1

Pęd i kręt.

Ćwiczenia 12

dr inż. Monika Kwacz

Pęd

Zasada zachowania pędu

Wstęp

zew

F

a

m









uwzględniając:

dt

d

a









zew

F

dt

d

m













dt

F

d

m

zew

















dt

F

m

d

zew













Impuls sił

zewnętrznych

oznaczając:











m

p

pęd





zew

F

dt

m

d













zew

F

dt

p

d









Wstęp

jeżeli:

const

m

p













0





zew

F



zew

F

dt

p

d









to:

Jeżeli

suma wszystkich sił zewnętrznych

działających na układ mechaniczny

jest

równa 0

to

pęd

układu pozostaje

niezmienny

.

Zasada zachowania pędu

Kręt

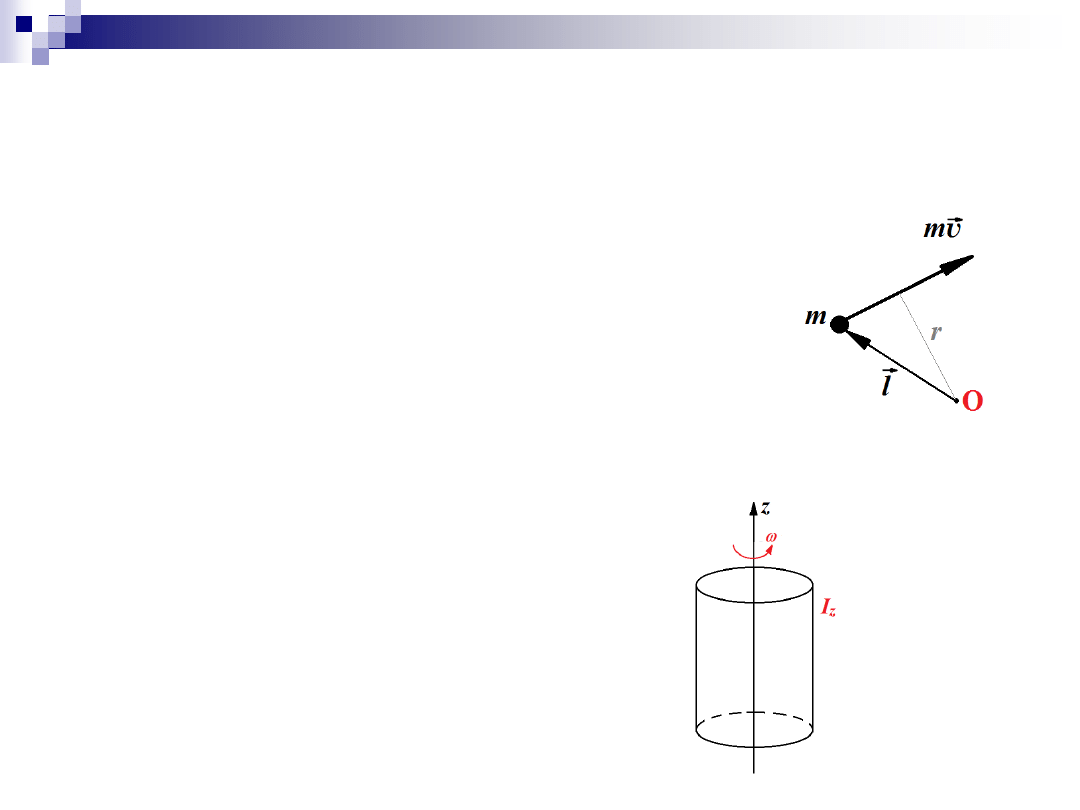
Kręt – definicja

Wstęp

Dla ruchu postępowego punktu:

Kręt = moment pędu









m

l

K

O





r

m

K

O







Dla ruchu obrotowego bryły:







z

z

I

K



Zasada zachowania krętu

Wstęp

zew

z

M

I











uwzględniając:

dt

d











zew

z

M

dt

d

I













dt

M

d

I

zew

z

















dt

M

I

d

zew

z













oznaczając:











z

z

I

K

kręt





zew

z

M

dt

I

d













zew

z

M

dt

K

d









Zasada zachowania krętu

Wstęp

jeżeli:

const

I

K

z

z













0





zew

M



to:

zew

z

M

dt

K

d









Jeżeli

suma momentów wszystkich sił zewnętrznych

działających na układ

mechaniczny jest

równa 0

to

kręt

układu pozostaje

niezmienny

.

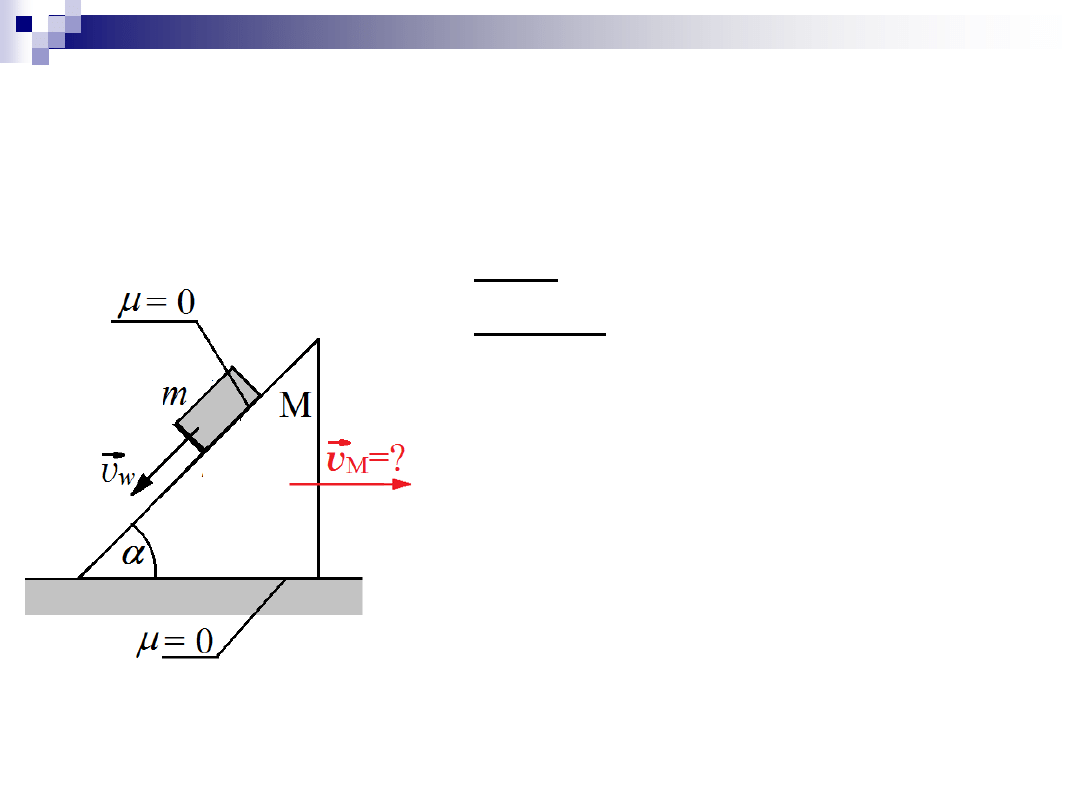
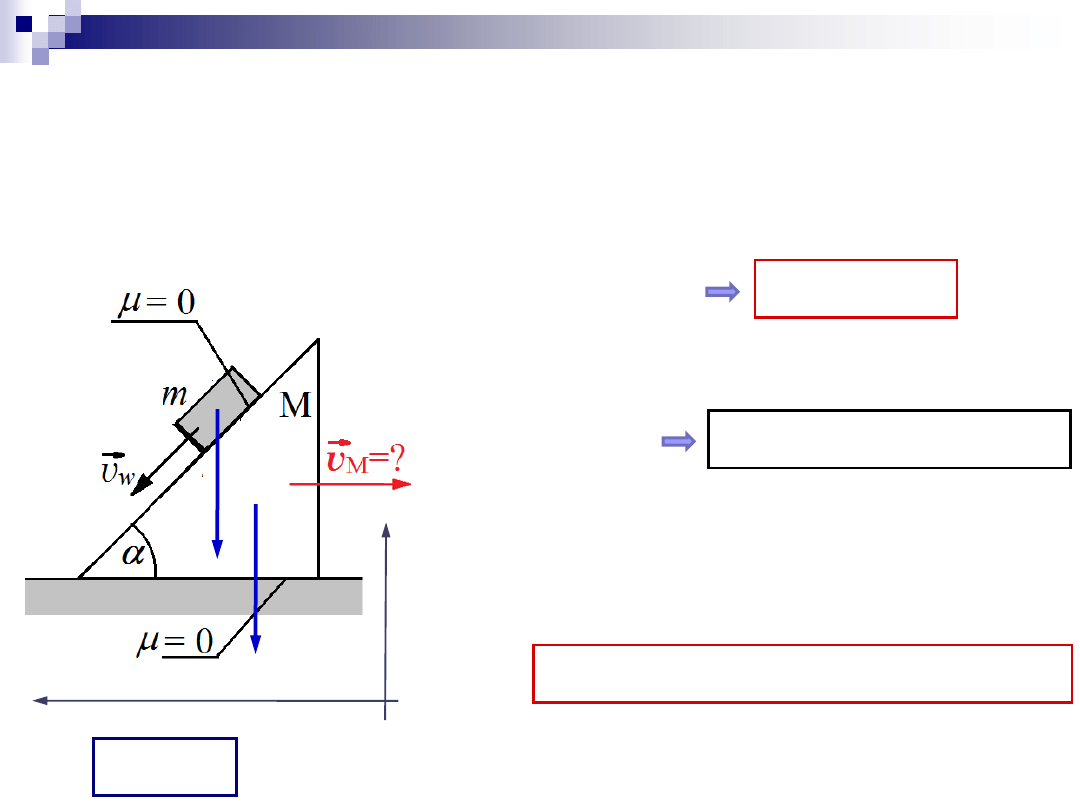
Zadanie 1

Dane: m, M,

a

,

Szukane:

v

M

(t)

– prędkość równi

Zadanie 1

2

t

b

w







Początkowo układ w spoczynku.

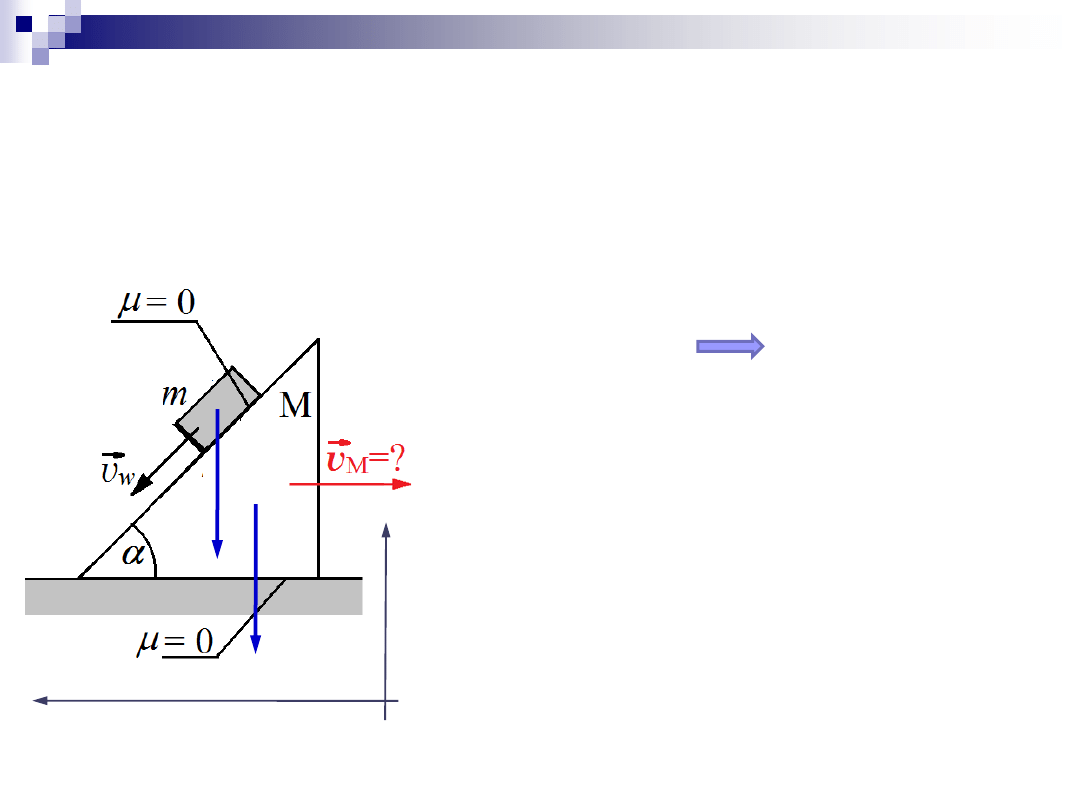
1. Siły zewnętrzne w układzie

Zadanie 1

mg

Mg

0





x

F



x

y

const

p

x





2. Pęd układu

Zadanie 1

mg

Mg

x

y

W chwili t=0:

W chwili t:

2

t

b

w







układ nieruchomy





0

0





t

p

x



układ ruchomy

 

M

mx

x

M

m

t

p



















gdzie:

w

M

w

u

m





























M

w

mx



a











cos

czyli:

 





M

M

w

x

M

m

t

p





a













cos

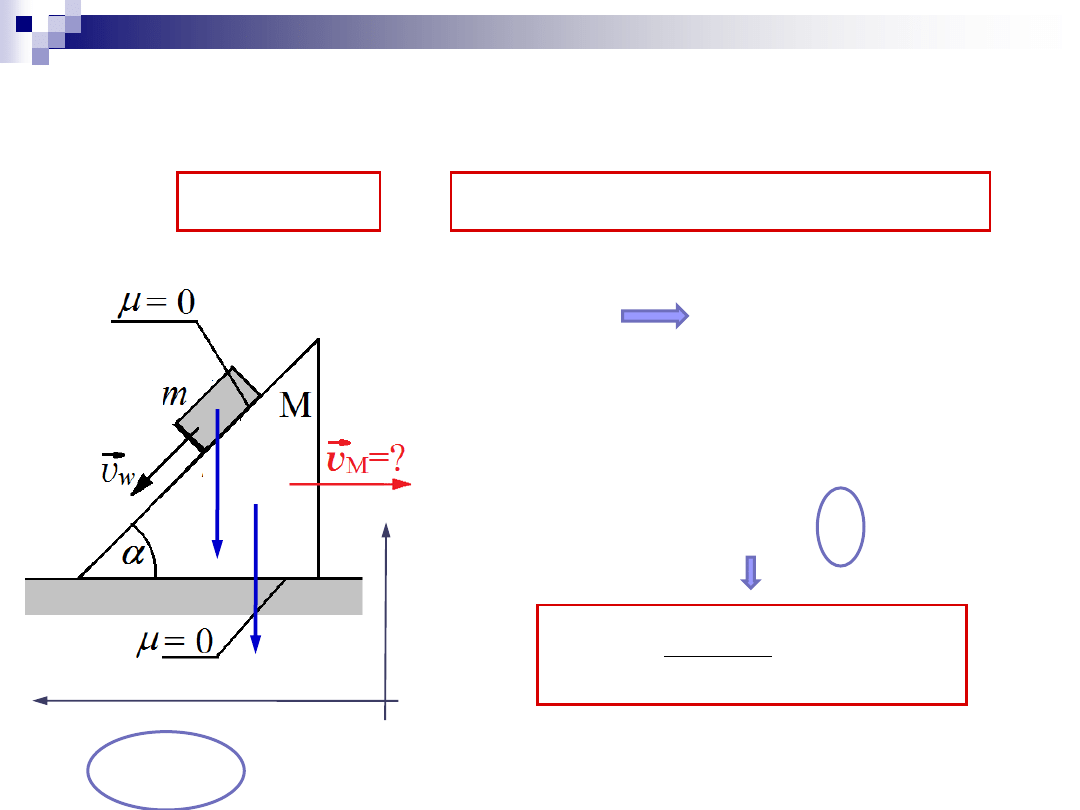
3. Zasada zachowania pędu

Zadanie 1

mg

Mg

x

y

2

t

b

w







0





x

F





 

t

p

t

p

x

x





0





0

0





t

p

x

 





M

M

w

x

M

m

t

p





a













cos





0

cos











M

M

w

M

m





a







a





cos

w

M

m

M

m









 

a



cos

2











t

b

M

m

m

t

M

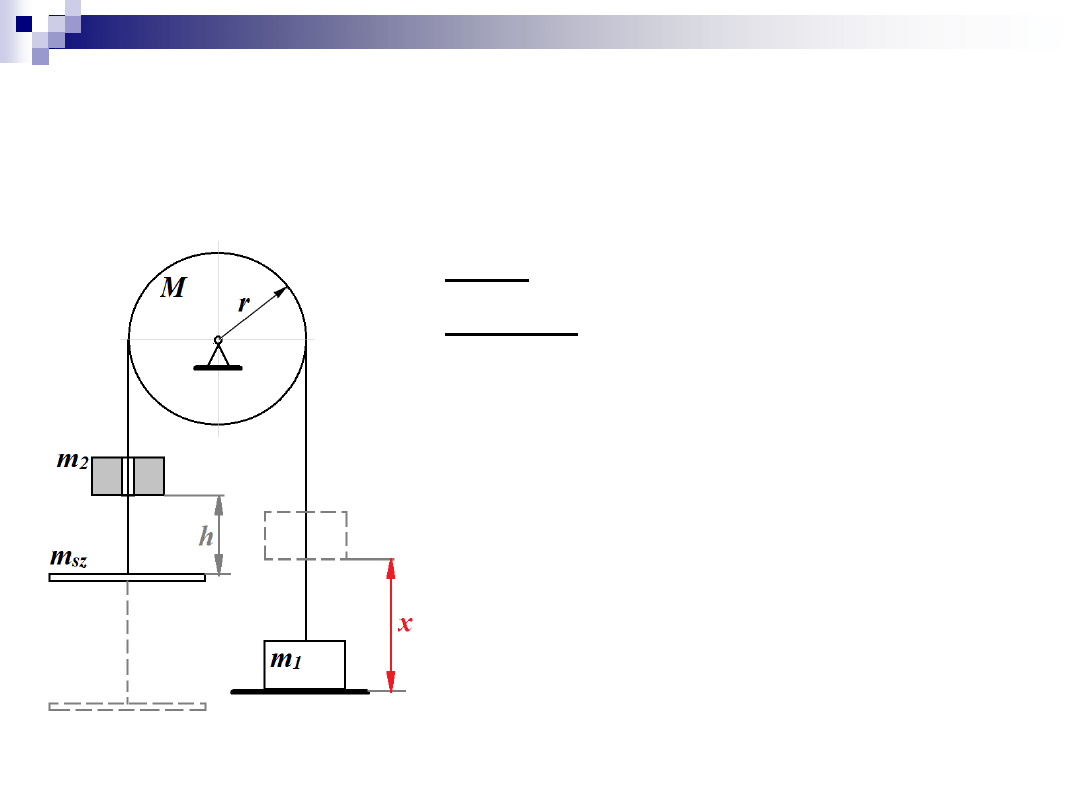
Zadanie 2

Zadanie 2

Dane: m

1

, m

2

, m

sz

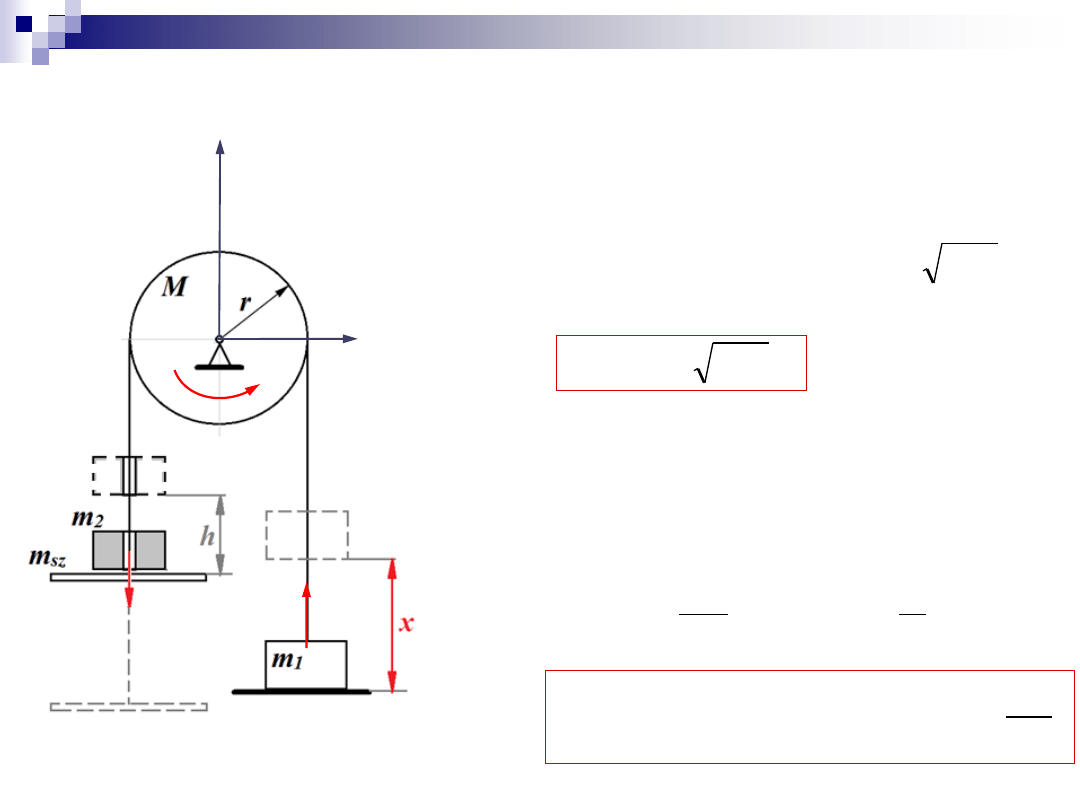
, M, r, h (wysokość spadku)

Szukane:

x –

wysokość na jaką zostanie

uniesiona masa

m

1

Na szalkę spada masa

m

2

z wysokości

h

.

Masa

m

2

pozostaje na szalce.

Linka stale napięta.

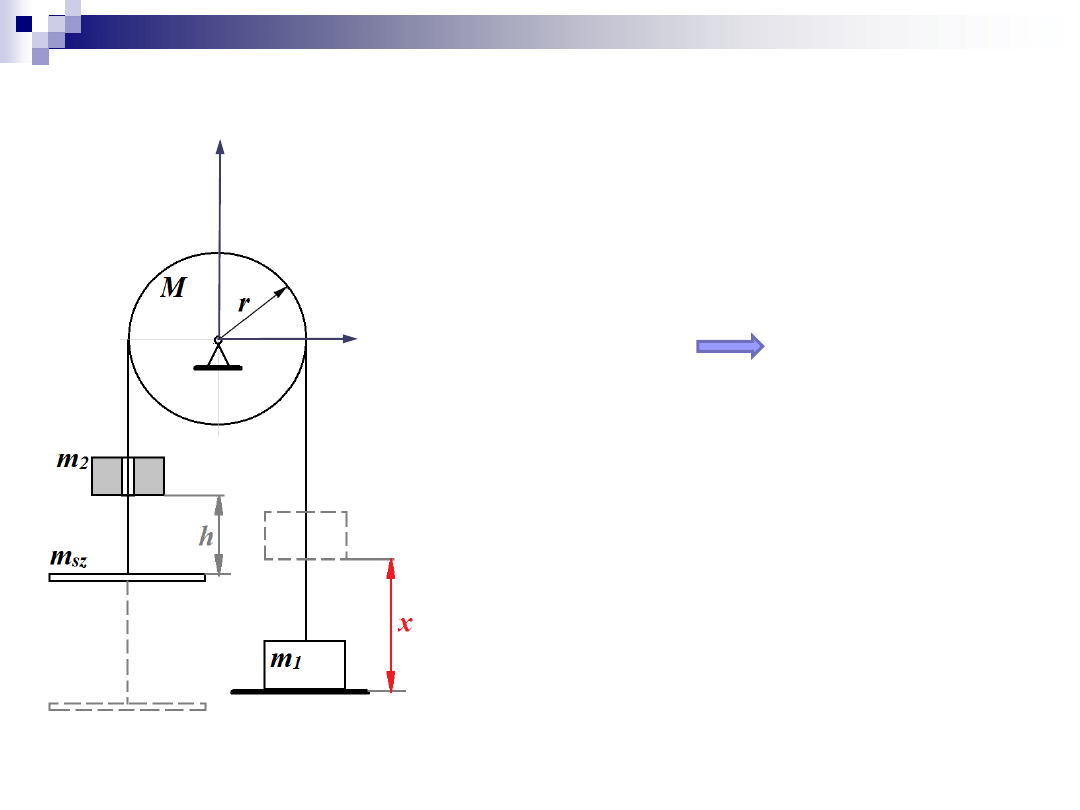
Zadanie 2

1. Kręt układu

W momencie zderzenia

0





t

const

K

z





x

y

czyli

2

1

z

z

K

K







gdzie:

K

z1

– kręt układu tuż przed zderzeniem

K

z2

– kręt układu tuż po zderzeniu

Zadanie 2

2. Kręt układu w kierunku osi

z

kręt układu tuż przed zderzeniem (w kierunku osi z) :

kręt układu tuż po zderzeniu (w kierunku osi z) :

r

m

K

z







1

2

1



gdzie:

gh

2

1





czyli:

r

gh

m

K

z







2

2

1









I

r

m

r

m

r

m

K

sz

z





















2

2

1

2

2

2

v

1

gdzie:

2

2

Mr

I



oraz

r

2







czyli:





























2

1

2

2

2

2

Mr

r

m

r

m

m

K

sz

z





v

2

v

2



x

y

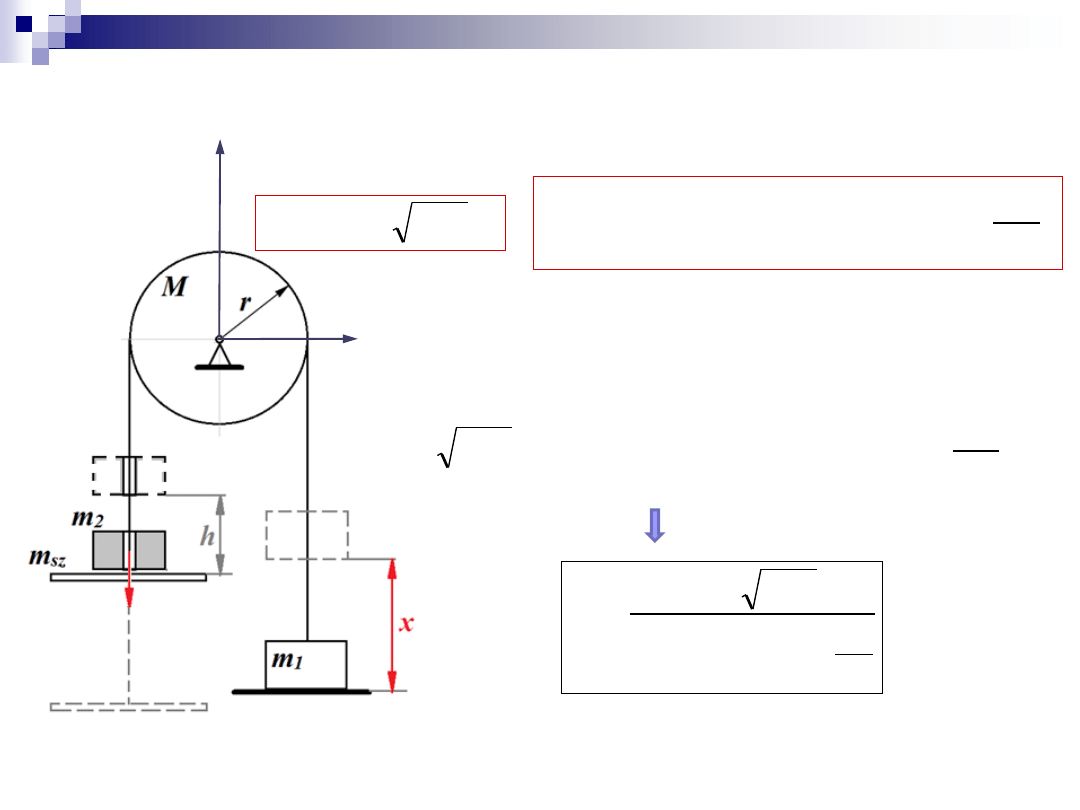
Zadanie 2

3. Zasada zachowania krętu

r

gh

m

K

z







2

2

1

v

1





























2

1

2

2

2

2

Mr

r

m

r

m

m

K

sz

z





2

1

z

z

K

K



































2

2

1

2

2

2

2

Mr

r

m

r

m

m

r

gh

m

sz





2

2

2

1

2

2

M

m

m

m

gh

m

sz













x

y

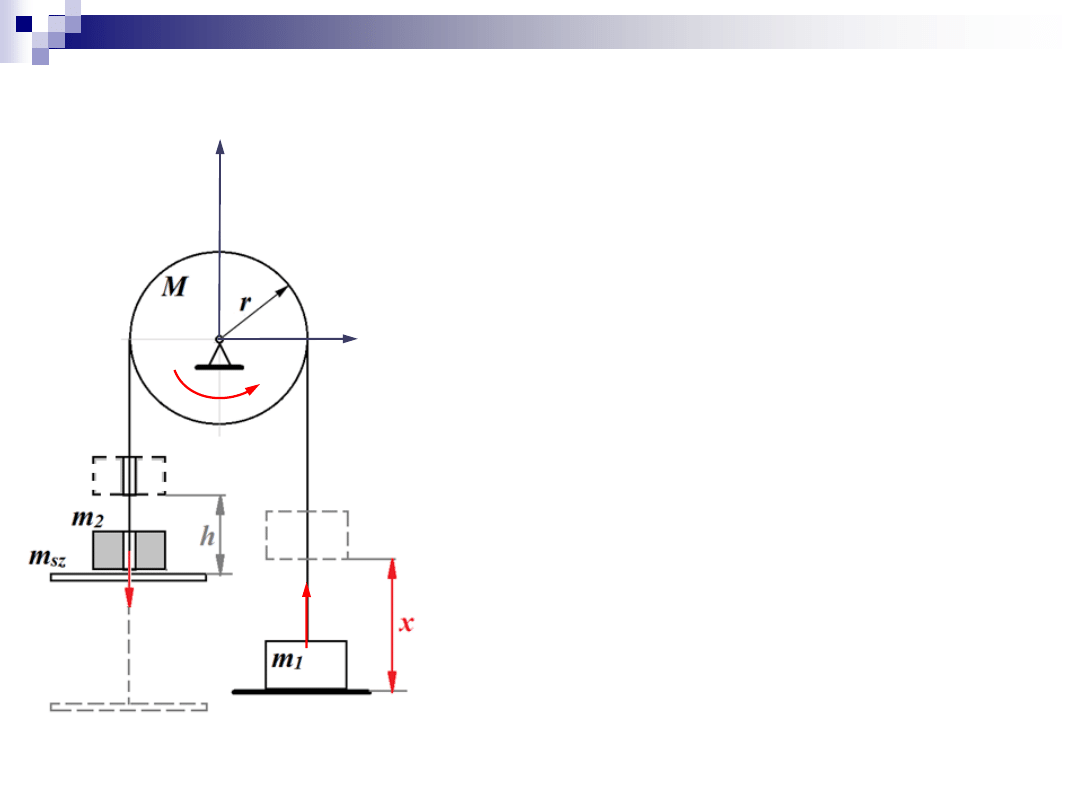
Zadanie 2

4. Wyznaczenie

x

v

1

v

2

v

2



Z zasady zachowania energii :

2

1

E

E



gdzie:

E

1

– energia układu tuż po zderzeniu

E

2

– energia układu w chwili gdy

m

1

na wysokości x

x

y

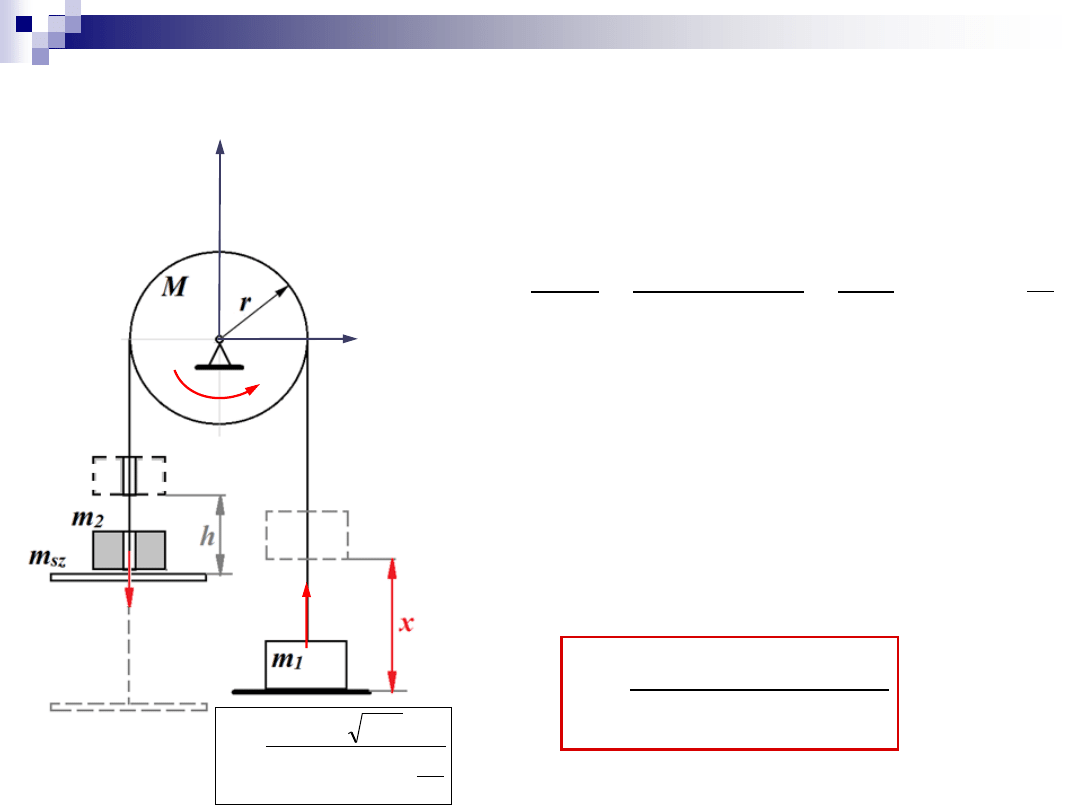
Zadanie 2

4. Wyznaczenie

x

v

1

2

2

2

1

2

2

M

m

m

m

gh

m

sz













v

2

v

2







2

2

2

2

2

2

2

2

2

1

1







I

m

m

m

E

sz









E

1

– energia układu tuż po zderzeniu

E

2

– energia układu w chwili gdy

m

1

na wysokości x





x

g

m

m

x

g

m

E

sz











2

1

2

x

y

2

1

E

E







sz

m

m

m

g

E

x







2

1

1

r

2







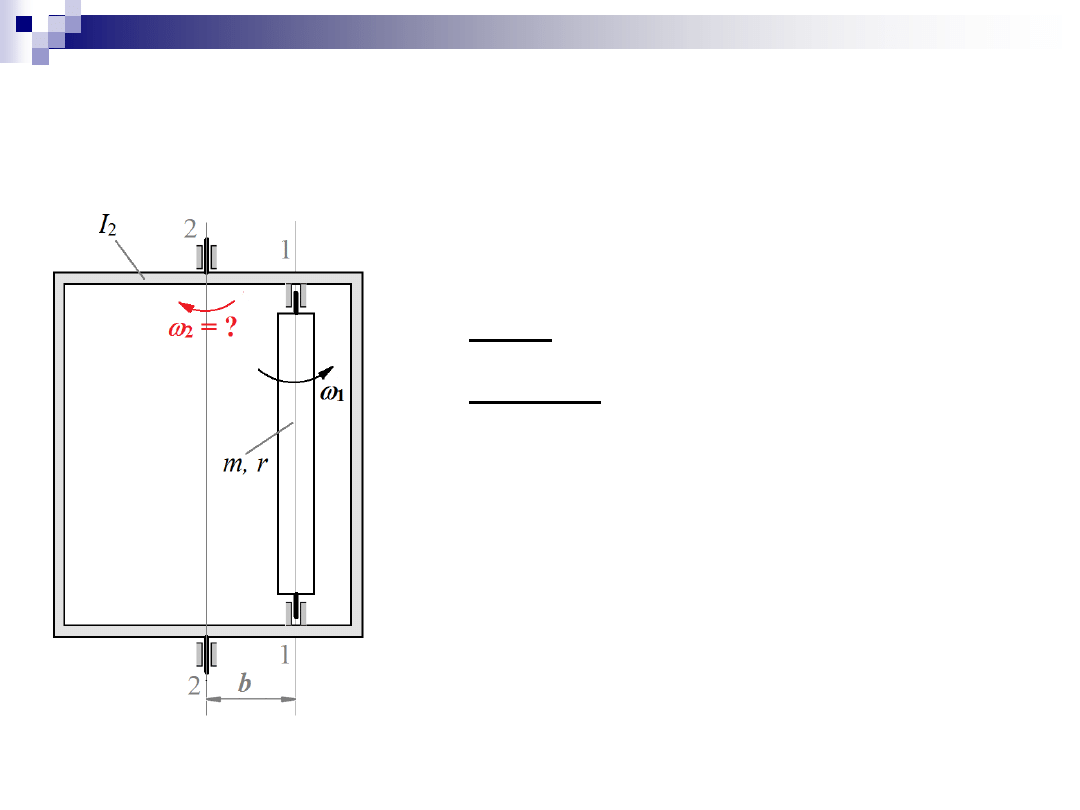
Zadanie 3

Zadanie 3

Dane: m, r, b, I

2

,



1

Szukane:



2

– prędkość kątowa ramki

Początkowo układ w spoczynku.

W pewnej chwili mechanizm zegarowy

nadaje walcowi prędkość kątową



1.

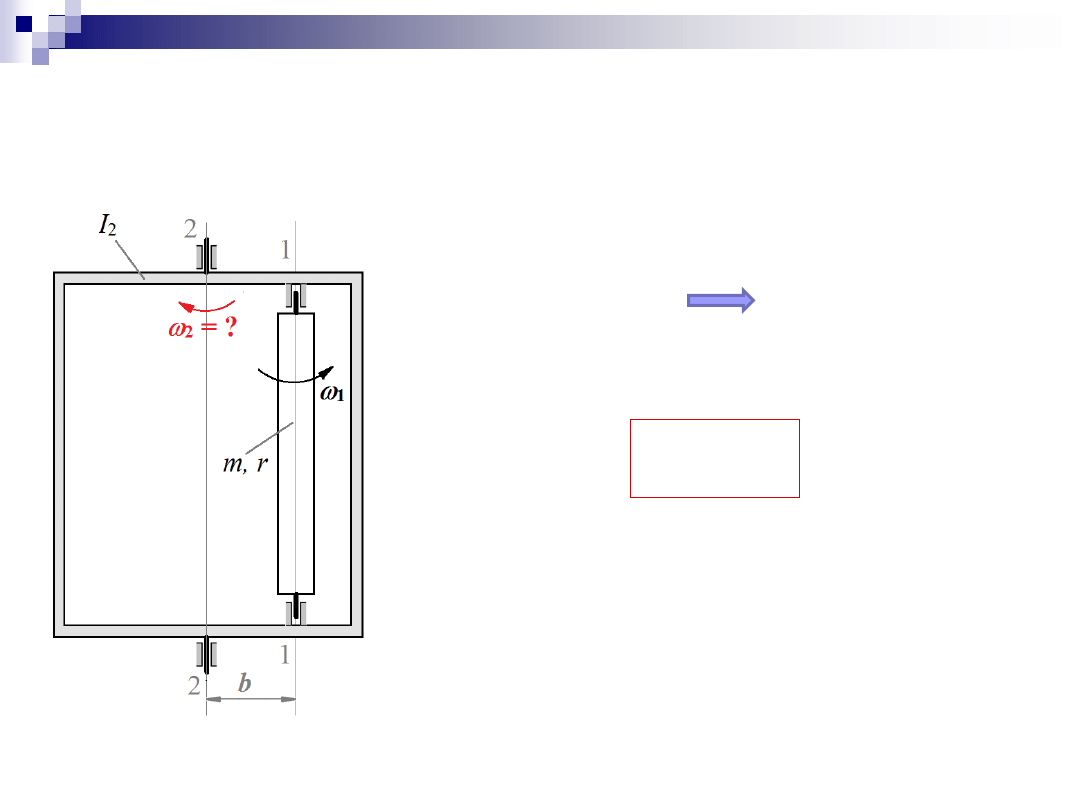
Zadanie 3

1. Kręt układu

const

K

ukladu





0





zew

M



czyli

2

1

K

K







gdzie:

K

1

– kręt początkowy

K

2

– kręt po nadaniu



1

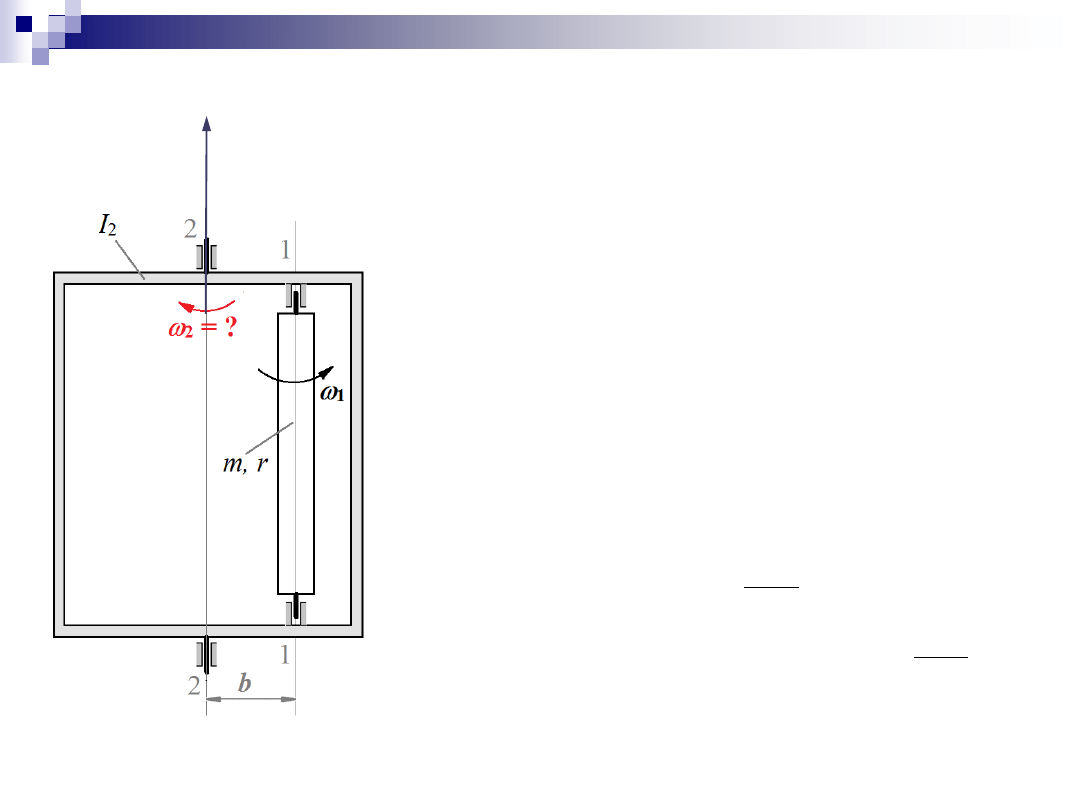
Zadanie 3

2. Kręt układu w kierunku

z

kręt początkowy :

0

1



z

K

kręt po nadaniu



1

:

2

2

2

2

2

1

1

1

1

1

2























I

I

I

K

z

z

gdzie:

2

2

1

1

1

mr

I





2

2

2

1

1

1

2

2

1

2

mb

mr

mb

I

I













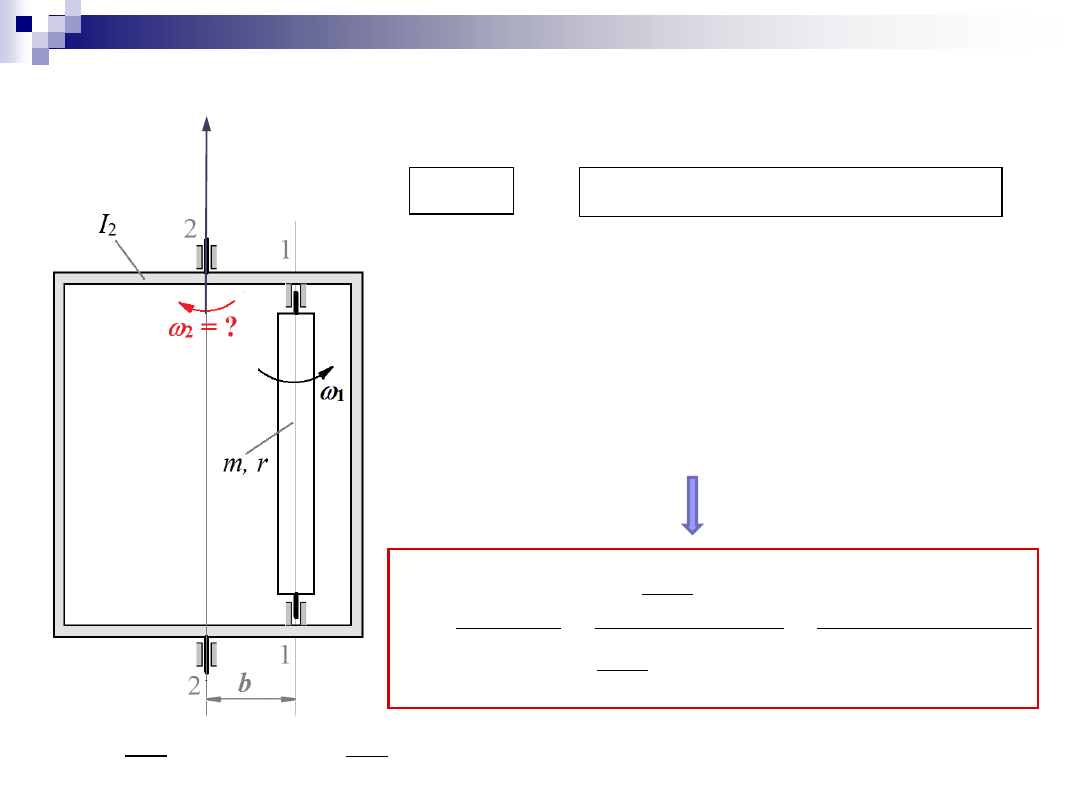
Zadanie 3

3. Zasada zachowania krętu

2

1

z

z

K

K



0

2

2

2

2

2

1

1

1

1

1























I

I

I

z

2

2

1

1

1

mr

I





2

2

2

2

1

2

mb

mr

I







0

1



z

K

2

2

2

2

2

1

1

1

1

1

2























I

I

I

K

z

czyli:

2

2

2

1

2

2

2

2

1

2

2

2

2

1

1

1

1

1

2

2

2

2

2

I

mb

mr

mr

I

mb

mr

mr

I

I

I



































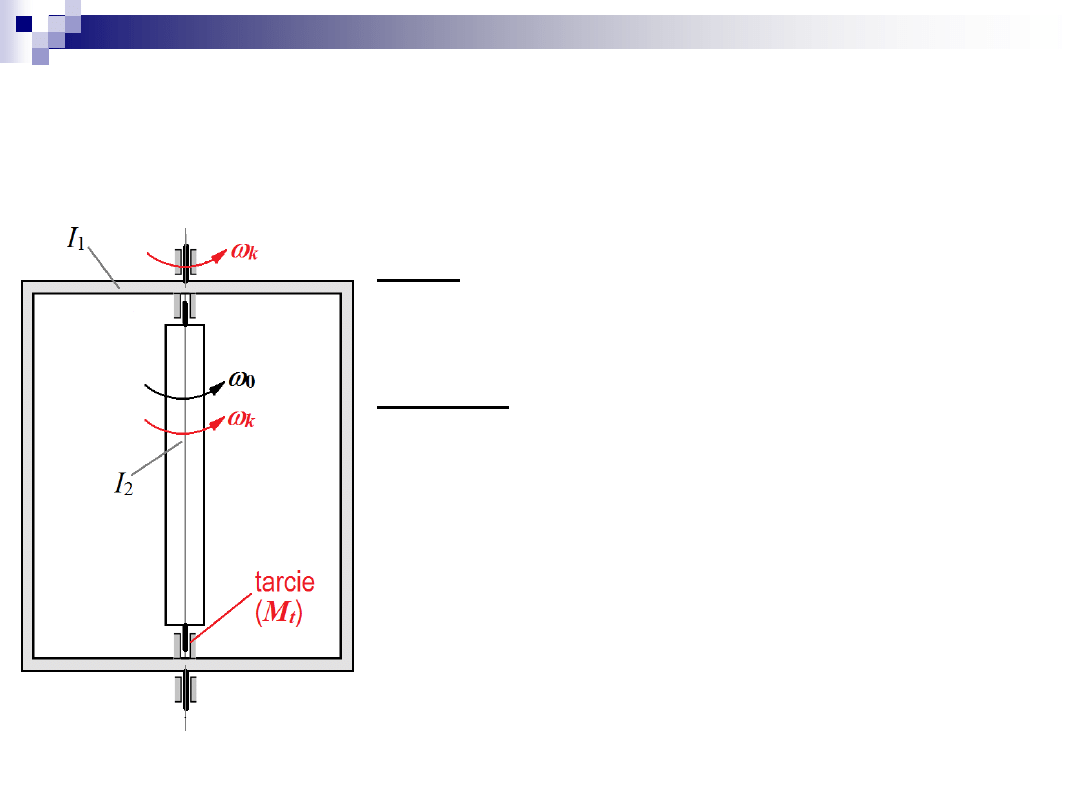
Zadanie 4

Zadanie 4

Dane: I

1

, I

2

,



0

= const,

t

1

– czas do wyrównania prędkości kątowych

Szukane:



k

– wspólna końcowa prędkość kątowa

M

t

– moment tarcia w łożyskach

Początkowo ramka unieruchomiona a płytka

obraca się z prędkością kątową



0

.

W pewnej chwili ramkę uwolniono.

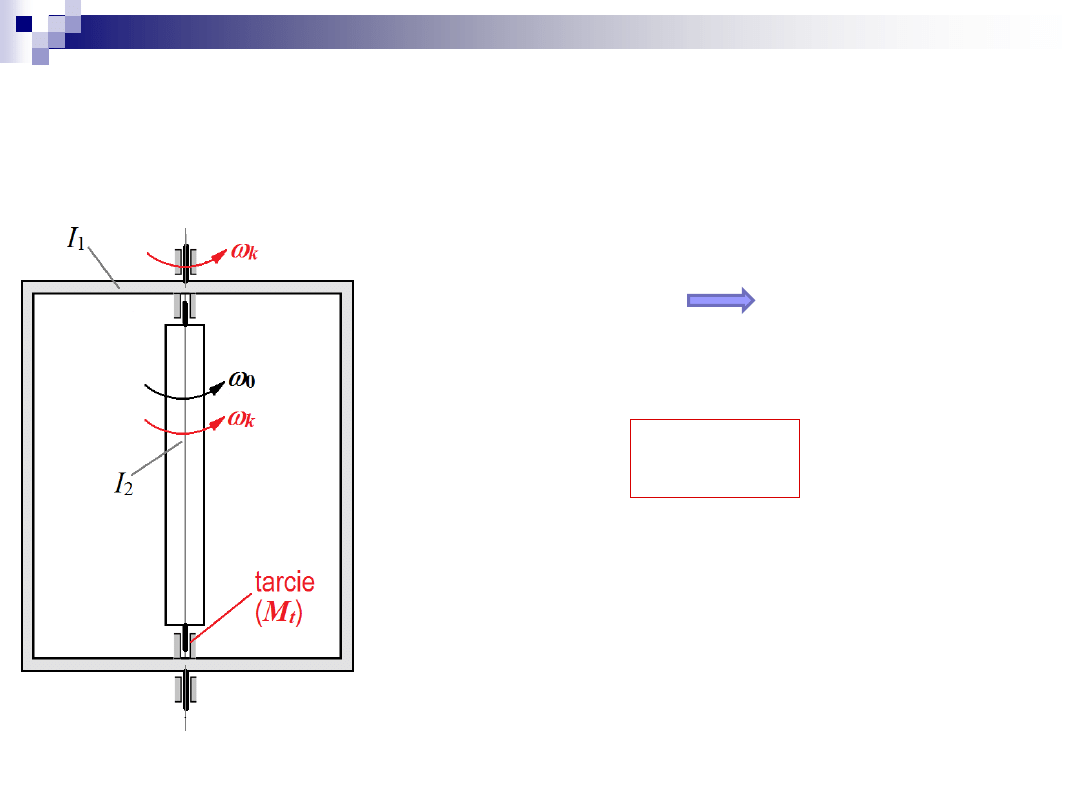
Zadanie 4

1. Kręt układu

const

K

ukladu





0





zew

M



czyli

2

1

K

K







gdzie:

K

1

– kręt początkowy

K

2

– kręt po czasie

t

1

M

t

– moment wewnętrzny w układzie ramka+płytka

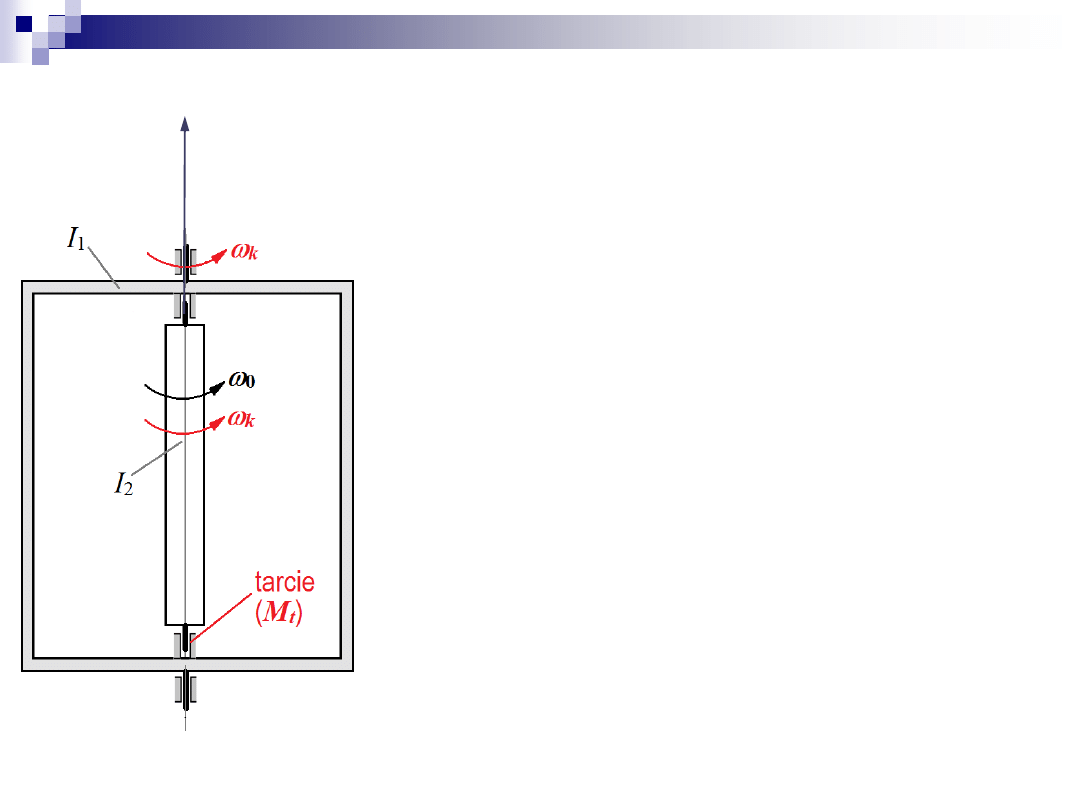
Zadanie 4

2. Kręt układu w kierunku

z

z

kręt początkowy :

0

2

1







I

K

z

kręt po czasie

t

1

:

k

k

z

I

I

K













1

2

2

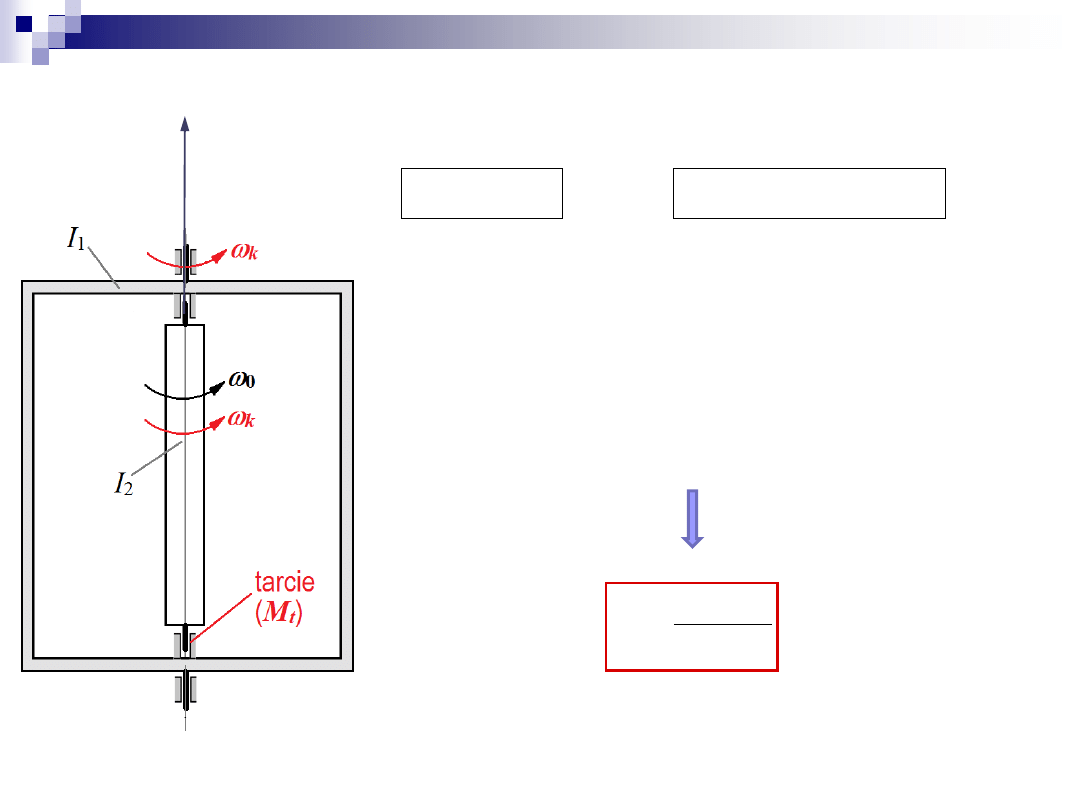
Zadanie 4

z

0

2

1







I

K

z

k

k

z

I

I

K













1

2

2

3. Zasada zachowania krętu

2

1

z

z

K

K



czyli:





0

2

1

2













I

I

I

k





1

2

0

2

I

I

I

k











Zadanie 4

z

4. Wyznaczenie

M

t

Dynamiczne równanie ruchu obrotowego ramki :

t

ramki

M

I







1

M

t

– moment zewnętrzny dla ramki

1

1

t

t

k

ramki













przy czym:





1

2

0

2

I

I

I

k











zatem:





1

2

1

0

2

1

1

1

t

I

I

I

I

t

I

M

k

t



















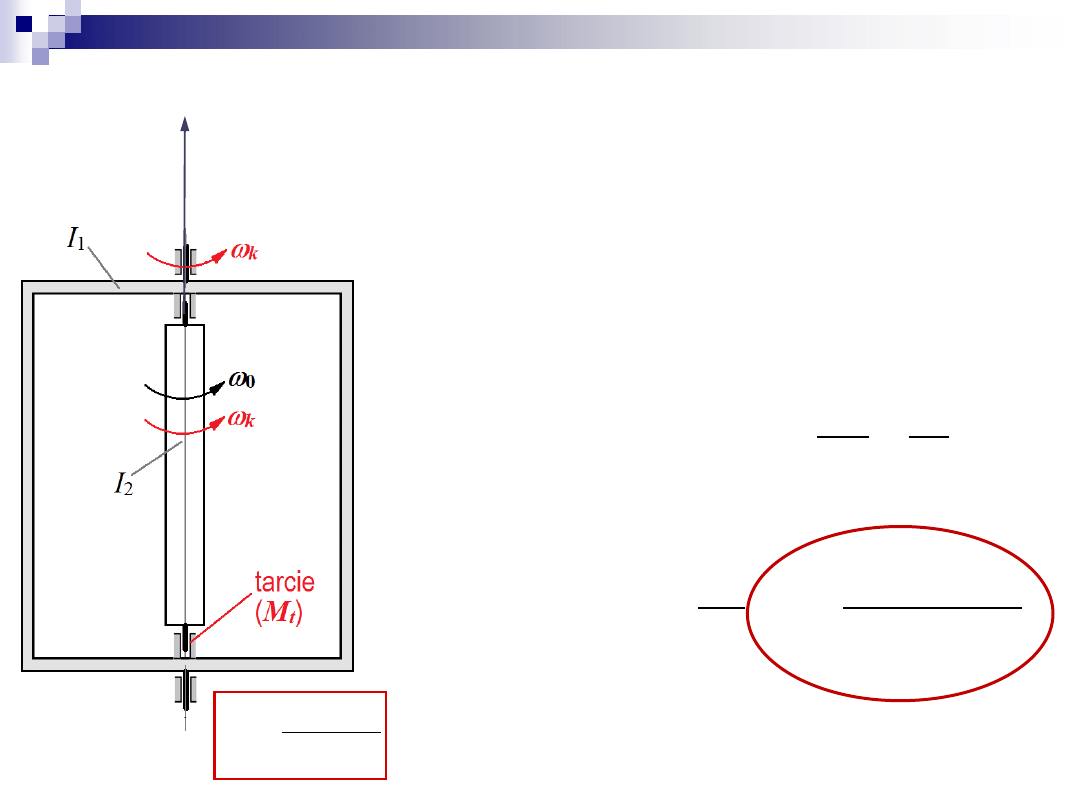
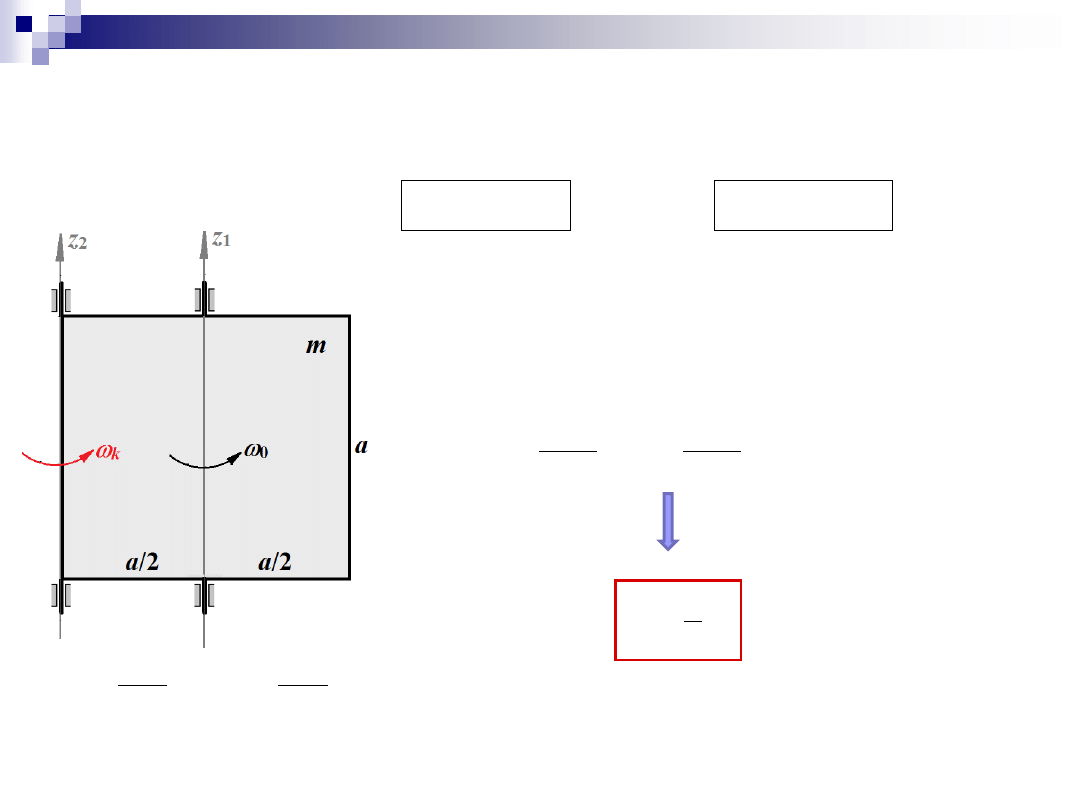
Zadanie 5

Zadanie 5

Dane: m, a,



0

= const

Szukane:



k

– prędkość kątowa po zmianie osi

Początkowo płytka obraca się z prędkością kątową



0

wokół osi

z

1

.

W pewnej chwili oswobodzono oś

z

1

i zatrzymano oś

z

2

.

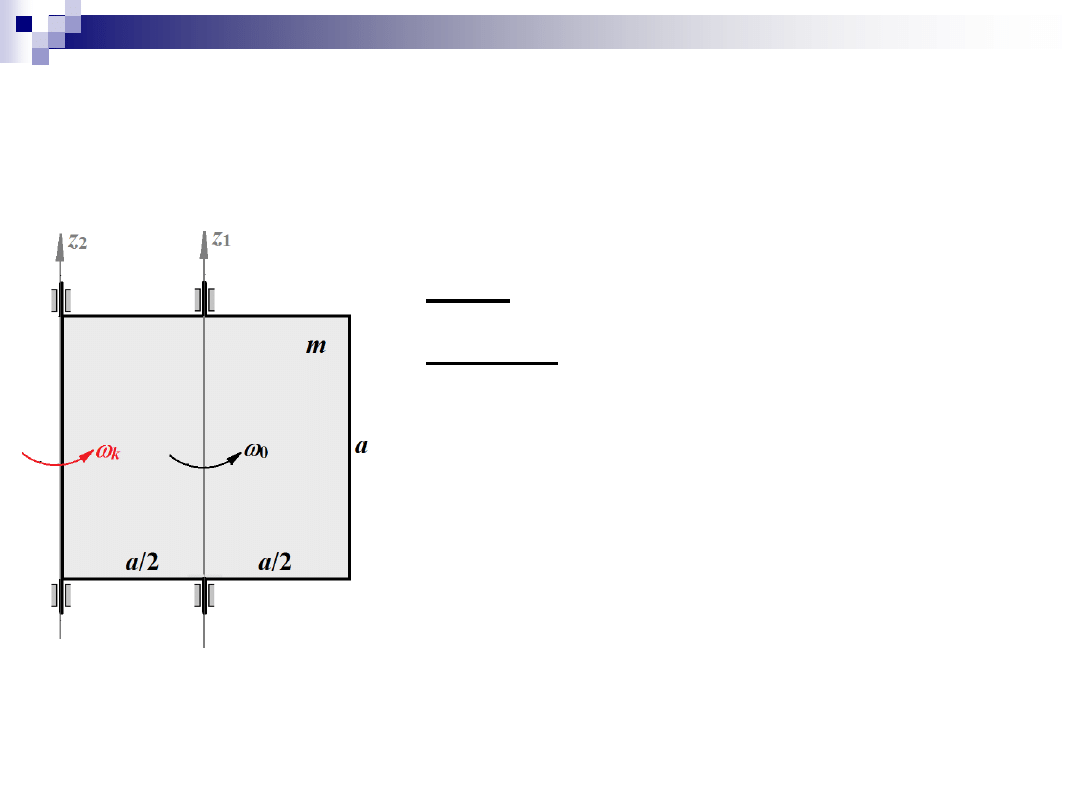
Zadanie 5

1. Kręt układu

const

K

ukladu





0





zew

M



czyli

2

1

K

K







gdzie:

K

1

– kręt przed zmianą osi

K

2

– kręt po zmianie osi

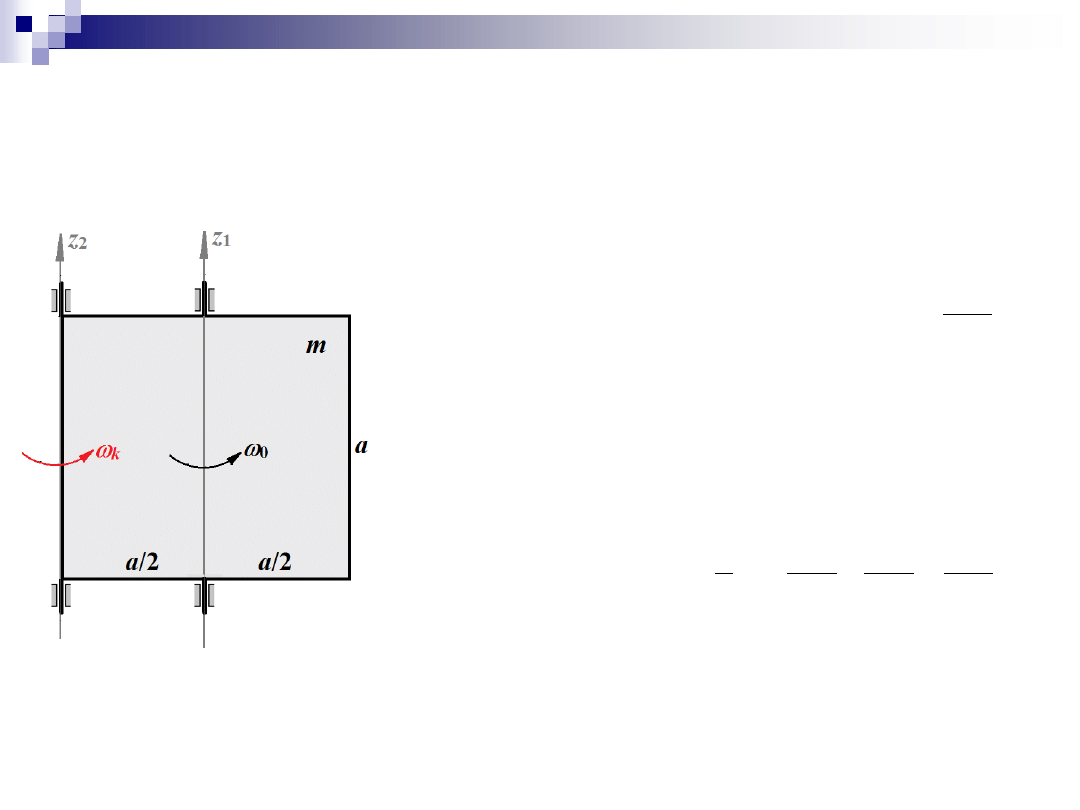
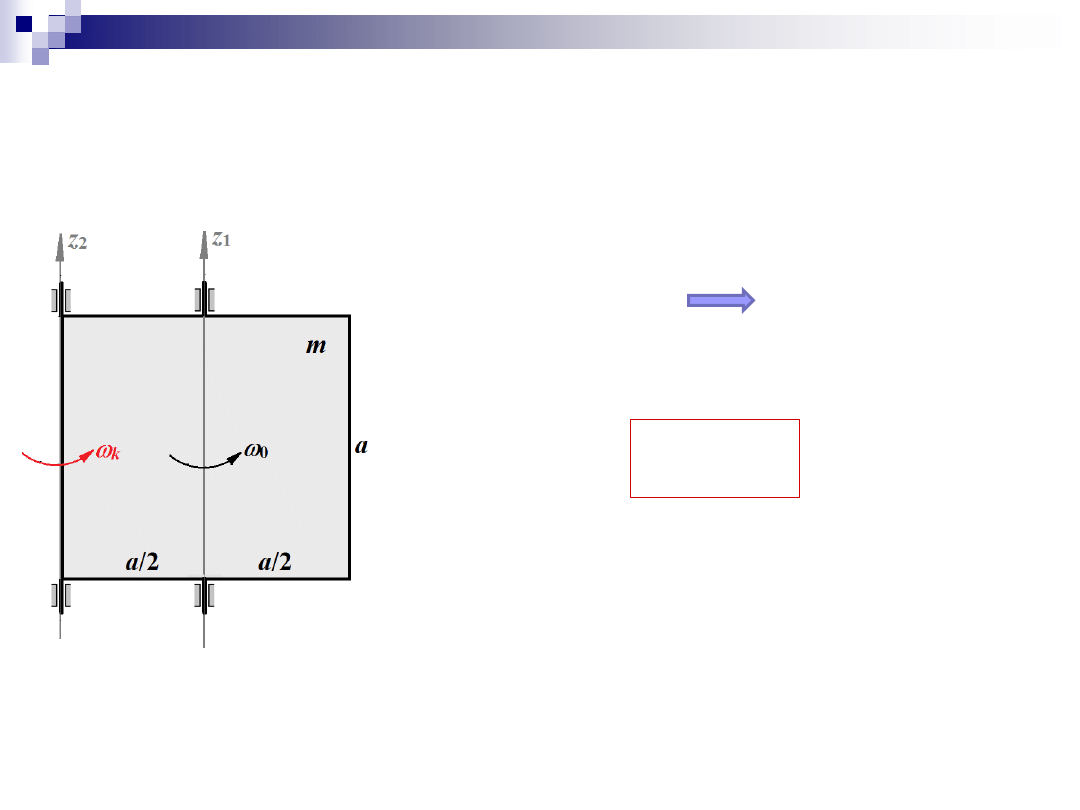
Zadanie 5

2. Kręt układu w kierunku

z

kręt przed zmianą osi :

0

1

1







z

z

I

K

kręt po zmianie osi :

k

z

z

I

K







2

2

gdzie:

12

2

1

ma

I

z



gdzie:

3

4

12

2

2

2

2

2

2

2

ma

ma

ma

a

m

I

I

z

z

























Zadanie 5

3. Zasada zachowania krętu

2

1

z

z

K

K



czyli:

k

ma

ma











3

12

2

0

2

0

4

1







k

0

1

1







z

z

I

K

k

z

z

I

K







2

2

12

2

1

ma

I

z



3

2

2

ma

I

z

