BIO-ALGORITHMS AND MED-SYSTEMS

JOURNAL EDITED BY MEDICAL COLLEGE – JAGIELLONIAN UNIVERSITY

Vol. 1, No. 1/2, 2005, pp. 3-8.

ANALIZA MOŻLIWOŚCI ZASTOSOWANIA METOD

SZTUCZNEJ INTELIGENCJI W MEDYCYNIE SĄDOWEJ

ANALYSIS OF ARTIFICIAL INTELLIGENCE METHODS

APPLICATION IN FORENSIC MEDICINE

E

LŻBIETA

F

ILIPOWICZ

*

,

J

OANNA

K

WIECIEŃ

**

,

M

AŁGORZATA

K

ŁYS

***

,

B

OGUSŁAW

F

ILIPOWICZ

**

*

Szpital Uniwersytecki, Collegium Medicum Uniwersytetu Jagiellońskiego,

Kraków, [e-mail]

**

Katedra Automatyki Akademii Górniczo-Hutniczej, Kraków, [e-mail]

***

Katedra Medycyny Sądowej, Collegium Medicum Uniwersytetu Jagiellońskiego,

Kraków, [e-mail]

Streszczenie. Artykuł opisuje zastosowanie nowych systemów
bioinformatycznych w medycynie sądowej. Systemy biome-
tryczne już znalazły zastosowanie między innymi w geome-
trycznej identyfikacji twarzy. Są one niezbędne w identyfikacji
osobowej oraz w poszukiwaniu osób zaginionych. W ostatnich
latach nastąpił bardzo szybki rozwój badań nad chromosomem
Y, co pozwoliło na postęp w medycynie sądowej. Metody
sztucznej inteligencji mogą być pomocne w badaniach spor-
nego ojcostwa i ewolucji człowieka. Bioinformatyka oraz metody
biologii molekularnej, metody multiplex PCR będą pełnić bardzo
ważną funkcję w analizie sądowej DNA oraz w historycznych
i genealogicznych badaniach.

Słowa kluczowe: medycyna sądowa, systemy biometryczne,
chromosom Y, multiplex PCR, pojedyncze nukleotydowe
polymorfizmy

Abstract. This article reviews new bioinformatic systems in
forensic medicine. Biometric systems are already used in
forensic medicine for face geometry identification. They are
necessary in personal identification and missing persons
investigations. The field of Y-chromosome analysis and its
application to forensic science has undergone rapid
improvement in recent years. Artificial Intelligence is usefull in
paternity testing and in human evolutionary study. Bioinformatic
systems and multiplex PCR assay will play an important role in
the future of forensic DNA typing and historical and
genealogical research.

Key words: forensic medicine, biometric systems, Y-chro-
mosome, multiplex PCR, single nucleotide polymorphisms

1. Możliwości zastosowania metod
sztucznej inteligencji w medycynie są-
dowej.

Systemy biometryczne mogą być stosowane do identyfi-

kacji osobowej w medycynie sądowej. Systemy biometryczne

są obecnie jednym z najszybciej rozwijających się działów

informatyki na świecie. Kontrola biometryczna oparta jest na
specyficznych cechach organizmu, które są charakterystyczne

dla każdego człowieka [2], [3], [10], [11]. W chwili obecnej

najpopularniejsze techniki biometryczne można podzielić na

następujące grupy:
- systemy oparte o rozpoznawanie linii papilarnych,
- systemy oparte o rozpoznawanie geometrii twarzy,
- systemy oparte o rozpoznawanie mowy,
- systemy oparte o rozpoznawanie cech charaktery-

stycznych tęczówki oka.

Aktualnie dostępne są nowe systemy:

- oparte o rozpoznawanie DNA,
- oparte o rozpoznawanie obrazu żył,

- oparte o rozpoznawanie dna oka.

Systemy biometryczne są potrzebne w medycynie sądo-

wej celem identyfikacji osobowej. Są proste w instalacji,

niezawodne i tanie, jeśli chodzi o koszty utrzymania oraz

konserwacji. Ogólne zasady biometryki opierają się na
zapisywaniu w pamięci komputera określonego i niepowta-

rzalnego wzoru wybranej cechy, przechowywaniu tej

informacji, a następnie dopasowaniu określonej cechy

podczas procesu weryfikacji w oparciu o zapisany wzorzec
[2], [3], [10], [11].

Identyfikacja w medycynie sądowej polega więc na auto-

matycznym rozpoznaniu nieznanej osoby poprzez badanie

jednej lub kilku jej cech biometrycznych. System porównuje
aktualny obraz zapisany przez odpowiednie urządzenie

z wzorcami zapisanymi w scentralizowanej bazie danych.

Liczone jest prawdopodobieństwo przyporządkowane

każdemu obrazowi. Jeśli przekracza ono ustaloną wartość
krytyczną, system uznaje, że nieznana osoba została

zidentyfikowana. Jeśli kilka obrazów przekracza ową wartość,

przyjmuje się najbardziej prawdopodobny obraz za praw-

dziwy.

Artificial in

telligence

E. Filipowicz et al., Analiza możliwości zastosowania metod sztucznej inteligencji w medycynie sądowej

4

Linie papilarne są bardzo ważną cechą każdego ludzkiego

organizmu, gdyż pozwalają jednoznacznie zidentyfikować

człowieka. Podstawę identyfikacji odcisków palców stanowią

tzw. minutie. Są to punkty, które zaznaczają początek i koniec
charakterystycznych miejsc oraz miejsca przecięcia, widoczne

nawet gołym okiem. Czytniki wykorzystujące systemy

biometryczne pozwalają na szybkie i dokładne identyfikowanie

danej osoby. Istnieją dwa rodzaje takich urządzeń: w jednym
weryfikacja odbywa się w samym czytniku, w drugim zaś

proces ten odbywa się w komputerze PC połączonym

z małym skanerem, niewymagającym trudnego oprogramo-

wania. Niektóre czytniki działają na zasadzie fotografowania
opuszki palca przyłożonego do czytnika. Kod opisujący palec

może być zapisany jako ciąg symboli liter i cyfr, a więc kodem

ASCII. Możemy go bez trudu przechowywać w dowolnej bazie

danych, a na dodatek zajmuje on bardzo mało miejsca
w pamięci [10], [11].

Ludzkie oko posiada wiele cech, które mają zastosowanie

w biometryce. Nie istnieją dwie tęczówki, których szczegółowy

opis matematyczny byłby identyczny, nawet bliźnięta
jednojajowe mają różne tęczówki. U każdego człowieka

występują odmienne tęczówki w prawym i w lewym oku; są

niezmienne począwszy od 18 miesiąca życia aż do śmierci.

Unikalność jest jednym z najważniejszych problemów
dotyczących systemów biometrycznych. Obrazem jest

siateczka tkanki łącznej oraz innych widzianych elementów.

Taki kod, zawierający skrócony opis punktów charakterystycz-

nych, jest następnie porównywany z zapisanym obrazem

w bazie danych [10], [11].

Systemy rozpoznające geometrię twarzy są najbardziej

naturalnymi sposobami identyfikacji biometrycznej. Technolo-

gia rozpoznawania twarzy obecnie jest rozwijana w dwóch

kierunkach: pomiaru twarzy i tzw. metody eigenface
(właściwych twarzy). Technologia pomiaru twarzy polega na

pomiarze specyficznych cech twarzy i relacji pomiędzy tymi

pomiarami [10], [11]. Punkty pomiarowe pokazano na rys. 1.

Rys. 1. Przykład punktów pomiarowych twarzy

Metoda eigenface polega na porównywaniu uzyskanego

obrazu z gotowymi wzorcami umieszczonymi w pamięci. Jest
podobna do metody stosowanej w kryminalistyce czyli

portretów pamięciowych. Technologia identyfikacji opierającej

się na eigenface jest w początkowym stadium rozwoju

i jest bardzo obiecująca.

Tworzenie modeli stochastycznych jest elastyczną

i najbardziej ogólną metodą wykorzystywaną do zagadnień

systemów biometrycznych. Istnieje wiele nie w pełni jasnych

i dających się z trudem zdefiniować aspektów, związanych

z rozpoznaniem danej cechy. Modele probabilistyczne są
bowiem najbardziej odpowiednie w rozwiązywaniu zagadnień

związanych z występowaniem niepewnych bądź niekomplet-

nych informacji. Modele stochastyczne są ukrytymi modelami

Markowa, które uznane są za najbardziej przydatne do

rozpoznawania właściwości cech. Gdy wzorzec sam służy

jako odniesienie i jest przechowywany w pamięci, podejście

bazujące na ukrytym modelu Markowa reprezentuje
odniesienie przez model, tym samym wykazując wyższy

stopień abstrakcji i elastyczności [2], [3], [4].

Ukryty model Markowa HMM jest procesem stochasty-

cznym w podwójnym sensie, ze szczególnym uwzględnieniem
procesu stochastycznego, który nie jest obserwowany

a ukryty, a pewne informacje o nim można wydobyć,

posługując się innym zbiorem procesów stochastycznych,

które produkują sekwencje obserwowanych symboli. Ukryty
model Markowa jest scharakteryzowany przez łańcuch

Markowa o skończonej liczbie stanów i zbiór dystrybucji

wyjściowych. Parametry przejścia pomiędzy stanami w

łańcuchu Markowa modelują zmiany widmowe. Analiza tych
dwóch typów zmian jest podstawą, na której opiera się

rozpoznawanie właściwości cech tęczówki czy geometrii

twarzy. W celu zdefiniowania symboli do utworzenia ukrytego

modelu Markowa, musi być opracowany proces wydobywania
cech oparty na analizie konturu. Aby ułatwić przetwarzanie

wzorców, zastosowano technikę zwaną transformacją

miejscowej projekcji konturu RPCT, która transformuje

złożony wzór lub wzór wielokonturowy w jeden zewnętrzny
kontur. Przy wykorzystaniu tej techniki miejscowa projekcja i

przetwarzanie konturu są dokonywanie współbieżnie.

Podstawowa zasada, na której się opiera ta metoda polega na

tym, że wszystkie piksele wzorca są rzutowane na podstawy

projekcyjne (ang. projection bases). Następnie dokonywana
jest ekstrakcja z wzorca łańcucha konturu (ang. contour

chain). Wszystkie te operacje przekształcają obraz w jeden

kontur. Metoda RPCT może zostać podzielona na cztery typy

technik transformacyjnych, w zależności od wyboru baz
projekcyjnych, jak przedstawiono na rys. 2.

Rys. 2. Cztery typy przekształcenia RPCT: a) HRPCT – pozioma
(ang. horizontal RPCT), b) VRPCT – pionowa (ang. vertical RPCT),
c) HVRPCT – poziomo-pionowa (ang. horinzontal-vertical RPCT),
d) DDRPCT – diagonalno-diagonalna (ang. diagonal-diagonal RPCT)

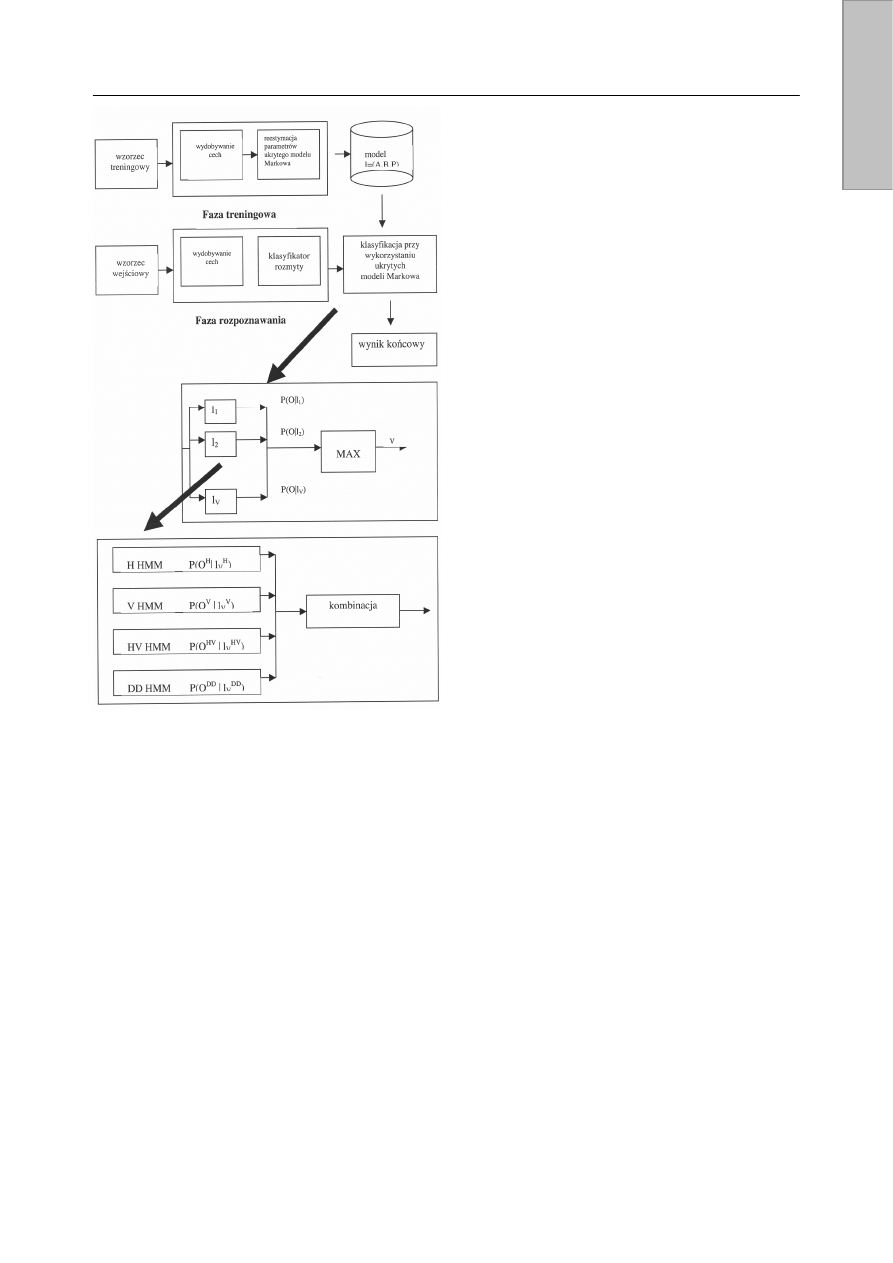
Rys. 3 przedstawia schemat blokowy ogólnej struktury

systemu rozpoznawania znaków należących do zbiorów

znaków o dużej liczności. Proces rozpoznawania znaków

składa się z fazy treningowej i fazy klasyfikacji. Zapropono-
wano również użycie preklasyfikatora, który odgrywa istotną

rolę w procesie wstępnej redukcji kandydatów do dalszego

rozpoznawania.

Artificial in

telligence

E. Filipowicz et al., Analiza możliwości zastosowania metod sztucznej inteligencji w medycynie sądowej

5

Rys. 3. Struktura systemu rozpoznawania cechy

Podsumowując, ukryty model Markowa opiera się na

grafie skierowanym o skończonej liczbie węzłów zwanych

stanami, przy czym dla każdego ze stanów dane są

prawdopodobieństwa zdarzenia, że proces właśnie od tego
stanu wystartuje oraz dane są prawdopodobieństwa przejść

do stanów następnych [2], [3], [4].

W każdym ze stanów modelu dokonywana jest generacja

jednego z możliwych do zaobserwowania symboli elementar-
nych oraz podane są prawdopodobieństwa generacji dla

każdego takiego symbolu. Dla każdego ze znaków należą-

cych do danego języka tworzony jest oddzielny ukryty model

Markowa, dla którego prawdopodobieństwo generacji tego
znaku, składającego się z pewnych elementarnych symboli

jest największe. Na początku, po przypisaniu początkowych

wartości prawdopodobieństw, ukryty model Markowa musi

zostać poddany fazie treningowej, w której modyfikowane są
wartości tych prawdopodobieństw w oparciu o dostarczony

przez uczącego zbiór znanych znaków. Po wykonaniu

odpowiedniej liczby iteracji, ukryte modele Markowa są już

gotowe do rozpoznania zadanych znaków. Faza ta jest zwana

fazą testującą. Dla każdego z ukrytych modeli Markowa
obliczane jest prawdopodobieństwo generacji przez niego

zaobserwowanego znaku, przy czym na końcu wybierany jest

model dający największe prawdopodobieństwo tego

zdarzenia. Z ukrytymi modelami Markowa związanych jest

kilka bardzo ważnych zagadnień [2], [3], [4]:
- dobór kryterium parametrów, liczby stanów oraz wybór

typu modeli,

- dobór liczby obserwowanych elementarnych symboli,
- problem klasyfikacji wyników dostarczonych przez

poszczególne modele,

- problem treningu modeli.

Opisane modele mają więc zastosowanie w medycynie

sądowej, aktualnie pracuje się nad zastosowaniem systemów

biometrycznych w analizie DNA w hemogenetyce.

Zastosowanie bioinformatyki w technikach biologii mole-

kularnej pozwoliło na szybki rozwój hemogenetyki

w medycynie sądowej [1], [7], [13], [14].

2. Metody i algorytmy sztucznej inteli-
gencji

Sztuczne sieci neuronowe, algorytmy genetyczne

i sztuczne systemy immunologiczne reprezentują grupę

metod i technik, które w pewnym stopniu są symulacją
rozwiązań stworzonych przez naturę.

Algorytm genetyczny operuje na zakodowanej części

informacji. Gen jako potencjalna cecha dla systemów

biometrycznych jest to potencjalny bit w algorytmach

genetycznych [4], [5]. Chromosom to binarny ciąg kodowy
składający się z zer i jedynek. Każdy pojedynczy bit jest

odpowiednikiem pojedynczego genu. Ze względu na sposób

ułożenia genów w chromosomie można wyróżnić trzy

podstawowe sposoby kodowania:

• klasyczne – geny są heterogeniczne, czyli geny na

różnych pozycjach przechowują różne informacje. Stosuje
się je wtedy, gdy mamy określone niejednorodne cechy

osobnika i chcemy dobrać im optymalne wartości.

• permutacyjne – geny są homogeniczne, czyli przechowują

podobne informacje i są wymienialne. Tego typu kodowa-

nie stosuje się do rozwiązywania problemów kombinato-

rycznych.

• drzewiaste – chromosom nie jest liniowym ciągiem genów,

ale złożoną strukturą drzewiastą. Kodowanie drzewiaste

znajduje zastosowanie w tzw. programowaniu genetycz-
nym, czyli wszędzie tam, gdzie ewolucji podlegają reguły

matematyczne

Genotyp jest to zbiór (struktura) jednego lub więcej chromo-

somów. Genotyp może być już pojedynczym osobnikiem
danej populacji. Fenotyp występuje w przyrodzie po interakcji

ze środowiskiem. Inaczej fenotyp to zbiór parametrów,

rozwiązanie, punkt.

Algorytmy genetyczne (AG) są to algorytmy poszukiwania

oparte na mechanizmach doboru naturalnego oraz dziedzicz-
ności [4], [5]. Algorytm genetyczny zawiera w sobie elementy

teorii ewolucji Darwina, która zakłada, że przeżywają tylko

najlepiej przystosowane osobniki. W każdym pokoleniu

powstaje nowy zespół sztucznych organizmów (ciągów
bitowych), utworzonych z połączenia fragmentów najlepiej

przystosowanych osobników poprzedniego pokolenia. AG

wykorzystują efektywnie przeszłe doświadczenia do

określania nowego obszaru poszukiwań o spodziewanej
podwyższonej wydajności.

Populacja jest to pewien zbiór osobników. Każdy algorytm

genetyczny rozpoczyna działanie od początkowej populacji

Artificial in

telligence

E. Filipowicz et al., Analiza możliwości zastosowania metod sztucznej inteligencji w medycynie sądowej

6

ciągów kodowych, po czym generuje kolejne populacje

ciągów. Najczęściej populację początkową dla AG wybiera się

drogą losową. W każdym kolejnym cyklu w algorytmach

genetycznych populacja ma stały rozmiar, wszystkie
chromosomy podlegają wymianie na nowe. Elementarny

algorytm genetyczny jest skonstruowany z trzech następują-

cych operacji: reprodukcji, krzyżowania oraz mutacji.

Reprodukcja jest to proces, polegający na powieleniu

indywidualnych ciągów kodowych w stosunku zależnym od

wartości, jakie przybiera funkcja celu. Istnieją różne sposoby

powielania ciągów. Najczęściej spotykanym sposobem jest

metoda ruletki.

Krzyżowanie to operacja genetyczna, składająca się

z dwóch etapów. Najpierw kojarzymy w sposób losowy ciągi

kodowe z puli rodzicielskiej w pary, a następnie każda para

przechodzi proces krzyżowania.

Mutacja polega na wymianie pojedynczego bitu w chro-

mosomie. Prawdopodobieństwo wystąpienia mutacji w AG

jest bardzo małe. Mutacja jest błądzeniem przypadkowym

w przestrzeni ciągów kodowych. Jest stosowana tylko na
wypadek utraty ważnych składników rozwiązania.

AG nie przetwarzają bezpośrednio parametrów zadania,

lecz ich zakodowaną część [4], [5]. Prowadzą poszukiwania,

wychodząc nie z pojedynczego punktu, ale z pewnej ich
populacji. AG korzystają tylko z funkcji celu, nie zaś z jej

pochodnych lub pomocniczych informacji. Ponadto stosują

probabilistyczne, a nie deterministyczne reguły wyboru.

Ważnym elementem w AG jest cel optymalizacji. Cel

optymalizacji to zwiększenie efektywności aż do osiągnięcia
pewnego optimum. Głównym celem optymalizacji jest

ulepszenie. Czyli w AG optymalizacja sprowadza się do

poszukiwania maksimum funkcji. W algorytmach tych dążymy

do znalezienia globalnego maksimum, ale pewne odmiany
potrafią znaleźć też optima lokalne [4], [5].

Pierwszym krokiem w AG jest utworzenie populacji po-

czątkowej. Polega on na wybraniu określonej liczby

chromosomów, reprezentowanych przez ciągi bitowe
określonej długości. Nasz algorytm rozpoczyna swoje

działanie właśnie od tej wybranej populacji początkowej

i generuje kolejne (z założenia coraz lepsze) populacje

ciągów. Do nas należy ustalenie liczby populacji początkowej
(należy pamiętać, że ta liczba nie może być zbyt mała ani zbyt

duża). Po wprowadzeniu populacji początkowej przychodzi

pora na ocenę osobników znajdujących się w populacji. Na

tym etapie badamy cechy poszczególnych osobników [4], [5].

Krzyżowanie ma na celu wymianę materiału genetycz-

nego pomiędzy dwoma osobnikami. Mutacja występuje

z bardzo małym prawdopodobieństwem. Wystąpienie mutacji

zależne jest od współczynnika mutacji.

Algorytm, teoretycznie, może się nie kończyć (działa

w nieskończoność). Jednak przeważnie wprowadza się jakieś

ograniczenia. Najczęściej stosowane ograniczenia to:

uzyskanie wartości znanej wcześniej, określona liczbę iteracji
oraz brak poprawy wyników. Zatrzymanie algorytmu zależy od

zadania jakie wykonujemy [4], [5].

Sztuczne sieci neuronowe, będące bardzo uproszczo-

nym modelem mózgu ludzkiego, składają się z dużej liczby
jednostek – neuronów, posiadających umiejętność przetwa-

rzania informacji. Każdy neuron wchodzący w skład sieci

powiązany jest z innymi neuronami za pomocą łączy

o parametrach (tzw. wagach synaptycznych) zmienianych
w trakcie procesu uczenia i służących do komunikacji między

neuronami. Na podstawie bieżącego stanu aktywacji neuronu

i sygnałów wejściowych obliczany jest sygnał, jaki neuron wy-

syła do sieci poprzez jedno wyjście do pozostałych neuronów

(węzłów sieci). W czasie transmisji sygnał ten podlega
osłabieniu lub wzmocnieniu w zależności od charakterystyki

łącza. Większość budowanych sieci neuronowych składa się

z kilku warstw: wejściowej – służącej do wprowadzania do

sieci danych wejściowych, wyjściowej – wyznaczającej końco-
we rozwiązanie i ukrytych – przetwarzających sygnały w taki

sposób, aby wydostać pewne dane pośrednie konieczne do

wyznaczenia końcowego rozwiązania. Istnieje wiele rodzajów

sieci, które różnią się między sobą strukturą i zasadą działania
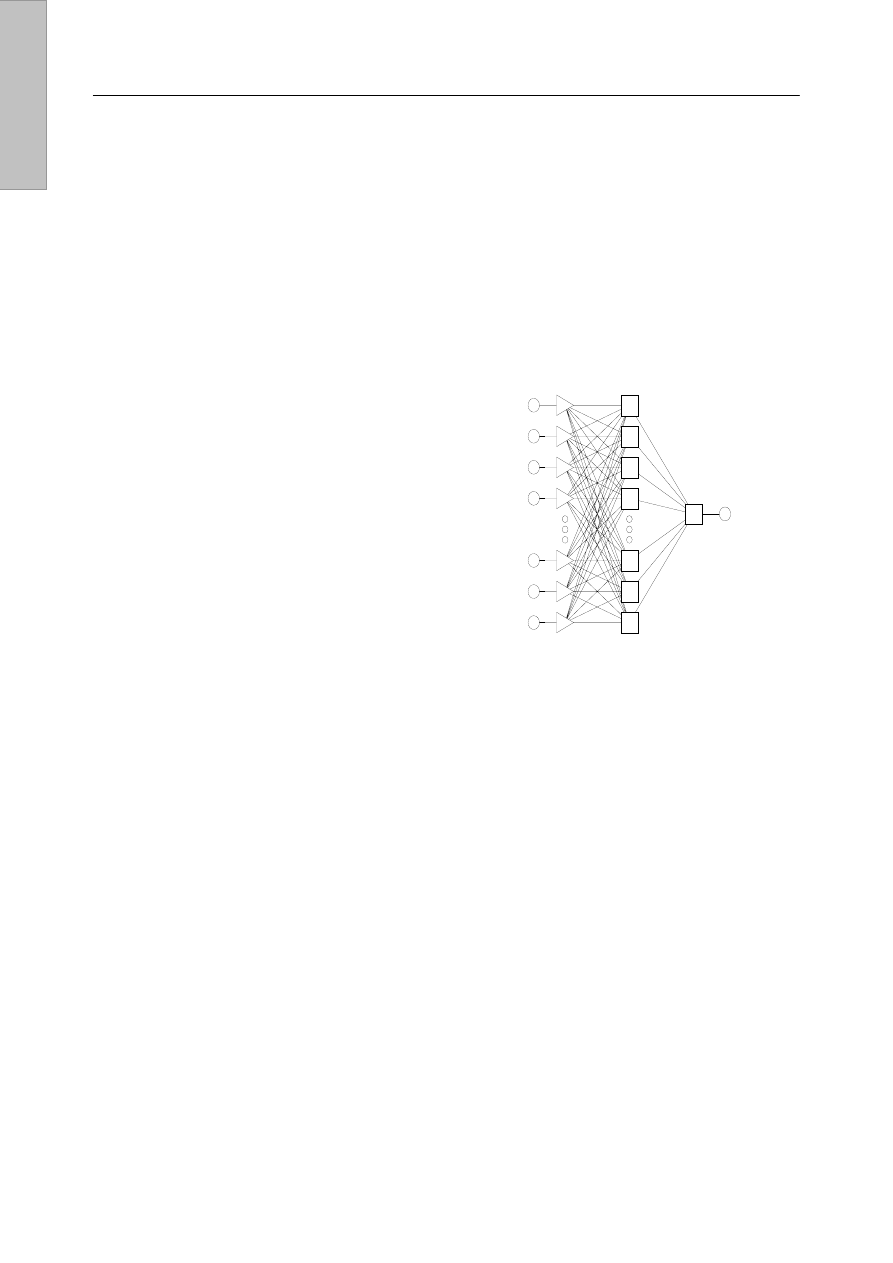
[8]. Najpopularniejszą obecnie strukturą sieci neuronowych są

perceptrony wielowarstwowe (MLP), należące do grupy sieci

z jednokierunkowymi połączeniami (rys. 4).

Rys. 4. Schemat trójwarstwowego MLP

Bardzo ważnym etapem całego procesu konstruowania

tych sieci jest określenie właściwej liczby warstw i neuronów

w warstwach. Okazuje się, że największe możliwości

posiadają nieliniowe sieci neuronowe o co najmniej trzech

warstwach, przy czym liczba neuronów w warstwach
wejściowej i wyjściowej jest określona przez rozwiązywany

problem, natomiast liczba neuronów w warstwie ukrytej zależy

od złożoności problemu, od typu funkcji aktywacji neuronów

tej warstwy, od algorytmu uczenia, od rozmiaru danych

uczących. Najpowszechniejszą metodą uczenia perceptronów
jest metoda wstecznej propagacji błędów. Chcąc właściwie

przeprowadzić proces uczenia sieci, napotykamy na wiele

trudności związanych m.in. z doborem odpowiedniego zbioru

uczącego oraz parametrów uczenia sieci [8].

Powolność i uciążliwość procesu uczenia metodą wstecz-

nej propagacji błędów w sieciach nieliniowych sprawiły, że

pojawiły się również inne rodzaje sieci neuronowych, między

innymi sieci rezonansowe (ART), sieci Hopfielda (ze
sprzężeniem zwrotnym), sieci Kohonena, sieci o radialnych

funkcjach bazowych (RBF), probabilistyczne sieci neuronowe

(PNN) [8].

Jednym z głównych problemów rozwiązywanych za po-

mocą sieci neuronowych jest klasyfikacja i rozpoznawanie

obrazów i dźwięków, wykorzystywane również w medycynie

sądowej. Sieci neuronowe (m.in. RBF) mogą być również

z powodzeniem stosowane do klasyfikacji chromosomów pod
warunkiem istnienia olbrzymiego zbioru danych, pozwalają-

cych na uczenie i testowanie sieci [6].

Artificial in

telligence

E. Filipowicz et al., Analiza możliwości zastosowania metod sztucznej inteligencji w medycynie sądowej

7

W ostatnich latach wśród metod sztucznej inteligencji

coraz większą popularnością cieszą się sztuczne systemy

immunologiczne. Natura układu immunologicznego (m.in.

selekcja klonalna, zdolność uczenia, pamięć immunologiczna,
samoorganizacja, odporność) czyni sztuczne systemy immu-

nologiczne przydatnymi do rozwiązywania problemów klasyfi-

kacyjnych, w szczególności problemów związanych z rozpo-

znawaniem znaków i analizy DNA. Obiektami systemu
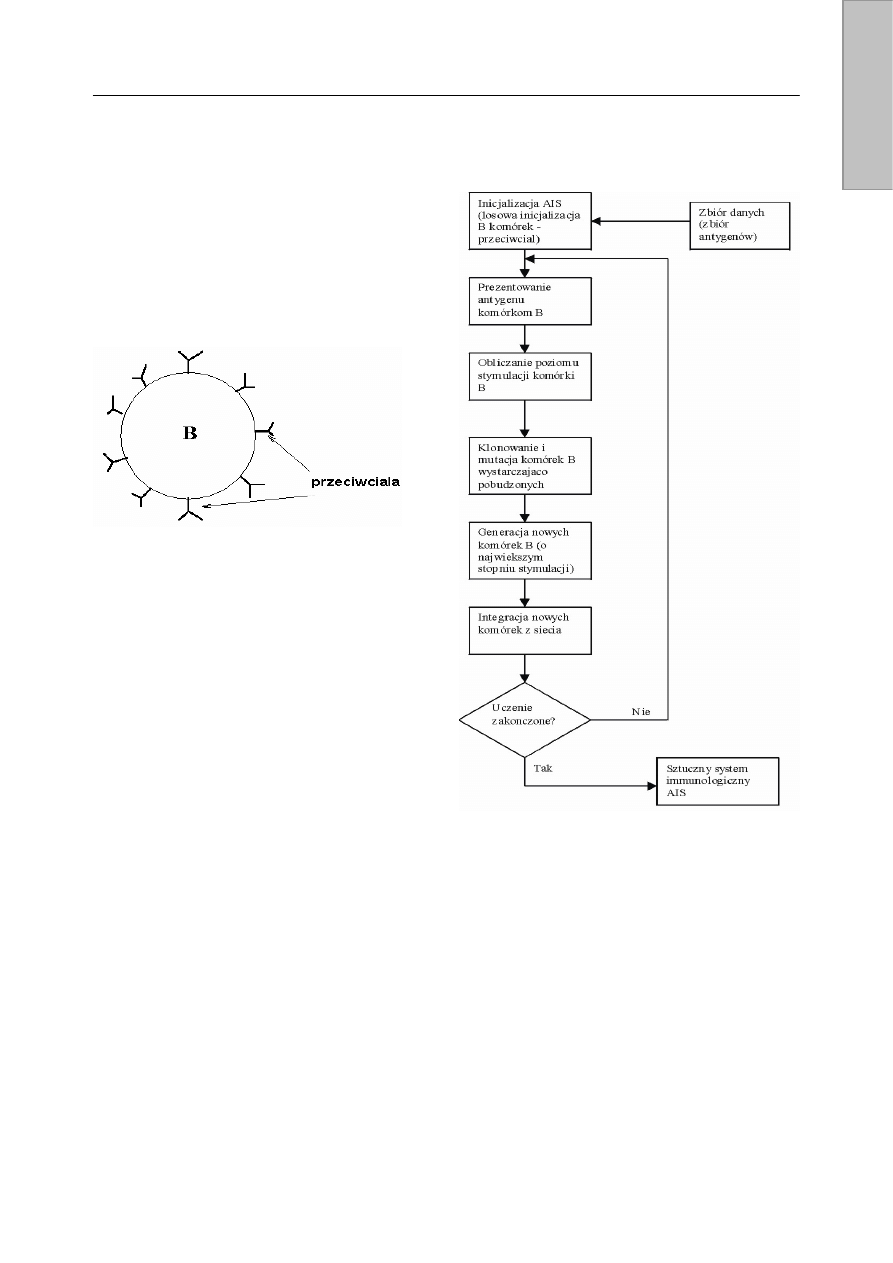
immunologicznego są limfocyty typu T – wspomagające

i wykorzystywane w detekcji anomalii oraz typu B – przeciw-

ciała (rys. 5) wykorzystywane w systemach analizy danych,

zdolne do rozpoznawania antygenów i reagowania na nie.

R

ys. 5. Schemat limfocytu typu B

Limfocyty, reagując na określony antygen wychwytują

istotne właściwości antygenu. Pobudzone limfocyty typu B są

intensywnie klonowane w celu wychwycenia wszystkich

antygenów (selekcja klonalna). Klony podlegają mutacji, dzięki

której możliwe jest również wychwycenie antygenów
podobnych. W sztucznych systemach immunologicznych

antygeny tworzą zbiór danych klasyfikowanych, zaś przeciw-

ciała tworzą wzorce tych danych. Przeciwciała tworzące sieć

idiotypową modyfikowaną wraz z rozpoznawaniem kolejnych
antygenów pogrupowane są na zasadzie podobieństwa.

Jeżeli żadne z przeciwciał nie jest w stanie rozpoznać

antygenu, produkowana jest nowa komórka na wzór

antygenu. Każde nowo utworzone przeciwciało wprowadzane
jest w sąsiedztwo przeciwciał do niego podobnych. Algorytm

uczenia sieci idiotypowej przedstawiony jest na rys. 6.

W procesie klasyfikowania określonej cechy (antygenu) ze

zbioru przeciwciał wybieranych jest n elementów wraz z ich
sąsiedztwem. Antygen porównywany jest z wybranymi

przeciwciałami i obliczany jest stopień ich dopasowania oraz

poziom stymulacji komórki. Przeciwciało, dla którego stopień

dopasowania do antygenu przekracza próg stymulacji,
nazywane jest węzłem klasyfikującym. Dla każdego węzła

klasyfikującego badane jest również jego sąsiedztwo. Spośród

wszystkich węzłów uporządkowanych malejąco względem

dopasowania wybieramy przeciwciało o największym dopa-
sowaniu, które stanowi rozwiązanie naszego problemu [9].

W większości przypadków stosowane jest kodowanie

binarne przeciwciał i antygenów. Dla sekwencjonowania DNA

stosujemy kodowanie ternarne, ponieważ łańcuch DNA
zbudowany jest z 4 nukleotydów: A, T, G i C.

Istotną cechą odróżniającą sztuczne systemy immunolo-

giczne od algorytmów genetycznych jest tzw. metadynamika

(dzięki zapamiętywaniu przez sieć wyuczonych wzorców
istnieje możliwość douczania sieci poprzez prezentowanie

nowych danych). Poza tym o zmianach „gatunkowej

różnorodności” w systemach immunologicznych decyduje

selekcja klonalna i mutacja, natomiast w AG selekcja,

krzyżowania i mutacja.

Rys. 6. Algorytm uczenia sieci idiotypowej

Dzięki opracowanej mapie chromosomu Y, zastosowaniu

analizy pojedynczych polimorfizmów nukleotydowych (ang.

single nucleotide polymorphism – SNP) oraz wykorzystaniu

krótkich odcinków powtarzających (ang. short tandem repeat

– STR) nastąpił znaczny rozwój w medycynie sądowej
w następujących dziedzinach [1], [7], [13], [14]:
- badanie spornego ojcostwa,
- identyfikacja sprawców gwałtu,
- identyfikacja nieznanych zwłok oraz zaginionych osób.

Dzięki zastosowaniu techniki multiplex PCR – reakcji

łańcuchowej polimerazy z wieloma starterami można uzyskać

analizę 246 Y-SNP [12].

Aktualnie bardzo ważne jest tworzenie bazy danych DNA

oraz rozwój wymiany informacji pomiędzy laboratoriami

hemogenetyki [5], [9], [10], [12].

Artificial in

telligence

E. Filipowicz et al., Analiza możliwości zastosowania metod sztucznej inteligencji w medycynie sądowej

8

2. Podsumowanie

Nasz artykuł przedstawia kilka przykładów zastosowania

systemów bioinformatycznych w medycynie sądowej.

Urządzenia wykorzystujące systemy biometryczne są
użyteczne w identyfikacji linii papilarnych, tęczówki oka czy

też geometrii twarzy.

Tworzenie modeli stochastycznych jest elastyczną i naj-

bardziej ogólną metodą wykorzystywaną w zagadnieniach
systemów biometrycznych. Istnieje wiele nie w pełni jasnych

i dających się z trudem zdefiniować aspektów związanych

z rozpoznaniem danej cechy. Ponadto znajomość oraz

zastosowanie algorytmów genetycznych wydaje się nie-
zbędne w hemogenetyce, między innymi w identyfikacji DNA

nieznanych zwłok oraz w oznaczaniu spornego ojcostwa.

Literatura cytowana

1. Butler J. M.: Recent developments in Y-single tandem repaet

and Y-single nucleotide polymorphism analysis, Forensic Sci
Rev, 15: 91-108, 2003.

2. Filipowicz B.: Modele stochastyczne w badaniach operacyjnych.

Analiza i synteza systemów obsługi i sieci kolejkowych, WNT,
Warszawa 1996.

3. Filipowicz B., Kwiecień J.: Optymalizacja sieci kolejkowych przy

użyciu algorytmów genetycznych, AUTOMATYKA, Półrocznik,
Uczelniane Wydawnictwa Naukowo-Dydaktyczne AGH, Kraków
2003.

4. Filipowicz B.: Modelowanie i optymalizacja systemów

kolejkowych cz. 1. Systemy Markowskie, Przedsiębiorstwo
Poligraficzne T. Rudkowski, Kraków 1995.

5. Goldberg D.: Algorytmy genetyczne i ich zastosowanie, WNT,

Warszawa 1998.

6. Musavi M. T. i in.: Mouse chromosome classification by radial

basis function network with fast orthogonal search, Neural
Networks 11, 769-777, 1998.

7. Opolska-Bogusz B., Sanak M., Turowska M.: Genetic variation at

STR-TH01 locus in the South Polish population, Arch Med
Sadowej Krymino, 52(2): 99-101, 2002.

8. Tadeusiewicz R.: Sieci neuronowe, Akademicka Oficyna

Wydawnicza, Warszawa 1993.

9. Wierzchoń S. T.: Sztuczne systemy immunologiczne. Teoria

i zastosowania, Akademicka Oficyna Wydawnicza EXIT,
Warszawa 2001.

10. www.biometryka.com
11. www.logistyka.net.pl
12. http://ycc.biosci.arizona.edu
13. www.relive.genetics.com
14. http://genome.ucsc.edu

INFORMATYK

NARZĘDZIA DO IDENTYFIKACJI

OSOBNICZEJ ORAZ RELACJI

MIĘDZY-OSOBNICZEJ

MEDYCYNA SĄDOWA

DANE O TRADYCYJNYCH I INNYCH

STOSOWANYCH METODACH

IDENTYFIKACJI

INFORMATYK

AUTOMATYCZNE PRZESYŁANIE ORAZ

KONSTRUKCJA BAZY DANYCH

STATYSTYK

PORÓWNAWCZA ANALIZA

STATYSTYCZNA WYNIKÓW

TRADYCYJNYCH ORAZ

WG PROPONOWANEGO MODELU

Artificial in

telligence