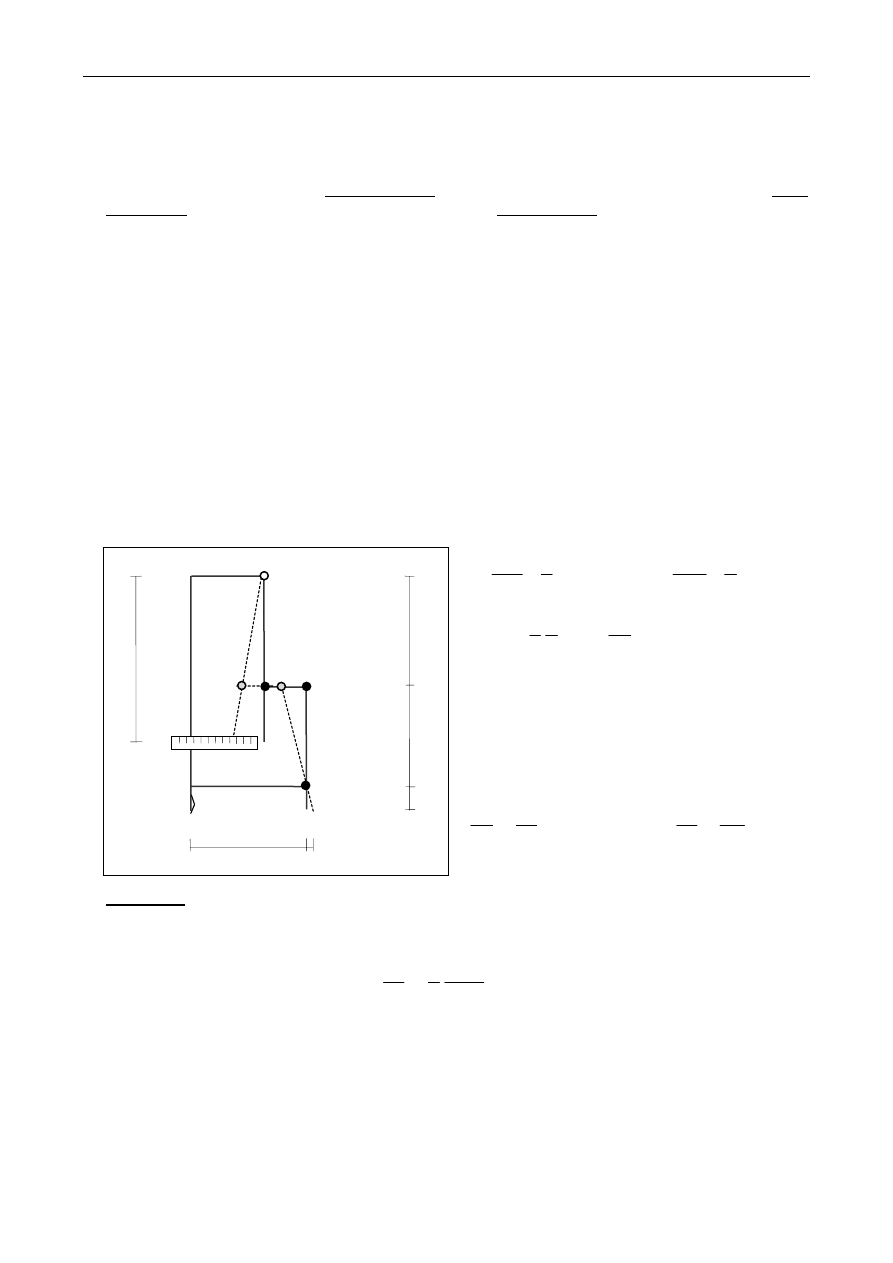
Podstawy tensometrii
1
1. Idea pomiarów tensometrycznych (łac. tensus = napięty + gr. metréô = mierzę)
∗
metody tensometryczne (MT) są podstawowym sposobem określania naprężeń w punktach na
powierzchni konstrukcji
∗
MT opierają się na pomiarze przemieszczeń na wybranym odcinku pomiarowym zwanym bazą
pomiarową o dług. L
0
, za pomocą urządzeń zwanych tensometrami
∗
pomiar przemieszczenia
∆ l, określenie przemieszczenia względnego ∆ l / L
0
=
ε (odkształcenie
liniowe na kierunku mierzonego przemieszczenia), obliczenie naprężenia w oparciu o przyjęty
związek fizyczny (np. równanie Hooke’a)
∗
baza tensometru powinna być jak najkrótsza, aby mierzone wartości uśrednione na długości
bazy były jak najbliższe wartości lokalnych w danym punkcie konstrukcji.
2. Typy tensometrów (ang. strain gauges)
∗ mechaniczne (tensometr Huggenbergera, t. zegarowe)
∗ ekstensometry (mechaniczno-elektryczno-fotooptyczne)
∗ czujniki elektooporowe
∗ indukcyjne
∗ optyczne
3. Tensometr Huggenbergera
∆L
BB
h
a
1
=
DD
CC
H
b
1
1
≅
∆L h
a
b
H
DD
bh
aH
DD
i DD
=
=
=
1
1
1
i = przełożenie
DD
s nR
1
= =
def
R = przemieszczenie jednostkowe
∆L
L
i s
L
0
0
=
⇒
ε =
=
s
L
i
n R
L
i
0
0
∗
Przykład:
baza tensometru L
0
= 5 mm, przełożenie i = 1/2000. Zdolność odczytu (najmniejsze
odkształcenie jakie można odczytać na tensometrze, odkształcenie odpowiadające jednostko-
wemu przemieszczeniu n R = 1mm) wynosi:
ε =
=
=
−
1
1
5
1
2000
10
4
L
i
0
maksymalna zdolność odczytu wynosi 5 x 10
-6
.
4. Zasada pomiaru przemieszczeń poprzez pomiar zmian oporu elektrycznego.
∗ drut elektrooporowy - drut o średnicy ~0.025 mm, charakteryzujący się liniową zależnością
zmiany oporu od odkształcenia
A
A
1
B
B
1
C
C
1
D
D
1
O
n
L
0
∆L
b
a
h
H
Podstawy tensometrii
2
R
L
A
L
r
=
=
ρ
ρ
π
2
dR
dL
r
L
r
dr
=
−
ρ
π
π
2
3
2
1
różniczka zupełna
∆
∆
∆
R
L
r
L r
r
=
−
ρ
π
π
2
3
2
/ : R
różnica skończona
∆
∆
∆
R
R
A
L
L
r
L r
r
=
−
ρ
ρ
π
π
2
3
2
∆
∆
∆
R
R
r
L r
L
L r
r
=
−
π
π
2
2
2
∆
∆
∆
R
R
L
L
r
r
=
− 2
dla drutu rozciąganego
ε
νε
y
x
= −
dla drutu rozciąganego o przekroju kołowym ∆
∆
r
r
L
L
= −ν
(
)
∆R
R
= +
1 2
ν ε
∗ względna zmiana oporu drutu jest wprost proporcjonalna do jego odkształcenia liniowego
∗ czujnik elektrooporowy - czujnik zbudowany z drutu elektrooporowego, odpowiednio
ukształtowanego w celu uzyskania jak największej dokładności odczytu zmian oporu
∆R
R
k
k
=
=
÷
ε
16 3 6
.
.
4.1.
Wymagania stawiane drutowi elektrooporowemu
∗ liniowa zależność między zmianą oporu, a przemieszczeniem
∗ wysoki współczynnik czułości (stała tensometryczna) k
∗ wysoka oporność właściwa pozwalająca budować czujniki o małych wymiarach
∗ niski współczynnik termicznej zmiany oporności
4.2.
Wymagania stawiane czujnikowi elektrooporowemu
∗ dobra przewodność cieplna (dobre odprowadzenie z czujnika ciepła wytworzonego przez
płynący prąd)
∗ niewrażliwość na odkształcenia poprzeczne do kierunku odkształceń mierzonych
∗ wysoka oporność izolacji
4.3.
Zalety czujników elektrooporowych
∗ duża dokładność
∗ możliwość stosowania w miejscach trudnodostępnych
∗ rozłączność czujnika i układu rejestrującego
∗ możliwość pomiarów statycznych i dynamicznych
2 r
A
L
ρ
Podstawy tensometrii
3
4.4.
Wady czujników elektrooporowych
∗ podatność na wpływy temperatury i wilgoci
∗ duża cena czujników (czujniki raz naklejone nie mogą być usunięte i ponownie użyte)
∗ rozłączność czujnika i układu rejestrującego - zdalny pomiar
∗ kosztowne badania (kwalifikowana obsługa)
5.
Układ pomiarowy w pomiarach tensometrycznych
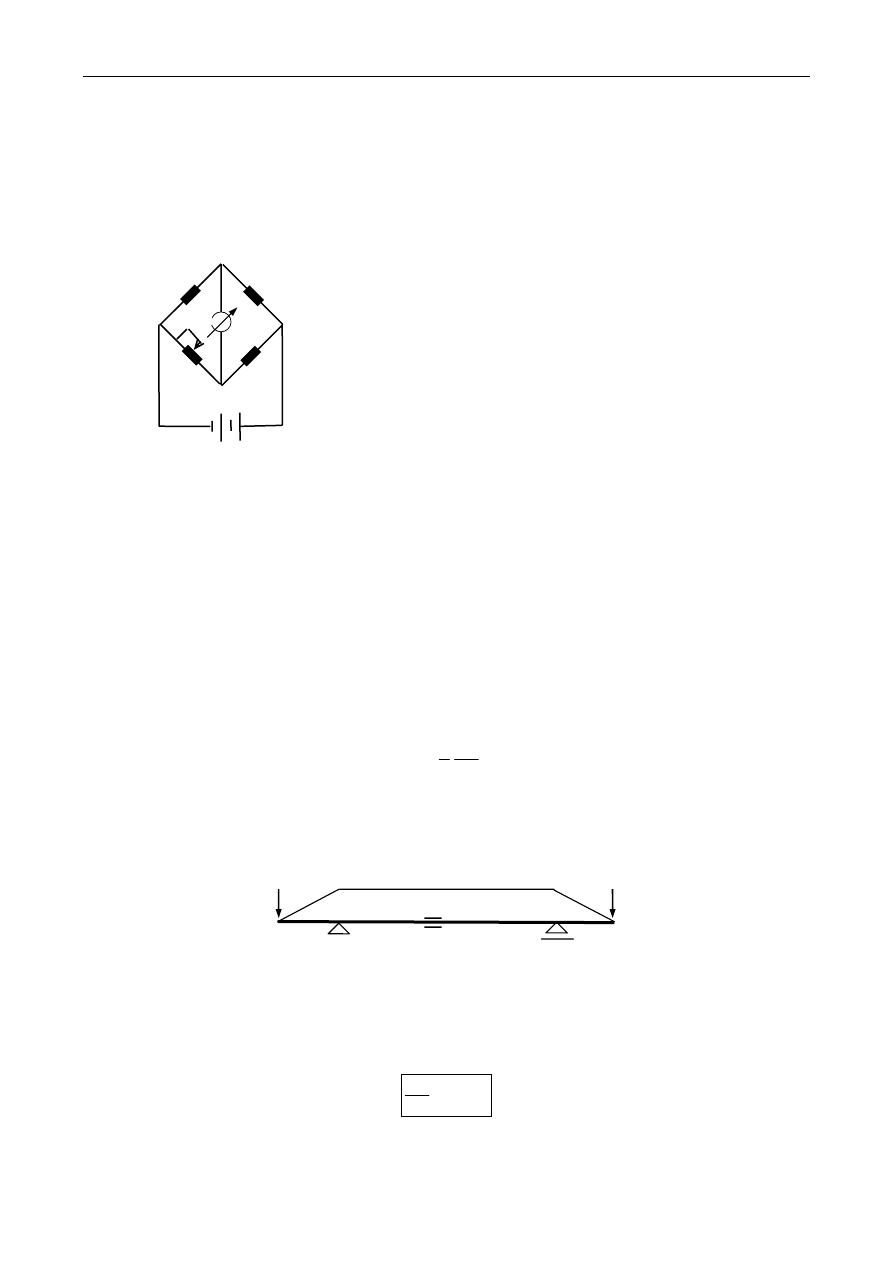
∗ zmiany oporności czujnika mierzy się w układzie mostka Wheatstone’a
R
c
- opór czynny
R
k
- opór kompensacyjny
R
1
- opór wewnętrzny regulowany
R
2
- opór wewnętrzny
∗ warunek zrównoważenia mostka (brak przepływu prądu przez galwanometr)
R R
R R
k
c
1
2
=
∗ czujnik kompensacyjny służy do kompensacji wpływu zmiany oporu przy zmianie temperatury o
∆T. Jest on identyczny jak czujnik czynny, ale jest nalepiony na nieobciążonej części konstrukcji
(lub oddzielnie)
5.1.
Układ kompensacyjny
∆
∆
R
k R
R
c
c
cT
=
+
ε
∆
∆
R
R
k
kT
=
∆
∆
∆
∆
∆
R
R
R
k R
R
R
c
k
c
cT
kT
=
−
=
+
−
ε
R
R
cT
kT
=
∆R k R
c
=
ε
ε = 1
k
R
R
c
∆
5.2.
Układ samokompensacyjny
∗ w przypadku belek o przekroju posiadającym oś symetrii prostopadłą do płaszczyzny obciąże-
nia, poddanych prostemu zginaniu, można umieścić dwa czujniki czynne na przeciwległych
włóknach skrajnych
∆
∆
R
k R
R
c
c
c
g
cT
=
+
ε
;
( )
∆
∆
R
k R
k
k
k
g
=
+
-
ε
R
kT
∆
∆
∆
∆
∆
R
k
g
g
=
−
=
+
+
−
R
R
R
R
k R
R
c
k
c
c
cT
k
k
kT
ε
ε
R
R
R
c
k
=
=
k
k
k
c
k
=
=
∆
∆
R
R
cT
kT
=
∆R
k R
g
= 2
ε
∆R
R
k
g
= 2 ε
∗ mostek wykazuje w ukł. samokompensacyjnym odkszt. dwa razy większe niż rzeczywiste.
R
1
R
2
R
k
R
c
G
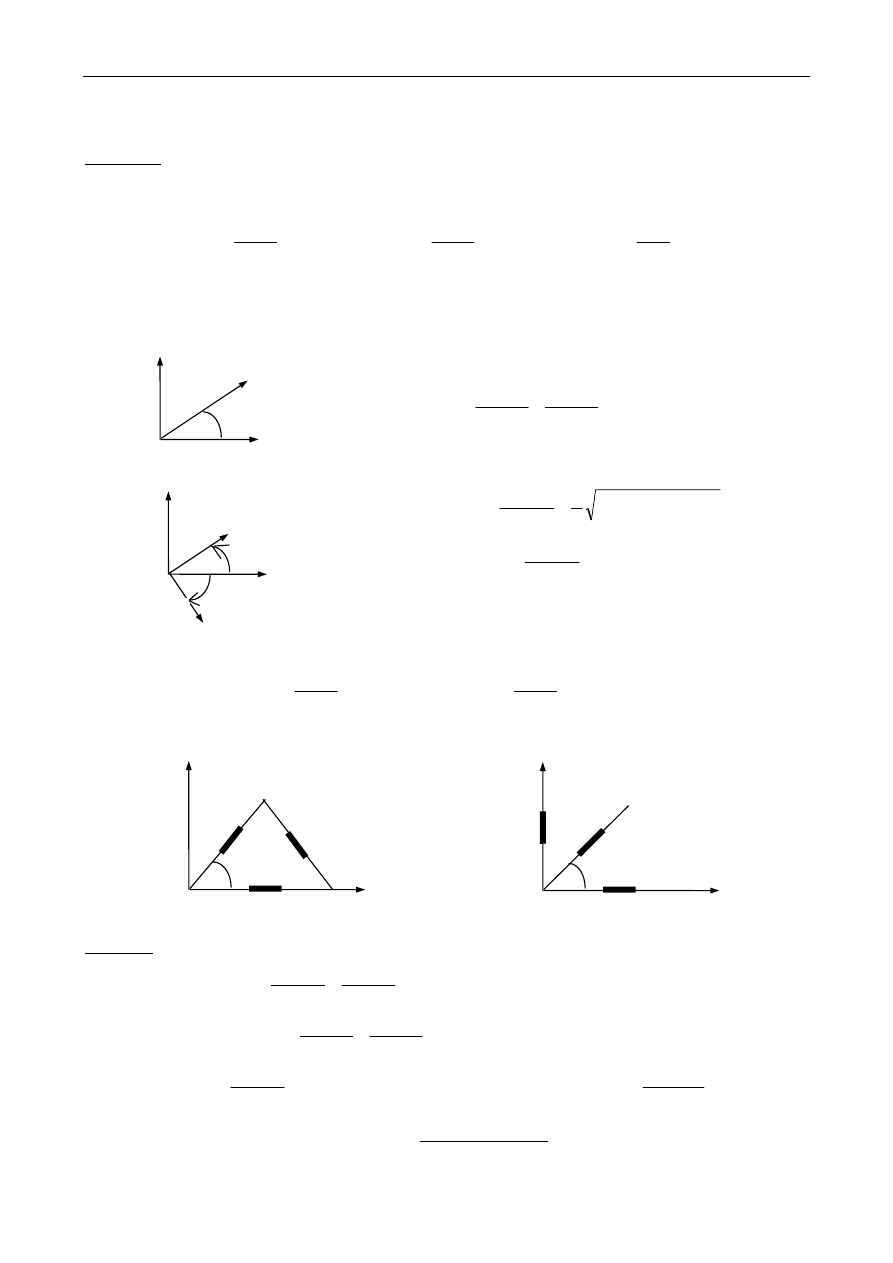
Podstawy tensometrii
4
6. Zastosowanie tensometrii elektrooporowej do doświadczalnej analizy naprężeń w
płaskim stanie naprężenia.
Problem :
Wyznaczyć naprężenia główne w dowolnym punkcie na powierzchni
konstrukcji
płaskiej
∗ na powierzchni ciała zawsze panuje płaski stan naprężenia
(
)
σ
ν
ε
ν ε
x
x
y
E
=
−
+
1
2
;
(
)
σ
ν
ε
ν ε
y
y
x
E
=
−
+
1
2
;
τ
ν
ε
xy
xy
E
=
+
1
∗ w celu wyznaczenia składowych tensora naprężenia należy znać odkształcenia
ε
x
,
ε
y
i
ε
xy
. Moż-
na je wyznaczyć znając odkształcenia w 3 dowolnych znanych kierunkach, korzystając z relacji
(transformacja tensora przy obrocie układu współrzędnych)
ε
ε
ε
ε
ε
α ε
α
α
=
+
+
−
+
x
y
x
y
xy
2
2
2
2
cos
sin
∗ odkształcenia i kierunki główne
(
)
ε
ε
ε
ε
ε
ε
1 2
2
2
2
1
2
4
,
=
+
±
−
+
x
y
x
y
xy
tan 2
2
ϕ
ε
ε
ε
= −
−
xy
y
x
∗ naprężenia główne
(
)
σ
ν
ε
ν ε
1
2
1
2
1
=
−
+
E
;
(
)
σ
ν
ε
ν ε
2
2
2
1
1
=
−
+
E
∗ rozety tensometryczne
typ „delta”
typ prostokątny
Przykład : rozeta prostokątna
ε
ε
ε
ε
ε
ε
0
2
2
=
+
+
−
=
x
y
x
y
x
⇒
ε
ε
x
=
0
ε
ε
ε
ε
ε
ε
90
2
2
=
+
−
−
=
x
y
x
y
y
⇒
ε
ε
y
=
90
ε
ε
ε
ε
45
2
=
+
+
x
y
xy
⇒
ε
ε
ε
ε
xy
=
−
+
45
0
90
2
(
)
tan 2
2
45
0
90
0
90
ϕ
ε
ε
ε
ε
ε
= −
−
+
−
x
y
α
α
x
y
α
=60
°
x
y
α
=45
°
x
y
ϕ
>0
1
1
ϕ
<0