X L V I I I K O N F E R E N C J A N AU K O W A

KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN

I KOMITETU NAUKI PZITB

Opole – Krynica

2002

Teresa PACZKOWSKA

1

Wiesław PACZKOWSKI

1

OCENA WIARYGODNOŚ CI

WYNIKÓ W OBCIĄŻ EŃ PRÓ BNYCH

WIADUKTU O KONSTRUKCJI ZESPOLONEJ

1. Badania tensometryczne wiaduktu

Standardowe badania prowadzone podczas statycznych obcią żeń próbnych obejmują przede
wszystkim pomiary ugię ć przę seł oraz przemieszczenia łożysk i podpór. W przypadku sto-
sowania rozwią zań nowatorskich zalecany jest pomiar odkształceń w celu uzyskania po-
twierdzenia, że przyję ty do obliczeń teoretyczny model zachowania się konstrukcji realizo-
wany jest w konstrukcji rzeczywistej. Pomiary przemieszczeń , o ile nie dojdzie do niekontro-
lowanych błę dów grubych, można uznać za obarczone jedynie błę dem wynikają cym z do-
kładności pomiaru. Błą d ten należy do klasy zjawisk określanych jako niepewność systema-
tyczna, co zapewnia na ogół wysoki stopień wiarygodności otrzymanych wyników.
W przypadku pomiarów tensometrycznych – szczególnie wykonywanych w warunkach po-
lowych – należy liczyć się z możliwością wystą pienia błę dów pomiarowych [1], których
wielkość znacznie przekroczy nominalną dokładność pomiaru.

Obcią żeniom próbnym poddano trójprzę słowy wiadukt o konstrukcji zespolonej [2].

Do zespolenia żelbetowej płyty pomostu ze stalowymi dźwigarami zastosowano w tym wia-
dukcie łą czniki listwowe [3]. Na etapie ustalania programu obcią żeń próbnych podję to decy-
zję o przeprowadzeniu pomiaru odkształceń w celu uzyskania informacji o osią gnię tym
stopniu zespolenia.

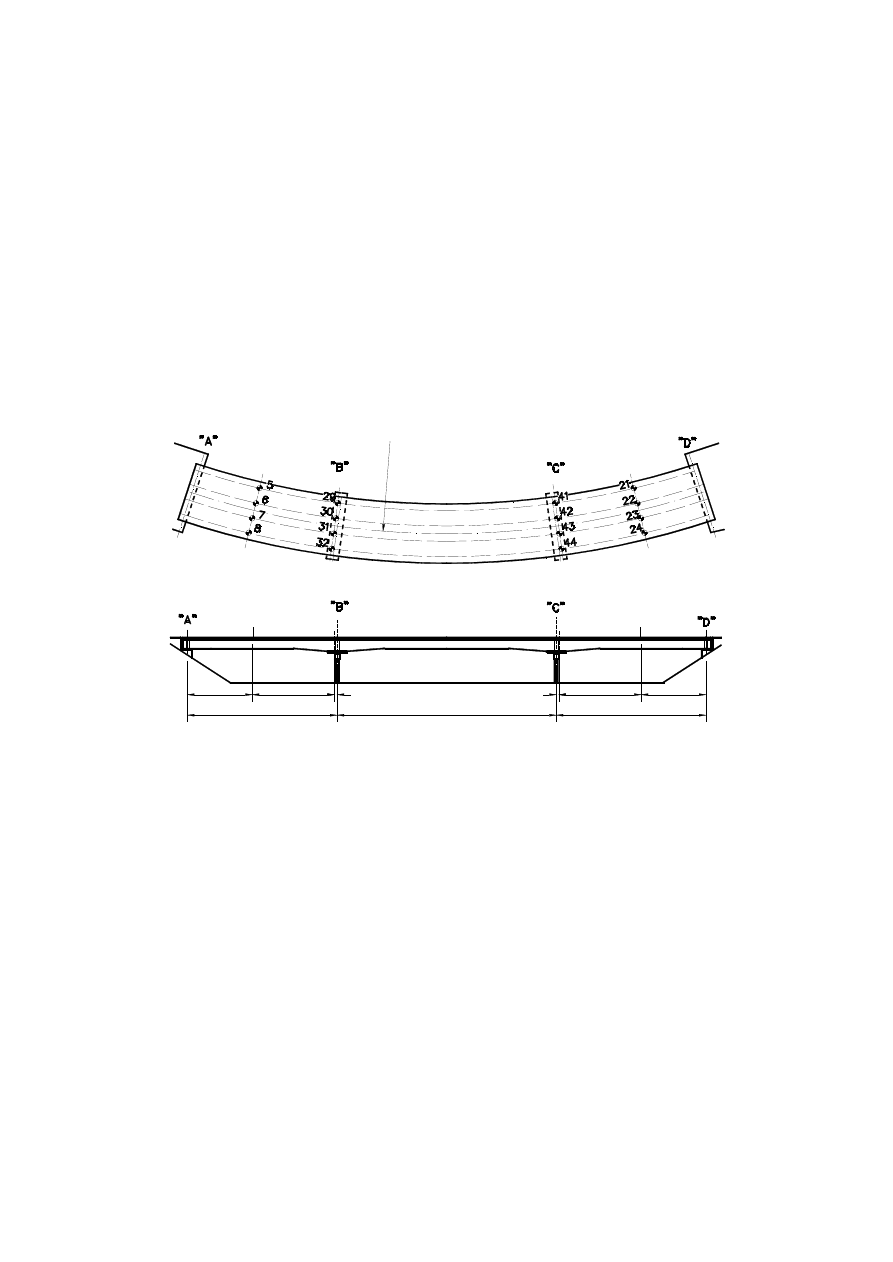
Badany wiadukt jest wiaduktem drogowym trójprzę słowym. Oś wiaduktu biegnie

w łuku poziomym R = 150 m (rys. 1) i w łuku pionowym R = 1500 m. Całkowita długość
obiektu wynosi 107,65 m, przy czym rozpię tości przę seł w osi jezdni wynoszą :

27,325 + 40,00 + 27,325 = 96,650 m

Konstrukcję nośną wiaduktu stanowią cztery stalowe dźwigary główne rozmieszczone
w rozstawie osiowym 2800 mm wykonane ze stali 18G2A. Dźwigary stalowe wykonano ja-
ko spawane blachownice o zmiennej wysokości: 1566 mm w przę śle i 2070 mm nad podpo-
rami pośrednimi. Pasy dolne w czę ści przę słowej przę seł skrajnych mają przekrój
350 x 25 mm wzmocniony nakładką 250 x 16 mm w dźwigarach zewnę trznych oraz przekrój

1

Dr inż., Wydział Budownictwa i Architektury Politechniki Szczeciń skiej

184

350 x 30 mm z taką samą nakładką w dźwigarach wewnę trznych. Pasy dolne wszystkich
dźwigarów przę sła środkowego mają przekrój 400 x 30 mm wzmocniony w czę ści środko-
wej nakładką 250 x 16 mm. Dodatkowo nad podporami pośrednimi pasy dolne wzmocniono
nakładkami 470 x 20 mm. Wszystkie pasy górne mają przekrój 350 x 20 mm. Dźwigary
główne powią zane są stę żeniami poprzecznymi pionowymi w postaci wykratowanej
w przę słach i w postaci blachownic nad podporami. Ponadto w poziomie pasów dolnych wy-
stę pują stę żenia poziome dolne w postaci wykratowań W i X.

Płytę żelbetową pomostu wykonano na mokro z betonu B40. Grubość płyty wynosi

20 cm z pogrubieniami 5 cm nad górnymi półkami dźwigarów stalowych. Do płyty stosowa-
no zbrojenie klasy A-I St3SX oraz klasy A-II 18G2. Całkowita szerokość pomostu wynosi
10,82 m z tego 10,22 m w świetle balustrad. Jezdnia ma 7,0 m szerokości, chodniki po obu
stronach mają szerokości 1,25 m.

D

Ź WIGAR D3

g

2

g

2

g

1

g

1

a

1

a

2

a

2

a

1

a

2

a

1

g

2

g

1

D

Ź WIGAR D2

D

Ź WIGAR D1

D

Ź WIGAR D4

R

=

1

5

0

.0

0

0

40.000

27.325

11.825

0.500

15.000

27.325

0.500

15.000

11.825

Rys. 1. Rzut i widok wiaduktu z zaznaczonymi symetrycznie rozmieszczonymi

punktami pomiarowymi

Na rys. 1 pokazano badany wiadukt oraz zaznaczono punkty pomiarowe przyję te do

analiz w niniejszym referacie. Używane tutaj poję cie punktu pomiarowego ma charakter or-
ganizacyjny i w istocie dotyczy wyróżnionego przekroju dźwigara głównego, w którym to
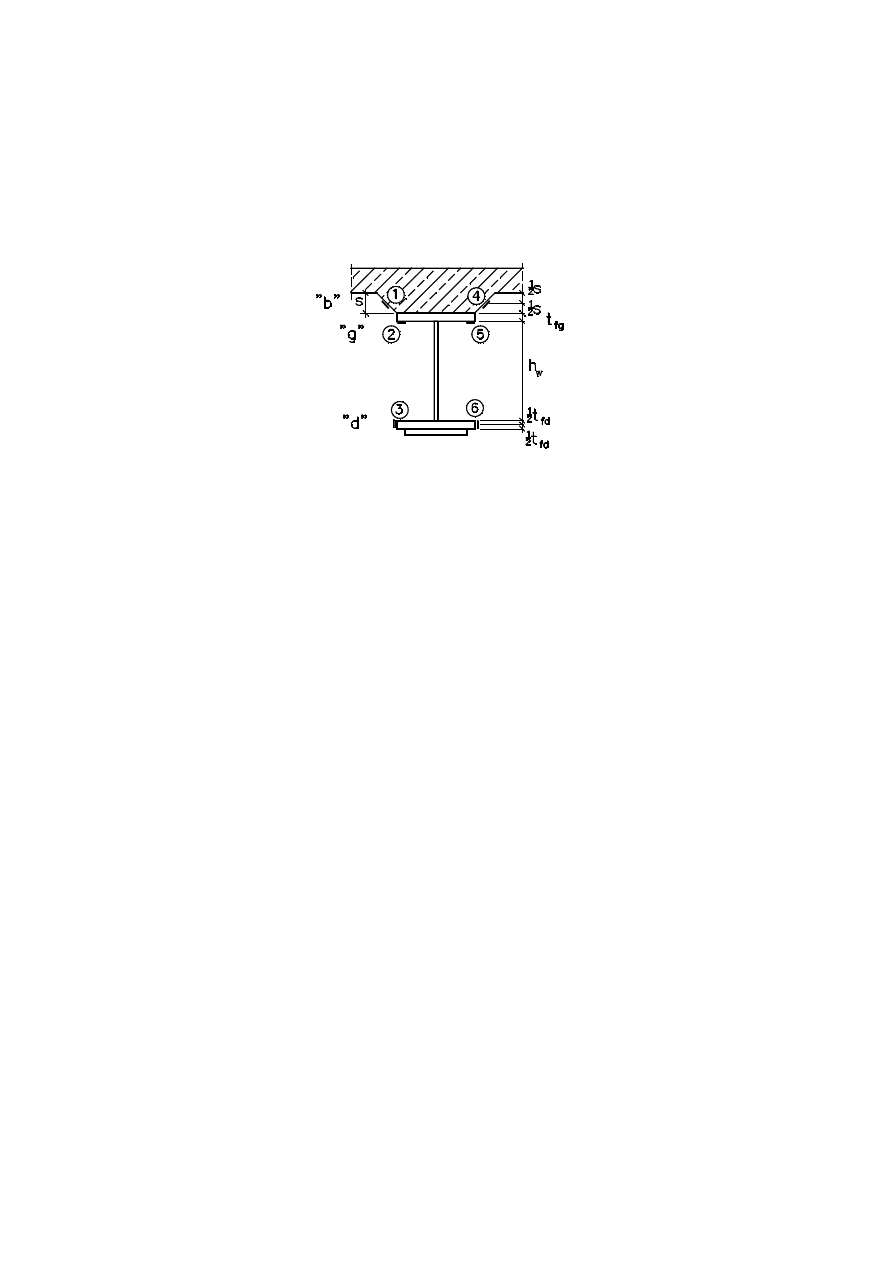
przekroju umieszczono po 2 tensometry na pasie górnym i dolnym oraz 2 tensometry na sko-
sach płyty żelbetowej (rys. 2). Badano zachowanie się konstrukcji w 20 punktach pomiaro-
wych, czyli dokonywano odczytu wskazań 120 tensometrów. Każde z przę seł poddane było
obcią żeniu w ustawieniu taboru od strony południowej oraz północnej, co dało 6 schematów
obcią żenia. W każdym schemacie obcią żenia rejestrowano odczyty w 4 punktach pomiaro-
wych przekroju przę słowego obcią żonego przę sła i w 4 punktach pomiarowych przekroju
przypodporowego danego przę sła jak zaznaczono na rys. 1. Metodologia badań przewidywa-
ła wstę pne obcią żenie konstrukcji na poziomie 50% obcią żenia pełnego oraz 6 schematów
obcią żeń , dla których wykonywano 2 odczyty przed obcią żeniem, odczyt po obcią żeniu, dal-
sze odczyty w odstę pach co 15 minut do ustabilizowania się przemieszczeń , odczyt po od-
cią żeniu oraz odczyty co 15 minut do ustabilizowania się przemieszczeń po odcią żeniu. W
sumie dokonano 2400 odczytów. Po ich obrobieniu wielkości odkształceń w 288 tensome-

185

trach (wyniki z jednego tensometru uwzglę dniano 2 lub 4 razy) przyję to do analizy pracy
konstrukcji.

PN

PD

Rys. 2. Układ tensometrów w punkcie pomiarowym

2. Wspó łczynnik podobieństwa wynikó w pomiaró w

Próbę ustalenia oceny wiarygodności wyników pomiarów otrzymanych w trakcie obcią żeń
próbnych przeprowadzono na przykładzie pomiaru odkształceń . Wszelkie pomiary terenowe,
w tym także wykonywane podczas obcią żeń próbnych prowadzone są w warunkach nie zaw-
sze sprzyjają cych uzyskiwaniu wiarygodnych wyników. Przykładowo jakość wyników ba-
dań tensometrycznych zależy od klasy użytej aparatury pomiarowej, ale także od czynników
takich jak np. długość kabli, skuteczność izolacji, wilgotność , temperatura. Prowadzenie po-
miarów, szczególnie na obiektach drogowych, napotykać może na ograniczenia natury for-
malno-organizacyjnej sprowadzają ce się najczę ściej do ograniczeń czasowych lub prze-
strzennych, a wię c zwią zanych z niedostę pnością określonych miejsc. Wreszcie istotnym
czynnikiem wystę pują cym w przypadku obcią żeń próbnych jest koszt taboru obcią żają cego,
co zmusza wykonawcę obcią żeń próbnych do ograniczenia czasu korzystania z taboru do
niezbę dnego minimum. Wszystkie te czynniki powodują , że najczę ściej pomiarów w warun-
kach terenowych nie daje się powtórzyć i jedynym sposobem ich weryfikacji staje się dodat-
kowa analiza prowadzona już w warunkach studyjnych.

Podstawę do oceny jakości pomiarów tworzy ich statystyczna obróbka [1]. W przypad-

ku konstrukcji o korzystnych cechach topologicznych, np. dla konstrukcji o 4 płaszczyznach
symetrii możliwe jest tworzenie 8-elementowych zbiorów wyników pomiarów poddają cych
się standardowej obróbce statystycznej, co pozwala w efekcie na zastosowanie wnioskowa-
nia bazują cego na weryfikacji hipotez statystycznych. W szczególności istotna jest możli-
wość odrzucenia pomiarów obcią żonym dużym błę dem.

W przypadku bę dą cym przedmiotem niniejszego opracowania wystę puje tylko jedna

płaszczyzna symetrii, która pozwala na dokonanie porównania wyników pomiarów dla od-
powiadają cych sobie symetrycznych schematów obcią żenia.

Dokonują c pomiarów odkształceń w różnych punktach złożonej konstrukcji rze-

czywistej trzeba liczyć się z możliwością wystą pienia efektów nie przewidywanych w
teoretycznych modelach obliczeniowych, z efektami losowymi bę dą cymi obiektywną
własnością konstrukcji, wreszcie z błę dami pomiarowymi. Oszacowanie w takiej sytu-
acji, czy w dwóch odpowiadają cych sobie punktach pomiarowych rejestrują cych po 6
odczytów otrzymano podobne wyniki pomiarów jest trudne i nie daje się wykonać bazu-
ją c na doświadczeniu lub intuicji. Wobec niemożności wykorzystania kryteriów staty-

186

stycznych proponuje się wprowadzenie współczynnika podobień stwa

a

pozwalają cego

oszacować stopień podobień stwa rozkładu wyników w porównywanych punktach po-
miarowych.

Teoretyczne określenie kryterium podobień stwa kształtu jest przedmiotem ocen

w teorii zbiorów rozmytych i jego zastosowanie przekraczałoby poziom praktycznego zna-
czenia oceny w omawianym przypadku. Z tego wzglę du zaproponowano uproszczoną ocenę
globalną z narzuconym kryterium oceny zgodności pojedynczych pomiarów. Dla dwóch cią -
gów liczbowych

}

...,

,

,

{

*

n

1

*

12

*

11

C

C

C

oraz

}

...,

,

,

{

*

n

2

*

22

*

21

C

C

C

poszukuje się miary

pozwalają cej oszacować podobień stwo obu cią gów. Owo podobień stwo jest warunkiem za-
akceptowania obu cią gów jako wiarygodnie opisują cych mierzone wielkości. Liczby tworzą -
ce oba cią gi są wynikami pomiaru n wielkości, przy czym ich uporzą dkowanie jest ściśle
określone, czyli

*

i

1

C

jest pomiarem z pierwszego cią gu dotyczą cym i-tego punktu, a

*

i

2

C

jest pomiarem z drugiego cią gu dotyczą cym odpowiadają cego punktu. Z góry zakłada się , że

dokonywane jest sprawdzenie

*

*

*

*

C

C

gr

i

2

i

1

i

D

D

£

-

=

eliminują ce odpowiadają ce sobie od-

czyty, gdy ich różnica przekracza przyję tą dla danego pomiaru wielkość

*

gr

D

.

Oba cią gi normuje się wybierają c najwię kszą co do wartości bezwzglę dnej wielkość

*

C

ij

i dzielą c przez nią wszystkie pozostałe wielkości. Zakładają c dla ustalenia uwagi, że

wielkość ta wystą piła w cią gu pierwszym oraz dodatkowo porzą dkują c wyrazy cią gu pierw-
szego tak, aby utworzyły cią g maleją cy (lokalnie może to być cią g nierosną cy) otrzymuje się

cią g unormowany

}

...,

,

,

1

{

n

1

12

C

C

. Dla cią gu drugiego porzą dkuje się wyrazy zachowu-

ją c ich odpowiedniość z cią giem pierwszym, co daje

}

...,

,

,

{

n

2

22

21

C

C

C

Współczynnik podobień stwa

a

definiuje się nastę pują co:

1

s

1

D

-

=

a

(1)

gdzie:

i

i

i

2

1

C

C

-

=

D

(2)

å

=

D

=

D

n

1

i

n

1

i

(3)

å

=

=

n

1

i

1

1

C

n

1

s

i

(4)

Cią gi identyczne dają wartość

1

=

a

, cią gi przekształcone liniowo dają

a

równe

współczynnikowi liniowego przekształcenia. Tak przyję te kryterium podobień stwa wykazuje
swą użyteczność w przypadku cią gów pomiarowych rzeczywiście do siebie zbliżonych, przy
czym ustalenie granicy przydatności tego kryterium wymaga osobnych badań . Zastosowanie
tego kryterium do cią gów silnie niepodobnych może doprowadzić do tego, że współczynnik
podobień stwa

a

nie spełni kryterium unormowania, czyli znajdzie się poza przedziałem

[1, -1] od dołu. Z teoretycznego punktu widzenia jest to istotne obcią żenie, natomiast
z praktycznego punktu widzenia współczynnik podobień stwa

a

spełni swe zadanie, gdyż

187

bę dzie to jednoznaczny sygnał o nieprzystawalności do siebie obu cią gów pomiarowych,
a wię c o konieczności natychmiastowej weryfikacji otrzymanych wyników.

Alternatywną możliwością oceny podobień stwa dwóch zestawów danych jest

zastosowanie korelacji liniowej. Zaletą tego podejścia jest przede wszystkim to, że
jest to podejście standardowe możliwe dla dowolnej liczebności cią gów pomiarowych.
Spełnia ona precyzyjnie kryterium unormowania [1, -1] oraz nie wprowadza problemów
zwią zanych ze zmiennością znaków różnic (2) oraz znaków wartości. Jego wadą jest
to, że współczynnik korelacji

r

bę dą cy w tym przypadku miarą stopnia podobień stwa

jest mało wrażliwy na zmienność danych i szczególnie przy dużej rozcią głości nie-
wielkiej liczby wyników osią ga z natury wartości bardzo bliskie 1. Ponadto w przy-
padku wystą pienia efektu przekształcenia liniowego dwóch porównywanych cią gów,
współczynnik

r

przyjmuje wartość 1 nie odzwierciedlają c wartości współczynnika

przekształcenia.

3. Przykład zastosowania wspó łczynnika podobieństwa

a

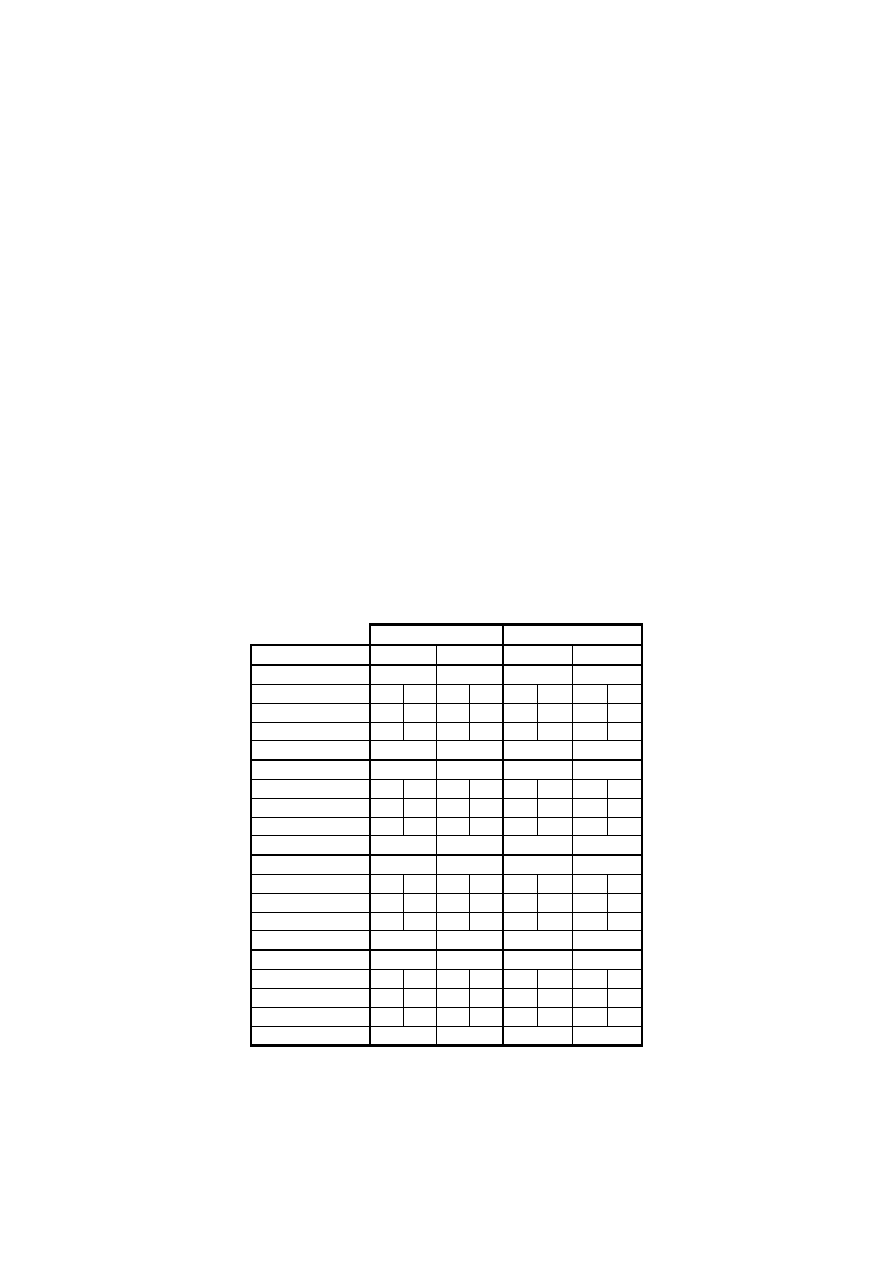
W tablicach 1 i 2 zestawiono wyniki odkształceń w

]

m

/

m

[

m

dla wszystkich tensometrów

we wskazanych na rys. 1 punktach pomiarowych. Dla każdej pary odpowiadają cych sobie
cią gów liczbowych wyliczono współczynnik podobień stwa

a

wpisują c go pod tym cią giem,

który stanowił podstawę normowania. Oznaczenia tensometrów są zgodne z rys. 2.

Tablica 1. Zestawienie odczytów tensometrycznych w

]

m

/

m

[

m

dla symetrycznych punktów

pomiarowych od obcią żenia na południowej (PD) stronie wiaduktu

Przekroje przę słowe Przekroje podporowe

Schemat obcią żeń

I

V

I

V

Punkt pomiarowy

5

21

29

41

b

-2

-1

-2

-2

6

6

2

2

g

14

0

12

1

3

2

0

3

d

141 56 145 54 -17 -33 -15 -15

a

0,9537

0,5224

Punkt pomiarowy

6

22

30

42

b

3

-4

2

2

12

4

5

2

g

22 10 17

2

4

4

0

0

d

125 208 144 216 -71 -60 -65 -57

a

0,8773

0,8323

Punkt pomiarowy

7

23

31

43

b

11

9

3

2

4

4

5

9

g

3

16 -19 21 -3

9

1

0

d

181 234 222 222 -72 -72 -82 -65

a

0,7907

0,7778

Punkt pomiarowy

8

24

32

44

b

4

6

2

5

4

4

8

14

g

8

23

8

15

4

3

2

3

d

130 223 149 233 -67 -64 -48 -45

a

0,9029

0,6301

188

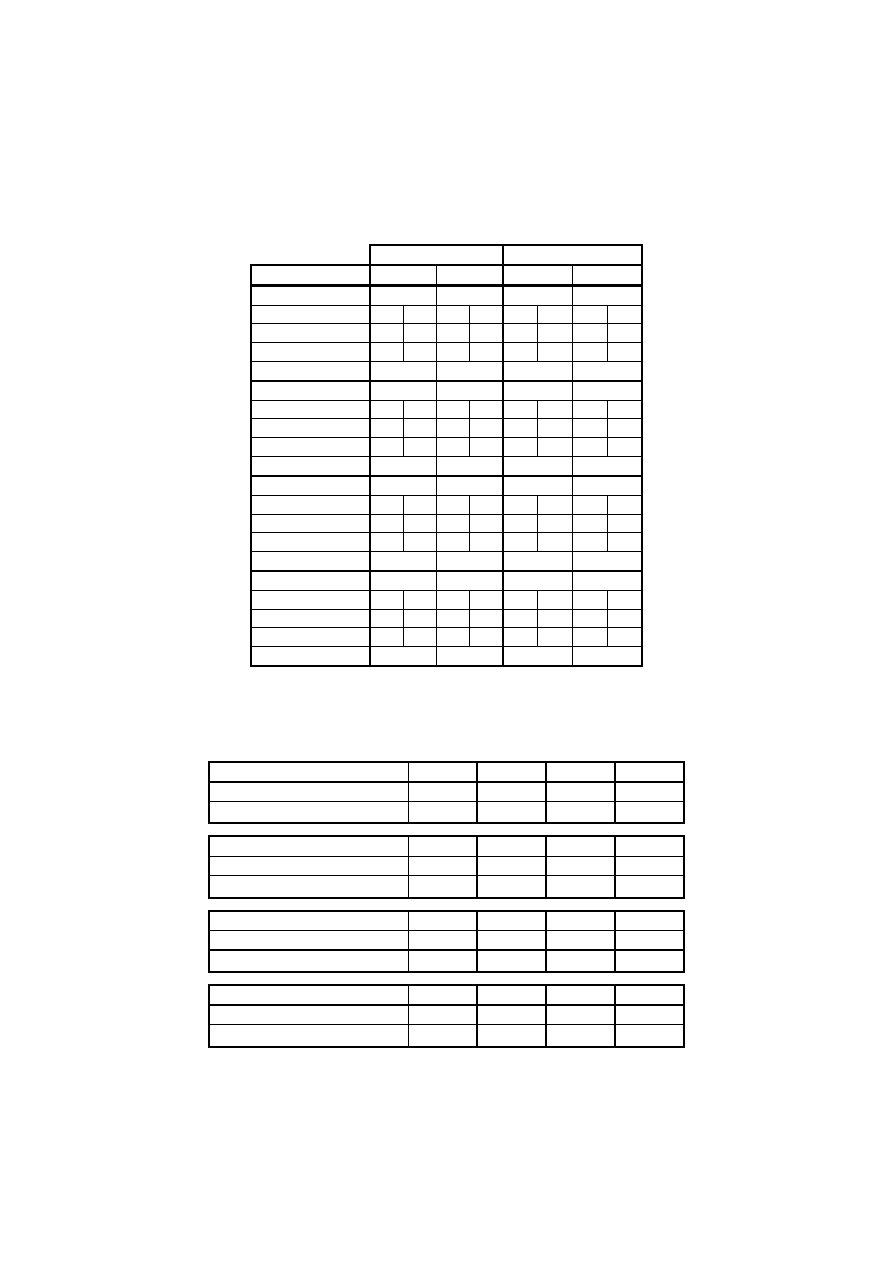
Tablica 2. Zestawienie odczytów tensometrycznych w

]

m

/

m

[

m

dla symetrycznych punktów

pomiarowych od obcią żenia na północnej (PN) stronie wiaduktu

Przekroje przę słowe Przekroje podporowe

Schemat obcią żeń

II

VI

II

VI

Punkt pomiarowy

5

21

29

41

b

-9

-9

2

2 -12 -1

7

2

g

29 -7 39

6

3

1

-1

1

d

196 101 206 112 -52 -52 -51 -50

a

0,8202

0,7603

Punkt pomiarowy

6

22

30

42

b

-18 -12 8

2

-7 -10

3

2

g

-10 -16 10 10 -14 -15

0

0

d

163 217 175 239 -93 -86 -83 -72

a

0,7297

0,6667

Punkt pomiarowy

7

23

31

43

b

-11 -4

-2

-6 -23

2

7

7

g

-10 -4 -15 25 -12 -14

0

0

d

145 166 175 175 -58 -58 -64 -50

a

0,7889

0,4141

Punkt pomiarowy

8

24

32

44

b

-1

3

2

0 -14 -14

3

4

g

3

3

3

6 -10 -3

2

2

d

65 137 90 165 -63 -24 -26 -9

a

0,7669

0,1875

Tablica 3. Zestawienie wartości współczynnika podobień stwa

a

i współczynnika korela-

cji

r

Porównywane zestawy danych PD-5/21 PD-8/24 PD-6/22 PD-30/42

a

0,9537

0,9029

0,8773

0,8323

r

0,999564 0,997836 0,996521 0,999116

Porównywane zestawy danych PN-5/21 PD-7/23 PN-7/23 PD-31/43

a

0,8202

0,7907

0,7889

0,7778

r

0,999936 0,984354 0,988438 0,983304

Porównywane zestawy danych PN-8/24 PN-29/41 PN-6/22 PN-30/42

a

0,7669

0,7603

0,7297

0,6667

r

0,997185 0,956676 0,998563 0,998623

Porównywane zestawy danych PD-32/44 PD-29/41 PN-31/43 PN-32/44

a

0,6301

0,5224

0,4141

0,1875

r

0,988888 0,937912 0,938525 0,960861

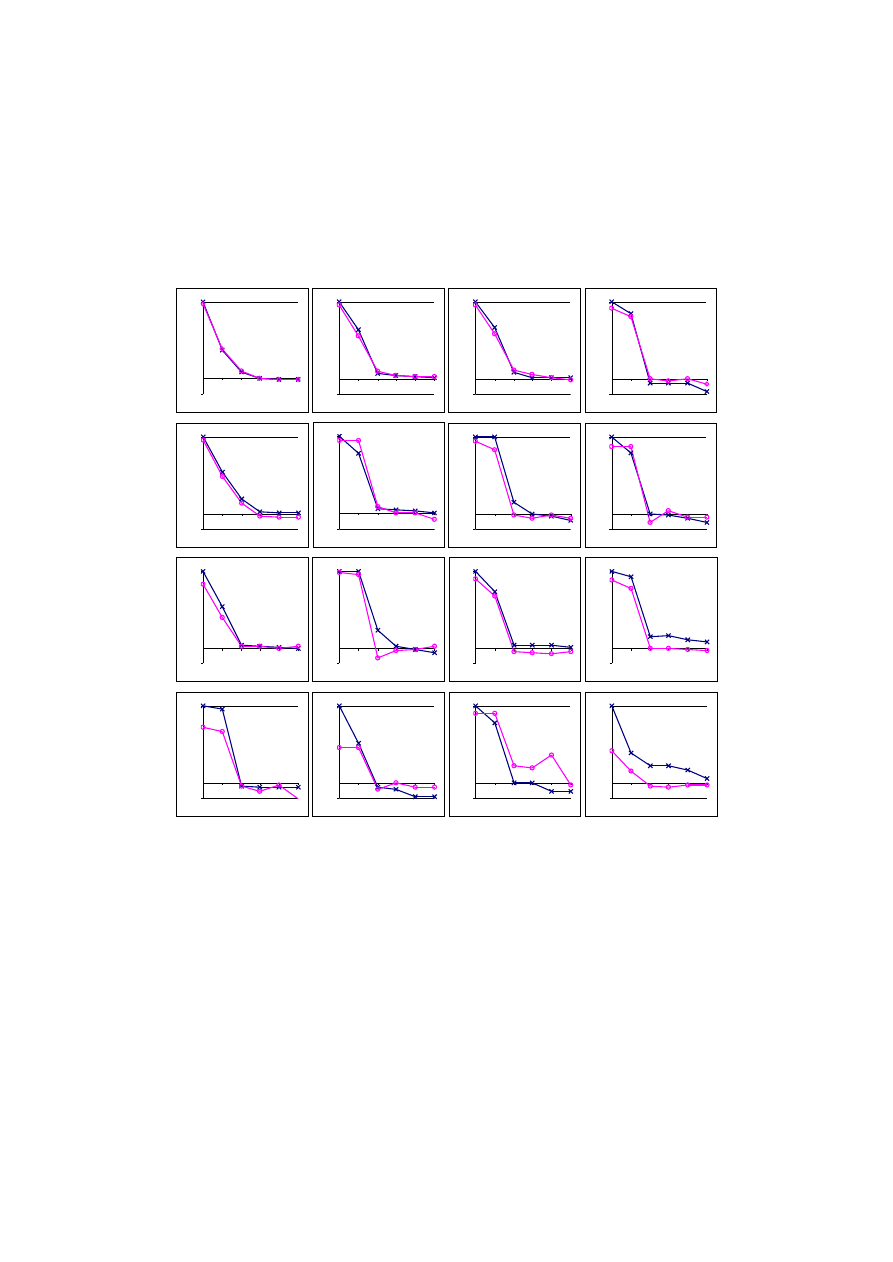
189

Ilustrację współczynnika

a

jako miary podobień stwa kształtu rozkładu mierzonych

wielkości przedstawiono na rys. 3. W tym celu dokonano zgodnie z opisaną procedurą
unormowania i uporzą dkowania w cią gi monotoniczne wyników pomiarów zestawionych
w tablicach 1 i 2.

PD-5/21

a

=0,9537

-0,2

1,0

1

2

3

4

5

6

PD-8/24

a

=0,9029

-0,2

1,0

1

2

3

4

5

6

PD-6/22

a

=0,8773

-0,2

1,0

1

2

3

4

5

6

PD-30/42

a

=0,8323

-0,2

1,0

1

2

3

4

5

6

PN-5/21

a

=0,8202

-0,2

1,0

1

2

3

4

5

6

PD-7/23

a

=0,7907

-0,2

1,0

1

2

3

4

5

6

PN-7/23

a

=0,7889

-0,2

1,0

1

2

3

4

5

6

PD-31/43

a

=0,7778

-0,2

1,0

1

2

3

4

5

6

PN-8/24

a

=0,7669

-0,2

1,0

1

2

3

4

5

6

PN-29/41

a

=0,7603

-0,2

1,0

1

2

3

4

5

6

PN-6/22

a

=0,7297

-0,2

1,0

1

2

3

4

5

6

PN-30/42

a

=0,6667

-0,2

1,0

1

2

3

4

5

6

PD-32/44

a

=0,6301

-0,2

1,0

1

2

3

4

5

6

PD-29/41

a

=0,5224

-0,2

1,0

1

2

3

4

5

6

PN-31/43

a

=0,4141

-0,2

1,0

1

2

3

4

5

6

PN-32/44

a

=0,1875

-0,2

1,0

1

2

3

4

5

6

Rys. 3. Ilustracja współczynnika podobień stwa

a

dokonana dla unormowanych

cią gów pomiarowych

Każdy wykres przedstawiony na rys. 3 ma przypisaną wartość współczynnika

a

, przy

czym kolejność wykresów ustalono wg maleją cej wartości

a

. Symbole PD i PN wskazują

na numer tablicy (odpowiednio 1 i 2), z której pochodzą dane wyjściowe, a liczby oznaczają
odpowiadają ce sobie symetryczne pary punktów pomiarowych.

W celu porównania miar uzyskiwanych za pomocą współczynnika podobień stwa

a

i współczynnika korelacji

r

dokonano ich zestawienia w tabl. 3. Porównywane zestawy da-

nych opisano stosują c konwencję oraz kolejność zastosowane na rys. 3. Kryterium porzą dku-
ją cym jest maleją ca wartość współczynnika

a

. Zwracają uwagę wysokie i mało zróżnico-

wane wartości współczynnika

r

.

190

4. Uwagi końcowe

Warunki techniczne, w jakich prowadzi się pomiary konstrukcji rzeczywistych mogą czę sto
w sposób istotny ograniczać wiarygodność otrzymanych wyników. Zazwyczaj minimalizację
skutków błę dów pomiarowych przeprowadza się na bazie obróbki statystycznej. Jeśli nie ma
podstaw do przeprowadzenia obróbki statystycznej, wówczas pojawia się problem uwiary-
godnienia otrzymanych wyników. Taką możliwość daje wykorzystanie symetrii wymiarów,
warunków brzegowych i obcią żenia. W pracy zaproponowano jednoparametrowy wskaźnik
pozwalają cy szacować podobień stwo wieloelementowych cią gów pomiarowych.

Zaproponowany współczynnik podobień stwa

a

jest ograniczony od góry przez 1 na-

tomiast ograniczenie od dołu wynika z przyję tej granicznej wielkości różnicy

*

gr

D

. Próby

prowadzone ze spełniają cym warunki unormowania [1, -1] współczynnikiem korelacji

r

uznano za nieudane, gdyż nie wystę powało wyraźne zróżnicowanie ewidentne różnią cych się
mię dzy sobą cią gów.

Współczynnik podobień stwa

a

pozwala na uproszczoną , ale za to szybką ocenę

podobień stwa porównywanych cią gów pomiarowych.

Na podstawie analizy otrzymanych wyników można przyjąć nastę pujące kryteria oceny:

8

0,

³

a

- dobre i bardzo dobre podobień stwo uwiarygodniają ce otrzymane wyniki,

8

0

6

0

,

,

<

£

a

- akceptowalne podobień stwo,

6

0,

<

a

- nieakceptowalny rozrzut wyników wymagają cy dodatkowych analiz.

Literatura

[1] SZYDŁ OWSKI H., Teoria pomiaró w. Warszawa, PWN, 1981
[2] PACZKOWSKA T., PACZKOWSKI W., Konstrukcje zespolone w nowej przeprawie

przez rzekę Regalicę w Szczecinie. Inżynieria i Budownictwo, nr 5/2001, s. 259-263.

[3] FURTAK K., Mosty zespolone. Warszawa–Kraków, WN PWN, 1999.

EVALUATION OF THE CREDIBILITY OF TEST

LOADING RESULTS OF A COMPOSITE BRIDGE

Summary

Test loading performed on a composite bridge gave series of results concerning strains dis-
tribution at different sections. A question of the credibility of the results arises. A proposal of
a similarity coefficient

a

is given. The value of the coefficient for corresponding symmetric

cross-sections is calculated and combined with the plots presenting distribution of strains.
A proposal of the credibility evaluation of the results based on the similarity coefficient
is given.