Lecture 9: Robust Design

Spanos

EE290H F05

1

Robust Design

A New Definition of Quality.
The Signal-to-Noise Ratio.
Orthogonal Arrays.

Lecture 9: Robust Design

Spanos

EE290H F05

2

The Taguchi Philosophy

Quality is related to the total loss to society due to
functional and environmental variance of a given product

Quality is related to the total loss to society due to
functional and environmental variance of a given product

Taguchi's method focuses on Robust Design through use of:

• S/N Ratio to quantify quality

• Orthogonal Arrays to investigate quality

Taguchi starts with a new definition of Quality:

Lecture 9: Robust Design

Spanos

EE290H F05

3

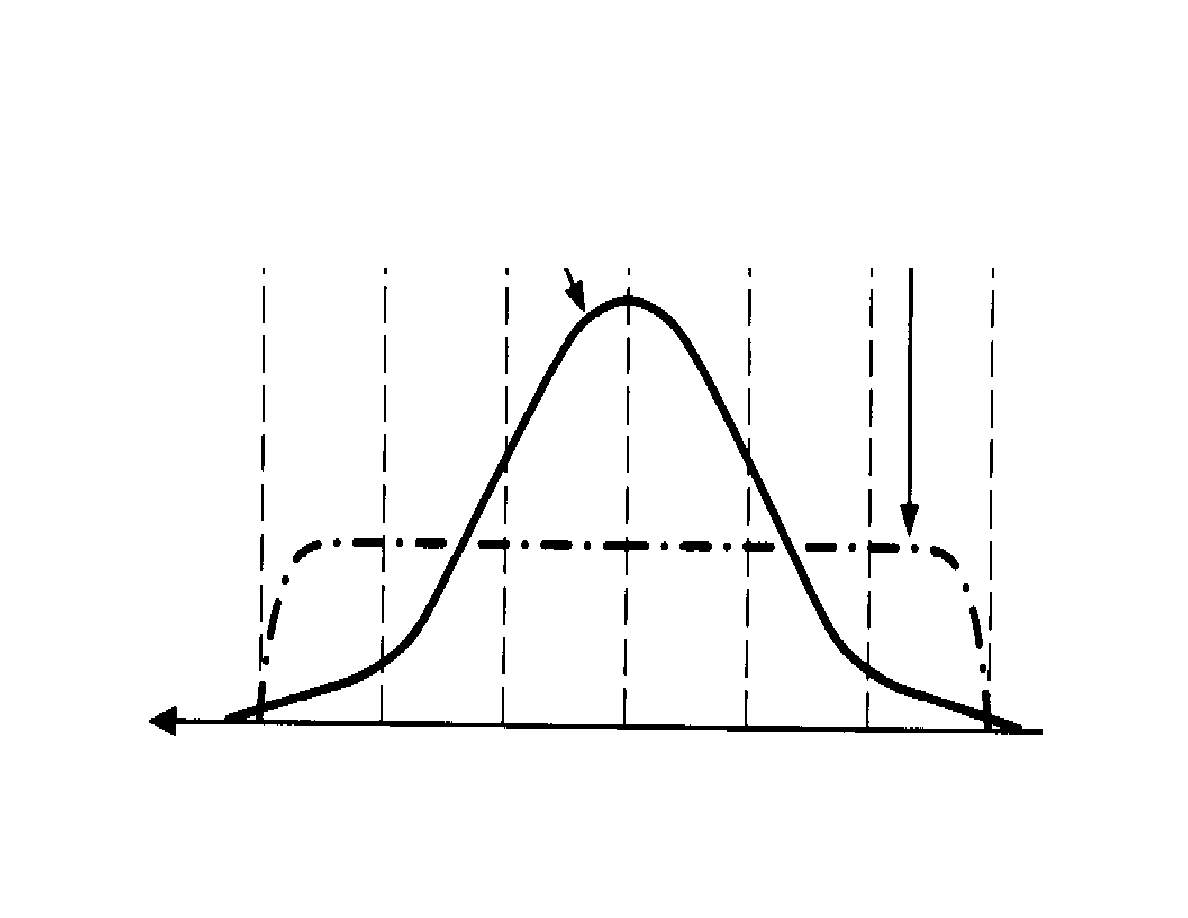
Meeting the specs vs. hitting the target

better quality

worse quality

m

m-5

m+5

Lecture 9: Robust Design

Spanos

EE290H F05

4

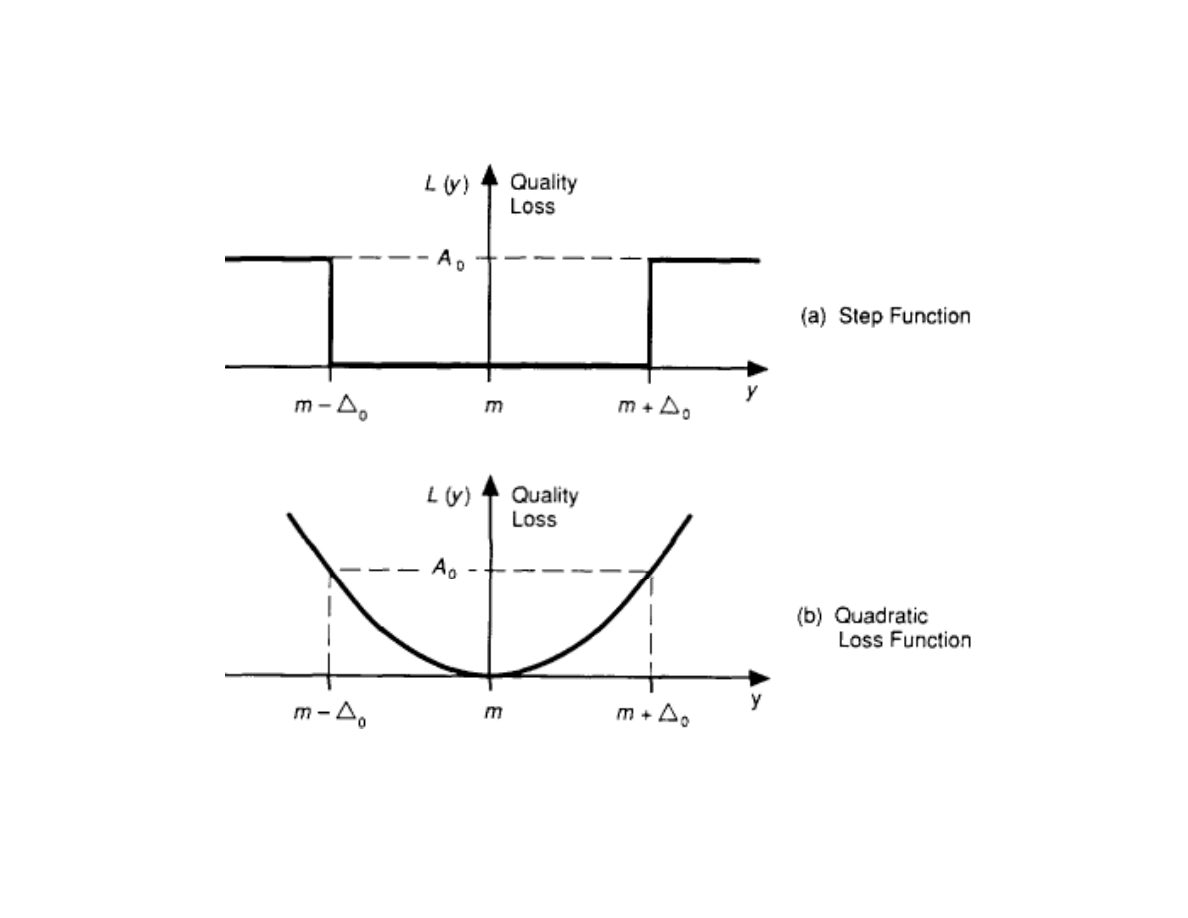
Quadratic Loss Function:

L(y) = k (y - m)

2

Fig 2.3 pp 18 from

Quality Engineering Using Robust Design

by Madhav S. Phadke

Prentice Hall 1989

Lecture 9: Robust Design

Spanos

EE290H F05

5

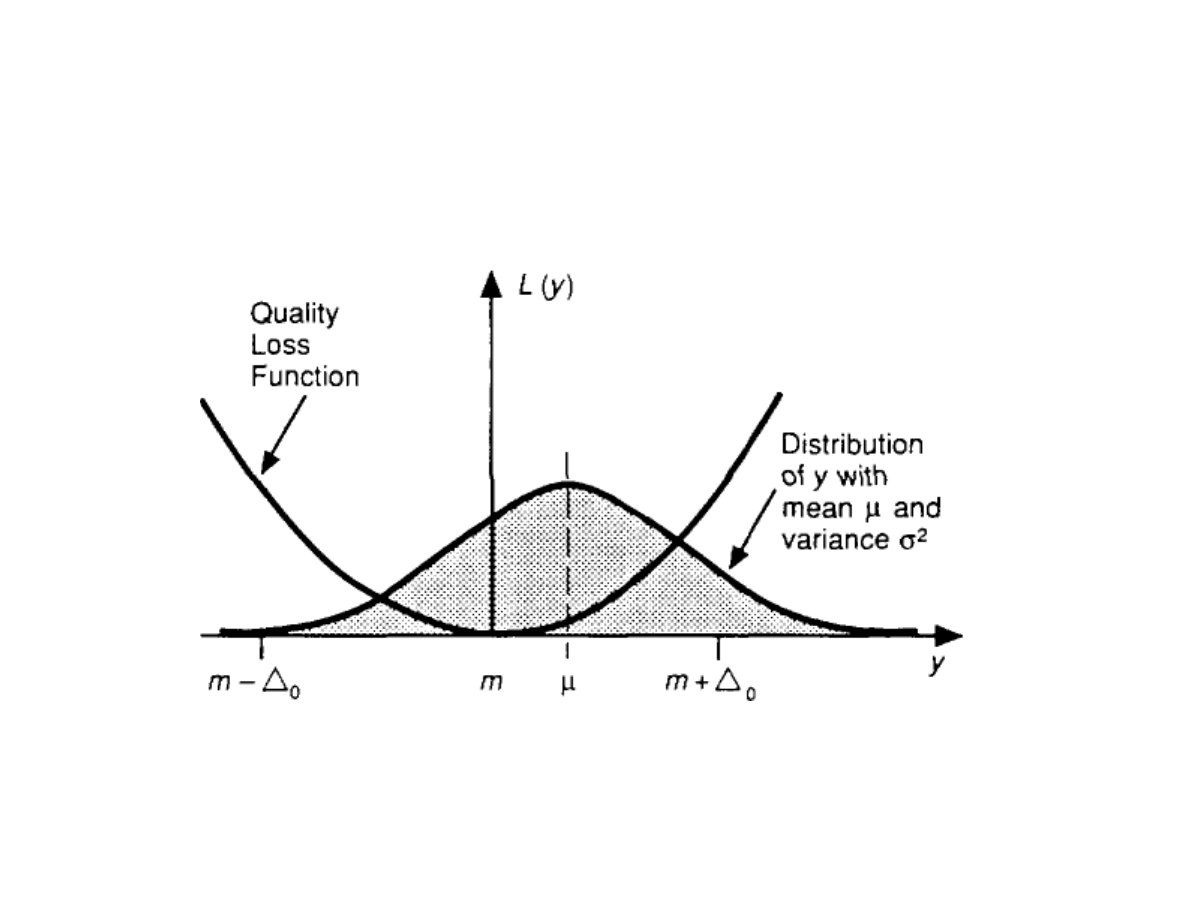
Quadratic Loss Function on Normal Distribution

Average quality loss due to µ and

σ:

Fig 2.5 pp 26

E(Q) = k [(µ-m) +

σ ]

2

2

Lecture 9: Robust Design

Spanos

EE290H F05

6

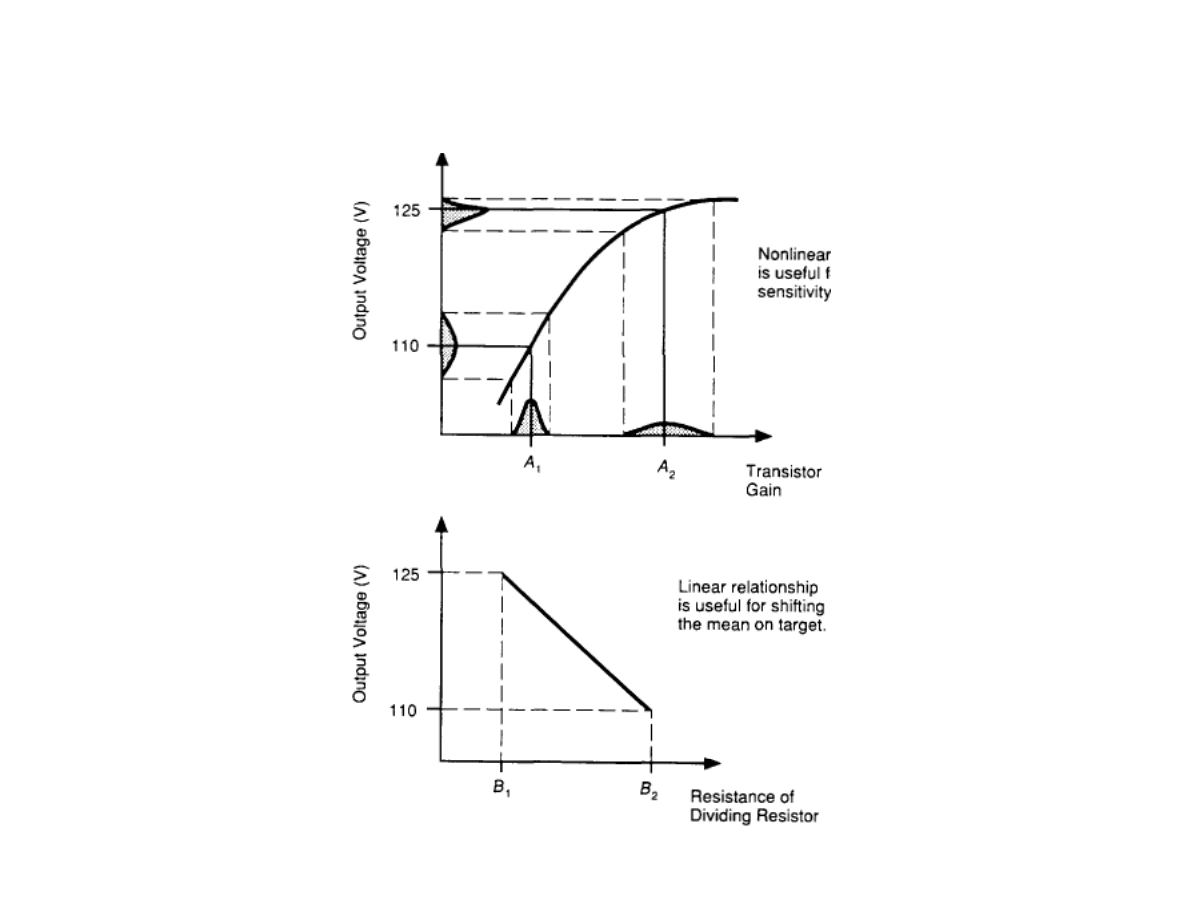
Exploiting non-linearity:

Fig 2.6 pp 28

Lecture 9: Robust Design

Spanos

EE290H F05

7

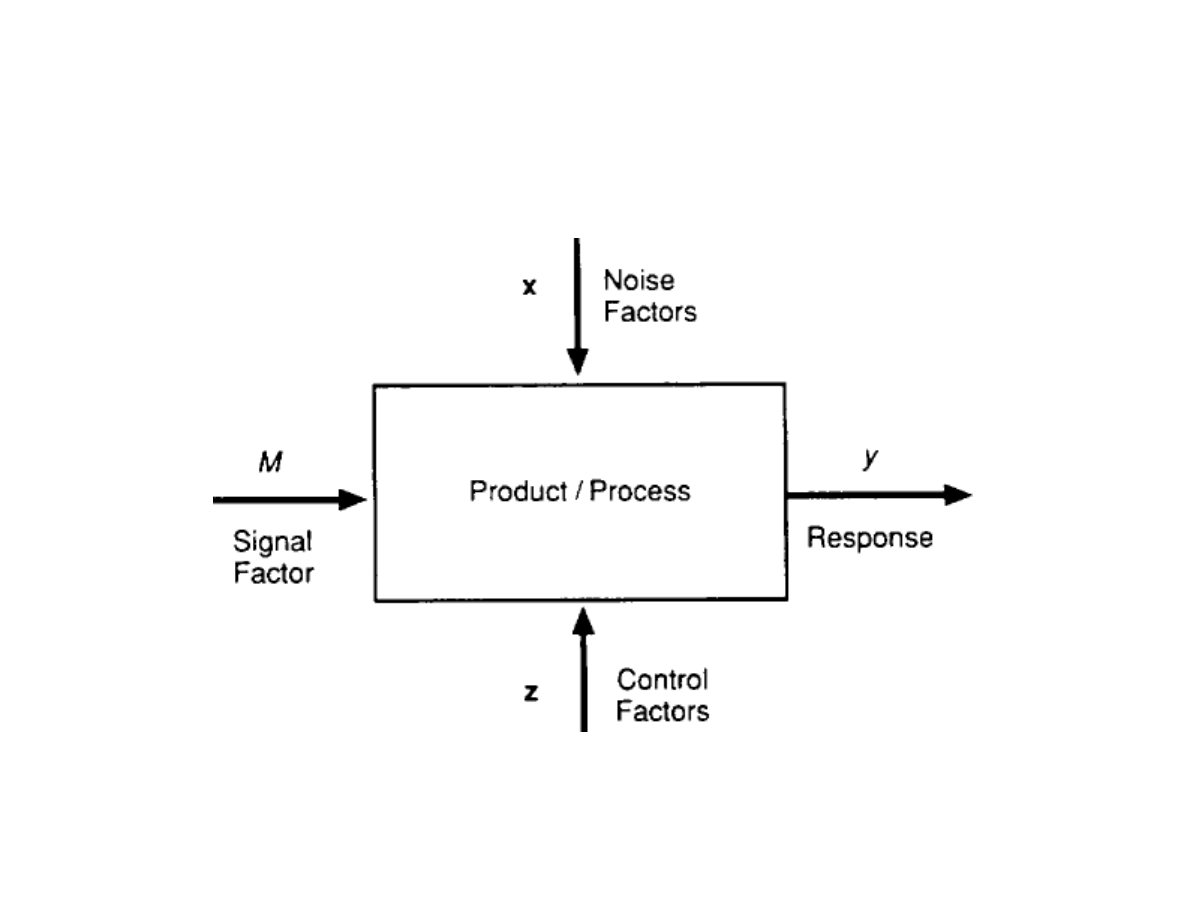
Parameters are classified according to function:

Fig 2.7 pp 30

Lecture 9: Robust Design

Spanos

EE290H F05

8

Orthogonal Arrays

b = (X

T

X)

-1

X

T

y

V(b) = (X

T

X)

-1

σ

2

During Regression Analysis, an orthogonal arrangement of
the experiment gave us independent model parameter
estimates:

Orthogonal arrays have the same objective:

For every two columns all possible factor combinations
occur equal times.

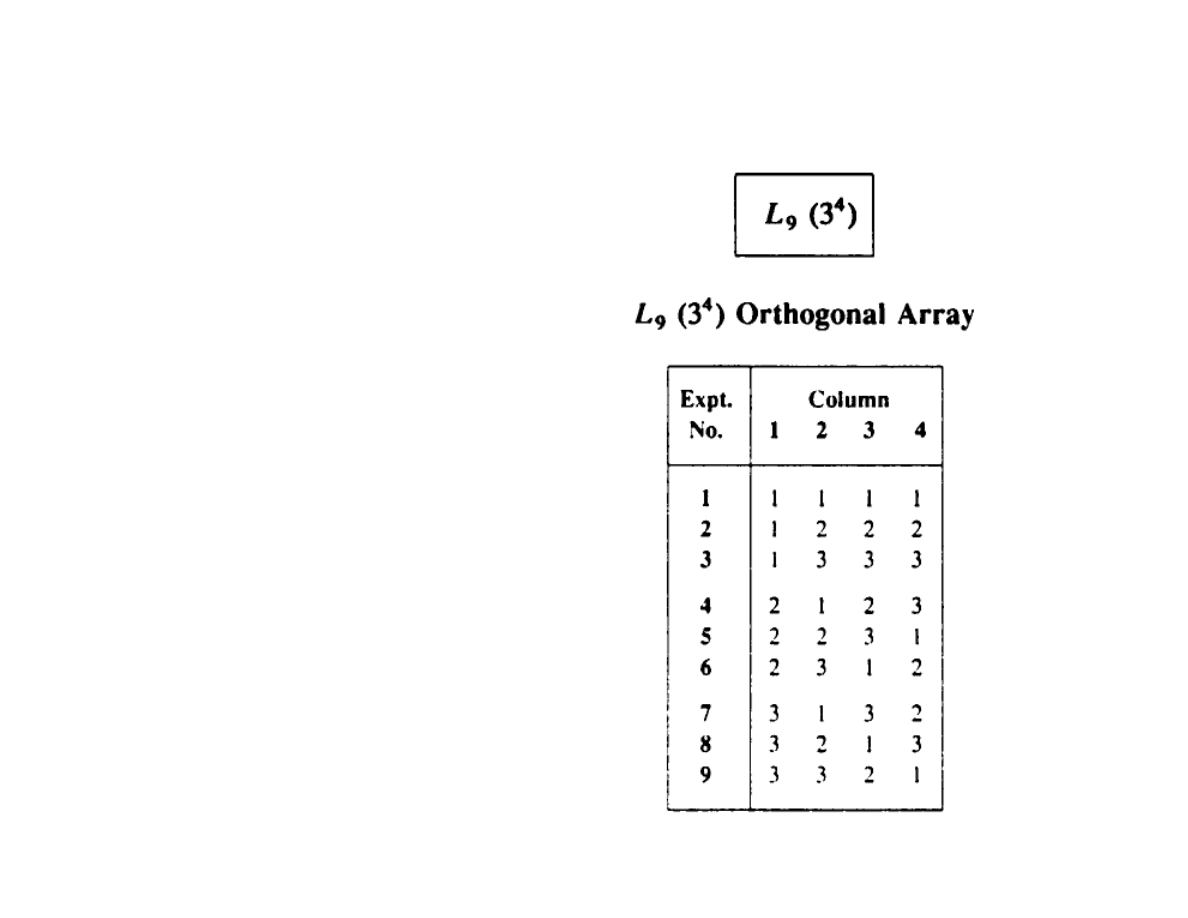
L

4

(2

3

) L

9

(3

4

) L

12

(2

11

) L

18

(2

1

x 3

7

)

Lecture 9: Robust Design

Spanos

EE290H F05

9

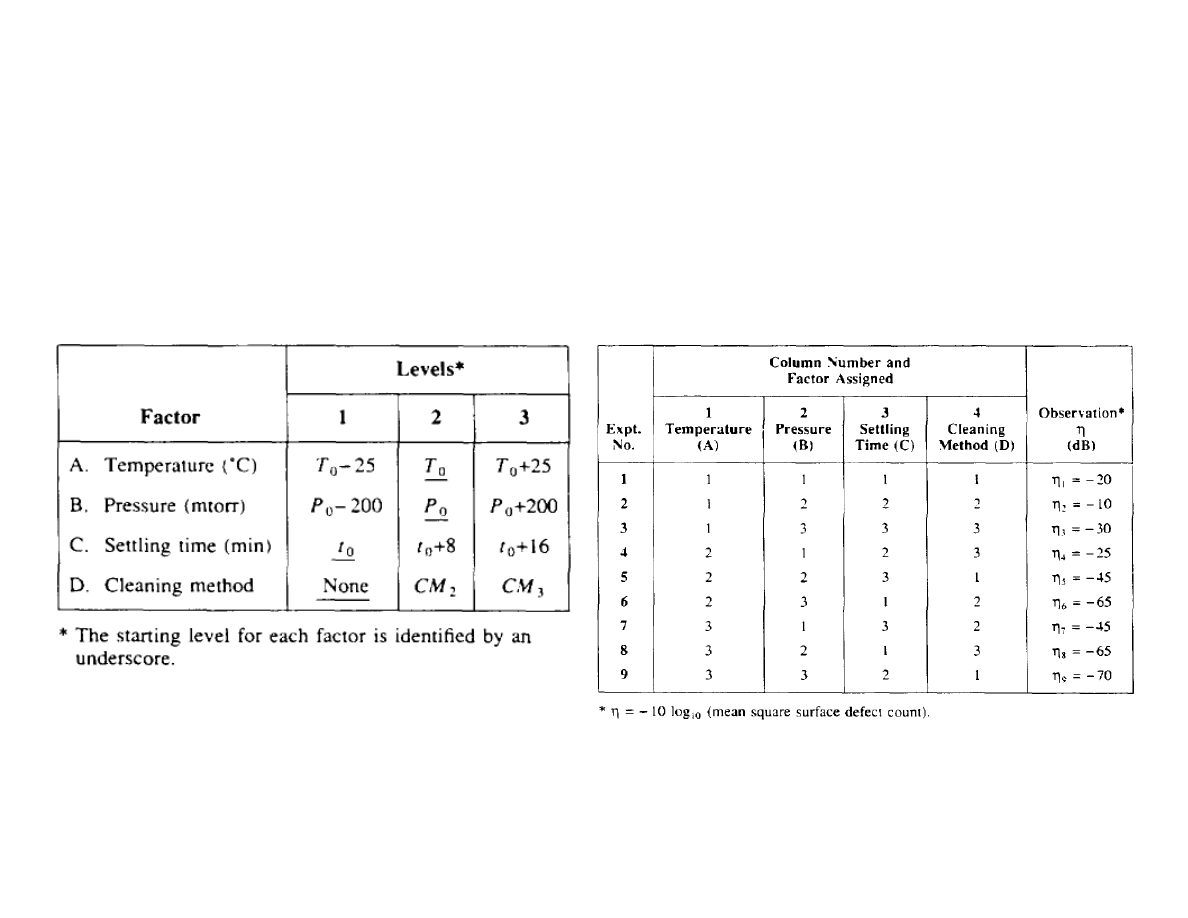
Simple CVD experiment for defect reduction

max n = -10 log (MSQ def)

10

Lecture 9: Robust Design

Spanos

EE290H F05

10

Simple CVD experiment for defect reduction (cont)

Using the L

9

orthogonal array:

Lecture 9: Robust Design

Spanos

EE290H F05

11

Estimation of Factor Effects (ANOM)

m = 1

9

η

1

+

η

2

+

η

3

+...+

η

9

m

A

1

= 1

3

η

1

+

η

2

+

η

3

m

A

2

= 1

3

η

4

+

η

5

+

η

6

m

A

3

= 1

3

η

7

+

η

8

+

η

9

...

m

B

2

= 1

3

η

2

+

η

5

+

η

8

...

m

D

3

= 1

3

η

3

+

η

4

+

η

8

η A

i

,B

j

,C

k

,D

l

= μ+α

i

+β

j

+γ

k

+δ

l

+e

α

i

= 0

Σ

β

i

= 0

Σ

γ

i

= 0

Σ

δ

i

= 0

Σ

Lecture 9: Robust Design

Spanos

EE290H F05

12

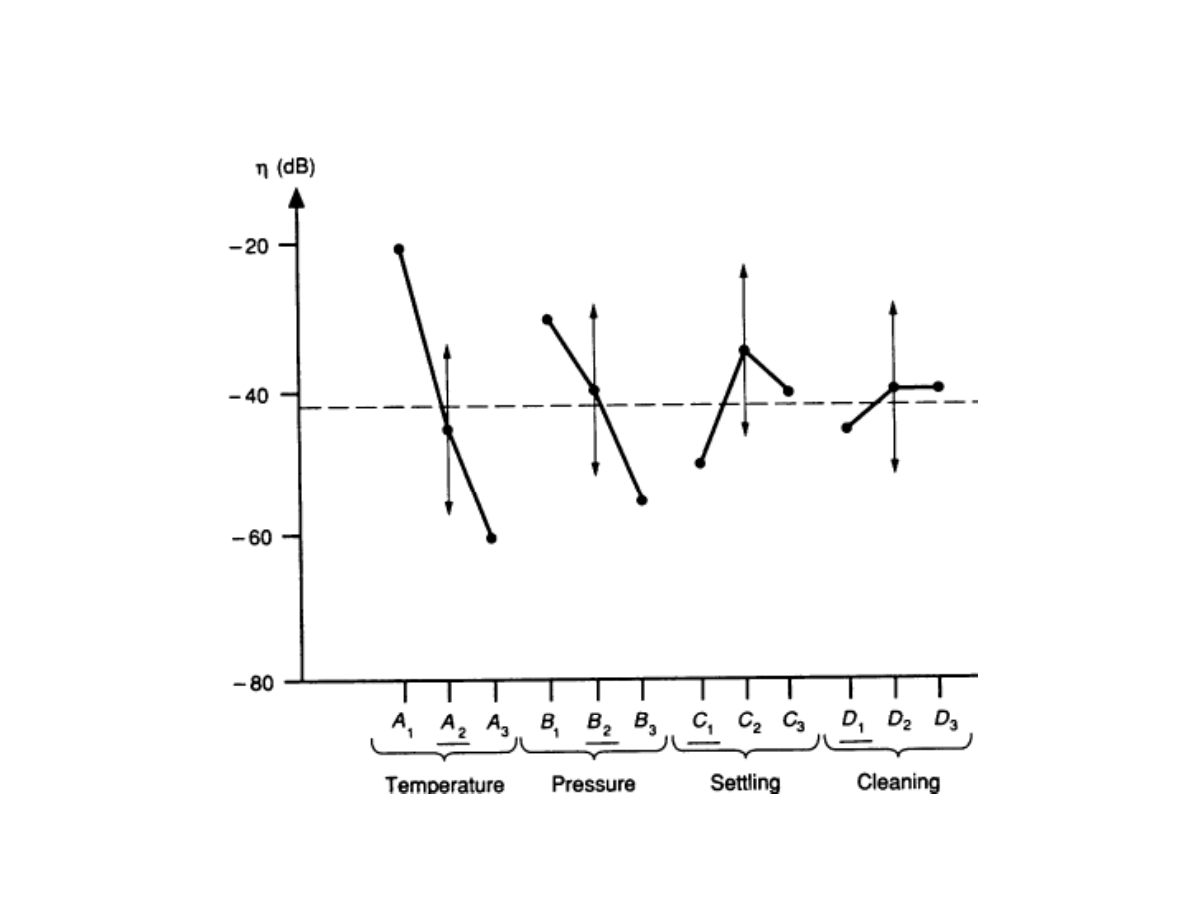
Analysis of CVD defect reduction experiment

Fig 3.1 pp 46
Tab 3.4 pp 55

Lecture 9: Robust Design

Spanos

EE290H F05

13

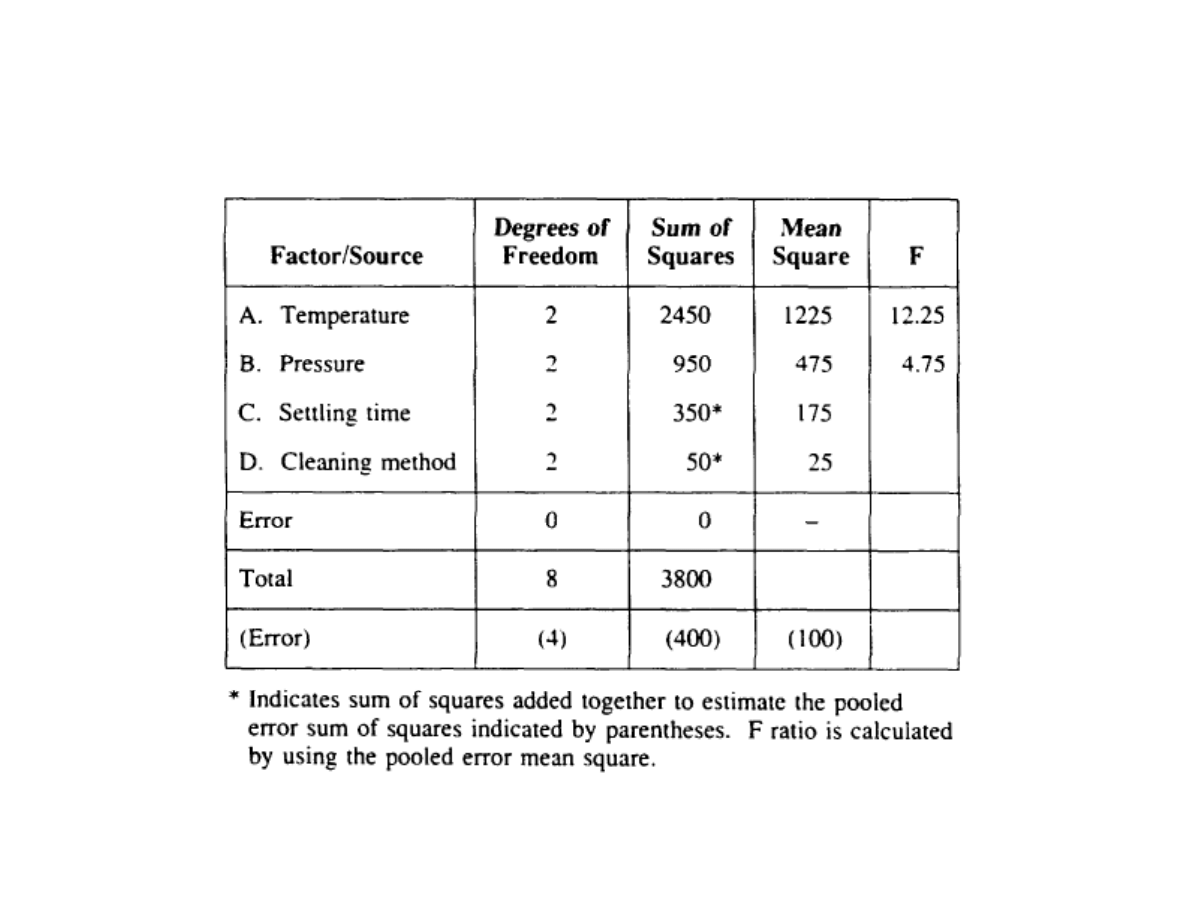
ANOVA for CVD defect reduction experiment

Grand total sum of squares:

η

i

2

= 19,425 (dB)

2

Σ

i=1

9

Total sum of squares:

η

i

-m

2

= 3,800 (dB)

2

Σ

i=1

9

Sum of squares due to mean:

m

2

= 15,625 (dB)

2

Σ

i=1

9

Sum of squares due to error:

e

i

2

= ??? (dB)

2

Σ

i=1

9

Sum of squares due to A: 3

m

A

i

-m

2

= 2,450 (dB)

2

Σ

i=1

3

Lecture 9: Robust Design

Spanos

EE290H F05

14

ANOVA for CVD defect reduction experiment (cont)

Lecture 9: Robust Design

Spanos

EE290H F05

15

Estimation of Error Variance

The experimental error is estimated from the ANOVA
residuals.

It is then used to estimate the error of the effects and to
determine their significance at the 5% level.

Lecture 9: Robust Design

Spanos

EE290H F05

16

Confirmation Experiment

Once the optimum choice has been made, it is tested by
performing a confirmation run.

This run is used to "validate" the model as well as confirm
the improvements in the process.

Variance of prediction (for the model)

σ

pred

2

=

σ

e

2

n

0

+

σ

e

2

n

r

This gives us +/-2

σ limits on the confirmation experiment.

1

n

0

σ

e

2

= 1

n +

1

n

A

1

- 1

n +

1

n

B

1

- 1

n σ

e

2

Lecture 9: Robust Design

Spanos

EE290H F05

17

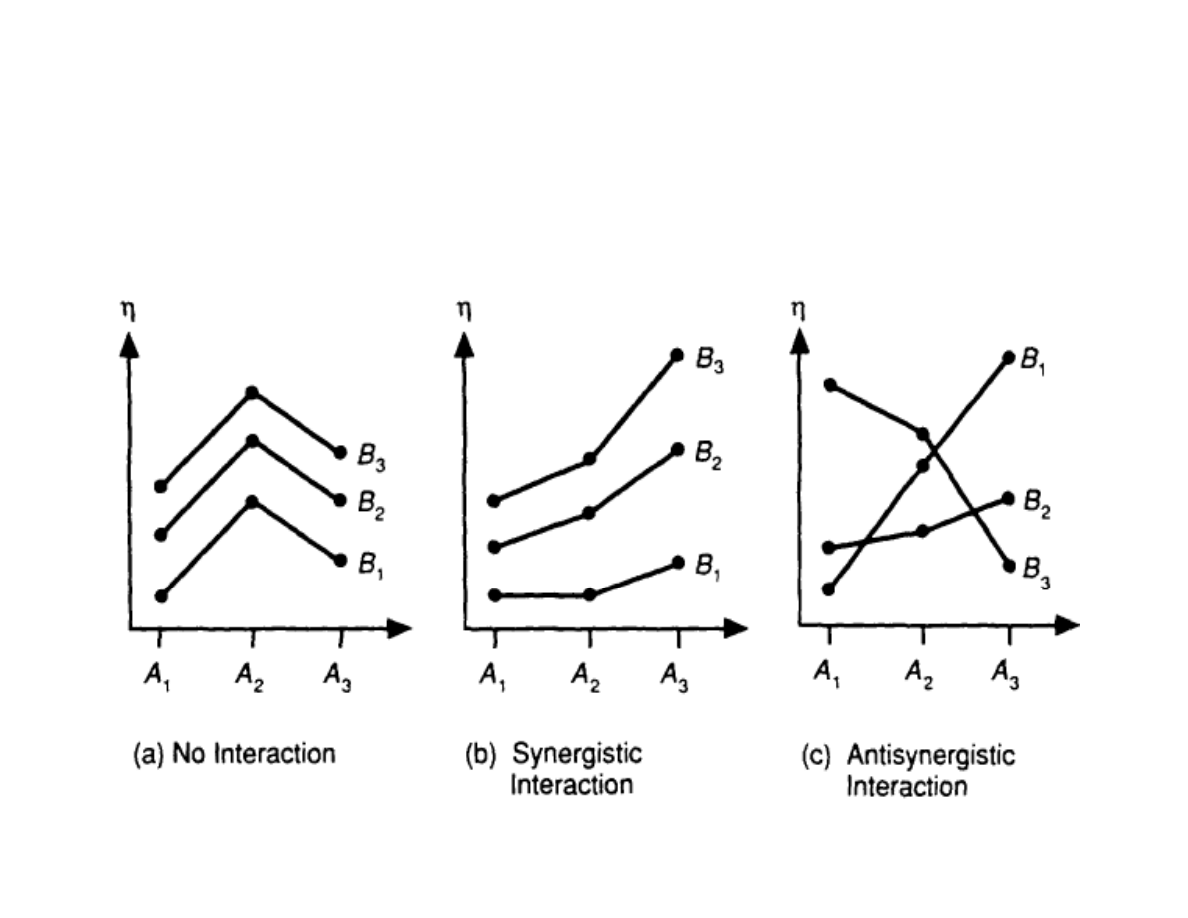
The additive model

Fig 3.3 pp 63, enlarged 120%

Since we assumed additive model, we must make sure
that there are no interactions:

Lecture 9: Robust Design

Spanos

EE290H F05

18

Example: Large CVD experiment.

Objectives:

a) reduce defects n = -10 log (MSQ Def)

b) maximize S/N of rate n'= 10 log (µ /

σ )

c) adjust poly thickness to a 3600 Å target.

10

10

2

2

Lecture 9: Robust Design

Spanos

EE290H F05

19

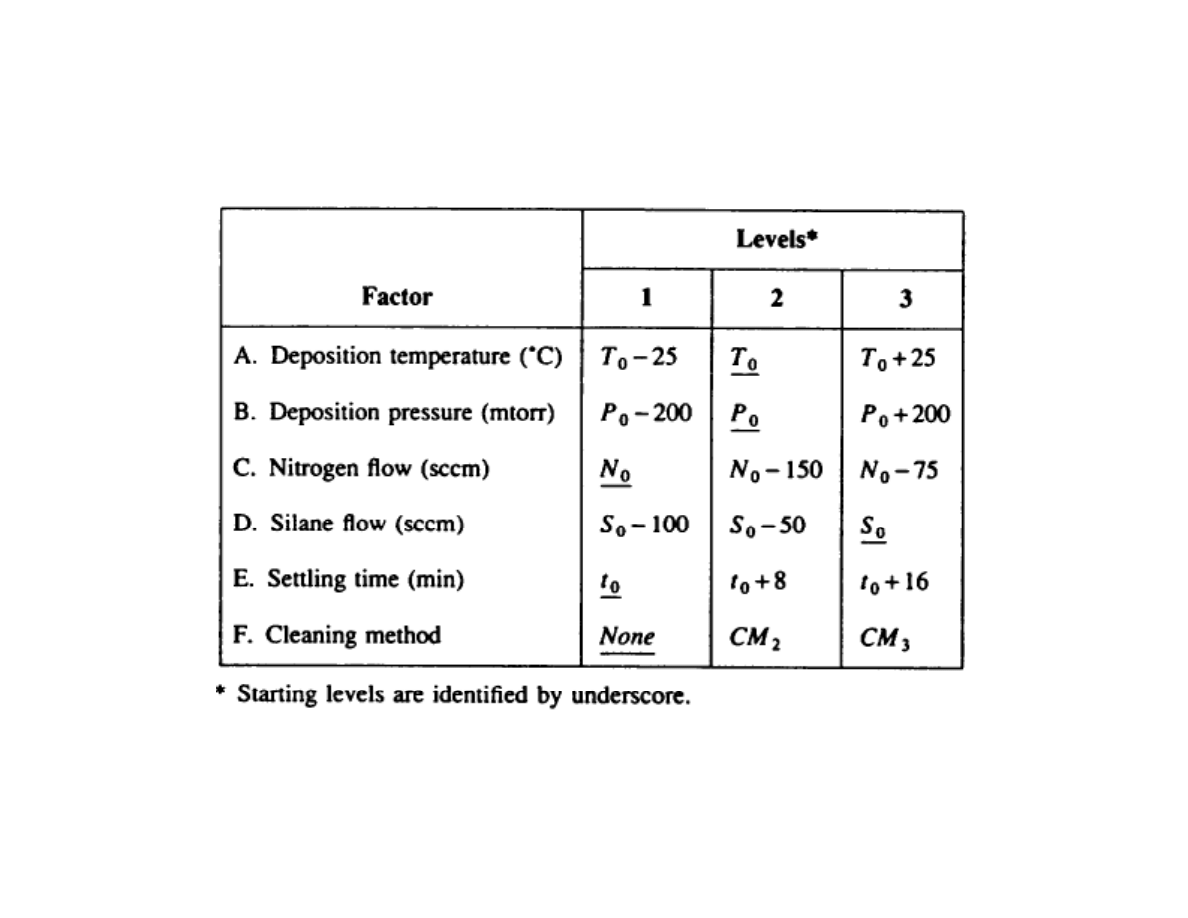
Choosing the Control Factors

Tab 4.6-7 pp 88-90

Lecture 9: Robust Design

Spanos

EE290H F05

20

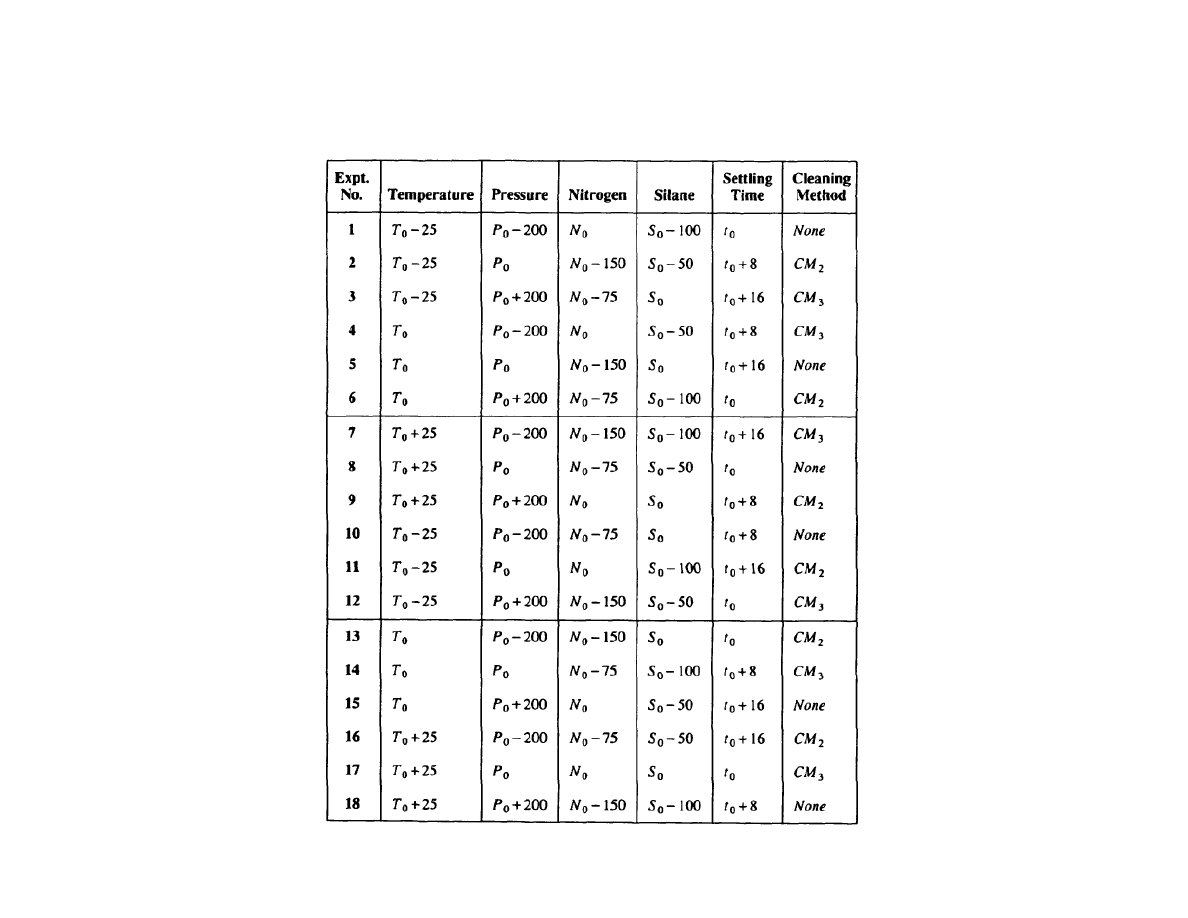
Using the L

18

orthogonal array...

Tab 4.3 pp 78, enlarged 120%

Lecture 9: Robust Design

Spanos

EE290H F05

21

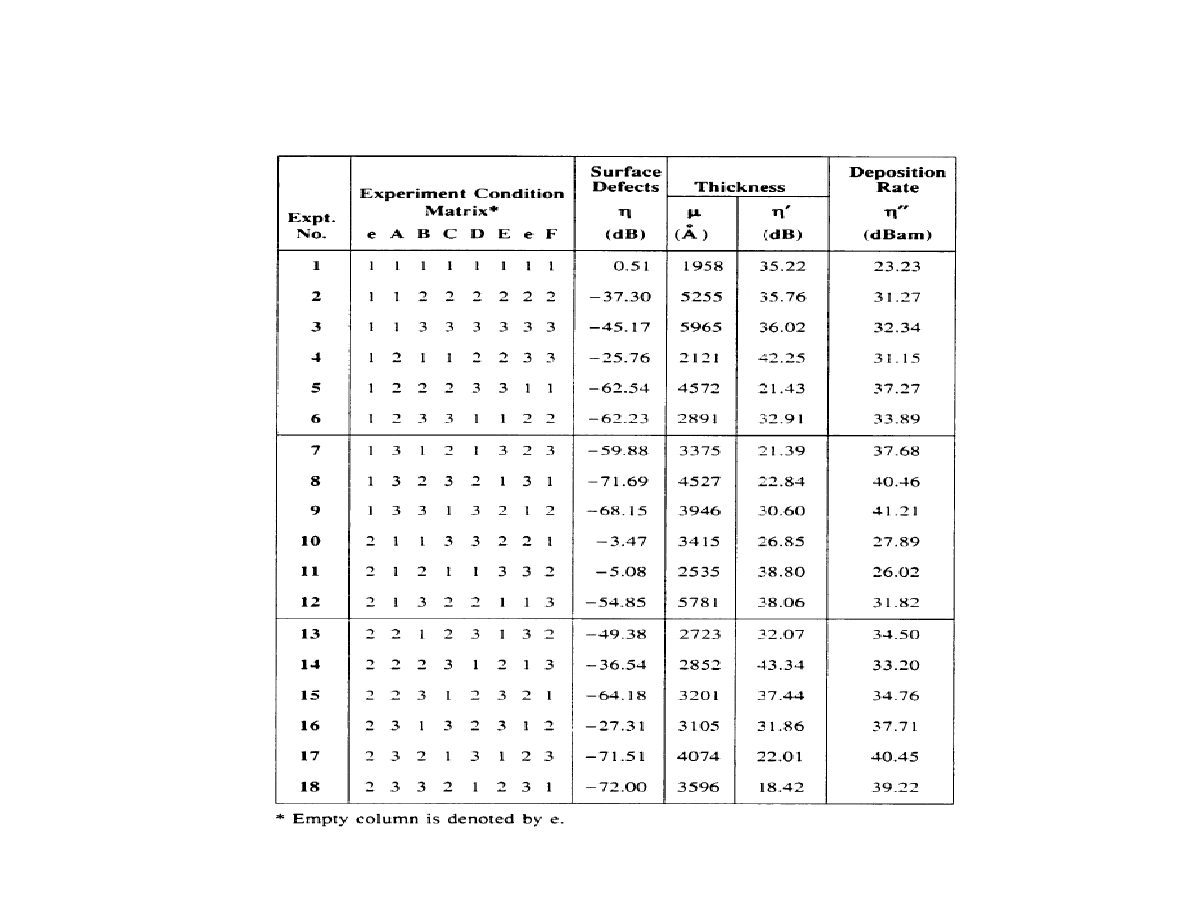
Data summary for large CVD experiment:

Tab 4.5 pp 85, enlarged 120%

Lecture 9: Robust Design

Spanos

EE290H F05

22

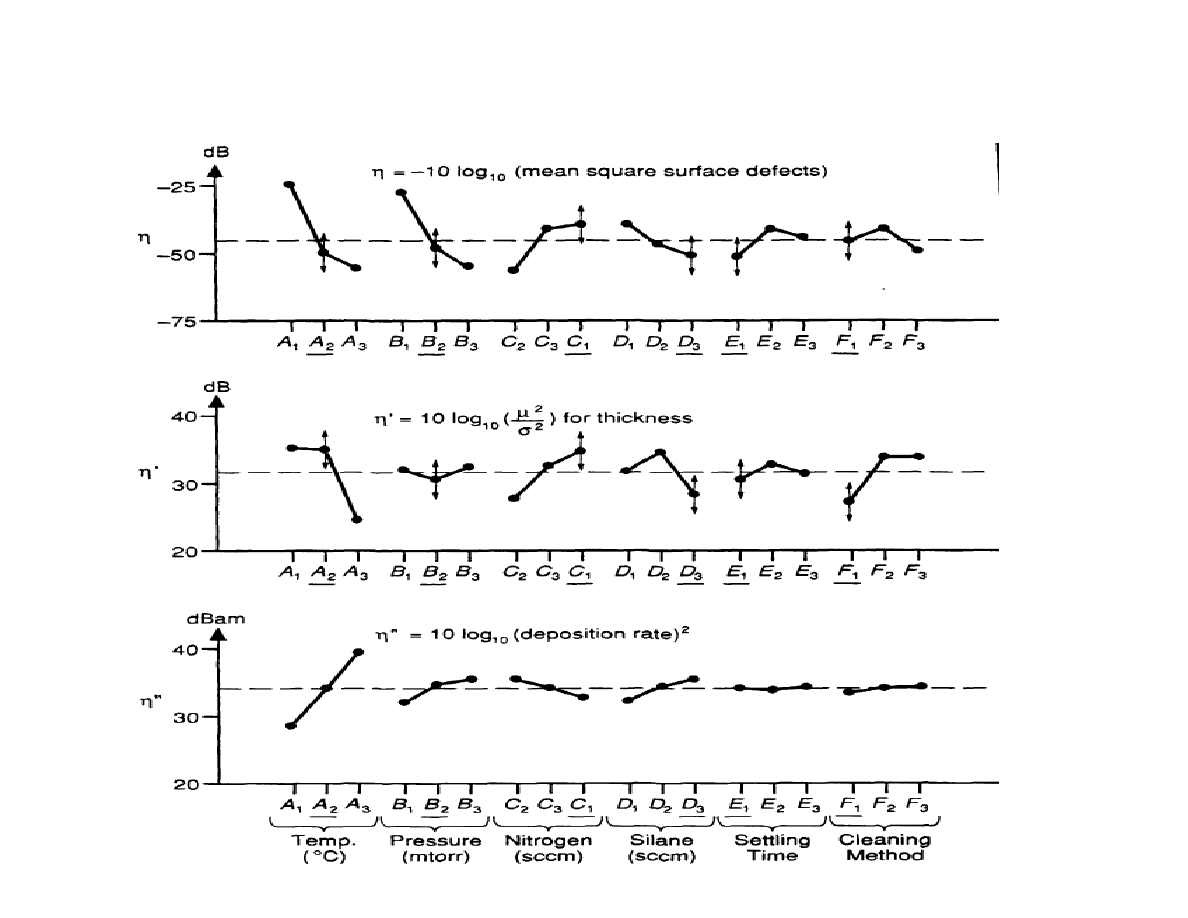
Data analysis for large CVD experiment (cont)

Fig 4.5 pp 86, enlarged 120%

Lecture 9: Robust Design

Spanos

EE290H F05

23

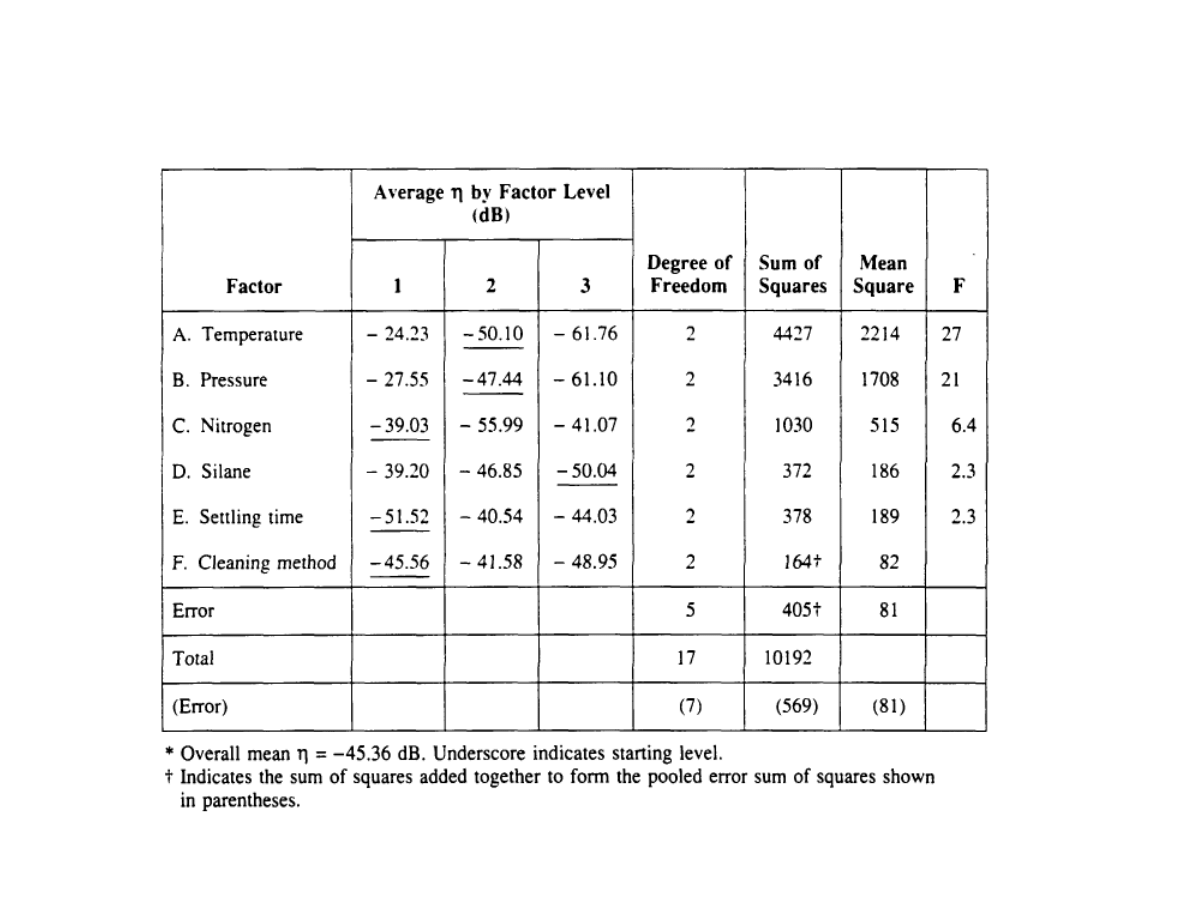
ANOVA table for large CVD experiment:

η

Lecture 9: Robust Design

Spanos

EE290H F05

24

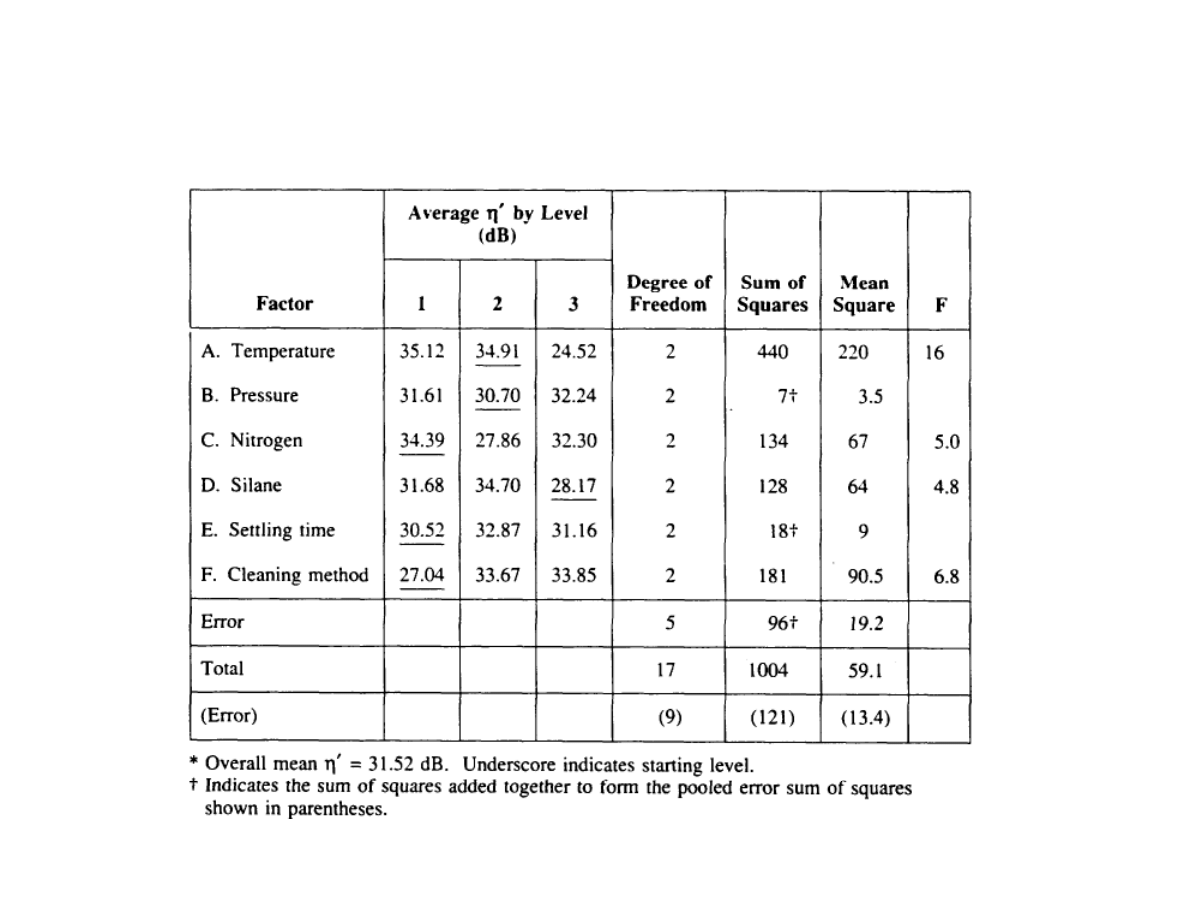
ANOVA table for large CVD experiment :

η’

Lecture 9: Robust Design

Spanos

EE290H F05

25

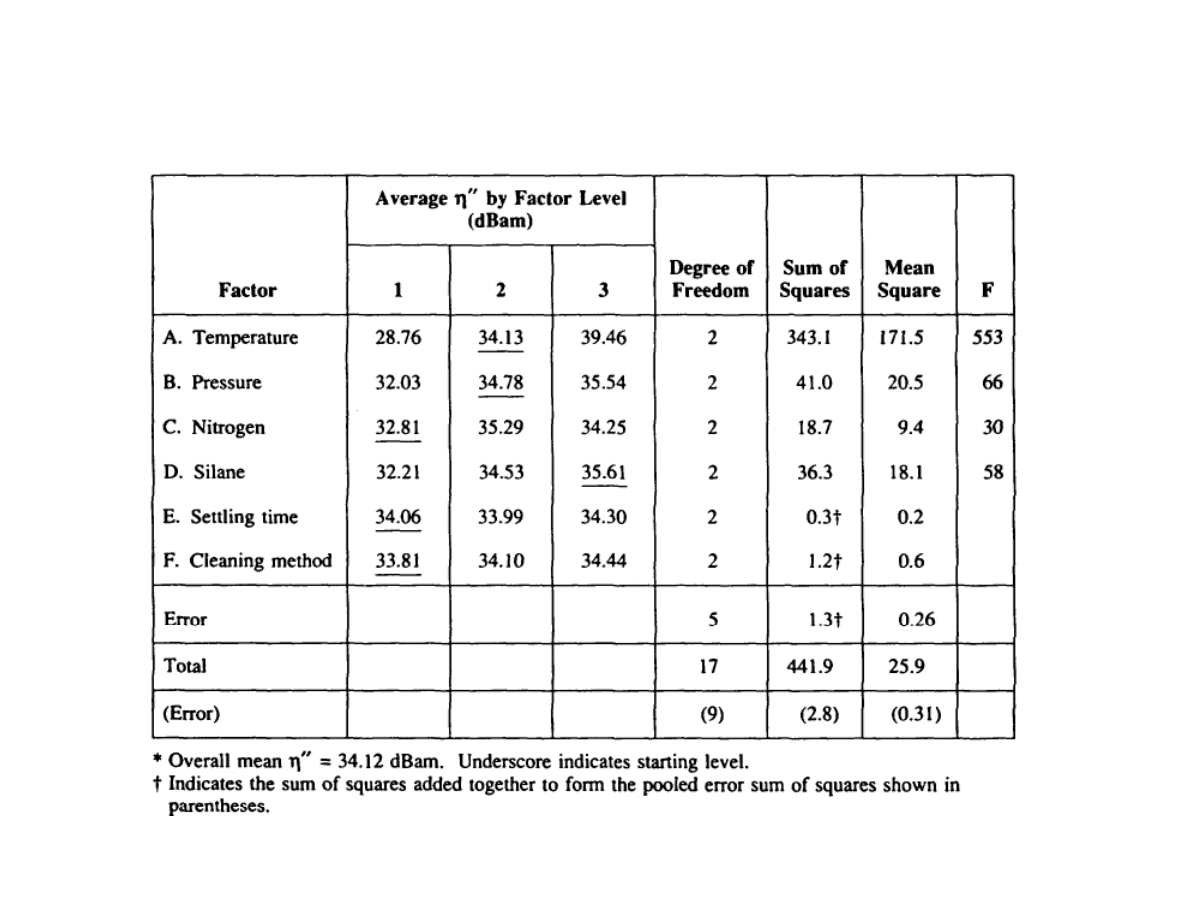
ANOVA tables for large CVD experiment:

η’’

Lecture 9: Robust Design

Spanos

EE290H F05

26

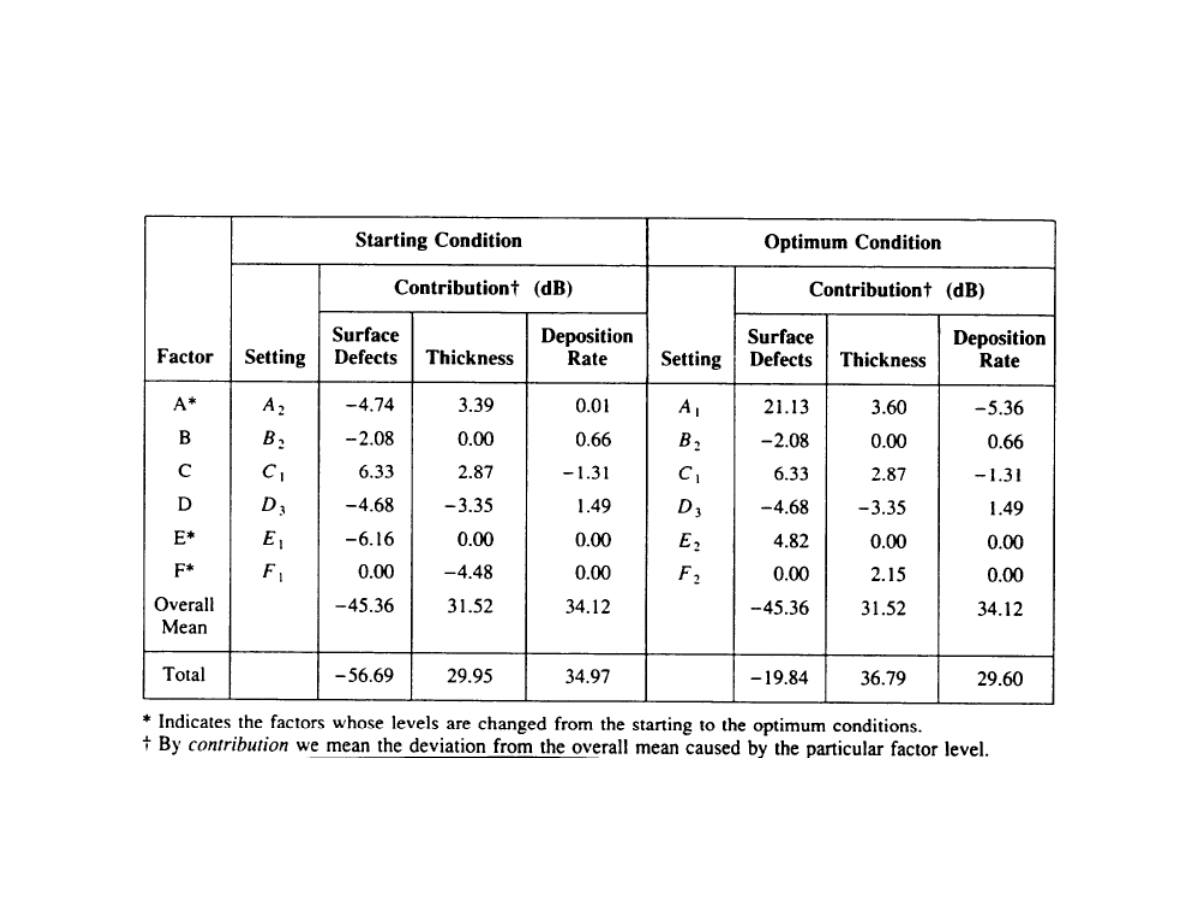
Combined Prediction Using the Additive Model

Tab 4.6-7 pp 88-90

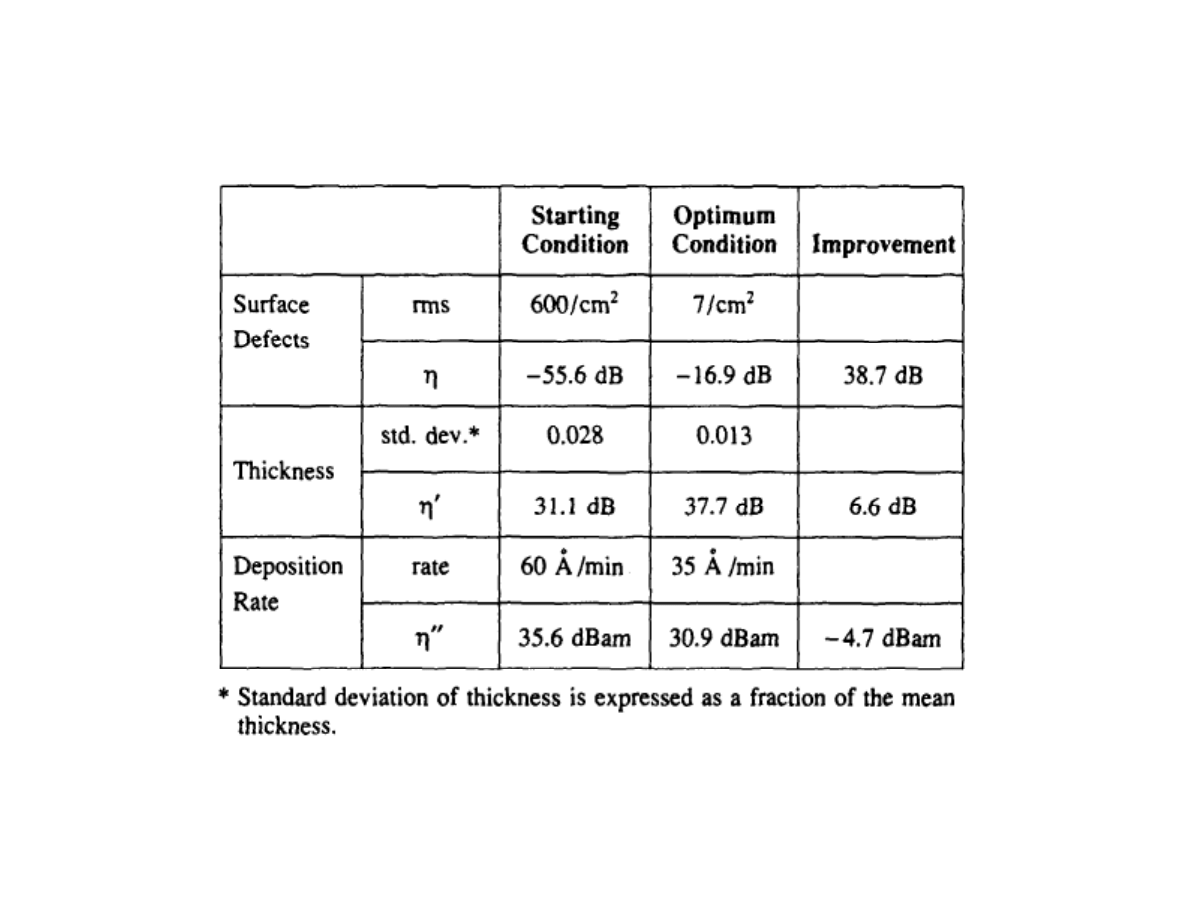
Lecture 9: Robust Design

Spanos

EE290H F05

27

Verification for large CVD experiment

Tab 4.10-11 pp 92

for further reading: Quality Engineering Using Robust Design by Madhav S. Phadke

Prentice Hall 1989

Lecture 9: Robust Design

Spanos

EE290H F05

28

“Inner” and “Outer” Arrays

•

Often one want to improve performance based on some “control”
factors, in the presence of some “noise” factors.

•

Two arrays are involved: the inner array explores the “control”
factors, and the entire experiment is repeated across an array of the
noise factors.

•

Inner arrays are typically orthogonal designs

•

Outer arrays are typically small, 2-level fractional factorial designs.

Lecture 9: Robust Design

Spanos

EE290H F05

29

Why use S/N Ratios?

• They lead to an optimum through a monotonic function.

• They help improve additivity of the effects.

⎟

⎠

⎞

⎜

⎝

⎛

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

∑

∑

i

i

STB

i

i

LTB

Y

n

N

S

Y

n

N

S

s

Y

N

S

2

2

2

2

1

log

10

1

1

log

10

log

10

Nominal is best:

Larger is better:

Smaller is better:

Lecture 9: Robust Design

Spanos

EE290H F05

30

Taguchi vs. RSM

Taguchi

RSM

Small number of runs

Explicit control of Interactions

Engineering Intuition

Statistical Intuition

“Complete” package

Training Issues

Additive Models

More General Models

Orthogonal Arrays

Fractional Factorials

A “Philosophy”

A Tool

Lecture 9: Robust Design

Spanos

EE290H F05

31

Design of Experiments

Comparison of Treatments
Blocking and Randomization
Reference Distributions
ANOVA
MANOVA
Factorial Designs
Two Level Factorials
Blocking
Fractional Factorials
Regression Analysis
Robust Design

Analysis

Modeling