1
IDENTYFIKACJA W OPARCIU O POMIAR CHARAKTERYSTYK W DZIEDZINIE
CZASU LUB CZĘSTOTLIWOŚCI
Znaczna grupa metod identyfikacji opiera się na wyznaczeniu charakterystyk
identyfikowanych obiektów w dziedzinie czasu lub częstotliwości. Wykorzystuje się tutaj
w szczególności charakterystyki impulsowe, skokowe lub częstotliwościowe.
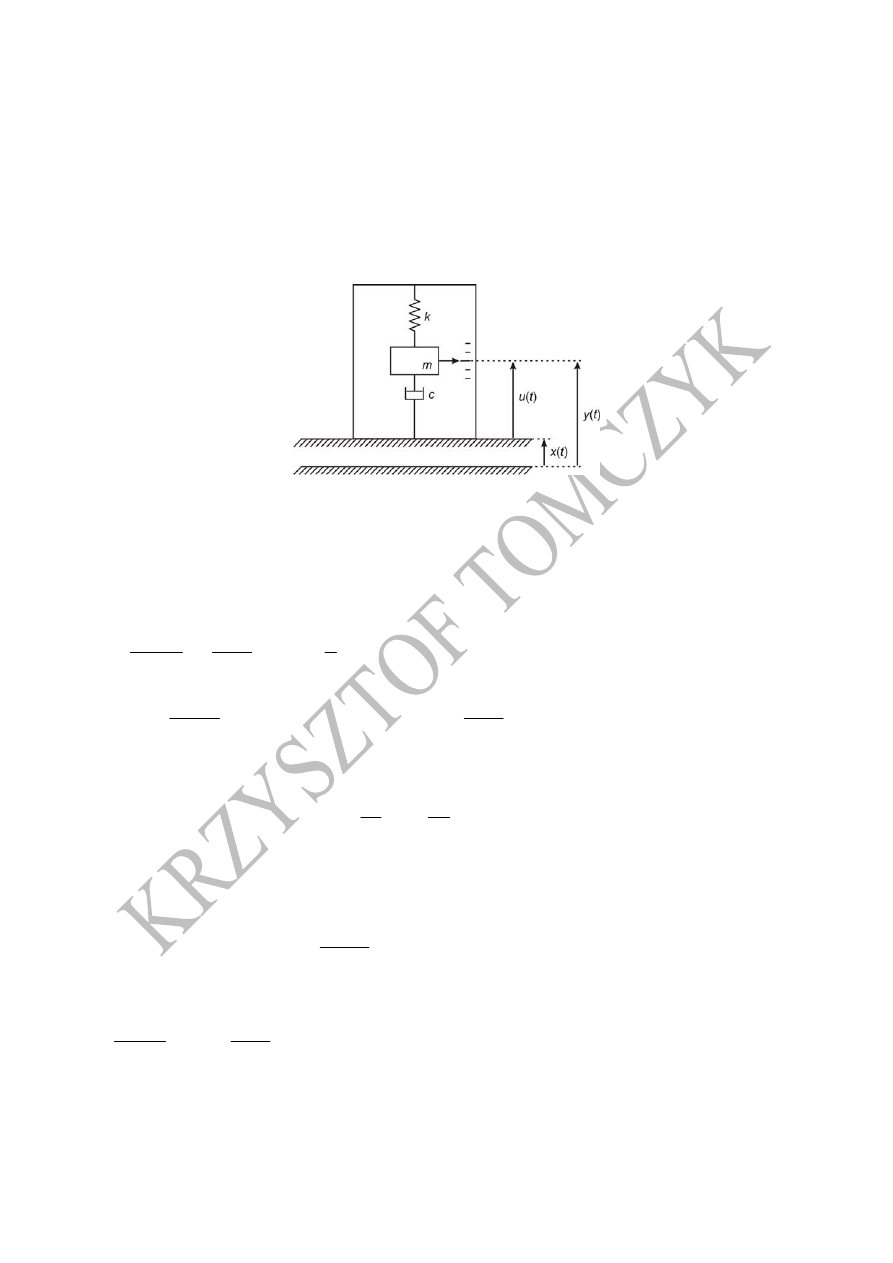
1. Układ 2-go rzędu
Rys 1. Mikromechanivzny model układu 2-go rzędu
Równanie ruchu przedstawionego na powyższym Rysunku układu można opisać za pomocą
równania różniczkowego 2-go rzędu, wykorzystując w tym celu równanie momentów. Mamy
zatem
)
(
)
(
)
(
)
(
t
x
k
t
ku
dt
t
du
c
dt
t
y
d
m
1
=
+
+
2
2
(1)
gdzie
2
2
dt
t
y
d
m
)
(
jest momentem bezwładności,
dt
t
du
c
)
(
jest momentem tłumiącym,
)
(t
ku
jest
momentem sprężystości,
)
(t
u
jest względnym przesunięciem masy,
)
(t
y
jest bezwzględnym
przesunięciem masy i
]
[kg
m
,
⎥⎦
⎤
⎢⎣
⎡
s
kg
c
,
⎥
⎦
⎤
⎢
⎣
⎡
2
s
kg
k
są odpowiednio: masą, współczynnikiem
tłumienia lepkiego i stałą sprężyny.
W przypadku pomiaru przyspieszenia wielkością wejściową jest druga pochodna
bezwzględnego przesunięcia
2
2
dt
t
x
d
)
(
, a wyjściem jest bezwzględne przesunięcie masy
)
(t
y
,
Z (1) wynika
)
(
)
(
)
(
)
(
t
x
a
t
u
dt
t
du
dt
t
u
d
2
0
0
2
2
=
+
2
+
ω
βω
(2)
gdzie:
)
(t
x
- sygnał wejściowy
2
)
(t
u
- sygnał wyjściowy
a
- współczynnik wzmocnienia statycznego
β
- współczynnik tłumienia
0
ω
- pulsacja drgań własnych nietłumionych oraz
2
0
=
ω
m
k
,
β
2
=
m
k
c
,
k
a
1
=
(3)
Wykonując operację transformaty Laplace’a na (2) mamy
)
(
)
(
)
(
)
(
s
X
a
s
U
s
sU
s
U
s
2
0
0
2
=
+
2
+
ω
βω
(4)
i w efekcie
2
0
0
2
2
0
+
2
+
=
=
ω
βω
ω
s
s
a
s
X
s
Y
s
K
)
(
)
(
)
(
(5)
Dla
1
≤
<
0
β
bieguny transmitancji (5), czyli pierwiastki równania:
0
=
+
2
+
=
2
0
0
2
ω
βω
s
s
s
M
)
(
(6)
wynoszą
2
0
0
∗
2
0
0
−
1
−
−
=
−
1
+
−
=
β
ω
βω
β
ω
βω
i
p
i
p
(7)
Transmitancja widmowa
)
(
)
(
)
(
)
(
)
(
)
(
ω
ϕ
ω
ω
ω
ω
ω
β
ω
ω
βωω
ω
ω
ω
ω
i
e
A
iQ
P
i
a
i
a
i
K
=
+
=
=
2
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
1
=
2
+
−
=
0
2
0
0
2
2
0
2
0
(8)
gdzie
)
(
ω
A
- charakterystyka wzmocnienia (magnitude characteristic)
)
(
ω
ϕ
- charakterystyka przesunięcia fazowego systemu (phase delay characteristic of system)
2
0
2
2
2
0
2
2
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
4
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
1
=
+
=
=
ω
ω
β
ω
ω
ω
ω
ω
ω
a
Q
P
i
K
A
)
(
)
(
)
(
)
(
(9)
3
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
1
2
−
=
2
0
0
ω
ω
ω
ω
β
ω
φ
arctg
)
(
(10)
Dla ),
(
ω
i
K
0
ω oraz
β
zachodzą następujące relacje:
(
)
0
2
2
0
2
0
0
2
0
2
0
0
2
0
2
2
0
0
2
0
0
0
2
2
0
2
0
2
2
2
0
0
2
0
0
0
2
0
0
2
0
0
0
∗
0
2
+
−
=
−
2
−
−
1
=
−
⎟
⎠
⎞
⎜
⎝
⎛
−
1
−
−
−
1
+
−
−
1
=
=
−
1
+
−
+
−
1
+
−
+
−
1
−
−
−
1
=
=
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
−
1
−
−
−
1
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
−
1
+
−
−
1
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
1
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
1
=
βωω
ω
ω
ω
ω
ω
βω
ω
ω
ω
β
ω
βω
β
ω
βω
ω
β
ω
ω
β
ω
β
ω
βω
ω
β
ω
βω
ω
β
ω
βω
ω
β
ω
βω
ω
ω
ω
ω
i
K
i
K
i
i
i
K
i
i
i
i
H
i
i
i
i
K
p
i
p
i
K
i
K
)
(
)
(
)
(
(11)
)
(
2
2
0
2
0
2
−
1
+
=
β
ω
ω
β
p
=
0
2
0
2
2
0
2
0
2
=
−
+
ω
ω
β
ω
ω
β
(12)
β
ω
βω
=
=
−
0
0
p
p)
Re(
(13)
gdzie
(
)
a
i
K
K
=
0
=
=
0
ω
(14)
Dla układu (1) pulsacja drgań własnych tłumionych
n
ω
oraz szczyt rezonansowy
r
M
wynoszą:
2
0
−
1
=
β
ω
ω
n
(15)
2
−
1
2
=
β
β
a
M
r
(16)
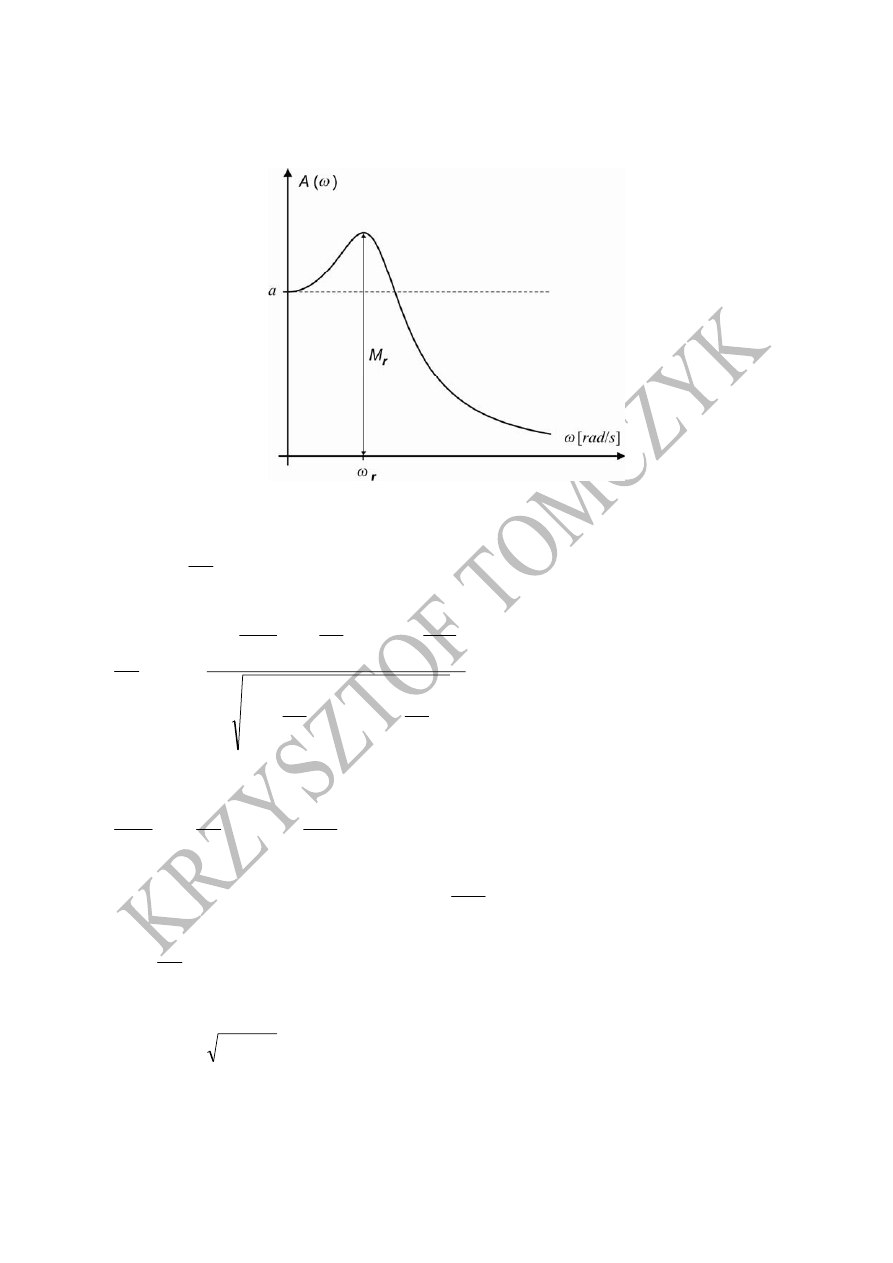
4
Rysunek 2 przedstawia charakterystykę amplitudowo-częstotliwościową układu
oscylacyjnego 2 rzędu.
Rys. 2. Charakterystyka amplitudowo-częstotliwościowa układu oscylacyjnego 2 rzędu
Wzór określający pulsację rezonansową
r
ω wyprowadza się poprzez przyrównanie
pochodnej
[
]
)
(
ω
ω
A
d
d
do zera
[
]
0
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
4
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
1
2
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
8
+
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
1
4
−
−
=
3
2
0
2
2
2
0
2
0
2
2
0
2
0
ω
ω
β
ω
ω
ω
ω
β
ω
ω
ω
ω
ω
ω
a
A
d
d
)
(
(17)
Wtedy
0
=
8
+
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
1
4
−
2
0
2
2
0
2
0
ω
ω
β
ω
ω
ω
ω
(18)
Mnożąc powyższe równanie obustronnie przez
ω
ω
4
2
0
otrzymujemy
0
=
2
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
1
−
2
2
0
β
ω
ω
(19)
i w efekcie
2
0
2
−
1
=
=
β
ω
ω
ω
r
(20)
5
Wyznaczenie odpowiedzi impulsowej
)
(t
k
metodą residuów
(
)
)
(
lim
)
(
s
K
p
s
s
K
res
i
i
p
s
i
p
s
−
=
→
=
∑
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
1
=
=
n
i
t
i
p
i
p
s
e
s
K
res
t
y
)
(
)
(
(21)
Bieguny transmitancji (5) opisuje (7). Zgodnie z (21) mamy
(
)
2
0
2
0
2
0
=
∗
2
0
∗
2
0
→
=
−
1
2
−
=
−
1
2
=
−
=
−
−
−
=
β
ω
β
ω
ω
ω
ω
ia
i
a
p
s
a
p
s
p
s
a
p
s
s
K
res
p
s
p
s
p
s
)
(
)
)(
(
lim
)
(
(22)
(
)
2
0
2
0
2
0
∗
=
2
0
∗
2
0
∗
∗
→
∗
=
−
1
2
=
=
−
1
2
−
=
−
=
−
−
−
=
β
ω
β
ω
ω
ω
ω
ia
i
a
p
s
a
p
s
p
s
a
p
s
s
K
res
p
s
p
s
p
s
)
(
)
)(
(
lim
)
(
(23)
oraz
t
i
t
t
i
t
e
e
ia
e
e
ia
t
k
2
−
1
0
−
0
−
2
0
2
−
1
0
0
−
2
0
−
1
2
+
−
1
2
−
=
β
ω
βω
β
ω
βω
β
ω
β
ω
)
(
(24)
Wykorzystując relacje
x
i
x
e
x
i
x
e
ix
ix
sin
cos
sin
cos
−
=
+
=
−
(25)
mamy
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
1
−
⎟
⎠
⎞
⎜
⎝
⎛
−
1
+
+
⎟
⎠
⎞
⎜
⎝
⎛
−
1
−
⎟
⎠
⎞
⎜
⎝
⎛
−
1
−
−
1
2
=
2
0
2
0
2
0
2
0
0
−
2
0
t
i
t
t
i
t
e
ia
t
k
t
β
ω
β
ω
β
ω
β
ω
β
ω
βω
sin
cos
sin
cos
)
(
(26)
Z (2.26) wynika
⎟
⎠
⎞
⎜
⎝
⎛
−
1
−
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
−
1
2
−
1
2
−
=
2
0
0
−
2
0
2
0
0
−
2
0
t
e
a
t
i
e
ia
t
k
t
t
β
ω
β
ω
β
ω
β
ω
βω
βω
sin
sin
)
(
(27)
W rezultacie mamy
( )
t
e
a
t
k
n
t
ω
β
ω
βω
sin
)
(
0
−
2
0
−
1
=
(28)
Z kolei odpowiedź skokową opisuje równanie
6
( )
( )
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
1
=
∫
=
0
0
−
0
t
t
e
a
d
k
t
h
n
n
n
t
t
ω
ω
β
ω
ω
τ
τ
βω
sin
cos
)
(
)
(
(29)
Drgania (29) są tłumione wykładniczo z wykładnikiem
a
t
t
h
+
⋅
⋅
−
±
=
0
1
)
exp(
)
(
ω
β
(30)
stanowiącym asymptoty dla przebiegu oscylacyjnego.
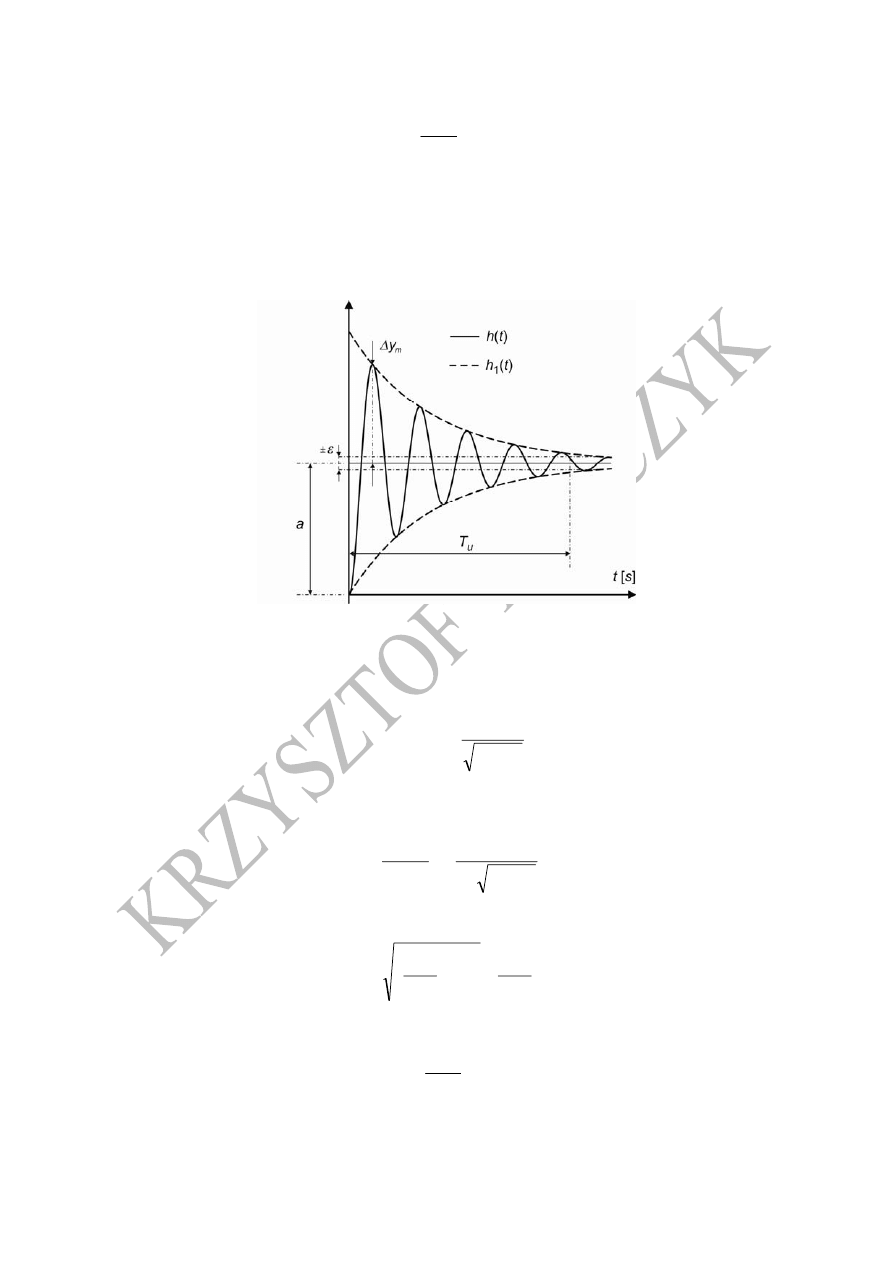
Rysunek 3 przedstawia odpowiedź skokową(29) układu (5).
Rys. 3. Odpowiedź skokowa układu oscylacyjnego 2 rzędu
Wartość współczynnika wzmocnienia odpowiada stanowi ustalonemu h(t).
Maksymalne odchylenie od stanu ustalonego odpowiedzi skokowej przedstawia (31).
m
y
∆
=
⎜⎜
⎜
⎝
⎛
⎟⎟
⎟
⎠
⎞
−
1
⋅
−
⋅
2
β
β
π
exp
a
(31)
Czas ustalania się wskazań, w którym przebieg h(t) odchyla się od swojego stanu ustalonego
o więcej niż
ε
± , określa (32).
u
T =
2
0
−
1
⋅
⋅
⋅
1
β
ε
ω
β
a
ln
(32)
Ze wzoru (31) wynika następująca zależność opisująca
β
β
=
α
π
α
π
⋅
2
−
1
+
⎜⎜
⎝
⎛
⎟
⎠
⎞
⋅
2
2
(33)
gdzie
⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
∆
=
m
y
a
ln
α
(34)
Dla przypadku odpowiedzi impulsowej współczynnik tłumienia wynosi
7
β
=
2
0
2
2
0
ln
4
ln
⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
+
⋅
⋅
n
n
A
A
n
A
A
π
(35)
i wyznacza się go na podstawie stosunku kolejnych amplitud
n
A odpowiedzi oscylacyjnej.
Ze wzoru (35) wynika pulsacja drgań własnych nietłumionych
0
ω
0
ω
=
u
T
a
⋅
−
1
⋅
2
β
β
ε
ln
(36)
Po wstawieniu (35) i (36) w (4) i (5) otrzymujemy szukany matematyczny model.
2. Przykład syntezy matematycznego modelu inercyjnego 1 rzędu w oparciu o pomiar
odpowiedzi skokowej
Transmitancja układu 1-go rzędu z opóźnieniem
)
(
)
(
s
X
s
Y
=
τ
s
e
T
s
k
−
⋅
+
1
(37)
Odpowiedź skokowa
τ
+
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ −
−
1
=
T
t
k
t
h
exp
)
(
(38)
Rysunek 4 przedstawia odpowiedź skokową (38) układu (37).
Rys. 4. Odpowiedź skokowa układu 1 rzędu z opóźnieniem