P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
1
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010
O
O
O
O
BLICZENIE
BLICZENIE
BLICZENIE
BLICZENIE
POŁĄCZENIA
POŁĄCZENIA
POŁĄCZENIA
POŁĄCZENIA
ŚRUBOWEGO
ŚRUBOWEGO
ŚRUBOWEGO
ŚRUBOWEGO
DOCZOŁOWEGO
DOCZOŁOWEGO
DOCZOŁOWEGO
DOCZOŁOWEGO
TYPU
TYPU
TYPU
TYPU
R1.3
R1.3
R1.3
R1.3
BELKI
BELKI
BELKI
BELKI
A
A
A
A
LGORYTM DO PROGRAMU
LGORYTM DO PROGRAMU
LGORYTM DO PROGRAMU
LGORYTM DO PROGRAMU MATHCAD
MATHCAD
MATHCAD
MATHCAD
P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
2
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010
Przyjęto stal St3SX o parametrach
E
205000 MPa
⋅
:=
G
80000 MPa
⋅
:=
Wytrzymałość obliczeniowa stali
f
d
215 MPa
⋅
:=
Obliczenie połączenia śrubowego doczołowego typu R1.3 belki
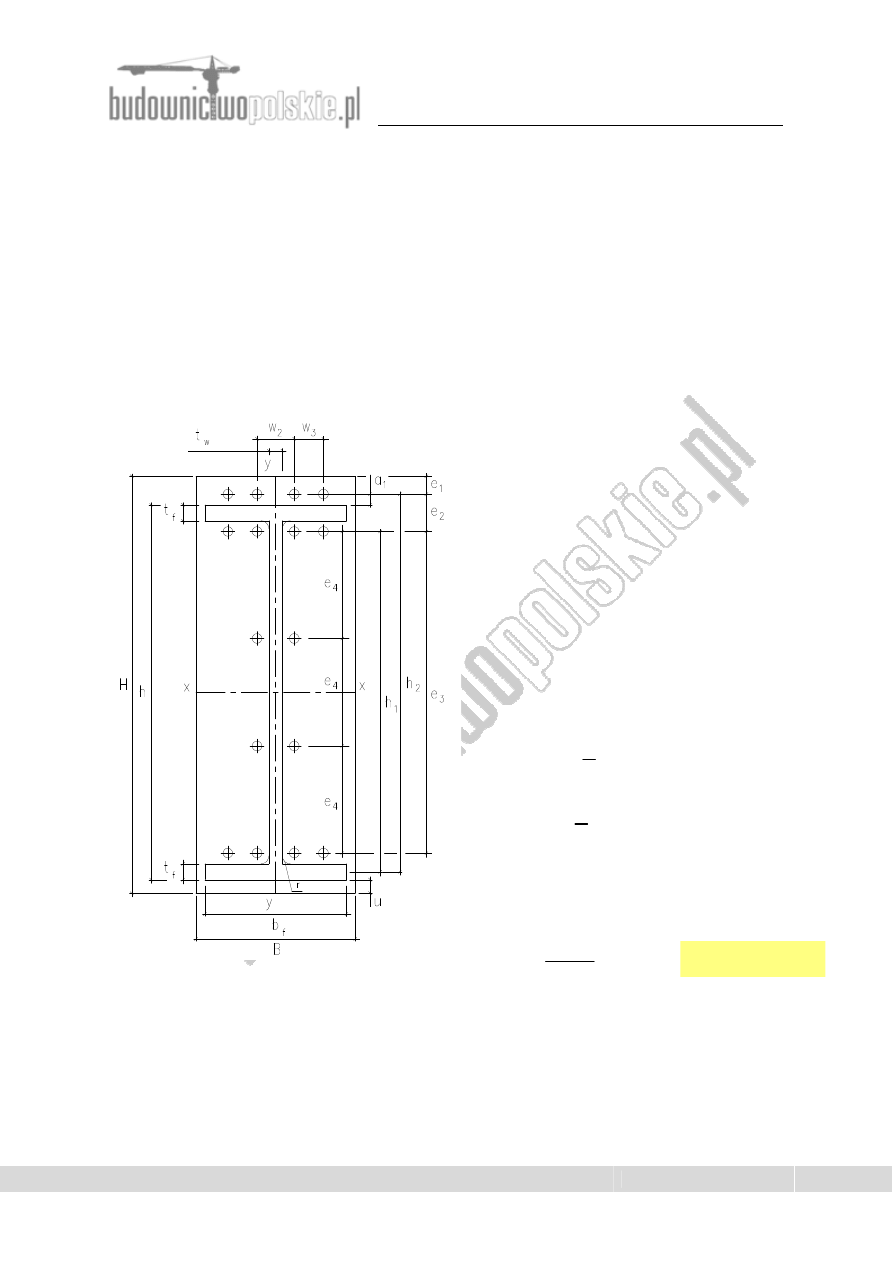
Charakterystyka geometryczna IKS 900x8x300x12, dane połączenia doczołowego
h
900 mm
⋅
:=
b
f
300 mm
⋅
:=
t
w
8 mm
⋅
:=
t
f
12 mm
⋅
:=
r
0 mm
⋅
:=
H
1010 mm
⋅
:=
B
340 mm
⋅
:=
a
1
40 mm
⋅
:=
e
1
50 mm
⋅
:=
w
2
80 mm
⋅
:=
e
2
100 mm
⋅
:=
w
3
60 mm
⋅
:=
e
4
260 mm
⋅
:=
t
bl
20 mm
⋅
:=
e
3
3 e
4
⋅
:=
e
3
78 cm
⋅
=
h
1
h
t
f
2
e
2
a
1
−
(
)
+
−
:=
u
20 mm
⋅
:=
h
1
83.4 cm
⋅
=
h
2
h
t
f
2
−
a
1
+
:=
h
2
93.4 cm
⋅
=
h
w
h
2 t
f
⋅
−
:=
h
w
87.6 cm
⋅
=
J
w
t
w
h
w
3
⋅
12
:=
J
w
44814.76 cm
4
⋅
=
Działające obciążenie
N
200 kN
⋅
:=
V
400 kN
⋅
:=
M
x
720 kNm
⋅
:=
P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
3
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010
Wielkości obliczeniowe
J
x
t
w
h
2 t
f
⋅
−
(
)
3
⋅
12
2
b
f
t
f
3
⋅
12
b
f
t
f
⋅
h
t
f
−
2
2
⋅
+
⋅
+
4 0.00755 r
4
⋅
r
2
0.2146
⋅
h
2 t
f
⋅
−
2 r
⋅
0.2234
⋅
−
2
2
⋅
+
⋅
+
...
:=
J
y
h
2 t
f
⋅
−
(
)
t
w
3
⋅
12
2 t
f
⋅
b
f
3
⋅
12
+
4 0.00755 r
4
⋅
0.2146 r
2
⋅
t
w
2
0.2234 r
⋅
+
2
⋅
+
⋅
+
:=
J
ω
J
y
h
t
f
−
(
)
2
⋅
4
:=
J
T
1.2
3
2 b
f
⋅
t
f
3
⋅
h
2 t
f
⋅
−
(
)
t
w
3
⋅
+
⋅
:=
A
2 b
f
⋅
t
f
⋅
h
2 t
f
⋅
−
(
)
t
w
⋅
+
4 r
2
⋅
0.2146
⋅
+
:=
i
x
J
x
A
:=
i
y
J
y
A
:=
W
x
2 J
x
⋅
h
:=
W
y
2 J
y
⋅
b
f
:=
J
x
186761.32 cm
4
⋅
=
J
T
59.41 cm
4
⋅
=
A
142.08 cm
2
⋅
=
J
y
5403.74 cm
4
⋅
=
J
ω
1.07
10
7
×
cm
6
⋅
=
G
m
A 7850
⋅
kg
m
3
⋅
:=
W
x
4150.25 cm
3
⋅
=
i
x
36.26 cm
⋅
=
G
m
111.53
kg
m
⋅
=
i
y
6.17 cm
⋅
=
W
y
360.25 cm
3
⋅
=
g
wk
G
m
g
⋅
:=
W
plx
1702 cm
3
⋅
:=
P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
4
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010
Parametry stateczności
ε
215 MPa
⋅
f
d
:=
λ
p
84
215 MPa
⋅
f
d
⋅
:=
ε
1
=
λ
p
84
=
Warunek smukłości dla równomiernie ściskanego pasa górnego
0.5 b
f
t
w
−
(
)
⋅
t
f
12.17
=
<
14
ε
⋅
14
=
Pas spełnia warunki smukłości klasy 3
σ
g
N
A
M
x
W
x
−
:=
σ
g
159.41
−
MPa
⋅
=
σ
d
N
A
M
x
W
x
+
:=
σ
d
187.56 MPa
⋅
=
ν
σ
g
σ
d
+
2
σ
g
⋅
:=
K
2
0.4
1
ν
−
(
)
:=
K
2
0.368
=
ν
0.09
−
=
Określenie klasy przekroju środnika przy zginaniu
42
K
2
ε
⋅
114.27
=
h
w
t
w
109.5
=
<
Ś
rodnik spełnia warunki smukłości klasy 3
Sprawdzenie warunków smukłości przekroju klasy 2
b
fd
b
f
:=
t
fd
t
f
:=
b
fg
b
f
:=
t
fg
t
f
:=
α
b
fd
t
fd
⋅
b
fg
t
fg
⋅
−
h
w
t
w
⋅
+
2t
w
h
w
⋅
:=
α
0.5
=
h
w
t
w
109.5
=
>
39
α
ε
⋅
78
=
P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
5
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010
Ś
rodnik nie spełnia warunku smukłości przekrojów klasy 2
Nośność przekroju przy zginaniu i rozciąganiu
M
RN
W
x
f
d
N
A
−
⋅
:=
M
RN
833.88 kNm
⋅
=
Określenie współczynnika niestateczności miejscowej przy ścinaniu
Graniczna smukłość klasy 3 przy ścinaniu wynosi
h
w
t
w
109.5
=
>
70
ε
⋅
70
=
K
0.8
:=
dla środnika bez żeber
Nośność w stanie krytycznym
λ
'
p
h
w
t
w
K
56
⋅
ε
⋅
:=
λ
'
p
1.56
=
φ
pV
1
λ
'
p
:=
φ
pV
0.64
=
Wielkość siły poprzecznej, jaką może przenieść środnik
A
v
h
w
t
w
⋅
:=
f
dv
f
d
3
:=
V
R
φ
pV
A
v
⋅
f
dv
⋅
:=
V
R
556.1 kN
⋅
=
V
V
R
0.72
=
>
0.6
M
RV
M
RN
1
J
w
J
x
V
V
R
2
⋅
−
⋅
:=
M
RV
730.36 kNm
⋅
=
>
M
x
720 kNm
⋅
=
Przyjęto na połączenie śruby M20 klasy 10.9
P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
6
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010
Obliczanie śrub
d
20 mm
⋅
:=
A
s
245 mm
2
⋅
:=
A
π
d
2
⋅
4
:=
R
e
940 MPa
⋅
:=
d
o
d
1 mm
⋅
+
:=
A
314.16 mm
2
⋅
=
R
m
1040 MPa
⋅
:=
A
v
0.8A
s
:=
m
1
:=
A
v
196 mm
2
⋅
=
Nośność obliczeniowa śruby na ścinanie
S
Rv
0.45 R
m
⋅
A
v
⋅
m
⋅
:=
S
Rv
91.73 kN
⋅
=
przyjęto
S
Rv
150 kN
⋅
:=
Nośność obliczeniowa śruby na rozciąganie
0.65 R
m
⋅
A
s
⋅
165.62 kN
⋅
=
S
Rt
166 kN
⋅
:=
0.85 R
e
⋅
A
s
⋅
195.75 kN
⋅
=
Nośność połączenia R1.4 ze względu na zerwanie
M'
o
0.9 h
1
⋅
0.7 h
2
⋅
+
(
)
4 S
Rt
⋅
0.5 h
t
f
−
(
)
⋅
N
⋅
−
:=
M'
o
843.72 kNm
⋅
=
Nośność połączenia R1.4 ze względu na rozwarcie
S
Rr
0.85 S
Rt
⋅
:=
M'
o
0.9 h
1
⋅
0.7 h
2
⋅
+
(
)
4 S
Rr
⋅
:=
M'
o
792.64 kNm
⋅
=
Nośność śrub na ścinanie w sąsiedztwie dolnego pasa belki
V'
o
4 S
Rv
⋅
:=
V'
o
600 kN
⋅
=
>
V
400 kN
⋅
=
a
f
0.7 t
f
⋅
:=
a
f
8.4 mm
⋅
=
a
w
0.2 t
bl
⋅
:=
a
w
4 mm
⋅
=
Przyjęto następujące grubości spoin:
- półki
a
f
8 mm
⋅
:=
- środnik a
w
4 mm
⋅
:=
P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
7
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010
Moment bezwładności układu spoin względem osi x-x:
- spoiny poziome
- spoiny pionowe
Jx
sh.1
2 a
f
⋅
b
f
⋅
a
f
3
h
2
+
2
⋅
:=
Jx
sv
2
a
w
h
2 t
f
r
+
(
)
⋅
−
3
⋅
12
⋅
:=
Jx
sh.2
2 a
f
⋅
b
f
t
w
−
2 r
⋅
−
(
)
⋅
h
2
t
f
−
a
f
3
−
2
⋅
:=
Jx
sv
44814.76 cm
4
⋅
=
Jx
sh
Jx
sh.1
Jx
sh.2
+
:=
Jx
sh
186896.87 cm
4
⋅
=
Jx
s
Jx
sh
Jx
sv
+
:=
Całkowity moment bezwładności układu spoin
względem osi x-x
Jx
s
231711.63 cm
4
⋅
=
Największe naprężenie w spoinie, wywołane momentem gnącym M'o
σ
M
M'
o
h
2
a
f
2
+
⋅
Jx
s
:=
σ
M
155.31 MPa
⋅
=
κ
0.7
:=
σ
p
σ
M
2
:=
σ
p
109.82 MPa
⋅
=
τ
p
σ
p
:=
σ
κ
σ
p
2
3
τ
p
2
⋅
+
⋅
:=
σ
153.74 MPa
⋅
=
<
f
d
215 MPa
⋅
=
Największe naprężenie w spoinie, wywołane siłą poprzeczną V
ls
v
2 h
2 t
f
r
+
(
)
⋅
−
⋅
:=
ls
v
175.2 cm
⋅
=
α
r
0.8
:=
τ
r
V
a
w
ls
v
⋅
:=
τ
r
57.08 MPa
⋅
=
<
α
r
f
d
⋅
172 MPa
⋅
=
Największe naprężenie w spoinie, wywołane momentem gnącym M'o w punkcie
połączenia środnika i półki
P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
8
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010
α
p
0.9
:=
σ
M1
M'
o
h
2 t
f
⋅
−
2
⋅
Jx
s
:=
σ
M1
149.83 MPa
⋅
=
α
r
0.8
:=
σ
M1
α
p
2
τ
r
α
r
2
+
181.12 MPa
⋅
=
<
f
d
215 MPa
⋅
=
κ
σ
M1
2
3
τ
p
2
τ
r
2
+
(
)
⋅
+
⋅
183.08 MPa
⋅
=
<
f
d
215 MPa
⋅
=
Sprawdzenie nośności spoin
b
s
2 b
f
⋅
t
w
−
:=
b
s
59.2 cm
⋅
=
f
ds
205 MPa
⋅
:=
κ
0.7
:=
∆
κ
2
⋅
:=
∆
0.99
=
M
Rj
a
f
b
s
⋅
f
ds
⋅
∆
N
2
−
h
t
f
−
(
)
⋅
:=
M
Rj
782.09 kNm
⋅
=
>
M
x
720 m kN
⋅
=
V
Rj
2 a
w
⋅
α
r
⋅
f
ds
⋅
h
2 t
f
⋅
−
(
)
⋅
:=
V
Rj
1149.31 kN
⋅
=
>
V
400 kN
⋅
=
P O M O C E N A U K O W E I D Y D A K T Y C Z N E
P O Ł Ą C Z E N I E Ś R U B O W E D O C Z O Ł O W E B E L K I T Y P U
R 1 . 3
9
P
R A W A A U T O R S K I E
–
B
U D O W N I C T W O
P
O L S K I E
.
P L
L
I S T O P A D
2010