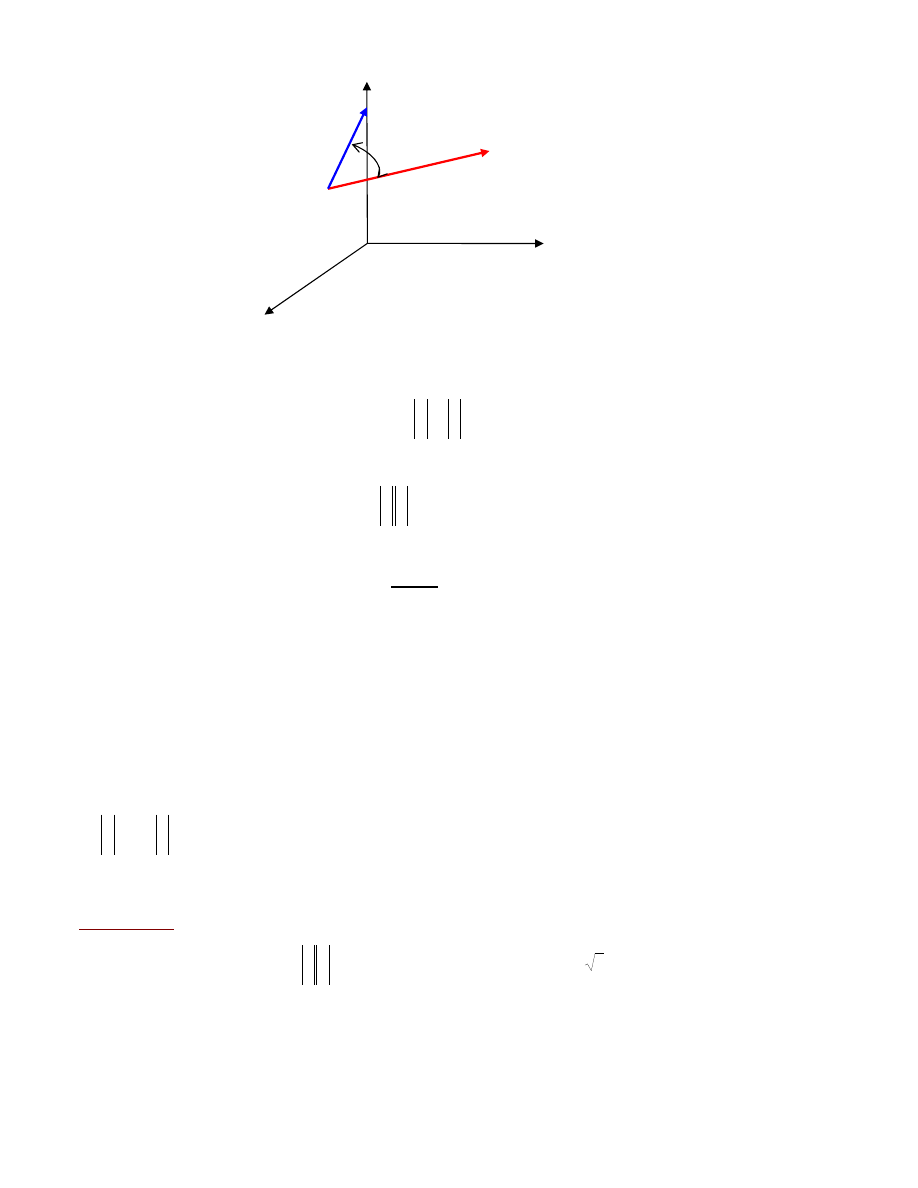
3 . Iloczyn skalarny
Iloczynem skalarnym
(oznaczanym
v
u
) dw
óch wektorów
v
,
u
nazywamy liczb
ê
r
ówn¹
iloczynowi d
ùugoœci tych wektorów
u
,
v
i cosinusa k
¹ta
zawartego
mi
êdzy nimi, czyli
cos
v
u
v
u
.
Nale
¿y pamiêtaã, ¿e iloczyn skalarny jest liczb¹
(skalarem), a nie wektorem.
Je
œli
z
y
x
u
,
u
,
u
u
i
z
y
x
v
,
v
,
v
v
, to iloczyn skalarny mo
¿emy wyliczyã ze wzoru
z
z
y
y
x
x
v
u
v
u
v
u
v
u
.
..........................................................................................
PRZYK£AD
Obliczy
ã ilocz
yn skalarny wektor
ów
v
,
u
je
œli:
a)
2
u
,
7
v
, a k
¹t
mi
êdzy wektorami
v
,
u
wynosi
o
30
;
b)
2
2
0
,
,
u
,
j
k
i
v
4
3
2
.
Rozwi
¹zanie
a) Zgodnie ze wzorem
cos
v
u
v
u
mamy
3
5
30
5
2
o
cos
v
u
.
b) Zapiszmy wektor
v
w postaci
3
4
2
,
,
v
.
Poniewa
¿
mamy dane wsp
óùrzêdne
wektor
ów wygodniej bêdzie
skorzysta
ã z drugiego wzoru na iloczyn skalarny
z
z
y
y
x
x
v
u
v
u
v
u
v
u
.
Mamy wi
êc
14
3
2
4
2
2
0
v
u
.
..........................................................................................
iloczyn skalarny
X
Y
Z
u
v
id4520234 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com

Przekszta
ùcaj¹c wzór
cos
v
u
v
u
otrzymamy wz
ór do wyznaczenia
cosinusa
k¹ta
miêdzy wektorami
v
,
u
v
u
v
u
cos
.
K
¹t miêdzy wektorami
v
,
u
symbolicznie zapisujemy
v
u
.
..........................................................................................
PRZYK£AD
Obliczy
ã cosinus k¹ta miêdzy wektorami
v
,
u
je
œli:
k
i
j
u
2
3
,
AB
v
,
gdzie
4
6
1 ,
,
A
,
1
5
3
,
,
B
.
Rozwi
¹zanie
Najpierw wyznaczamy wsp
óùrzêdne wektora
AB
v
.
5
1
4
4
1
6
5
1
3
,
,
,
,
AB
i wektora
1
3
2
,
,
u
.
Nast
êpnie dùugoœci wektorów
v
,
u
14
1
3
2
2
2
2
u
42
5
1
4
2
2
2
v
Iloczyn skalarny wyznaczamy ze wzoru
z
z
y
y
x
x
v
u
v
u
v
u
v
u
Mamy wi
êc
10
5
1
1
3
4
2
v
u
.
Ostatecznie mo
¿emy wyliczyã
cosinus k
¹ta
v
,
u
21
3
5
3
14
10
14
42
10
v
u
v
u
cos
.
..........................................................................................
cosinus k
¹ta
mi
êdzy
wektorami

Wùasnoœci iloczynu skalarnego wektorów
Niech
w
,
v
,
u
b
êd¹ dowolnymi wektorami,
dowoln
¹ liczb¹
.
Wtedy:
1.
u
v
v
u
2.
w
v
w
u
w
v
u
3.
v
u
v
u
4.
2
u
u
u
5.
0
0
u
u
u
6.
v
u
v
u
0
7.
Iloczyn skalarny jest dodatni je
œli k¹t pomiêdzy wektorami jest ostry
i ujemny je
œli k¹t ten jest rozwarty.
..........................................................................................
PRZYK£AD
Obliczy
ã iloczyn skalarny wektorów
v
,
u
je
œli
q
p
u
2
,
p
q
v
2
3
,
2
p
,
3
q
,
a k
¹t
mi
êdzy wektorami
q
,
p
wynosi
o
60
.
Rozwi
¹zanie
Poniewa
¿ wektory
v
,
u
nie s
¹ dane
za pomoc
¹ wspóùrzêdnych nie mo¿emy
stosowa
ã wzoru
z
z
y
y
x
x
v
u
v
u
v
u
v
u
.
Przy obliczaniu iloczyn
v
,
u
wykorzystamy
w
ùasnoœci iloczynu skalarnego
i dane z przyk
ùadu:
13
10
2
1
3
2
10
3
3
6
4
2
4
6
2
3
4
6
2
3
2
3
2
2
2
1
4
3
2
cos
q
p
q
p
q
p
q
p
q
p
p
q
q
q
p
p
q
p
p
q
q
p
v
u
iloczynu
.
def
i
.
wù
i
.
wù
Ostatecznie
13
v
u
..........................................................................................
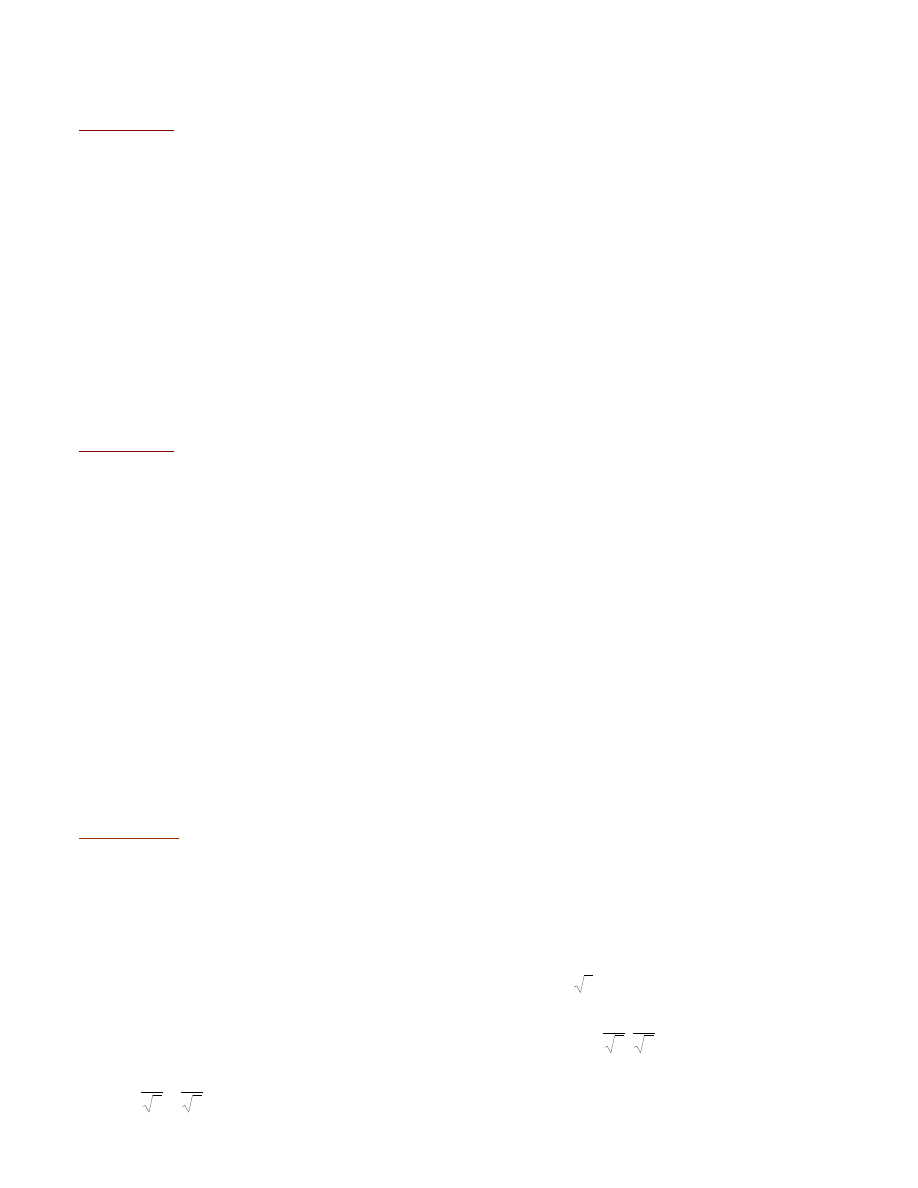
PRZYK£AD
Czy wektory
2
2
0
,
,
u
,
1
4
3 ,
,
v
s
¹ prostopadùe?
Rozwi
¹zanie
Obliczamy iloczyn skalarnych wektor
ów
v
,
u
6
1
2
4
2
3
0
v
u
.
Poniewa
¿
0
v
u
, to stwierdzamy
¿e wektory
v
,
u
nie s
¹ prostopadùe.
..........................................................................................
PRZYK£AD
Dla jakiej warto
œci parametru m
wektory
2
2
m
,
m
,
m
u
,
2
5
4
,
,
v
s
¹
prostopad
ùe?
Rozwi
¹zanie
Poniewa
¿ wektory s¹ prostopadùe
wtedy i tylko wtedy gdy ich iloczyn skalarny jest
r
ówny
zero. Wyznaczamy iloczyn skalarnych wektor
ów
v
,
u
i przyr
ównujemy g
o do
zera.
4
4
2
2
5
2
4
m
m
m
m
v
u
0
4
4
0
m
v
u
, st
¹d
1
m
.
Dla
1
m
wektory
v
,
u
s
¹ prostopadùe.
..........................................................................................
PRZYK£AD
Znale
êã dowolny wektor jednostkowy prostopadùy do wektora
3
3
2
,
,
u
.
Rozwi¹zanie
Poszukamy najpierw jakiegokolwiek wektora (niezerowego)
v
prostopad
ùego do
u
Przyjmijmy dwie pierwsze jego wsp
óùrzêdne dowoln
e, byleby nie by
ùy jednoczeœnie
r
ówne 0
np.
.
z
,
,
v
u
2
0
Z warunku prostopad
ùoœci
0
v
u
dostajemy
,
z
u
0
3
6
st
¹d
.
z
u
1
D
ùugoœã
tak wyznaczonego wektora
1
2
0 ,
,
v
wynosi
5
. Wyznaczymy
teraz wektor
w
jednostkowy r
ównolegùy do wektora
v
5
1
5
2
0
,
,
w
(lub
5
1
5
2
0
,
,
w
). Wektor ten spe
ùnia warunki zadania
(jest prostopad
ùy do
wektora
u
i
1
w
).
..........................................................................................
PRZYK£AD
Wyznaczy
ã dùugoœã wektora
u
je
œli
q
p
u
2
,
4
p
,
2
q
,
q
p
.
Rozwi
¹zanie
Poniewa
¿ wektory
u
nie jest dany za pomoc
¹ wspóùrzêdnych nie mo¿emy
stosowa
ã wzoru
2
2
2
z
y
x
u
u
u
u
.
Przy obliczaniu d
ùugoœã wektora
u
wykorzystamy wz
ór
2
u
u
u
i inne w
ùasnoœci
iloczynu skalarnego:
32
4
4
16
4
4
4
2
2
2
2
6
2
2
4
1
3
2
2
.
wù
i
.
wù
i
.
wù
q
q
p
p
q
q
p
q
q
p
p
p
q
p
q
p
u
u
u
2
4
32
32
2
u
u
.
..........................................................................................
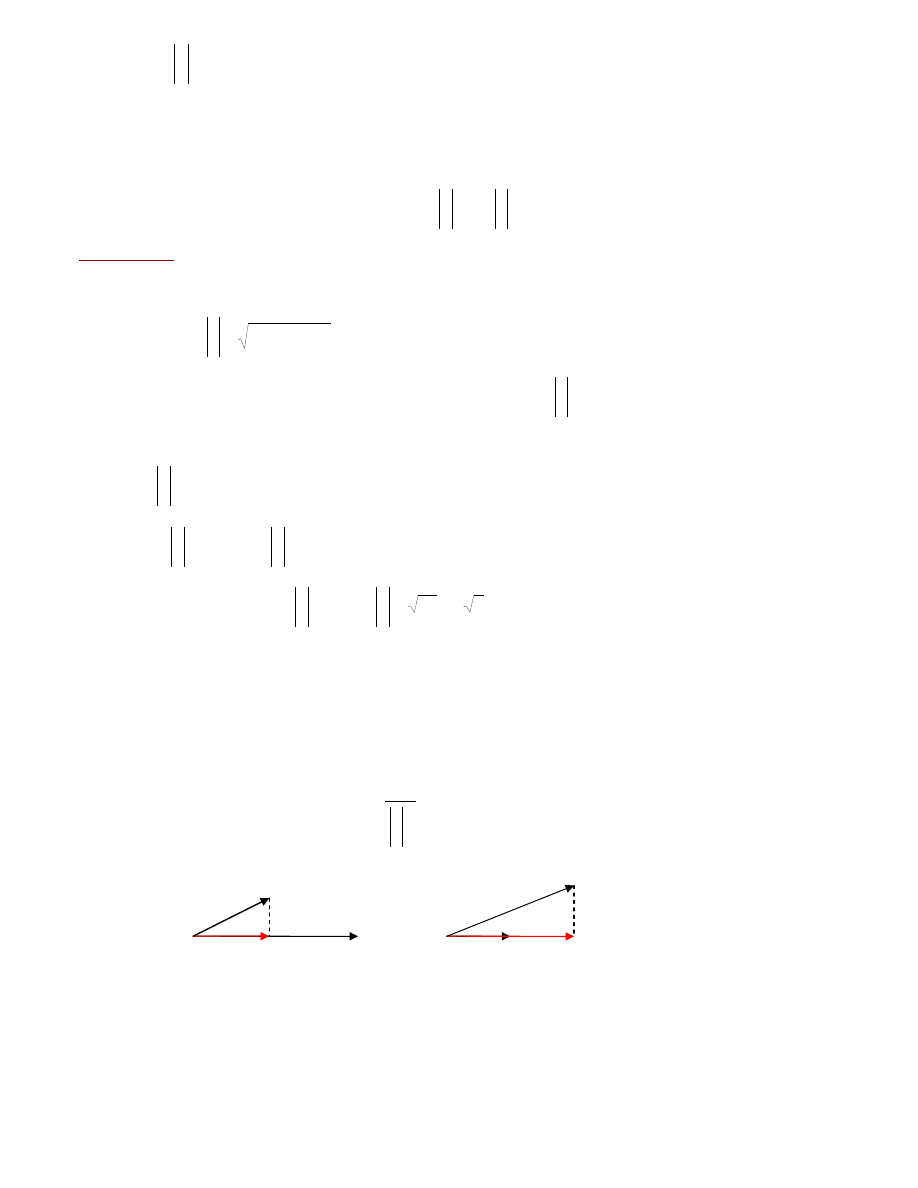
Korzystaj
¹c z wùasnoœci iloczynu skalarnego mo¿na wyprowadziã
wz
ór
na wektor
v
u
b
êd¹cy rzutem p
rostok
¹tny
m wektora
u
na o
œ o kierunku wektora
v
v
v
v
u
u
v
2
lub
u
v
v
u
u
v
v
u

..........................................................................................
PRZYK£AD
Znale
êã rzut prostok¹tny wektora
2
3
1
,
,
u
na wektor
3
5
4
,
,
v
.
Rozwi
¹zanie
Wyznaczamy najpierw
25
v
u
i
2
5
50
v
, a nast
êpnie szukany wektor
v
u
ze wzoru
v
v
v
u
u
v
2
, mamy wi
êc
2
3
2
5
2
3
5
4
2
1
3
5
4
2
5
25
2
,
,
,
,
,
,
u
v
.
..........................................................................................
Wyszukiwarka
Podobne podstrony:
Algebra 1 06 iloczyn skalarny
iloczyn skalarny iloczyn wektorowy
Iloczynn skalarny
Iloczyn skalarny wektorowy
matematyka, iloczyn, Iloczyn skalarny wektorów
fiz-indukcja elektromagnetyczna, Strumień indukcji magnetycznej - jest równy iloczynowi skalarnemu w
Prez iloczyn skalarny id 389685 Nieznany
W[1].3.Iloczyn skalarny
Matematyka I (Ćw) Lista 06 Wektory Iloczyn skalarny, wektorowy, mieszany
matematyka, Iloczyn skalarny, Iloczyn skalarny wektorów
iloczyn skalarny, macierze, wyznaczniki, wektory
Algebra 1 06 iloczyn skalarny
ILOCZYN PRZEZ ROZKŁAD NA DZIESIĄTKI, materiały szkolne
iloczyn rozpuszczalności
więcej podobnych podstron