1

Maksymalizacja funkcji dwóch zmiennych

W sytuacji gdy funkcja celu y=f(x

1

,x

2

) jest funkcją dwóch zmiennych, znalezienie maksimum tej funkcji

wymaga spełnienia dwóch warunków:

1) Po pierwsze obie pochodne cząstkowe tej funkcji muszą byd równe zeru:

2) po drugie wyznacznik macierzy kwadratowej drugich pochodnych cząstkowych musi byd

dodatnich, co jest równoznaczne ze stwierdzeniem, iż spełniona musi byd następująca
nierównośd:

co oznacza iż:

przy czym:

Przykład

1

. Zysk Przedsiębiorstwa π (mierzony w tysiącach złotych) zależy od ceny produktu

P (w złotych) i wydatków na reklamę A (w tysiącach złotych). Funkcję zysku można przedstawid
następująco:

Należy obliczyd, jaka cena i jaka wielkośd wydatków reklamowych pozwolą zmaksymalizowad zysk
firmy. Należy w tym celu znaleźd pochodne cząstkowe funkcji zysku i przyrównad do zera. Wynoszą
one:

1

Wykorzystano przykład z: A. Solek, Optymalne decyzje. Ekonomia menedżerska w zadaniach, Wydawnictwo

Uniwersytetu Ekonomicznego w Krakowie, Kraków 2008, str. 17-18

2

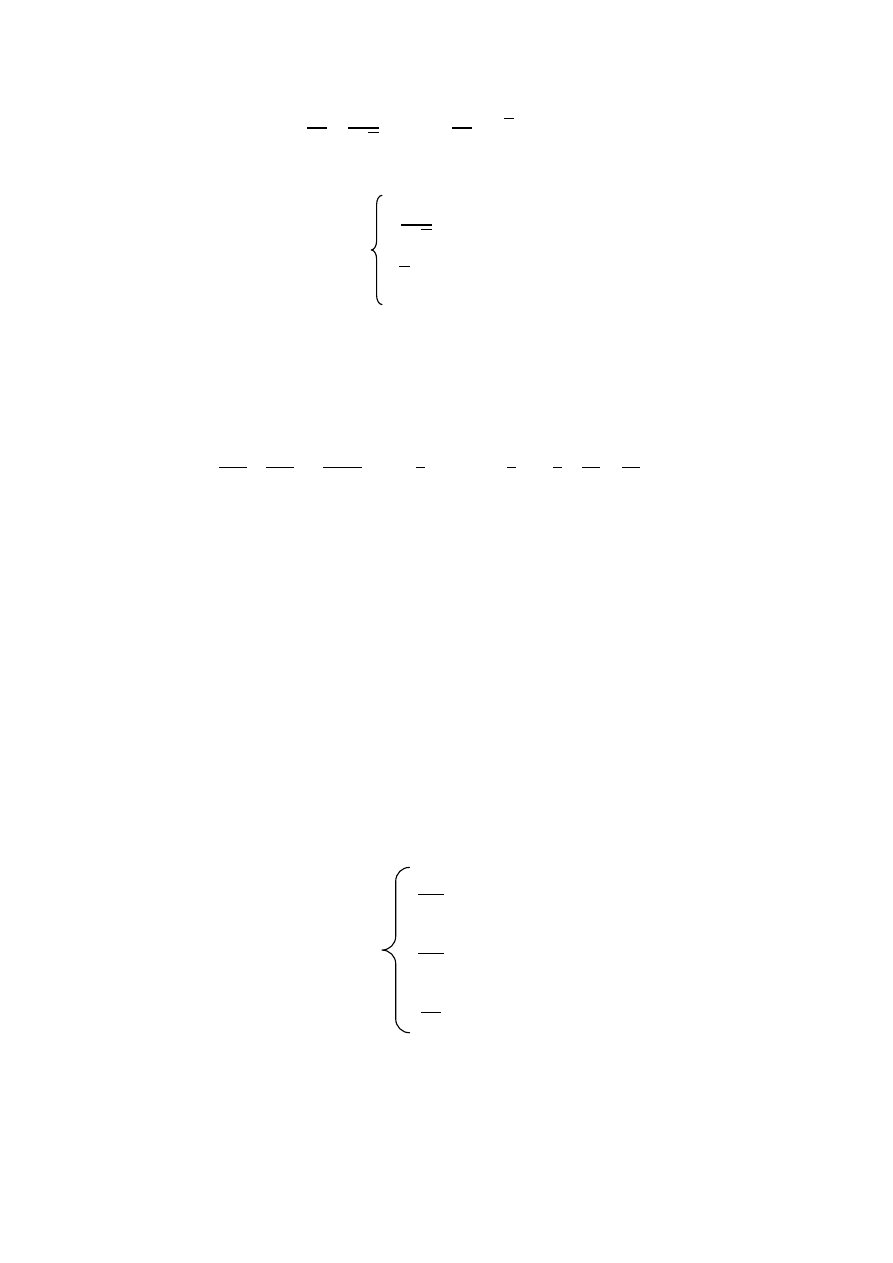
Następnie tworzymy układ równao:

Po wyliczeniu z pierwszego równania: A=2P

1/2

i podstawieniu do drugiego otrzymujemy: P=4(zł),

A=4(tys. zł).

W dalszej kolejności sprawdzamy drugi warunek:

Ponieważ warunki są spełnione firma osiąga największy zysk przy cenie 4 zł i poziomie wydatków na
reklamę 4 tys. zł.

Na funkcję celu y=f(x

1

,x

2

) mogą byd nałożone pewne ograniczenia. W takiej sytuacji jej maksimum

można znaleśc stosując metodę mnożników Lagrange’a. Ograniczenie to może dotyczyd przeróżnych
okolicznośd jak np. funduszu na wynagrodzenia lub pojemności magazynu. Funkcję ograniczenia
można zapisad wzorem:

Wykorzystując ją możliwym jest skonstruowanie funkcji Langrange’a Z:

gdzie to tzw. mnożnik Lagrange’a. Funkcja ta jest sumą funkcji celu oraz funkcji ograniczenia
pomnożonej przez λ. Gdy policzymy kolejne pochodne cząstkowe tej funkcji otrzymamy układ
równao:

Którego rozwiązanie pozwoli znaleźd optymalne wielkości zmiennych.

3

Przykład

2

. Przedsiębiorstwo chce zmaksymalizowad wielkośd produkcji jako funkcję ilości

wykorzystanych czynników produkcji:

Za każdą roboczogodzinę firma musi zapłacid 3 euro, za jednostkę kapitału 5 euro. Na produkcję
można przeznaczyd łącznie 1200 euro. Jakiego podziału środków powinien dokonad menedżer firmy,
by przy danym ograniczeniu budżetowym osiągnąd jak największą wielkośd produkcji?

Na początek zapiszemy funkcję ograniczenia. Wykorzystując L godzin pracy, przedsiębiorstwo zapłaci
kwotę 3 euro, zaś na K jednostek kapitału wyda 5K euro. Maksymalny poziom wydatków na czynniki
produkcji można więc zapisad następująco:

co jest równoważne:

Teraz tworzymy funkcję Lagrange’a:

Liczymy pochodne cząstkowe tej funkcji i przyrównujemy do zera:

Zauważy, że ostatnie równanie jest funkcją ograniczenia.

Najłatwiej rozwiązad powyższy układ wyliczając λ z dwóch pierwszych równao - przyrównując je do
siebie. Otrzymamy: 5K=3L. Do funkcji ograniczenia podstawiamy K=0,6L i wyliczamy:

Firma powinna zatrudnid 200 jednostek pracy i 120 jednostek kapitału. Osiągnie wtedy największy
możliwy poziom produkcji, równy Q=6*200+10*120+200*120=26400.

WAŻNE: Funkcję Lagrange’a można również wykorzystad do znalezienia minimum oraz w analogiczny
do przedstawionego powyżej sposób zastosowad do funkcji więcej niż tylko dwóch zmiennych.

2

Wykorzystano przykład z: A. Solek, Optymalne decyzje. Ekonomia menedżerska w zadaniach, Wydawnictwo

Uniwersytetu Ekonomicznego w Krakowie, Kraków 2008, str. 19-20

4

Zadania

3

.

1. Przedsiębiorstwo może w swoim zakładzie produkcyjnym wytwarzad dwa produkty

jednocześnie. Ceny, po jakich może je sprzedad, wynoszą odpowiednio: 12 i 18. Koszt
produkcji określa funkcja: TC=2x

2

+xy+2y

2

+24, gdzie x to wielkośd produkcji pierwszego dobra,

a y to wielkośd produkcji drugiego dobra. Jaka wielkośd produkcji maksymalizuje zysk firmy
i ile on wówczas wynosi?

2. Fabryka urządzeo elektronicznych stosuje w produkcji pracę ludzi i (lub) maszyn. Zarząd firmy

chce zmaksymalizowad wielkośd produkcji, która wyraża się wzorem: Q=2K+5L+KL, gdzie L –
liczba pracowników, K liczba maszyn. Ma jednak organiczny budżet – koszt produkcji nie
może przekroczyd 69 tys. zł tygodniowo. Stawka opłaty leasingowej wynosi 3 tys. zł,
a wynagrodzenie pracownika 6 tys. zł. Jaką wielkośd nakładów kapitału i pracy należy
zatrudnid w ciągu tygodnia? Ile urządzeo zostanie wówczas wyprodukowanych?

Odpowiedzi do zadao z poprzedniej części:

1. Q=3000; π=2000000
2. Odpowiednio:

a. Q=5; π=90
b. Q=6; π=27
c. Q=8; π=2000
d. Q=3500; π=600000

3

Wykorzystano przykład z: A. Solek, Optymalne decyzje. Ekonomia menedżerska w zadaniach, Wydawnictwo

Uniwersytetu Ekonomicznego w Krakowie, Kraków 2008, str. 23-24