1

OPTYMALIZACJA W WARUNKACH JEDNEJ ZMIENNEJ DECYZYJNEJ.

Podejmowanie decyzji ekonomicznych wiąże się z poniesieniem pewnych w kosztów (TC – Total Cost
– koszt całkowity) w celu uzyskania pewnych korzyści (TB – Total Benefit – korzyśd całkowita. Celem
racjonalnego decydenta powinno byd zatem takie rozwiązanie problemu ekonomicznego by
nadwyżka korzyści nad kosztami była jak największa. W takim przypadku funkcja celu może byd
zdefiniowana jako:

gdzie NB oznacza korzyśd netto (net benefit).

By znaleźd największy poziom nadwyżki korzyści całkowitej nad kosztem całkowitym można
wykorzystad analizę matematyczną. Jeżeli korzyści i koszty zależą od jednego typu aktywności (a-
activity) to zarówno TB, jak i TC są funkcjami tej aktywności:

W tej sytuacji koniecznym jest określenie zależności pomiędzy poziomem a oraz wielkością TB oraz
TC. Można dokonad tego stosując pochodne. Zakładając, że wzrost natężenia prowadzenia danej
działalności prowadzi zarówno do wzrostu korzyści, jak i kosztu całkowitego odpowiednie pochodne
mają następujące znaki:

׀

׀

Ponieważ funkcje zostały zapisane w postaci ogólnej to nie możemy nic powiedzied na temat tempa
przyrostu żadnej z tych funkcji w miarę wzrostu a. Jednak z drugiej strony wykorzystując posiadane
informacje możemy określid wartości kraocowe:

- korzyśd kraocowa – to przyrost korzyści całkowitej wynikający z nieskooczenie małego

przyrostu aktywności:

׀

- koszt kraocowy – to przyrost korzyści całkowitej wynikający z nieskooczenie małego

przyrostu aktywności:

׀

Wykorzystując wielkości kraocowe można określid maksymalną wielkośd nadwyżki korzyści

całkowitej nad kosztem całkowitym znajdując ekstremum – maksimum – tej funkcji. By można było
mówid o ekstremum NB muszą wystąpid dwa warunki:

-WARUNEK KONIECZNY – pierwsza pochodna jest równa zero:

2

wynika stąd, iż warunkiem równorzędnym dla powyższego jest równośd korzyści całkowitej i

kosztu całkowitego.

-WARUNEK WYSTARCZAJĄCY – druga pochodna jest:

a. większa od zera – wtedy funkcja przyjmuje minimum;

b. mniejsza od zera – wtedy funkcja przyjmuje maksimum – wartośd nadwyżki korzyści
całkowitej nad kosztem całkowitym jest maksymalna:

wynika stąd, iż warunkiem równorzędnym dla powyższego wyższośd drugiej pochodnej

kosztu całkowitego nad drugą pochodną korzyści całkowitej.

Powyższe rozważania można łatwo zaaplikowad do analizy decyzji przedsiębiorstwa.

Przedsiębiorstwo chcące maksymalizowad zysk (π=TR-TC) musi maksymalizowad nadwyżkę przychodu
całkowitego (Total Revenue – TR=P*Q) nad kosztem całkowitym. Zakładając (zgodnie ze
stylizowanymi faktami), iż:

możemy sformułowad warunki na maksymalizację zysku

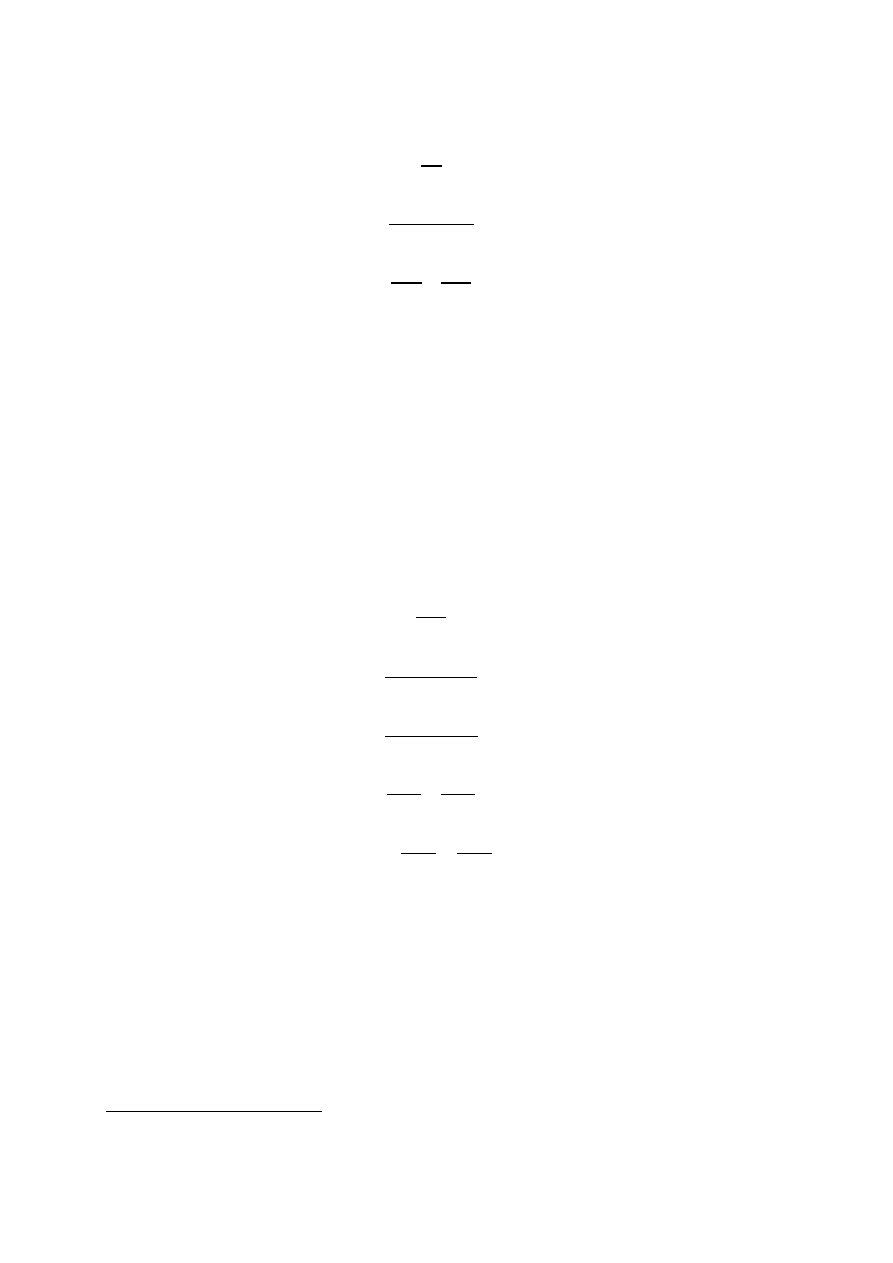
3

-WARUNEK KONIECZNY – pierwsza pochodna jest równa zero:

wynika stąd, iż warunkiem równorzędnym dla powyższego jest równośd korzyści całkowitej i

kosztu całkowitego.

-WARUNEK WYSTARCZAJĄCY – druga pochodna jest:

a. większa od zera – wtedy funkcja przyjmuje minimum;

b. mniejsza od zera – wtedy funkcja przyjmuje maksimum – wartośd nadwyżki korzyści
całkowitej nad kosztem całkowitym jest maksymalna:

wynika stąd, iż warunkiem równorzędnym dla powyższego jest wyższośd drugiej pochodnej

kosztu całkowitego nad drugą pochodną utargu całkowitego.

Przykład

1

. Funkcja popytu zgłaszanego w ciągu tygodnia na wyroby przedsiębiorstwa sprzedającego

deskorolki wyraża się wzorem: P=520-3Q, zaś funkcja kosztu produkcji ma postad:
TC=0,5Q

2

+100Q+4000. Oblicz, ile deskorolek firma powinna dostarczyd na rynek, by osiągnąd

największe zyski i ile one wynoszą?

11

Wykorzystano przykład z: A. Solek, Optymalne decyzje. Ekonomia menedżerska w zadaniach, Wydawnictwo

Uniwersytetu Ekonomicznego w Krakowie, Kraków 2008, str. 15-16

4

Rozwiązując to zadanie drugą z podanych wyżej metod, musimy przyrówna do siebie MR i

MC. W tym celu najpierw trzeba znaleźd funkcję TR, a następnie wyliczyd MR.

Koszt kraocowy liczymy następująco:

Teraz przyrównujemy obie wielkości kraocowe i wyliczamy optymalną wielkośd produkcji:

Sprawdzamy jeszcze, czy pochodna funkcji korzyści kraocowej jest mniejsza od pochodnej kosztu
kraocowego.

Oznacza to, że firma powinna wytwarzad 60 sztuk tygodniowo. Uzyska wtedy zysk w wysokości:

To samo rozwiązanie można też znaleźd, konstruując funkcję zysku całkowitego i znajdując jej
maksimum. Funkcja ta ma postad:

Następnie przyrównujemy jej pochodną, czyli zysk kraocowy, do zera, by wyliczyd Q:

Sprawdzamy na koniec znak drugiej pochodnej:

5

Rozwiązanie jest więc identyczne jak poprzednio.

Zadania

2

:

1.W firmie wytwarzającej urządzenia elektroniczne funkcja utargu całkowitego wyraża się wzorem:
TR=-1/3Q

2

+4000Q. Funkcja kosztu całkowitego ma postad: TC=2000Q+1000000; Q oznacza liczbę

podzespołów wytworzonych w ciągu miesiąca. Jaka wielkośd produkcji pozwoli zmaksymalizowad
zysk?

2. Oblicz optymalną – z punktu widzenia przedsiębiorstwa maksymalizującego zysk – wielkośd
produkcji, znając funkcję popytu na jego produkty oraz koszt całkowity produkcji. Jaki jest największy
poziom zysku w każdym z przykładów?

a)
b)

c)

d)

2

Wykorzystano przykład z: A. Solek, Optymalne decyzje. Ekonomia menedżerska w zadaniach, Wydawnictwo

Uniwersytetu Ekonomicznego w Krakowie, Kraków 2008, str. 15-16