Ćwiczenie 1

Temat:

OBWÓD SZEREGOWY I RÓWNOLEGŁY 

RLC PRZY WYMUSZENIU SINUSOIDANYM 

– REZONANS NAPIĘĆ I PRĄDÓW

I. ZAGADNIENIA

1.

Badanie   własności   obwodu   RLC   przy   szeregowym   i   równoległym 
połączeniu elementów w stanie ustalonym.

2.

Pomiar prądów i napięć oraz wyznaczanie mocy; wykresy wektorowe.

3.

Rezonans fazowy napięć i prądów.

4. Dobroć cewki rzeczywistej, kondensatora rzeczywistego, dobroć obwodu 

rezonansowego i jego związek z pasmem przepuszczania.

II. WIADOMOŚCI PODSTAWOWE

W obwodach prądu zmiennego zawierających elementy indukcyjne i pojemno-
ściowe   następuje   ciągła   zamiana   energii   pola   elektrycznego   w   energię   pola 
magnetycznego i na odwrót. Rzeczywiste cewki i kondensatory oprócz induk-
cyjności L i pojemności C charakteryzują się też pewną rezystancją R, Część 
energii   doprowadzonej   do   obwodu   zostaje   stracona   na   ciepło   na   wszystkich 
rezystancjach obwodu.

1.1. GAŁĄŹ SZEREGOWA R, L, C, REZONANS NAPIĘĆ

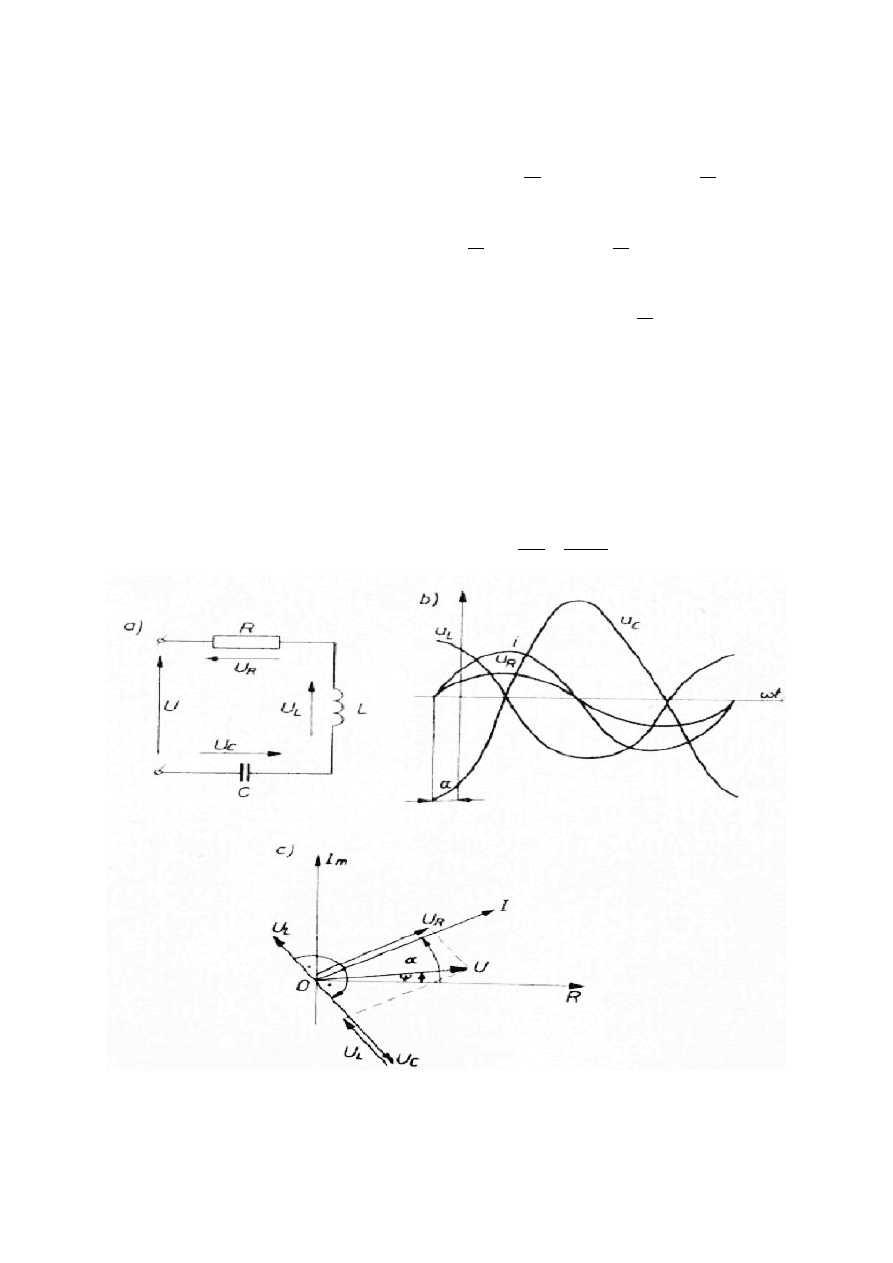
Do obwodu złożonego z szeregowo połączonych elementów idealnych R, L, C 
doprowadzone   jest   napięcie   sinusoidalnie   zmienne   (rys.1.la).   Przepływający 
przez te elementy prąd wywołuje na nich napięcia UR, UL, UC, przy czym 
zgodnie z drugim prawem Kirchhoffa dla wartości chwilowych możemy z2-
sać:

u=u

R

+u

L

+u

C

 

(1.1)

lub:

∫

+

+

•

=

idt

C

1

dt

di

L

i

R

u

 

(1.2)

Zakładamy, że prąd w omawianym obwodzie ma też charakter sinusoidalny:

i=I

m

 sin(ωt+α)

 (1.3)

gdzie α jest fazą początkową prądu.
Równanie (1.1) lub (1.2) możemy również zapisać:

)

2

sin(

)

2

sin(

)

sin(

Π

−

+

•

+

Π

+

+

•

+

+

•

=

α

ω

α

ω

α

ω

t

U

t

U

t

U

u

Cm

Lm

Rm

  (1.4)

Ponieważ:

)

2

sin(

)

2

sin(

Π

+

+

−

=

Π

−

+

α

ω

α

ω

t

t

 

(1.5)

to równanie (1.4) możemy zapisać w postaci:

)

2

sin(

)

(

)

sin(

Π

+

+

•

−

+

+

•

=

α

ω

α

ω

t

U

U

t

U

u

Cm

Lm

Rm

 

(1.5)

gdzie:

m

C

Cm

m

L

Lm

m

Rm

I

X

U

I

X

U

I

R

U

•

=

•

=

•

=

,

,

 

(1.6)

lub dla wartości skutecznych:

fC

C

X

I

X

U

fL

L

X

I

X

U

I

R

U

C

C

C

L

L

L

R

Π

=

=

•

=

Π

=

=

•

=

•

=

2

1

1

2

,

ω

ω

 

(1.7)

Rys 1.1

Dodając rzędne poszczególnych sinusoid u

R

, u

L

, u

c

 dla tego samego czasu t lub 

kąta   (ωt)   otrzymujemy   sinusoidę   wypadkową   napięcia   zasilającego 
rozpatrywany obwód:

)

sin(

ψ

ω

+

•

=

t

U

u

m

 

(1.8)

W wyniku takiego sumowania otrzymujemy sinusoidę o tym samym okresie T 
(lub częstotliwości f), co sinusoidy składowe. Z rys. 1.lb możemy bezpośrednio 
odczytać   amplitudę   U   oraz   fazę   początkową   sinusoidy   wypadkowej.   Aby 
uzyskać dokładny wynik, rysunek należałoby wykonać bardzo precyzyjnie na 
papierze   milimetrowym,   co   jest   uciążliwe   i   pracochłonne,   zwłaszcza   w  z2-
dku sumowania więcej niż dwóch sinusoid.
Przedstawiając   przebieg   sinusoidalny   w   postaci   kolejnych   rzutów   wektora, 
wirującego ze  stałą prędkością kątową ω, na oś  rzędnych, możemy zastąpić 
sumowanie   sinusoid   geometrycznym   dodawaniem   wektorów   (rys.   3.1c). 
Długości   wektorów   odpowiadają   amplitudom   lub   wartościom   skutecznym 
poszczególnych   wielkości   sinusoidalnych,   a   kąty,   jakie   tworzą   te   wektory   z 
dodatnim   kierunkiem   osi   liczb   rzeczywistych,   odpowiadają   fazom   począt-
kowym tych przebiegów.
Na podstawie wykresu wektorowego łatwo możemy wyznaczyć amplitudę (lub 
wartość skuteczną) przebiegu wypadkowego. W naszym przypadku amplituda 
napięcia zasilającego szeregowy obwód RLC wynosi:

2

2

)

(

Cm

Lm

Rm

m

U

U

U

U

−

+

=

 

(1.9)

Korzystając z odpowiedniości pomiędzy przebiegiem sinusoidalnym i wektorem 
wirującym,   można   przedstawić   wymuszenie   i   odpowiedź   odpowiednio   w 
postaci   wektorów   wirujących.   Następnie,   przechodząc   do   wektorów  z2-
chomych (zakładając t=0) i do wartości skutecznych zespolonych, otrzymujemy 
dla szeregowego, obwodu RLC wyrażenie zwane prawem Ohma w postaci z2-
olonej:

I

Z

I

C

L

j

R

U

•

=









−

+

=

)

1

(

ω

ω

 

(1.10)

nazywamy impedancją zespoloną gałęzi szeregowej RLC, R= Re [Z] – rezystan-
cja tej gałęzi, zaś X

L

-X

C

 = X = Im [Z] - reaktancją, która w zależności od 

charakteru obwodu może być indukcyjna, pojemnościowa lub mieć wartość z2-
. 
Impedancję zespoloną można zapisać również w postaci wykładniczej jako:

2

2

)

(

C

L

j

X

X

R

Z

gdzie

Ze

Z

−

+

=

=

ϕ

 

(1.12)

φ- kąt przesunięcia fazowego wnoszony przez rozpatrywany obwód.

Przesunięcie fazowe (φ jest to kąt, jaki tworzy wektor napięcia z wektorem 

prądu. Obliczamy go ze wzoru:

R

X

X

tg

Z

X

X

C

L

C

L

−

=

−

=

ϕ

ϕ

lub

sin

 

(1.13)

Kąt φ może być dodatni, ujemny lub zerowy, zależnie od charakteru obwodu. 

W przypadku, gdy X

L

>Xc, obwód ma charakter indukcyjny i kąt φ ma wartość 

dodatnią, co oznacza, że przebieg napięcia wyprzedza przebieg prądu. Dla z2-
du o charakterze pojemnościowym, tzn., gdy X

C

>X

L

 kąt φ ma wartość ujemną i 

wówczas przebieg napięcia na gałęzi RLC opóźnia się o kąt φ za przebiegiem 
prądu.

Jeśli X

c

  = X

L

, reaktancja  X  obwodu i kąt φ są równe zeru. W obwodzie 

występuje wówczas tzw. rezonans napięć, gdyż napięcia U

L

 i U

C

 są sobie równe 

co do wartości, lecz przeciwne co do fazy (przesunięte w fazie o 180°), wobec 
czego kompensują się.

Ponieważ impedancja obwodu zgodnie ze wzorem (1.11) równa jest przy 

rezonansie napięciowym tylko rezystancji R, prąd w obwodzie osiąga wartość 
największą, równa: U/R, a gdy rezystancja zmierza do zera, prąd osiąga war-
tość nieskończenie dużą.

W chwili rezonansu prąd i napięcie są ze sobą w fazie. Z warunku rezonansu 

napięciowego:

L

C

ω

ω

=

1

 

(1.14)

wynika, że rezonans można uzyskać zmieniając częstotliwość źródła przy  z2-
ienionych parametrach obwodu, lub gdy będziemy zmieniać parametry obwodu 
L lub C przy stałej częstotliwości.

Pulsacja   rezonansowa  

LC

1

0

=

ω

  a   odpowiadająca   jej   częstotliwość   rezonan-

sowa: 

LC

f

π

2

1

0

=

W przypadku rezonansu lub w jego pobliżu mogą wystąpić na elementach bier-
nych obwodu przepięcia, tzn. napięcia o wartościach większych od napięcia na 
zaciskach obwodu. Wynika to z proporcji:

C

C

L

L

rez

X

U

X

U

R

U

I

=

=

=

 

(1.15)

więc U

L

 > U gdy X

L

 > R, oraz Uc > U przy X

c

 > R.

Jak stąd wynika, warunkiem wystąpienia przepięć jest rezonans napięć i więk-
sza wartość reaktancji (indukcyjnej lub pojemnościowej) niż rezystancji.

Na rys. 1.2. wykonane są wykresy wektorów napięć i prądu dla obwodów 

o charakterze   indukcyjnym,   pojemnościowym   i   rezystancyjnym.   Dla   uprosz-
czenia przyjęto fazę początkową wektora prądu równą zeru.

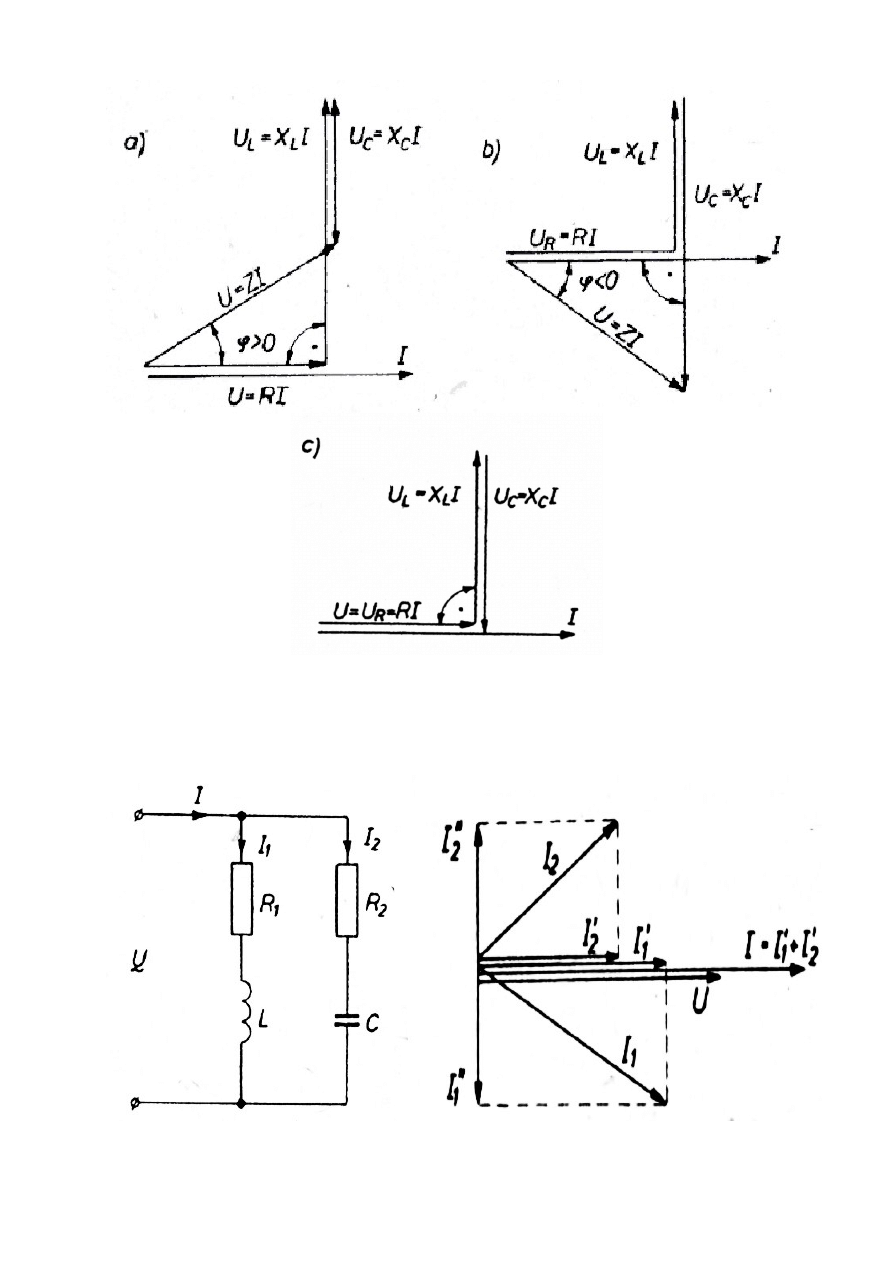
Rys 1.2

1.2. OBWÓD RÓWNOLEGŁY R, L, C, REZONANS PRĄDÓW

Rozważmy obwód jak na rys. 1.3:

Rys 1.3 

Rys 1.4

W obwodzie  tym wystąpi rezonans  prądów,  gdy składowe bierne  prądów  w 
gałęziach zrównają się (rys. 1.3): I

1

”

= I

2

”

. Całkowity prąd pobierany  ze źródła 

jest równy w chwili rezonansu tylko sumie składowych czynnych obu prądów 
gałęziowych, czyli osiąga minimum i jest w fazie z napięciem zasilającym obie 
gałęzie. Ponieważ:

2

2

1

2

2

1

1

1

1

1

)

(

)

(

L

R

L

U

j

L

R

UR

L

j

R

U

Z

U

I

ω

ω

ω

ω

+

−

+

=

+

=

=

 

(1.16)

2

2

2

2

2

2

2

2

2

2

)

1

(

1

)

1

(

1

C

R

C

U

j

C

R

UR

C

j

R

U

Z

U

I

ω

ω

ω

ω

+

+

+

=

+

=

=

 

(1.17)

gdzie: 

V

Ue

U

o

j0

=

, więc:

2

2

2

2

2

1

)

1

(

1

)

(

C

R

C

U

L

R

L

U

ω

ω

ω

ω

+

=

+

 

(1.18)

Ostatecznie warunek rezonansu w rozpatrywanym obwodzie ma postać:

2

2

2

2

2

1

C

C

L

L

X

R

X

X

R

X

+

=

+

 (1.19)

czyli: B

1

=B

2

Rezonans prądów można uzyskać nie zmieniając częstotliwości źródła zasilania, 
a   tylko   wielkości   R

1

,R

2

,L,C.   Przy   zmianie   indukcyjności   lub   pojemności 

możliwy jest nie jeden, lecz nawet dwa stany rezonansu; wynika to z warunku 
(1.19), z którego otrzymać można równanie kwadratowe względem L lub C.

III. POMIARY

1. Obwód szeregowy RLC – rezonans napięć

1.1. Schemat układu pomiarowego:

V

U

cos

ϕ

A

V

V

V

R

R

L

C

L

1

2

3

1.2

Zmierzyć wartości napięć i prądu w układzie jak na rysunku.

1.3

Wyznaczyć na podstawie pomiarów parametry układu (XL, XC, R, RL).

UWAGA: uwzględnić rezystancję cewki.

1.4

Obliczyć   moc   czynną,   bierną,   pozorną   oraz   cos

ϕ

  całego   układu   dla 

wybranego pomiaru.

1.5

Wykonać w skali wykres wektorowy napięć, prądu oraz przeprowadzić 
wektorowe sumowanie.

1.6

Przy stałej wartości napięcia zasilania U i stałych wartościach R i L zdjąć 
charakterystyki:

        UL = f1(C) ,  UR = f2(C) ,  UC = f3(C) ,  I = f4(C)   i sporządzić wykresy.
1.7  Z powyższych wykresów określić wartość C, przy której wystąpił 

rezonans napięć.

1.8   Wyznaczyć teoretycznie wartość reaktancji rezonansowej XC, prądu Ir 

oraz porównać wyniki z otrzymanymi z pomiarów.

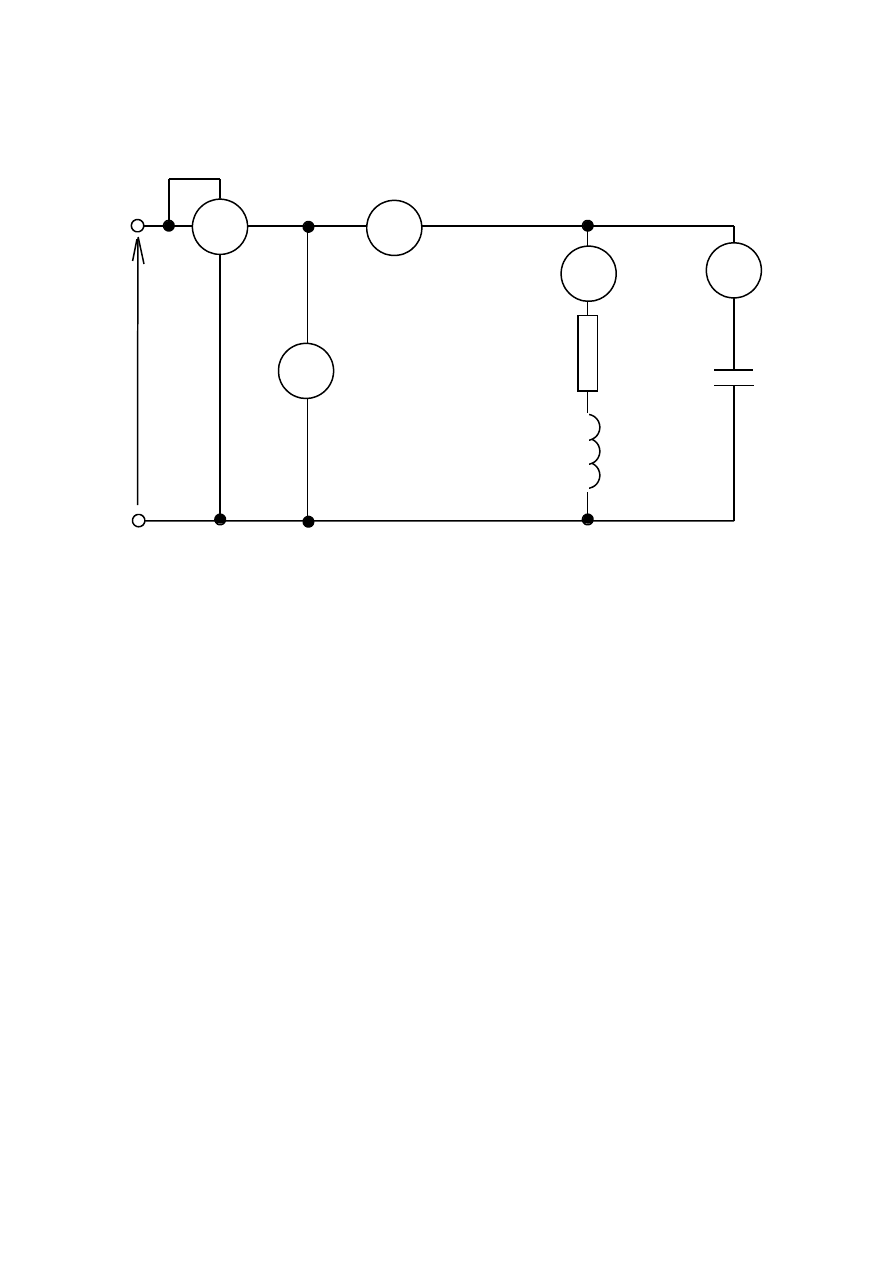
2. Obwód równoległy RLC – rezonans prądów

2.1

Schemat układu pomiarowego:

V

U

cos

ϕ

A

A

A

R

L

C

L

1

2

2.2

Zmierzyć napięcie i prądy w układzie jak na rysunku.

2.3

Obliczyć   moc   czynną,   bierną,   pozorną   oraz   cos

ϕ

  całego   układu   dla 

wybranego pomiaru.

2.4

Wykonać w skali wykres wektorowy prądów i napięcia oraz przeprowa-
dzić wektorowe sumowanie prądów I1, I2.

2.5

Przy stałej wartości napięcia zasilania U i stałych wartościach R, L i f 
zmieniając C i mierząc prądy, zdjąć charakterystyki: I1 = f1(C), I2 = f2(C) 
i sporządzić wykresy.

2.6

Obliczyć pojemność, przy której wystąpi rezonans prądów w powyższym 
układzie, wartość prądu Ir oraz porównać wyniki z otrzymanymi w pkt. 

2.7

Wykonać w skali wykres wektorowy rezonansu prądów.

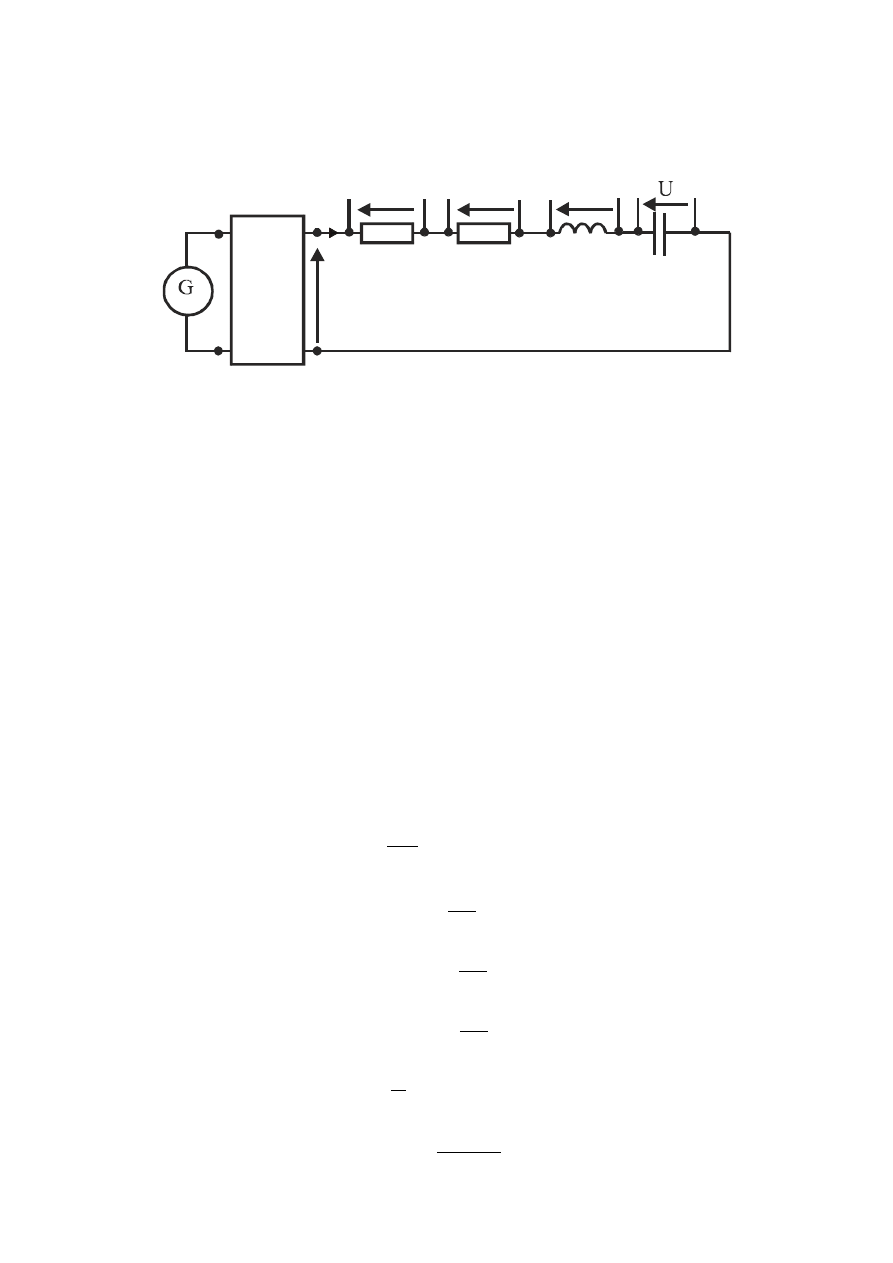
3. Badanie układu rezonansowego przy zmianie częstotliwości

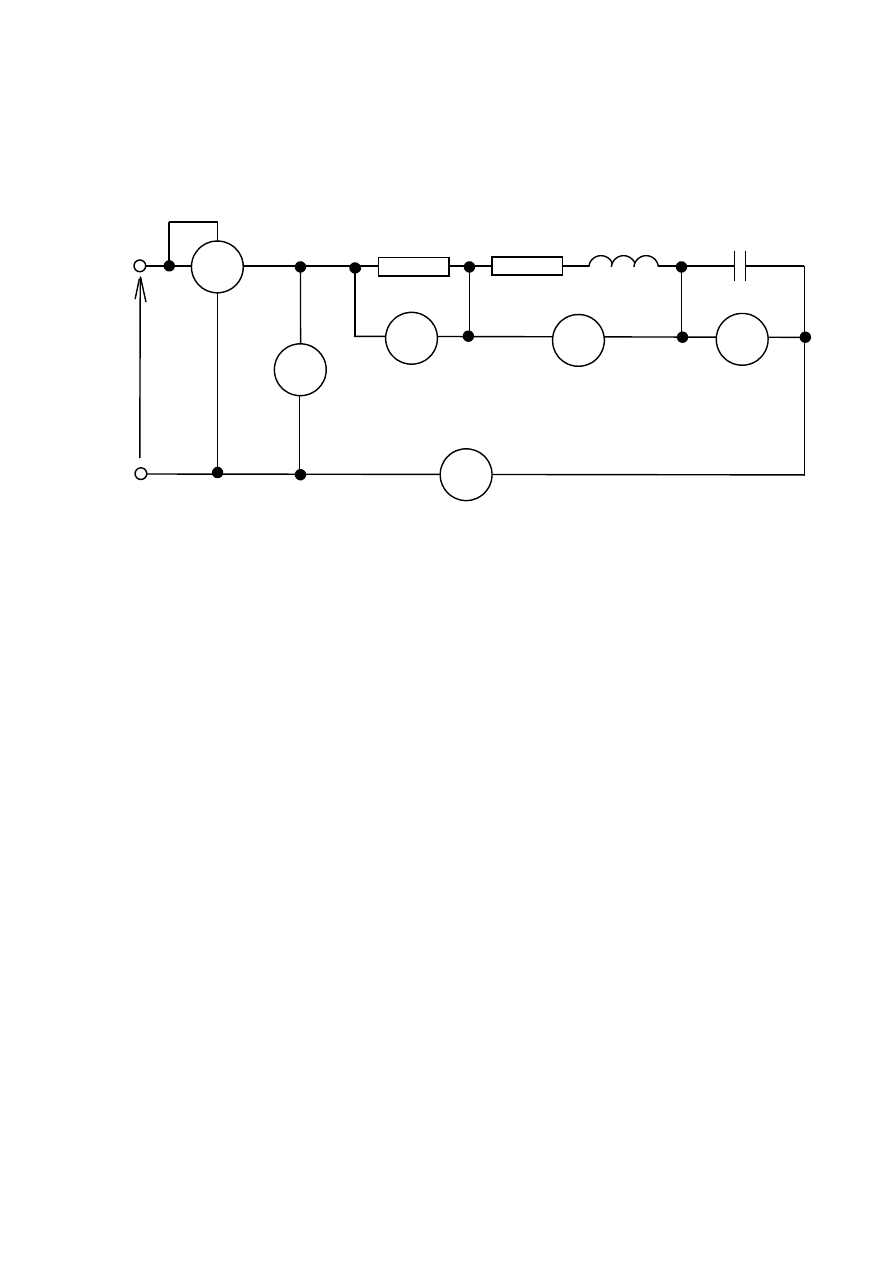
3.1  Układ o szeregowym połączeniu elementów RLC
3.1.1 Schemat układu pomiarowego:

R

L

C

U

R

U

L

C

R

w

U

w

model

źródła

napięcia

U=const

I

Wartości elementów RLC:

R1 = 22

Ω

L1 = 69 mH

C1 = 143 nF 

R

w

 = 100 

R2 = 52

Ω

L2 = 153 mH

C2 = 547 nF

R3 = 82

Ω

3.1.2

Multimetr cyfrowy ustawić na pomiar napięcia zmiennego,

3.1.3 Ustawić wartość napięcia zasilającego U na około 1 V,
3.1.4 Zmieniając częstotliwość f napięcia od ok. 100 Hz do 2 kHz z krokiem 

ok. 100 Hz (20 pomiarów) zmierzyć wartości skuteczne napięć U

R

, U

L

, U

C 

na poszczególnych elementach R, L, C oraz napięcie U

w

  na rezystorze 

wzorcowym   R

w

  podłączając   kolejno   woltomierz   do   odpowiednich   z2-

sków   na   modelu,   oraz   zapisać   częstotliwość,   przy   której   napięcie   U

w 

osiąga wartość maksymalną,

3.1.5

Zmienić wartość indukcyjności L, pomiary powtórzyć,

3.1.6

Zmienić wartość pojemności C, pomiary powtórzyć, 

3.1.7 Zmienić wartość rezystancji R, pomiary powtórzyć,
3.1.8 Obliczenia:

Korzystając ze wzorów (1, 2, 3, 4, 5, 6):

w

w

R

U

I

=

(1)

I

U

R

R

=

(2)

I

U

X

L

L

=

(3)

I

U

X

C

C

=

(4)

I

U

Z

=

(5)









−

=

R

C

L

U

U

U

arctg

ϕ

(6)

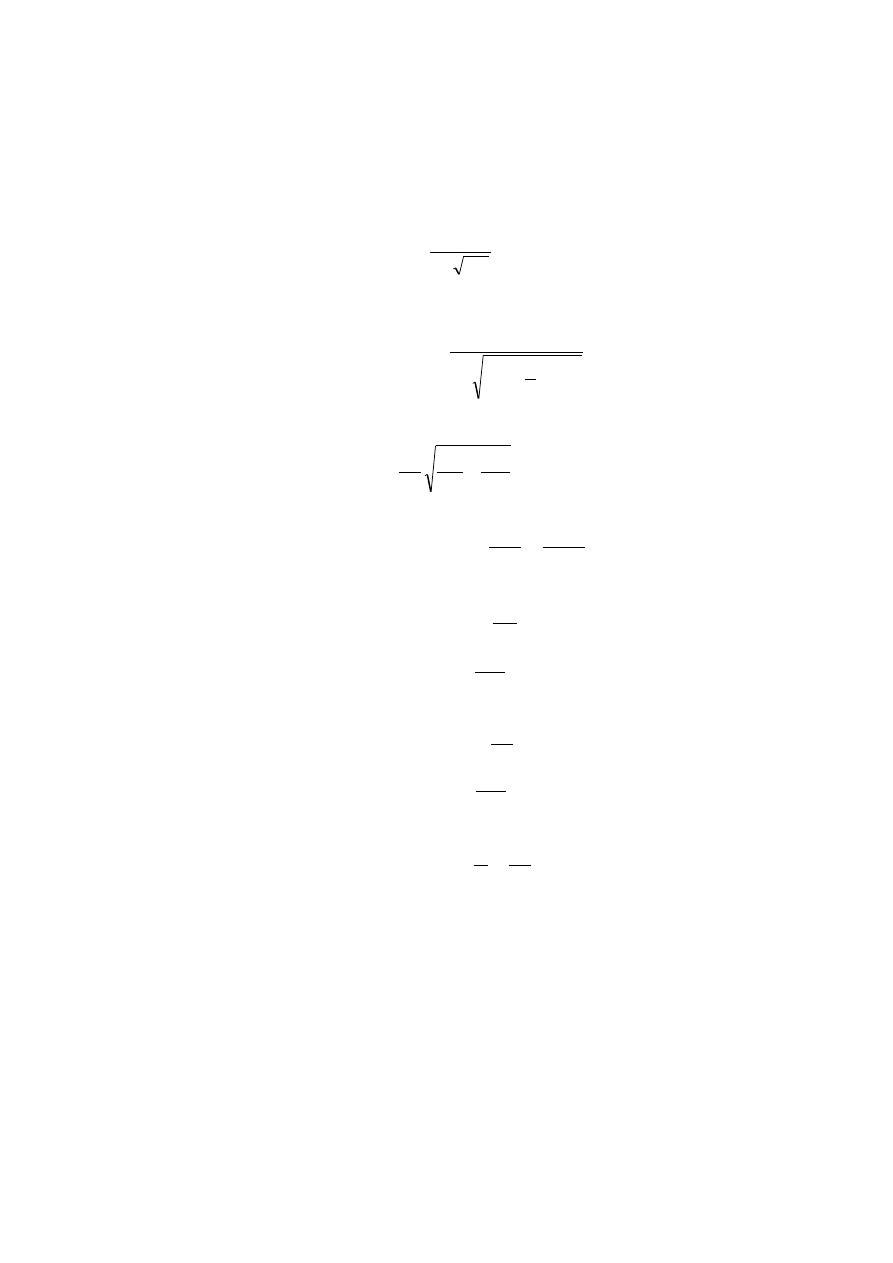
obliczyć wartości I, R, X

L

, X

C

, X

L

  – X

C

, Z oraz kąta przesunięcia fazowego  

ϕ 

pomiędzy napięciem a prądem w obwodzie i zapisać.

Korzystając ze wzorów (7, 8, 9, 10, 11, 12, 13) obliczyć:

-

częstotliwość rezonansowa

LC

f

π

2

1

0

=

(7)

-

częstotliwość 

1

f

 przy której napięcie 

L

U

 osiąga maksimum

2

2

1

2

1

2

1

C

R

LC

f

−

=

π

(8)

-

częstotliwość 

2

f

 przy której napięcie 

c

U

 osiąga maksimum

2

2

2

4

1

2

1

L

R

LC

f

−

=

π

(9)

-

dobroć cewki

R

L

f

R

L

Q

0

0

2

π

ω

=

=

(10)

-

dolna częstotliwość przepuszczania

L

R

2

0

1

−

=

ω

ω

L

R

f

f

π

4

0

1

−

=

(11)

-

górna częstotliwość przepuszczania

L

R

2

0

2

+

=

ω

ω

L

R

f

f

π

4

0

2

+

=

(12)

-

pasmo przepuszczania

Q

L

R

0

1

2

ω

ω

ω

=

=

−

=

−

1

2

f

f

(13)

Dla różnych kombinacji elementów R, L, C wykreślić (uwzględniając na 

wykresie 

punkty U

wmax

):

a)

charakterystyki zmian prądu I w obwodzie w funkcji częstotliwości f; 

( )

f

f

I

=

.

b)

charakterystyki reaktancji X

L

 i X

C

 oraz charakterystykę X

L

 – X

C

 w funkcji 

częstotliwości f;  

( )

f

f

X

L

=

, 

( )

f

f

X

C

=

, 

( )

f

f

X

X

C

L

=

−

.

c)

charakterystyki zmian impedancji Z oraz kąta przesunięcia fazowego  w 
funkcji częstotliwości f;  

( )

f

f

Z

=

, 

( )

f

f

=

ϕ

.

Z wykresów odczytać:

-

Wartość częstotliwości przy której prąd I osiąga wartość maksymalną.

-

Wartość częstotliwości przy której X

L

 – X

C

 równa się zero.

-

Wartość   częstotliwości   przy   której   Z   osiąga   wartość   minimalną   a    
wynosi zero.

-

Wyznaczyć pasmo przepuszczania prądu i dobroć obwodu Q.

-

Określić wpływ R na dobroć obwodu.

-

Określić wpływ R i L na szerokość pasma przepuszczania w obwodzie 
RLC.

-

Zakładając stałą wartość napięcia w obwodzie RLC wykreślić krzywe: 

( )

f

f

I

=

,  

( )

f

f

U

R

=

,  

( )

f

f

U

C

=

,  

( )

f

f

U

L

=

. Obliczyć teoretycznie i  z2-

ytać z wykresów częstotliwość  

1

f

  i  

2

f

  przy których napięcia  

L

U

  i  

C

U

 

osiągają wartość maksymalne. Zbadać wpływ rezystancji na częstotliwo-
ść  

1

f

  i  

2

f

  (szerokość   pasma   przepuszczania   B).   Porównać   wyniki 

pomiarów z wynikami obliczeń teoretycznych.

Komentarz:

Gdy częstotliwość napięcia zasilającego U równa jest częstotliwości rezonan-

sowej f

r

 to X

L

 = X

C

 i obwód ma charakter czysto rezystancyjny. Wówczas war-

tość skuteczna prądu I osiąga maksimum, zgodnie ze wzorem 14. Jest to jeden 
ze   sposobów   znalezienia   częstotliwości   rezonansowej   szeregowego   obwodu 
RLC.

(

)

2

2

C

L

X

X

R

U

Z

U

I

−

+

=

=

(14)

Gdy częstotliwość napięcia zasilającego U równa jest częstotliwości rezonan-

sowej obwodu f

r

  to reaktancja indukcyjna X

L

  równa jest reaktancji pojemno-

ściowej X

C

  i ich różnica wynosi zero. Jest to kolejny sposób na znalezienie 

częstotliwości rezonansowej szeregowego obwodu RLC.
Wraz   ze   wzrostem   częstotliwości   zmienia   się   charakter   obwodu   z   czynno   - 
pojemnościowego na czynno - indukcyjny. Ilustruje to wykres X

L

 – X

C

.

Rezystancja R jest stała w funkcji częstotliwości, reaktancja indukcyjna X

L

 jest 

wprost proporcjonalna a reaktancja pojemnościowa X

C

 odwrotnie proporcjonal-

na do częstotliwości napięcia zasilającego (zgodnie ze wzorami 15, 16, 17):

R = const

(15)

L

f

2

X

L

⋅

π

=

(16)

C

f

2

1

X

C

⋅

π

=

(17)

Wraz ze wzrostem częstotliwości impedancja Z maleje do wartości minimal-

nej   a   następnie   rośnie.   Zmienia   się   wówczas   charakter   obwodu   z   czynno   - 
pojemnościowego na czynno - indukcyjny. Kąt przesunięcia fazowego 

ϕ

 rośnie 

od wartości ujemnych (prąd wyprzedza napięcie) do wartości dodatnich (z2-
ęcie wyprzedza prąd) poprzez wartość zerową. Wtedy prąd jest w fazie z  z2-
ęciem zasilającym (

ϕ

 = 0°) i obwód ma charakter czysto rezystancyjny (wzory 

18, 19):

(

)

2

C

L

2

X

X

R

Z

−

+

=

(18)













−

=

R

X

X

C

L

arctg

ϕ

(19)

Inne obliczenia:

Dla   podanych   wartości   elementów   R,   L,   C   obliczyć   teoretyczną   wartość 

częstotliwości rezonansowej f

0

 i porównać z wartością otrzymaną z pomiarów. 

Do obliczeń można wykorzystać wzór (20)

C

L

f

⋅

=

π

2

1

0

(20)

lub przydatny w praktyce wzór (21) (L podstawić w mH, C w F)

C

L

f

⋅

=

5033

0

(21)

Dla obliczonej częstotliwości rezonansowej f

0

  wyliczyć rezystancję charakte-

rystyczną obwodu 

ρ

 w stanie rezonansu napięć (wzór 22) oraz dobroć obwodu Q 

dla tego stanu (wzór 23).

C

L

C

1

L

r

r

=

ω

=

ω

=

ρ

(22)

C

L

R

1

R

Q

=

ρ

=

(23)

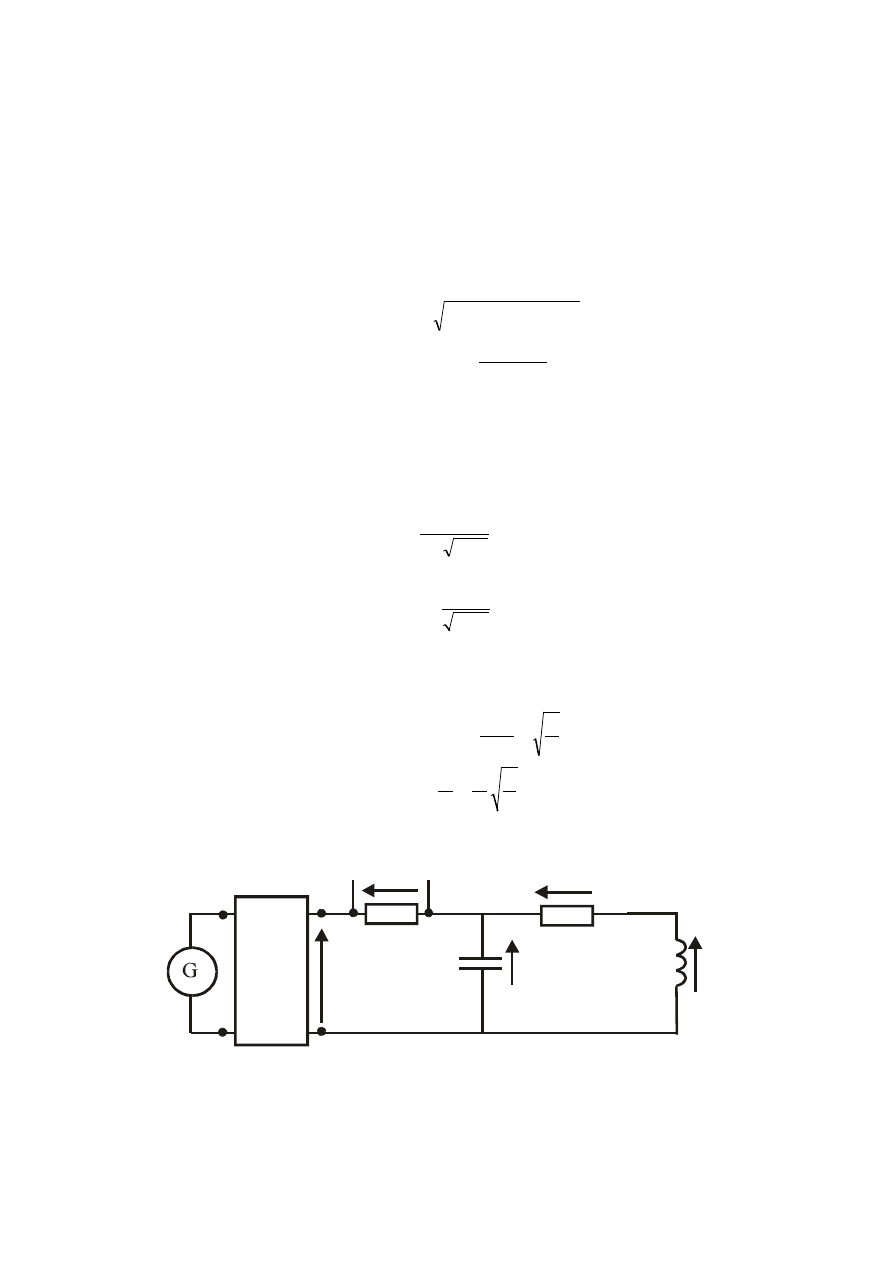
3.2  Układ o równoległym połączeniu elementów RLC
3.2.1 Schemat układu pomiarowego:

R

L

C

U

R

U

L

U

C

R

w

U

w

U=const

model
źródła

napięcia

Zasilając dwójnik równoległy RLC przedstawiony na rys. z idealnego źródła z2-
ęcia o stałej wartości skutecznej wyznaczyć charakterystykę częstotliwościową 
prądu.

Ustawić wartość napięcia zasilającego U na około 1V. Zmierzyć i zapisać 

jego wartość.

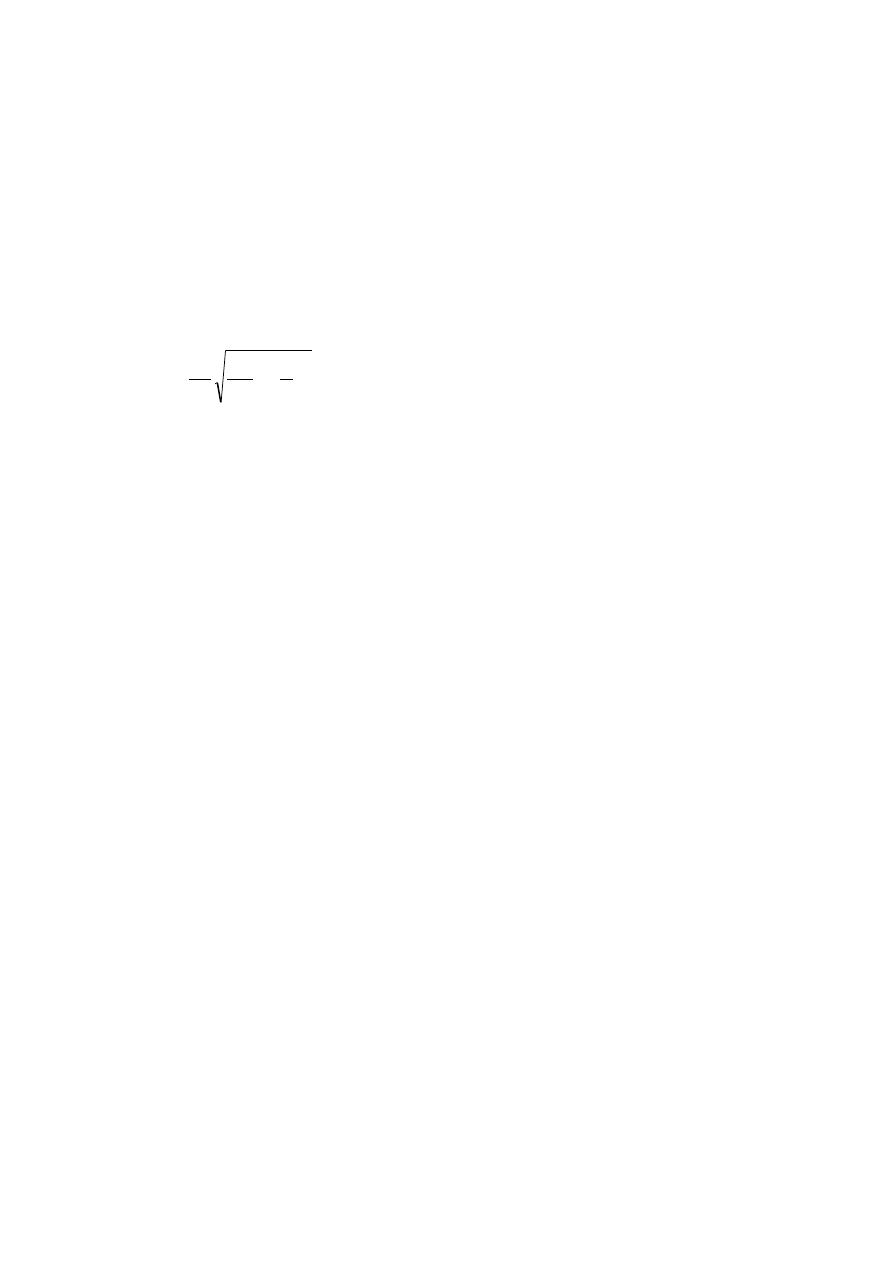
Zapisać wartości nastawionych elementów R, L, C.

Zmieniając częstotliwość f napięcia od ok. 200 Hz do 2,5 kHz z krokiem ok. 

100 Hz (23 pomiarów) zmierzyć wartość skuteczną napięcia U

w

  na rezystorze 

wzorcowym R

w

 podłączając woltomierz do odpowiednich zacisków na modelu. 

Wyniki   zapisać.   Znając   wartość   rezystora   R

w

  obliczamy   wartość   prądu 

płynącego w układzie.

Zmieniając częstotliwość napięcia z generatora, zapisać częstotliwość przy 

której napięcie U

w

 osiąga wartość minimalną.

Pomiary przeprowadzić dla różnych wartości rezystancji R.

Korzystając ze wzoru:

2

0

1

2

1













−

=

L

R

LC

f

π

obliczyć teoretyczną wartość częstotliwości rezonansowej