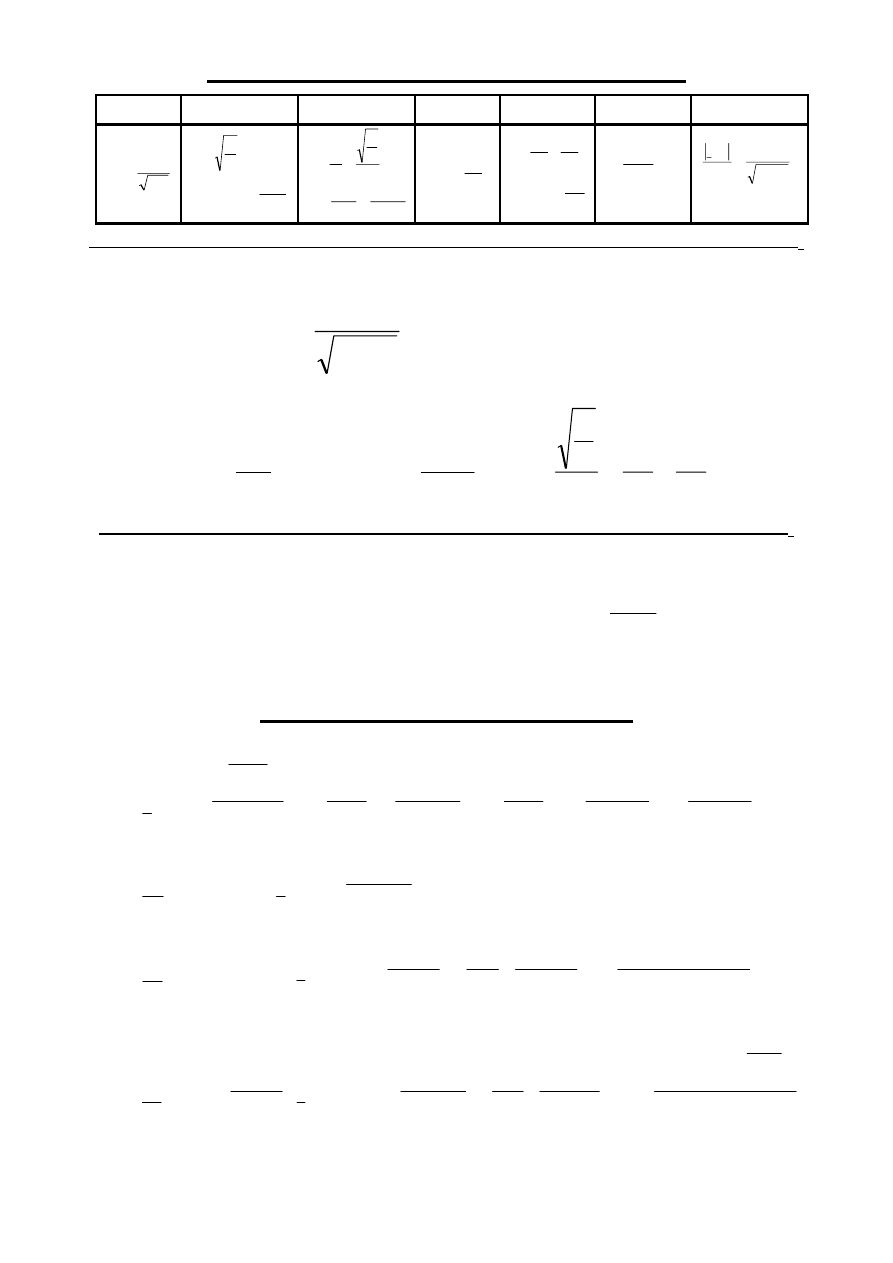
Zestawienie wielkości opisujących SOR

Pulsacja

rezonansowa

Opór

charakterystyczny

Dobroć SOR

Pulsacja

unormowana

Rozstrojenie

względne

Rozstrojenie
bezwzględne

Uniwersalne krzywe

rezonansowe

LC

1

ω

0

=

C

ω

1

L

ω

C

L

ρ

0

0

=

=

=

=

CR

ω

1

R

L

ω

R

C

L

R

ρ

Q

0

0

=

=

=

=

0

n

ω

ω

=

Ω

n

n

0

0

1

ω

ω

ω

ω

ν

Ω

−

Ω

=

−

=

Qν

R

)

X(ω

ξ

=

=

)

arctg(ξ

)

ξ

(

ξ

1

1

I

ξ)

(

I

2

max

r

−

=

+

=

α

Napięcie wymuszające oraz prąd SOR dla pulsacji różnej od pulsacji rezonansowej

ω

0

[ ]

[ ]

⎪

⎩

⎪

⎨

⎧

−

+

=

=

A

))

arctg(ξ

ω

cos(

ξ

1

I

)

(

V

)

ω

cos(

E

)

(

2

max

r

m

t

t

i

t

t

e

przy czym:

[ ]

;

ω

ω

ω

ω

R

C

L

Qν

R

)

X(ω

ξ

;

A

R

E

I

0

0

m

max

r

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

=

=

=

=

Napięcie wymuszające oraz prąd SOR dla pulsacji równej pulsacji rezonansowej

ω

0

X(

ω

0

)

≡ 0 – w SOR występuje rezonans typu szeregowego i wtedy ξ = 0

[ ]

[ ]

⎩

⎨

⎧

=

=

A

)

ω

cos(

I

)

(

V

)

ω

cos(

E

)

(

0

max

r

0

m

t

t

i

t

t

e

;

[ ]

;

A

R

E

I

m

max

r

=

Napięcia na elementach SOR

( )

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

−

+

⋅

⎟

⎠

⎞

⎜

⎝

⎛

=

+

−

⋅

⎟

⎠

⎞

⎜

⎝

⎛

=

+

⎟

⎠

⎞

⎜

⎝

⎛

=

2

2

m

2

m

m

ξ

1

ξ

j

ξ

1

1

R

E

ξ

1

ξ

j

1

R

E

ξ

j

1

R

E

ξ

I

( )

( )

ξ

j

1

E

ξ

I

R

ξ

U

m

R

+

=

⋅

=

( )

( )

(

)

ξ

j

1

E

Q

j

ξ

j

1

E

ω

ω

R

L

ω

j

ξ

I

L

ω

j

ξ

U

n

m

m

0

0

L

+

Ω

⋅

⋅

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

=

⋅

=

( )

( )

ξ

j

1

1

E

Q

j

ξ

j

1

E

ω

ω

CR

ω

1

j

ξ

I

C

ω

j

1

ξ

U

n

m

m

0

0

C

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Ω

⋅

⋅

−

=

+

⎟

⎠

⎞

⎜

⎝

⎛

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

⋅

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Napięcia na elementach SOR w stanie rezonansu

ω = ω

0

→ Ω

n

= 1

oraz

ξ = 0

( )

m

R

E

ξ

U

=

( )

(

)

m

L

E

Q

j

ξ

U

⋅

+

=

( )

(

)

m

C

E

Q

j

ξ

U

⋅

−

=

W stanie rezonansu SOR amplitudy napięć na elementach L oraz C są Q-krotnie
większe od amplitudy napięcia zasilającego. Zjawisko to nazywa się przepięciem
rezonansowym – jeśli nie jest ono kontrolowane to może zagrozić „całości” SOR.

Przykład

R= 50

Ω

( typowa wartość stosowana w telekomunikacji )

, L= 6,25 mH, C= 80,00 pF

Amplituda napięcia sygnału PR1 w Krakowie |E

1

|

≈ 0,094 mV .

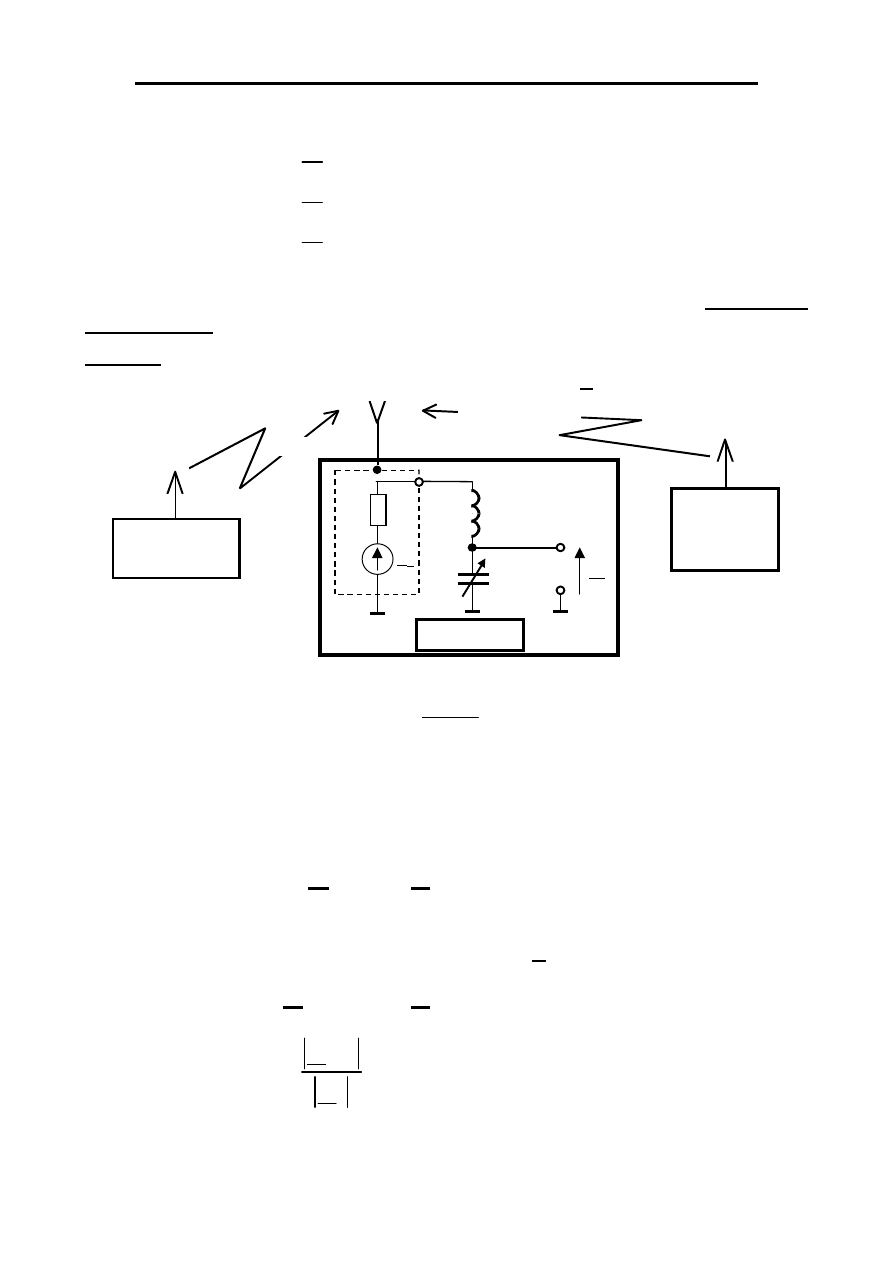
Mo

de

l a

nt

en

y

L

C

U

R

E

A

TX

f

1

≈ 113,5 kHz

TX PR 1

f = 225 kHz

Solec Kujawski

Zakłócenie

Sygnał użyteczny

BC RX

Pulsacja rezonansowa:

⎥⎦

⎤

⎢⎣

⎡

=

s

Mrad

414

,

1

ω

0

;

[ ]

kHz

225

f

0

≈

Opór charakterystyczny:

[ ]

Ω

=

k

839

,

8

ρ

Dobroć:

77

,

176

Q

=

Amplituda napięcia wyjściowego SOR:

|U

1

| = Q

⋅|E

1

|

=

16,62 mV

Zły TX f

TX

= 113,5 kHz: f

2

≈ 227 kHz w odległości l = 5 km i mocy 2-giej

harmonicznej P= 50 mW co daje w przybliżeniu: |E

1TX

|

≈ 0,199

mV

|U

1TX

| = Q

⋅|E

1TX

|

=

35,26 mV

Poziom zakłócenia:

dB

,53

6

ˆ

12

,

2

U

U

1

TX

1

=

=

( DWA razy głośniejsze ! )

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

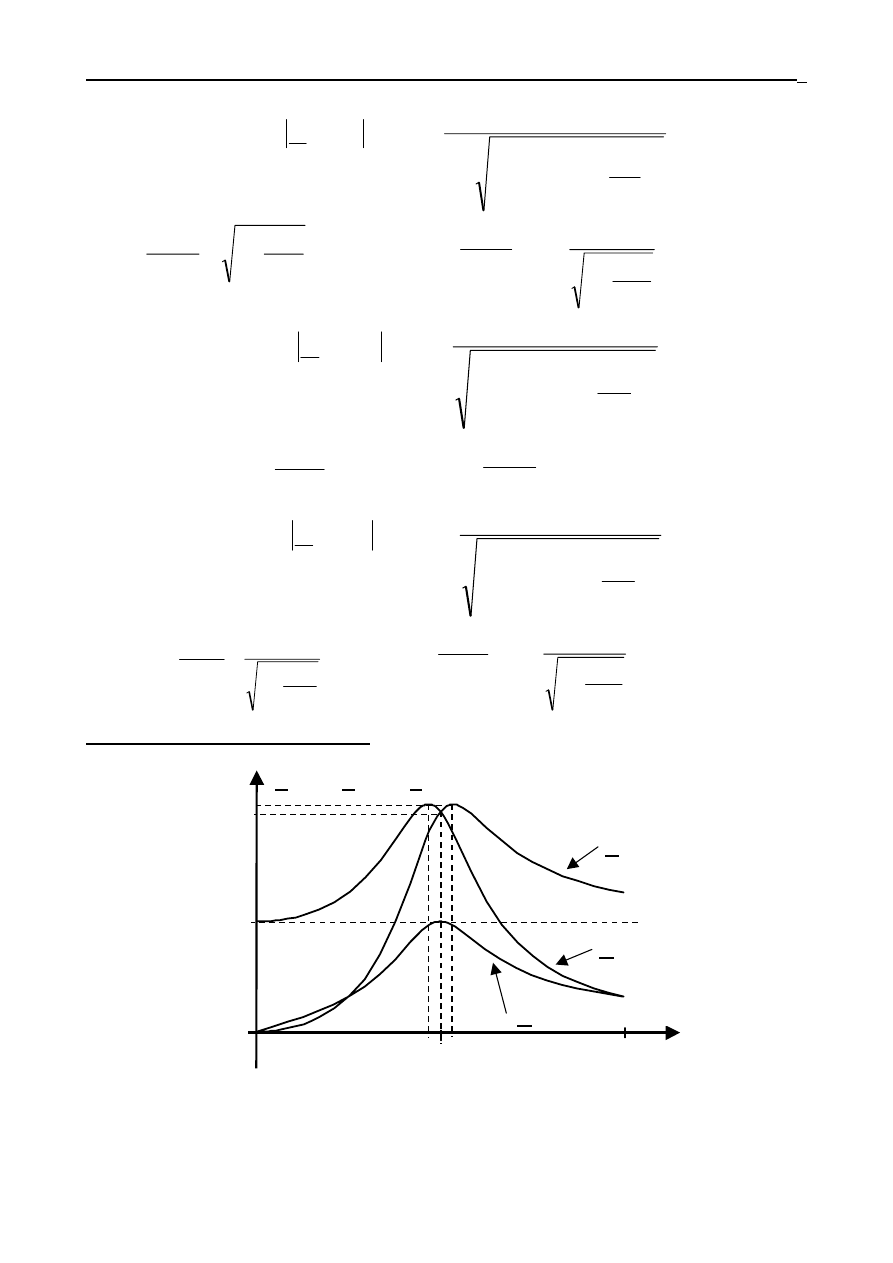
Zmiany amplitud napięć SOR w funkcji pulsacji unormowanej

Ω

n

( )

2

n

n

2

n

m

n

C

Cm

1

Q

1

1

QE

U

U

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Ω

−

Ω

+

Ω

⋅

=

Ω

=

;

1

Q

2

1

1

ω

ω

2

0

max

C

<

−

=

;

m

m

2

max

0

max

C

Cm

QE

E

Q

4

1

1

Q

ω

ω

U

>

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

( )

2

n

n

2

m

n

R

Rm

1

Q

1

1

E

U

U

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Ω

−

Ω

+

⋅

=

Ω

=

;

1

ω

ω

0

max

R

=

;

m

max

0

max

R

Rm

E

ω

ω

U

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

( )

2

n

n

2

n

m

n

L

Lm

1

Q

1

QE

U

U

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Ω

−

Ω

+

Ω

⋅

=

Ω

=

;

1

Q

2

1

1

1

ω

ω

2

0

max

L

>

−

=

;

m

m

2

max

0

max

L

Lm

QE

E

Q

4

1

1

Q

ω

ω

U

>

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

W praktyce dla SOR o dobroci Q > 5:

0

max

L

max

C

ω

ω

ω

=

≅

,

.

m

max

Lm

max

Cm

QE

U

U

=

≅

E

m

QE

m

1

2

Ω

n

|U

L

(

Ω

n

)|

|U

C

(

Ω

n

)|

|U

R

(

Ω

n

)|

|U

L

(

Ω

n

)|, |U

C

(

Ω

n

)|, |U

R

(

Ω

n

)|

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

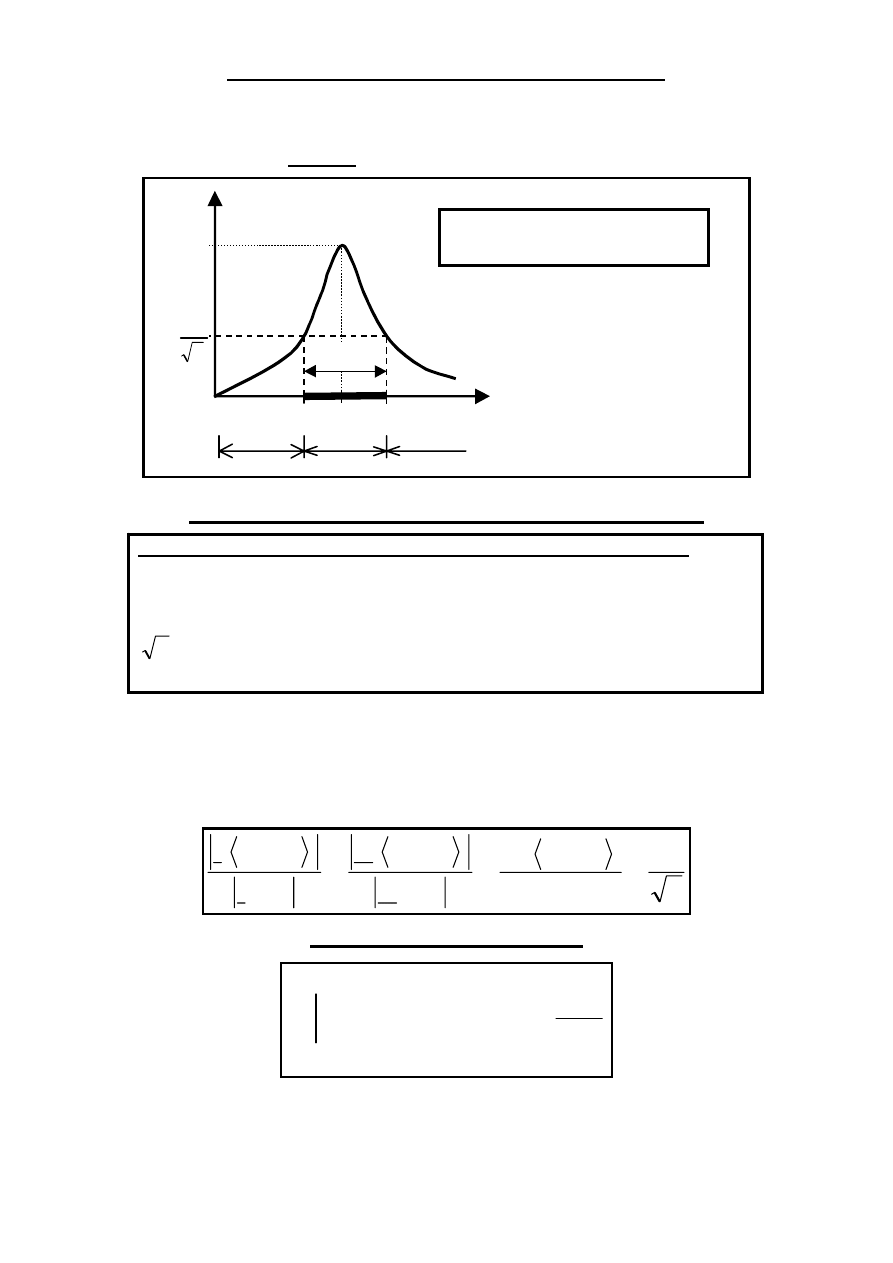
SOR jako filtr środkowoprzepustowy.

SOR przenosi z małymi zniekształceniami ( amplitudy i fazy ) sygnały
o pulsacjach

ω

s

bliskich jego pulsacji rezonansowej

ω

0

, natomiast

silnie zniekształca ( filtruje ) sygnały o pulsacjach odległych od

ω

0

.

ω

0

ω

1

ω

2

ω

I

m

(

ω)

I

mr

I

mr

PZ

PP

PZ

PZ – pasmo zaporowe

PP – pasmo przepustowe

SOR jako

Filtr – środkowoprzepustowy

ω

1

– dolna granica PP

ω

2

– górna granica PP

2

B|

3-dB

Trzydecybelowe ( 3-dB ) pasmo przepustowe

Trzydecybelowym ( 3-dB ) pasmem przepustowym ( PP ) SOR ( filtru
środkowoprzepustowego ) nazywamy przedział pulsacji [

ω

1

,

ω

2

], dla

których przy stałej amplitudzie E

m

napięcia wymuszającego

amplituda I

m

prądu płynącego w obwodzie maleje nie więcej niż

2

-krotnie w stosunku do maksymalnej amplitudy prądu I

mr

wymuszonego przez napięcie o pulsacji rezonansowej

ω

0

.

Przepustowe pasmo 3-dB to przedział pulsacji sygnału napięciowego
wymuszającego prąd w SOR, dla którego rozstrojenie bezwzględne

ξ

spełnia zależność:

⎪ξ⎪≤

1

W 3-dB paśmie przepustowym zachodzi związek

(

)

(

)

(

)

2

1

)

ω

(

I

ω

,

ω

I

)

ω

(

Y

ω

,

ω

Y

)

ω

(

I

ω

,

ω

I

0

m

2

1

m

0

2

1

0

2

1

≥

=

=

Szerokość pasma 3-dB

Q

ω

ω

ω

B

0

1

2

dB

-

3

=

−

=

∆

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Moc czynna SOR

( )

[ ]

( )

( )

[ ]

(

)

[

]

ξ

j

1

R

Re

ξ

1

R

E

2

1

ξ

Z

Re

ξ

I

2

1

I

U

Re

2

1

ξ

P

2

2

m

2

*

+

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

=

⋅

=

⋅

=

( )

2

2
m

ξ

1

1

R

E

2

1

ξ

P

+

⋅

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

W stanie rezonansu:

ξ= 0 i wtedy moc czynna SOR osiąga maksimum

( ) ( )

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

=

=

=

R

E

2

1

P

ξ

P

ξ

P

max

2
m

max

0

ξ

ξ

Moce czynne SOR na krańcach przepustowego pasma 3-dB

(

)

(

)

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

=

+

=

=

−

=

R

E

4

1

P

2

1

1

ξ

P

1

ξ

P

2
m

max

2

1

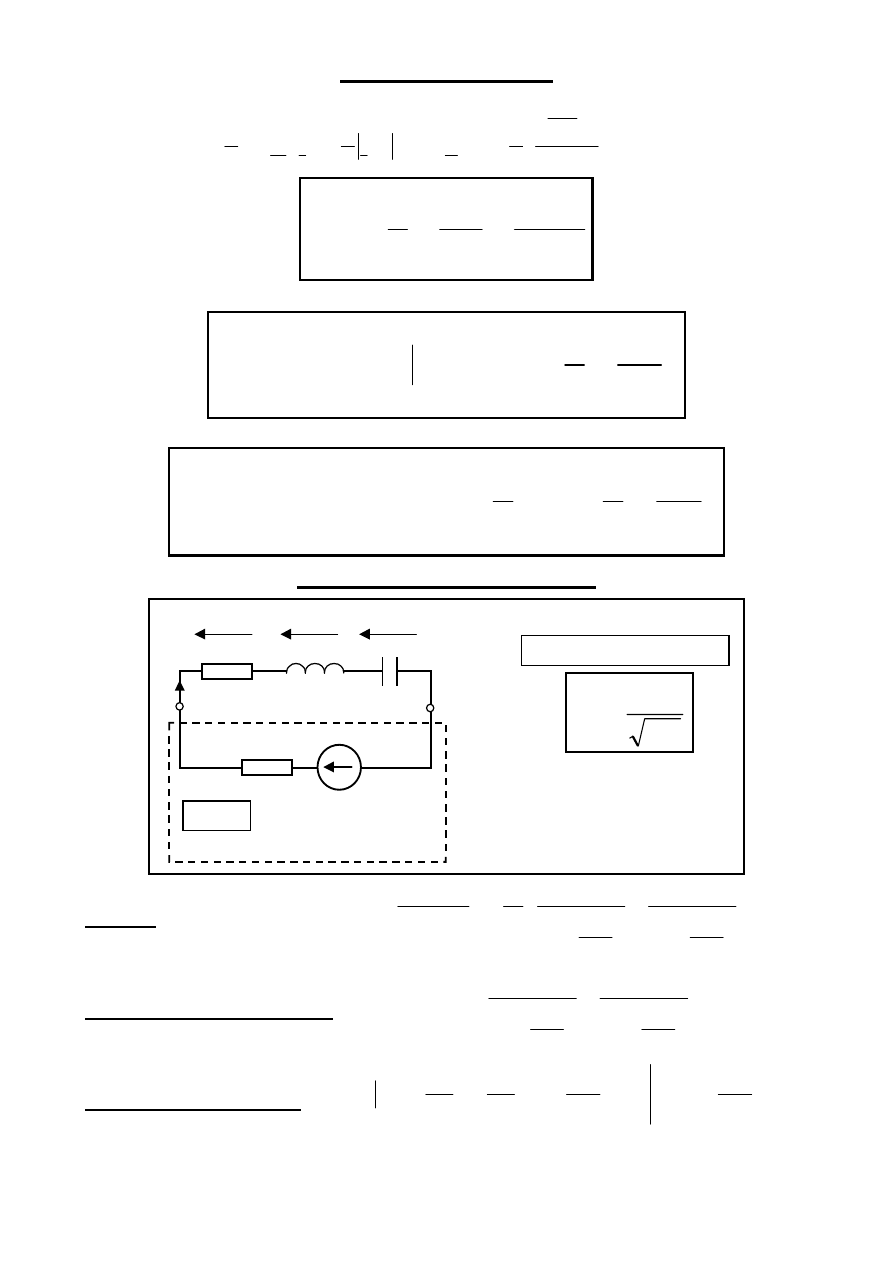
Współpraca SOR z NZE

C

R

L

ω ∈ (0,+∞) rad/s

e(t) = E

m

sin

ωt

u

R

u

L

u

C

i

LC

1

ω

0

=

Pulsacja rezonansowa

R

R

w

NZE

Dobroć:

⎟

⎠

⎞

⎜

⎝

⎛ +

=

⎟

⎠

⎞

⎜

⎝

⎛ +

⎟

⎠

⎞

⎜

⎝

⎛

=

+

=

′

R

R

1

Q

R

R

1

1

R

ρ

R

R

ρ

Q

w

w

w

Rozstrojenie bezwzględne:

( )

⎟

⎠

⎞

⎜

⎝

⎛ +

=

⎟

⎠

⎞

⎜

⎝

⎛ +

=

′

=

′

R

R

1

ξ

R

R

1

1

Qν

ν

Q

ξ

w

w

Szerokość pasma 3-dB:

⎟

⎠

⎞

⎜

⎝

⎛ +

=

⎟

⎠

⎞

⎜

⎝

⎛ +

⎟

⎠

⎞

⎜

⎝

⎛

=

′

=

′

R

R

1

B

R

R

1

Q

ω

Q

ω

B

w

dB

3

w

0

0

dB

3

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

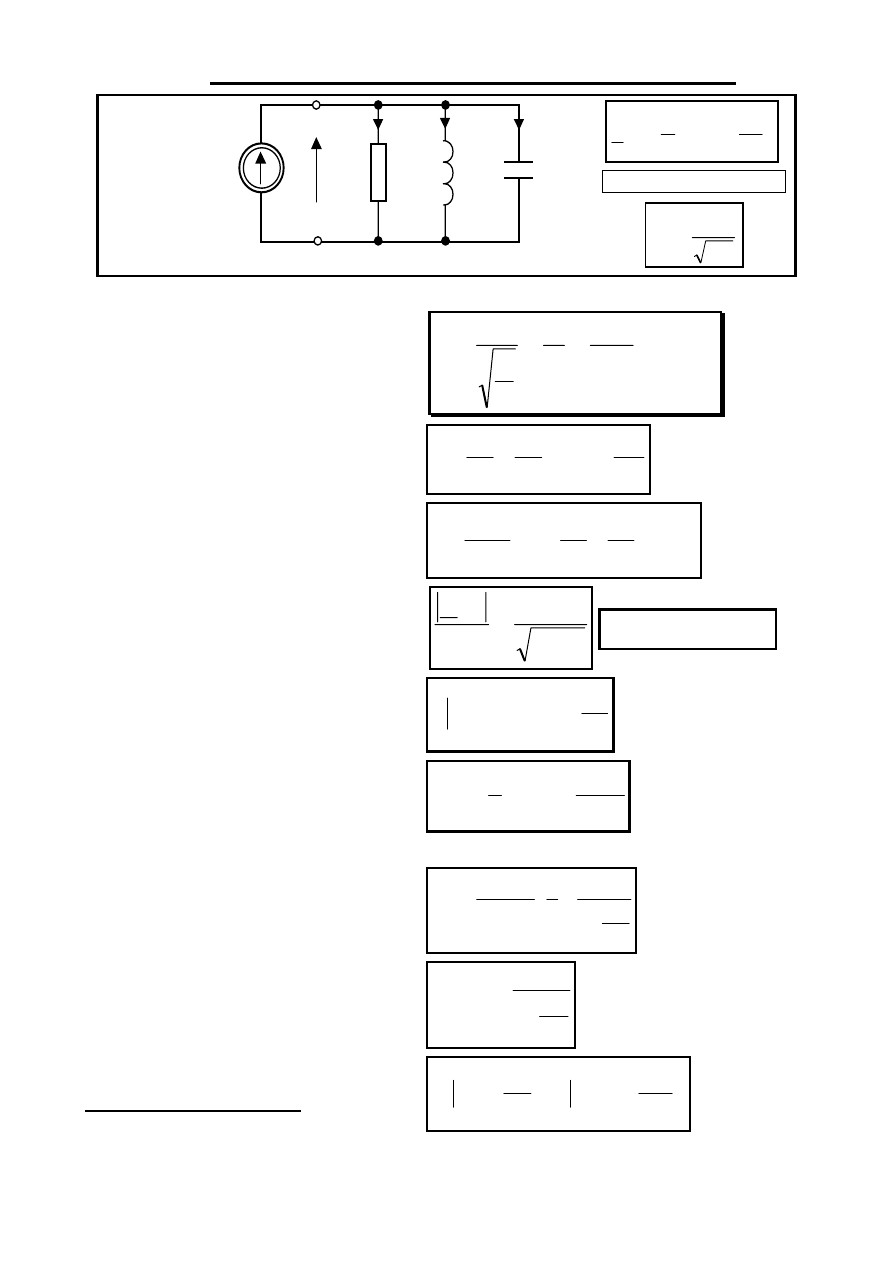
Równoległy obwód rezonansowy ( ROR )

L

ω ∈ (0,+∞) rad/s

j(t) = J

m

cos

ωt

i

R

i

L

i

C

u

LC

1

ω

0

=

Pulsacja rezonansowa

R

C

( )

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

=

L

ω

1

C

ω

j

R

1

ω

Y

Ponieważ ROR ma strukturę dualną do SOR więc jego analiza przebiega analogicznie z zastosowaniem zasad dualizmu.

Dobroć:

CR

ω

L

ω

R

ρ

R

C

L

R

Q

0

0

=

=

=

=

Rozstrojenie względne:

n

n

0

0

1

ω

ω

ω

ω

ν

Ω

−

Ω

=

−

=

Rozstrojenie bezwzględne:

( )

ν

Q

ω

ω

ω

ω

Q

G

ω

B

ξ

0

0

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

=

Uniwersalne krzywe rezonansowe:

2

m

ξ

1

1

U

)

(ξ

U

+

=

r

ξ

arctg

ξ)

(

−

=

ϕ

Szerokość pasma 3-dB:

Q

ω

ω

ω

B

0

1

2

dB

-

3

=

−

=

∆

Moc czynna ROR:

( )

( )

2

2
m

ξ

1

1

R

J

2

1

ξ

P

+

⋅

⋅

=

Współpraca z PZE:

w

w

w

R

R

1

Q

ρ

1

R

R

R

R

Q

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

′

Rozstrojenie bezwzględne:

w

R

R

1

ξ

ν

Q

ξ

+

=

′

=

′

Szerokość pasma 3-dB:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

′

=

′

w

dB

3

0

dB

3

R

R

1

B

Q

ω

B

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Przykład SOR C= 2 nF, R

1

= 2

Ω zestrojony na f

0

= 300 kHz ma przenosić pasmo B|

3dB

=

10 kHz. Dobrać rezystancję oporu korygującego R

k

oraz wyliczyć wymaganą wartość

indukcyjności cewki L.

[ ]

π

600

f

π

2

ω

s

krad

0

0

=

=

(

)

mH

281

,

0

10

2

10

π

600

1

C

ω

1

L

LC

1

ω

9

2

3

2
0

0

≅

⋅

⋅

=

=

→

=

−

+

[ ]

s

krad

3dB

π

20

f

π

2

B

=

=

30

π

20

π

600

B

ω

Q

Q

ω

B

3dB

0

0

3dB

=

=

=

→

=

Ω

≅

⋅

⋅

⋅

⋅

=

=

→

=

−

+

842

,

8

0

3

10

2

10

π

600

1

CQ

ω

1

R

CR

ω

1

Q

9

3

0

0

R > R

1

:

R= R

1

+ R

k

Æ

R

k

= R – R

1

= 6,842

Ω

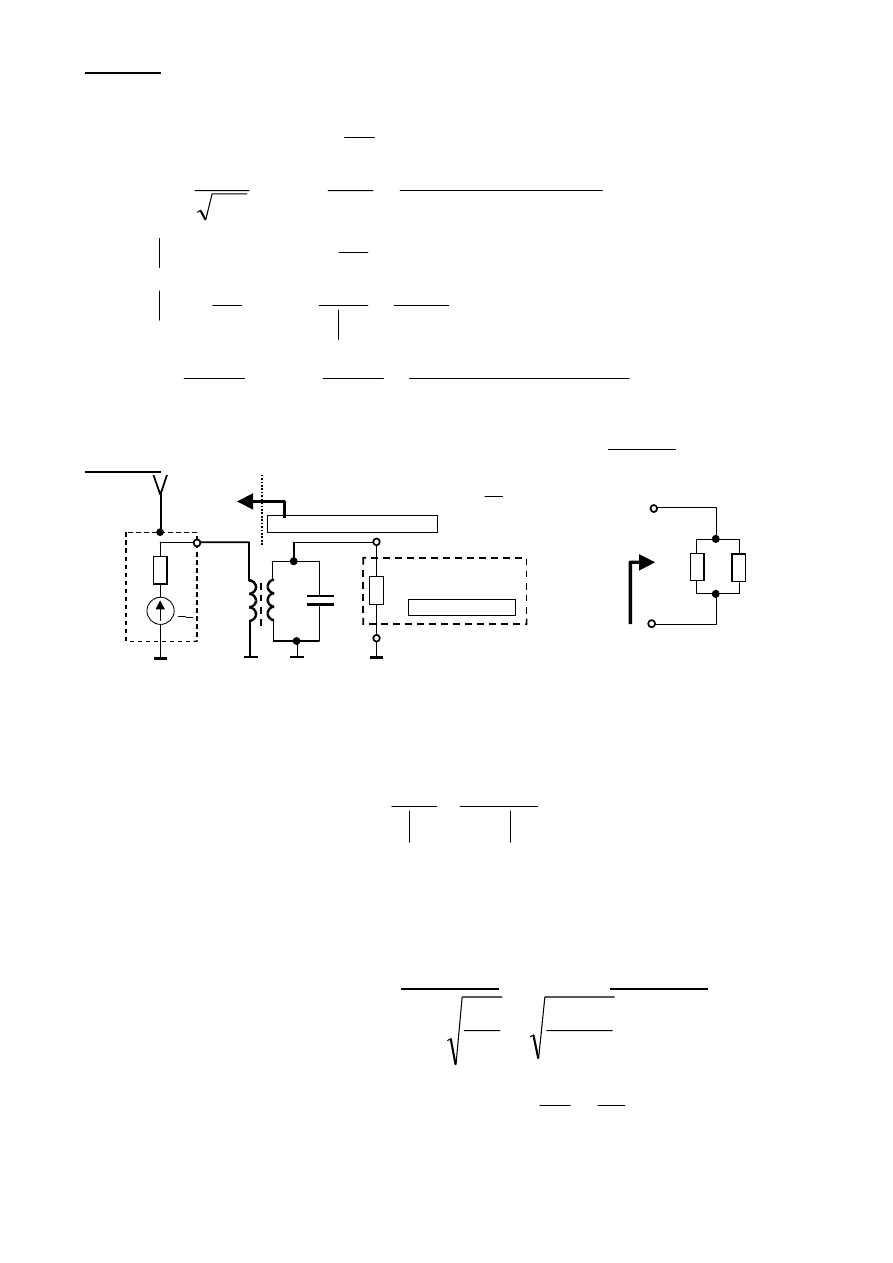
Przykład

Długofalowy ( LW ) niestrojony obwód wejściowy.

Mo

de

l a

nt

en

y

L

C

R

A

E

A

R

w

L

A

Kolejny stopień RX

A

2

1

R

η

R

≈

R

w

R

1

R

0

A

L

n

n

η

=

(n

A

)

(n

L

)

Opór wnoszony przez sprzężenie

– przekładnia zwojowa

L= 6,2 mH; n

L

= 250 zw.; R

A

= 50

Ω

Pasmo:

f

∈<150,300> kHz;

(2

∆f)= (f

g

–f

d

)= 150 kHz

Środek

pasma:

f

0

= 225 kHz;

ω

0

= 450

π krad/s

Szerokość pasma:

B = 2

π(f

g

–f

d

) = 2

π150 krad/s = 300 π krad/s

Dobroć:

5

,

1

f)

(2

f

B

ω

Q

dB

3

0

dB

3

0

=

∆

=

=

Opór R

0

ROR L–C:

Ω

=

⋅

⋅

⋅

=

⋅

=

k

13,148

6,2

π

450

1,5

L

ω

Q

R

0

0

Przyjmujemy:

R

w

= R

1

= 2R

0

( można inaczej, ale tak aby:

R

0

= R

1

⎢⎢R

w

)

R

w

= 26,296 k

Ω;

R

1

= 26,296 k

Ω

wtedy przekładnia zwojowa:

23

50

26296

R

R

η

A

1

≈

=

=

.

zw.

11

50

2

23

1

η

n

n

L

A

≈

=

=

Czyli uzwojenie antenowe L

A

musi mieć:

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

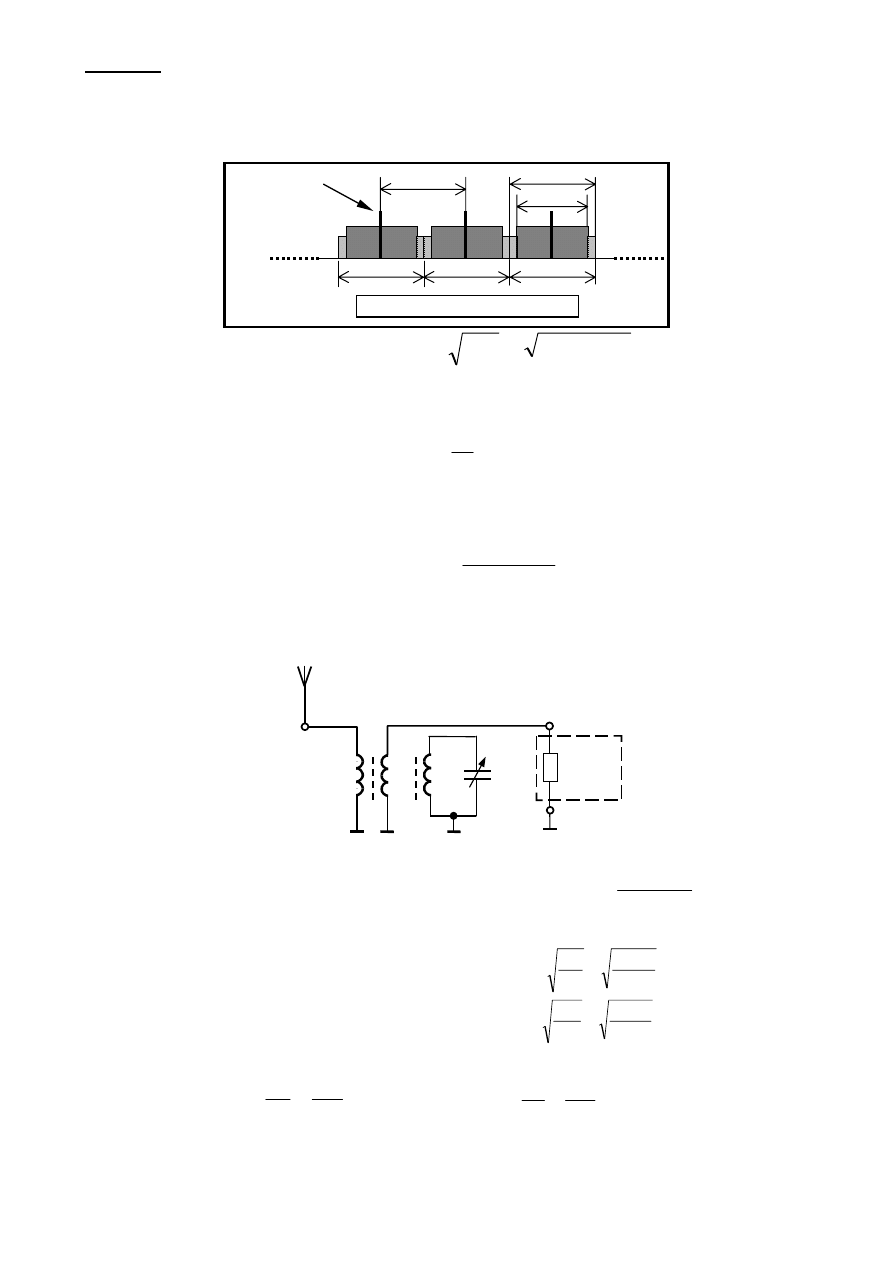
Przykład Wejściowy strojony ROR fal średnich ( Ś, MW ) AM.

( obliczenia uproszczone )

Pasmo

MW: f

∈<510, 1620> kHz = <0,51, 1,62> MHz;

(2

∆f)= (f

g

–f

d

)= 1110 kHz

Kanał radiowy MW AM :

∆f = 9 kHz ( f

mod

= 4 kHz )

9 kHz

9 kHz

8 kHz

Kanał

Kanał

Kanał

częstotliwość

nośna f

n

kanału

Kanały radiowe fal D i Ś ( AM )

Środek pasma MW AM:

kHz

95

,

908

1620

510

f

f

f

g

d

0

=

⋅

=

=

Przyjmujemy:

f

0

= 900 kHz

( u nas częstotliwość projektowa ROR)

Szerokość pasma ROR:

B = 30 kHz

( mniej więcej trzy kanały )

Dobroć:

30

B

f

Q

0

=

=

Uwaga ! W dalszej części pomijamy straty r

L

oraz r

C

.

C kondensatora strojącego:

C= 150 pF

( wynika z innych rozważań )

Wymagany

opór:

(

)

Ω

≈

⋅

=

k

35

C

f

2π

Q

R

0

0

Rezystancja

anteny:

R

A

= 50

Ω

Rezystancja R

w

I-stopnia:

R

w

= 2 k

Ω

L

C

R

w

= 2 k

Ω

L

A

(n

A

)

(n

L

)

L

s

(n

s

)

R

A

= 50

Ω

Rezystancje wnoszone do ROR L-C winny spełniać związek

( połączenie równoległe

R

A

oraz R

we

)

wynikający z dopasowania energetycznego:

we

A

we

A

0

R

R

R

R

R

′

+

′

′

′

=

Przyjmujemy:

R

′

A

= R

′

we

= 70 k

Ω

Przekładnia zwojowa od strony anteny:

37

50

70000

R

R

η

A

A

A

≈

=

′

=

Przekładnia zwojowa od strony obciążenia:

6

2000

70000

R

R

η

we

we

s

≈

=

′

=

Przyjmujemy: n

L

= 175 zw. i z tego:

zw.

5

,

4

37

175

η

n

n

A

L

A

≈

=

=

zw.

30

6

175

η

n

n

s

L

s

≈

=

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

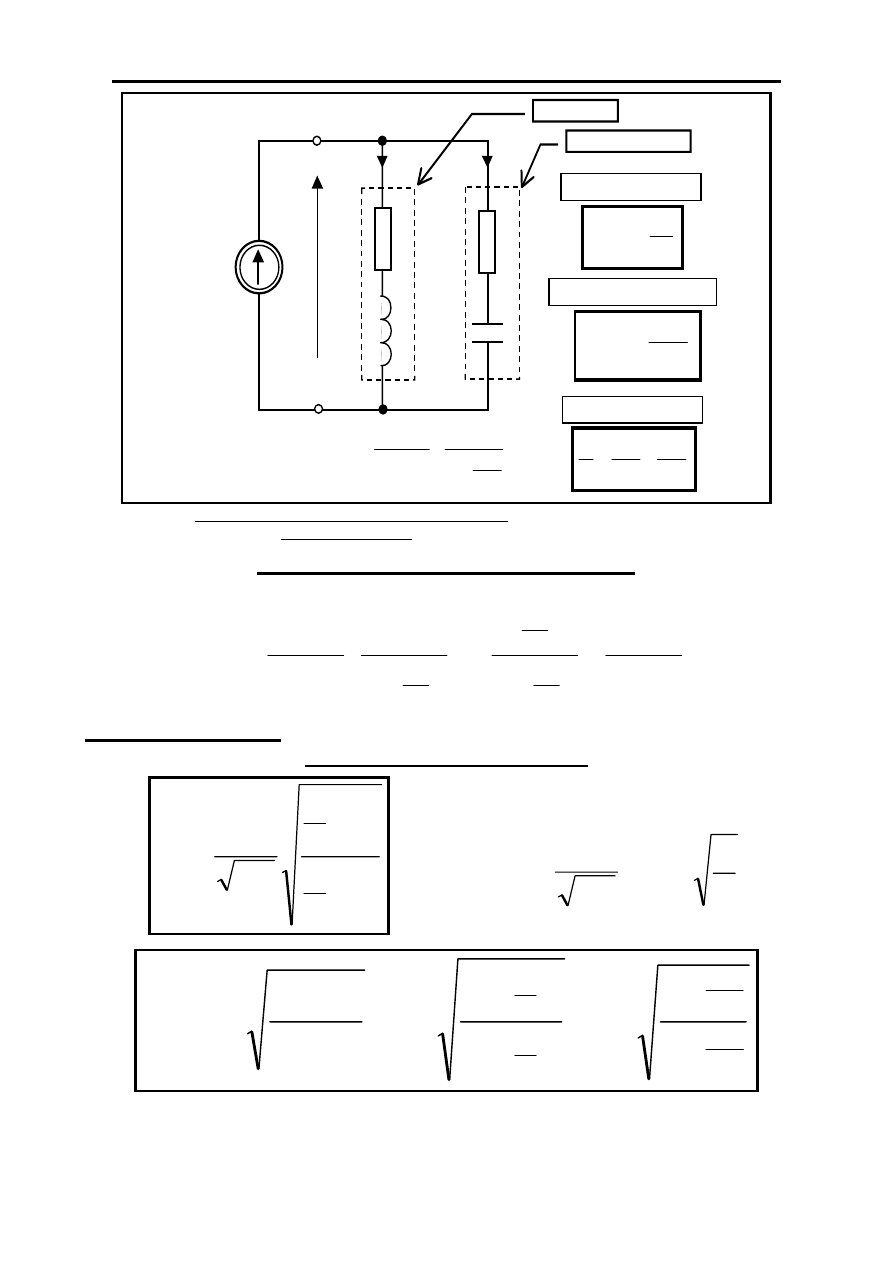
Dwugałęźny równoległy obwód rezonansowy ( DROR )

ω ∈ (0,+∞) rad/s

j(t) = J

m

cos

ωt

i

L

i

C

u

r

C

C

r

L

L

Model Cewki

Model Kondensatora

Dobroć cewki

L

L

r

ωL

ω)

(

Q

=

Dobroć kondensatora

C

C

ωCr

1

ω)

(

Q

=

C

jω

1

r

1

L

jω

r

1

)

b(ω

j

)

g(ω

)

Y(ω

C

L

+

+

+

=

+

=

Dobroć DROR

Co

Lo

Q

1

Q

1

Q

1

+

=

W praktyce przeważnie spełnione są nierówności: Q

L

(

ω) >> 1 oraz Q

C

(

ω) >> 1,

z których wynika, że: X

L

(

ω) >> r

L

oraz X

C

(

ω) >> r

C

.

Pulsacja rezonansowa DROR

( )

( )

⎟

⎟

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎜

⎜

⎝

⎛

+

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

⎟

⎟

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎜

⎜

⎝

⎛

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

+

=

2

2

L

2

2

C

2

2

C

2

2

L

L

L

ω

r

L

ω

C

ω

1

r

C

ω

1

j

C

ω

1

r

1

L

ω

r

r

)

Y(ω

Warunek rezonansu b(

ω) = 0.

Pulsacja rezonansowa DROR

2

C

2

L

r

r

C

L

r

C

L

LC

1

ω

−

−

=

LC

1

ω

0

=

C

L

ρ

=

( )

( )

2

Co

2

Lo

C

L

Q

1

Q

1

0

2

ρ

r

2

ρ

r

0

2

C

2

2

L

2

0

r

1

1

ω

1

1

ω

r

ρ

r

ρ

ω

ω

−

−

=

−

−

=

−

−

=

gdzie: Q

Lo

– dobroć cewki dla pulsacji

ω

o

;

Q

Co

– dobroć kondensatora dla pulsacji

ω

o

;

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Jeśli w DROR spełnione są nierówności: Q

Lo

>>1 i Q

Co

>>1 można z dobrym przybliżeniem

przyjąć:

LC

1

ω

ω

0

r

=

≈

. W

szczególności, gdy r

L

= r

C

, to

ω

r

=

ω

0

.

Opór dynamiczny DROR

Założenia: Z1). Dobroci cewki i kondensatora są duże:

Q

Lo

>>1 i Q

Co

>>1;

Z2). DROR badamy w małym otoczeniu pulsacji rezonansowej

ω

r

.

Z Z1 wynika:

( )

( )

C

2

L

2

r

ωC

1

i

r

ωL

>>

>>

( )

( )

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

≈

L

ω

1

C

ω

j

C

ω

1

r

L

ω

r

)

Y(ω

2

C

2

L

Z Z2 wynika:

r

ρ

r

L

ω

Q

r

ωL

Q

L

L

0

Lo

L

L

=

=

≈

=

ρ

L

ω

ωL

0

=

≈

r

ρ

Cr

ω

1

Q

ωCr

1

Q

C

C

0

Co

C

C

=

=

≈

=

ρ

C

ω

1

ωC

1

0

=

≈

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

⎟

⎠

⎞

⎜

⎝

⎛ +

≈

L

ω

1

C

ω

j

ρ

r

r

)

Y(ω

2

C

L

W stanie rezonansu DROR jest reprezentowany przez opór dynamiczny R

d

o wartości:

(

)

C

r

r

L

r

r

ρ

R

C

L

C

L

2

d

+

=

+

=

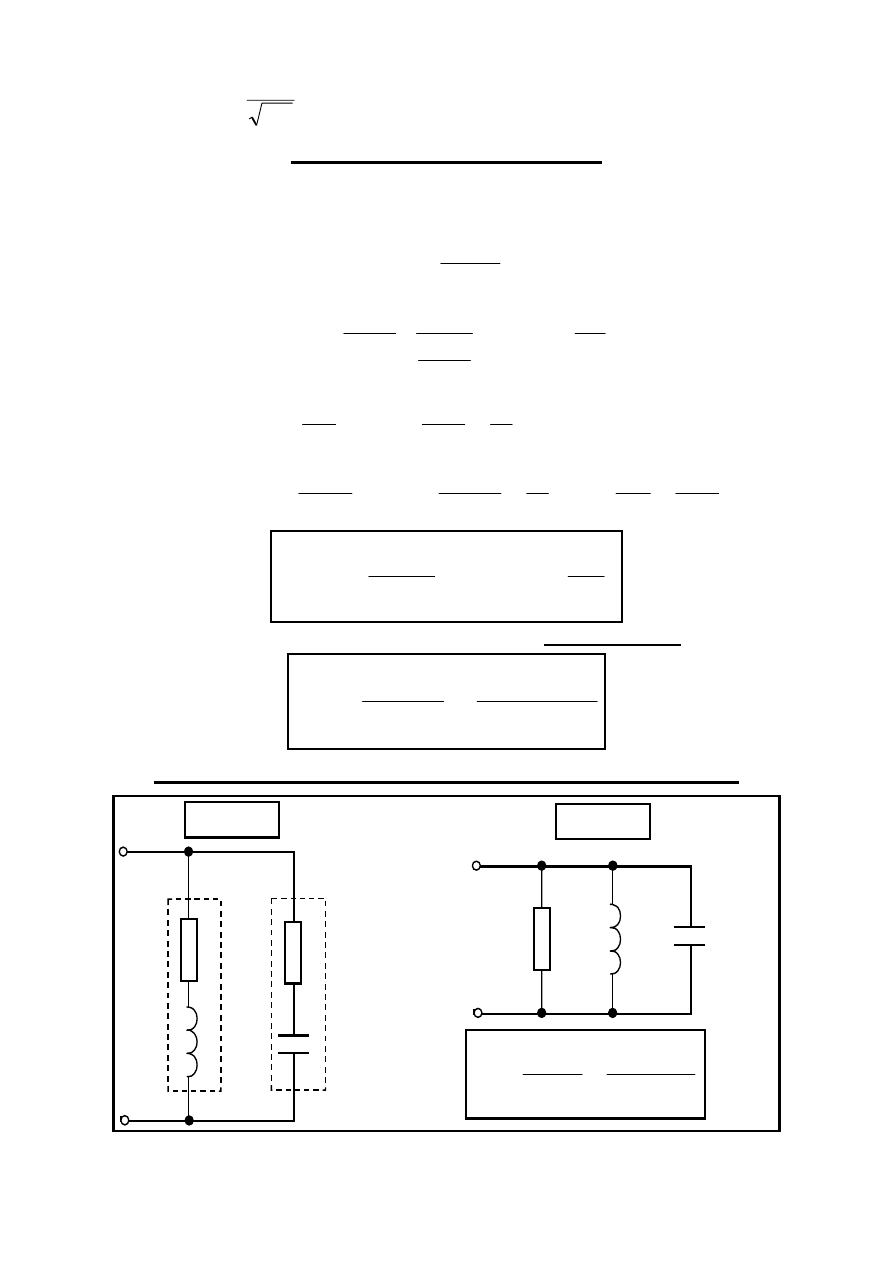
ROR równoważny DROR w stanie rezonansu

r

C

C

r

L

L

L

R

d

C

DROR

ROR

(

)

C

r

r

L

r

r

ρ

R

C

L

C

L

2

d

+

=

+

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

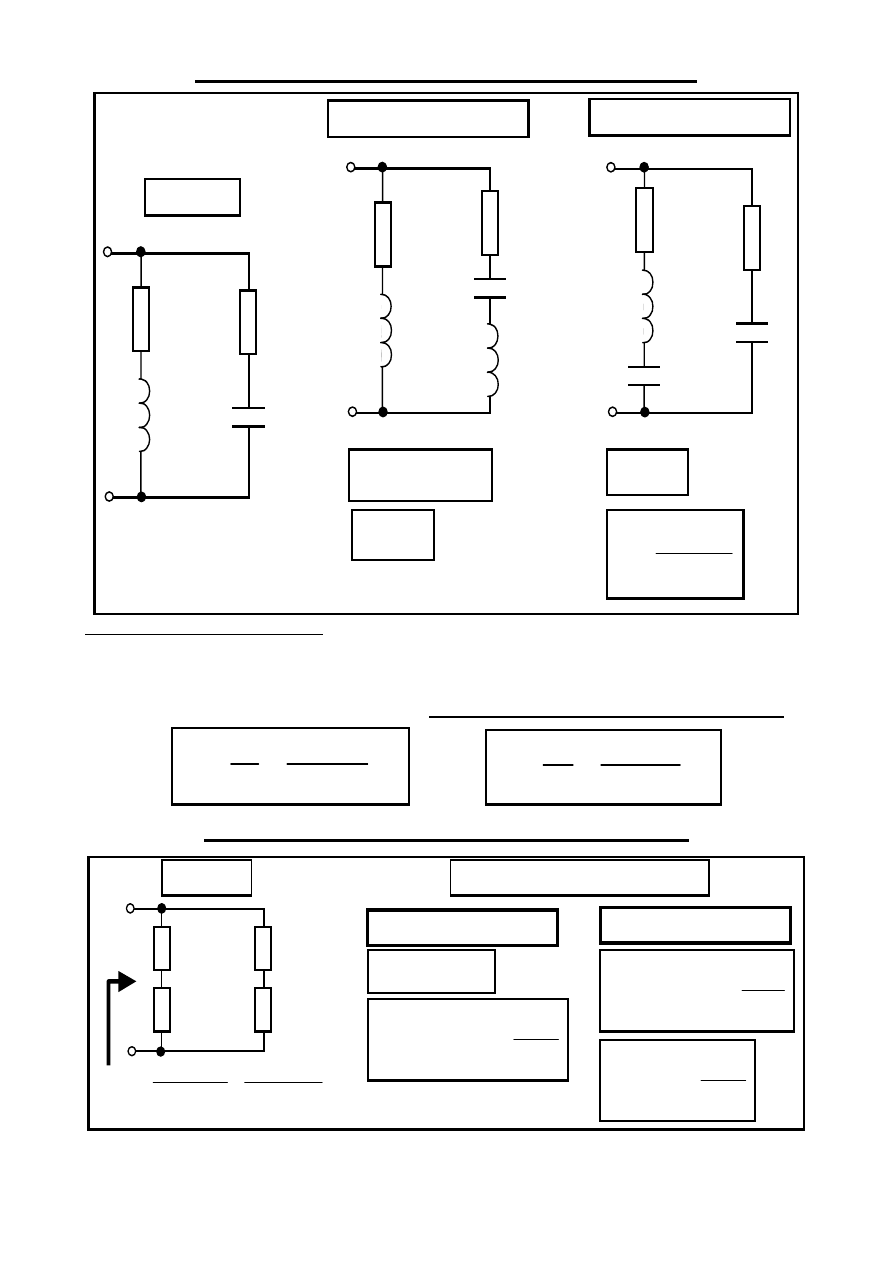
Obwody DROR z dzielonymi elementami

r

2

C

2

r

1

L

1

r

2

C

r

1

L

L

2

DROR

DROR – dzielona L

DROR – dzielona C

r

2

C

2

r

1

L

1

C

1

2

1

L

L

L

+

=

2

C

C

=

1

L

L

=

2

1

2

1

C

C

C

C

C

+

=

DROR z dzielonymi elementami mają mniejszą wartość oporu dynamicznego R

d

niż wyjściowy

obwód DROR, natomiast pulsacja i dobroć są takie same.
W DROR z dzielonymi elementami można regulować wartość rezystancji oporu
dynamicznego R

d

( pozwala to uzyskać dopasowanie energetyczne ), przy stałej pulsacji

rezonansowej i stałej dobroci poprzez dobór współczynników podziału dzielonych elementów:

1

L

L

L

L

L

p

2

1

1

1

L

<

+

=

=

lub

1

C

C

C

C

C

p

2

1

1

2

C

<

+

=

=

Admitancje DROR z dzielonymi elementami

r

2

r

1

DROR

DROR – dzielona L

DROR – dzielona C

( )

1

1

ωL

ω

x

=

x

1

(ω)

x

2

(ω)

( )

2

2

2

ωC

1

ωL

ω

x

−

=

( )

1

1

1

ωC

1

ωL

ω

x

−

=

( )

2

2

ωC

1

ω

x

−

=

Reaktancje gałęzi DROR

)

ω

(

x

j

r

1

)

ω

(

x

j

r

1

)

Y(ω

2

2

1

1

+

+

+

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

−

+

+

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

+

=

)

ω

(

x

r

)

ω

(

x

)

ω

(

x

r

)

ω

(

x

j

)

ω

(

x

r

r

)

ω

(

x

r

r

)

Y(ω

2
2

2

2

2

2

1

2

1

1

2
2

2

2

2

2

1

2

1

1

Jeśli

|x

1

(

ω)| >> r

1

oraz

|x

2

(

ω)| >> r

2

, to

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

≈

)

ω

(

x

1

)

ω

(

x

1

j

)

ω

(

x

r

)

ω

(

x

r

)

Y(ω

2

1

2
2

2

2

1

1

i przybliżona pulsacja rezonansowa

ω

0

dana jest równaniem:

0

)

ω

(

x

)

ω

(

x

0

2

0

1

=

+

z którego wynika:

LC

1

ω

0

≈

W pobliżu pulsacji rezonansowej dla obu typów DROR zachodzi:

2

0

2
2

0

2

1

p

C

L

)

ω

(

x

)

ω

(

x

=

=

oraz

2

2

1

d

p

)C

r

(r

L

R

+

=

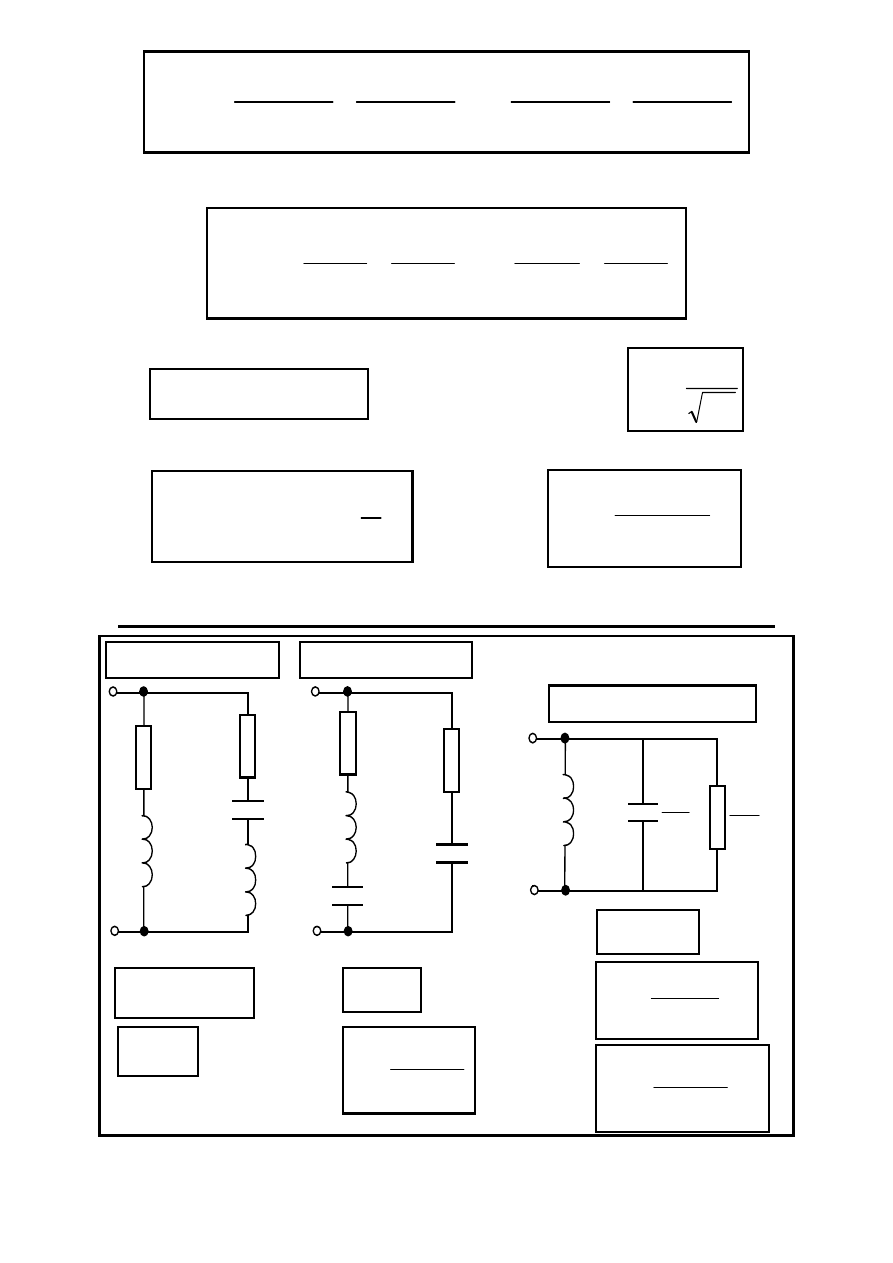
ROR równoważny DROR z dzielonymi elementami

r

2

C

2

r

1

L

1

2

p

C

L

p

2

L

2

Równoważny ROR

DROR – dzielona L

r

2

C

2

r

1

L

1

C

1

2

1

L

L

L

+

=

2

C

C

=

1

L

L

=

2

1

2

1

C

C

C

C

C

+

=

DROR – dzielona C

2

p

rC

L

2

1

r

r

r

+

=

1

L

L

L

p

2

1

1

L

<

+

=

1

C

C

C

p

2

1

1

C

<

+

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

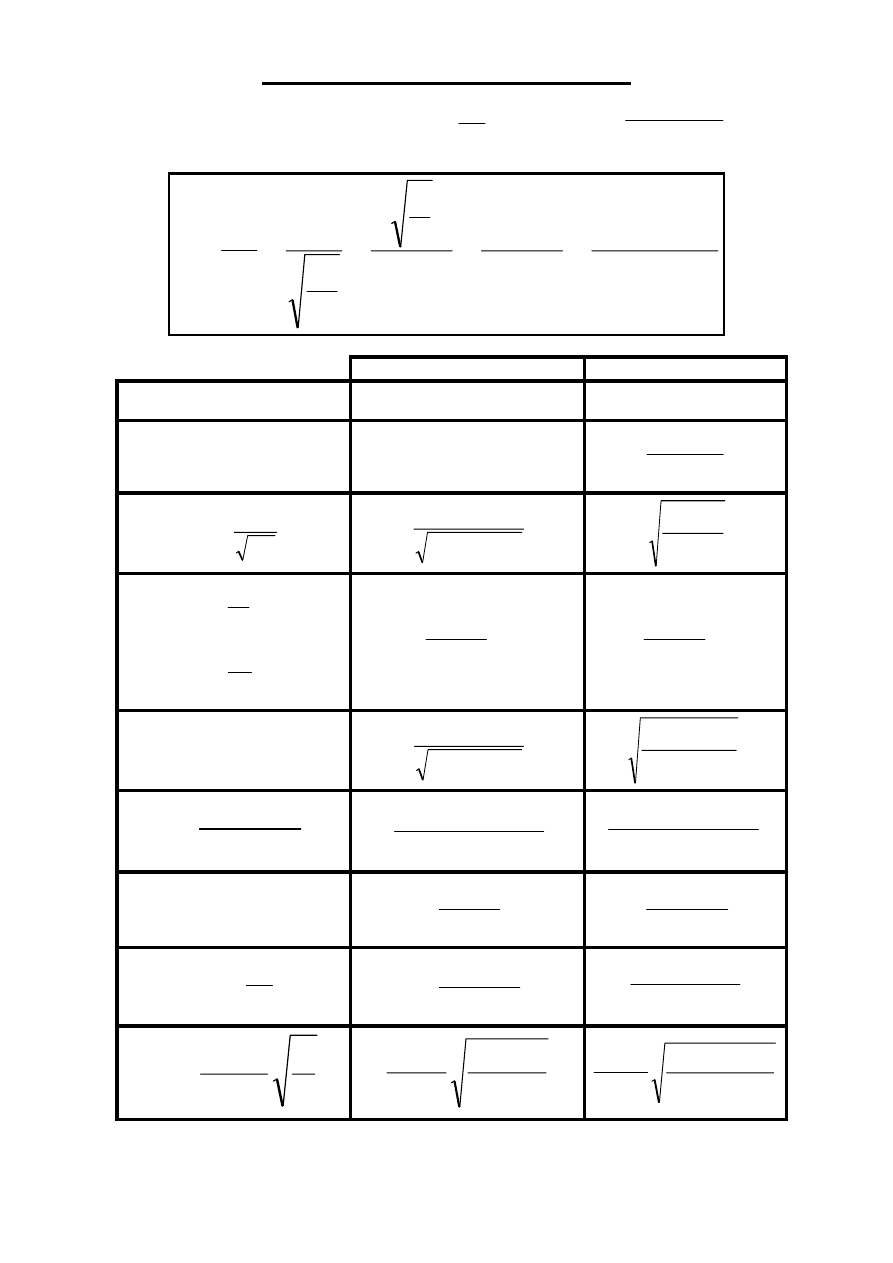
Dobroć równoważnego ROR

Oznaczenia:

2

r

Lp

L

=

2

r

p

C

C

=

2

2

1

d

p

C

)

r

(r

L

R

+

=

)

r

C(r

ω

1

)

r

(r

L

ω

)

r

(r

C

L

C

L

R

ρ

R

Q

2

1

0

2

1

0

2

1

r

r

d

d

+

=

+

=

+

=

=

=

Dzielona

indukcyjność Dzielona

pojemność

L

2

1

L

L

+

1

L

C

2

C

2

1

2

1

C

C

C

C

+

LC

1

ω

0

≈

(

)

2

2

1

C

L

L

1

+

2

1

1

2

1

C

C

L

C

C

+

1

C

C

p

1

L

L

p

2

C

1

L

<

=

<

=

1

L

L

L

2

1

1

<

+

1

C

C

C

2

1

1

<

+

|

x

1

(

ω

0

)

|

=

|

x

2

(

ω

0

)

|

(

)

2

2

1

1

C

L

L

L

+

(

)

2

2

1

1

1

C

C

C

C

L

+

2

2

1

d

p

C

)

r

(r

L

R

+

=

(

)(

)

2

2

1

2

1

2

1

C

L

L

r

r

L

+

+

(

)(

)

2

2

1

2

1

1

1

C

C

C

r

r

C

L

+

+

2

r

Lp

L

=

2

1

2

1

L

L

L

+

(

)

2

2

1

2

1

1

C

C

C

L

+

2

r

p

C

C

=

(

)

2

1

2

2

1

2

L

L

L

C

+

(

)

1

2

1

2

C

C

C

C

+

C

L

r

r

1

Q

2

1

+

=

2

2

1

2

1

C

L

L

r

r

1

+

+

(

)

2

1

2

1

1

2

1

C

C

C

C

L

r

r

1

+

+

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

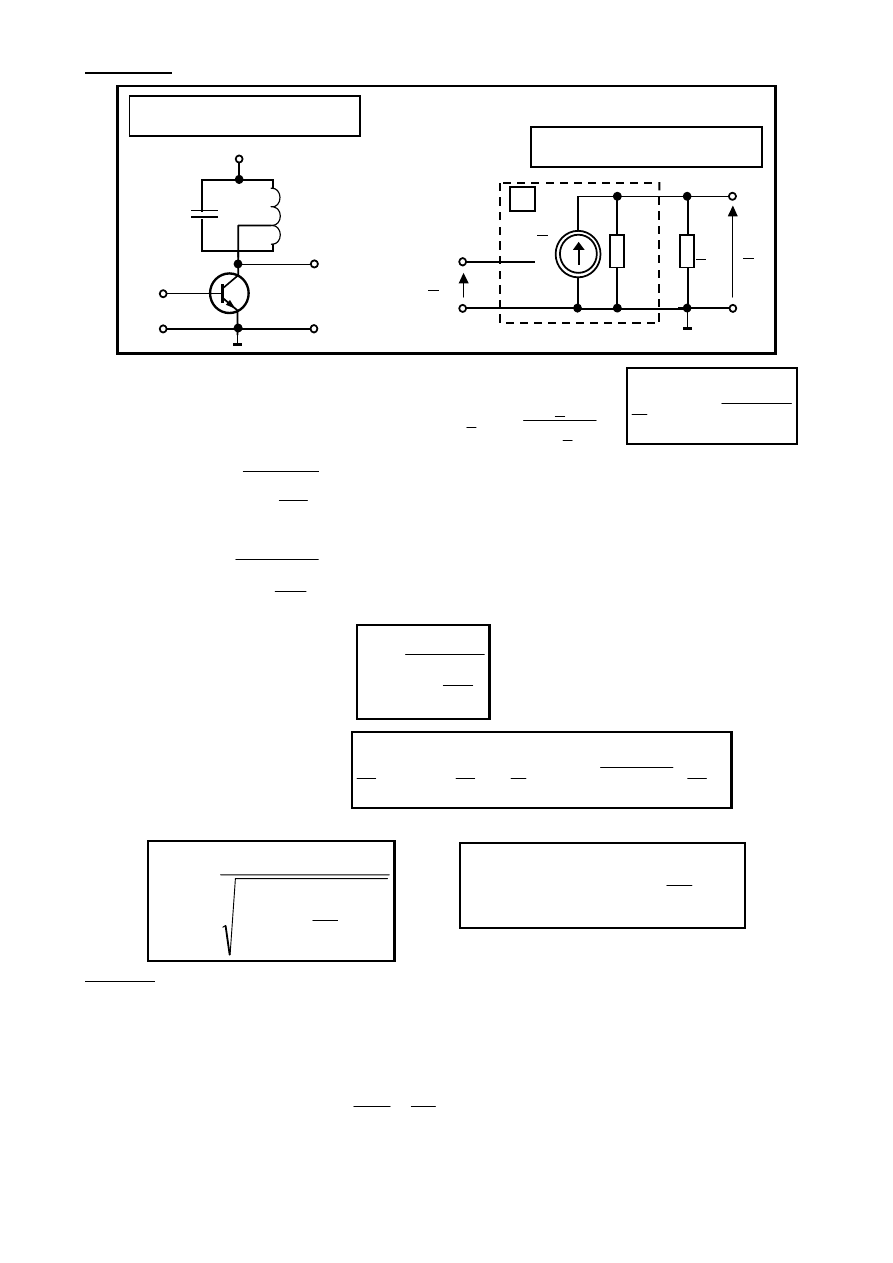
Przykład. Tranzystorowy wzmacniacz rezonansowy

( dzielone L )

małych sygnałów.

C

L

+U

s

We

Wy

–

g⋅U

we

R

w

Z(ω) U

wy

Schemat wzmacniacza

rezonansowego małych sygnałów

Model wzmacniacza

rezonansowego małych sygnałów

T

T

U

we

Impedancja zastępcza obciążająca ZPSN:

ω)

(

Z

R

ω)

(

Z

R

ω)

(

Z

w

w

z

+

=

.

z

dz

z

jξ

1

R

ω)

(

Z

+

=

gdzie:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

w

d

d

dz

R

R

1

R

R

– zastępcza oporność dynamiczna;

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

w

d

z

R

R

1

ξ

ξ

– zastępcze rozstrojenie bezwzględne.

Dobroć:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

w

d

z

R

R

1

Q

Q

Napięcie wyjściowe:

we

z

dz

z

we

wy

U

jξ

1

gR

ω)

(

Z

U

g

U

⋅

+

−

=

⋅

−

=

Charakterystyki częstotliwościowe:

2

r

2
z

dz

1

ω

ω

Q

4

1

gR

ω)

(

A

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

=

⎥

⎦

⎤

⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

=

1

ω

ω

Q

2

arctg

π

ω)

(

r

z

ϕ

Przykład

Wzmacniacz rezonansowy z poprzedniego przykładu ma następujące parametry: f

r

=28 MHz, Q= 95,

ρ= 430 Ω, p= 0,6, g= 20 mA/V, R

w

= 15 k

Ω. Wyznaczyć wartość wzmocnienia dla pulsacji rezonansowej i

szerokość pasma przepustowego wzmacniacza.

Opór

dynamiczny:

R

d

= p

2

ρQ= 14,71 kΩ

Zastępczy opór dynamiczny:

R

dz

= 7,43 k

Ω

Dla pulsacji rezonansowej

ω

r

:

A(

ω

r

) = g

R

dz

= 148,6 =>

α

0

= 20

log

A(

ω

r

)= 43,44 dB

Pasmo

3-dB:

MHz

584

,

0

kHz

77

,

583

Q

f

π

2

B

z

r

3dB

=

=

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE