Mechanika techniczna

przykładowe pytania i zadania

statyka

1. Zacytować i zilustrować zasadę równoległoboku (zasada statyki).
2. Kiedy dwie siły przyłożone do ciała sztywnego równoważą się ?
3. Pokazać, że w statyce siły przyłożone do ciała sztywnego można przesuwać wzdłuż

linii działania tych sił.

4. Zacytować i zilustrować zasadę działania i przeciwdziałania (zasada statyki).
5. Zacytować i zilustrować zasadę oswobodzenia od więzów (zasada statyki).
6. Zilustrować układ sił zbieżnych (centralnych) działających na ciało sztywne. Jaki jest

warunek równowagi układu sił zbieżnych ?

7. Zacytować twierdzenie „o trzech siłach” , zilustrować przykładem.
8. Zdefiniować pojęcie momentu siły względem punktu (na płaszczyźnie).
9. Co to jest para sił i ile wynosi moment pary sił ?

10. Podać twierdzenie „o równoległym przenoszeniu siły” (na płaszczyźnie).
11. Podać warunki równowagi dowolnego płaskiego układu sił.
12. Co to jest siła tarcia?
13. Podać prawa tarcia Coulomba-Morena.
14. Co to jest moment siły względem osi? Kiedy jest on równy zeru?
15. Podać zależność na wyznaczanie środka masy dla ciał składających się z „kawałków”,

dla których znamy masy i położenia środków mas.

16. Jaki jest warunek sztywności kratownicy płaskiej ?
17. Co to są pręty zerowe, jak je identyfikujemy w kratownicy płaskiej i jaka jest ich rola ?

kinematyka

18. Zdefiniować położenie, prędkość i przyspieszenie punktu w kartezjańskim układzie

odniesienia?

Zdefiniować położenie, prędkość i przyspieszenie punktu w biegunowym układzie

współrzędnych na płaszczyźnie.

19. Jak zorientowana jest prędkość punktu względem trajektorii ruchu ?
20. Zdefiniować kierunki: styczny i normalny a następnie składowe prędkości i

przyspieszenia na tych kierunkach.

Co to jest ruch postępowy? Prędkość i przyspieszenie punktów ciała sztywnego w

ruchu postępowym.

21. Opisać ruch punktu po okręgu: położenie, prędkość i przyspieszenie. Podać

najważniejsze zależności kinematyczne.

22. Opisać zależności kinematyczne w ruchu obrotowym ciała wokół stałej osi (prędkość

kątowa, przyspieszenie kątowe).

23. Zdefiniować ruch płaski.
24. Podać metody wyznaczania prędkości w ruchu płaskim, zilustrować przykładami.
25. Podać metody wyznaczania przyspieszenia w ruchu płaskim, zilustrować przykładami.

Click here to get your free novaPDF Lite registration key

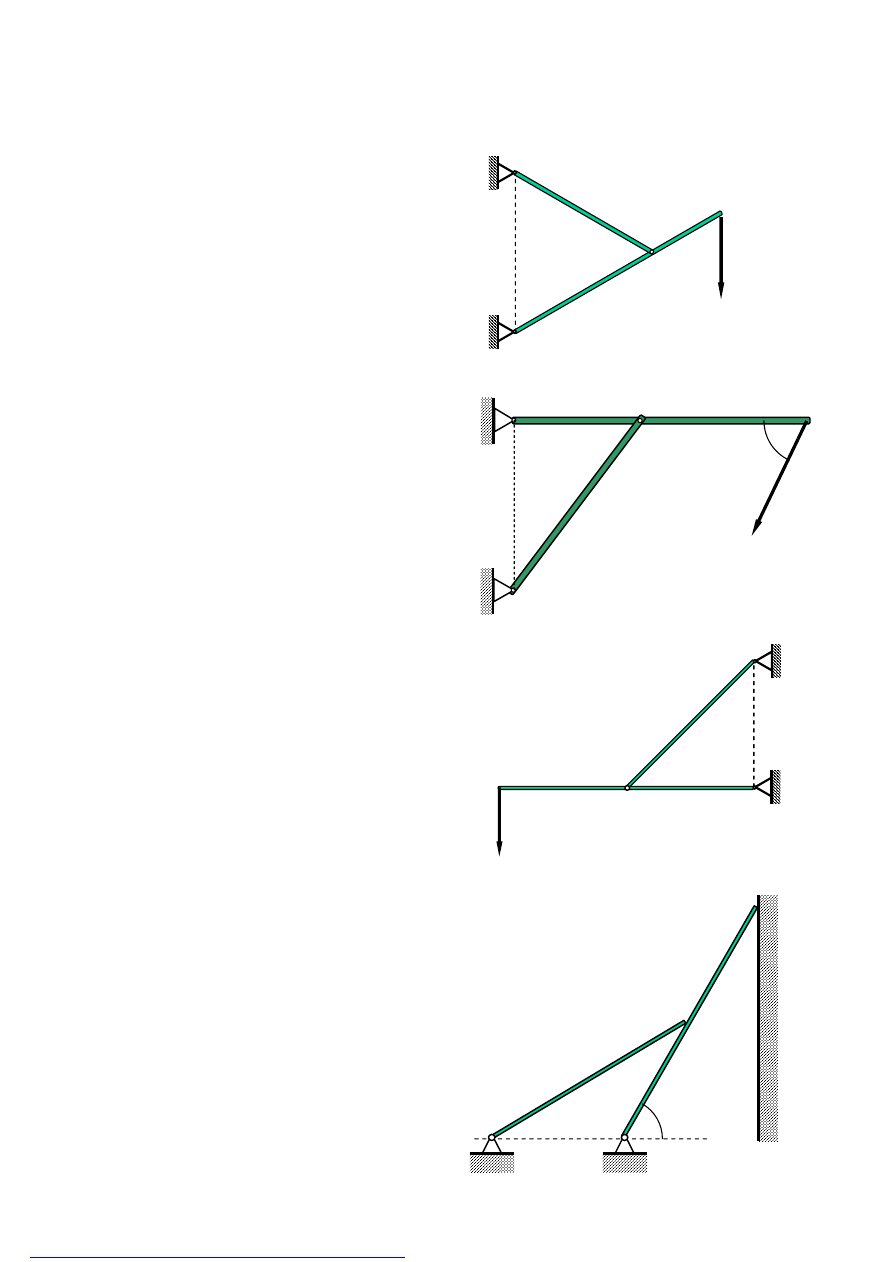
Zadania – statyka

Zadanie 1
Pomijając

ciężar

własny

prętów

wyznaczyć reakcje w przegubach A, B
i C konstrukcji pokazanej na rysunku
obciążonej siłą G.






Zadanie 2
Konstrukcja

złożona

jest

z

dwóch

nieważkich prętów połączonych ze sobą
przegubowo

w

przegubie

B

oraz

podpartych przegubowo na podporach A
i C. W punkcie D obciążona jest siłą P
nachyloną pod kątem . Wyznaczyć
reakcje w przegubach A, B oraz C. Dane
są wymiary a i b.




Zadanie 3
Wspornik pokazany na rysunku zbudowany
jest z cienkich, jednorodnych prętów AB i CD
połączonych ze sobą przegubowo w węźle B.
Ciężar jednostkowy prętów wynosi q[N/m].
W punkcie D wspornik obciążono pionową
siłą P=4qa.
Wyznaczyć reakcje w przegubach A, B i C.
Dany jest wymiar a.



Zadanie 4
Jednorodna belka AB o ciężarze G
podparta jest przegubowo w punkcie A
i opiera się o gładką jednorodną belkę CD
o ciężarze Q. Belka CD podparta jest na
końcu C przegubowo, zaś końcem D
opiera się o gładką, pionową ścianę.
Wyznaczyć reakcje podpór A i C oraz
reakcje w punktach B i D.
AC=BC=BD=b, =60

0

.

A

C

B

D

2a

a

2a

2a

G

P

a

a

a

A

B

C

D

D

A

B

C

α

b

b

b

C



P

D

b

a

b

B

A

Click here to get your free novaPDF Lite registration key

Zadanie 5
Jednorodny walec o ciężarze Q i promieniu
r spoczywający na chropowatej równi
utrzymywany jest w położeniu równowagi
za pomocą nieważkiej nici AB.
Jaki musi być współczynnik tarcia



pomiędzy walcem a równią, aby możliwa
była

równowaga

układu

przy

kącie

nachylenia równi wynoszącym

?

Opór toczenia pominąć.


Zadanie 6
Jednorodny cienki, ciężki pręt opiera się w
punkcie A o chropowatą płaszczyznę
natomiast w punkcie B o gładkie naroże. Ile
co najmniej musi wynosić współczynnik
tarcia

 pomiędzy prętem i płaszczyzną, aby

układ pozostawał w równowadze? Dany jest
kąt

=30

0

oraz wymiar a.

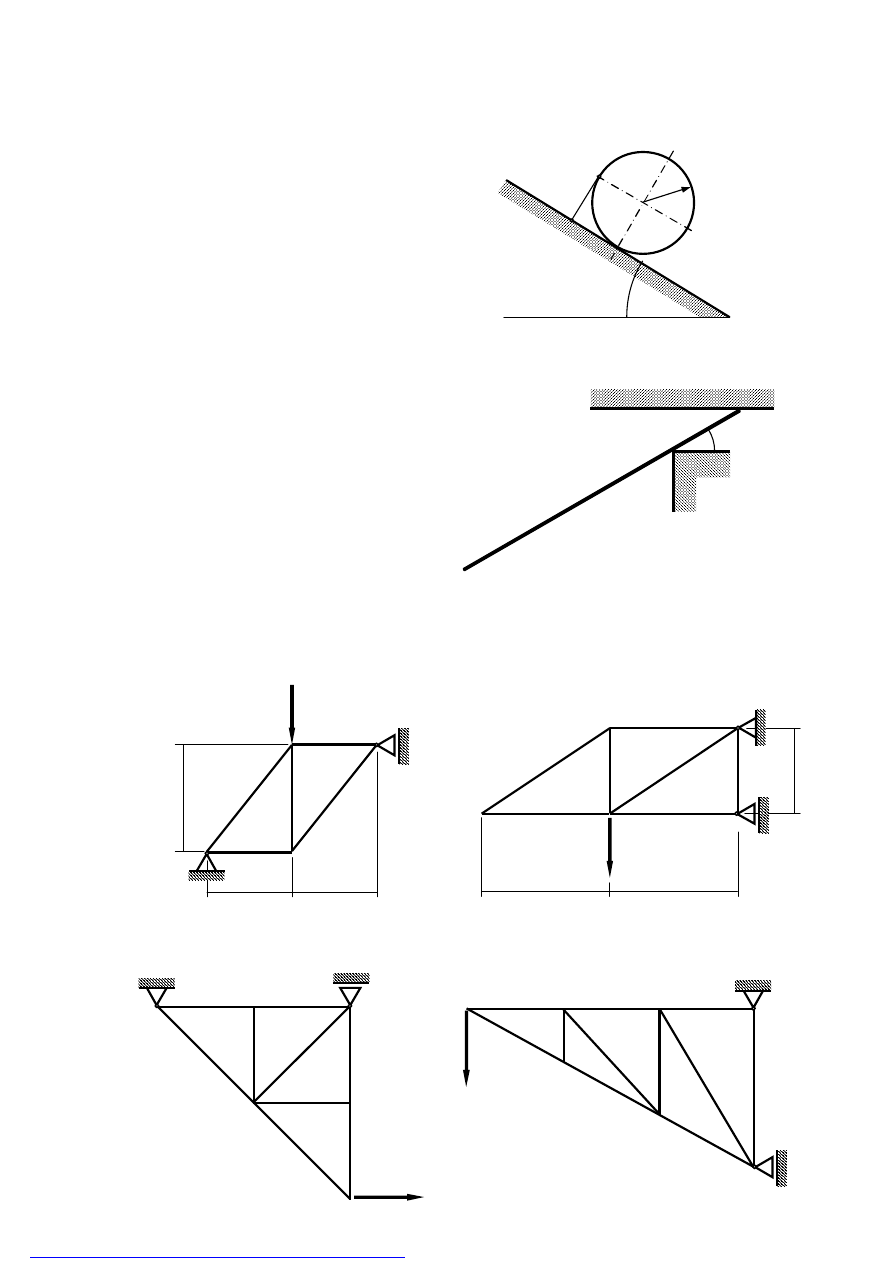
Zadanie 7
Obliczyć siły w prętach kratownic pokazanych na rysunkach.


a) b)










c) d)

r

A

α

B

a

1

6

5

4

3

2

7

8

9

a

a

a

P

5a

3a

1

6

5

4

3

2

7

8

9

10

11

P

3a

3a

P

1

2

3

4

5

6

7

a

b

a

P

1

2

3

4

5

a

b

a

A

B

C



3a

a

Click here to get your free novaPDF Lite registration key

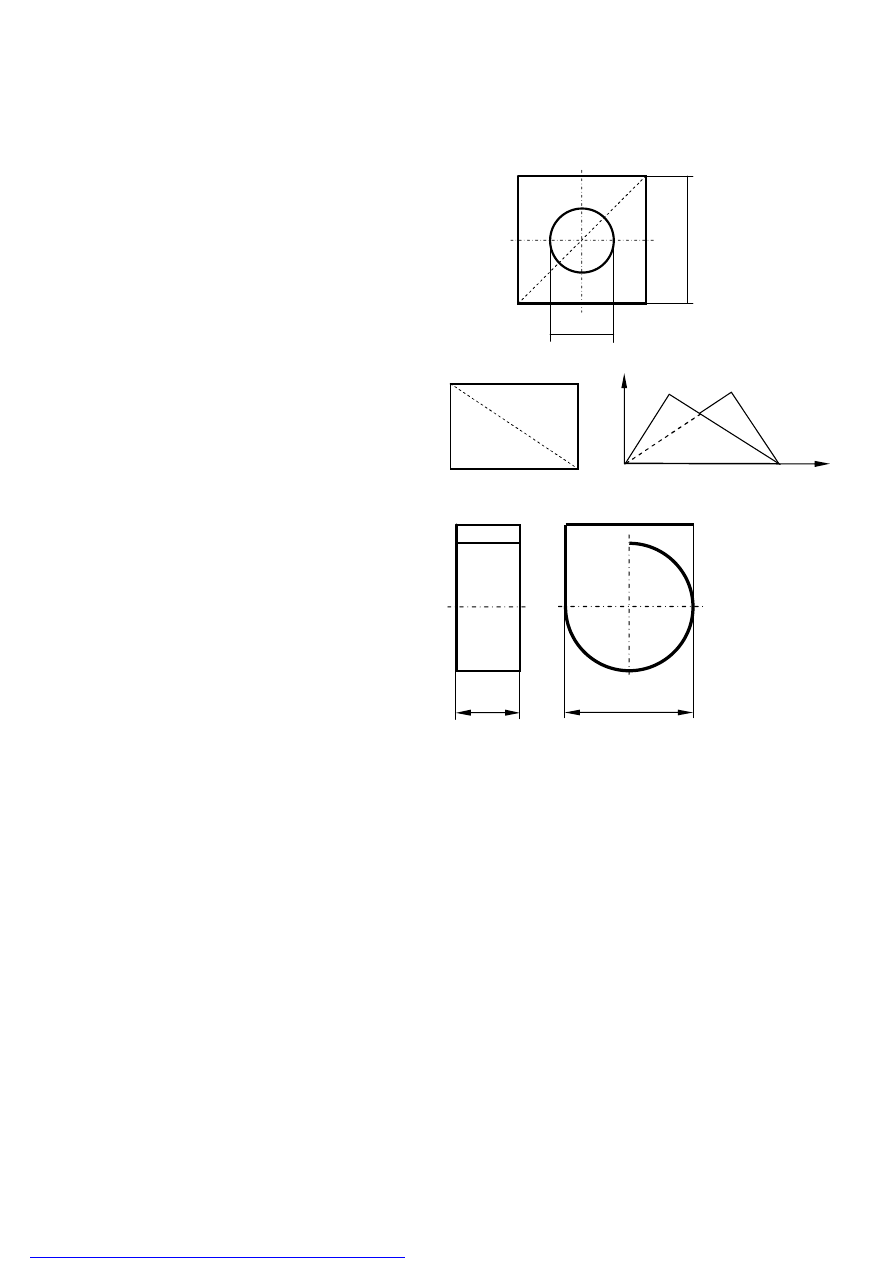
Zadanie 8
Kwadratową płytkę o boku 2a, z wyciętym
symetrycznie otworem o średnicy a, wykonaną
z cienkiej blachy, zagięto pod kątem prostym
wzdłuż linii A-C.
Wyznaczyć położenie środka ciężkości tak
powstałej figury.



Zadanie 9
Prostokątny arkusz ABCD cienkiej blachy
o wymiarach ab zagięto pod kątem 180

0

wzdłuż przekątnej. Wyznaczyć położenie
środka ciężkości otrzymanej figury.



Zadanie 10
Pasek cienkiej blachy o długości 8a
i szerokości a wygięto jak na rysunku.
Wyznaczyć położenie środka ciężkości
powstałej bryły.

A

B

C

D

a

2a

D

C

B

A

b

a

x

C

A

B

D

y

2a

a

Click here to get your free novaPDF Lite registration key

Zadania - kinematyka

Zadanie 1
Równania ruchu punktu poruszającego się w jednej płaszczyźnie mają postać:

a)

3

3

4

3

3

t

y

t

x









b)

3

3

4

2

2







t

y

t

x

c)

2

2

4

3

3

t

y

t

x







d)

3

3

4

3

3







t

y

t

x

1) Narysować tor ruchu punktu.
2) Podać położenie punktu na torze w chwili początkowej.
3) Po jakim czasie ts punkt przebędzie drogę s

=

10? Obliczyć prędkość i przyspieszenie

punktu po przebyciu przez niego tej drogi.

Zadanie 2
Punkt porusza się w jednej płaszczyźnie zgodnie z równaniami
a)

0

,

,

cos

sin

2







k

b

a

kt

b

y

kt

a

x

b)

t

y

t

x

2

sin

5

1

2

cos

4

2









c)

0

,

,

sin

2

cos







k

b

a

kt

b

y

kt

a

x

1) Narysować tor ruchu punktu,
2) zaznaczyć położenie punktu na torze w chwili początkowej,
3) obliczyć prędkość i przyspieszenie punktu w charakterystycznych punktach toru.


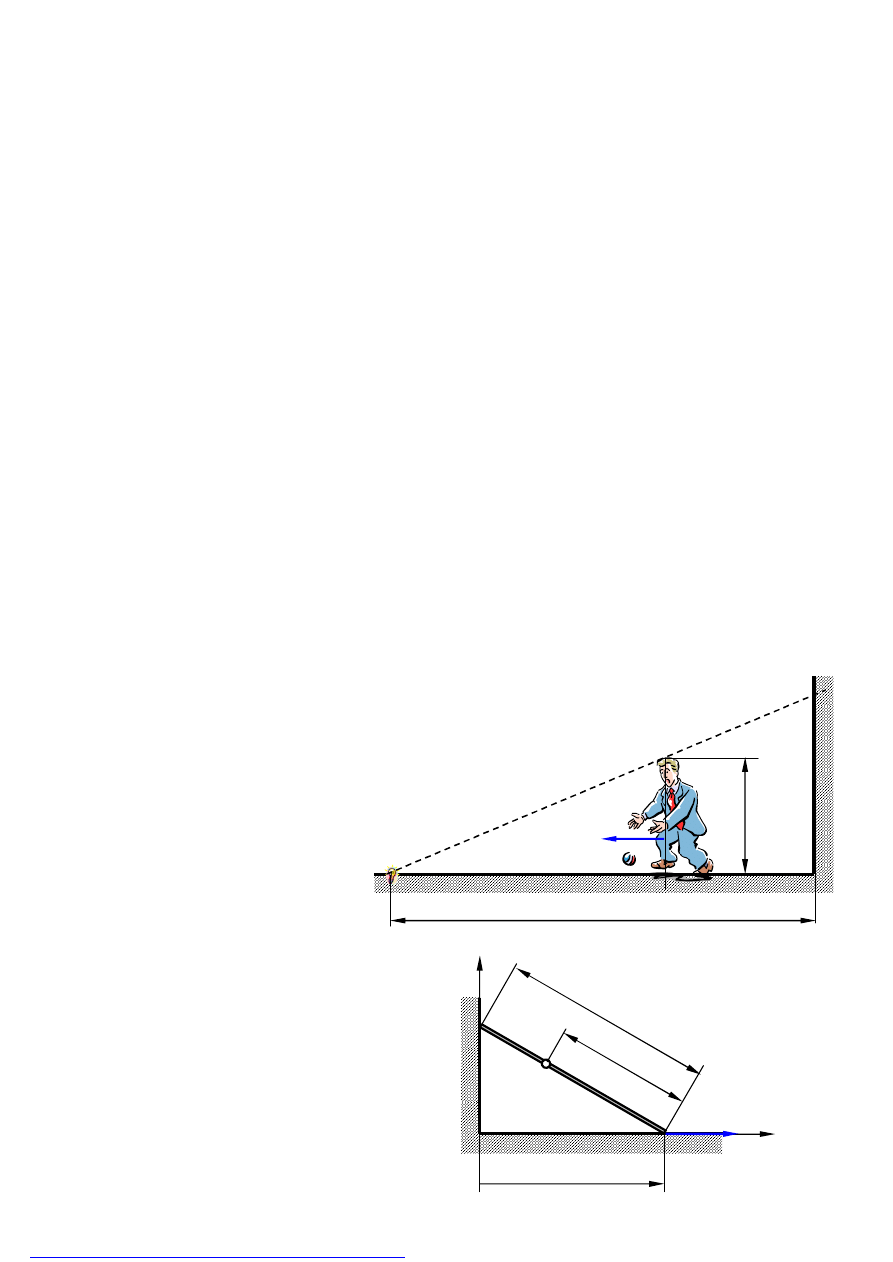
Zadanie 3
Człowiek o wzroście h zbliża się
ze stałą prędkością  do źródła
światła (punkt A) znajdującego się
w odległości AB=l od pionowej
ściany. Obliczyć z jaką prędkością
i przyspieszeniem porusza się
wierzchołek cienia tego człowieka
po ścianie (punkt C). W chwili
początkowej człowiek znajdował
się przy ścianie (punkt B).



Zadanie 4
Pręt AB o długości l porusza się w ten
sposób, że jego końce ślizgają się po
dwóch wzajemnie prostopadłych pros-
tych. Obliczyć prędkość punktu M,
znajdującego się w odległości a od
końca A, w zależności od położenia x

A

i prędkości



A

końca A.

h

A

B

C



l

x

y

l

a

M

B

A

x

A



A

Click here to get your free novaPDF Lite registration key

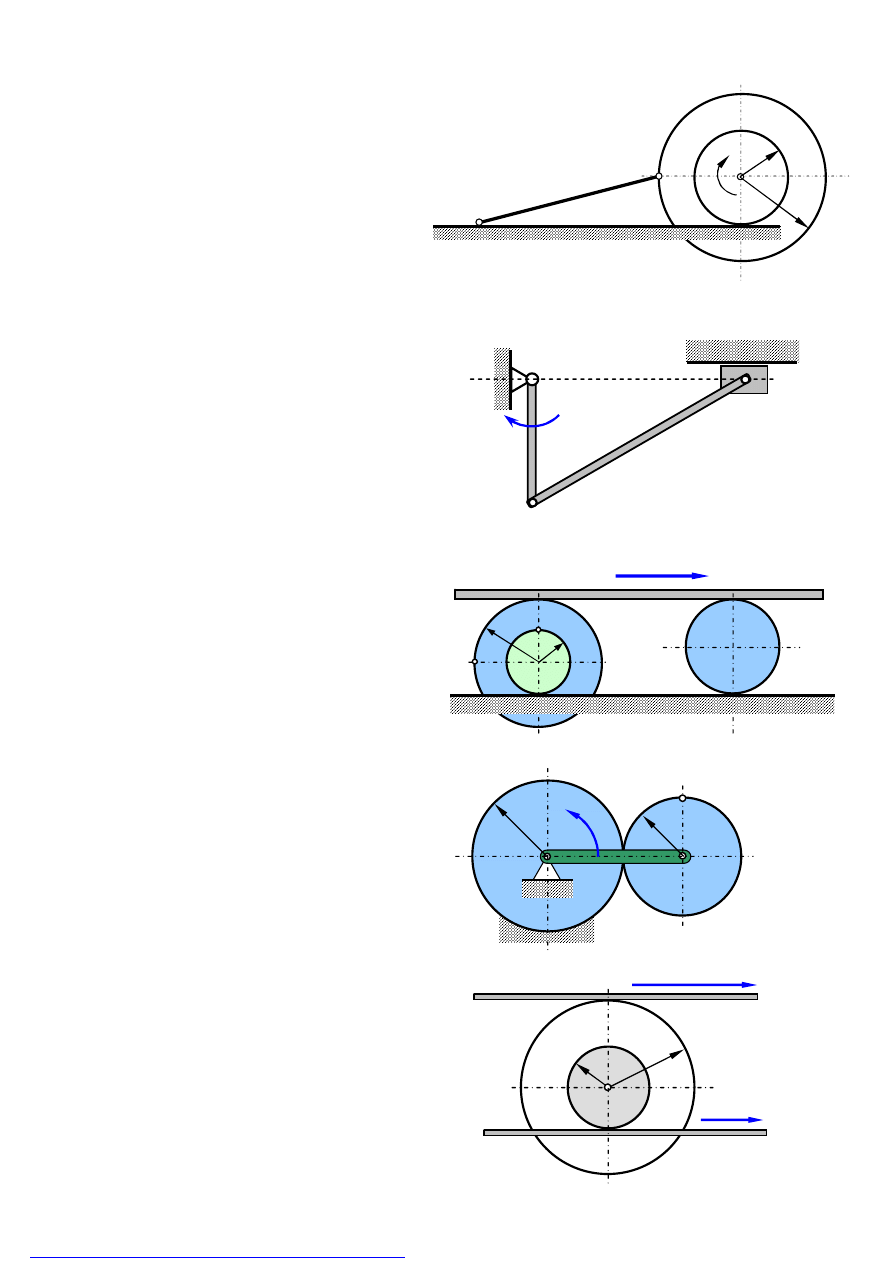
Zadanie 5
Ze szpulą o środku O i promieniach r oraz
R, toczącą się bez poślizgu po płaszczyźnie
ze stałą prędkością kątową





, połączono

przegubowo pręt AB o długości 4r, którego
koniec B ślizga się po tejże płaszczyźnie.
Obliczyć prędkość kątową





pręta oraz

prędkość



B

punktu B.

Zadanie 6
W mechanizmie korbowym pokazanym na
rysunku korba OA o długości r obraca się ze
stałą prędkością kątową



0

wokół nieruchomej

osi O. Wyznaczyć prędkość i przyspieszenie
tłoka B, w położeniu pokazanym na rysunku,
umieszczonego na końcu korbowodu AB
o długości l.




Zadanie 7
Deska oparta na szpuli o promieniach r i 2r
oraz na rolce przesuwa się z prędkością

.

Wyznaczyć prędkości punktów A i B szpuli.

Zadanie 8

W mechanizmie planetarnym pokaza-
nym na rysunku łącznik O

1

O

2

obraca się

z prędkością kątową

 wokół nieru-

chomej osi O

1

powodując toczenie się

koła 2 po nieruchomym kole 1. Obliczyć
prędkość kątową



2

koła 2 oraz pręd-

kość punktu A.

Zadanie 9

Szpula o promieniach r i 2r toczy się bez
poślizgu między dwiema równoległymi
listwami posiadającymi prędkości  oraz
. Obliczyć prędkość kątową szpuli
oraz prędkość jej środka.

O

4r

B

A

R

r



0

O

B

l

r

A



0



2r

r

B

A

r

1

r

2

O

1

O

2



A

koło 1 koło 2

2

2r

r



Click here to get your free novaPDF Lite registration key