1
Zadania do rozwiązania na zajęciach z badań operacyjnych
w semestrze zimowym roku akademickiego 2012/2013
(zadania lub pomysły zadań zaczerpnięto m.in. z następujących pozycji: Wayne L.Winston,
Operations Research. Applications and Algorithms. Duxbury Press, Belmont 1994; Alpha
C.Chiang, Podstawy ekonomii matematycznej. Państwowe Wydawnictwo Ekonomiczne.
Warszawa 1994; Jack Hirshleifer, John G.Riley, The Analytics of Uncertainty and
Information. Cambridge University Press, Cambridge 1994)
Zad. 1: Rozwiąż układ równań liniowych
b
Ax
=
, w którym: (a)
−
−
=
1
2
1
2
1
3
1
5
2
A
,
=
3
2
1
x
x
x
x
oraz
=
6
9
7
b
; (b)
−
−
−
=
1
1
1
1
1
1
1
1
1
A
,
=
3
2
1
x
x
x
x
,
−
−
=
3
7
1
b
.
Zad. 2: Wyznacz przebieg zmienności funkcji: (a)
14
x
5
x
y
2
−
−
=
, (b)
4
x
2
x
2
y
2
−
+
=
.
Zad. 3: W przedsiębiorstwie wytwarza się dwa wyroby (
A i B ) zużywając w procesie
produkcyjnym 3 czynniki produkcji (
1
S
,
2
S
,
3
S ). Normy zużycia poszczególnych czynników
produkcji na jednostkę każdego wyrobu oraz ich zasoby przedstawia poniższa tabela.
Czynnik
produkcji
Wyrób
Zasób
A
B
1
S
1
1
12
2
S
2
4
42
3
S
1
0
11
Wiedząc, że zyski jednostkowe ze sprzedaży obu wyrobów wynoszą odpowiednio 3 i 4 złote:
(i) sformułuj zagadnienie pierwotne i dualne; (ii) wyznacz wielkości produkcji obu wyrobów,
które maksymalizują zysk przedsiębiorstwa; użyj metody simpleks; (iii) oblicz maksymalny
zysk przedsiębiorstwa i podaj o ile on wzrośnie, gdy zasób czynnika wzrośnie o jednostkę,
ceteris paribus; (iv) zadecyduj, czy zasoby wszystkich czynników produkcji zostaną
całkowicie wykorzystane; jeśli nie, to podaj ich nazwy i określ niewykorzystane wielkości;
(v) sporządź rysunek ilustrujący rozwiązanie problemu.
Zad. 4: Jesteś dyrektorem agencji reklamowej, która promuje nowy typ dezodorantu. Budżet
kampanii reklamowej wynosi 200000 zł. Promocja odbywa się poprzez umieszczanie 30
sekundowych reklam w telewizji oraz kolorowych, dwukolumnowych ogłoszeń w tygodniku
o zasięgu ogólnokrajowym. Jednorazowa emisja reklamówki w telewizji kosztuje 20000 zł,
natomiast opublikowanie ogłoszenia w tygodniku – 5000 zł. Przeprowadzona przez
pracowników agencji analiza oglądalności programu telewizyjnego i poczytności prasy
wykazała, że używając telewizji dociera się średnio do 400000 widzów, wybierając zaś
tygodnik – dociera się do 150000 osób. Zadecyduj o sposobie i częstości reklamowania
nowego dezodorantu w taki sposób, aby o jego pojawieniu się na rynku dowiedziała się jak
największa liczba osób.
2
Zad 5: Jesteś dyrektorem przedsiębiorstwa, w którym wytwarza się dwa rodzaje sztućców:
noże i widelce. Proces produkcji obejmuje tłoczenie i polerowanie. Wyposażenie tłoczni i
polerni w maszyny jest takie, że umożliwia obróbkę sztućców przez odpowiednio 70 i 100
maszynogodzin czasu pracy tygodniowo na każdym wydziale. Do wytworzenia kompletu
noży potrzeba 12 minut czasu pracy maszyn do tłoczenia i 30 minut czasu pracy maszyn do
polerowania, natomiast do wytworzenia kompletu widelców – 24 i 15 minut czasu pracy
maszyn odpowiedniego typu. Przedsiębiorstwo może sprzedać całą wytworzoną produkcję
sztućców uzyskując za komplet noży 12 złotych, a za komplet widelców – 9 złotych. Określ
tygodniowe wielkości produkcji obu rodzajów sztućców maksymalizujące zysk
przedsiębiorstwa wiedząc, że koszt wytworzenia kompletu noży wynosi 4 złote, a koszt
wytworzenia kompletu wielcy – 3 złote.
Zad. 6: Spodziewasz się, że w 2007 roku 1 akcja zwykła First National Bank of Upper Sopot
(FNBUS) przyniesie Ci 50 zł zysku, natomiast 1 akcja zwykła First National Bank of Lower
Sopot (FNBLS) – tylko 35 zł zysku. Załóż, że 31 grudnia 2006 roku posiadasz 1 mln zł, które
przeznaczasz na zakup tych akcji po cenach równych odpowiednio 1250 i 750 zł. Określ
ilości akcji obu banków, które zakupisz, jeśli wiesz, że będziesz mógł zakupić co najwyżej
750 akcji FNBLS. Ile jest ,,warta” 1 złotówka kapitału przeznaczonego na zakup akcji? O ile
zwiększy się Twój zysk, gdybyś mógł zakupić o jedną akcję FNBLS więcej? Rozwiązanie
zilustruj odpowiednim(i) rysunkiem(ami).
Zad. 7: Załóż, że funkcją użyteczności Marka jest
2
1
x
5
x
10
U
+
=
, gdzie
i
x
– wielkość
spożycia odpowiednio ciasta (kg) i lemoniady (litry). Niech kilogram ciasta i litr lemoniady
kosztują odpowiednio 10 i 5 złotych. Wyznacz optymalne wielkości spożycia obu dóbr
wiedząc, że Marek może zjeść co najwyżej 8 kg ciasta i przeznaczyć na konsumpcję co
najwyżej 100 złotych. O ile zmieni się użyteczność Marka, gdyby mógł zjeść o 1 kg ciasta
(przeznaczyć na konsumpcję o 1 zł) więcej?
Zad. 8: Janek otrzymuje od rodziców kieszonkowe w wysokości 100 zł miesięcznie, które
przeznacza na zakłady piłkarskie. Z każdej złotówki postawionej na Legię uzyskuje
przeciętnie 15 gr zysku, natomiast złotówka postawiona na Górnika przynosi mu przeciętnie
20 groszy zysku. Wyznacz optymalne wielkości zakładów na obie drużyny, jeśli wiesz, że
Janek stawia na Górnika co najwyżej 40 zł. Wyznacz przeciętny miesięczny zysk z zakładów
piłkarskich. O ile zmieni się ten zysk, jeśli rodzice zwiększą Jankowi kieszonkowe o 1 zł?
Zad. 9: W tartaku przecina się deski o szerokości 10 cm w deski o mniejszej szerokości.
Określ sposób realizacji zlecenia klienta na 90 desek o szerokości 6 cm i 120 desek o
szerokości 3 cm, który minimalizuje odpad drewna powstający w trakcie przecinania. Załóż,
ż
e na rozmiary odpadu nie ma wpływu szerokość ostrza tnącego. O ile zmieni się odpad
drewna, jeśli zlecenie na deski o szerokości 3 cm wzrośnie o 1 szt?
Zad. 10: Dom inwestycyjny Midas rozważa zaangażowanie się w dwa przedsięwzięcia.
Kierownictwo domu oczekuje, że zysk z zaangażowania złotówki w pierwsze przedsięwzięcie
wyniesie 25 gr a zysk z zaangażowania złotówki w drugie przedsięwzięcie – 40 gr. Określ
optymalne zaangażowanie w oba przedsięwzięcia, jeśli wiadomo, że łączne zaangażowanie
nie może przekroczyć 100 mln zł, a zaangażowanie w pierwsze przedsięwzięcie – 40 mln zł.
O ile zmieni się zysk domu inwestycyjnego, jeśli jego łączne zaangażowanie wzrośnie o 1
mln zł?
3
Zad. 11: Duża ferma hoduje świnie, które skarmia się paszą będącą mieszaniną trzech
rodzajów ziarna. Każde z nich zawiera 4 składniki odżywcze: białko, wapń, proteiny oraz
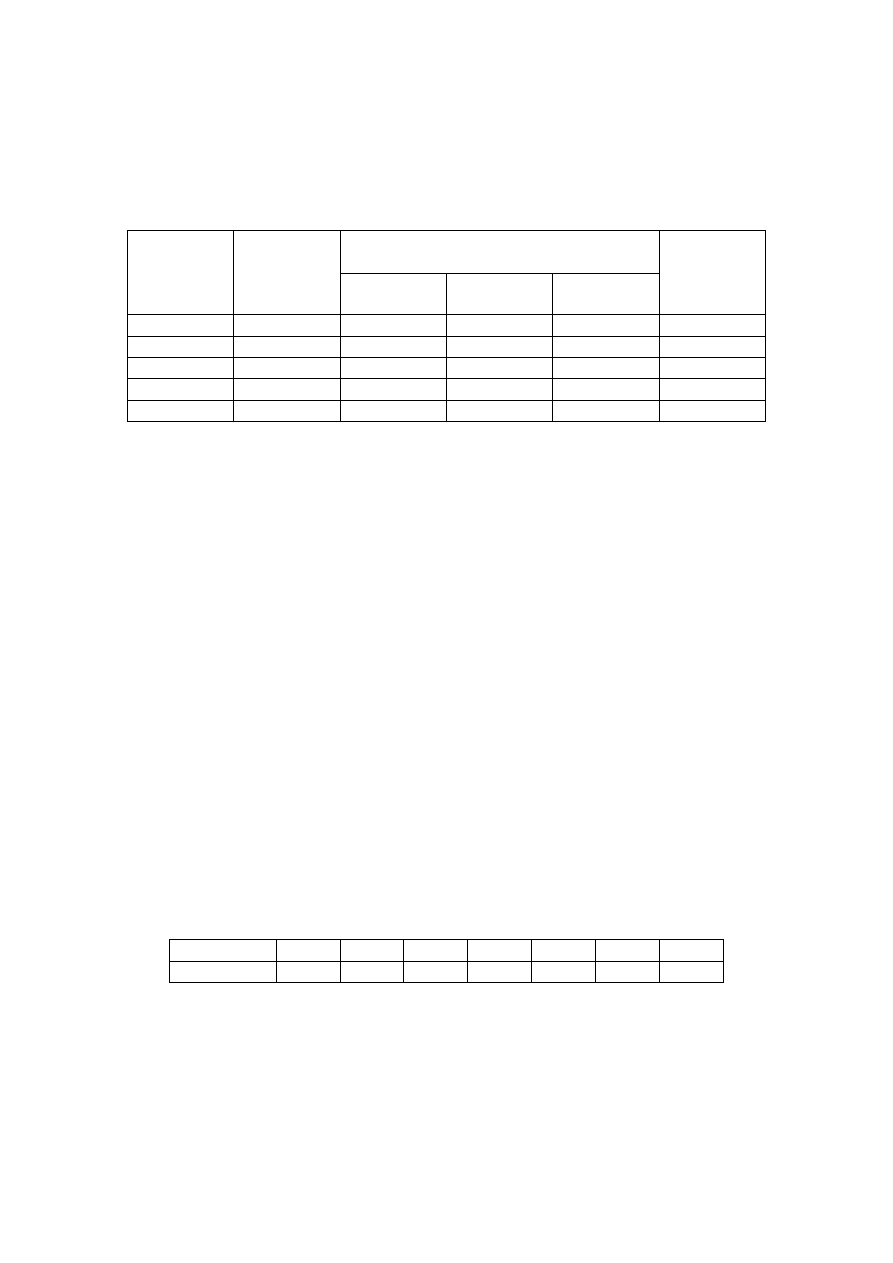
witaminę A. Informacje o przeciętnej zawartości poszczególnych składników odżywczych w
jednostce wagowej ziarna, minimalnym dziennym zapotrzebowaniu stada na składniki oraz
cenie jednostkowej ziarna zamieszczono w poniższej tabeli.
Składnik
Odżywczy
Jednostka
miary
Zawartość składnika w jednostce wagowej
ziarna rodzaju
Minimalne
dzienne
zapotrzebow
anie
I
II
III
Białko
mg
2,0
3,0
7,0
1250,0
Wapń
mg
1,0
1,0
0,0
250,0
Proteiny
mg
5,0
3,0
0,0
900,0
Witamina A mg
0,6
0,25
1,0
232,5
Cena ziarna
zł/jed wag
41,0
35,0
96,0
Pomóż właścicielowi fermy dobrać skład paszy w taki sposób, aby była ona najtańsza z
możliwych.
Zad. 12: Zamierzasz otworzyć wytwórnię słodyczy. Rozważasz w niej produkcję dwóch
rodzajów cukierków ( A i B ), do której używa się cukru, orzeszków i czekolady. W chwili
obecnej posiadasz zapas 100 kg cukru, 20 kg orzeszków oraz 30 kg czekolady. Masa, z której
formuje się cukierki typu A musi zawierać co najmniej 20% orzeszków, natomiast masa, z
której formuje się cukierki typu B musi składać się z co najmniej 10% orzeszków i 10%
czekolady. Zapisz i rozwiąż odpowiednie zagadnienie programowania liniowego wiedząc, że
sprzedaż 1 kg cukierków typu A zapewni Ci 2,5 zł zysku, a sprzedaż 1 kg cukierków typu B
– 2 zł zysku. Za kryterium optymalności przyjmij łączny zysk ze sprzedaży (produkcji) obu
rodzajów cukierków.
Zad. 13: Litr soku malinowego kosztuje 2 złote i zawiera 20 mg witaminy C i 30 mg wapnia,
natomiast litr soku mango – kosztuje 3 zł i zawiera odpowiednio 50 i 20 mg każdego ze
składników odżywczych. Skonstruuj taką mieszaninę soków malinowego i mango, w której
znajduje się co najmniej 250 mg witaminy C i 150 mg wapnia i która jest zarazem najtańsza
ze wszystkich możliwych mieszanin. Określ jej koszt oraz wartość ekonomiczną składników
odżywczych zawartych w 1 litrze soku malinowego. Rozwiązanie zilustruj odpowiednim(i)
rysunkiem(ami).
Zad. 14: W poszczególne dni tygodnia na poczcie potrzebna jest następująca liczba
pracowników pełnoetatowych do sprawnej obsługi klientów:
Dzień tyg
Pon
Wt
Ś
r
Czw
Pt
Sob
Nd
Pracownicy
17
13
15
19
14
16
11
Wiedząc, że pracownicy muszą pracować przez 5 kolejnych dni, po czym korzystają z
dwudniowej przerwy w pracy, wyznacz optymalną liczbę zatrudnionych w każdym dniu
tygodnia w taki sposób, aby zminimalizować ogólną liczbę zatrudnionych na poczcie.
Zad. 15: Jesteś dyrektorem mleczarni. Planujesz wprowadzenie do sprzedaży w następnym
kwartale 3 rodzajów jogurtów: X , Y i Z . Na ten cel przeznaczasz ze środków własnych
kwotę 50000 złotych. Pozostałe wydatki osobowe i rzeczowe (przekraczającą powyższą
4
kwotę) zostaną sfinansowane z kredytu bankowego udzielonego przez Bank Rozwoju
Rolnictwa. Bank ten oferuje kwartalną linię kredytową z limitem 300000 złotych.
Oprocentowanie kredytu wyniesie 3% w stosunku kwartalnym. Warunkiem dostępu do
kredytu jest utrzymanie przez mleczarnię współczynnika wypłacalności szybkiej na poziomie
równym 0,04 (4%) oraz zobowiązanie się mleczarni do spłaty odsetek pod koniec
rozważanego kwartału. Bank wymaga również, aby w celach promocji produkcji udział
jogurtu X w całości produkcji stanowił co najmniej 20%. Z kolei dystrybutor jogurtów żąda,
aby udział jogurtu Y w produkcji był co najmniej taki sam jak pozostałych jogurtów.
Produkcja jogurtów odbywa się na 3 wydziałach produkcyjnych: produkcji właściwej,
kontroli jakości oraz paczkowania. Informacje o cenach, kosztach oraz procesie
technologicznym przedstawia poniższa tabela.
Jogurt
Cena
sprzedaży
Koszt
wytworze
nia
Normy technologiczne
prod wł
kontr jak
paczkowa
nie
zł/litr
godz/litr
X
0,88
0,65
0,16
0,03
0,08
Y
0,82
0,54
0,12
0,045
0,06
Z
1,02
0,87
0,18
0,04
0,05
Wiedząc, że mleczarnia może przeznaczyć na nową produkcję 400000 godzin czasu pracy
maszyn na wydziale produkcji właściwej, 80000 godzin czasu pracy maszyn na wydziale
kontroli jakości oraz 150000 godzin czasu pracy maszyn na wydziale paczkowania określ
wielkości produkcji jogurtów wszystkich rodzajów maksymalizujące zysk przedsiębiorstwa.
Zad. 16: Zakład oczyszczania miasta w Gdyni usuwa z jej terenu trujące odpadki organiczne i
nieorganiczne, poddaje je działaniu detergentu neutralizującego ich szkodliwe oddziaływanie
na środowisko oraz spala pozostałości tego procesu w specjalnie do tego celu
zaprojektowanej instalacji. Pracownicy zakładu ustalili, że przeróbka kilograma odpadków
organicznych kosztuje 2 złote, a przeróbka kilograma odpadków nieorganicznych – 3 złote.
W zakładzie można przerobić w ciągu tygodnia do 9 milionów kilogramów odpadków. W
wyniku spalania pozostałości po przerobionych odpadkach powstaje gruboziarnisty popiół i
pewien produkt mineralny. Każdy z nich jest mieszaniną składników organicznych i
nieorganicznych, której proporcje zależą od ustawienia procesu technologicznego. Nabywcą
popiołu jest producent nawozów sztucznych, a nabywcą produktu mineralnego – producent
proszku do prania. Ten pierwszy kupuje tygodniowo do 7 milionów kilogramów popiołu,
płacąc po 4 złote za jego kilogram, ten drugi zaś – do 6 milionów kilogramów produktu
mineralnego, płacąc po 5 złotych za jego kilogram. Producent nawozów sztucznych wymaga,
aby zawartość składników organicznych w popiele nie przekraczała 60% jego wagi.
Producent proszku do prania żąda natomiast, ażeby zawartość składników nieorganicznych w
produkcie mineralnym stanowiła przynajmniej 50% i nie więcej niż 75% jego wagi. Będąc
kierownikiem zakładu określ takie wielkości produkcji popiołu i produktu mineralnego
(składników organicznych i nieorganicznych zawartych w każdym z nich), przy których zysk
przedsiębiorstwa jest największy. Jak zmienią się optymalne wielkości produkcji, jeśli
producent nawozów sztucznych dodatkowo ustali swoje minimalne tygodniowe
zapotrzebowanie na popiół na poziomie nie mniejszym od 4 milionów kilogramów?
Zad. 17: Jesteś odpowiedzialny za transakcje walutowe w banku. Zasoby walutowe banku na
otwarcie dnia wynoszą (w mln): $ 8, £ 1, DM 8, ¥ 0. Zapotrzebowanie na zamknięcie
kształtuje się w wysokości odpowiednio $ 6, £ 3, DM 1 oraz ¥ 10. Jakich transakcji
5
powinieneś dokonać w trakcie dnia chcąc zmaksymalizować wartość zasobów walutowych na
zamknięcie wyrażoną w dolarach, jeśli kursy wymiany na rynku w tym dniu kształtowały się
następująco: 1 $= £ 0,58928 = DM 1,743 = ¥ 138,3. Dla uproszczenia przyjmij, że kurs kupna
jest równy kursowi sprzedaży, a dokonują transakcji nie płacisz prowizji. Czy Twoje decyzje
ulegną zmianie, jeśli celem Twojego działania stanie się maksymalizacja wartości zasobów
walutowych wyrażona w markach?
Zad. 18: Dana jest tablica K , której elementy
ij
k charakteryzują koszt przewozu jednostki
pewnego towaru od i -tego dostawcy do j -tego odbiorcy:
=
50
70
90
160
130
100
90
120
60
140
90
80
K
.
Załóż, że popyty i podaże wynoszą odpowiednio: 45, 20, 30, 30 oraz 35, 50 i 40 jednostek.
Sformułuj zagadnienie programowania liniowego, którego użyjesz do wyznaczenia planu
przewozów minimalizującego łączny koszt przewozu oraz odpowiadające mu zagadnienie
dualne. Rozwiąż problem stosując metodę kąta północno-zachodniego (minimalnego kosztu).
Wyznacz macierz przewozów minimalizującą łączny koszt przewozu oraz minimalny koszt
przewozu.
Zad 19: Operatorka przedsiębiorstwa taksówkowego odebrała trzy wezwania od pasażerów.
Dysponuje pięcioma wolnymi wozami. Czas dojazdu poszczególnych taksówek do pasażerów
(min) przedstawiono w tabeli poniżej.
Taksówka Pasażer
1
P
2
P
3
P
1
T
10
11
18
2
T
6
7
7
3
T
7
8
5
4
T
5
6
4
5
T
9
4
7
Pomóż operatorce skierować wozy do klientów w taki sposób, aby zminimalizować łączny
czas dojazdu.
Zad. 20: Przedsiębiorstwo ,,Robótki domowe'' zatrudnia 5 studentów do sprzątania.
Posprzątanie Twojego domu polega na odkurzaniu elektroluksem, czyszczeniu kuchni,
czyszczeniu łazienki oraz trzepaniu dywanów. Czas wykonania poszczególnych czynności
(w godz) przez każdego studentka podano w poniższej tablicy.
Student
Czynność
odkurzanie
czyszczenie
trzepanie
dywanów
kuchni
łazienki
1
S
6
5
2
1
2
S
9
8
7
3
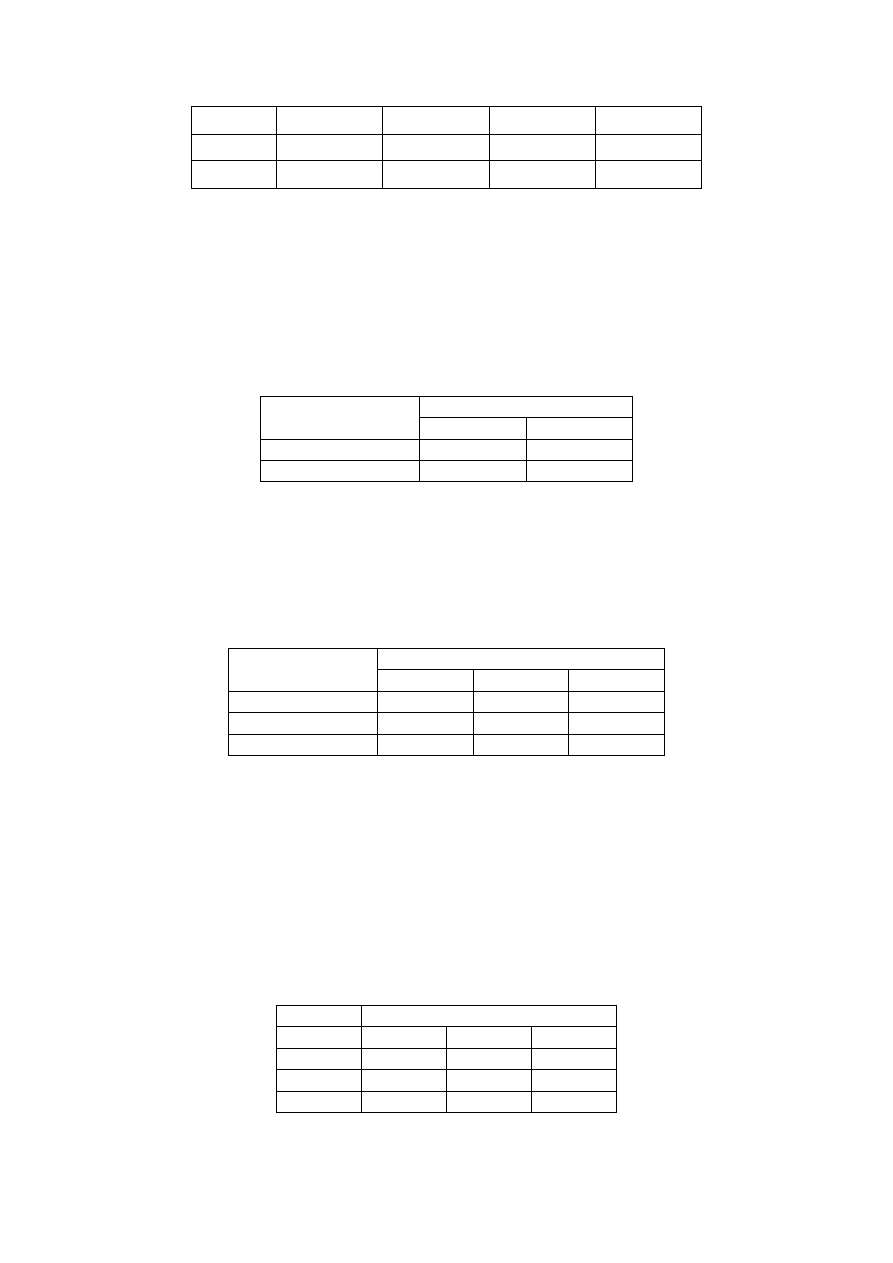
6
3
S
8
5
9
4
4
S
7
7
8
3
5
S
5
5
6
4
Pomóż kierownikowi przedsiębiorstwa przydzielić poszczególne prace studentom w taki
sposób, aby sprzątanie zajęło im jak najmniej czasu. Pamiętaj, że każdy student może
wykonać tylko jedną czynność. Sformułuj odpowiednie zadanie programowania liniowego.
Zad. 21: Janek i Stefan dojeżdżają samochodem na zajęcia w szkole. Za każdym razem
wybierają jedną z dwóch tras: obwodnicę miejską lub drogę przez centrum miasta. Informacje
o czasie przejazdu każdą z tras w zależności od natężenia ruchu w centrum przedstawia
poniższa tabela.
Decyzja
Natężenie ruchu w centrum
małe
duże
Jazda przez centrum 10
40
Jazda obwodnicą
20
30
Wyruszając do szkoły chłopcy nie znają natężenia ruchu w centrum miasta. Załóż, że Janek
jest pesymistą a Stefan optymistą. Którą drogę wybierze każdy z nich? Odpowiedź uzasadnij.
Zad. 22: Musisz zadecydować o sposobie pomnożenia swojego kapitału. Charakterystykę
Twoich możliwości inwestycyjnych (zysków) w zależności od przebiegu koniunktury
przedstawia poniższa tablica.
Rodzaj inwestycji Stan gospodarki
recesja
stabilizacja ekspansja
Lokata bankowa
10000
10000
10000
Obligacje
5000
20000
25000
Akcje
10000
15000
50000
Na podstawie analizy przebiegu koniunktury w przeszłości ustaliłeś, że prawdopodobieństwo
recesji, stabilizacji i ekspansji wynosi odpowiednio: 0,3, 0,5 i 0,2. Twój doradca inwestycyjny
zaleca zakup obligacji. Wyjaśnij, w jaki sposób doszedł on do takiej konkluzji? Jaka będzie
Twoja decyzja inwestycyjna?
Zad. 23: Zarząd małej miejscowości wypoczynkowej w górach rozważa trzy warianty
rozwoju bazy narciarskiej: A – zakup dodatkowego sprzętu do sztucznego zaśnieżania tras
narciarskich, B – modyfikację sprzętu zainstalowanego, C – odłożenie decyzji do
następnego sezonu. Wielkości spodziewanego tygodniowego zysku miasta z realizacji
każdego wariantu (w mln Pln) w zależności od stanu pogody przedstawia poniższa tabela.
Wariant
Opad śniegu
mały
ś
redni
duży
A
15000
10000
-5000
B
12000
8000
-1000
C
-6000
0
4000
7
Jaka będzie decyzja zarządu miasta, jeśli przy wyborze wariantu inwestycyjnego jego
członkowie kierowali się będą kryterium straty alternatywnej? Jaka będzie Twoja decyzja,
jeśli posłużysz się kryterium Hurwicza i za współczynnik optymizmu przyjmiesz liczbę 0,6?
Zad. 24: W poniższej tablicy przedstawiono koszt całkowity realizacji dwóch wariantów
pewnego przedsięwzięcia (w Pln) w zależności od stanu natury.
Wariant
Stan natury
1
S
2
S
3
S
4
S
I
5
2
1
-4
II
-3
0
2
4
Wiedząc, że:
2
,
0
)
S
(
P
1
=
,
4
,
0
)
S
(
P
2
=
,
3
,
0
)
S
(
P
3
=
,
1
,
0
)
S
(
P
4
=
podaj decyzje wynikające z
zastosowania kryterium oczekiwanej wartości pieniężnej, oczekiwanej straty alternatywnej
oraz największej wiarygodności.
Zad. 24: Zarząd przedsiębiorstwa rozważa podjęcie produkcji jednego z trzech wyrobów: A ,
B lub C . Zysk z ich produkcji (sprzedaży) zależy od stanu koniunktury na rynku.
Odpowiednie informacje zawiera poniższa tabela.
Decyzja
Stan rynku
dobry
zły
A
18
13
B
11
15
C
7
32
Określ decyzję zarządu, jeżeli na podstawie informacji historycznych ocenia on wstępnie
prawdopodobieństwo wystąpienia dobrej koniunktury na
8
,
0
)
S
(
P
1
=
. Czy decyzja zarządu
ulegnie zmianie, gdy uzyska on dodatkową informację o stanie rynku w postaci:
6
,
0
)
S
|
I
(
P
1
1
=
i
7
,
0
)
S
|
I
(
P
2
2
=
. Określ maksymalną kwotę, jaką zarząd skłonny będzie
wydatkować na pozyskanie dodatkowej informacji.
Zad. 25: Kierownik restauracji w miejscowości wypoczynkowej nad Morzem Bałtyckim
planuje zaopatrzenie w żywność i napoje z jedniodniowym wyprzedzeniem, stosownie do
przewidywanego natężenia ruchu turystycznego, które zależy od stanu pogody. Za każdym
razem składa zamówienie standardowe ( A ), jeśli spodziewa się złej pogody, bądź też
zamówienie ponadprzeciętne ( B ), jeśli uważa, ze pogoda będzie sprzyjała wycieczkowiczom.
Odgadnięcie, bądź też nieodgadnięcie, właściwego stanu pogody i złożenie odpowiedniego
zamówienia skutkuje różnicowaniem się zysku eksploatacyjnego. Informacje o jego
wielkości (w tys zł), wynikającej ze złożenia zamówienia i realizacji danego stanu natury,
zawiera poniższa tabela.
Zamówienie Pogoda
zła
dobra
)
S
(
P
1
)
S
(
P
2
A
25
30
B
-50
80
8
Jaka będzie decyzja kierownika, jeśli z poczynionych przez niego obserwacji pogody w
ostatnim kwartale wynika, ze
4
,
0
)
S
(
P
1
=
? Odpowiedź uzasadnij.
Zad. 26: Bierzesz udział w grze polegającej na odgadnięciu, w której z trzech,
ponumerowanych od 1 do 3, skrytek znajduje się cenna nagroda. Nie posiadasz żadnej
informacji odnośnie do umiejscowienia nagrody, wybierasz więc losowo jedną ze skrytek, np.
o numerze 1. Wówczas prowadzący grę przed otworzeniem wybranej przez Ciebie skrytki
otwiera jedną z pozostałych, np. o numerze 2, która okazuje się pusta, i pyta, czy zechcesz
zmienić swoją pierwotną decyzję. Jaka będzie Twoja odpowiedź?
Zad. 27: Załóż, że kierownik restauracji z zad. 16 wysłuchuje codziennie wieczorem
prognozy pogody na dzień następny, nadawanej przez lokalną stację radiowa, a następnie
składa przez telefon zamówienie u dostawcy. Prognoza w podsumowaniu kończy się jednym
z dwóch komunikatów: jutro będzie zła (
1
I
) lub dobra (
2
I
) pogoda. Kierownik od dłuższego
czasu porównuje prognozy z rzeczywistością, co pozwala mu sądzić, iż
8
,
0
)
S
|
I
(
P
1
1
=
oraz
6
,
0
)
S
|
I
(
P
2
2
=
. Jakie zamówienie powinien złożyć kierownik, jeśli dziś przez radio usłyszy,
ż
e jutro będzie zła pogoda? Odpowiedź uzasadnij.