Błądzenie losowe

1

Błądzenie losowe

Błądzenie losowe to pojęcie z zakresu matematyki i fizyki określające sformalizowane przedstawienie procesu,

polegającego na podejmowaniu kolejnych kroków, każdy w losowo wybranym kierunku. Błądzenie losowe jest

przykładem prostego procesu stochastycznego.

Własności

Najprostszy przykład błądzenia losowego to ścieżka skonstruowana według następujących zasad:

• Istnieje punkt początkowy

• Odległość od jednego punktu ścieżki do następnego jest stała

• Kierunek od jednego punktu ścieżki do drugiego jest wybierany losowo i żaden z kierunków nie jest bardziej

prawdopodobny od drugiego

Średnia odległość w linii prostej pomiędzy punktem początkowym i punktem końcowym po n krokach rośnie

zgodnie z

. Jeśli przez "średnią" będziemy rozumieć średnią kwadratową, wtedy średnia odległość po n

krokach wyniesie dokładnie

.

Przykład

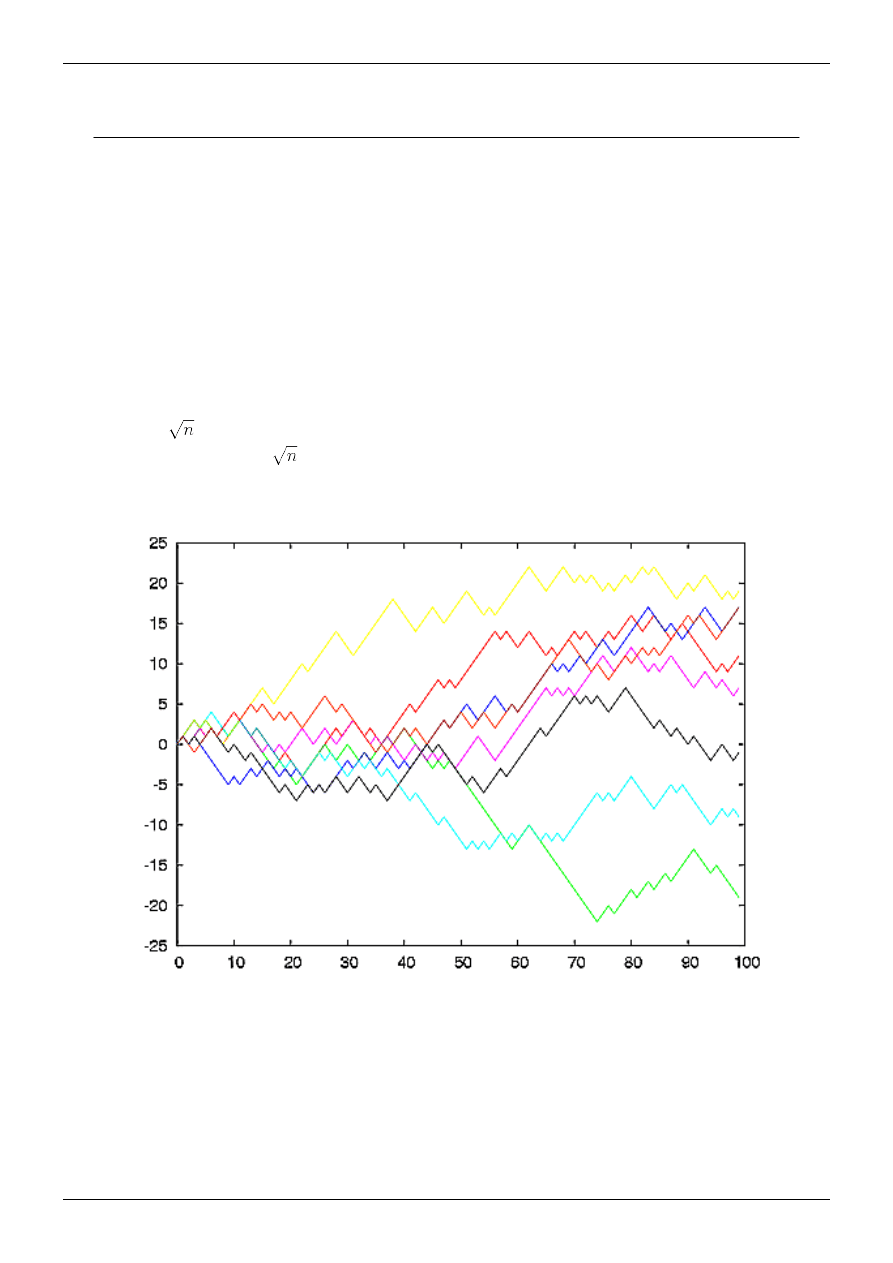
Wykres (n,R(n)) ośmiu różnych symulacji błądzenia losowego zaczynających się w 0.

Wykres przedstawia osiem przykładów błądzenia losowego, każdy o długości 100 kroków. W każdym kroku proces

może pójść do góry lub na dół. Można zauważyć, że pozostają one skupione wokół punktu początkowego, a średnia

odległość od tego punktu zwiększa się, ale wolniej niż liniowo.

Błądzenie losowe

2

Większa liczba wymiarów

Wyobraźmy sobie pijaka spacerującego po mieście. Miasto jest nieskończone i całkowicie uporządkowane, a na

każdym skrzyżowaniu pijak ma do wyboru jedną z czterech dróg (włączając tę, którą przyszedł). Formalnie jest to

proces błądzenia losowego na płaszczyźnie o całkowitych współrzędnych. Czy pijak kiedykolwiek wróci z baru do

domu? Okazuje się, że prawdopodobieństwo powrotu pijaka do domu wynosi 1 (!) – matematycy mówią w takiej

sytuacji: prawie na pewno. Jest to wielowymiarowa wersja problemu przekraczania poziomu, opisanego wcześniej.

Jednak podobieństwa na tym się kończą. W trzech i więcej wymiarach to twierdzenie nie jest prawdziwe. Innymi

słowy, pijany ptak mógłby zawsze błądzić w przestrzeni, nigdy nie trafiając do swojego gniazda. Opisując rzecz

formalnie, błądzenie losowe w 1 i 2 wymiarach jest procesem stochastycznym ze stanami powtarzającymi się,

natomiast błądzenie losowe w 3 wymiarach to proces o stanach chwilowych. Udowodnił to w 1921 roku George

Pólya.

Trajektoria błądzenia losowego to kolekcja miejsc odwiedzonych przez proces, rozważana jako zbiór bez brania pod

uwagę kiedy proces osiągnął dany punkt. W jednowymiarowej przestrzeni trajektoria to po prostu wszystkie punkty

pomiędzy minimalną wysokością osiągniętą przez proces a maksymalną wysokością (obie rosną średnio zgodnie z

). Przy większej liczbie wymiarów dostajemy dyskretny fraktal, to znaczy zbiór, który w dużej skali wykazuje

własność samopodobieństwa, ale w mniejszej skali zobaczymy wpływ siatki, na której odbywa się proces.

Błądzenie losowe na grafie

Przypuśćmy teraz, że nasze miasto nie jest uporządkowane. Kiedy pijak dociera do skrzyżowania, może wybrać

jedną z wielu dróg, każdą z jednakowym prawdopodobieństwem. Jeśli ze skrzyżowania wybiega siedem dróg, pijak

wybierze każdą z nich z prawdopodobieństwem 1/7. Taki problem nazywamy błądzeniem losowym na grafie. Czy

nasz pijak ciągle ma szansę na powrót do domu? Okazuje się, że przy pewnych łagodnych założeniach odpowiedź

ciągle brzmi: tak. Na przykład jeśli długość wszystkich bloków pozostanie w przedziale od 10 metrów do 10

kilometrów (albo pomiędzy dwoma innymi dowolnymi liczbami), wtedy pijak prawie na pewno dotrze do domu.

Ciekawe jest, że nie zakładamy przy tym, że graf jest planarny, tzn. że w mieście mogą być tunele i mosty. Jeden z

dowodów opiera się na związkach z sieciami elektrycznymi. Weźmy mapę miasta i umieśćmy rezystor na każdym

bloku. Teraz zmierzmy "opór pomiędzy danym punktem a nieskończonością". Innymi słowy, wybierzmy liczbę R i

weźmy wszystkie punkty w sieci elektrycznej odległe o więcej niż R od naszego punktu i połączmy je razem. Mamy

skończoną sieć elektryczną i jesteśmy w stanie zmierzyć opór od naszego punktu do połączonych punktów.

Zwiększajmy R do nieskończoności. Granicę nazwiemy oporem pomiędzy punktem i nieskończonością. Okazuje się,

że prawdą jest:

Twierdzenie: proces błądzenia losowego na grafie posiada stany chwilowe wtedy i tylko wtedy, gdy opór pomiędzy

punktem i nieskończonością jest skończony. Nie jest ważne, jaki punkt wybierzemy.

Okazuje się, że taki opis procesów ze stanami chwilowymi i powtarzającymi się jest bardzo wygodny i w

szczególnym przypadku pozwala na analizę przypadku miasta na płaszczyźnie z ograniczonymi odległościami.

Nie należy mylić błądzenia losowego na grafie z łańcuchem Markowa. W przeciwieństwie do łańcuchów Markowa,

błądzenie losowe na grafie posiada własność symetrii względem czasu lub odwracalności. Oznacza to mniej więcej,

że prawdopodobieństwa przejścia danej trasy w jednym lub drugim kierunku są ze sobą w prosty sposób powiązane

(jeśli graf jest regularny są po prostu równe). Okazuje się, że ta własność pociąga za sobą ważne konsekwencje.

Źródła i autorzy artykułu

3

Źródła i autorzy artykułu

Błądzenie losowe  Źródło: http://pl.wikipedia.org/w/index.php?oldid=21166916  Autorzy: 4C, AI, Izik, Jarekt, Kbsc, Mciura, Mg20170, Michalgarbowski, MichałRadecki, Przykuta, Qblik, 1
anonimowych edycji

Źródła, licencje i autorzy grafik

Plik:Random Walk example.png  Źródło: http://pl.wikipedia.org/w/index.php?title=Plik:Random_Walk_example.png  Licencja: GNU Free Documentation License  Autorzy: ChongDae,
Darapti, Mdd, Ordoon, Toobaz, 1 anonimowych edycji

Licencja

Creative Commons Attribution-Share Alike 3.0 Unported
http:/

/

creativecommons.

org/

licenses/

by-sa/

3.

0/