W 4.1

1024

512

256

128

64

64 128 256

512

1024

Obliczanie
za pomoc

ą

FFT

Obliczanie
za pomoc

ą

DFT

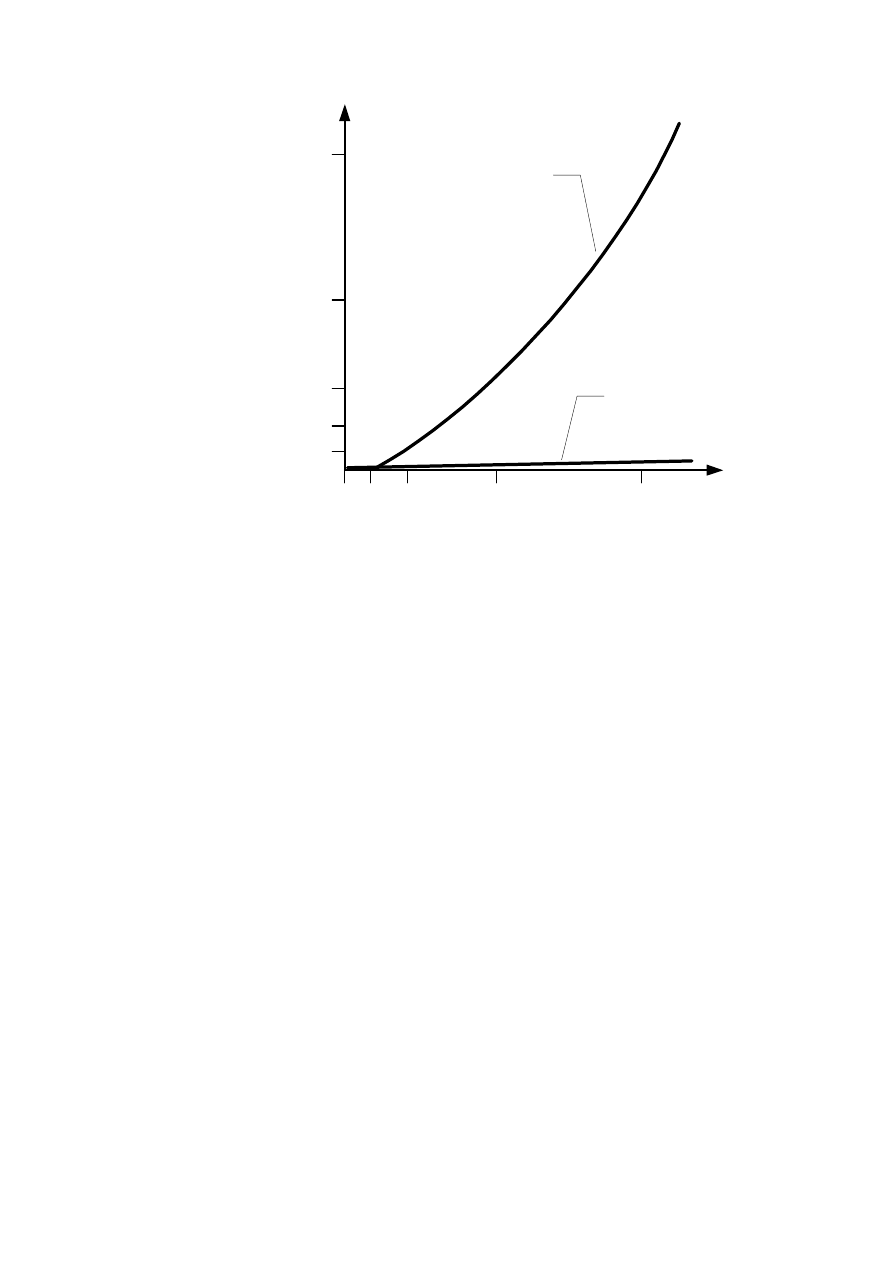
Operacje[tys]

N

Rys. Porównanie szybkości algorytmu DFT oraz FFT

Przykład
Niech N=8. Wówczas X

n

współczynników DFT ma postać

4

n

0

W

Z

Y

X

W

Z

Y

X

W

Z

Y

X

W

Z

Y

X

3

3

3

3

2

2

2

2

1

1

1

1

0

0

0

0

<

≤













+

=

+

=

+

=

+

=

4

n

0

W

Z

Y

W

Z

Y

X

W

Z

Y

W

Z

Y

X

W

Z

Y

W

Z

Y

X

W

Z

Y

W

Z

Y

X

3

3

3

7

3

3

7

2

2

2

6

2

2

6

1

1

1

5

1

1

5

0

0

0

4

0

0

4

<

≤













−

=

+

=

−

=

+

=

−

=

+

=

−

=

+

=

W 4.2

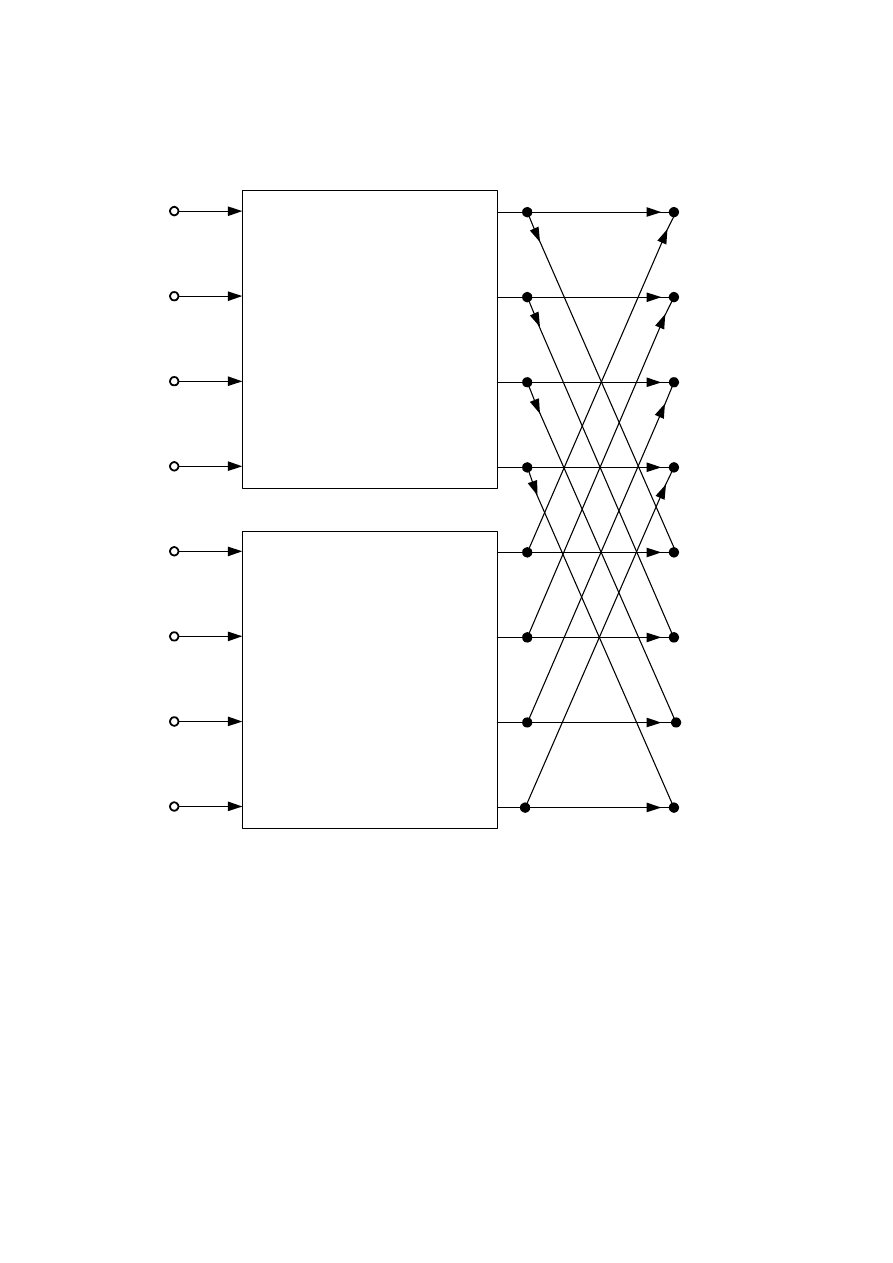
Schematycznie proces obliczeniowy współczynników X

n

dla 8-punktowej

DFT z podziałem na dwie 4-punktowe DFT przedstawiono na rysunku.

DFT

(N=4)

DFT

(N=4)

0

x

2

x

4

x

6

x

1

x

3

x

5

x

7

x

0

y

1

y

2

y

3

y

0

z

1

z

2

z

0

z

0

Z

1

Z

2

Z

3

Z

4

X

5

X

6

X

7

X

4

W

5

W

6

W

7

W

0

W

1

W

2

W

3

W

0

X

1

X

2

X

3

X

3

Y

2

Y

1

Y

0

Y

Rys. Dwupunktowy algorytm FFT

Uwagi

1. Węzły oznaczają zmienne przekształcenia (współczynniki Fouriera

dla ciągów y

k

oraz z

k

).

2. Strzałki oznaczają wkład zmiennych do sumarycznych wartości

poszczególnych współczynników DFT.

3. W

n

oznacza wagi z jakimi współczynnikami sumują się w węzłach.

W 4.3

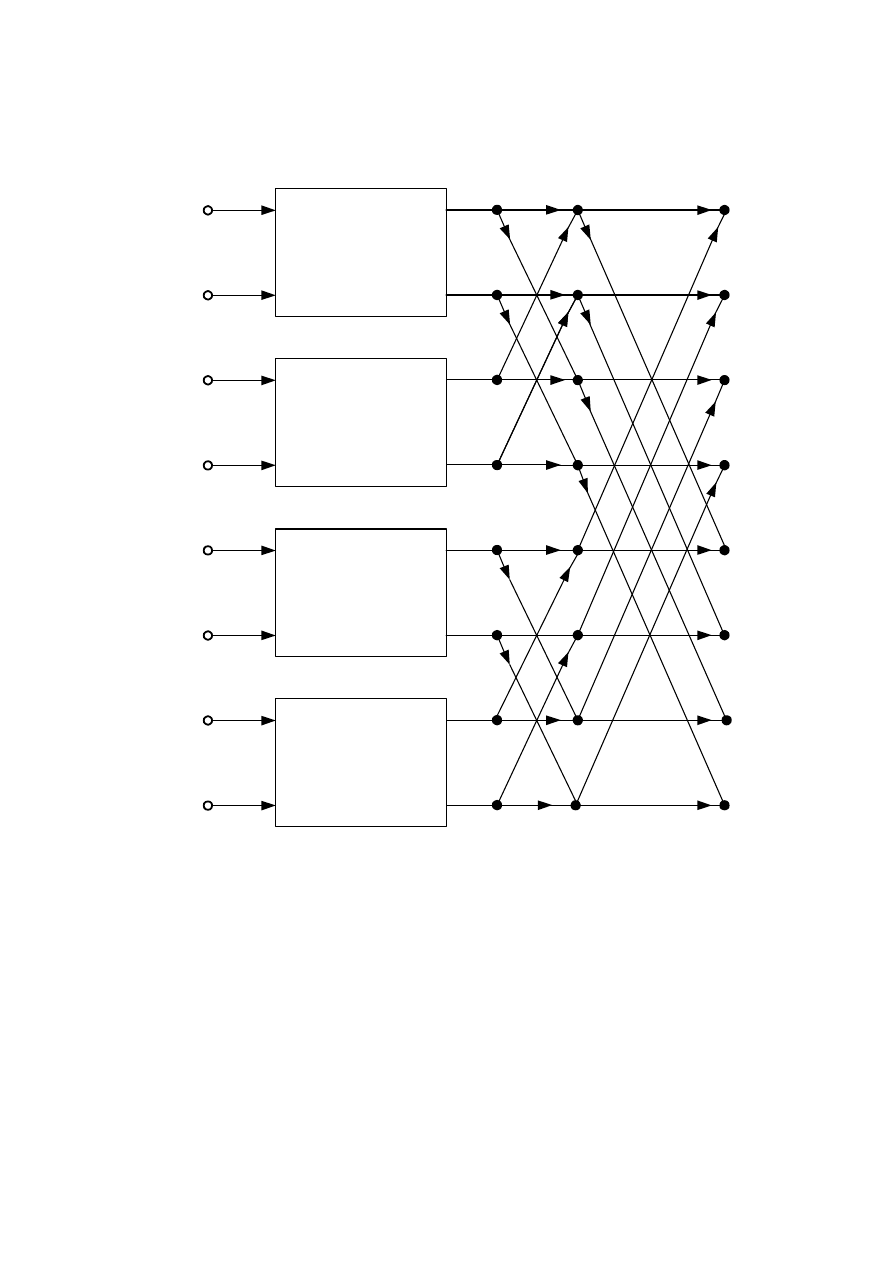
Proces obliczeniowy współczynników X dla 8-punktowej DFT z podziałem
na cztery 2-punktowe DFT przedstawiono schematycznie na rysunku.

DFT

(N=2)

DFT

(N=2)

4

X

5

X

6

X

7

X

4

W

5

W

6

W

7

W

0

W

1

W

2

W

3

W

0

X

1

X

2

X

3

X

6

W

4

W

2

W

0

W

6

W

4

W

2

W

0

W

DFT

(N=2)

DFT

(N=2)

1

x

3

x

5

x

7

x

0

x

2

x

4

x

6

x

Rys. Czteropunktowy algorytm FFT