KAS 2011

Przetwarzanie via FFT

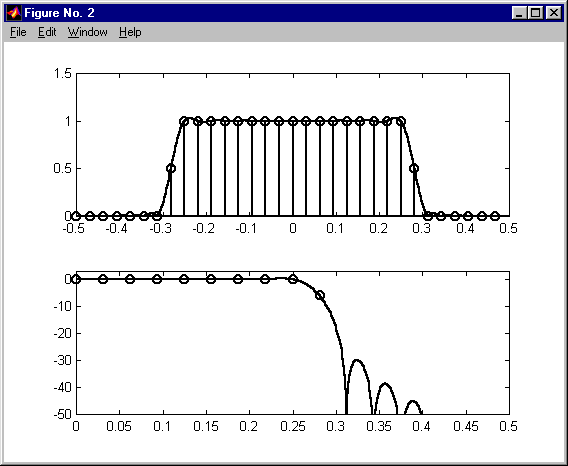
• projektowanie filtrów metodą próbkowania w dziedzinie częstotliwości

• filtracja w dziedzinie częstotliwości

- założona a uzyskana charakterystyka częstotliwościowa

- alias w dziedzinie czasu

- zjawisko przecieków

• koncepcja filtracji overlap-add / overlap-save : szybki splot

• przetwarzanie via FFT długich ciągów

- fragmenty nie nakładające się

- fragmenty z uzupełnianiem zerami

- nakładające się fragmenty sygnału

• metody pomiaru jakości przetwarzania segmentowego

- odpowiedź impulsowa lub chirp nie nadaje się ze względu na brak stacjonarności

- szum biały (ew. powyższe sygnały) - podejście statystyczne (może TPE)

- ew. testowanie sygnałem monochromatycznym KAS 2011

projektowanie filtrów metodą próbkowania w dziedzinie częstotliwości KAS 2011

1

KAS 2011

KAS 2011

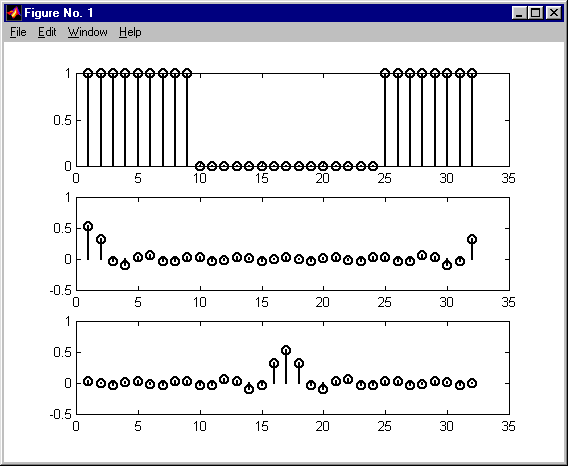
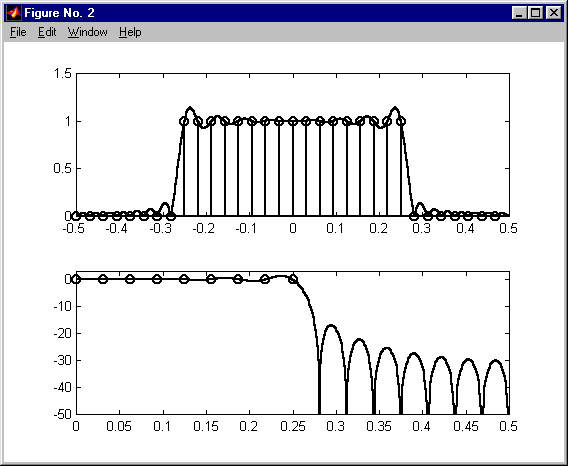
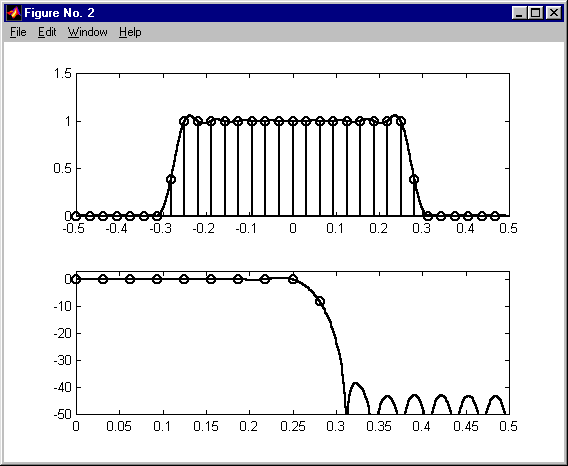
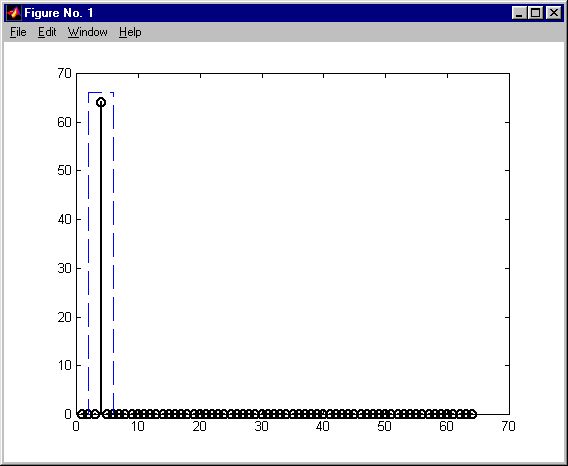
alias w dziedzinie czasu

[n,cc] = size(x);

m = 2^nextpow2(n);

y = fft(real(x),m);

if m ~= 1

h = [1; 2*ones(fix((m-1)/2),1);...

ones(1-rem(m,2),1);...

zeros(fix((m-1)/2),1)];

y(:) = y.*h(:, ones(1,cc) );

end

y = ifft(y,m);

y = y(1:n,:);

KAS 2011

2

KAS 2011

przecieki a filtracja w dziedzinie częstotliwości KAS 2011

koncepcja filtracji overlap-add / overlap-save : szybki splot x[ n]

n

Filter each block x [ n]

x [ n]

i

y [ n]

i

i

with the impulse

response h[ n]

Partition input

in non-overlapping

blocks x [ n]

i

y[ n]

Adding the over-lapping

outputs y [ n] from each block i

to obtain the output y[ n]

n

Overlap-add sectioning of convolution x[ n]

n

Filter each block x [ n]

x [ n]

i

y [ n]

i

i

with the impulse

response h[ n]

Partition input

in overlapping

blocks x [ n]

i

y[ n]

Select the output from

appropriate block y [ n]

i

(discard over-lap)

n

Overlap-save sectioning of convolution KAS 2011

3

KAS 2011

filtracja overlap-add / overlap-save

%Overlap-add

%Overlap-save

function y=fftfilt(h, x, Nfft)

function y=fftfiltS(h, x, Nfft)

H=fft(h, Nfft);

N=length(h);

N=length(h);

H=fft(h, Nfft); %fft with zeropadding M=Nfft-N+1; %section length

M=Nfft-N+1; %section length

%make sure that length(x) is multiple of M

x=[zeros(1,N-1) x];

LenOut=length(x);

%make sure that length(x) is

if rem(LenOut,M)~=0

% Nfft plus multiple of M

x(ceil(LenOut/M)*M)=0;

LenOut=length(x)

end;

if LenOut<Nfft

x(Nfft)=0;

y=zeros(1,N);

elseif rem(LenOut-Nfft,M)~=0

for indX=1:M:length(x)

x(ceil((LenOut-Nfft)/M)*M+Nfft)=0;

x_seg=x(indX:(indX+M-1)); %segment of x[n]

end;

X=fft(x_seg, Nfft); %fft with zeropadding Y=X.*H;

y=[];

y_seg=ifft(Y);

for indX=1:M:(length(x)-Nfft+1)

y(indX:(indX+N-2))=y(indX:(indX+N-2))+y_seg(1:(N-1)); x_seg=x(indX:(indX+Nfft-1));

y((indX+N-1):(indX+Nfft-1))=y_seg(N:Nfft);

%segment of Nfft samples of x[n]

end;

X=fft(x_seg);

Y=X.*H;

% check if output signal should be purely real y_seg=ifft(Y);

if ~any(imag(h)) & ~any(imag(x))

y=[y y_seg((Nfft-M+1):Nfft)];

y=real(y);

end;

end;

% check if output signal should be purely real if ~any(imag(h)) & ~any(imag(x))

y=real(y);

end;

KAS 2011

FFTFILT Overlap-add method of FIR filtering using FFT.

Y = FFTFILT(B,X) filters X with the FIR filter B using the overlap/add method, using internal parameters (FFT

size and block length) which guarantee efficient execution.

Y = FFTFILT(B,X,N) allows you to have some control over the internal parameters, by using an FFT of at least N points.

If X is a matrix, FFTFILT filters its columns.

See also FILTER.

--- Algorithmic details ---

The overlap/add algorithm convolves B with blocks of X, and adds the overlapping output blocks. It uses the FFT to compute the convolution.

Particularly for short filters and long signals, this algorithm is MUCH faster than the equivalent numeric function FILTER(B,1,X).

Y = FFTFILT(B,X) -- If you leave N unspecified: (RECOMMENDED) Usually, length(X) > length(B). Here, FFTFILT chooses an FFT length (N) and block length (L) which minimize the number of flops required for a length-N FFT times the number of blocks ceil(length(X)/L).

If length(X) <= length(B), FFTFILT uses a single FFT of length nfft = 2^nextpow2(length(B)+length(X)-

1), essentially computing ifft(fft(B,nfft).*fft(X,nfft)).

Y = FILTFILT(B,X,N) -- If you specify N: In this case, N must be at least length(B); if it isn't, FFTFILT sets N to length(B). Then, FFTFILT uses an FFT of length nfft = 2^nextpow2(N), and block length L = nfft - length(B) + 1.

CAUTION: this can be VERY inefficient, if L ends up being small.

KAS 2011

4

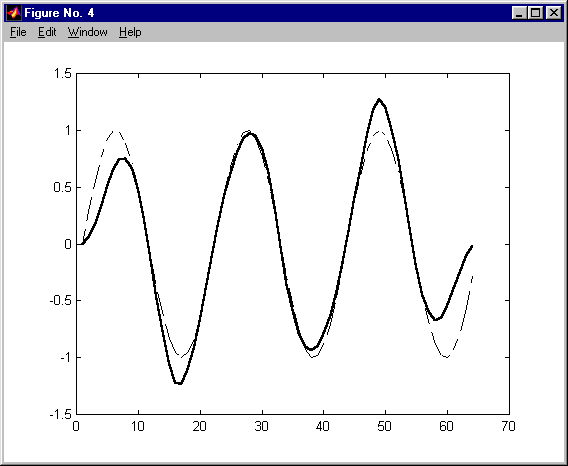
KAS 2011

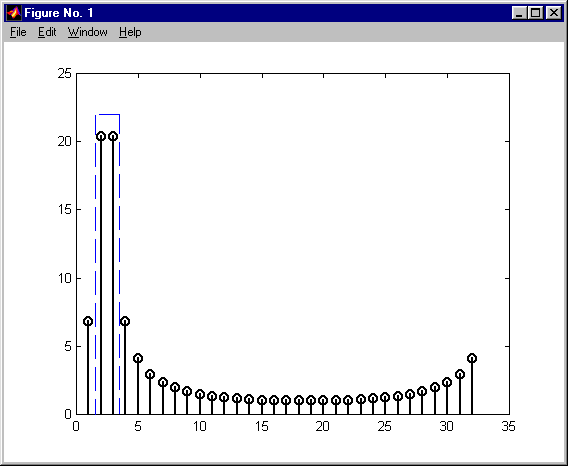
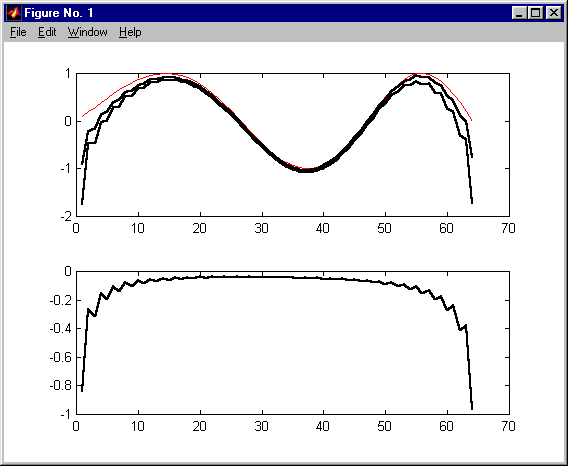
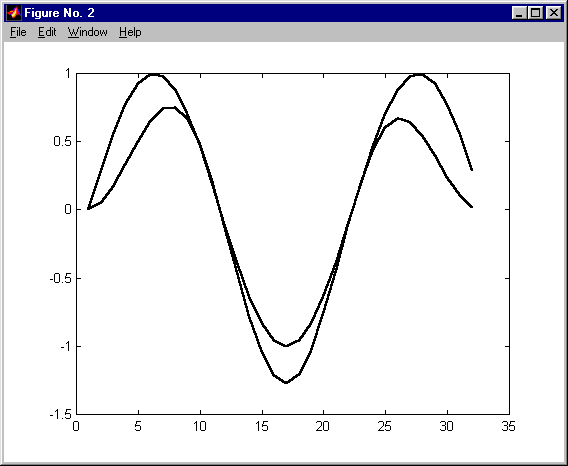
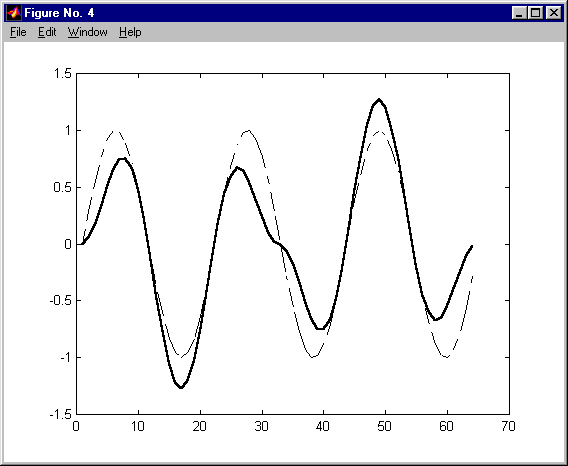
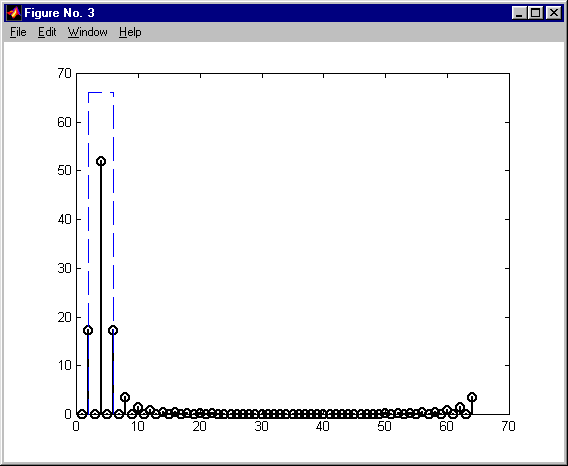
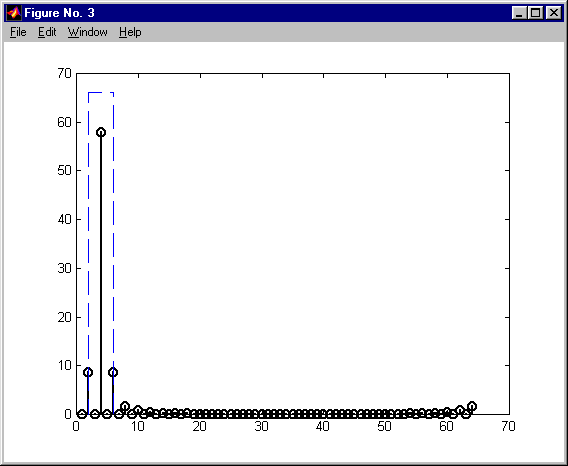
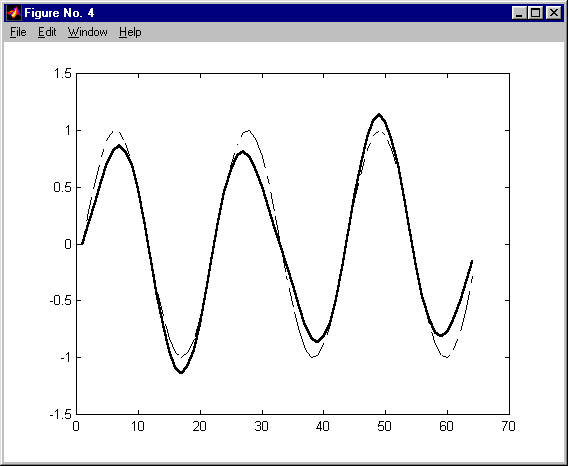
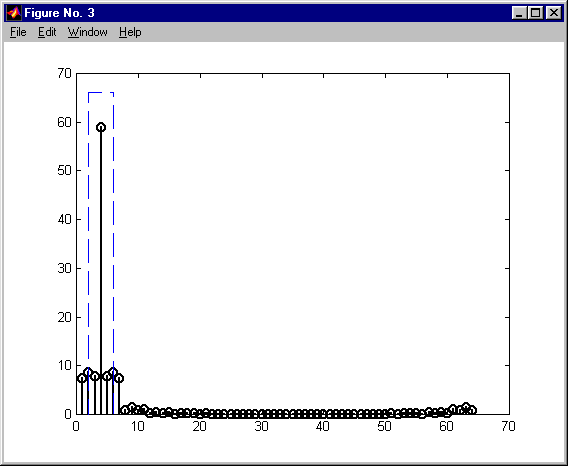
przetwarzanie via FFT długich ciągów - nie nakładające się ciągi KAS 2011

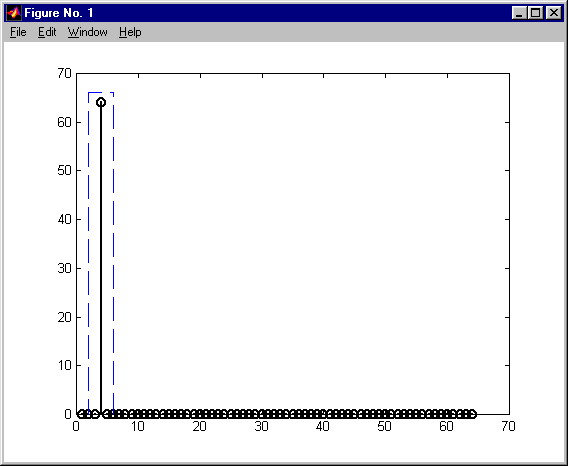
przetwarzanie via FFT długich ciągów KAS 2011

5