Laboratorium Programowanie procesorów sygnałowych

Szybka transformacja Fouriera (FFT)

Poznań 2005

Politechnika Poznańska
Instytut Elektroniki i Telekomunikacji
Zakład Systemów Telekomunikacyjnych

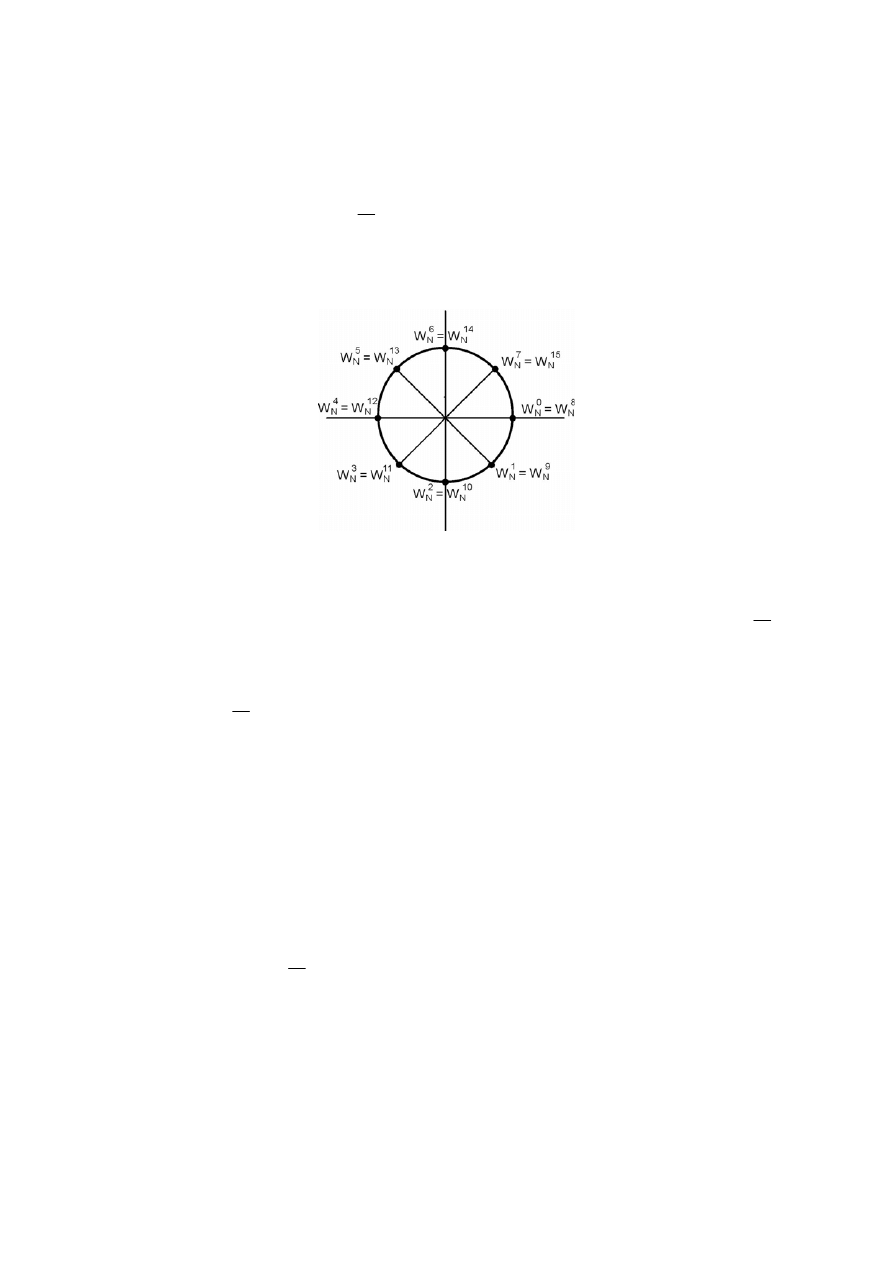
1. Wstęp

1.1 Dyskretna transformacja Fouriera

( )

( )

∑

−

=

−

=

1

0

1

N

n

kn

N

W

n

x

N

k

X

, k=0,1,2,…,N-1

Obliczenie DFT z definicji wymaga

mnożeń zespolonych i N(N-1)

dodawań:

2

N

1.2 Szybka transformacja Fouriera (ang. Fast Fourier Transform - FFT)

Ponieważ DFT charakteryzuje się złożonością obliczeniowa rzędu

, dzieląc sygnał

na dwie części i transformując je osobno, musimy wykonać dwa razy po

2

N

2

)

2

(

N

operacji plus niewielką liczbę operacji potrzebnych na „skonsolidowanie” widm
częściowych. Przykładowo dla N=1024, zamiast wykonywać

mnożeń

wykonuje się

1048676

2

=

N

524288

)

2

(

2

2

=

N

mnożeń, czyli dwa razy mniej.

Oczywiście podziału zbioru próbek można dokonywać dalej –aż do uzyskania
zbiorów dwuelementowych.
W dalszej części niniejszej instrukcji zostanie zaprezentowany algorytm radix-2 DIT
(ang. Decimation In Time), ze względu na prostotę realizacji i powszechność
stosowanego podejścia.
W algorytmie tym zakłada się, że transformowany sygnał posiada

próbek, a

następnie:

p

N

2

=

1) dokonuje się zmiany kolejności próbek (realizowane jest to sprzętowo przez
adresowanie z inwersją bitów), dzieląc je rekurencyjnie na próbki o indeksach
parzystych i nieparzystych, aż do uzyskania zbiorów dwuelementowych;

2) wykonuje się serię

)

2

(

N dwupunktowych przekształceń DFT;

3) następnie składa się widma dwukrążkowe (będące wynikiem przekształceń DFT z
pkt. 2) w widma czterokrążkowe. Procedurę powtarza się aż do momentu „złożenia”
pełnego -N - punktowego widma.

Dla danego N algorytm FFT w wersji radix-2 DIT *(decymacja w czasie) wymaga
wykonania

mnożeń i tyle samo dodowań zespolonych

N

N

2

log

• *-szybsza wersja algorytmu redukuje liczbę mnożeń do połowy tej wielkości.

Politechnika Poznańska
Instytut Elektroniki i Telekomunikacji
Zakład Systemów Telekomunikacyjnych

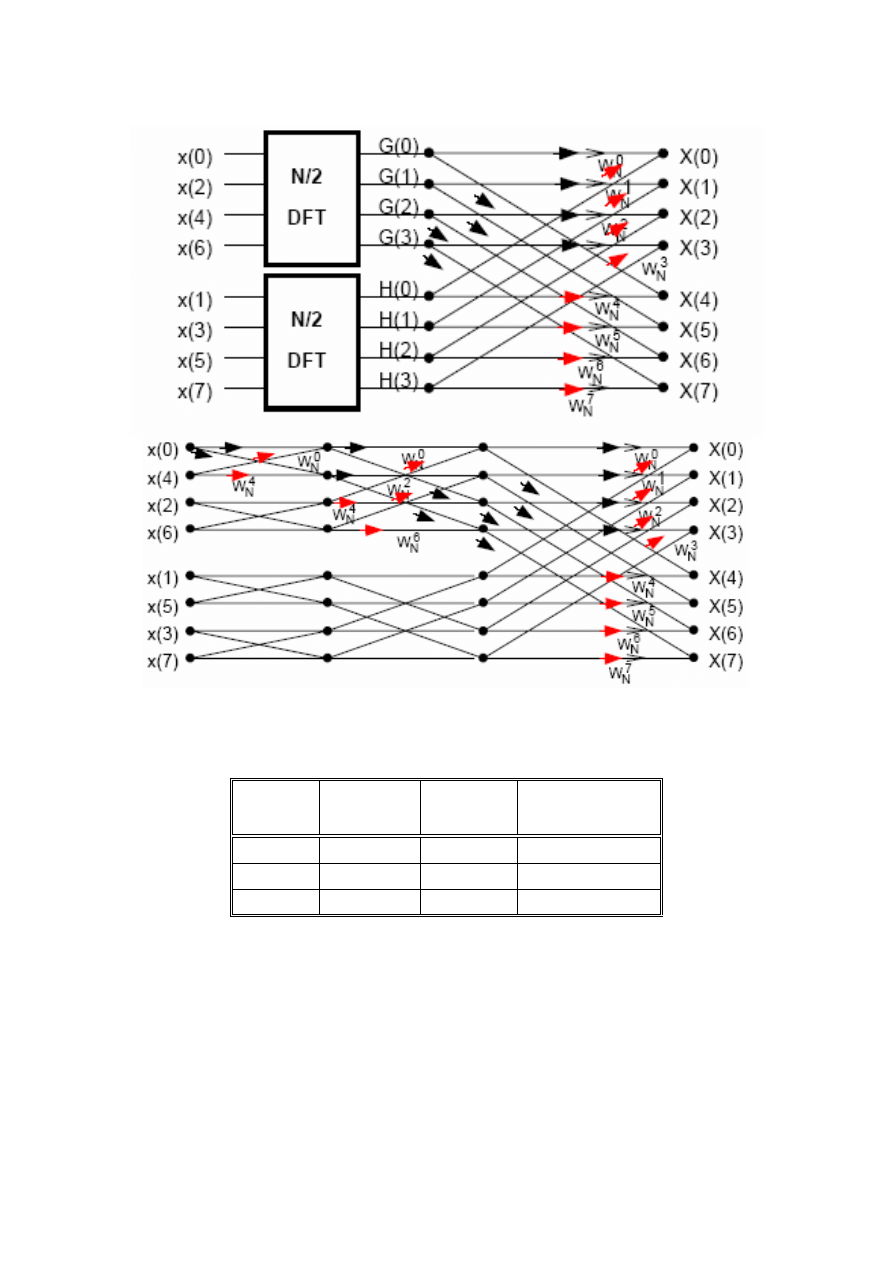
Próbki sygnału x(n) są uporządkowane według zasady inwersji bitów
indeksu.

N

2

N

N

N

2

log

2

N /

N

N

2

log

8

64

24

2.67

64

4096

384

10.7

1024 1048576 10240

102.4

Liczbę mnożeń można jeszcze zmniejszyć zastępując operacje motylkowe:

Politechnika Poznańska
Instytut Elektroniki i Telekomunikacji
Zakład Systemów Telekomunikacyjnych

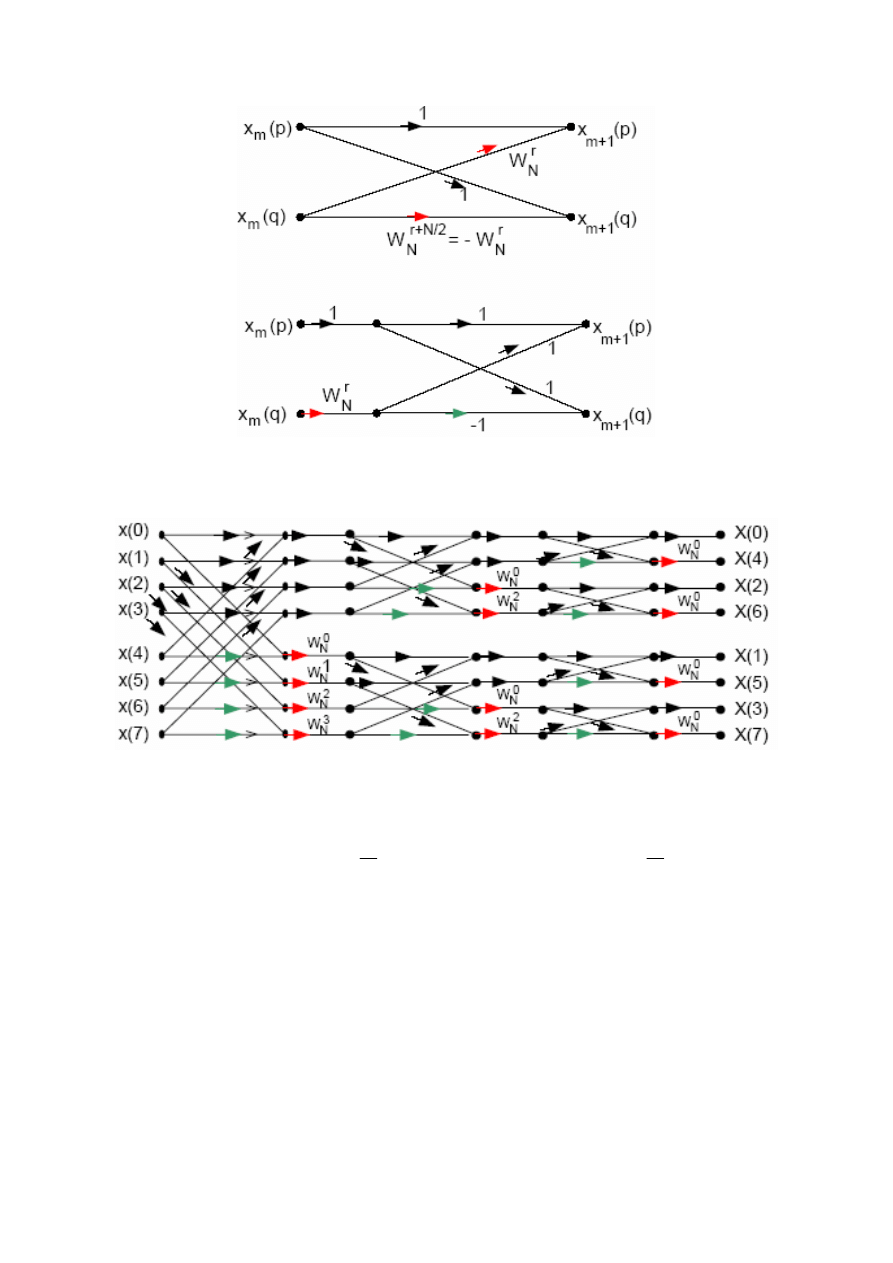
W podobny sposób można opisać algorytm z podziałem częstotliwości (tutaj
decymacja ma miejsce „po stronie” częstotliwości):

Przedstawiony powyżej algorytm radix-2 DIT nie jest jedynym szybkim algorytmem
typu DIT pozwalającym na wyznaczenie DFT. W literaturze przedstawiono wiele
wersji algorytmów FFT, w tym efektywniejsze od radix-2 algorytmy radix-4 (4

„części”), gdzie wykonuje się

⎟

⎠

⎞

⎜

⎝

⎛

4

3

N mnożenia zespolone, zamiast

⎟

⎠

⎞

⎜

⎝

⎛

2

N mnożeń

(radix-2),ale etapów jest dwa razy mniej.

2. Zawartość katalogu z zestawem plików dot. ADSP-21160 EZ-KIT Lite FFT

Celem obecnego ćwiczenia laboratoryjnego jest przedstawienie algorytmu
realizowanego na zmiennoprzecinkowym procesorze sygnałowym Analog Devices
21160.

Zawartość katalogu po rozpakowaniu załączonego archiwum:

fft.dpj -plik projektu w środowiskuVisualDSP
Main.c – główny moduł obliczeniowy projektu
ADSP_21160_EzKit.c – moduł inicjalizacji

Politechnika Poznańska
Instytut Elektroniki i Telekomunikacji
Zakład Systemów Telekomunikacyjnych

21160_EZKIT_Lite.ldf -plik opisu Linkera
ADSP_21160_EzKit.h – plik nagłówkowy- prototypy fukcji
Audio_Processing_ISR.asm - Codec moduł tx and rx
1000Hz_Sine.wav – wejściowy plik audio – sygnał sinusoidalny o częstotliwości
1000Hz
1500Hz_Triangle.wav – wejściowy plik audio – sygnał trójkątny o częstotliwości
1500Hz Sine Wave FFT.vps – rysowanie FFT dla sygnału sinusoidalnego

Sine Wave Input.vps – rysowanie wejściowego sygnału sinusoidalnego
Triangle FFT.vps - rysowanie FFT dla sygnału trójkątnego
Triangle Input.vps - rysowanie wejściowego sygnału trójkątnego

3. Opis funkcjonalny.

Niniejszy przykład demonstruje inicjalizacje interfejsu SPORT w celu umożliwienia
połączenia AC-97 pomiędzy ADSP 21160 a kodekiem AD1881. W przykładzie tym
użyto interfejs SPORT0 umożliwiający pozwalający na połączenie z przetwornikiem
AD1881. Próbki sygnału dźwiękowego otrzymane z AD1881 kierowane SA do
wejściowego bufora używając DMA (pominięcie rejestrów procesora - interfejs
bezpośredniego dostępu do pamięci – ang. Direct Memory Access). Kolejnym
etapem jest przetworzenie próbek przez ADSP-21160 i umieszczenie ich w buforze
wyjściowym, po czym następuje z powrotem przesłanie przetworzonych próbek do
AD1881.
Transformacja FFT realizowana jest na lewym i prawym kanale wejściowym.
Podczas, gdy FFT realizowane jest na jednym kanale, na drugim następuje zbieranie
danych. Używając metody buforów cyklicznych, zależnej od miejsca zatrzymania
programu sygnał wejściowy może być nieznacznie zniekształcany. Niemniej jednak
powyższe zniekształcenie nie ma wpływu na sam zbiór próbek FFT.

4. Opis implementacji.

Zadaniem modułu inicjalizacji jest inicjalizacja:

1. Transmisję i odbieranie danych w konfiguracji wielokanałowej;
2. Transmisyjne i wejściowe rejestry kontroli DMA oraz rejestry buforów

automatycznych;

3. Rejestry kontrolujące interfejs SPORT0 ;
4. Przetwornika A/C C/A poprzez wpis do jego rejestrów kontrolnych;
5. FFT poprzez wykonanie funkcji rfft128 na pobranym wektorze próbek sygnału

wejściowego.

Następnie wizualizowane jest widmo amplitudowe.

6. Opis ćwiczenia – instrukcje do samodzielnego wykonania w trakcie

zajęć.

1. Trzymając przycisk control uruchomić aplikację Visual DSP++ Æ wczytać

sesję domyślną sesję w oknie wyboru sesji.

2. Otworzyć plik projektu FFT.dpj (fileÆopen Project file)
3. Zbudować projekt (ProjectÆ Build Project)
4. Załadować plik FFT.dxe do ADSP-21160.

Politechnika Poznańska
Instytut Elektroniki i Telekomunikacji
Zakład Systemów Telekomunikacyjnych

5. Połączyć liniowe wyjście karty dźwiękowej PC z wejściem liniowym zestawu

uruchomieniowego ADSP-21160 EZ-KIT Lite.

6. Upewnić się, że suwak poziomu głośności nie jest ustawiony na wartość

maksymalną.

7. Uruchomić odtwarzanie pliku audio 1500Hz_Triangle.wav (np. Winamp lub

Windows Media Player).

8. Uruchomić wykonanie programu FFT na ADSP-21160 EZ-KIT Lite

(DebugÆRun).

9. Sygnał wyjściowy powinien być słyszalny w słuchawkach.
10. Zatrzymać działanie procesora (DebugÆHalt).
11. Zobaczyć sygnał wejściowy i jego transformatę FFT (ViewÆDebug

WindowsÆPlotÆRestore) i wybrać odpowiednio Triangle Input.vps oraz
Triangle FFT.vps.

12. Powtórzyć procedurę przedstawioną w punktach 2-11 zastępując sygnał

trójkątny przez sinusoidalny (patrz zawartość katalogu użytego w bieżącym
ćwiczeniu lab.)

7. Sprawozdania z wykonania ćwiczenia laboratoryjnego.

W sprawozdaniu należy zawrzeć:

A. Wydruki przebiegów czasowych analizowanych sygnałów
B. Wydruki transformat FFT ze stosownym komentarzem
C. Fragment kodu realizujący FFT
D. Wnioski

Politechnika Poznańska
Instytut Elektroniki i Telekomunikacji
Zakład Systemów Telekomunikacyjnych

8. Dodatek – bufory cykliczne.

Operacje MAC (ang. Multiply and Accumulate) w procesorach DSP są najistotniejszymi

instrukcjami, które wpływają na szybkość ich przetwarzania w przypadku cyfrowej obróbki danych.
Zasada ich działania opiera się na sprzętowych rozwiązaniach gwarantujących optymalizację
wykonywanych przez nie zadań (tzn. mnożenia i jednoczesnej akumulacji),
Rozwiązaniami tymi są specjalnie zaprojektowane układy adresujące pamięć DAGs (ang. Data
Address Generatorors) oraz odpowiednie towarzyszące im zbiory rejestrów indeksujących.
Wykorzystują one tryb pracy polegający na organizowaniu pamięci w bufory adresowanie w sposób
cykliczny.
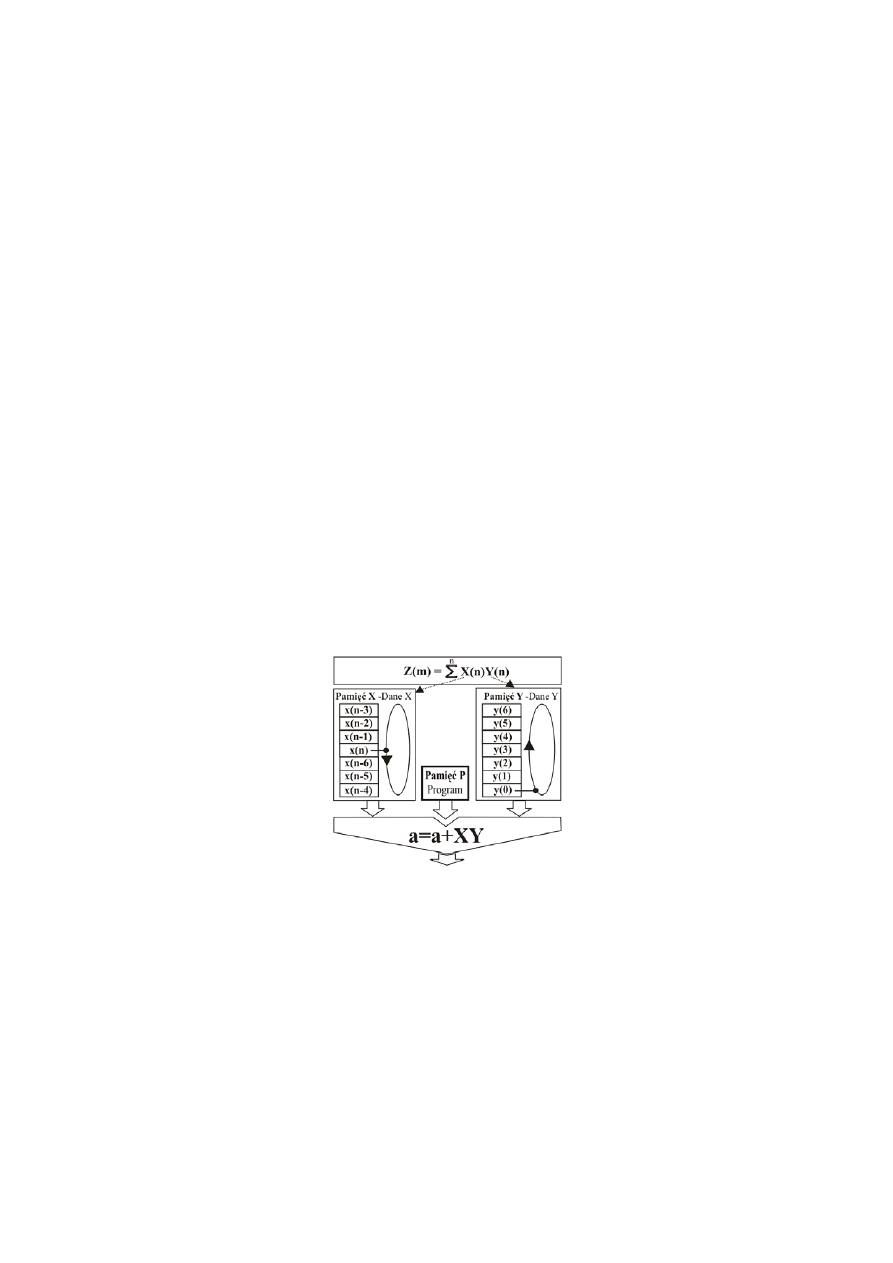
Zasada takiego adresowania polega na tym, że najmłodsza pobrana próbka wchodzi na miejsce
najstarszej, a wartości wskaźników indeksujących próbki są odpowiednio modyfikowane tak, aby
wskazywały odpowiednio ich sekwencyjną kolejność. Na rysunku 1 najstarszą wartością w buforze
cyklicznym (kołowym) jest wartość x(n-6). W jej miejsce zapisywana jest aktualna wartość x(n), a
dotychczasowa wartość x(n) staje się wartością x(n-1), wartość x(n-1) wartością x(n-2) itd. Wymagana
w obliczeniach aktualna wartość próbki x(n), dzięki odpowiedniemu wskazywaniu jej przez stosowne
rejestry indeksujące, przemieszcza się w sposób cykliczny po całym adresowanym buforze. Zaletą
tego jest to, że próbki nie muszą być fizycznie przesuwane tak jak w buforze przesuwnym -
„przesunięcie” dokonywane jest tylko poprzez modyfikację stosownych rejestrów wskazujących ich
odpowiednią kolejność.

Dodatkowo układy DAGs posiadają możliwość adresowania polegającą na bitowym

odwracaniu adresów (ang. Bit Reverse Addressing). Własność ta jest szczególnie przydatna w
przypadku obliczeń korzystających z algorytmów szybkiej transformacji Fouriera (FFT).

Rys 1. Zasada działania buforów cyklicznych oraz bazującej na tej koncepcji operacji MAC.

W celu zobrazowania omawianej idei rozważmy fragment kodu procesora firmy Motorola DSP

560xx.

rep #liczba_mnożeń
mac x0,y0,a x(r1)+,x0 y(r5)-,y0

Politechnika Poznańska
Instytut Elektroniki i Telekomunikacji
Zakład Systemów Telekomunikacyjnych

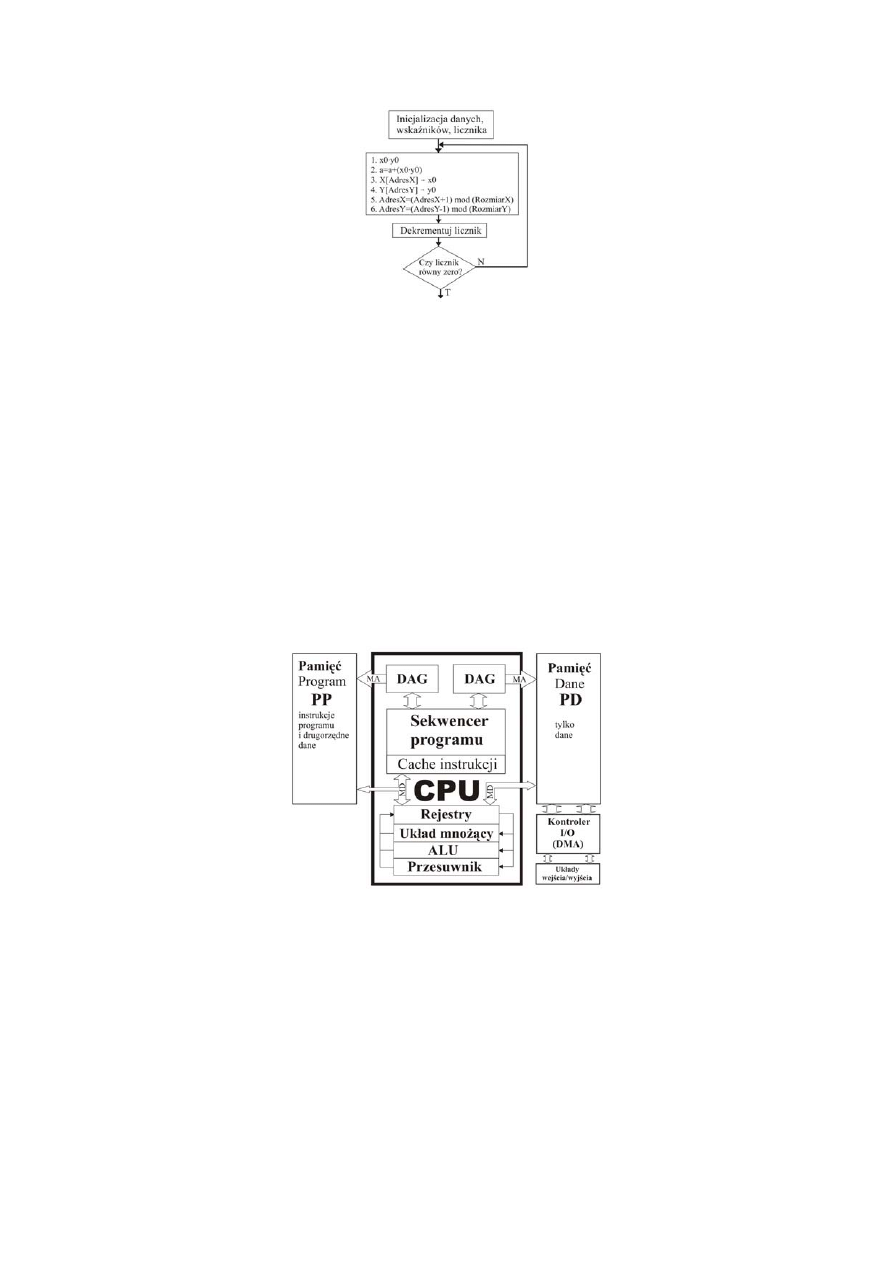
Rys. Algorytm demonstrujący zasadę działania instrukcji mac w procesorze firmy Motorola DSP
560xx. Zademonstrowany jest również sprzętowo działający licznik programu.

Wartości znajdujące się odpowiednio w rejestrach x0 i y0 są wymnażane przez siebie, a wynik tej
operacji dodawany jest do stanu aktualnie przechowywanego przez akumulator a. Następnie z
pamięci X spod adresu przechowywanego w rejestrze r1 (wartość AdresX) pobierana jest kolejna
mnożna do rejestru x0, zaś z pamięci Y spod adresu znajdującego się w rejestrze r5 (wartość AdresY)
pobierany jest kolejny mnożnik do rejestru y0. Wartości w rejestrach r1 (AdresX) i r5 (AdresY) są
następnie modyfikowane w taki sposób - aby wskazywały na kolejne wartości danych z pamięci, które
w następnym cyklu zostaną przez siebie przemnożone. AdresX jest inkrementowany o 1, natomiast
AdresY jest dekrementowany o 1. Wartości w tych rejestrach są adresowane modulo względem
rozmiarów buforów przechowujących kolejne mnożne i mnożniki (bufor ma strukturę kołową).
Cały cykl operacji instrukcji mac wykonywany jest tyle razy - ile wynosi wartość zmiennej
liczba_mnożeń.
Sama operacja MAC (realizowana instrukcją mac, w innych procesorach nazewnictwo jest inne)
byłaby nie tak efektywna, gdyby w pamięci przechowywany był programowo zaimplementowany
licznik, zliczający ilość dokonanych mnożeń, a następnie go modyfikujący i sprawdzający warunek
wyzerowania (rysunek 2). W procesorach DSP licznik ten jest zaimplementowany i zarządzany
sprzętowo, dzięki czemu w znaczny sposób odciąża jednostkę obliczeniową.

Rys. Schemat blokowy układu DSP, który dzięki odpowiednio zaprojektowanej i zarządzanej
architekturze umożliwia sprawne wykonywanie operacji MAC.

Politechnika Poznańska
Instytut Elektroniki i Telekomunikacji
Zakład Systemów Telekomunikacyjnych