1

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

1

transport masy

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

2

herbata

herbata
z cukrem

dyfuzja jest samorzutnym, nieodwracalnym procesem mieszania

wywołanym ró

ż

nic

ą

st

ęż

e

ń

natura d

ąż

y do wyrównania istniej

ą

cych ró

ż

nic st

ęż

e

ń

. Proces

odwrotny wymaga nakładu pracy. Proces dyfuzji jest w wielu
aspektach

podobny do transportu ciepła

. Opis dyfuzji b

ę

dzie

bazowa

ć

na wykorzystaniu istniej

ą

cych analogii

cukier

2

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

3

ró

ż

ne rodzaje dyfuzji

Transport masy mo

ż

e by

ć

wywołany przez

• ró

ż

nic

ę

st

ęż

e

ń

-

zwykła dyfuzja

(w skrócie

dyfuzja

)

• ró

ż

nic

ę

ci

ś

nie

ń

–

dyfuzja ci

ś

nieniowa

istotna tylko przy bardzo du

ż

ych

ró

ż

nicach ci

ś

nie

ń

np. w ultrawirówkach przy separacji izotopów

•

siły inne ni

ż

ró

ż

nica ci

ś

nie

ń

- dyfuzja wymuszona.

Np. ruch

cz

ą

stek naładowanych lub namagnesowanych w polu elektromagnetycznym

•

gradient temperatury-termodyfuzja

(efekt Soreta)

Dyfuzja w porach o rozmiarach mniejszych ni

ż ś

rednia droga swobodna

cz

ą

steczki –

dyfuzja Knudsena

Dyfuzja w porach o rozmiarach porównywalnych z rozmiarami cz

ą

steczki –

dyfuzja powierzchniowa

, zaadsorbowane cz

ą

steczki poruszaj

ą

si

ę

wzdłu

ż

ś

cian porów

Ruch cz

ą

stek o wymiarach poni

ż

ej 1

µµµµ

m (sadza, mgła) -

ruchy Browna

na ogół efekty te s

ą

pomijalne.

W ramach tego kursu nie b

ę

d

ą

omawiane

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

4

wektor strumienia masy i-tego składnika kg/m

2

s

τ

=

dSd

dm

i

i

j

i

m

masa i-tego składnika wyra

ż

ona w kg

S

powierzchnia

analogiem wektora g

ę

sto

ś

ci strumienia ciepła

q

jest wektor

g

ę

sto

ś

ci strumienia masy

j

τ

czas

i

im

i

im

i

w

D

D

∇

ρ

−

=

ρ

∇

−

=

j

analogiem prawa Fouriera jest prawo Ficka

im

D

współczynnik dyfuzji i-tego składnika przez mieszanin

ę

innych składników. m

2

/s

i

ρ

g

ę

sto

ść

i-tego składnika kg/m

3

V

m

i

i

/

=

ρ

V

obj

ę

to

ść

System oparty na kilogramie

mas

ę

mo

ż

na wyra

ż

a

ć

w kg lub kmol.

i

w

ułamek masowy i-tego składnika

ρ

g

ę

sto

ść

mieszaniny kg/m

3

3

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

5

wektor strumienia masy i-tego składnika kmol/m

2

s

τ

=

dSd

dn

i

i

J

i

n

masa i-tego składnika wyra

ż

ona w kmol

S

powierzchnia

analogiem wektora g

ę

sto

ś

ci strumienia ciepła

q

jest wektor

g

ę

sto

ś

ci strumienia masy

J

τ

czas

i

im

i

im

i

y

cD

c

D

∇

−

=

∇

−

=

J

analogiem prawa Fouriera jest prawo Ficka

im

D

współczynnik dyfuzji i-tego składnika przez mieszanin

ę

innych składników. m

2

/s

i

c

koncentracja molowa i-tego składnika kmol/m

3

V

n

c

i

i

/

=

V

obj

ę

to

ść

System oparty na kilomolu

i

y

ułamek molowy i-tego składnika

c

g

ę

sto

ść

molowa (koncentracja) mieszaniny kmol/m

3

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

6

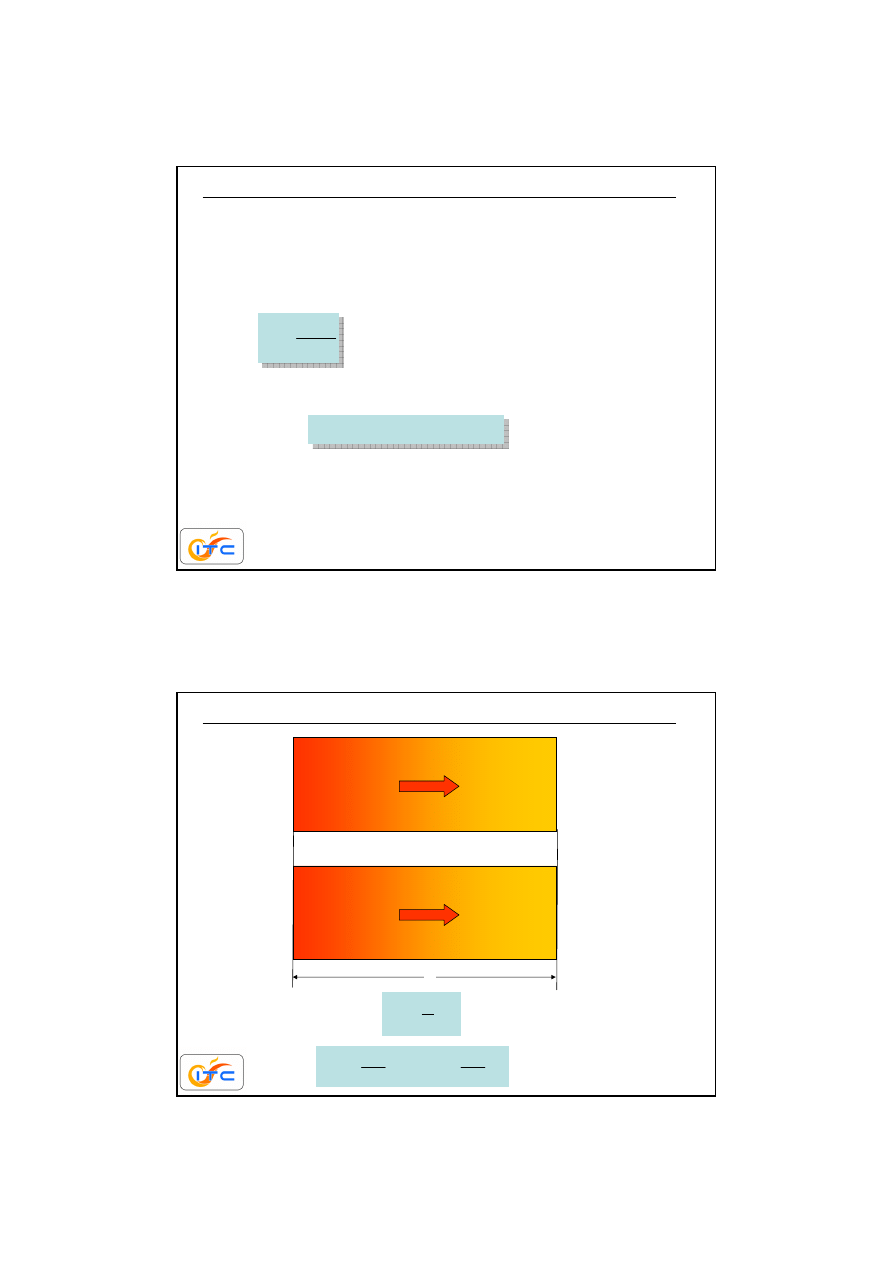
przewodzenie
ciepła

T

L

=

9

0

0

C

T

r

=

1

0

0

C

strumie

ń

ciepła

T

S

S

Q

∇

λ

−

=

=

q

y

L

=

9

0

%

y

r

=

1

0

%

strumie

ń

masy

i-tego składnika

i

im

i

i

SD

S

m

ρ

∇

−

=

=

j

T

S

q

∆

δ

λ

=

i

im

i

im

i

c

D

S

n

D

S

m

∆

δ

=

ρ

∆

δ

=

przewodzenie
ciepła

dyfuzja masy

δ

dyfuzja
masy

4

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

7

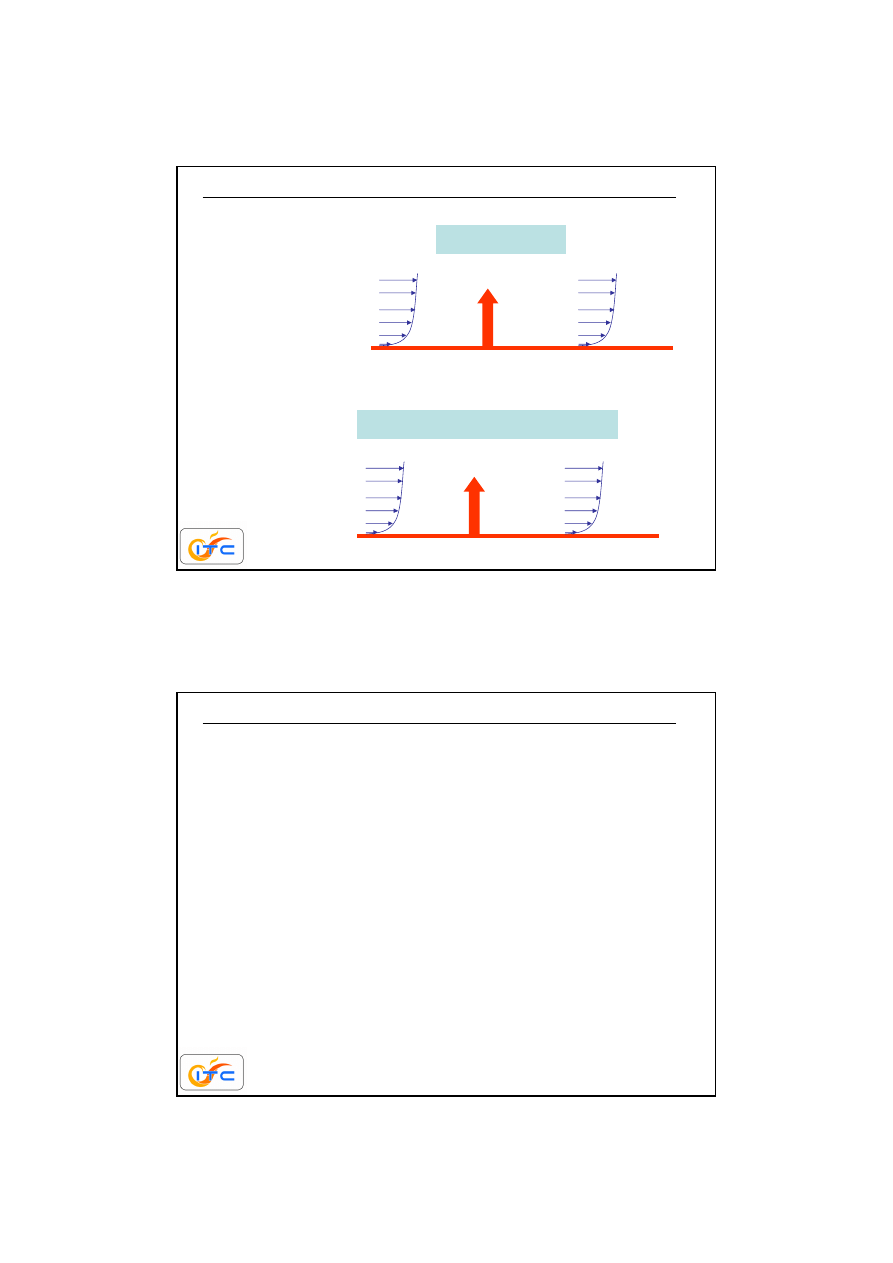
konwekcyjny transport ciepła

konwekcyjny
strumie

ń

ciepła

)

(

∞

−

α

=

T

T

S

Q

w

C

T

w

0

100

=

C

T

0

10

=

∞

konwekcyjny
strumie

ń

masy

)

(

)

(

∞

∞

−

βρ

=

ρ

−

ρ

β

=

y

y

S

S

m

w

w

i

%

70

=

w

y

%

10

=

∞

y

gaz

powierzchnia
cieczy

gaz

konwekcyjny transport masy

α

warstwa
przy

ś

cienna

warstwa
przy

ś

cienna

ś

cianka

współczynnik
wnikania ciepła
W/m

2

K

β

współczynnik
wnikania masy
m/s

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

8

radiacyjny transport ciepła

brak odpowiednika w transporcie masy

5

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

9

Równanie transportu masy w poruszaj

ą

cym si

ę

płynie

Ω

’

Γ

’

Ω

Γ

n’

J

i

R

i

'

'd '

d '

dif

i

i

n

J

′

Γ

Γ

= −

= −

⋅

Γ

Γ

∫

∫

J n

strumie

ń

masy i-tego składnika transportowany przez dyfuzj

ę

d

gen

i

i

n

R

′

Ω

′

=

Ω

∫

d

acc

i

i

n

c

′

Ω

∂

∂

′

=

Ω

∂

∂

∫

τ

τ

J

i

–

wektor g

ę

sto

ś

ci strumienia masy

,

kmol/m

2

s, J

i

-

składowa normalna

R

i

– wydajno

ść

reakcji chemicznych

tworz

ą

cych i-ty składnik kmol/s m

3

pr

ę

dko

ść

tworzenie i-tego składnika na skutek reakcji

'

'd '

d '

adv

i

i

i

n

c

c

′

Γ

Γ

= −

= −

υ

⋅

Γ

Γ

∫

∫

v n

strumie

ń

masy i-tego składnika transportowany przez adwekcj

ę

pr

ę

dko

ść

akumulacji masy w obj

ę

to

ś

ci kontrolnej

'

i

i

J

= ⋅

J n

v

–

wektor pr

ę

dko

ś

ci płynu

,

m/s -

υ

składowa normalna

'

= ⋅

v n

υ

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

10

bilans masy

acc

dif

adv

gen

i

i

i

i

n

n

n

n

+

+

=

∂τ

∂

'

'

'

'

'

'

'

'

i

i

i

Jd

c d

R d

d

c

Γ

Γ

Ω

Ω

∂τ

−

Γ −

υ Γ +

Ω =

Ω

∂

∫

∫

∫

∫

wprowadzaj

ą

c definicj

ę

strumieni

zamieniaj

ą

c całki powierzchniowe na obj

ę

to

ś

ciowe (tw. Gaussa o dywergencji)

'

(

)

'

0

i

i

i

i

c

R

d

c

Ω

∂τ





−∇⋅ −∇⋅

+ −

Ω =









∂

∫

J

v

słuszne dla dowolnej obj

ę

to

ś

ci kontrolnej, tylko wtedy gdy

(

)

i

i

i

i

c

R

c

∂τ

−∇⋅ − ∇⋅

+ =

∂

J

v

wstawiaj

ą

c prawo Fick’a

[

]

(

)

i

im

i

i

i

D

c

c

R

c

∂τ

∇⋅

∇ − ∇⋅

+ =

∂

v

prawo zachowania masy
i-tego składnika

i

im

i

D

c

=

∇

J

6

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

11

2

2

2

2

2

2

(

)

(

)

(

)

i

i

y

i x

i z

i

i

i

im

i

c v

c v

c v

c

c

c

D

R

x

y

z

x

y

z

c

∂τ

∂





∂

∂

∂

∂

∂

+

+

+

=

+

+

+





∂

∂

∂

∂

∂

∂





∂

w współrz

ę

dnych kartezja

ń

skich przy stałym współczynniku dyfuzji

dla nieruchomego o

ś

rodka i stałego wsp. dyfuzji

2

2

2

2

2

2

i

i

i

i

im

i

c

c

c

D

R

x

y

z

c

∂τ





∂

∂

∂

=

+

+

+





∂

∂

∂





∂

dla nieruchomego o

ś

rodka, stałego wsp. dyfuzji i braku reakcji chemicznych

2

2

2

2

2

2

i

i

i

i

im

c

c

c

D

x

y

z

c

∂τ





∂

∂

∂

=

+

+





∂

∂

∂





∂

dla nieruchomego o

ś

rodka, stałego wsp. dyfuzji, braku reakcji chemicznych i 1D

2

2

i

i

im

c

D

x

c

∂τ

∂

=

∂

∂

dla nieruchomego o

ś

rodka, stałego wsp. dyfuzji, braku reakcji chemicznych, 1D

i stanu ustalonego

2

2

d

0

d

i

c

x

=

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

12

reakcje chemiczne –

ź

ródło substancji i-tego składnika

1

i

i

R

k c

= −

1

i

k

j

R

k c c

=

1

1

r

i

i

j

R

k c

k c

= −

+

1

1

r

i

k l

i

j

R

k c c

k c c

=

−

i

j

→

k

j

i

+ →

i

j

k

l

i

j

+

+

2

1

i

j

R

k c

=

2 j

i

→

przykładowe równanie reakcji

równanie kinetyki reakcji tworzenia produktu

składnik i bierze udział w jednej reakcji

1

1

i

i

R

k c

= −

1

2

1

i

k

R

k c

=

1

1

1

r

i

i

j

R

k c

k c

= −

+

i

j

→

i

j

1

2

1

i

i

R

k c

= −

2

i

j

→

przykładowe równania reakcji

równania kinetyki reakcji

składnik i bierze udział w dwu reakcjach

i

j

k

+ →

i

j

k

l

+

+

k

i

i

j

k

+ →

2

2

i

i

j

R

k c c

= −

2

2

2

r

i

i

j

k l

R

k c c

k c c

=

−

2

k

i

→

2

2

2

r

i

k

i

R

k c

k c

=

−

2

2

2

r

i

i

j

k

R

k c c

k c

= −

−

ź

ródło jest sum

ą

równa

ń

kinetycznych ka

ż

dej z reakcji

w której bierze udział i-ty składnik

1

M

m

i

i

m

R

R

=

=

∑

m

kolejny numer reakcji w której bierze udział i-ty składnik

M

liczba takich reakcji

7

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

13

uwaga 1:

równanie reakcji nie musi odpowiada

ć

równaniu kinetyki.

Cz

ę

sto wzory opisuj

ą

ce kinetyk

ę

wyznacza si

ę

empirycznie.

W procesach biochemicznych cz

ę

sto wyst

ę

puje równanie

uwaga 2:

stałe reakcji odwracalnych s

ą

powi

ą

zane przez równowag

ę

chemiczn

ą

.

Np. dla

1

1

r

i

k l

i

j

R

k c c

k c c

=

−

1

1

r

k l

i

j

k c c

k c c

=

w stanie równowagi sumaryczna pr

ę

dko

ść

reakcji jest zerowa

1

1

r

k

K k

=

poniewa

ż

i

j

k l

c c

K

c c

=

stała równowagi chemicznej

1

2

1

i

i

i

k c

R

k c

= −

+

Michaelisa-Mentena

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

14

transport masy na drodze dyfuzji mo

ż

e wyst

ę

powa

ć

w gazie,

cieczy lub ciele stałym

Warto

ś

ci współczynników dyfuzji otrzymuje si

ę

eksperymentalnie

•gaz przez gaz – rz

ą

d 10

-5

m

2

/s

s

ą

wzory teoretyczne

•ciecz przez ciecz – rz

ą

d 10

-9

m

2

/s

•gaz przez ciało stałe – rz

ą

d od 10

-10

do 10

-25

m

2

/s

współczynniki zale

żą

silnie od temperatury i

ci

ś

nienia – dla gazów

p

T

D

ij

/

2

/

3

∝

dla cieczy i ciał stałych rosn

ą

z temperatur

ą

np. wsp. dyfuzji w

ę

gla w stali przy wzro

ś

cie temperatury

z 500 do 1000C ro

ś

nie 6000 razy.

8

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

15

warunki brzegowe

• zadane st

ęż

enie 1-go rodzaju (Dirichlet)

• zadana składowa normalna g

ę

sto

ś

ci strumienia masy

2-go rodzaju (Neumann)

warunek konwekcyjny 3-go rodzaju (Robin)

i

i

i

i

c

c

y

y

=

=

dn

dc

D

J

dn

dy

D

j

j

i

im

i

i

im

i

i

=

ρ

−

=

=

)

(

)

(

∞

∞

−

β

=

−

βρ

=

c

c

J

y

y

j

w

i

w

i

temperatura na powierzchni brzegowej jest funkcj

ą

ci

ą

gł

ą

,

st

ęż

enie najcz

ęś

ciej doznaje skoku na powierzchni mi

ę

dzyfazowej

gaz

ś

cianka

temperatura

ułamek
masowy H

2

0

(w fazie
ciekłej
y

h20

=1)

woda

powietrze

skok st

ęż

enia

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

16

powietrze
p=92kPa
T=15C

skok st

ęż

enia

definiuj

ą

c zadane st

ęż

enie brzegowe,

trzeba dodatkowo poda

ć

której z faz dotyczy

0185

.

0

,

powietrze

2

=

O

H

y

1

,

woda

2

=

O

H

y

woda
T=15C

warto

ś

ci st

ęż

e

ń

po obu stronach powierzchni mi

ę

dzyfazowej

zwi

ą

zane s

ą

przez warunek równowagi termodynamicznej

warunek 1 rodzaju (Dirichleta)

9

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

17

odparowanie cieczy – krzywa nasycenia

)

(

,

,

gaz

gaz

T

f

y

p

p

i

i

=

⋅

=

absorpcja gazu w cieczy

ciecz

gaz

gaz

,

,

,

i

i

i

Hy

y

p

p

=

⋅

=

H

stała Henry’ego wyra

ż

ona w paskalach zale

ż

y praktycznie tylko od temperatury

du

ż

y zbiór warto

ś

ci stałej Henry’ego dost

ę

pny jest w sieci www.henrys-law.org

Prawo Henry’ego - małe st

ęż

enia (gazy słabo rozpuszczalne w cieczach)

Prawo Raoulta - du

ż

e st

ęż

enia (gazy dobrze rozpuszczalne w cieczach

np. amoniak w wodzie)

)

(

,

,

,

ciecz

gaz

gaz

T

p

y

y

p

p

si

i

i

i

=

⋅

=

p

si

ci

ś

nienie nasycenia i-tego składnika

sublimacja ciała stałego – krzywa nasycenia

)

(

,

,

gaz

gaz

T

f

y

p

p

i

i

=

⋅

=

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

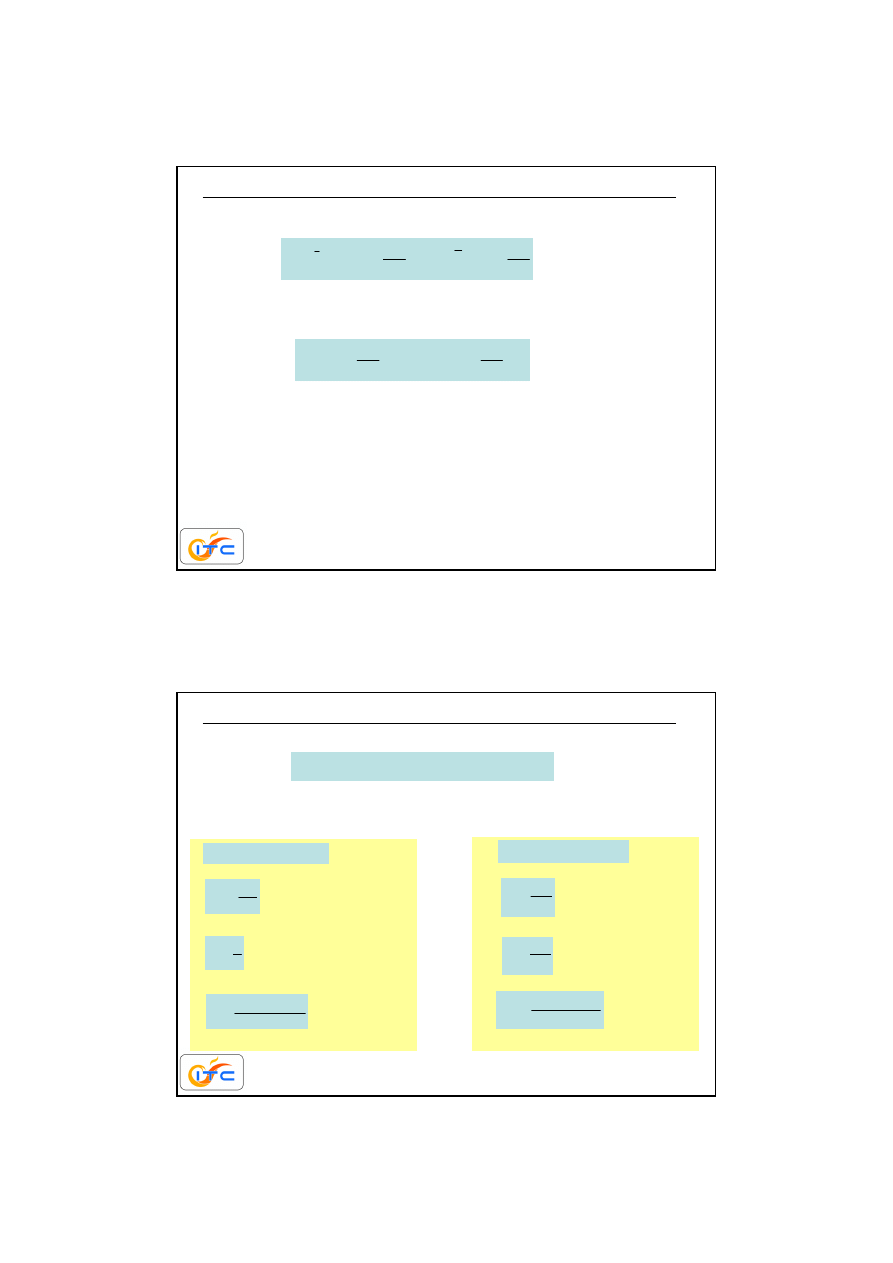
18

gaz

stale

cialo

,

,

i

i

p

c

⋅

χ

=

dyfuzja gazu przez ciało stałe

χ

rozpuszczalno

ść

kmol/m

3

Pa

dyfuzja cieczy przez ciało stałe

ciecz

stale

cialo

,

,

i

i

c

c

⋅

φ

=

φ

stała równowagi rozpuszczania (bezwymiarowa)

rozpuszczanie ciała stałego w cieczy

ciecz

,

( )

i

T

ρ

= σ

σ

rozpuszczalno

ść

kg/m

3

Uwaga: stałe równowagi wyst

ę

puj

ą

ce w tych równaniach np. stała

Henry’ego, rozpuszczalno

ść

mog

ą

by

ć

wyra

ż

ane w innych jednostkach

ciecz

gaz

,

ciecz

gaz

,

ciecz

gaz

,

,

,

,

i

yc

i

i

cc

i

i

yy

i

c

H

y

c

H

c

y

H

y

=

=

=

gaz

stale

cialo

,

gaz

stale

cialo

,

,

,

i

yc

i

i

cc

i

c

y

c

c

χ

⋅

χ

=

10

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

19

warunek 2 rodzaju (Neumanna)

najcz

ęś

ciej warunek nieprzepuszczalno

ś

ci

ś

cianki

dn

dc

D

J

J

dn

dy

D

j

j

i

im

i

i

i

im

i

i

=

=

ρ

−

=

=

0

0

0

0

=

⇒

=

=

⇒

=

dn

dc

J

dn

dy

j

i

i

i

i

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

20

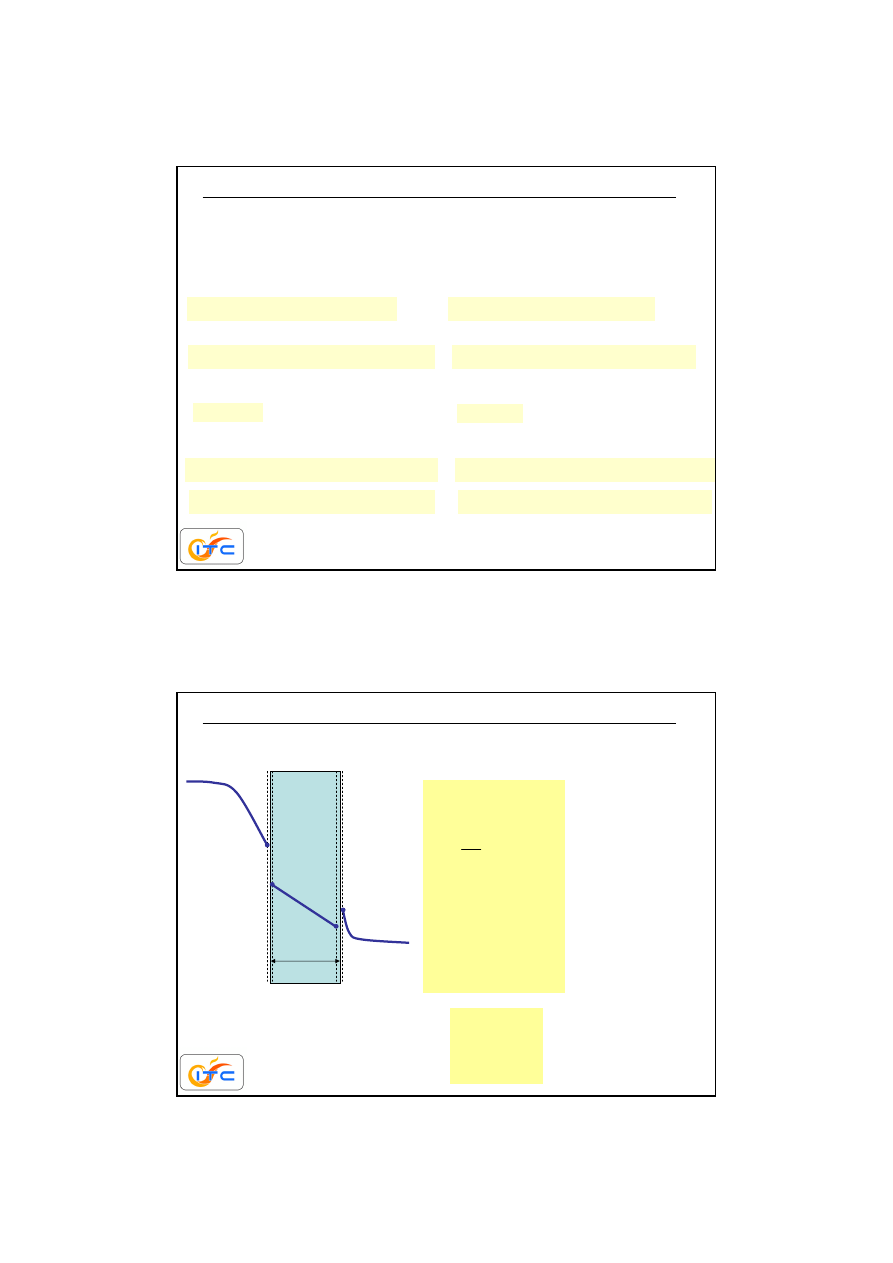
warunek 3 rodzaju (Robina)

)

(

)

(

∞

∞

−

β

=

−

βρ

=

c

c

J

y

y

j

w

i

w

i

warto

ść

współczynnika wnikania masy

ββββ

otrzymuje si

ę

z równa

ń

kryterialnych analogicznych do równa

ń

wyst

ę

puj

ą

cych w konwekcyjnym

transporcie ciepła

)

Gr

Pr,

(Re,

Nu

f

=

)

Gr

,

Sc

(Re,

Sh

m

f

=

λ

α

=

L

Nu

im

D

L

β

=

Sh

liczba Sherwooda

a

ν

=

Pr

im

D

ν

=

Sc

liczba Schmidta

liczba Nusselta

liczba Prandtla

2

3

)

(

Gr

ν

−

β

=

∞

L

T

T

g

s

liczba Grashofa

liczba Grashofa

2

3

m

)

(

Gr

ρν

ρ

−

ρ

=

∞

L

g

w

β

współczynnik

rozszerzalno

ś

ci

obj

ę

to

ś

ciowej

β

współczynnik

wnikania masy

ruch ciepła

ruch masy

11

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

21

6

.

0

Pr

Pr

Re

664

.

0

Nu

3

/

1

5

.

0

>

=

analogia mi

ę

dzy ruchem masy i ciepła – równania kryterialne s

ą

cz

ę

sto

(nie zawsze!) podobne. Analogia dotyczy małych strumieni dyfunduj

ą

cej

masy (wpływ na pr

ę

dko

ść

głównego strumienia), gładkich powierzchni

5

.

0

Sc

Sc

Re

664

.

0

Sh

3

/

1

5

.

0

>

=

przepływ laminarny wzdłu

ż

płaskiej płyty

Re<5 10

5

160

Pr

7

.

0

Pr

Re

023

.

0

Nu

4

.

0

8

.

0

<

<

=

160

Sc

7

.

0

Sc

Re

023

.

0

Sh

4

.

0

8

.

0

<

<

=

przepływ turbulentny w rurze

Re>10

5

w pełni rozwini

ę

ty przepływ laminarny w rurze

Re<2300

66

.

3

Nu

=

konwekcja swobodna z pionowej

ś

cianki

66

.

3

Sh

=

9

5

4

/

1

10

Pr

Gr

10

Pr)

Gr

(

59

.

0

Nu

<

<

=

9

m

5

4

/

1

m

10

Pr

Gr

10

)

Sc

Gr

(

59

.

0

Sh

<

<

=

13

9

3

/

1

10

Pr

Gr

10

Pr)

Gr

(

1

.

0

Nu

<

<

=

13

m

9

3

/

1

m

10

Pr

Gr

10

)

Sc

Gr

(

1

.

0

Sh

<

<

=

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

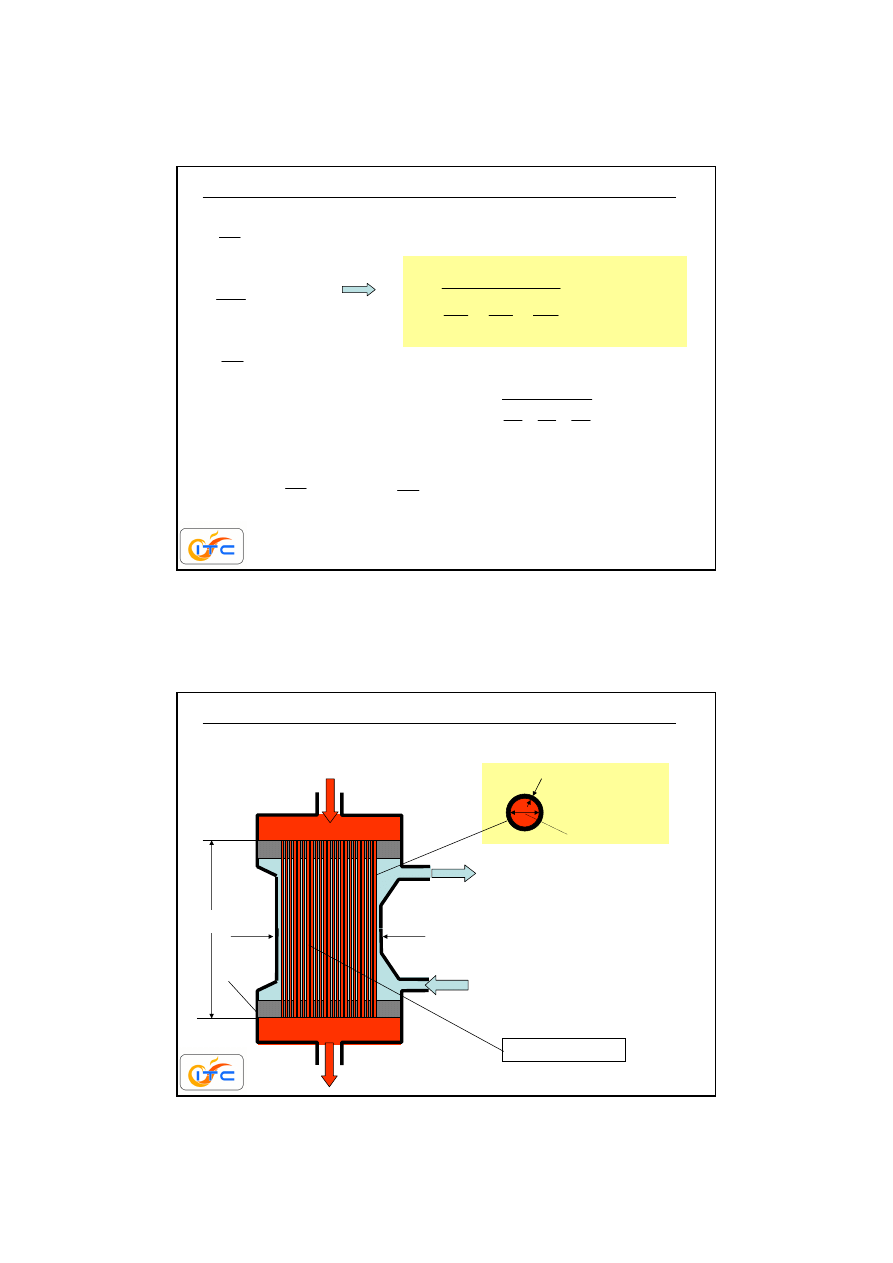
22

ustalone przenikanie masy przez membran

ę

układ ciecz-membrana-ciecz

L

c

∞

ciecz

m

e

m

b

ra

n

a

ciecz

L

w

c

L

m

c

R

m

c

R

w

c

R

c

∞

L

β

R

β

)

(

L

w

L

L

c

c

J

−

β

=

∞

)

(

R

m

L

m

c

c

D

J

−

δ

=

)

(

R

R

w

R

c

c

J

∞

−

β

=

wnikanie od cieczy do

membrany

dyfuzja w membranie

wnikanie z membrany

do cieczy

L

m

L

L

w

c

c

φ

=

R

m

R

R

w

c

c

φ

=

warunki równowagi

na obu brzegach

membrany

L

m

L

w

c

c

φ

=

R

m

R

w

c

c

φ

=

w biotechnologii ciecz po

obu stronach membrany

zwykle zbli

ż

ona do wody,

stałe równowagi

praktycznie te same

δ

dla uproszczenia zapisu opuszczono

indeks transportowanego czynnika

12

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

23

L

w

L

L

c

c

J

−

=

β

∞

R

m

L

m

c

c

D

J

−

=

δφ

R

R

w

R

c

c

J

∞

−

=

β

)

(

1

1

R

L

m

R

L

R

L

c

c

k

D

c

c

J

∞

∞

∞

∞

−

=

β

+

δφ

+

β

−

=

R

L

m

D

k

β

+

δφ

+

β

=

1

1

1

sumowanie oporów transportu masy –

analogicznie jak w ruchu ciepła

współczynnik przenikania masy

L

L

L

w

J

c

c

β

−

=

∞

warto

ś

ci st

ęż

e

ń

na brzegach membrany

φ

=

/

L

w

L

m

c

c

R

R

R

w

J

c

c

β

+

=

∞

φ

=

/

R

w

R

m

c

c

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

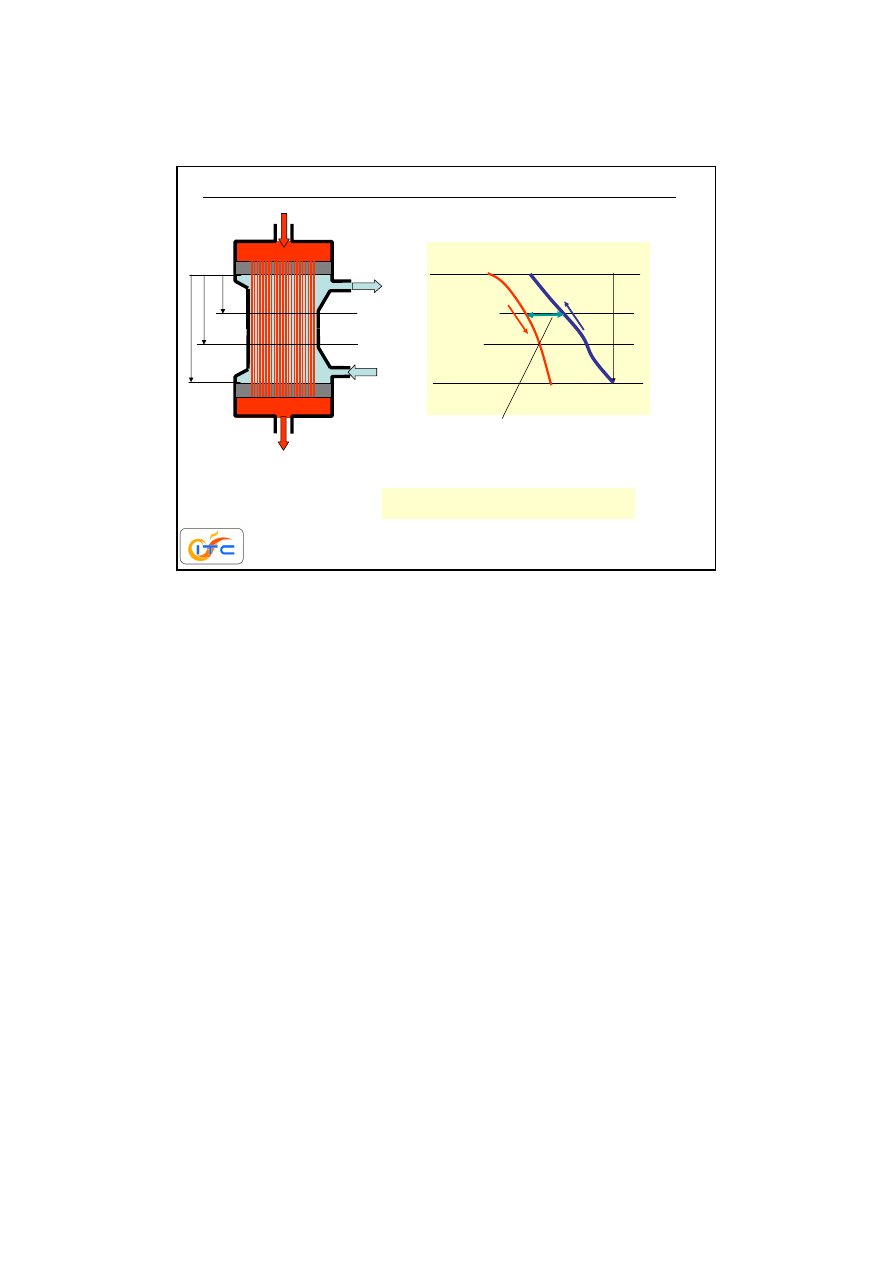
24

sztuczna nerka

krew +

metabolity

krew oczyszczona

dializat

(woda+sole)

dializat

(woda+sole+metabolity)

20 cm

4 cm

200

µµµµ

m

30

µµµµ

m

przekrój

przez

kapilar

ę

ok. 10 tys kapilar

dno
sitowe

13

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

25

out

B

c

∞

)]

'

(

)

'

(

)[

'

(

z

c

z

c

z

k

dS

dJ

D

B

m

∞

∞

−

=

ró

ż

niczkowy strumie

ń

metabolitów usuni

ę

tych z krwi

poprzez ró

ż

niczkow

ą

powierzchni

ę

dS

kapilar

z

'

z

L

'

z

z

L

in

D

c

∞

out

D

c

∞

in

B

c

∞

out

B

c

∞

rozkład st

ęż

e

ń

metabolitów

w sztucznej nerce

in

B

c

∞

in

D

c

∞

out

D

c

∞

)

'

(

)

'

(

z

c

z

c

D

B

∞

∞

−

siła nap

ę

dowa wymiany

masyw przekroju z’

całkowanie wzdłu

ż

kapilar daje całkowity strumie

ń

usuni

ę

tych

metabolitów