http://zcht.mfc.us.edu.pl/∼mm

CHEMIA KWANTOWA

MONIKA MUSIAŁ

POSTULATY

Ćwiczenia

• Literatura

•

Lucjan Piela,

Idee chemii kwantowej, PWN, Warszawa

2003.

•

Włodzimierz Kołos,

Chemia kwantowa, PWN, Warszawa

1978.

•

Alojzy Gołębiewski,

Elementy mechaniki i chemii kwan-

towej, PWN, Warszawa 1982.

http://zcht.mfc.us.edu.pl/∼mm

• Dygresja → układy współrzędnych

•

w dwóch wymiarach: biegunowy

x

= r cos ϕ

y

= r sin ϕ

0

¬ r ¬ ∞

0

¬ ϕ ¬ 2π

r

=

r

x

2

+ y

2

ϕ

= arc cos

x

√

x

2

+ y2

•

w trzech wymiarach: sferyczny

x

= r sin ϑ cos ϕ

y

= r sin ϑ sin ϕ

z

= r cos ϑ

r

=

r

x

2

+ y

2

+ z

2

ϑ

= arc cos

z

√

x

2

+ y

2

+ z

2

ϕ

= arc tg

y

x

http://zcht.mfc.us.edu.pl/∼mm

• Dygresja → zamiana zmiennych

Zamiana zmiennych przy całkowaniu:

∞

Z

−∞

∞

Z

−∞

f

(x, y)dxdy =

2π

Z

0

(

∞

Z

0

g

(r, ϕ)rdr)dϕ

∞

Z

−∞

∞

Z

−∞

∞

Z

−∞

f

(x, y, z)dxdydz =

∞

Z

0

π

Z

0

2π

Z

0

g

(r, ϑ, ϕ)r

2

sin ϑdrdϑdϕ

http://zcht.mfc.us.edu.pl/∼mm

• Dygresja → użyteczne całki

+

∞

Z

0

e

−ax

dx

=

1

a

+

∞

Z

0

x

n

e

−ax

dx

=

n

!

a

n+1

+

∞

Z

−

∞

e

−ax

2

dx

=

v

u

u

u

t

π

a

+

∞

Z

−

∞

x

2

e

−ax

2

dx

=

1
2

v

u

u

u

t

π

a

3

http://zcht.mfc.us.edu.pl/∼mm

http://zcht.mfc.us.edu.pl/∼mm

Aksjomatyczna konstrukcja mechaniki kwantowej:

pięć aksjomatów zwanych postulatami

• Postulaty

•

Postulat pierwszy

: Stan układu kwantowomechanicznego opisuje

funkcja falowa Ψ(r

1

, r

2

, ..., r

N

, t

) zwana także funkcj¸a stanu taka, że

kwadrat jej modułu:

|Ψ|

2

= Ψ

∗

Ψ pomnożony przez element objętości

dτ

określa prawdopodobieństwo, że w chwili t cząstka znajduje się w

elemencie objętości dτ .

dW

(r

1

, r

2

, ...

; t) =

|Ψ(r

1

, r

2

, ...

; t)

|

2

dτ

= ρ(r

1

, r

2

, ...

; t)dτ

gdzie:

ρ

oznacza gęstość prawdopodobieństwa ρ =

dW

dτ

r

i

- współrzędne (x,y,z) i-tej cząstki

dτ

= dV

1

dV

2

· · · dV

N

http://zcht.mfc.us.edu.pl/∼mm

• Postulaty

•

Postulat drugi

: Każdej wielkości mechanicznej zapisanej jako funk-

cja F współrzędnych i pędów, F (r

1

, r

2

, ..., p

1

, p

2

, ...

) przypisujemy ope-

rator kwantowomechaniczny ˆ

F zgodnie z następującymi regułami (Jor-

dan):

p

xi

→ −i¯h

∂

∂x

i

,

p

yi

→ −i¯h

∂

∂y

i

,

p

zi

→ −i¯h

∂

∂z

i

x

i

→ x

i

·,

y

i

→ y

i

·,

z

i

→ z

i

·

•

Postulat trzeci

: równanie Schr¨odingera zawierające czas:

ˆ

H

Ψ = i¯

h

∂

Ψ

∂t

określa zmianę funkcji falowej Ψ w czasie

http://zcht.mfc.us.edu.pl/∼mm

• Postulaty

•

Postulat czwarty

: Równanie stanu charakterystycznego wielkości

F (zagadnienie własne operatora ˆ

F): jeżeli spełnione jest równanie

ˆ

F

Φ

i

= f

i

Φ

i

f

i

wartość własna

Φ

i

funkcja własna.

Wynikiem pomiaru wielkości F może być tylko jedna z wartości wła-
snych operatora ˆ

F

. Jeżeli Φ

i

jest funkcją stanu układu to zmienna F

ma w tym stanie dokładnie wartość f

i

.

•

Postulat piąty

: o wartości średniej. Wartość spodziewana ¯

f

wiel-

kości mechanicznej F, której odpowiada operator ˆ

F dana jest wyraże-

niem:

¯

f

=

Z

Ψ

∗

ˆ

F

Ψdτ

Zakładamy, że funkcja falowa jest unormowana.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Postulat I

Funkcja porządna:

skończona, ciągła, jednoznaczna.

jednoznaczność, np.: ϕ zmienna w układzie biegunowym

f

(ϕ) = f (ϕ + 2π)

f

(ϕ) = sin aϕ

jednoznaczna tylko dla a = 0,

±1, ±2, . . .

Funkcje klasy Q - całkowalne z kwadratem modułu.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Normalizacja

funkcji falowej

Funkcja unormowana gdy:

Z

|Ψ(r

1

, r

2

, ..., t

)

|

2

dτ

= 1

Jeżeli:

Z

|Ψ(r

1

, r

2

, ..., t

)

|

2

dτ

= N

to

Ψ =

1

√

N

Ψ

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

• Unormować funkcj¸e falow¸a Ψ(ϕ) = Ne

imϕ

określon¸a w przedziale

[0,2π] przy czym m jest liczb¸a całkowit¸a:

N

2

2π

Z

0

e

−imϕ

e

imϕ

dϕ

= N

2

2π

Z

0

dϕ

= N

2

2π = 1

czyli

N

=

1

√

2π

Postać funkcji unormowanej: Ψ(ϕ) =

1

√

2π

e

imϕ

• Unormować funkcj¸e falow¸a Ψ(r, ϑ, ϕ) = Ne

−ar

określon¸a w całej

przestrzeni (

wskazówka: skorzystaj z wyniku

∞

R

0

r

n

e

−ar

dr

=

n!

a

n+1

):

N

2

(

∞

Z

0

e

−2ar

r

2

dr

ϑ

Z

0

sinϑdϑ

2π

Z

0

dϕ

) = N

2

π

a

3

= 1

czyli

N

= (

a

3

π

)

1
2

Postać funkcji unormowanej: Ψ(r, ϑ, ϕ) = (

a

3

π

)

1
2

e

−ar

http://zcht.mfc.us.edu.pl/∼mm

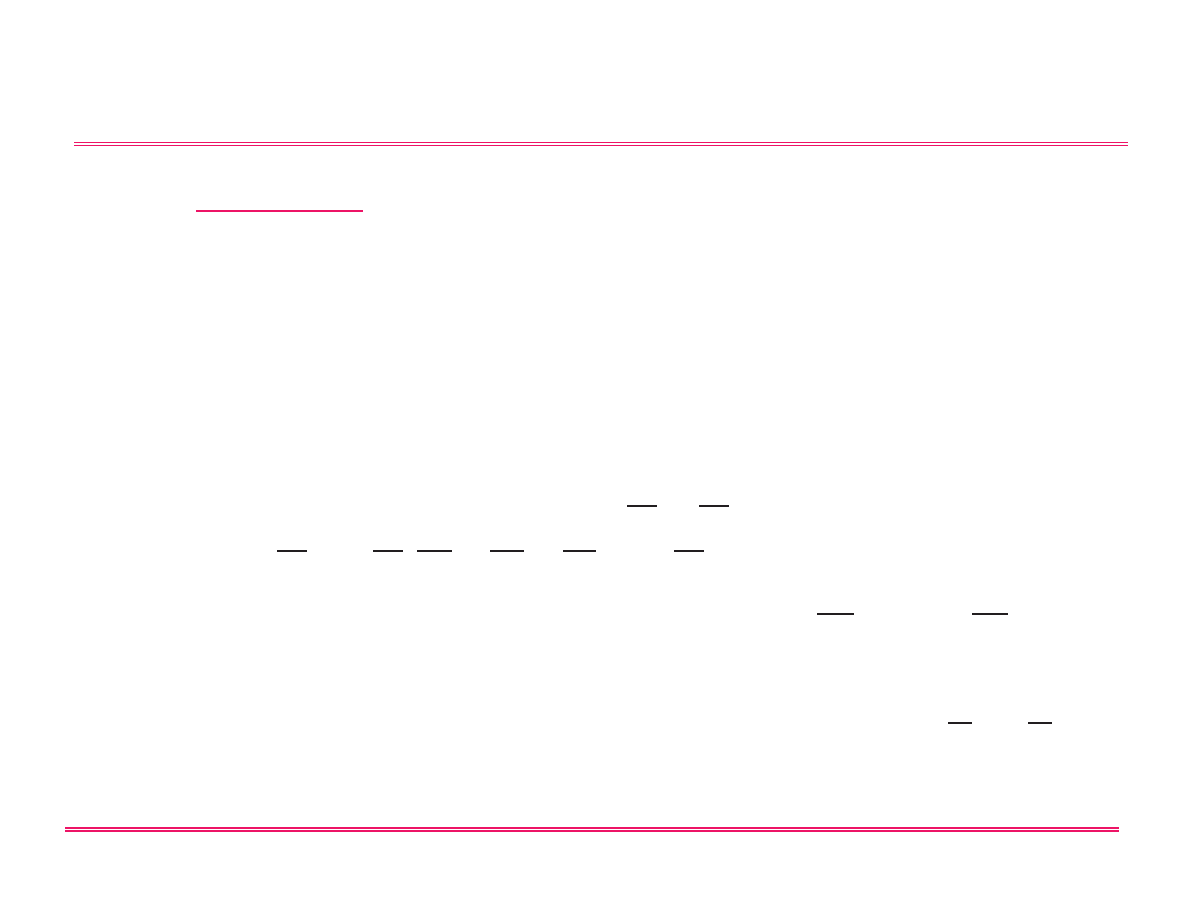
• Konsekwencje wynikające z postulatów

Postulat II

funkcja:

x

−→ y

operator:

f

(x)

−→ g(x)

Przykłady operatorów:

- energia kinetyczna elektronu (T =

p

2

2m

=

1

2m

(p

2
x

+ p

2
y

+ p

2
z

)):

ˆ

T

=

ˆ

p

2

2m

=

−

¯

h

2

2m

(

∂

2

∂x

2

+

∂

2

∂y

2

+

∂

2

∂z

2

) =

−

¯

h

2

2m

△

- energia oddziaływania elektronu z j¸adrem (V = −

Ze

2

r

): ˆ

V

=

−

Ze

2

r

- energia całkowita (hamiltonian): ˆ

H

= ˆ

T

+ ˆ

V

- składowa x momentu p¸edu (M

x

= yp

z

− zp

y

): ( ˆ

M

x

=

−i¯h(y

∂

∂z

− z

∂

∂y

)

- etc.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Operatory

liniowe

:

ˆ

F

(Ψ

1

+ Ψ

2

) = ˆ

F

Ψ

1

+ ˆ

F

Ψ

2

ˆ

F

(cΨ) = c ˆ

F

Ψ

ˆ

F

(c

1

Ψ

1

+ c

2

Ψ

2

) = c

1

ˆ

F

Ψ

1

+ c

2

ˆ

F

Ψ

2

gdzie c

1

, c

2

s¸a stałymi (również zespolonymi)

Np. operatory różniczkowania, całkowania s¸a operatorami liniowymi a

np. operatory pot¸egowania, sprz¸eżenia nie.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Operatory

hermitowskie

dla funkcji klasy Q:

Z

Ψ

∗

1

ˆ

F

Ψ

2

dτ

=

Z

Ψ

2

( ˆ

F

Ψ

1

)

∗

dτ

• Sprawdzić czy operator ˆ

F

= 2i jest operatorem hermitowskim

Z

Ψ

∗

1

2iΨ

2

dτ

=

−

Z

Ψ

2

(2iΨ

1

)

∗

dτ

Operator ˆ

F

= 2i nie jest operatorem hermitowskim.

• Sprawdzić czy operator ˆ

F

= 8 jest operatorem hermitowskim

Z

Ψ

∗

1

8Ψ

2

dτ

=

Z

Ψ

2

(8Ψ

1

)

∗

dτ

Operator ˆ

F

= 8 jest operatorem hermitowskim.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

• Sprawdzić czy operator ˆ

F

=

d

dx

jest operatorem hermitowskim

(

wskazówka: skorzystać z całkowania przez cz¸eści)

+

∞

Z

−∞

Ψ

∗

1

d

dx

Ψ

2

dx

= Ψ

∗

1

Ψ

2









+

∞

−∞

|

{z

}

0

−

+

∞

Z

−∞

Ψ

2

d

dx

Ψ

∗

1

dx

=

=

−

+

∞

Z

−∞

Ψ

2

(

d

dx

Ψ

1

)

∗

dx

Operator ˆ

F

=

d

dx

nie jest operatorem hermitowskim.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Działania na operatorach:

suma: ( ˆ

F

+ ˆ

G

)Ψ = ˆ

F

Ψ + ˆ

G

Ψ

iloczyn: ( ˆ

F ˆ

G

)Ψ = ˆ

F

( ˆ

G

Ψ)

potęga: ˆ

F

2

Ψ = ˆ

F

( ˆ

F

Ψ)

Komutator

Komutatorem operatorów ˆ

F

i ˆ

G

nazywamy operator:

ˆ

K

= [ ˆ

F , ˆ

G

]

df

= ˆ

F ˆ

G

− ˆ

G ˆ

F

Gdy komutator sprowadza si¸e do mnożenia przez 0, wówczas mówimy,

że operatory ˆ

F

i ˆ

G

s¸a przemienne, czyli komutuj¸a.

http://zcht.mfc.us.edu.pl/∼mm

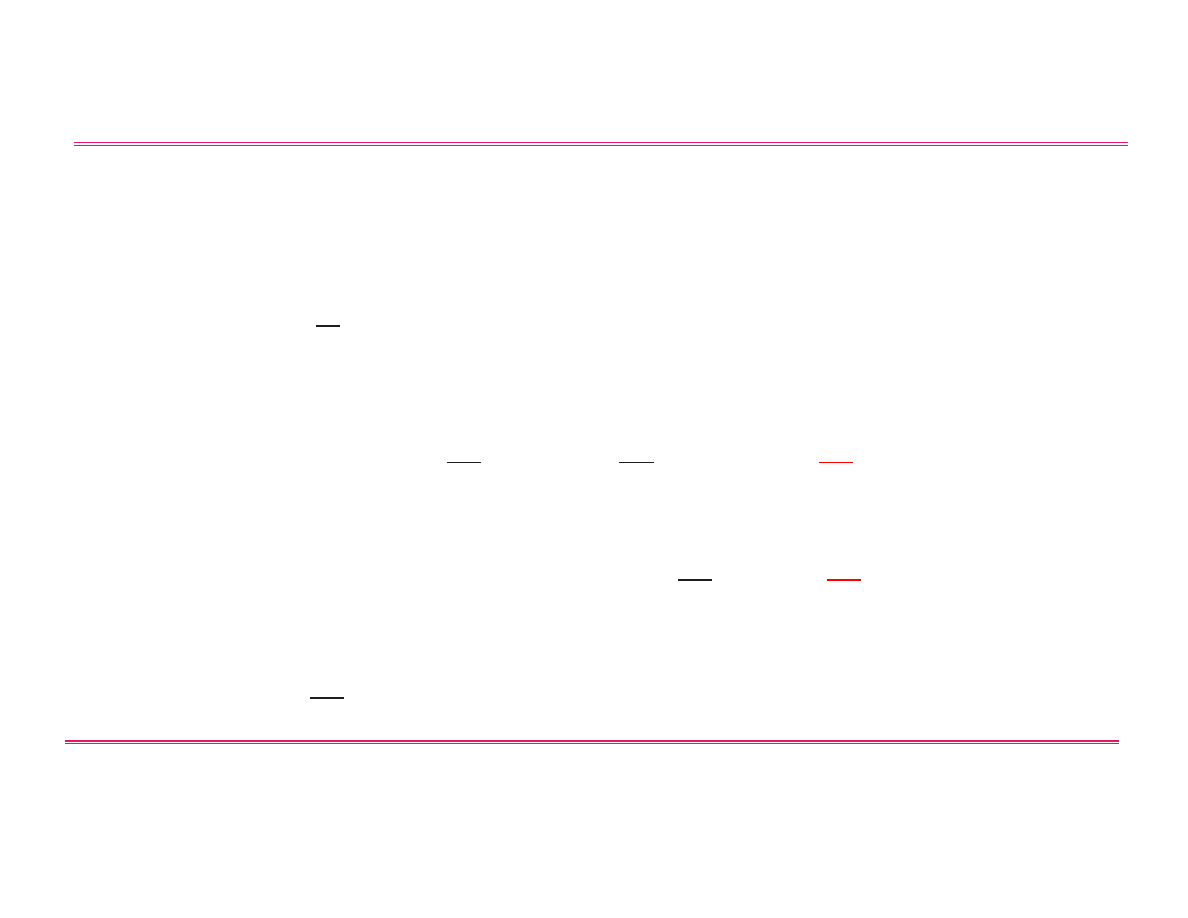
• Konsekwencje wynikające z postulatów

W celu sprawdzenia czemu równy jest komutator, działamy nim na

jak¸aś dowoln¸a funkcj¸e.

Np. ˆ

F

=

d

dx

ˆ

G

= x:

[ ˆ

F , ˆ

G

]f (x) = [

d

dx

, x

]f (x) =

d

dx

(xf (x))

−

x

(

d

dx

f

(x))

=

f

(x) + x

d

dx

f

(x)

−

x

d

dx

f

(x)

= f (x)

czyli

[

d

dx

, x

] = 1

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Własności komutatorów:

• [ ˆ

A, ˆ

B

] =

−[ ˆ

B, ˆ

A

]

• [ ˆ

A, ˆ

A

n

] = 0

n

= 1, 2, 3, ....

• [k ˆ

A, ˆ

B

] = [ ˆ

A, k ˆ

B

] = k[ ˆ

A, ˆ

B

]

k

− stała

• [ ˆ

A, ˆ

B

+ ˆ

C

] = [ ˆ

A, ˆ

B

] + [ ˆ

A, ˆ

C

]

• [ ˆ

A

+ ˆ

B, ˆ

C

] = [ ˆ

A, ˆ

C

] + [ ˆ

B, ˆ

C

]

• [ ˆ

A ˆ

B, ˆ

C

] = ˆ

A

[ ˆ

B, ˆ

C

] + [ ˆ

A, ˆ

C

] ˆ

B

• [ ˆ

A, ˆ

B ˆ

C

] = [ ˆ

A, ˆ

B

] ˆ

C

+ ˆ

B

[ ˆ

A, ˆ

C

]

http://zcht.mfc.us.edu.pl/∼mm

• Moment p¸edu

Ujęcie klasyczne:

Moment pędu jest iloczynem wektorowym: wektora promienia wodzącego

r i wektora pędu p:

M = r × p

Moment pędu jest wektorem o składowych:

M

x

= yp

z

− zp

y

M

y

= zp

x

− xp

z

M

z

= xp

y

− yp

x

M

2

= M

2

x

+ M

2

y

+ M

2

z

http://zcht.mfc.us.edu.pl/∼mm

• Moment p¸edu

Ujęcie kwantowe:

Konstrukcja operatorów dla składowych momentu pędu:

ˆ

M

x

=

−i¯h(y

∂

∂z

− z

∂

∂y

)

ˆ

M

y

=

−i¯h(z

∂

∂x

− x

∂

∂z

)

ˆ

M

z

=

−i¯h(x

∂

∂y

− y

∂

∂x

)

http://zcht.mfc.us.edu.pl/∼mm

• Komutatory

Własności komutacyjne operatorów momentu pędu:

[ ˆ

M

x

, ˆ

M

y

] = i¯

h ˆ

M

z

[ ˆ

M

y

, ˆ

M

x

] =

−i¯h ˆ

M

z

[ ˆ

M

z

, ˆ

M

x

] = i¯

h ˆ

M

y

[ ˆ

M

x

, ˆ

M

z

] =

−i¯h ˆ

M

y

[ ˆ

M

y

, ˆ

M

z

] = i¯

h ˆ

M

x

[ ˆ

M

z

, ˆ

M

y

] =

−i¯h ˆ

M

x

[ ˆ

M

2

, ˆ

M

x

] = [ ˆ

M

2

, ˆ

M

y

] = [ ˆ

M

2

, ˆ

M

z

] = 0

Z reguł komutacji wynika, iż:

Równocześnie ostro mierzalne są: kwadrat momentu
pędu i jedna ze składowych.
Dwie dowolne składowe momentu pędu nie mogą być
równocześnie dowolnie dokładnie zmierzone.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Postulat III

Stany stacjonarne:

Hamiltonian nie zależy od czasu lub (równoważnie)

gęstość prawdopodobieństwa nie zależy od czasu

˜

Ψ(r

1

, r

2

, ..., t

) = Ψ(r

1

, r

2

, ..., r

N

)e

−i

E

¯

h

t

E jest energią całkowitą układu.
Po podstawieniu do równania Schr¨odingera:

ˆ

H

Ψ = EΨ

Jest to równanie Schr¨odingera nie zawierające czasu.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Postulat IV

Założenie: ˆ

F

jest operatorem hermitowskim.

Teza:

wartości własne operatora ˆ

F są rzeczywiste.

ˆ

F

Φ

i

= f

i

Φ

i

ˆ

F

∗

Φ

∗

i

= f

∗

i

Φ

∗

i

Mnożąc przez Φ

∗

i

i Φ

i

:

Z

Φ

∗

i

F

Φ

i

dτ

= f

i

Z

Φ

∗

i

Φ

i

dτ

Z

Φ

i

F

∗

Φ

∗

i

dτ

= f

∗

i

Z

Φ

∗

i

Φ

i

dτ

Lewe strony są równe więc

f

i

= f

∗

i

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Założenie: ˆ

F

jest operatorem hermitowskim

wartości własne f

i

i f

j

są różne

Teza:

funkcje własne są ortogonalne:

ˆ

F

Φ

i

= f

i

Φ

i

ˆ

F

∗

Φ

∗

j

= f

∗

j

Φ

∗

j

Mnożąc przez Φ

∗

i

i Φ

i

:

Z

Φ

∗

j

F

Φ

i

dτ

= f

i

Z

Φ

∗

j

Φ

i

dτ

Z

Φ

i

F

∗

Φ

∗

j

dτ

= f

j

Z

Φ

i

Φ

∗

j

dτ

Lewe strony są równe więc

(f

i

− f

j

)

Z

Φ

i

Φ

∗

j

dτ

= 0

i

Z

Φ

i

Φ

∗

j

dτ

= 0

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Jednoczesna mierzalność wielkości fizycznych

Kiedy dwie wielkości fizyczne (obserwable), którym odpowiadają opera-
tory ˆ

F

i ˆ

G

sa równocześnie dokładnie mierzalne ?

Z postulatu IV wynika, że ostro można określić wartość wielkości
F, gdy funkcja stanu Ψ jest funkcją własną operatora ˆ

F

. Zatem jeśli dwie

wielkości F i G mają być równocześnie ostro mierzalne to funkcja Ψ winna
być funkcją własną obu operatorów ˆ

F

i ˆ

G

.

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Zasada superpozycji stanów:

zbiór funkcji własnych

{Φ

i

} do-

wolnego operatora kwantowomechanicznego F tworzy tzw. zbiór zupełny.
Każdą funkcję porządną Ψ możemy rozwinąć:

Ψ =

X

i

c

i

Φ

i

a kwadrat współczynnika

|c

i

|

2

= c

∗

i

c

i

jest prawdopodobieństwem, że stan

Ψ może mieć własności opisane przez Φ

i

http://zcht.mfc.us.edu.pl/∼mm

• Konsekwencje wynikające z postulatów

Postulat V

Wynika pośrednio z zasady superpozycji. Jeżeli prawdopodobieństwo

udziału funkcji Φ

i

w funkcji opisującej stan układu, czyli prawdopodobień-

stwo wystąpienia wielkości f

i

wynosi

|c

i

|

2

to

średnia wartość wielko-

ści F

jest zgodnie z zasadami statystyki jako:

¯

f

=

X

i

|c

i

|

2

f

i

W oparciu o postulat V obliczymy:

¯

f

=

Z

Ψ

∗

ˆ

F

Ψdτ =

X

i,j

c

∗

i

c

j

Z

Φ

∗

i

ˆ

F

Φ

j

dτ

=

X

i

c

∗

i

c

i

f

i

http://zcht.mfc.us.edu.pl/∼mm

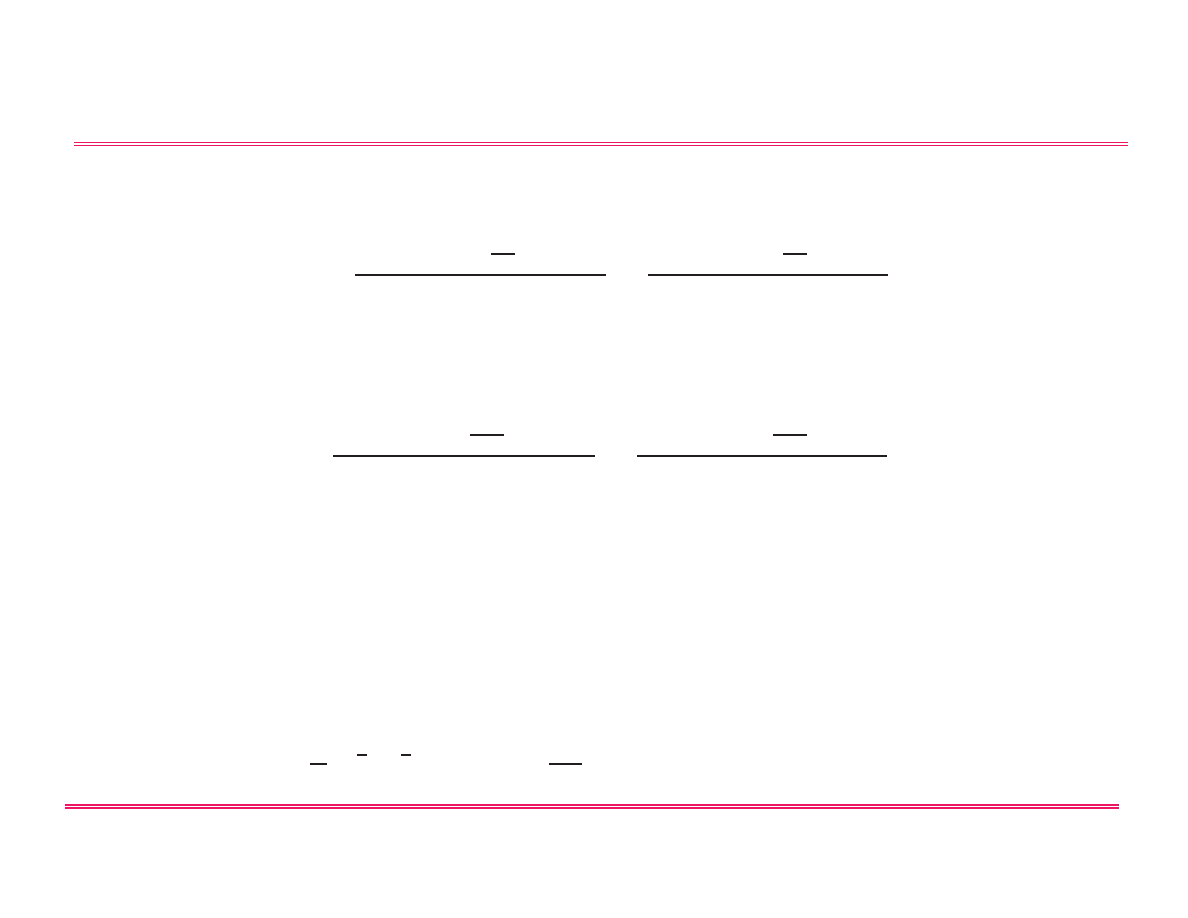
• Konsekwencje wynikające z postulatów

• Oblicz ¯p

x

jeśli funkcja jest postaci Ψ = e

ikx

¯

p

x

=

R

e

−ikx

(

−i¯h

d

dx

)e

ikx

dx

R

e

−ikx

e

ikx

dx

=

−i¯h

R

e

−ikx d

dx

e

ikx

dx

R

dx

= ¯

hk

• Oblicz ¯p

2
x

jeśli funkcja jest postaci Ψ = e

ikx

¯

p

2
x

=

R

e

−ikx

(

−¯h

2 d

2

dx

2

)e

ikx

dx

R

e

−ikx

e

ikx

dx

=

−¯h

2

R

e

−ikx d

2

dx

2

e

ikx

dx

R

dx

= ¯

h

2

k

2

• Oblicz wartość spodziewan¸a

– energii kinetycznej
– energii potencjalnej
– energii całkowitej
w przypadku oscylatora harmonicznego w stanie podstawowym, gdzie

Ψ(x) = (

Π

a

)

−

1
4

e

−

1
2

ax

2

a

=

mω

¯

h

http://zcht.mfc.us.edu.pl/∼mm

• Dygresja → notacja Diraca

Notacja Diraca:

Z

Φ

∗

i

ˆ

F

Φ

j

dτ

df

=

hΦ

i

|F |Φ

j

i

Z

Φ

∗

i

Φ

j

dτ

=

Z

Φ

∗

i

ˆ1Φ

j

dτ

df

=

hΦ

i

|1|Φ

j

i = hΦ

i

|Φ

j

i

http://zcht.mfc.us.edu.pl/∼mm