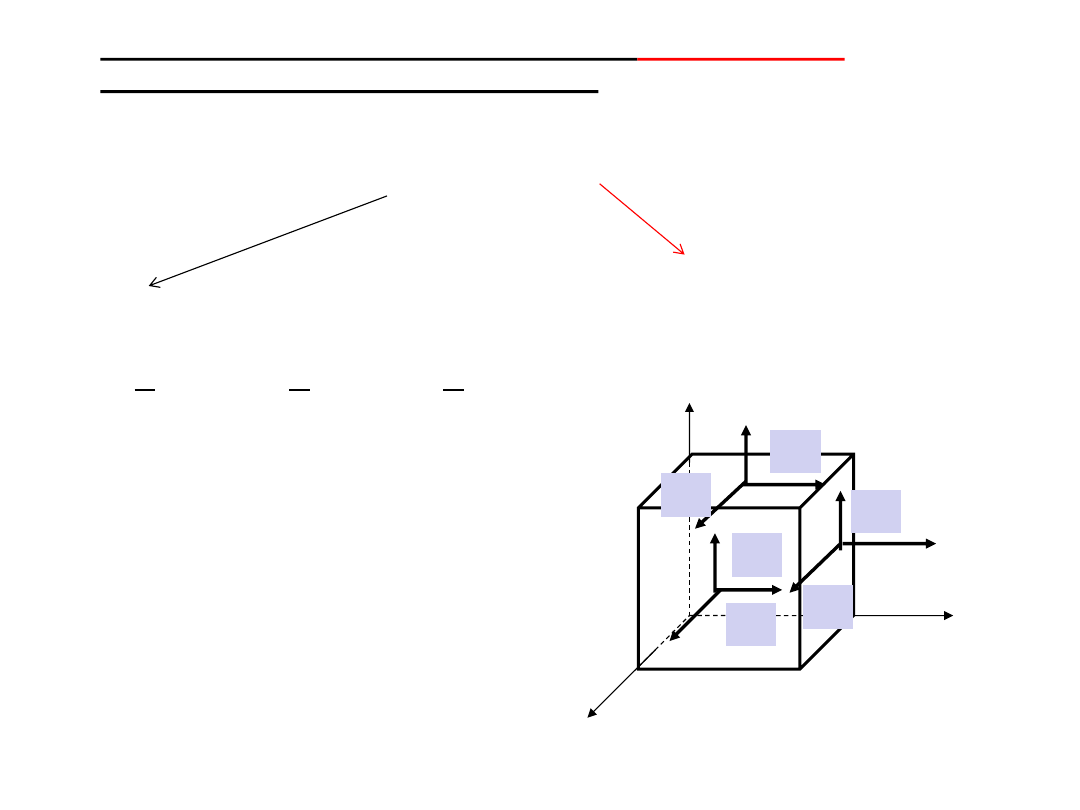
Uogólnione prawo Hooke’a dla materiału

anizotropowego

Dowolny przestrzenny stan naprężenia

{

ε

ij

}=[S

ijkl

]{

σ

kl

}

i= x,y,z
j= x,y,z

k= x,y,z

l= x,y,z

zx

yz

xy

z

y

x













,

,

,

,

,

zx

zx

yz

yz

xy

xy

z

y

x



















2

1

,

2

1

,

2

1

,

,

,







36 współczynników S

ijkl

ale tylko

21 niezależnych stałych sprężystych!!!

{

ε

ij

}

– macierz kolumnowa odkształceń

{

σ

kl

}

– macierz kolumnowa naprężeń

[S

ijkl

]

– macierz podatności

x

y

z



x

τ

zy



z



y

τ

zx

τ

yz

τ

yx

τ

xy

τ

xz

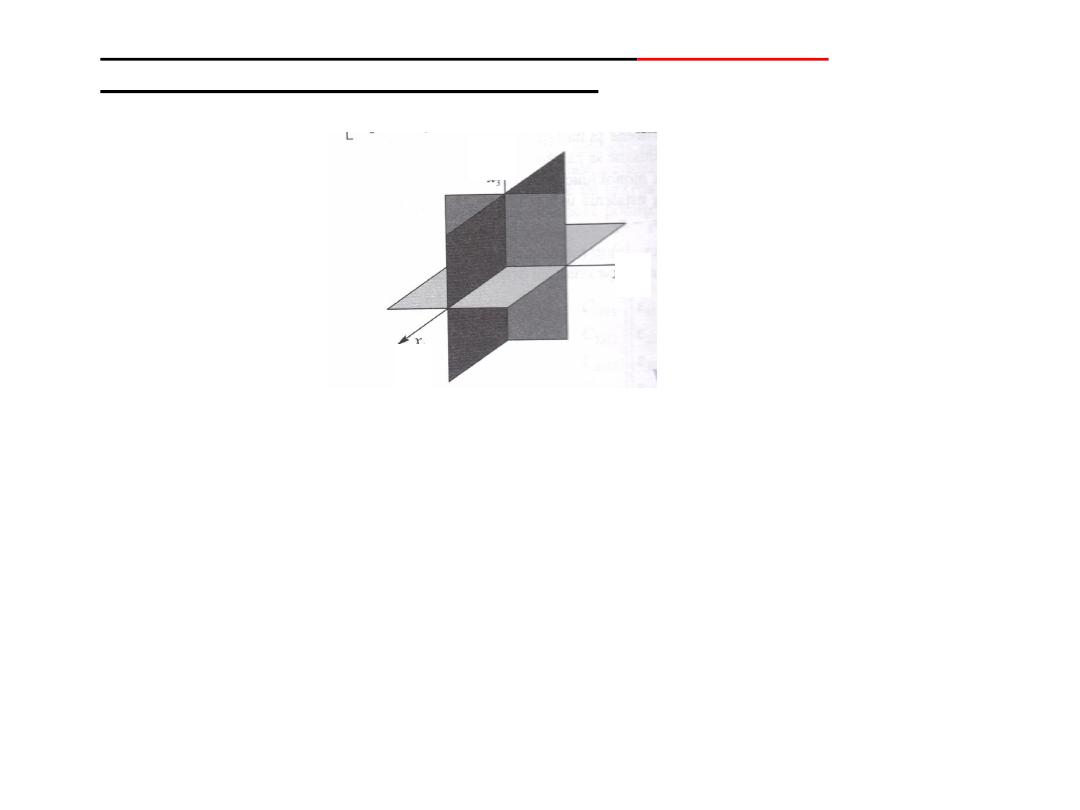
Uogólnione prawo Hooke’a dla materiału

ortotropowego

Dowolny przestrzenny stan naprężenia

x

z

y

3 prostopadłe płaszczyzny symetrii właściwości sprężystych

12 współczynników S

ijkl

ale tylko

9 niezależnych stałych sprężystych!!!

,

,

,

,

,

,

,

,

,

zx

yz

xy

zx

yz

xy

z

y

x

G

G

G

E

E

E







moduły Younga w głównych kierunkach ortotropii

liczby Poissona w głównych kierunkach ortotropii

moduły Kirchhoffa w głównych kierunkach ortotropii

zx

zx

zx

z

z

y

z

zy

x

z

zx

z

yz

yz

yz

z

y

yz

y

y

x

y

yx

y

xy

xy

xy

z

x

xz

y

x

xy

x

x

x

G

E

E

E

G

E

E

E

G

E

E

E

















































1

;

1

1

;

1

1

;

1































;

;

;

z

zx

x

xz

z

zy

y

yz

y

yx

x

xy

E

E

E

E

E

E



















Uogólnione prawo Hooke’a dla materiału

ortotropowego

Dowolny przestrzenny stan naprężenia

WYBRANE HIPOTEZY

WYTRZYMAŁOŚCIOWE

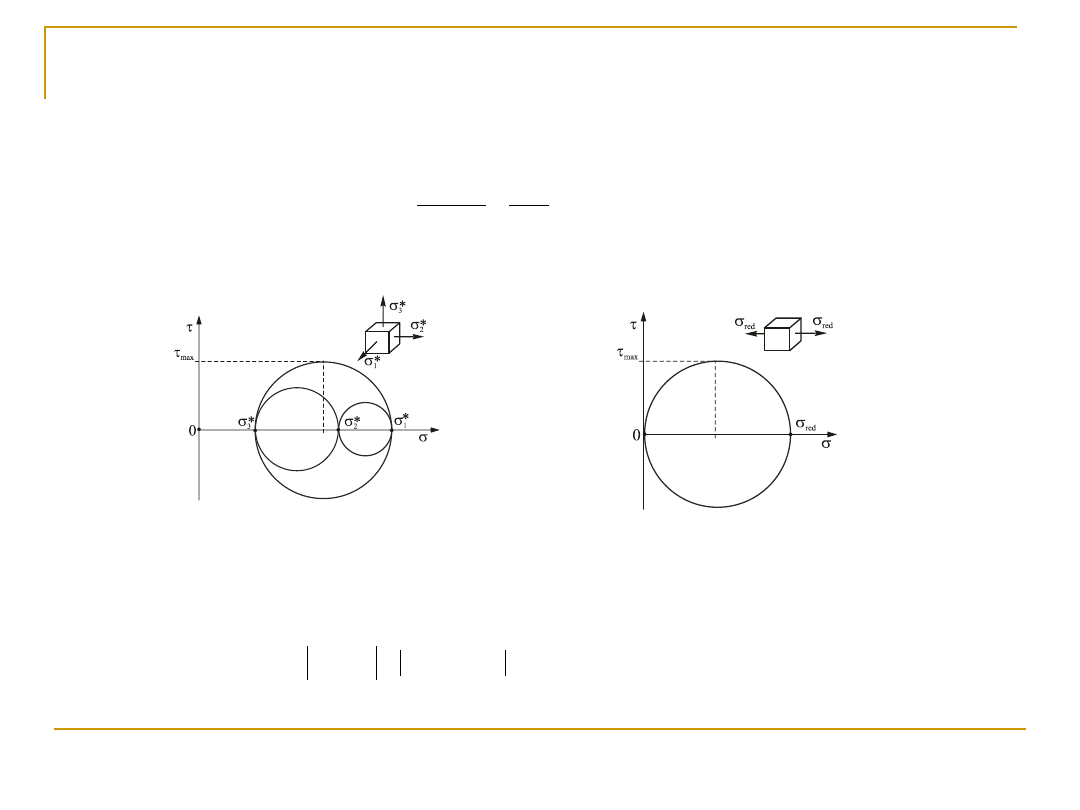
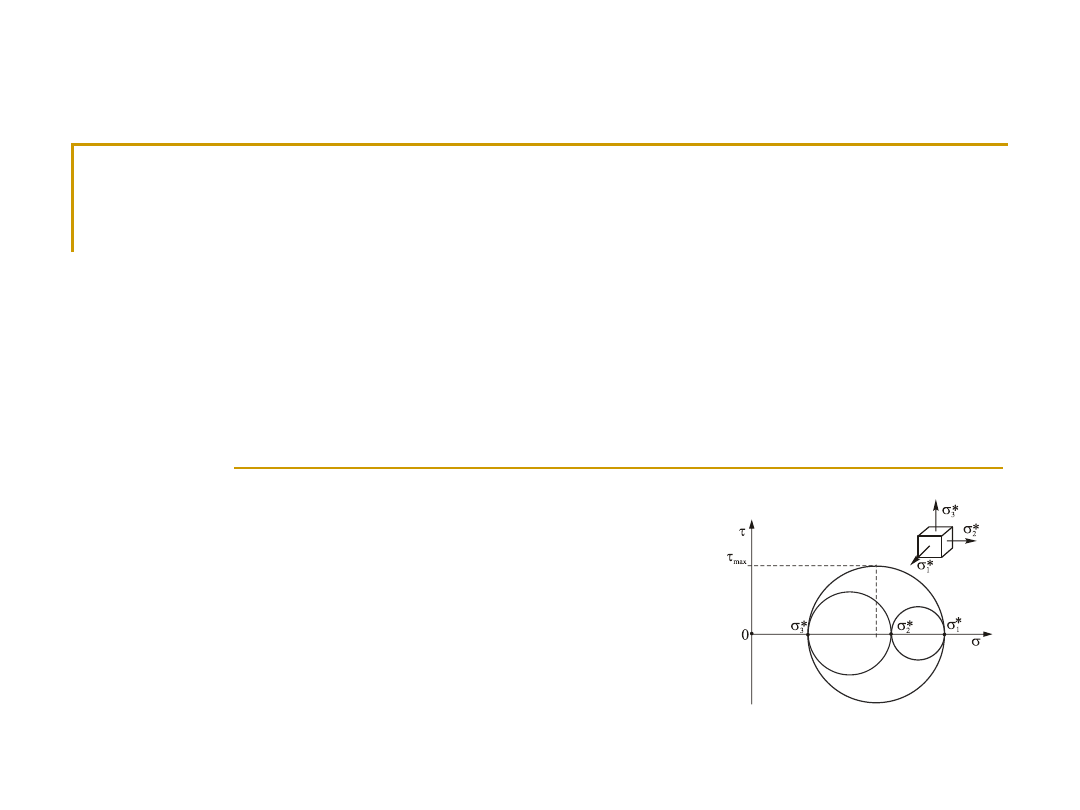
Hipoteza największego naprężenia stycznego (

max



)

2

2

*

3

*

1

max

red















(5.2)

(a) (b)

Rys. 5.1. Maksymalne naprężenia styczne według hipotezy największego naprężenia

stycznego

min

max

*

3

*

1



















red

, gdzie

*

3

*

2

*

1











(5.3)

2

2

*

3

*

1

max

red















(5.2)

(a) (b)

Rys. 5.1. Maksymalne naprężenia styczne według hipotezy największego naprężenia

stycznego

min

max

*

3

*

1



















red

, gdzie

*

3

*

2

*

1











(5.3)

(a) (b)

Rys. 5.1. Maksymalne naprężenia styczne według hipotezy największego naprężenia

stycznego

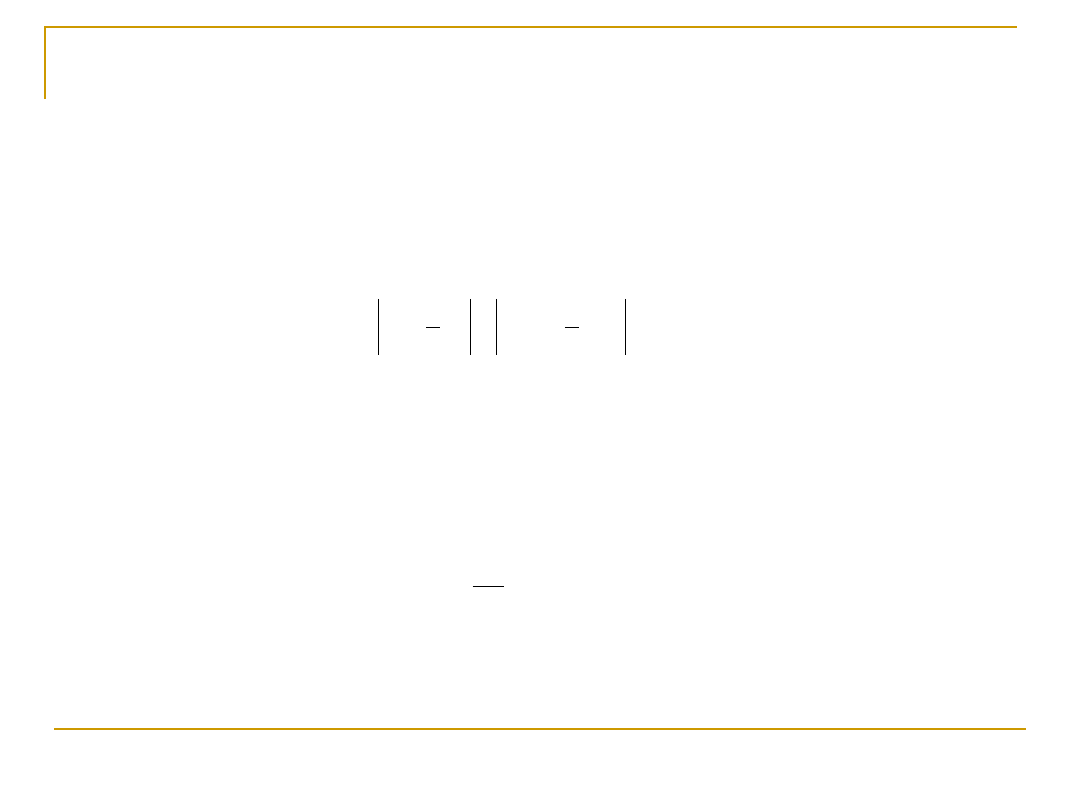
Hipoteza Mohra

W przypadku materiału izotropowego mającego różną wytrzymałość na rozciąganie i

ściskanie Mohr zaproponował modyfikację hipotezy

max



w postaci ogólnej:

min

max

*

3

*

1

1

1



















z

z

red

(5.4)

gdzie stosunek wytrzymałości na ściskanie i rozciąganie:

m

c

R

R

z



(5.5)

W przypadku materiału izotropowego mającego różną wytrzymałość na rozciąganie i

ściskanie Mohr zaproponował modyfikację hipotezy

max



w postaci ogólnej:

min

max

*

3

*

1

1

1



















z

z

red

(5.4)

gdzie stosunek wytrzymałości na ściskanie i rozciąganie:

m

c

R

R

z



(5.5)

W przypadku materiału izotropowego mającego różną wytrzymałość na rozciąganie i

ściskanie Mohr zaproponował modyfikację hipotezy

max



w postaci ogólnej:

min

max

*

3

*

1

1

1



















z

z

red

(5.4)

gdzie stosunek wytrzymałości na ściskanie i rozciąganie:

m

c

R

R

z



(5.5)

W przypadku materiału izotropowego mającego różną wytrzymałość na rozciąganie

i ściskanie Mohr zaproponował modyfikację hipotezy

max



w postaci ogólnej:

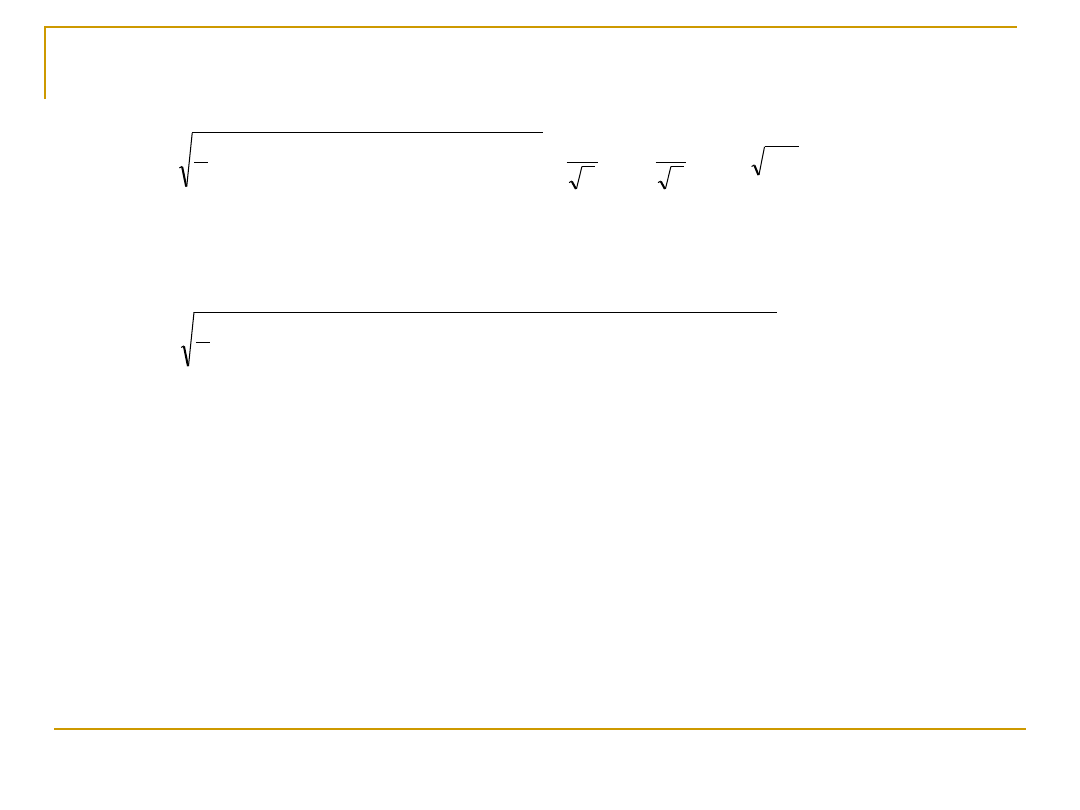
Hipoteza Hubera





d

oct

red

I

3

2

3

2

3

)

(

)

(

)

(

2

1

2

2

*

1

*

3

2

*

3

*

2

2

*

2

*

1







































(5.6)

lub postać:





)

(

6

)

(

)

(

)

(

2

1

2

31

2
23

2

12

2

11

33

2

33

22

2

22

11







































red

(5.7)

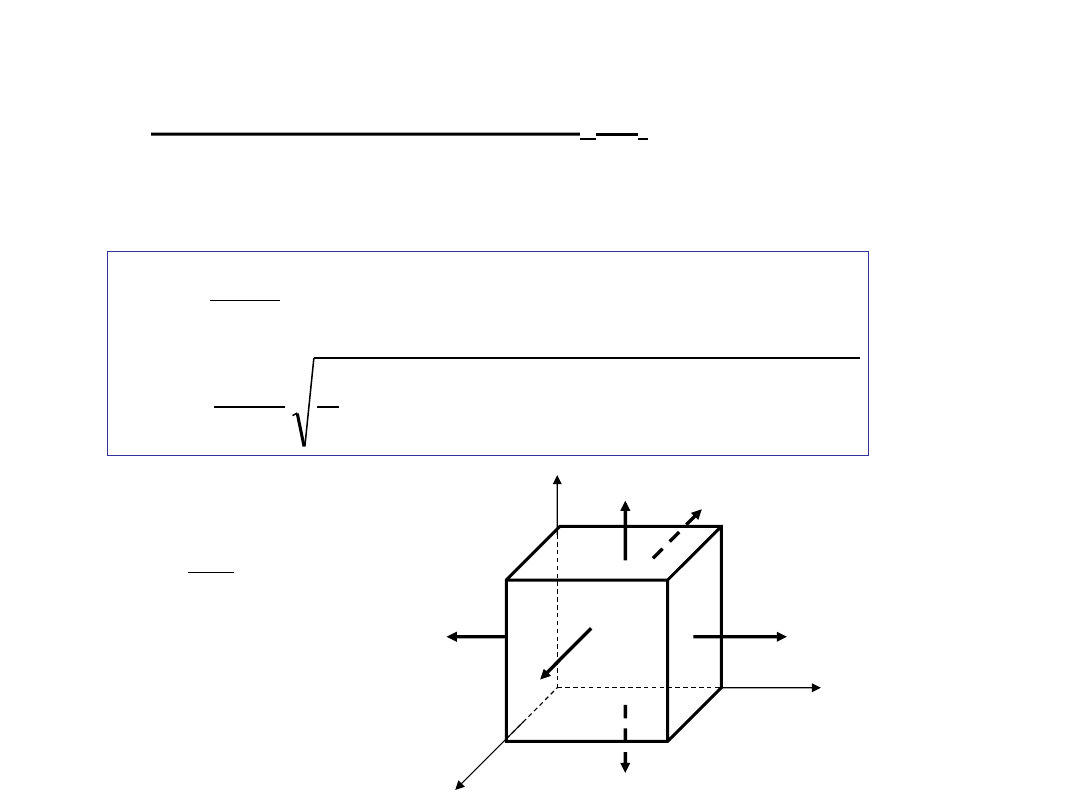
Materiały izotropowe o różnych R

m

i R

c

Hipoteza Burzyńskiego dla przypadku naprężeń głównych







 

 







2

1

3

2

3

2

2

2

1

3

2

1

2

1

2

1

2

1





















































red

m

c

R

R





x

y

z



1



1



3



2



2



3

Kryterium maksymalnych odkształceń - płaski stan odkształcenia

t

m

c

m

c































12

2

2

2

1

1

1

12

12

2

2

2

1

1

1

2

2

2

1

1

1

/ G

R

E

R

E

R

E

R

E

R

t

m

m

m

m

c

c

c

c





















Płaski dowolny stan naprężenia

Kryterium Hilla

– wzajemne oddziaływanie naprężeń

1

1

1

1

1

2

12

2

2

2

2

2

2

1

2

1

2

1

2

1



















t

m

m

m

m

R

R

R

R

R

R

m1

=R

c1

– wytrzymałość na rozciąganie/ściskanie w kierunku 1

R

m2

=R

c2

– wytrzymałość na rozciąganie/ściskanie w kierunku 2

R

t

– wytrzymałość na ścinanie

1,2

– główne kierunki ortotropii



1





12



1



2



2

2

12

2

2

1

2

2

2

2

2

1

2

1

2

1

2

1

2













t

m

m

m

m

m

red

R

R

R

R

R

R









Kryteria interakcji naprężeń niszczących

Kryterium Hilla

Definiując naprężenie efektywne (zredukowane)



eff

(2.48) dla płaskiego stanu naprężenia w sposób

podobny do kryterium Hubera-Misesa-Hencky’ego sformułowanego dla materiałów izotropowych,
kryterium Hilla można zapisać w postaci:

2

12

3

2

1

12

2

2

2

2

1

1

2

eff

2

red

3















a

a

a

a











(6.51)

gdzie:

12

2

1

,

,







są składowymi naprężenia w głównych kierunkach ortotropii,

3

1

a

a



nazywane są

parametrami anizotropii,



eff

oznacza naprężenie efektywne, zaś



red

naprężenia zredukowane.

Kryteria interakcyjne dla materiałów o różnych właściwościach na rozciąganie i ściskanie

W kryterium Hilla przyjmuje się jednakowe wytrzymałości na rozciąganie i ściskanie w głównych

kierunkach ortotropii

2

1



. Omówione pierwsze dwa kryteria nie uwzględniają oddziaływania pomiędzy

formami zniszczenia. Kryteria zniszczenia, w których uwzględniono różnice pomiędzy zachowaniem się
materiałów podczas rozciągania i ściskania można zapisać w najbardziej znanej i najczęściej stosowanej
postaci:

1

3

2

12

33

2

1

12

2
2

22

2

1

11

2

2

1

1





























k

k

k

k

k

k

f

(6.56)

gdzie:

1

1

1

1

1

C

T

k





,

1

1

11

1

C

T

k



,

2

2

2

1

1

C

T

k





,

2

2

22

1

C

T

k



,

2

33

3

1

S

k



(6.57)

Wartości współczynnika

12

k mogą być określane w różny sposób:



kryterium Tsai-Wu [33,34]:

2

2

1

1

12

1

C

T

C

T

k



(6.58)



kryterium Hoffmana [14]:

1

1

12

1

C

T

k



(6.59)



kryterium Wilczyńskiego [37]:

2

1

2

1

12

2

C

C

T

T

k





(6.60)



kryterium Cui, Wisnoma i Jonesa [6]:

0

12



k

(6.61)



kryterium Pucka [29]:

0

12



k

oraz ponadto

1

1

T





;

1

1

C







(6.62)