Dr inż. Janusz Dębiński

1

5. Analiza statyczna płaskich układów prętowych

Definicja siły

5.1. Siła

Siła jest wektorową miarą oddziaływania jednego ciała na drugie.

W niniejszym kursie Mechaniki ogólnej będziemy rozpatrywać tylko oddziaływanie ciał będących

w bezpośrednim kontakcie.

Siła jest jednoznacznie określona przez swoją wartość czyli długość wektora, kierunek

oraz zwrot.

Dla większości naszych obliczeń nie będzie miało znaczenia to, że siła może się poruszać po

prostej pokrywającej się z kierunkiem jej działania. Jest więc ona wektorem ślizgającym.

Istnieją jednak przypadki, kiedy siłę traktujemy jako wektor związany.

Dr inż. Janusz Dębiński

2

5. Analiza statyczna płaskich układów prętowych

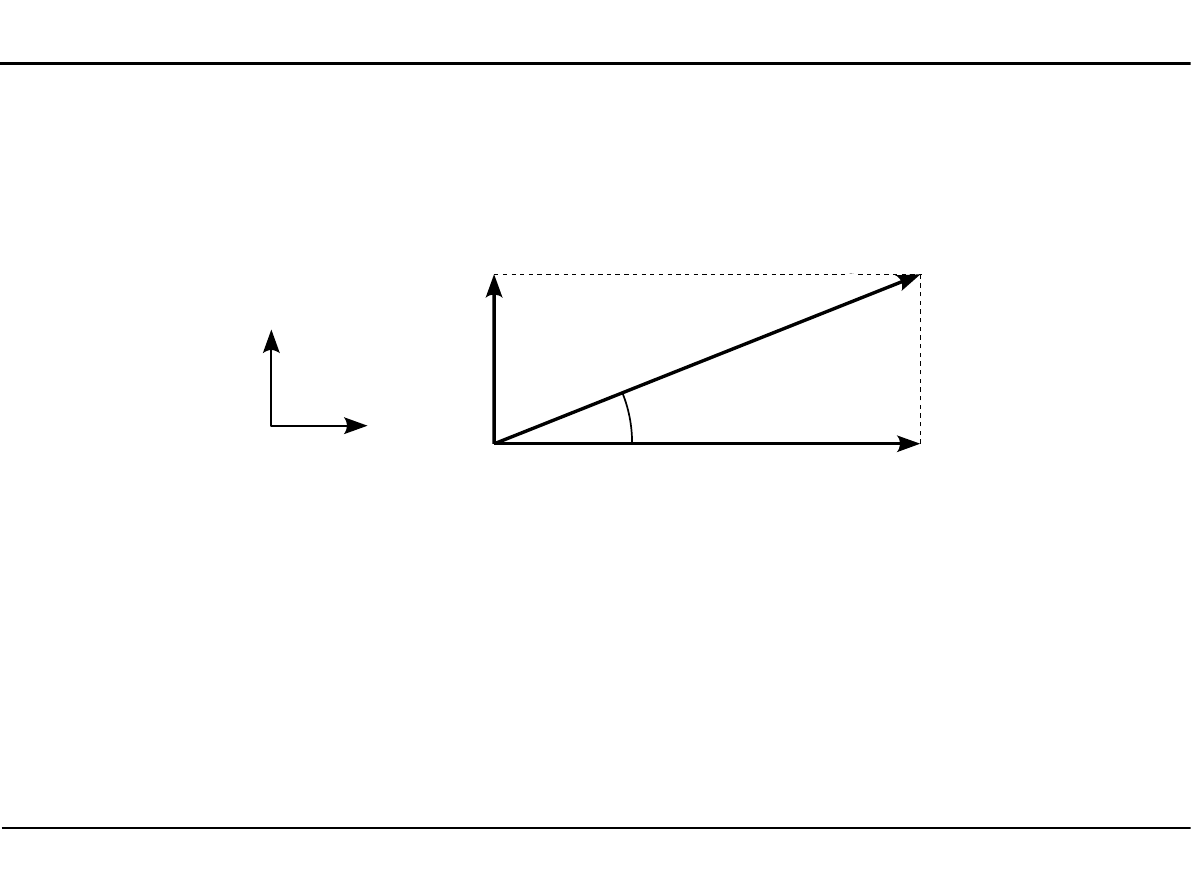
Rozkładanie siły na kierunek poziomy i pionowy

5.1. Siła

X

Y

P

P

X

P

Y

α

P

X

=

P⋅cos







P

Y

=

P⋅sin







Wartości sił składowych

Wartość siły składowej jest dodatnia, jeżeli siła ma zwrot zgodny ze zwrotem osi.

Dr inż. Janusz Dębiński

3

5. Analiza statyczna płaskich układów prętowych

a

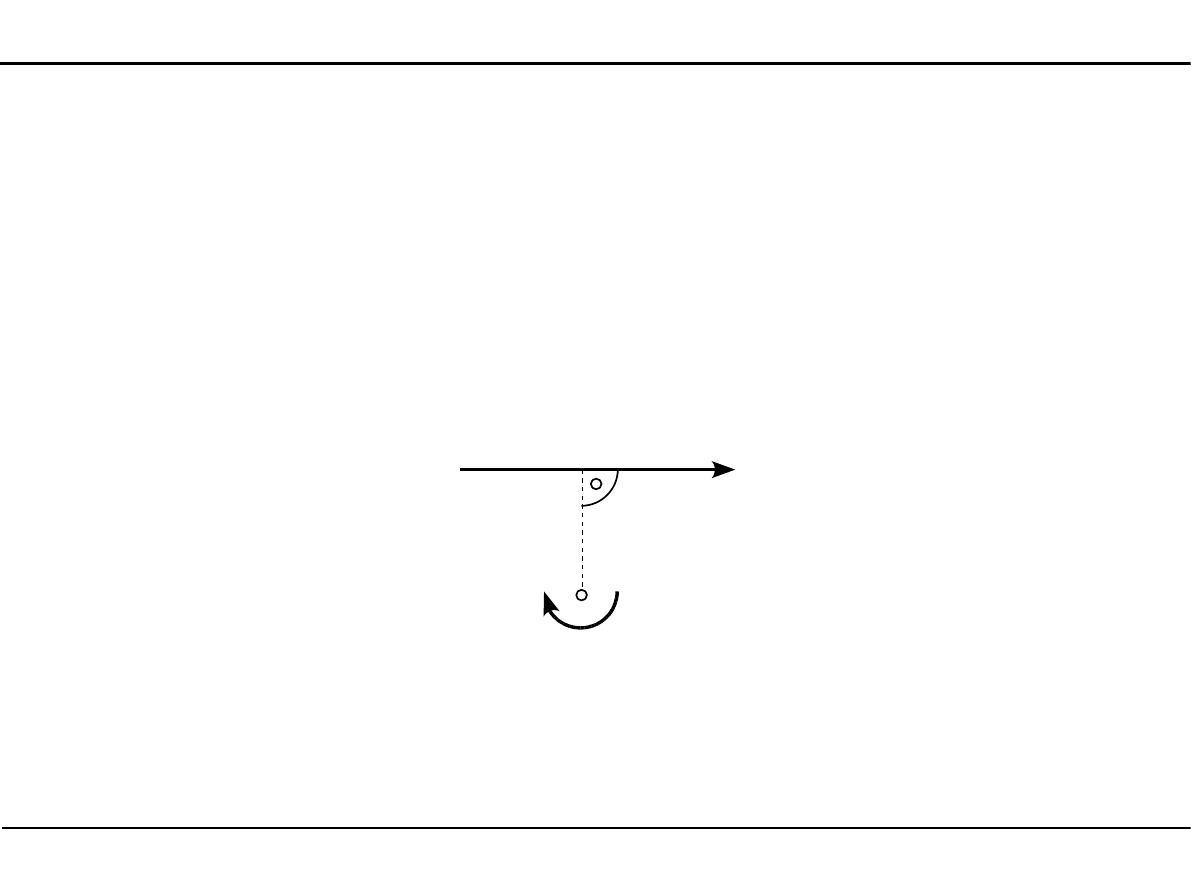
Moment siły względem punktu

5.1. Siła

M

O

=

∣

P

∣

⋅

a =∣P∣⋅a

a - odległość kierunku siły od punktu O

P - wartość siły.

P

O

M

O

W niniejszym kursie Mechaniki ogólnej będziemy przyjmować, że dodatni moment siły

względem punktu kręci zgodnie z ruchem wskazówek zegara.

Dr inż. Janusz Dębiński

4

5. Analiza statyczna płaskich układów prętowych

a

3

a

1

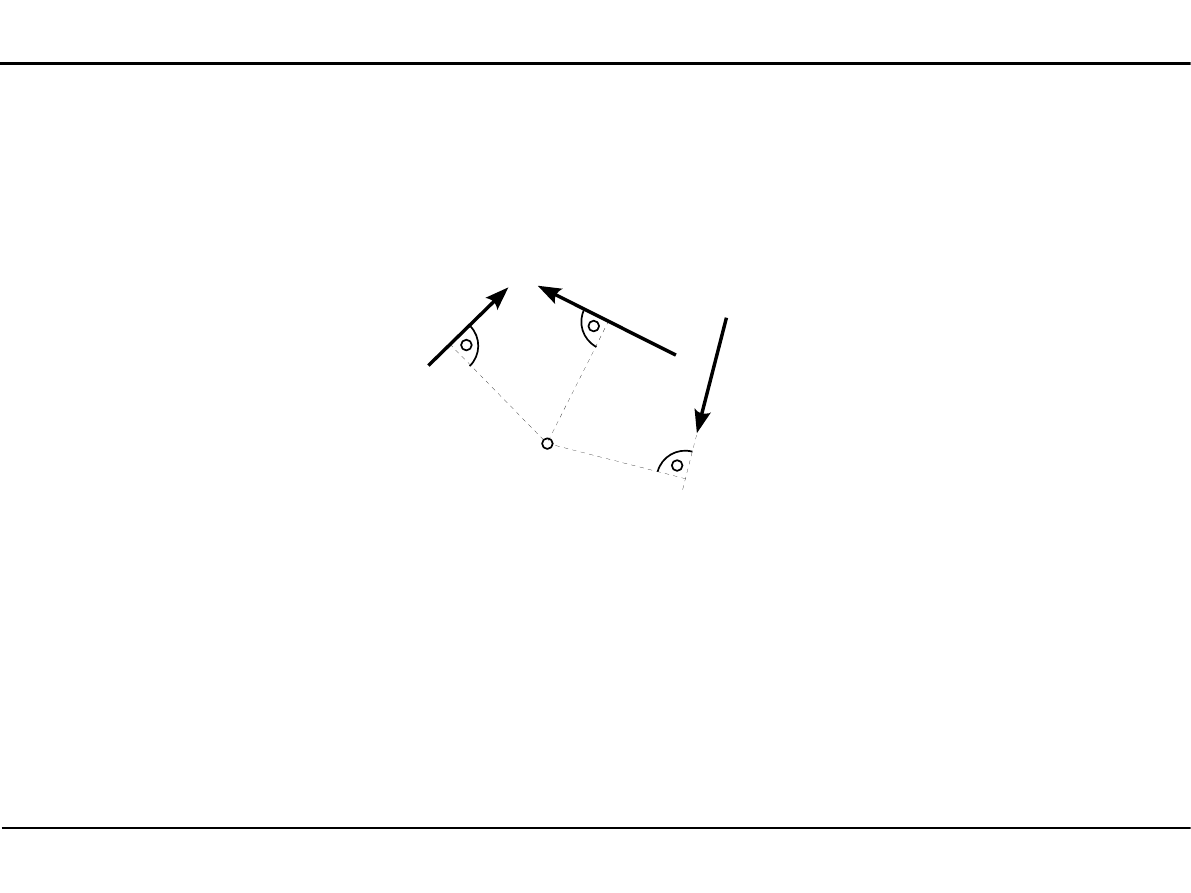
Moment siły względem punktu

5.1. Siła

P

1

P

2

P

3

O

a

2

M

O

=

∣

P

1

∣

⋅

a

1

−

∣

P

2

∣

⋅

a

2



∣

P

3

∣

⋅

a

3

Dr inż. Janusz Dębiński

5

5. Analiza statyczna płaskich układów prętowych

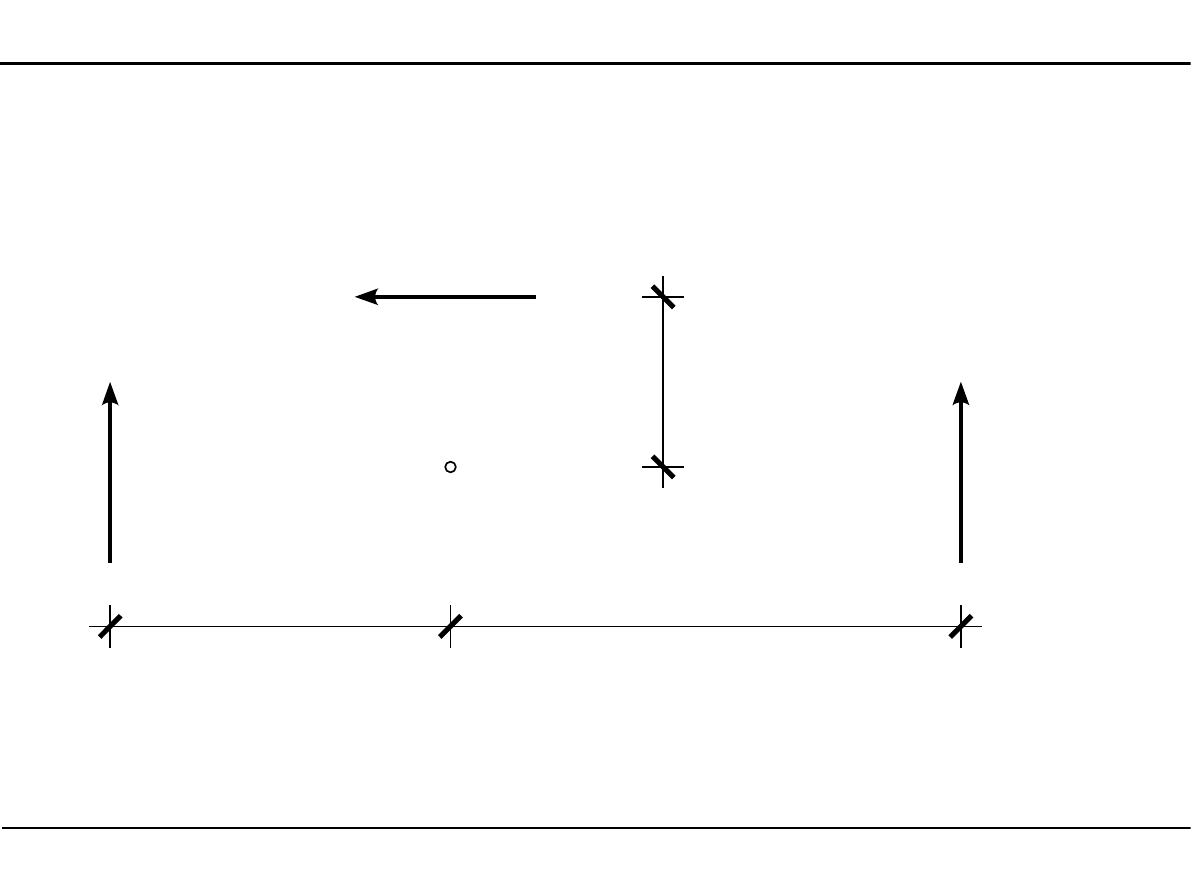
Moment siły względem punktu

5.1. Siła

2,

0

kN

5,0 kN

3,

0

kN

A

[m]

1,

0

2,0

3,0

M

A

=

2,0⋅2,0

−

5,0⋅1,0

−

3,0⋅3,0=−10,0 kN⋅m

Dr inż. Janusz Dębiński

6

5. Analiza statyczna płaskich układów prętowych

x

5.1. Siła

Para sił

M

O

=−∣

P∣⋅



xa



∣

P∣⋅x=−∣P∣⋅a

P

P

O

a

Jak więc widać wartość tego momentu jest zawsze taka sama bez względu na to,

w którym miejscu znajduje się punkt O.

Moment ten nazywamy momentem obrotowym, a jego wartość równa się iloczynowi wartości siły

P przez odległość tych sił od siebie a.

Jeżeli para sił kręci względem siebie zgodnie z ruchem wskazówek zegara, to moment obrotowy

jest dodatni, jeżeli przeciwnie, to ujemny.

Wektor momentu pary sił M

0

jest wektorem swobodnym, ponieważ możemy go przyłożyć

w dowolnym punkcie płaszczyzny i ma on zawsze ten sam zwrot, wartość i kierunek.

Dr inż. Janusz Dębiński

7

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

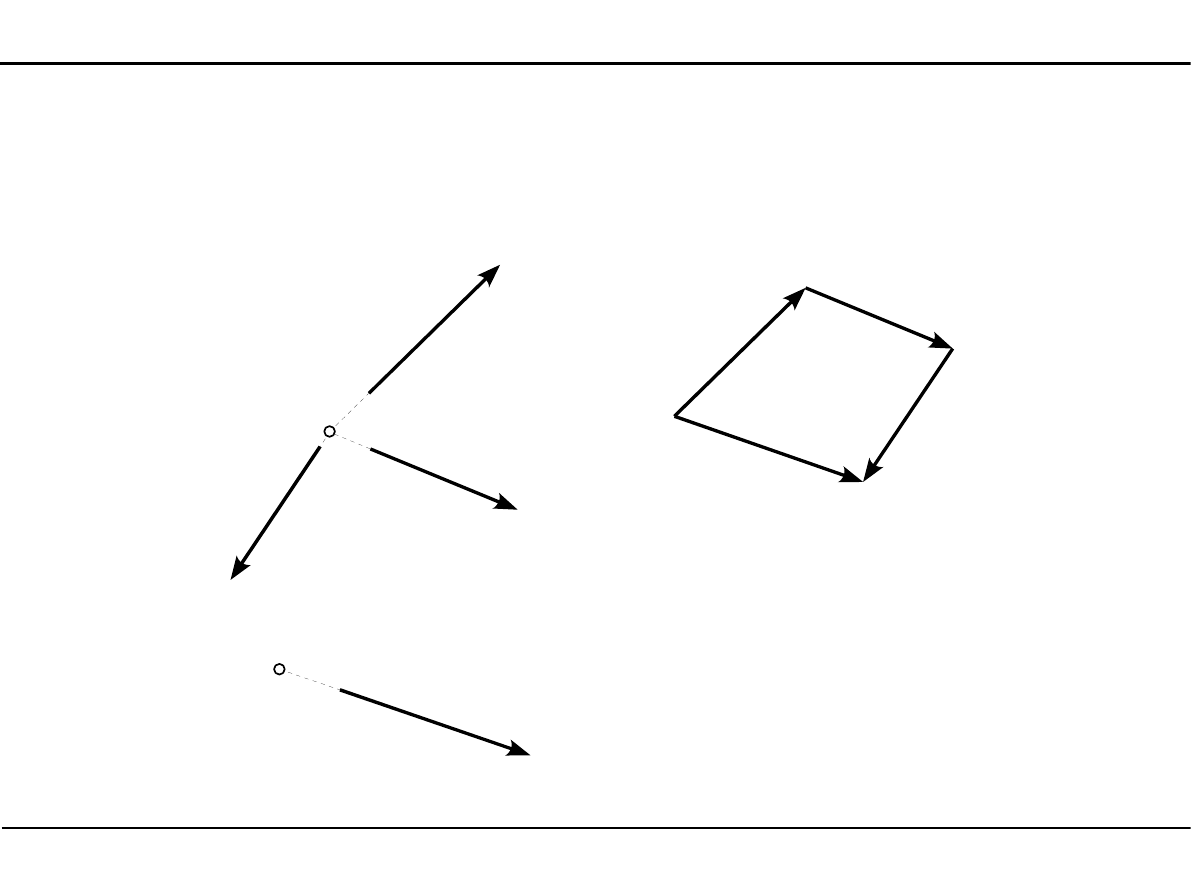
Płaski układ sił zbieżnych

Płaskim układem sił zbieżnych nazywamy siły, których kierunki leżą na jednej płaszczyźnie

i przecinają się wszystkie w jednym punkcie O.

Aby znaleźć siłę wypadkową z płaskiego układu sił zbieżnych zastosujemy wielobok sił.

Kierunek siły wypadkowej przechodzi przez punkt O.

Dr inż. Janusz Dębiński

8

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

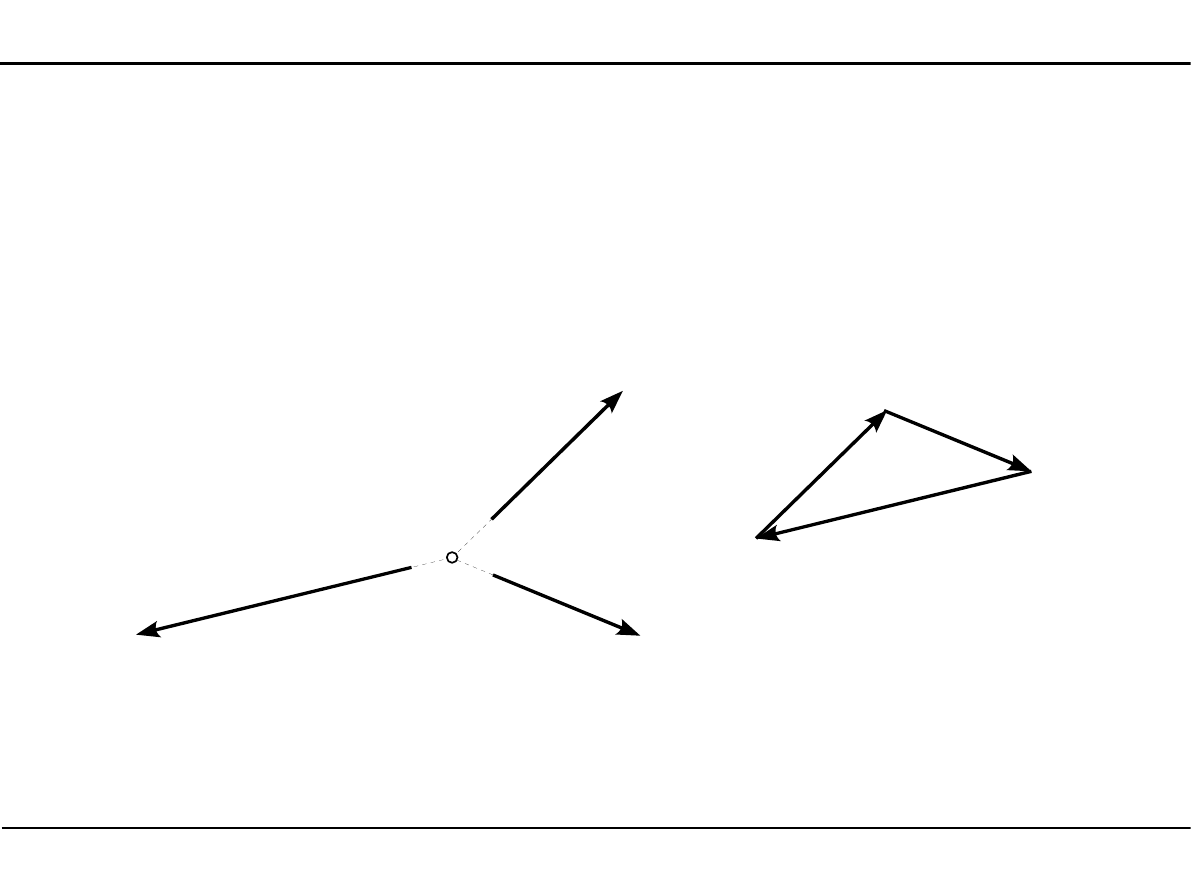
Płaski układ sił zbieżnych

P

1

P

2

P

3

O

P

1

P

2

P

3

W

O

W

Dr inż. Janusz Dębiński

9

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

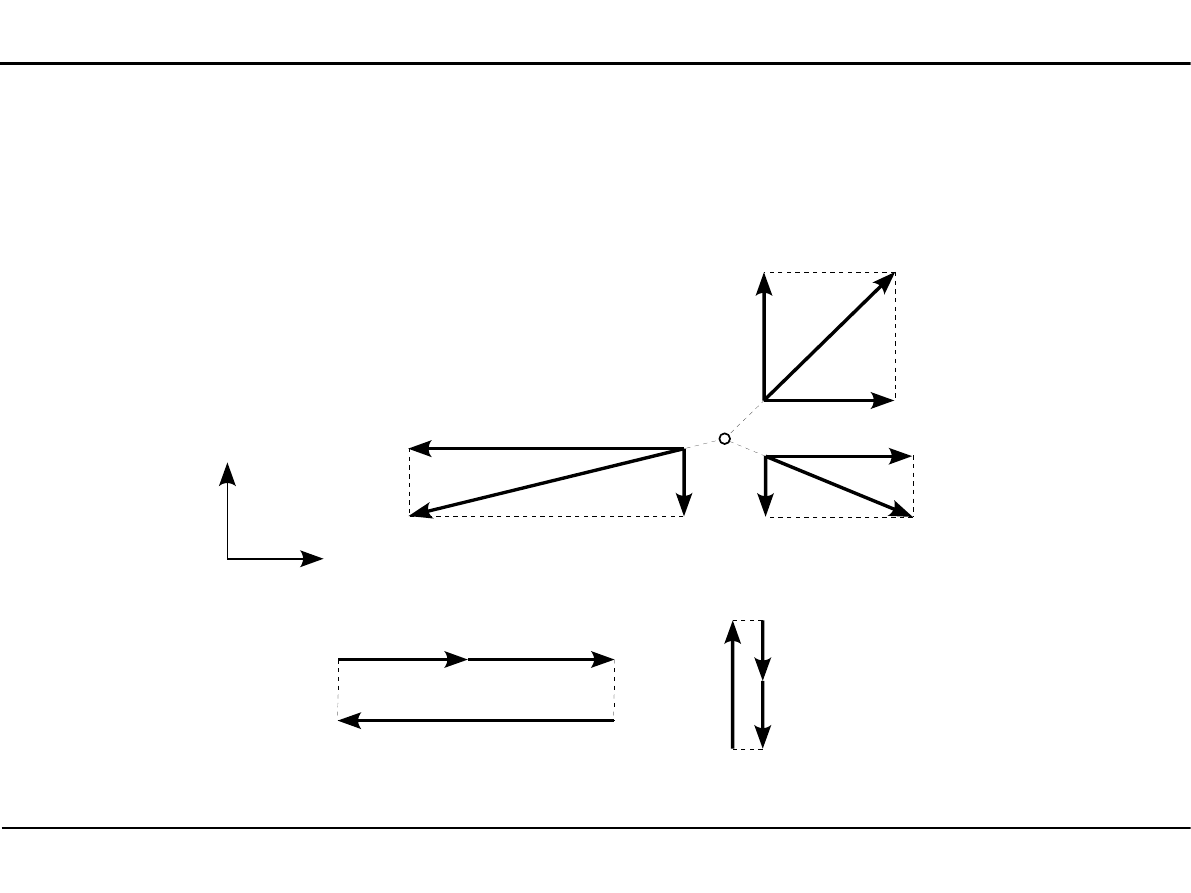
Płaski układ sił zbieżnych

Aby płaski układ sił zbieżnych znajdował się w równowadze, wielobok sił musi być wielobokiem

zamkniętym. Oznacza to, że siła wypadkowa z takiego układu musi być równa zero.

P

1

P

2

P

3

O

P

1

P

2

P

3

Dr inż. Janusz Dębiński

10

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

Płaski układ sił zbieżnych

P

1

O

P

2

P

3

X

Y

P

1X

P

1Y

P

2X

P

2Y

P

3X

P

3Y

P

1X

Siły są wektorami związanymi.

P

2X

P

3X

P

2Y

P

3Y

P

1Y

Dr inż. Janusz Dębiński

11

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

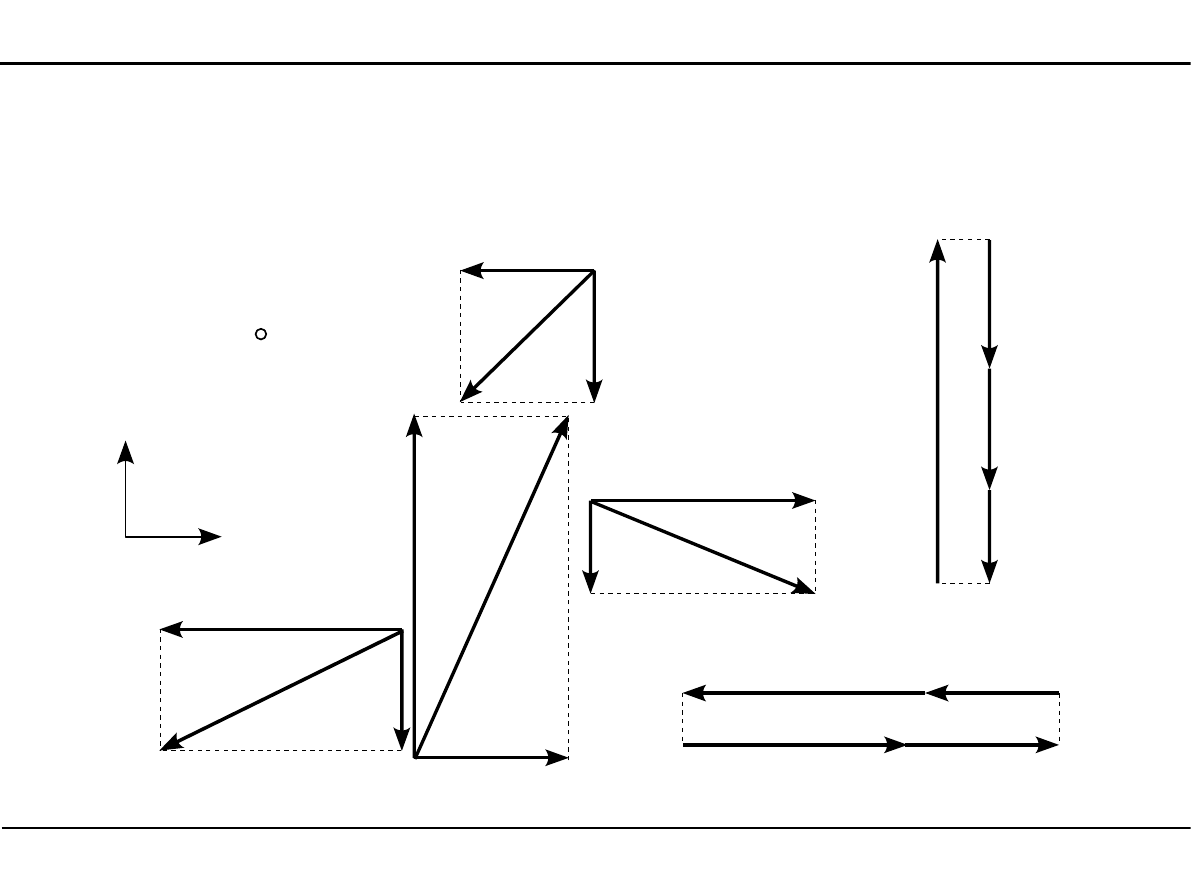
Płaski układ sił zbieżnych

Aby płaski układ sił zbieżnych znajdował się w równowadze muszą więc być spełnione równania

równowagi.

∑

i=1

i=n

P

iX

=

0

∑

i=1

i=n

P

iY

=

0

Dr inż. Janusz Dębiński

12

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

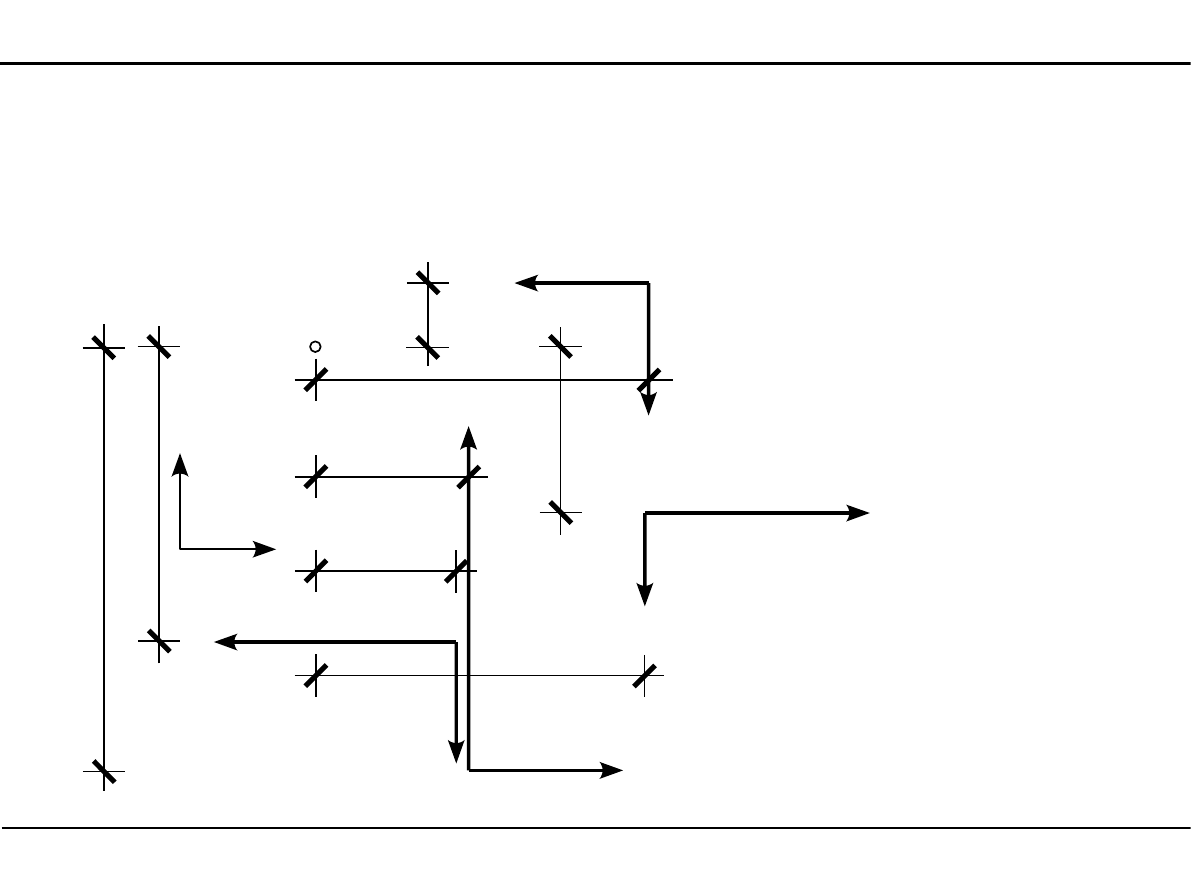
Płaski układ sił niezbieżnych

P

1

P

2

P

3

P

4

X

Y

P

1X

P

1Y

P

2X

P

2Y

P

3X

P

3Y

P

4X

P

4Y

P

1X

P

3X

P

2X

P

4X

P

4Y

P

1Y

P

3Y

P

2Y

O

Dr inż. Janusz Dębiński

13

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

Płaski układ sił niezbieżnych

M

O

=

∑

i=1

i=n



∣

P

iX

∣

⋅

a

iY



∣

P

iY

∣

⋅

a

iX



P

1X

P

1Y

P

2X

P

2Y

P

3X

P

3Y

P

4X

P

4Y

X

Y

O

a

1X

a

2X

a

3X

a

4X

a

1

Y

a

2

Y

a

3Y

a

4

Y

Dr inż. Janusz Dębiński

14

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

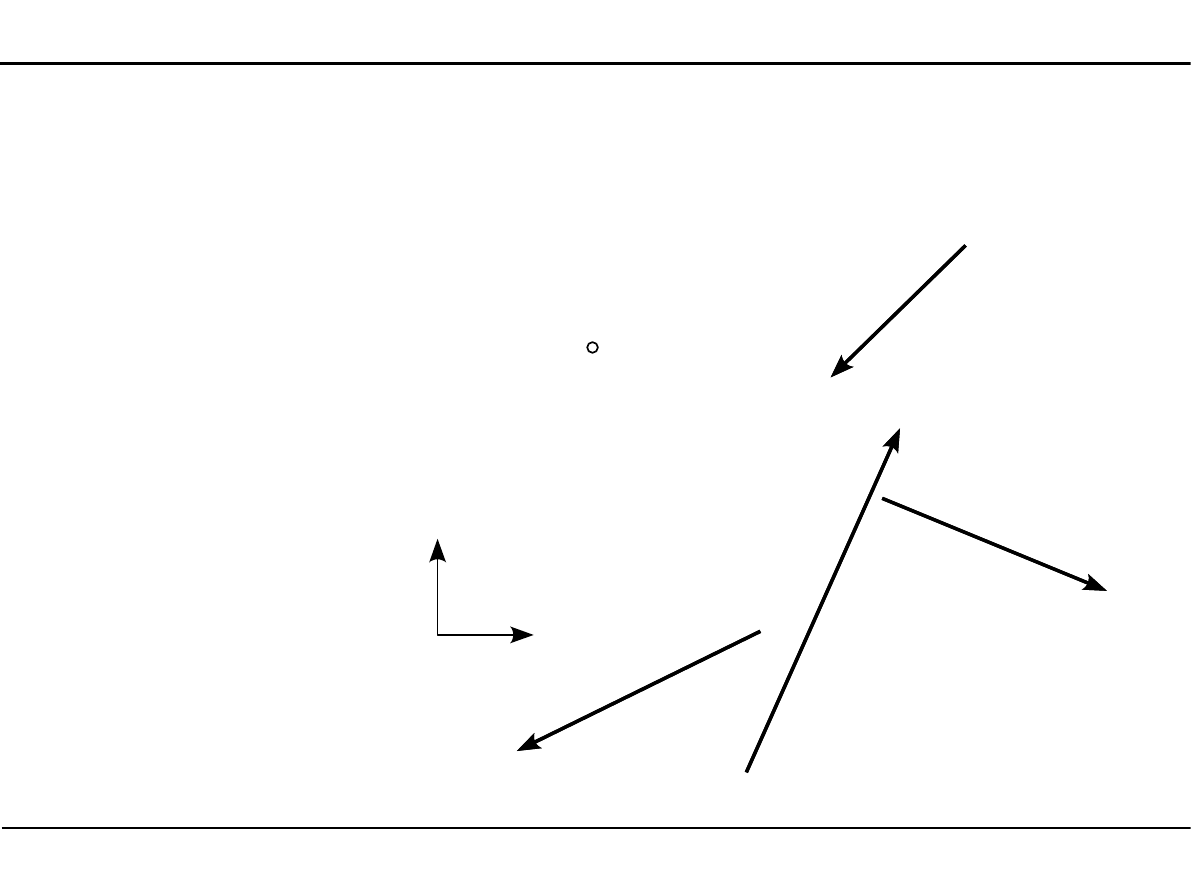
Płaski układ sił niezbieżnych

Aby płaski układ sił niezbieżnych znajdował się w równowadze muszą być spełnione równania

równowagi:

∑

i=1

i=n

P

iX

=

0

∑

i=1

i=n

P

iY

=

0

∑

i=1

i=n

M

O

=

0

P

1

P

2

P

3

P

4

P

1

P

2

P

3

P

4

X

Y

O

Dr inż. Janusz Dębiński

15

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

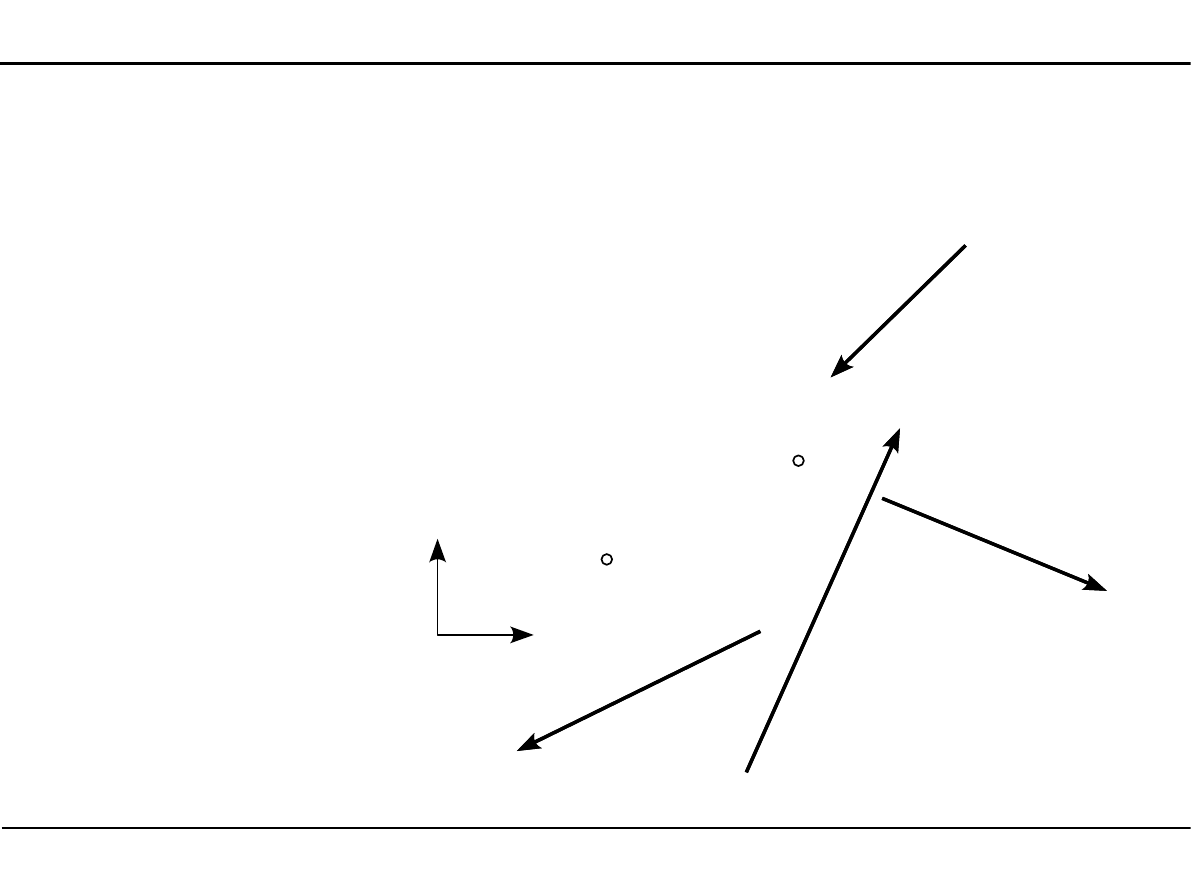
Płaski układ sił niezbieżnych

Aby płaski układ sił niezbieżnych znajdował się w równowadze muszą być spełnione równania

równowagi:

∑

i=1

i=n

P

iX

=

0

∑

i=1

i=n

M

O 1

=

0

∑

i=1

i=n

M

O 2

=

0

P

1

P

2

P

3

P

4

P

1

P

2

P

3

P

4

X

Y

O

1

O

2

Punkty O

1

, O

2

nie mogą

leżeć na prostej

równoległej do osi X.

Dr inż. Janusz Dębiński

16

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

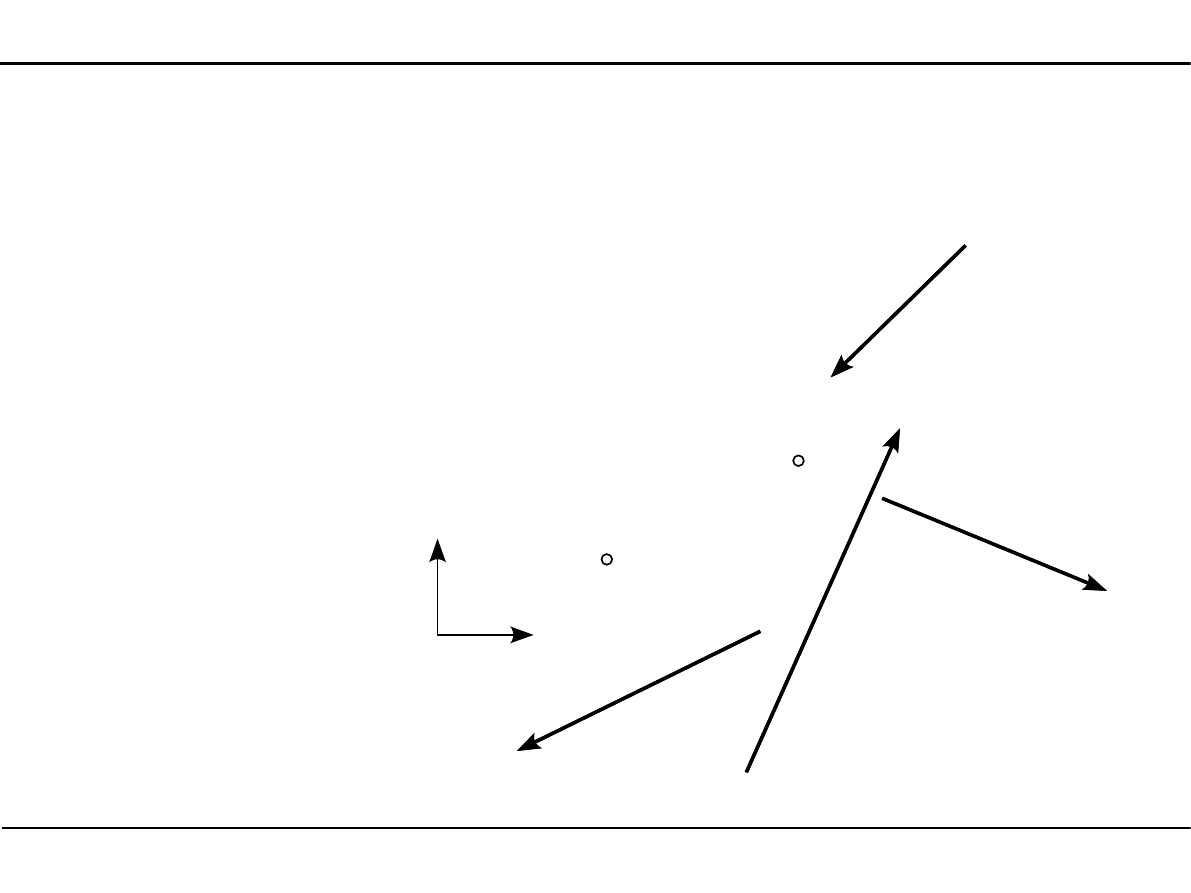
Płaski układ sił niezbieżnych

Aby płaski układ sił niezbieżnych znajdował się w równowadze muszą być spełnione równania

równowagi:

∑

i=1

i=n

M

O 1

=

0

∑

i=1

i=n

M

O 2

=

0

P

1

P

2

P

3

P

4

P

1

P

2

P

3

P

4

X

Y

O

1

O

2

∑

i=1

i=n

P

iY

=

0

Punkty O

1

, O

2

nie mogą

leżeć na prostej

równoległej do osi Y.

Dr inż. Janusz Dębiński

17

5. Analiza statyczna płaskich układów prętowych

5.1. Siła

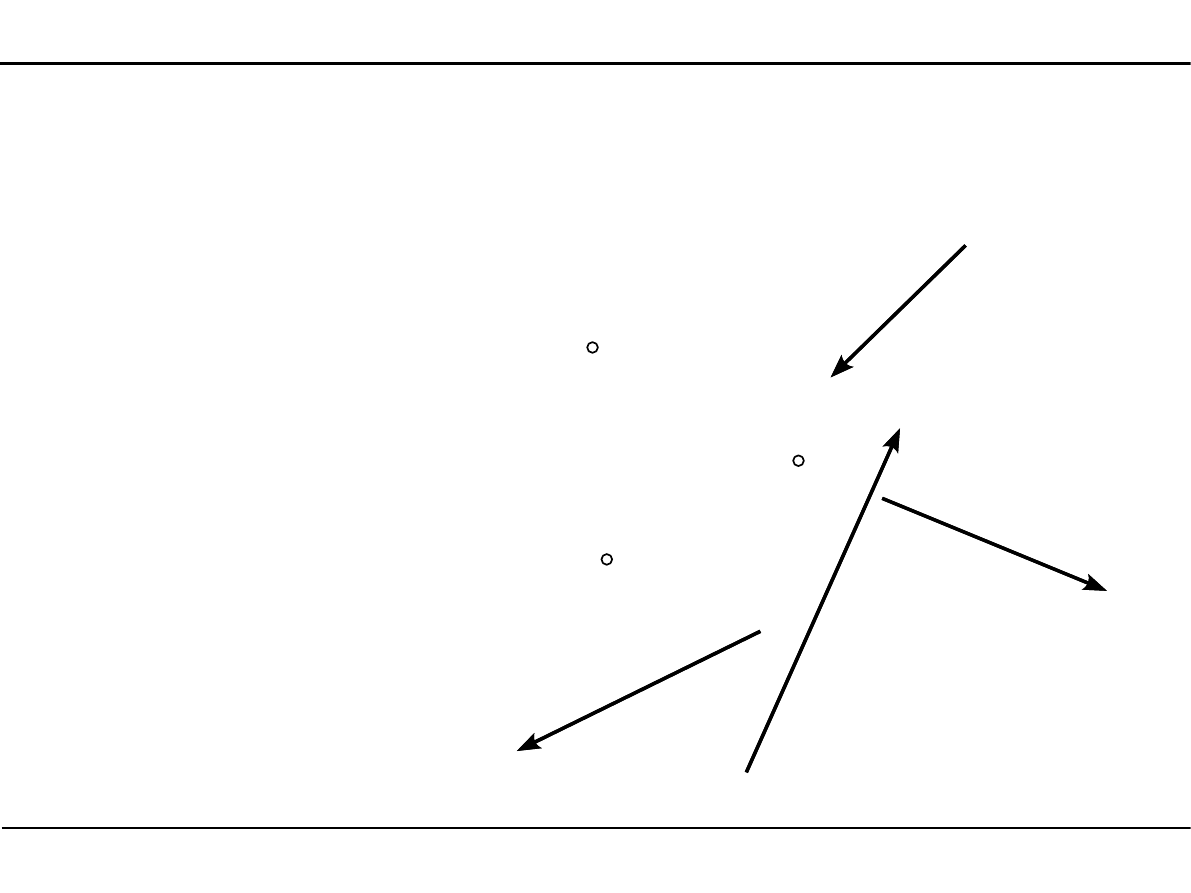
Płaski układ sił niezbieżnych

Aby płaski układ sił niezbieżnych znajdował się w równowadze muszą być spełnione równania

równowagi:

∑

i=1

i=n

M

O 1

=

0

∑

i=1

i=n

M

O 2

=

0

∑

i=1

i=n

M

O 3

=

0

P

1

P

2

P

3

P

4

P

1

P

2

P

3

P

4

O

1

O

2

O

3

Punkty O

1

, O

2

i O

3

nie mogą

leżeć na jednej prostej.

Dr inż. Janusz Dębiński

18

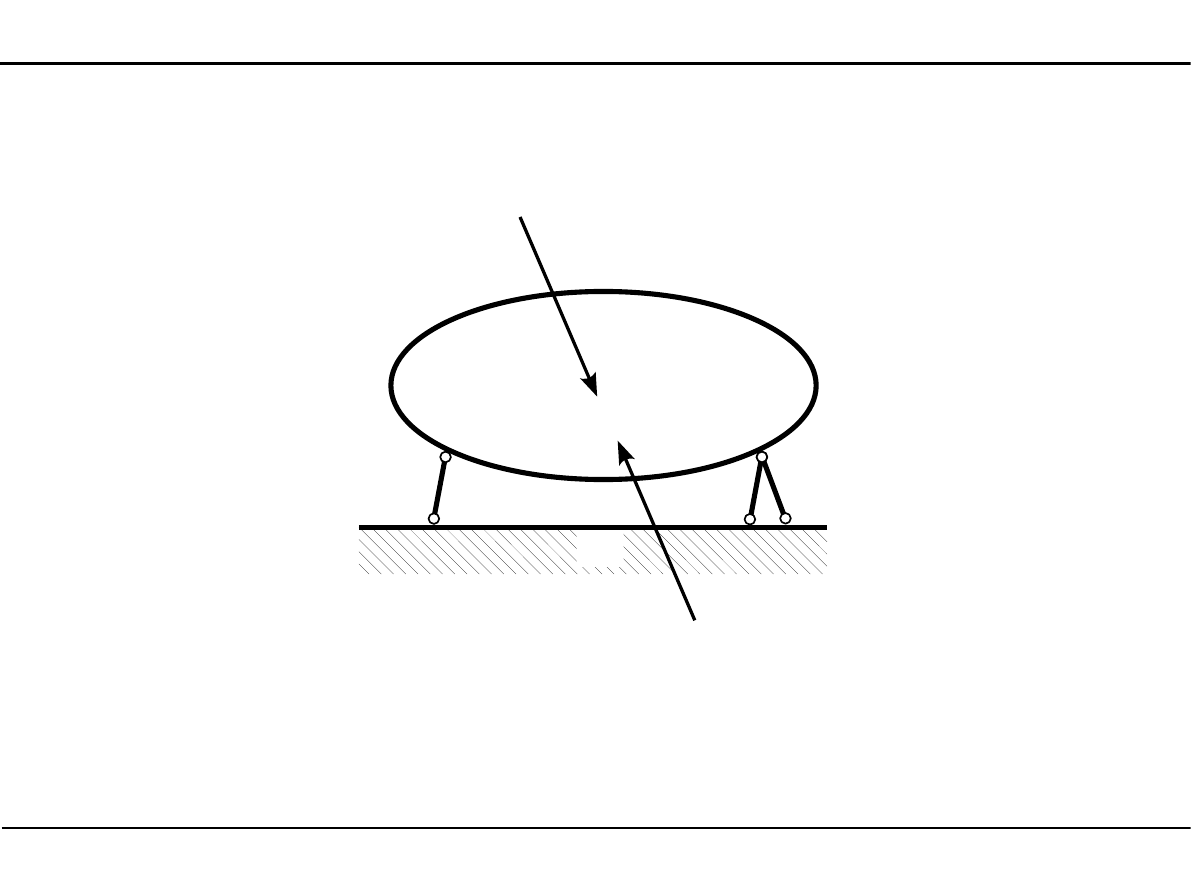
5. Analiza statyczna płaskich układów prętowych

5.2. Analiza statyczna

Siły czynne i reakcje

TP

1

2

3

P

P - siła czynna

R

R - reakcja czyli siła bierna

I

Analiza statyczna - wyznaczanie wartości i zwrotów reakcji.

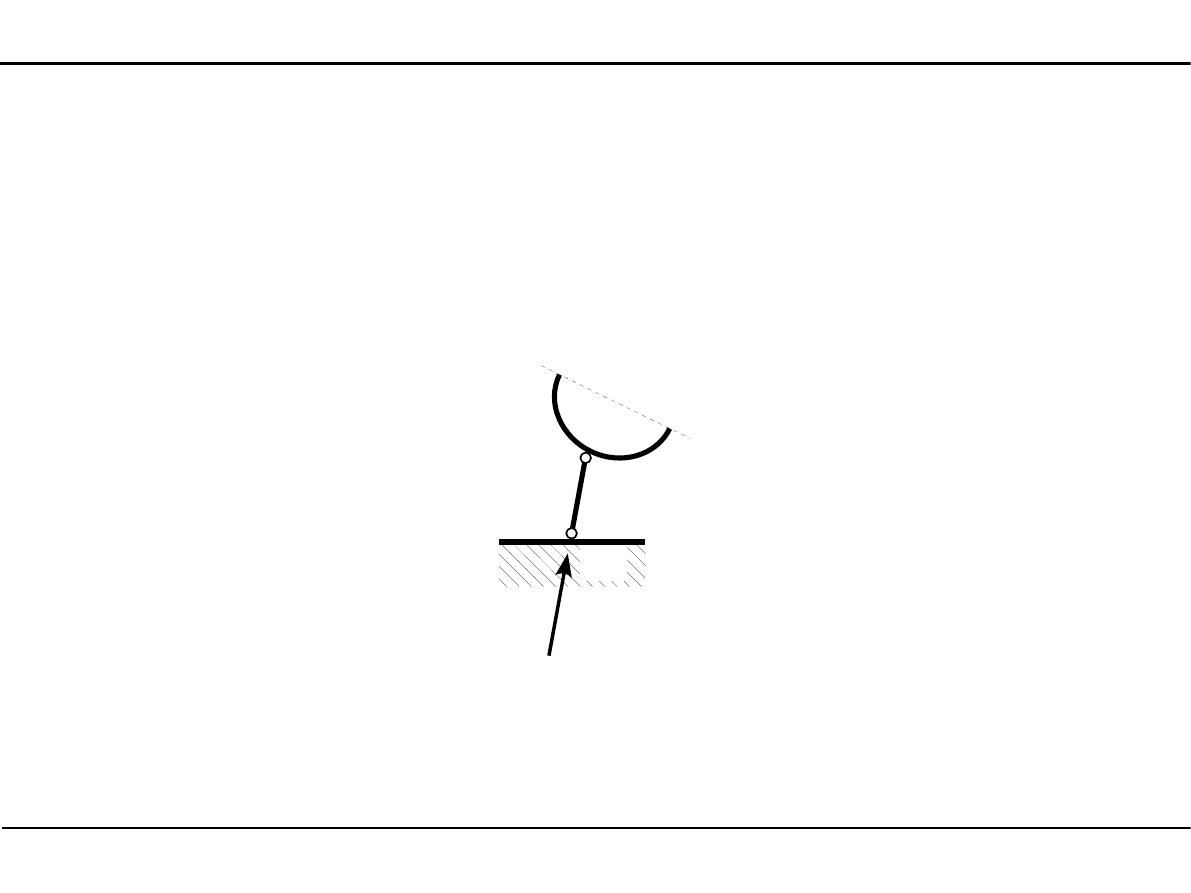
Dr inż. Janusz Dębiński

19

5. Analiza statyczna płaskich układów prętowych

5.2. Analiza statyczna

Reakcja w pręcie podporowym

W pręcie podporowym łączącym tarczę sztywną z tarczą podporową działa tylko jedna reakcja,

której kierunek działania pokrywa się z kierunkiem pręta podporowego.

TP

1

R

1

Dr inż. Janusz Dębiński

20

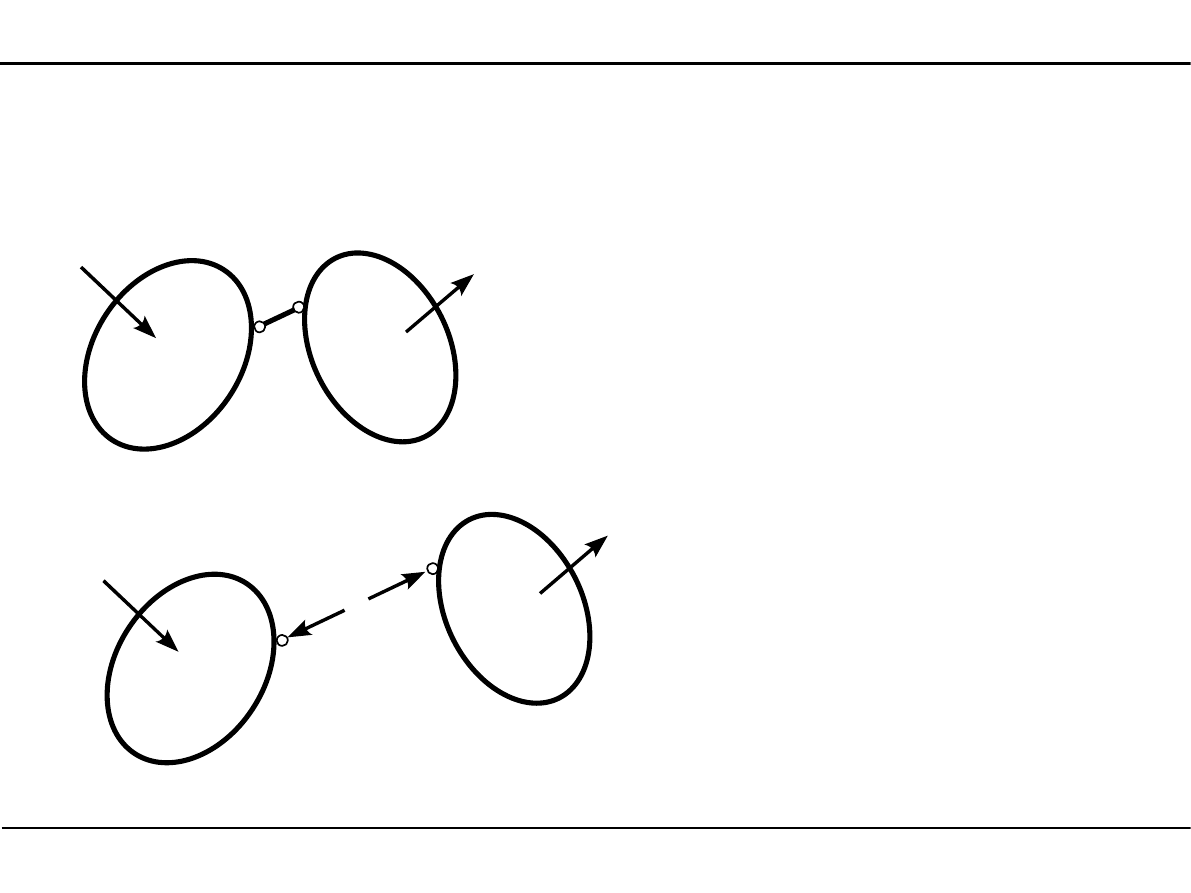
5. Analiza statyczna płaskich układów prętowych

5.2. Analiza statyczna

Reakcja w pręcie podporowym

Jeżeli pręt podporowy numer 1 łączy

dwie tarcze sztywne, z których żadna nie jest

tarczą podporową.

I

II

1

P

1

P

2

I

II

P

1

P

2

R

1

(I)

R

1

(II)

R

1



I

=

R

1



II

Jeżeli rozpatrujemy obie tarcze sztywne

razem, to reakcje te równoważą się.

Dr inż. Janusz Dębiński

21

5. Analiza statyczna płaskich układów prętowych

α

5.2. Analiza statyczna

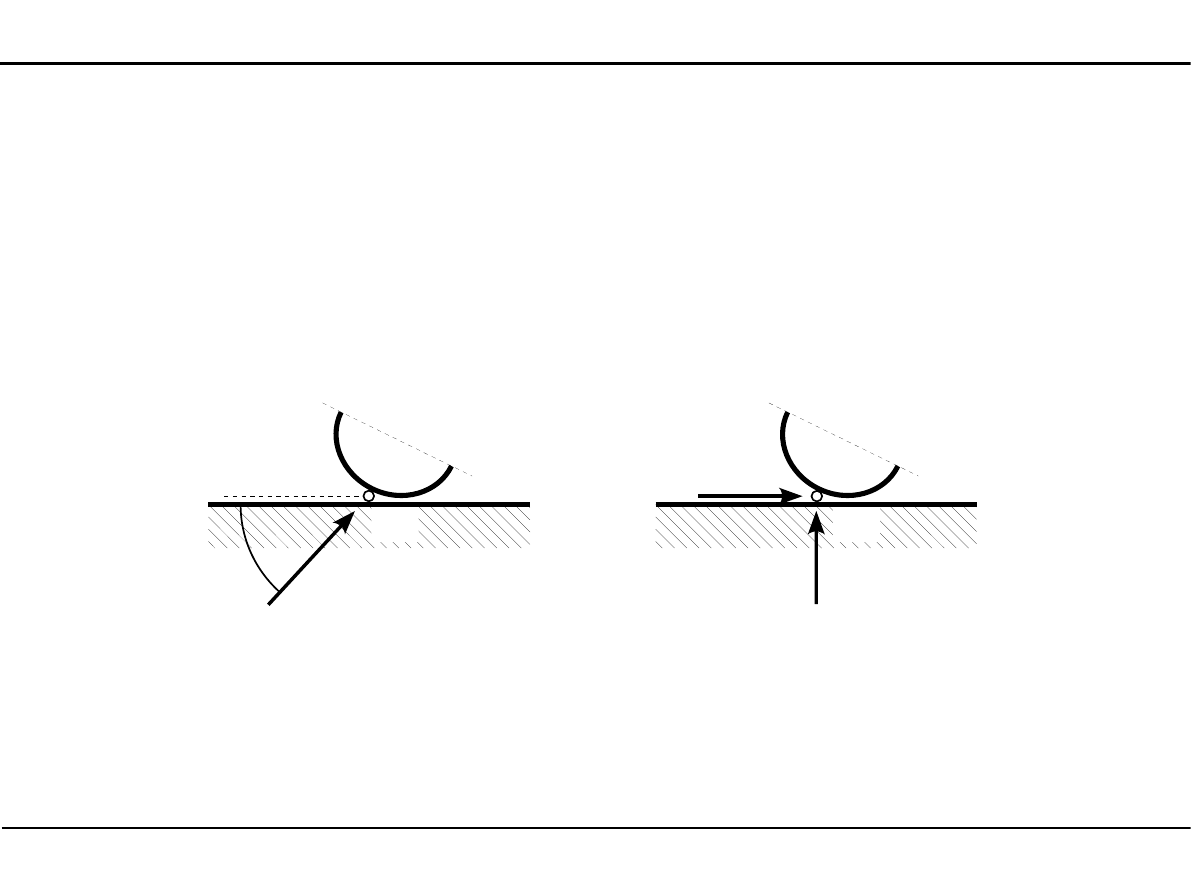
Reakcja w przegubie

W przegubie łączącym tarczę sztywną z tarczą podporową działa także jedna reakcja, której

kierunek działania przechodzi przez ten przegub.

W przeciwieństwie do pręta podporowego nie znamy kąta nachylenia kierunku jej działania.

Aby wyznaczyć reakcję, rozkładamy ją więc na dwie reakcje składowe: poziomą i pionową.

TP

A

R

A

TP

A

V

A

H

A

Dr inż. Janusz Dębiński

22

5. Analiza statyczna płaskich układów prętowych

5.2. Analiza statyczna

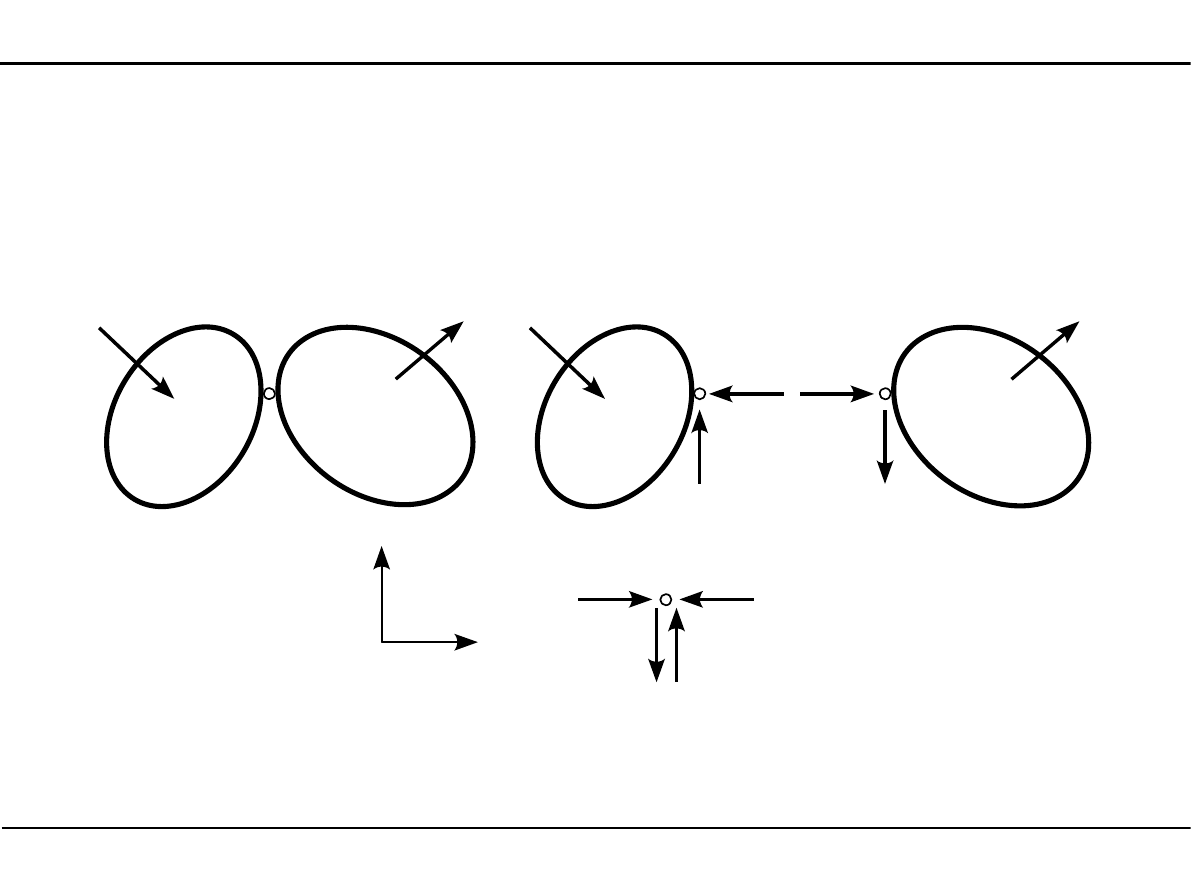
Reakcja w przegubie

Przegub łączący dwie tarcze sztywne, z których żadna nie jest tarczą sztywną.

I

II

A

P

1

P

2

I

II

A

A

P

1

P

2

V

A

(I)

V

A

(II)

H

A

(I)

H

A

(II)

A

H

A

(I)

H

A

(II)

V

A

(I)

V

A

(II)



X =H

A



I

−

H

A



II

=

0



Y =−V

A



I



V

A



II

=

0

X

Y

H

A

(I)

=H

A

(II)

V

A

(I)

=V

A

(II)

Dr inż. Janusz Dębiński

23

5. Analiza statyczna płaskich układów prętowych

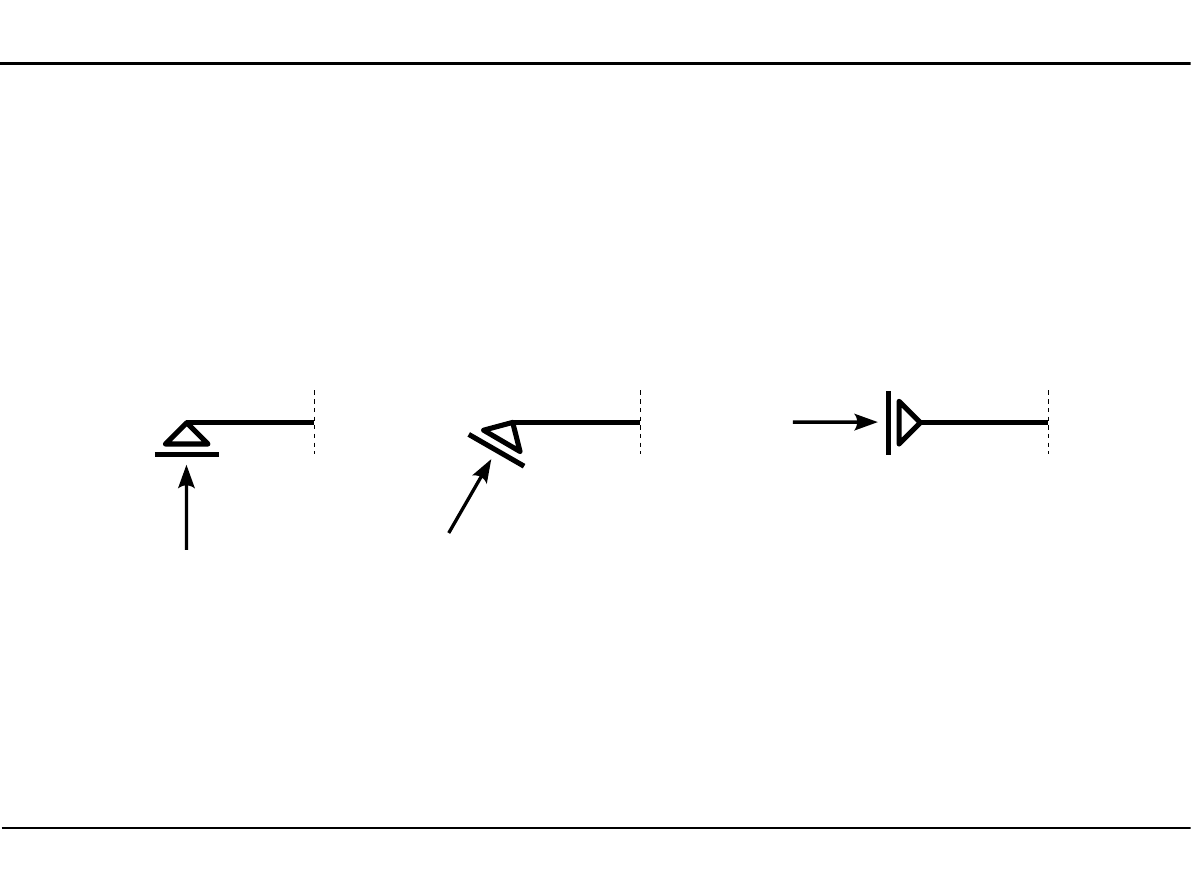
5.2. Analiza statyczna

Reakcja na podporze przegubowo-przesuwnej

Na podporze przegubowo-przesuwnej działa reakcja, której kierunek jest prostopadły

do kreski oznaczającej tę podporę.

R

R

R

Dr inż. Janusz Dębiński

24

5. Analiza statyczna płaskich układów prętowych

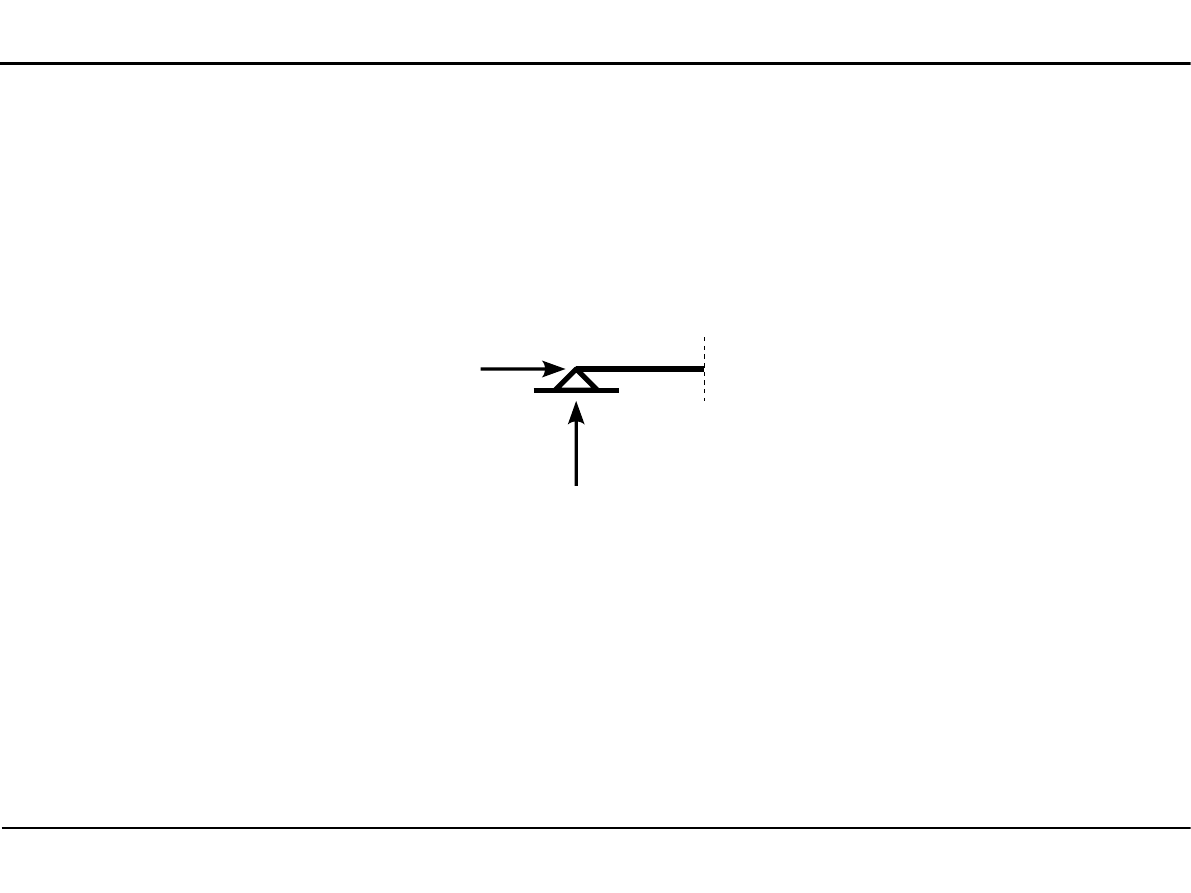
5.2. Analiza statyczna

Reakcje na podporze przegubowo-nieprzesuwnej

V

H

Na podporze tej działają dwie składowe składowe reakcje: pozioma H oraz pionowa V.

Dr inż. Janusz Dębiński

25

5. Analiza statyczna płaskich układów prętowych

5.2. Analiza statyczna

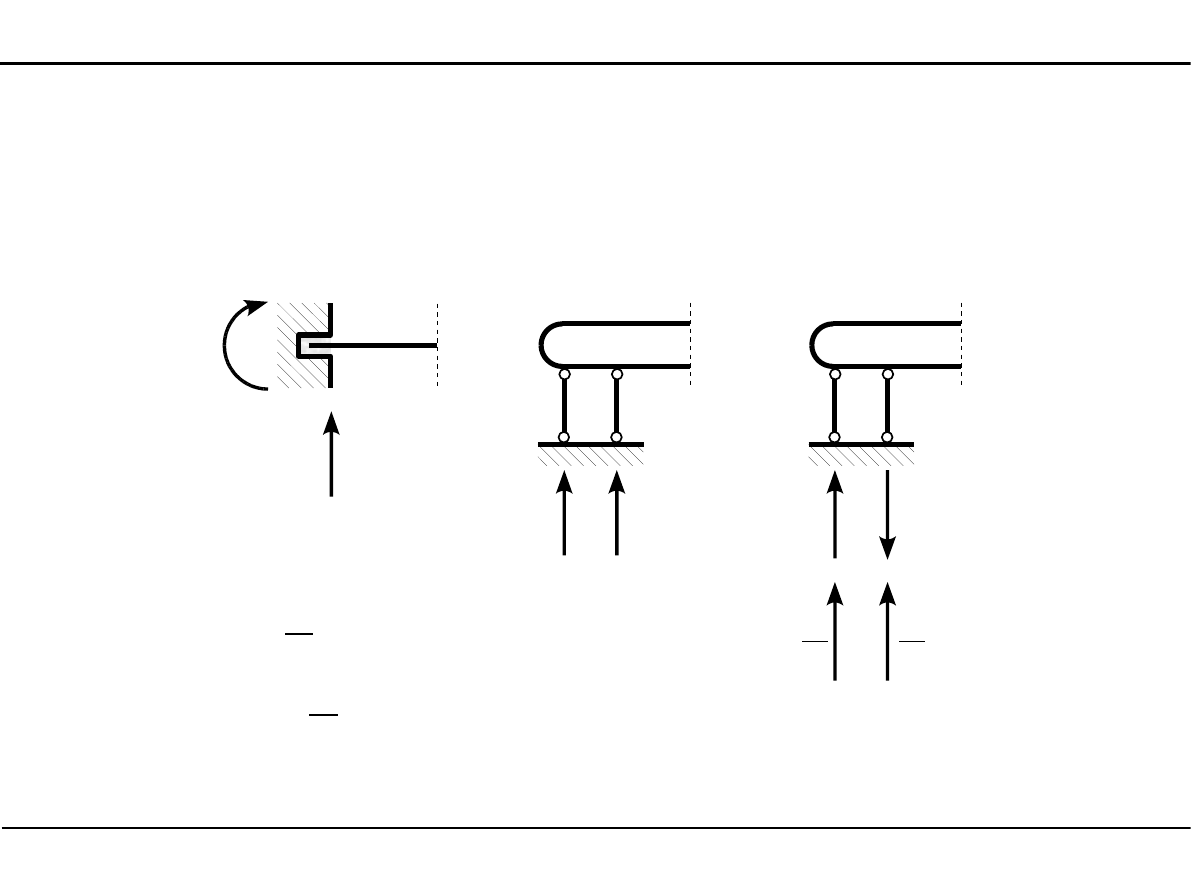
Reakcje na podporze teleskopowej

1

2

1

2

R

1

R

2

R

R

V

2

V

2

{

R

1

=

R V

2

R

2

=−

R V

2

V

M

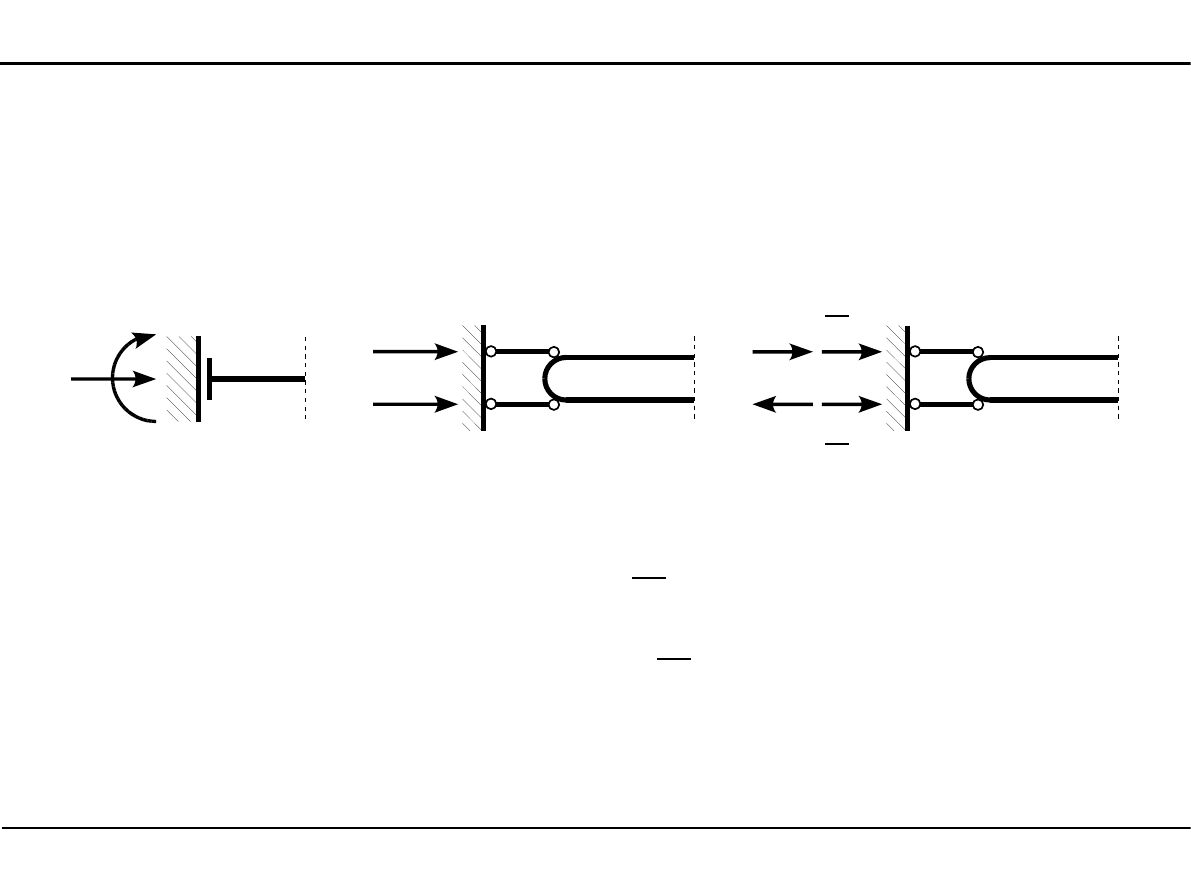
Dr inż. Janusz Dębiński

26

5. Analiza statyczna płaskich układów prętowych

5.2. Analiza statyczna

Reakcje na podporze ślizgowej

1

2

1

2

R

1

R

2

R

R

H

2

H

2

H

M

{

R

1

=

R H

2

R

2

=−

R H

2

Dr inż. Janusz Dębiński

27

5. Analiza statyczna płaskich układów prętowych

5.2. Analiza statyczna

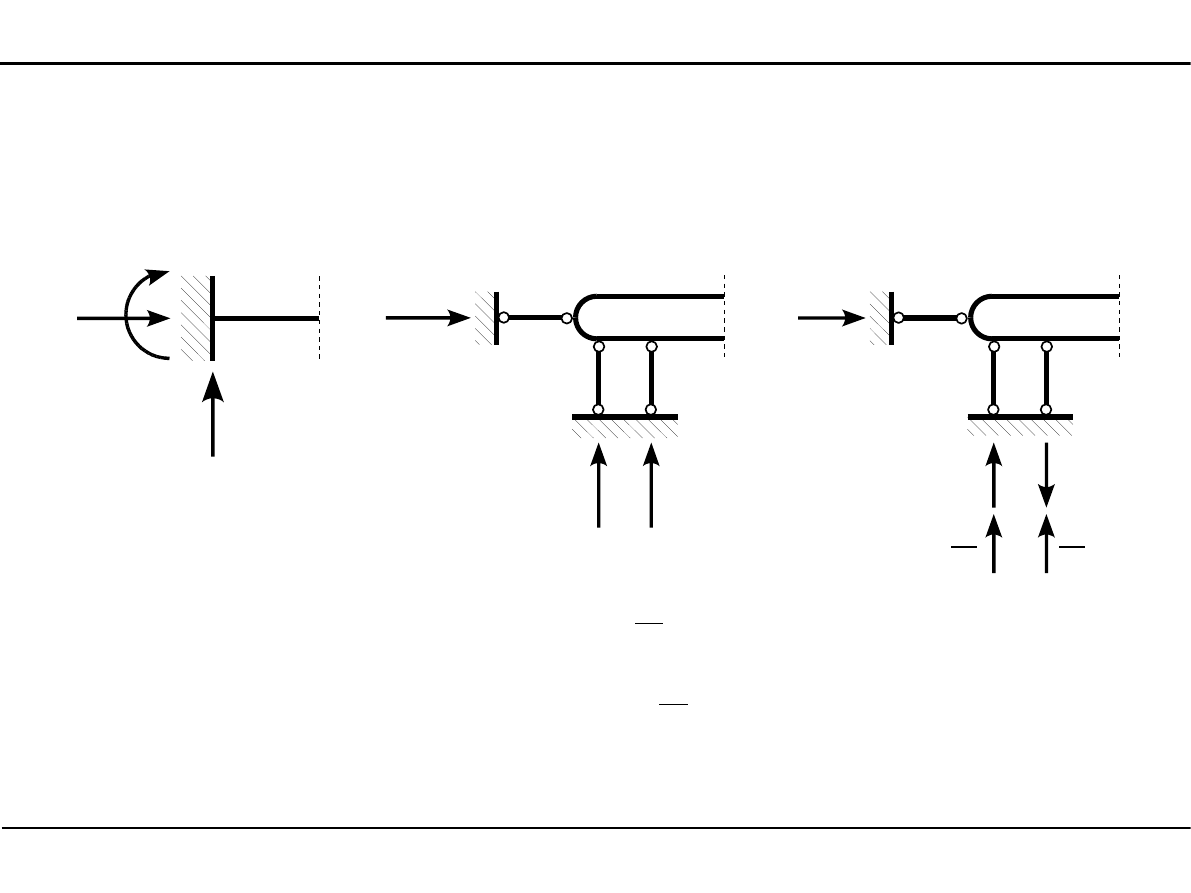
Reakcje w utwierdzeniu

1

2

1

2

R

1

R

2

H

H

R

R

V

2

V

2

V

H

M

{

R

1

=

R V

2

R

2

=−

R V

2

Dr inż. Janusz Dębiński

28

5. Analiza statyczna płaskich układów prętowych

5.3. Obciążenia prętów

Siła i moment obrotowy

Siłą będziemy obciążać wszystkie rodzaje płaskich konstrukcji prętowych.

Jednostką siły jest Niuton [N].

W niniejszym kursie Mechaniki ogólnej będziemy używać wielokrotności kiloniutona [kN].

Momentem obrotowym będziemy obciążać belki, ramy i łuki płaskie.

Jest on równoważny parze sił.

Jednostką momentu obrotowego jest [N∙m], w niniejszym kursie Mechaniki ogólnej

będziemy używać wielokrotności [kN∙m].

M

M

P

P

P

P

Dr inż. Janusz Dębiński

29

5. Analiza statyczna płaskich układów prętowych

5.3. Obciążenia prętów

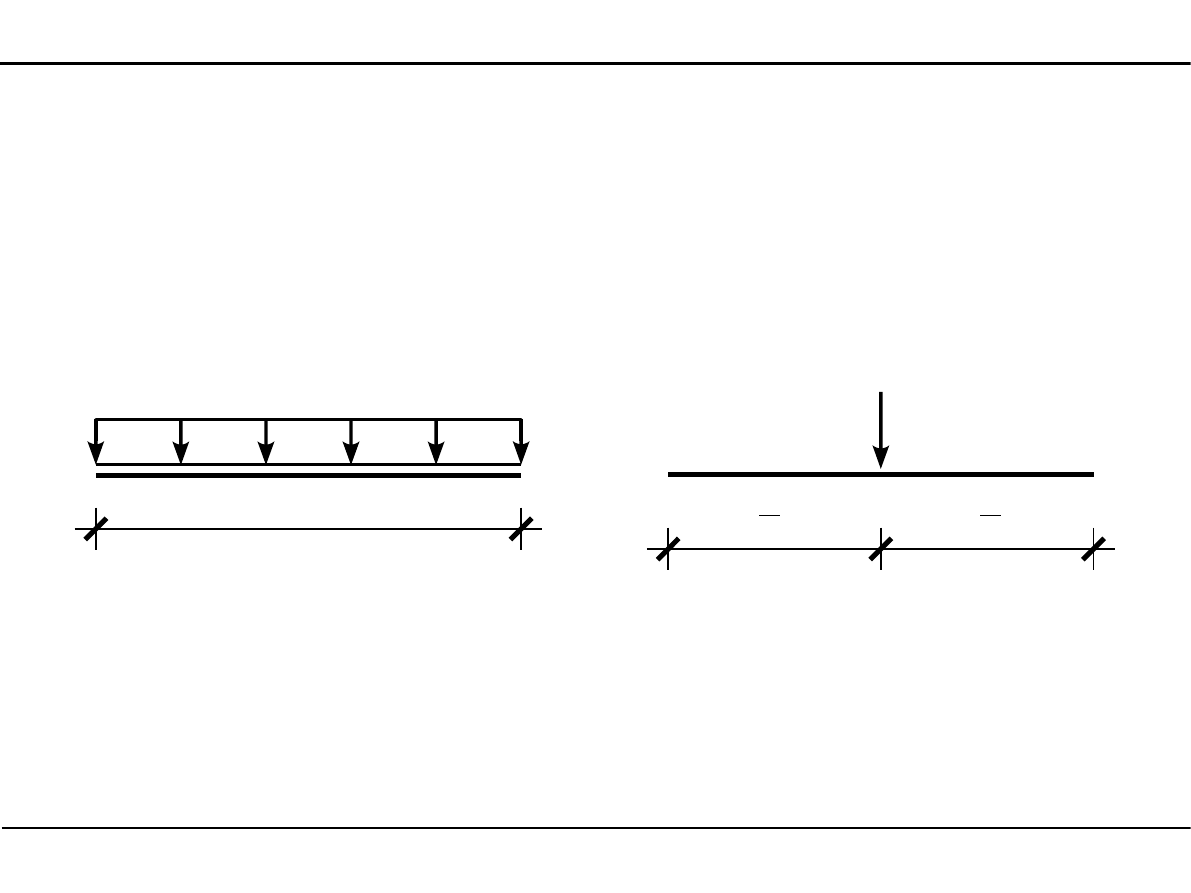
Obciążenie ciągłe równomiernie rozłożone prostopadłe do osi pręta

Jednostką tego obciążenia jest N/m, w niniejszym kursie Mechaniki ogólnej będziemy

używać kN/m.

A

B

L

q

A

B

q∙L

L

2

L

2

Siła wypadkowa z obciążenia ciągłego q ma ten sam zwrot co to obciążenie.

Dr inż. Janusz Dębiński

30

5. Analiza statyczna płaskich układów prętowych

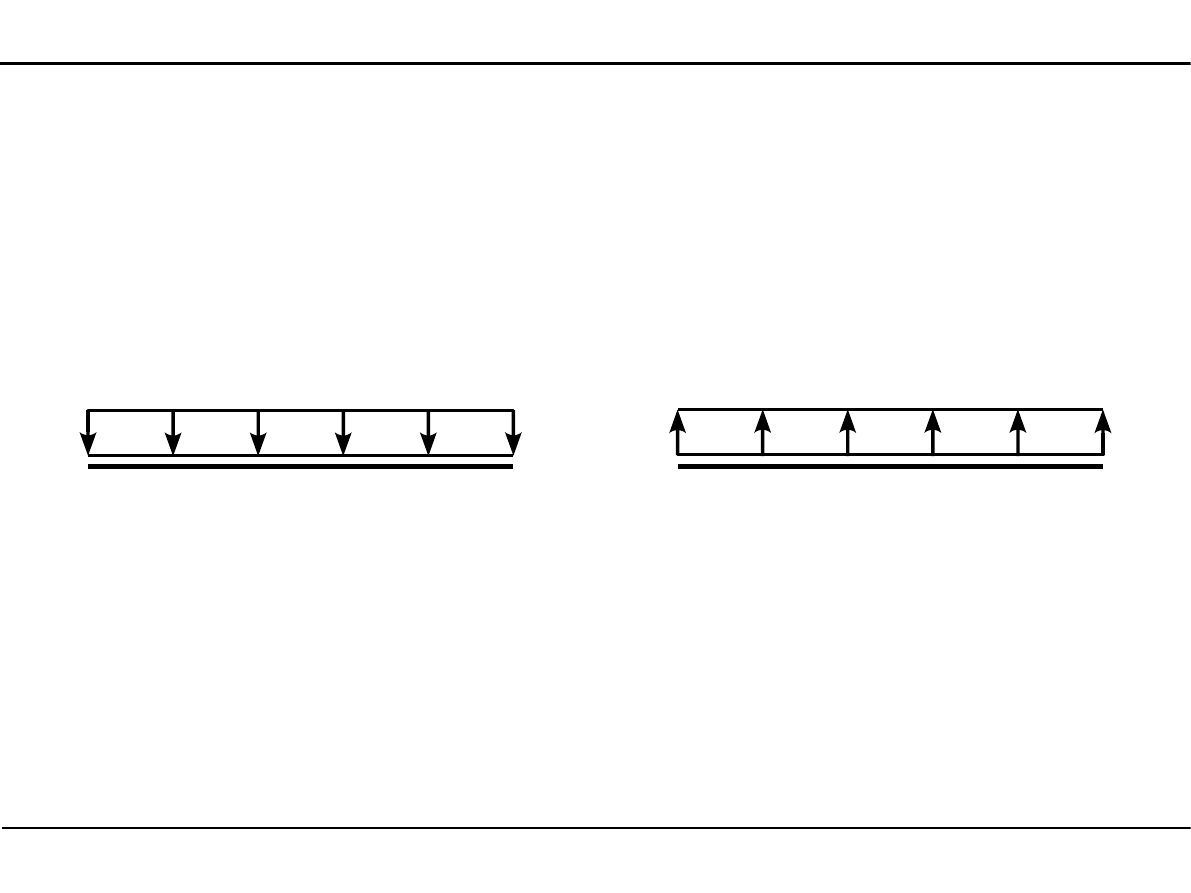
5.3. Obciążenia prętów

Obciążenie ciągłe równomiernie rozłożone prostopadłe do osi pręta

Dodatnie obciążenie q będzie w prętach poziomych działało w dół.

A

B

q > 0

A

B

q < 0

Dr inż. Janusz Dębiński

31

5. Analiza statyczna płaskich układów prętowych

5.3. Obciążenia prętów

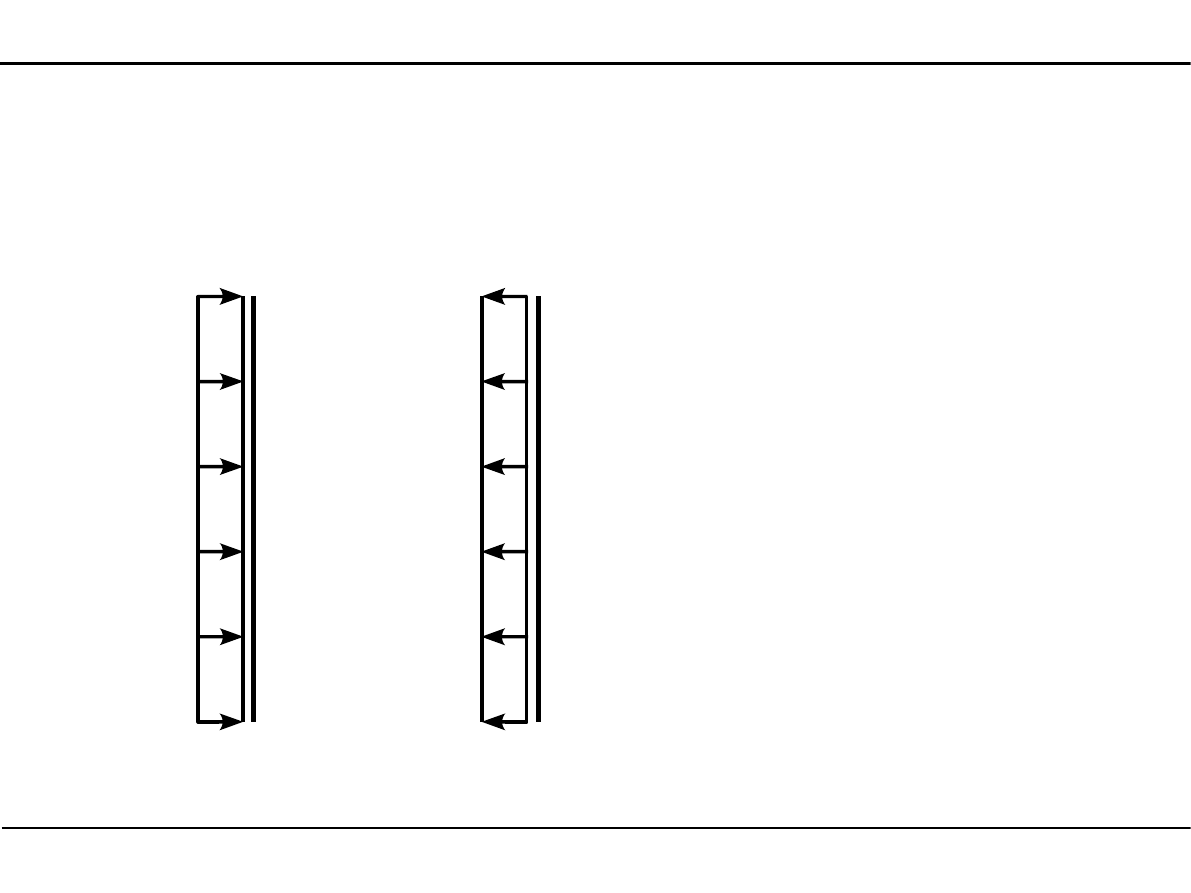
Obciążenie ciągłe równomiernie rozłożone prostopadłe do osi pręta

Dodatnie obciążenie q będzie w prętach

pionowych działało w prawo.

A

B

q > 0

A

B

q < 0

Dr inż. Janusz Dębiński

32

5. Analiza statyczna płaskich układów prętowych

5.3. Obciążenia prętów

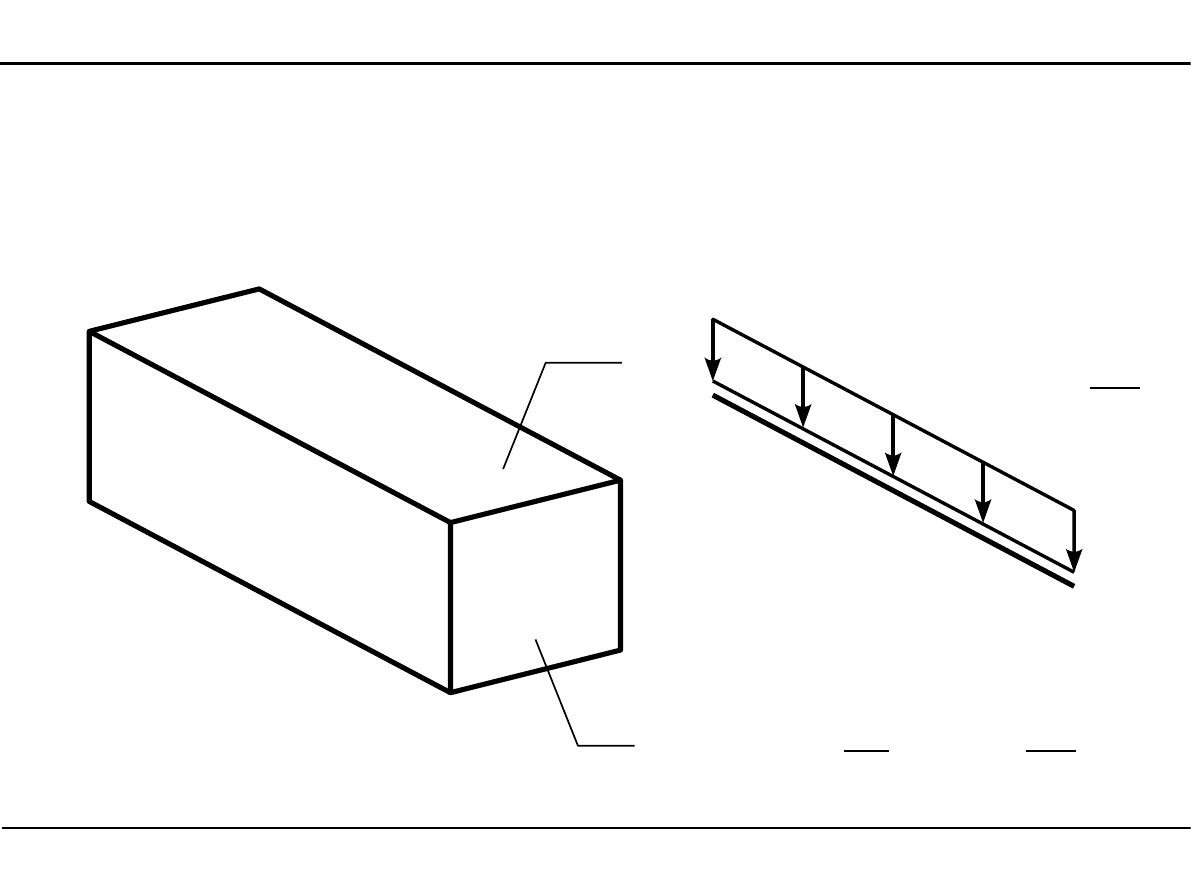
Obciążenie ciągłe równomiernie rozłożone prostopadłe do osi pręta

Ciężar własny - siła ciężkości działająca

na jednostkę objętości.

Wyrażony w N/m

3

. Najczęściej używaną

jednostką jest kN/m

3

.



[

kN

m

3

]

q=⋅A

γ

A

A - pole powierzchni przekroju

pręta.

q

[

N

m

3

]

⋅

[

m

2

]

=

[

kN

m

]

Dr inż. Janusz Dębiński

33

5. Analiza statyczna płaskich układów prętowych

5.3. Obciążenia prętów

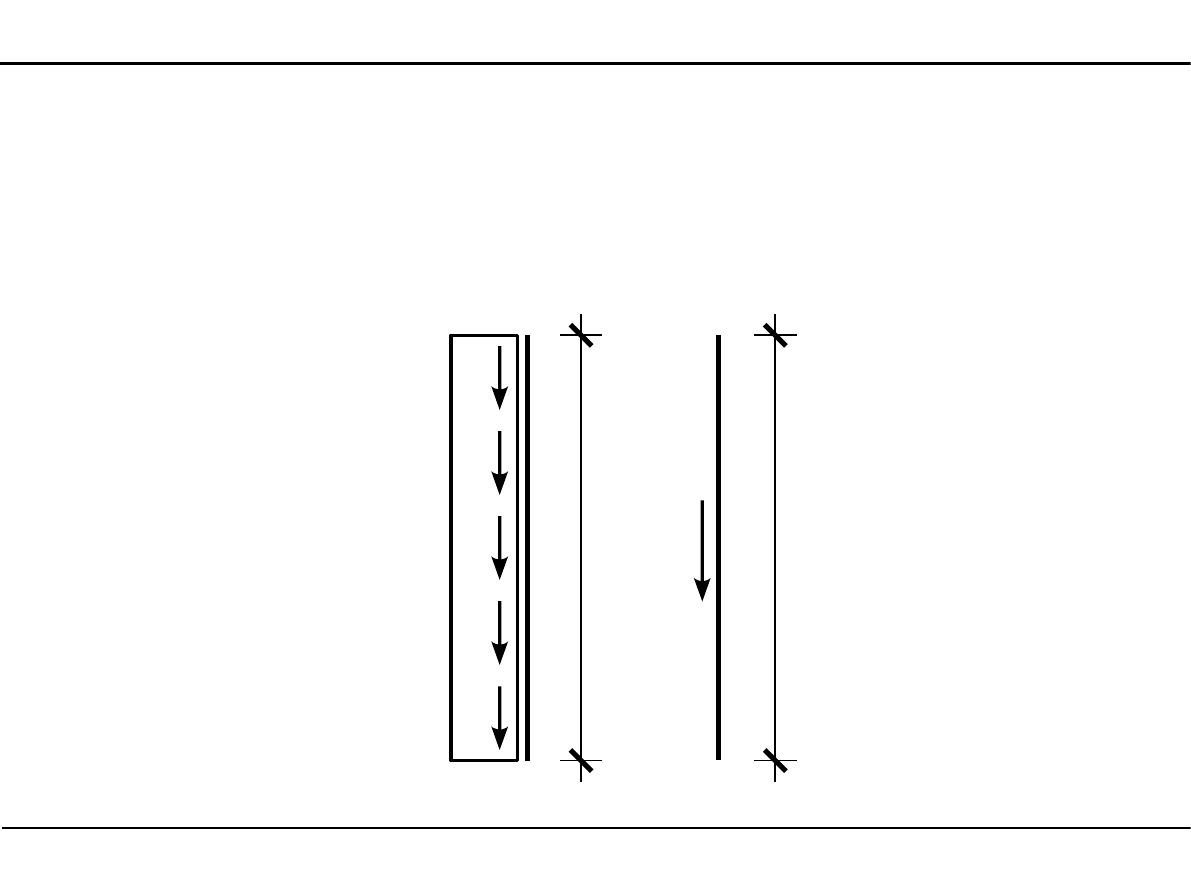
Obciążenie ciągłe równomiernie rozłożone równoległe do osi pręta

Jednostką tego obciążenia jest N/m, w niniejszym kursie Mechaniki ogólnej będziemy

używać kN/m.

L

h

L

h∙L

Dr inż. Janusz Dębiński

34

5. Analiza statyczna płaskich układów prętowych

5.3. Obciążenia prętów

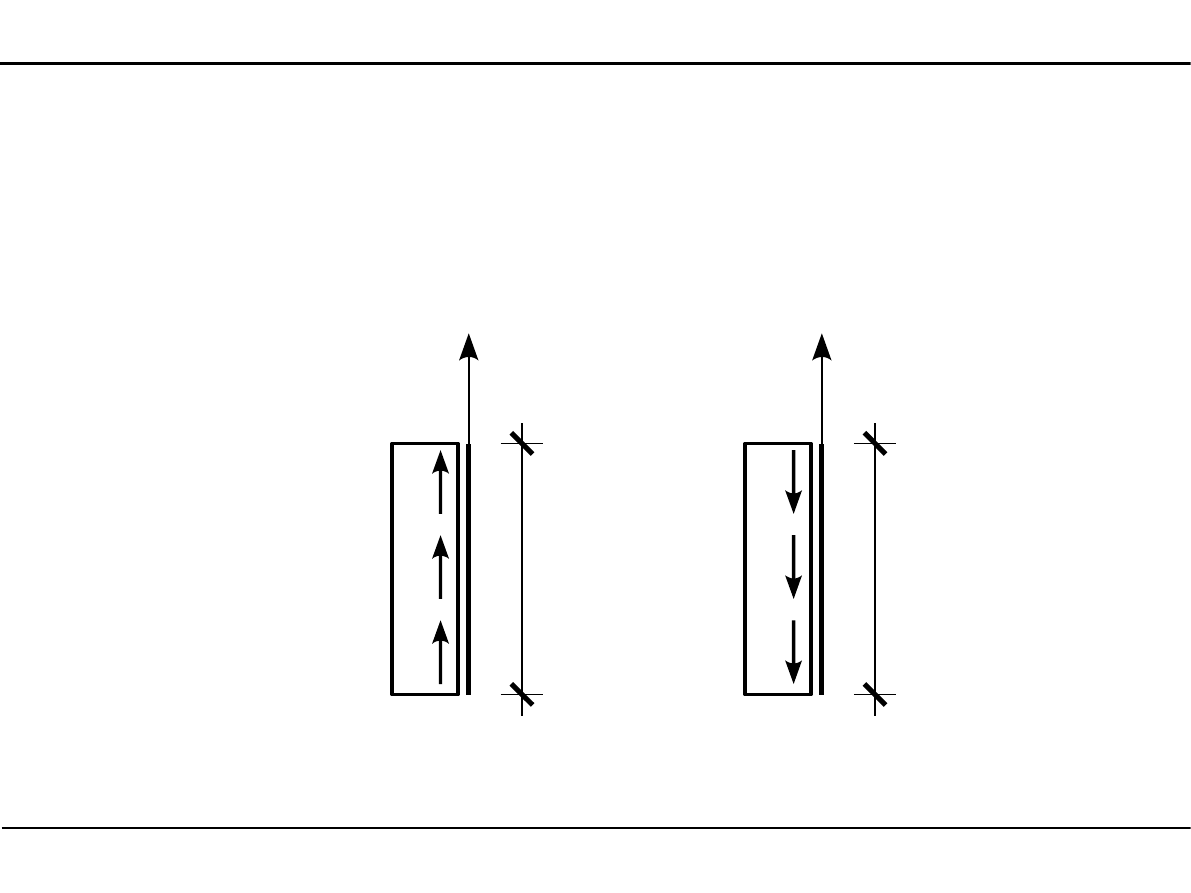
Obciążenie ciągłe równomiernie rozłożone równoległe do osi pręta

Dodatnie obciążenie h będzie działało zgodnie ze zwrotem osi X.

x

X

h > 0

x

X

h < 0

Dr inż. Janusz Dębiński

35

5. Analiza statyczna płaskich układów prętowych

5.3. Obciążenia prętów

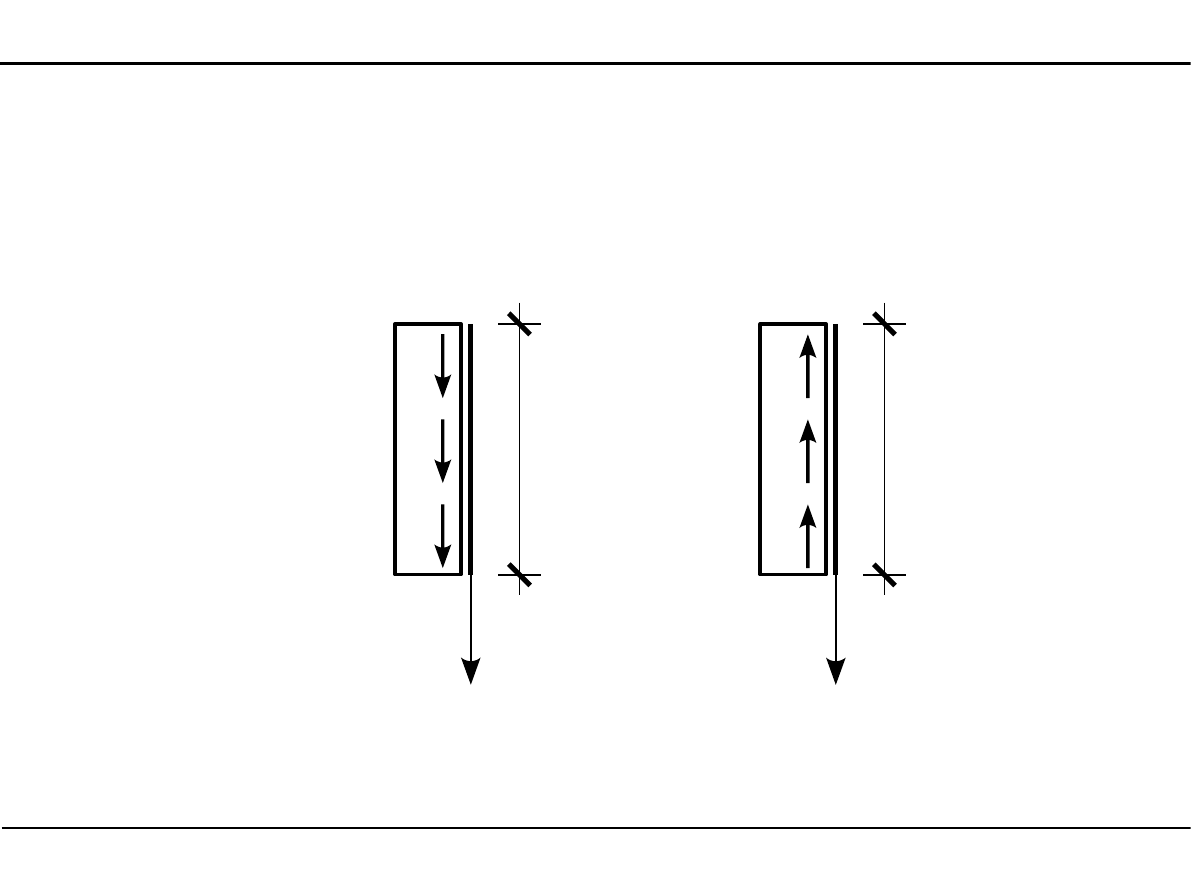
Obciążenie ciągłe równomiernie rozłożone równoległe do osi pręta

Dodatnie obciążenie h będzie działało zgodnie ze zwrotem osi X.

x

X

h > 0

x

X

h < 0

Dr inż. Janusz Dębiński

36

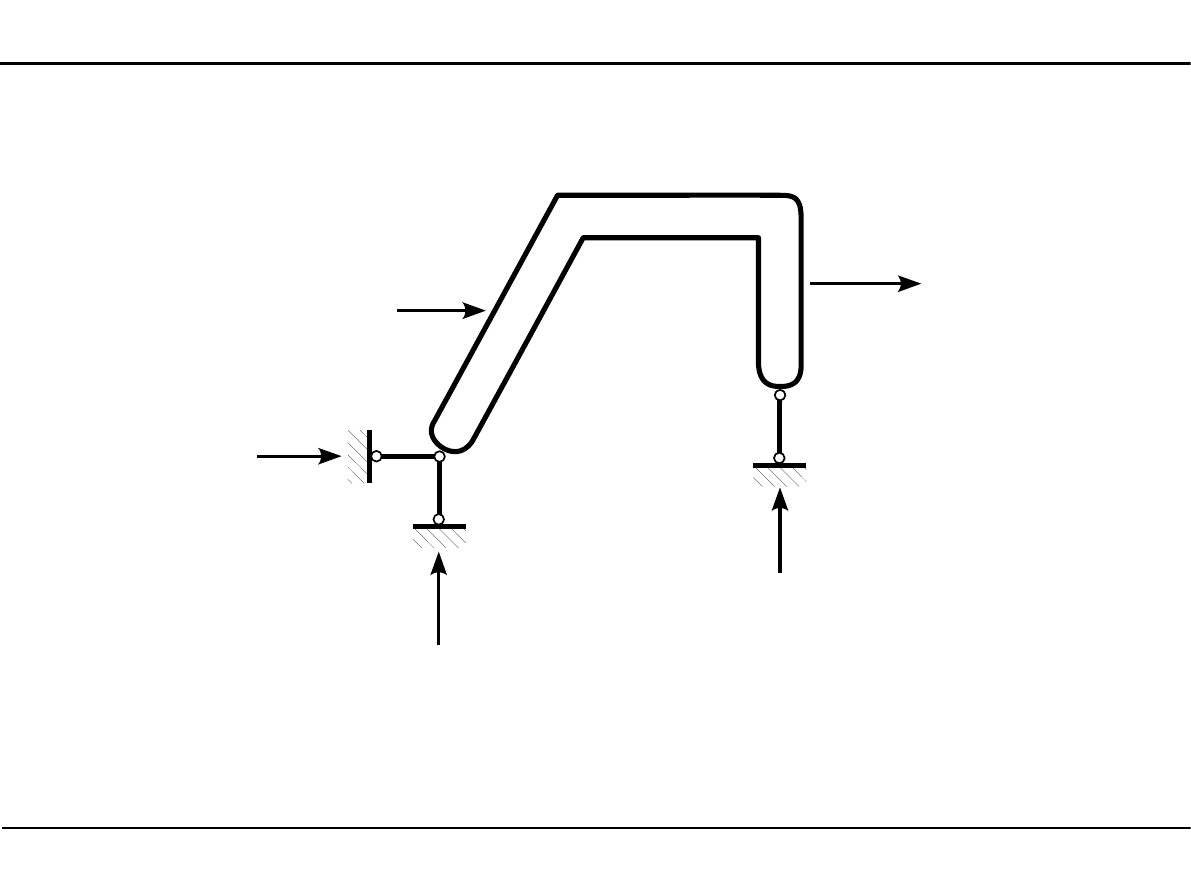
5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

I

1

2

3

P

1

P

2

R

1

R

2

R

3

Rama płaska znajduje się w równowadze.

Dr inż. Janusz Dębiński

37

5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

P

2

R

1

I

1

2

R

2

P

1

I

3

R

3

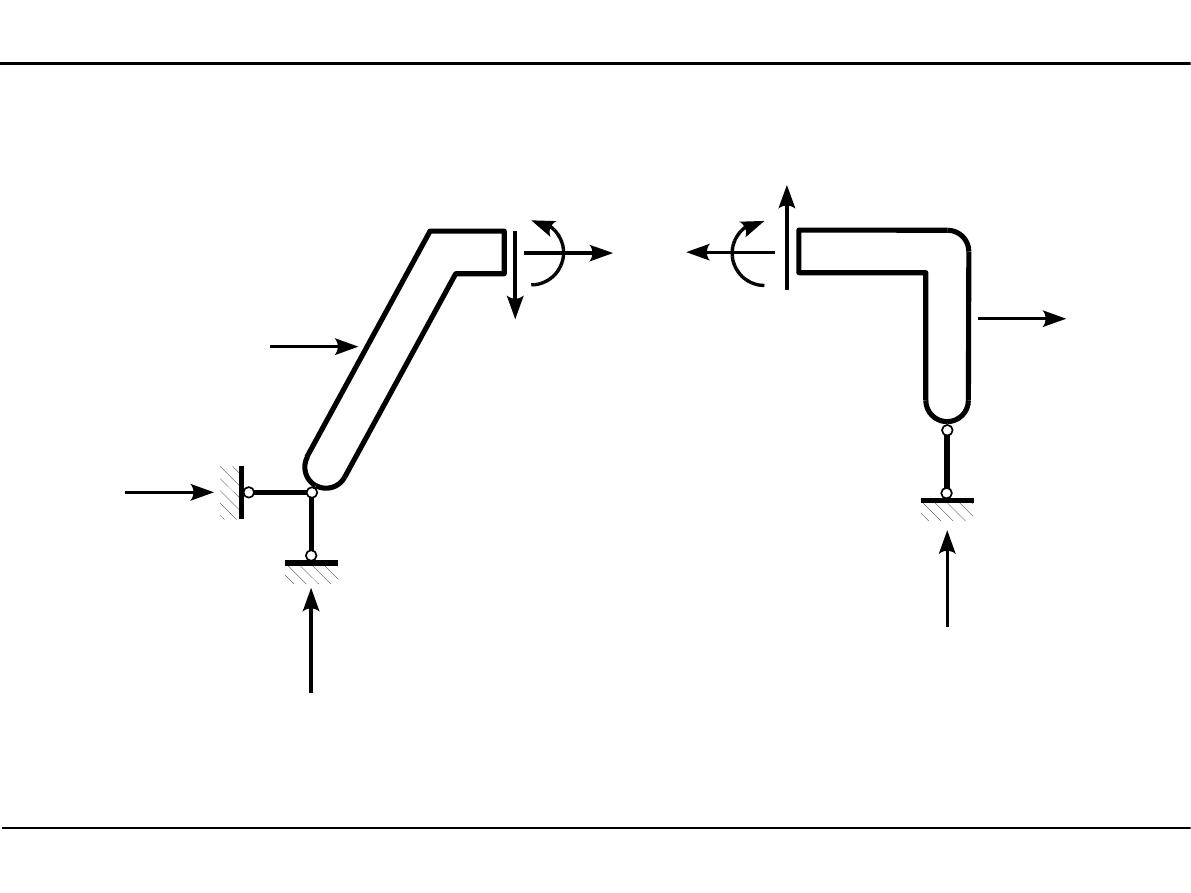
N

N

N - siła normalna

T

T

T - siła poprzeczna (tnąca)

M

M

M - moment zginający

Dr inż. Janusz Dębiński

38

5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

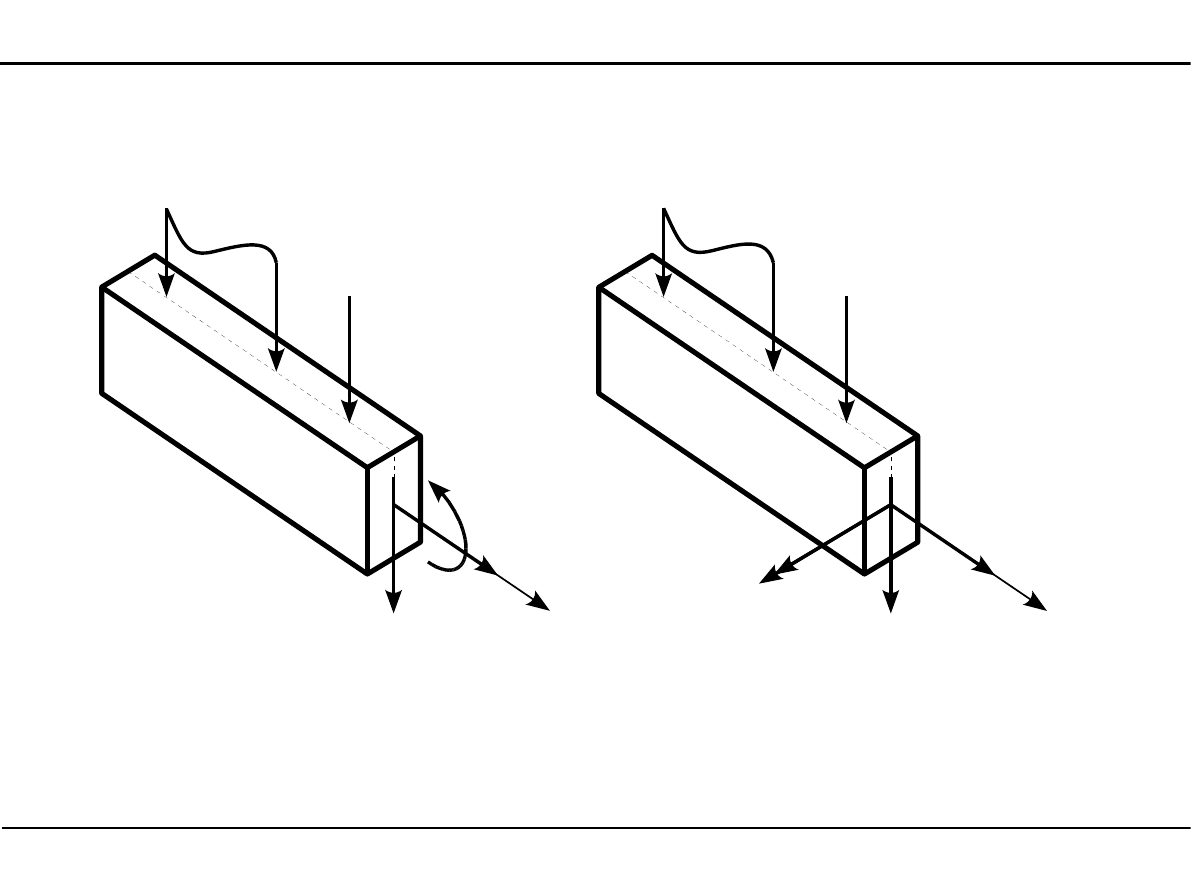
X

q(x)

P

N

T

M

P

X

N

T

q(x)

M

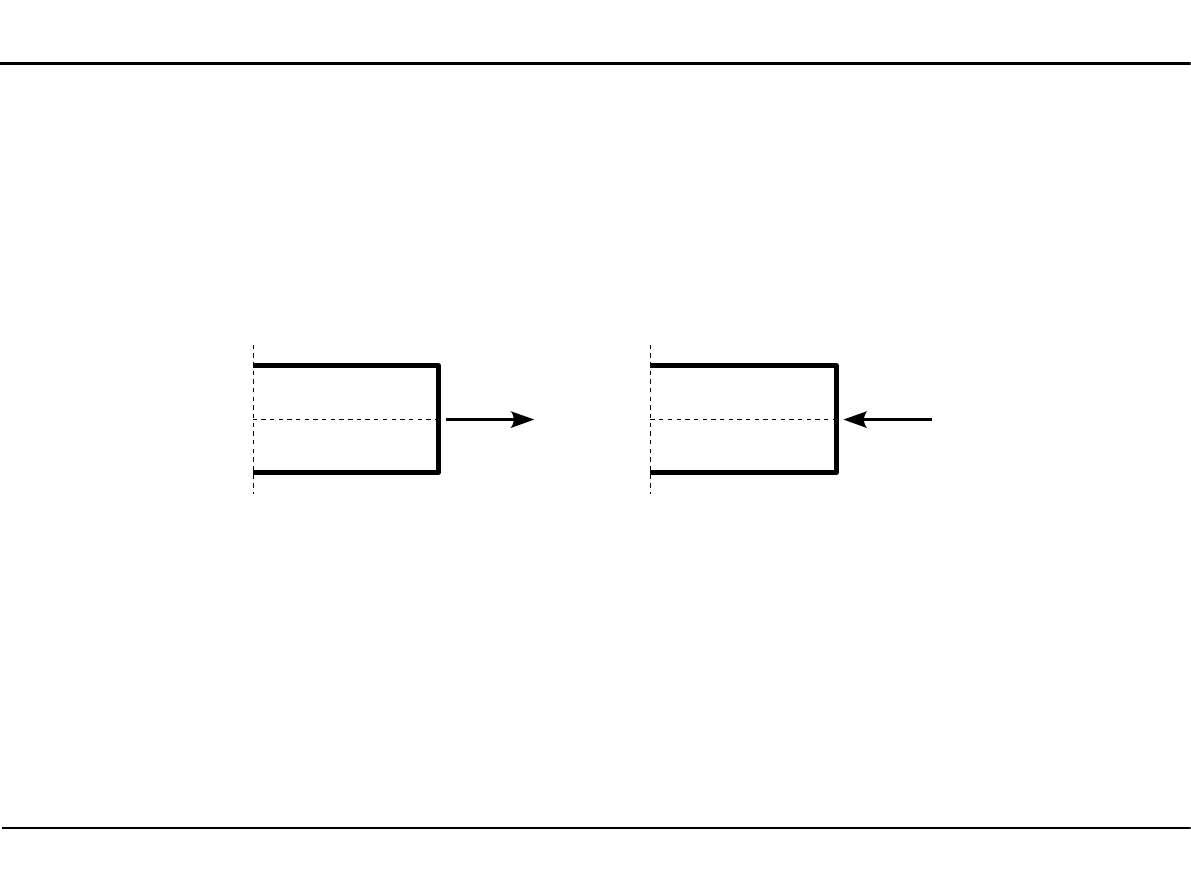
Dr inż. Janusz Dębiński

39

5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

Zasady znakowania sił przekrojowych

Siła normalna jest dodatnia, jeżeli rozciąga ona pręt.

N>0

N<0

Dr inż. Janusz Dębiński

40

5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

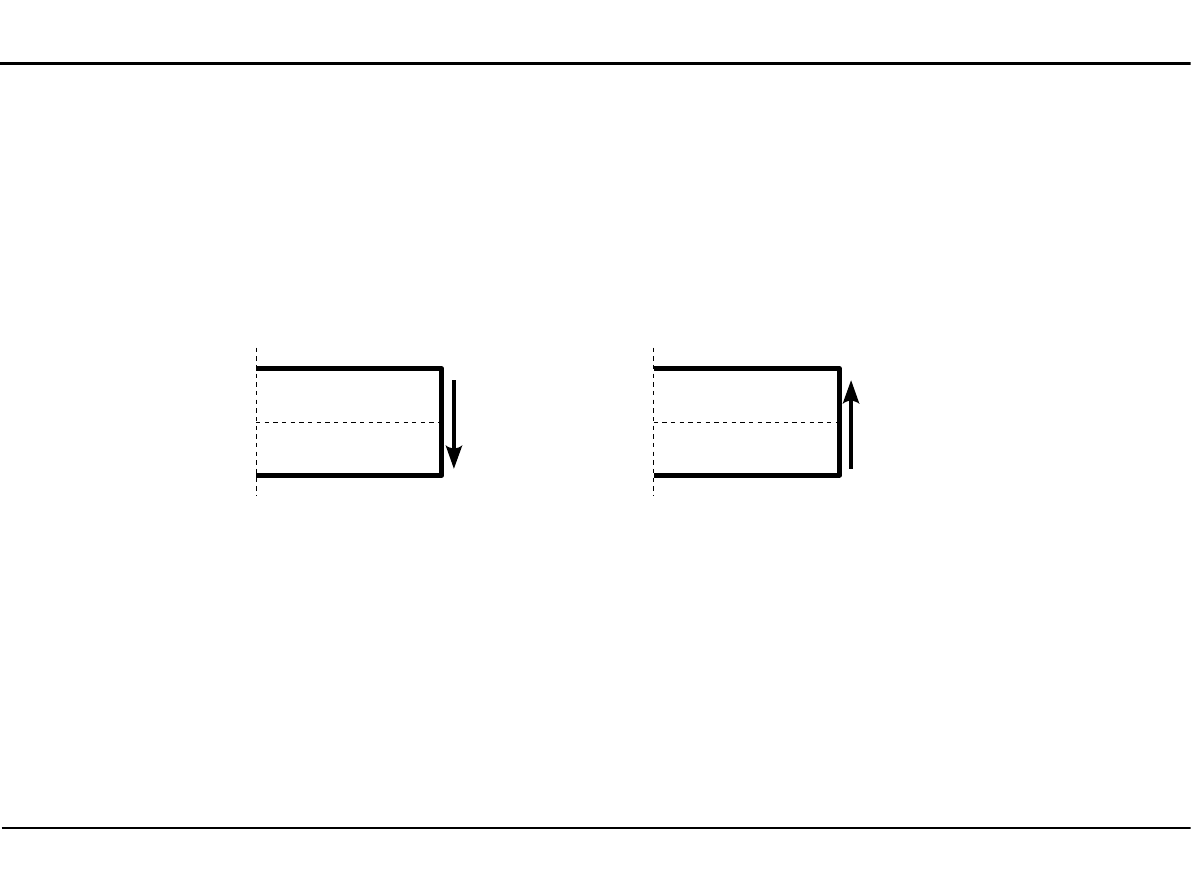
Zasady znakowania sił przekrojowych

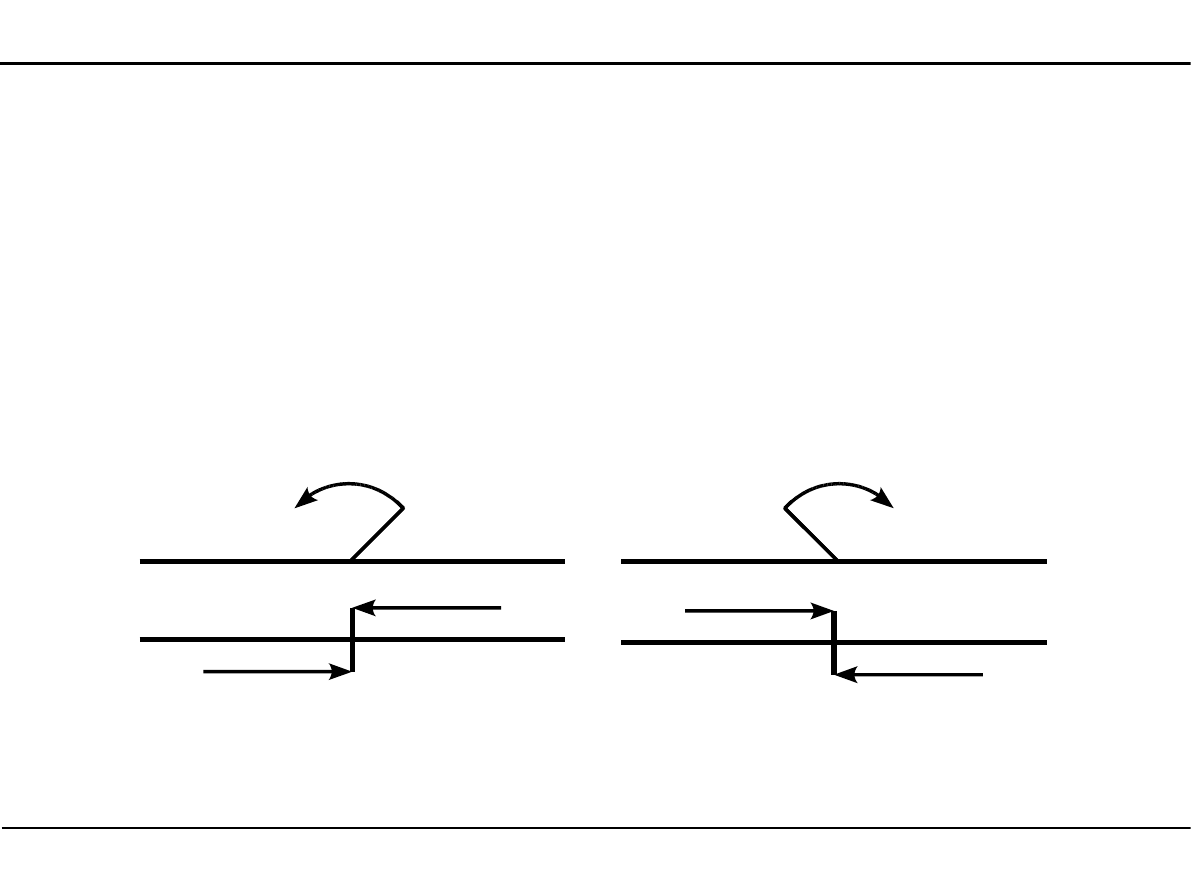
Siła poprzeczna jest dodatnia, jeżeli kręci ona odciętą częścią pręta

zgodnie z ruchem wskazówek zegara.

T>0

T<0

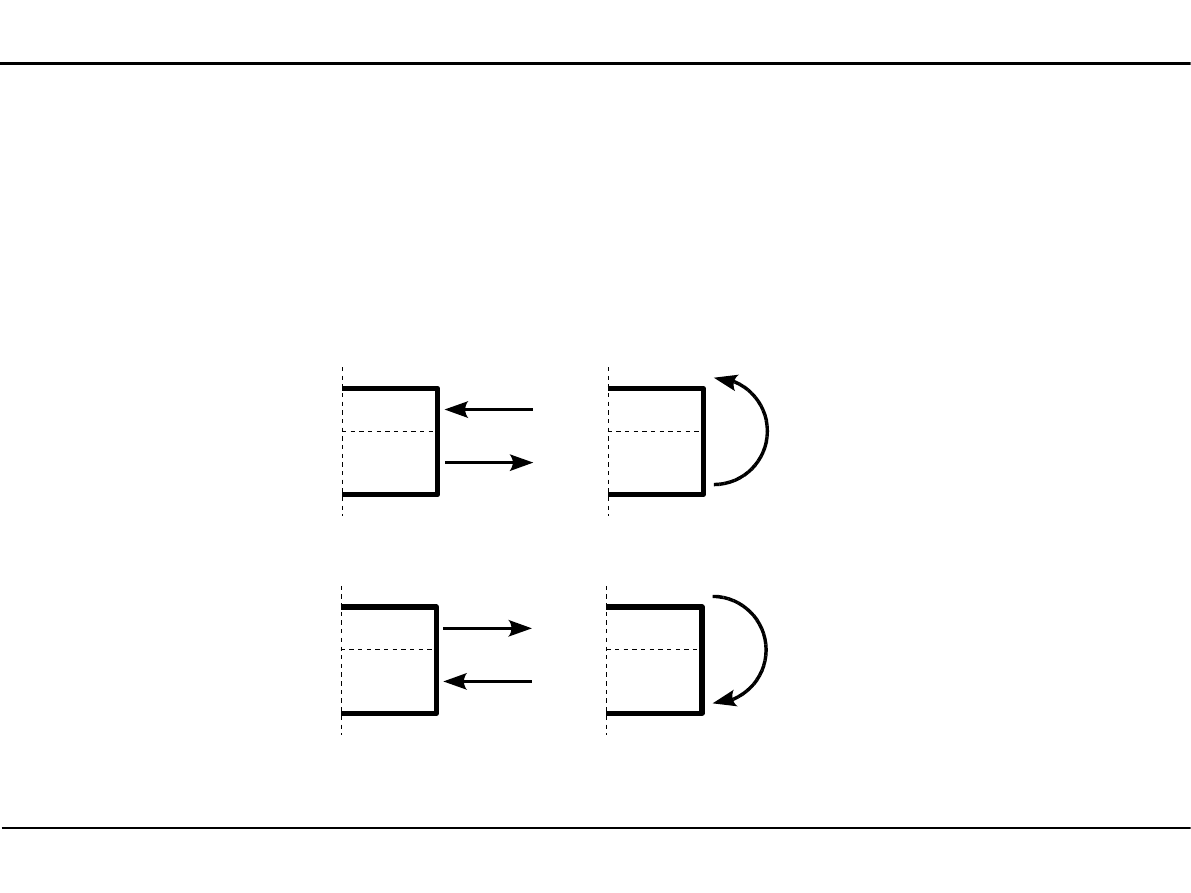
Dr inż. Janusz Dębiński

41

5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

Zasady znakowania sił przekrojowych

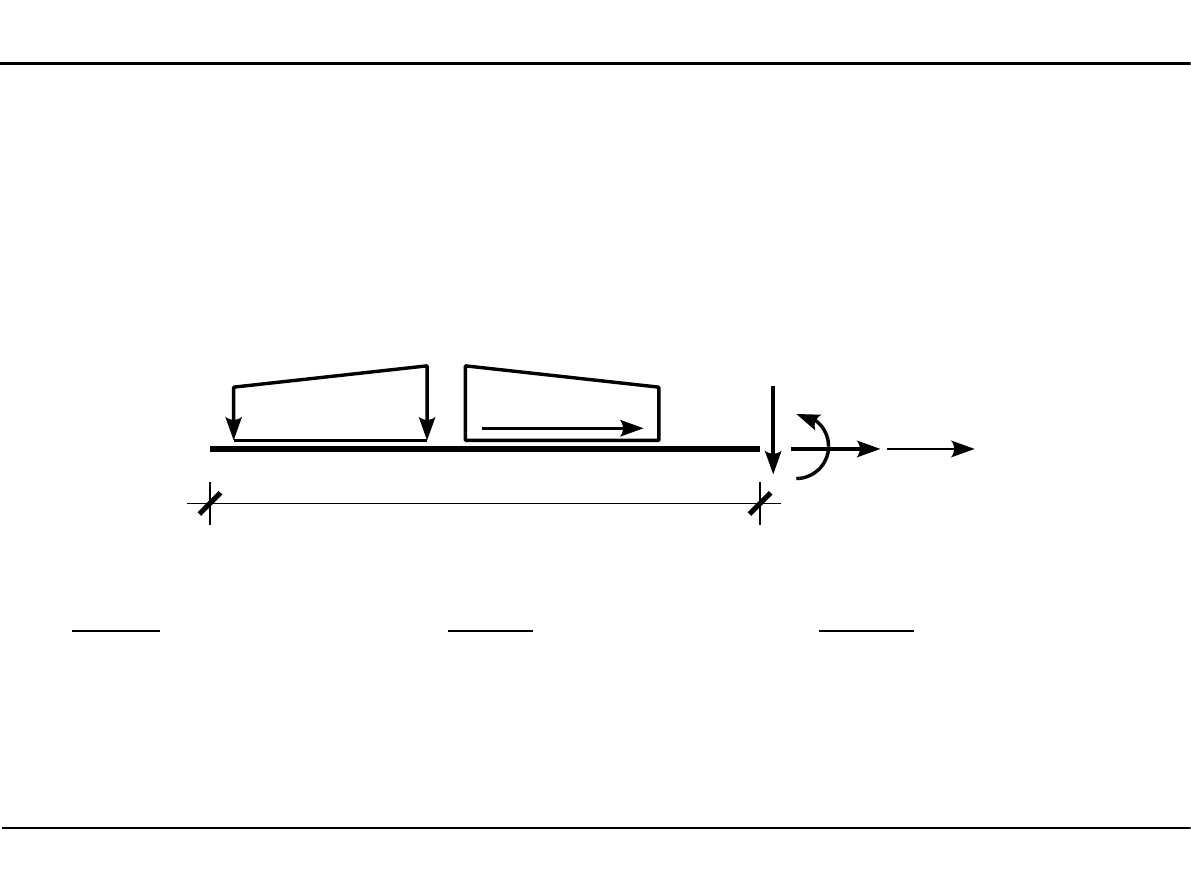
Moment zginający jest dodatni, jeżeli rozciąga on dolną część pręta.

W przypadku prętów pionowych, jako dolną część przyjmiemy prawą część pręta.

P

P

M>0

P

P

M>0

Dr inż. Janusz Dębiński

42

5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

Równania różniczkowe równowagi

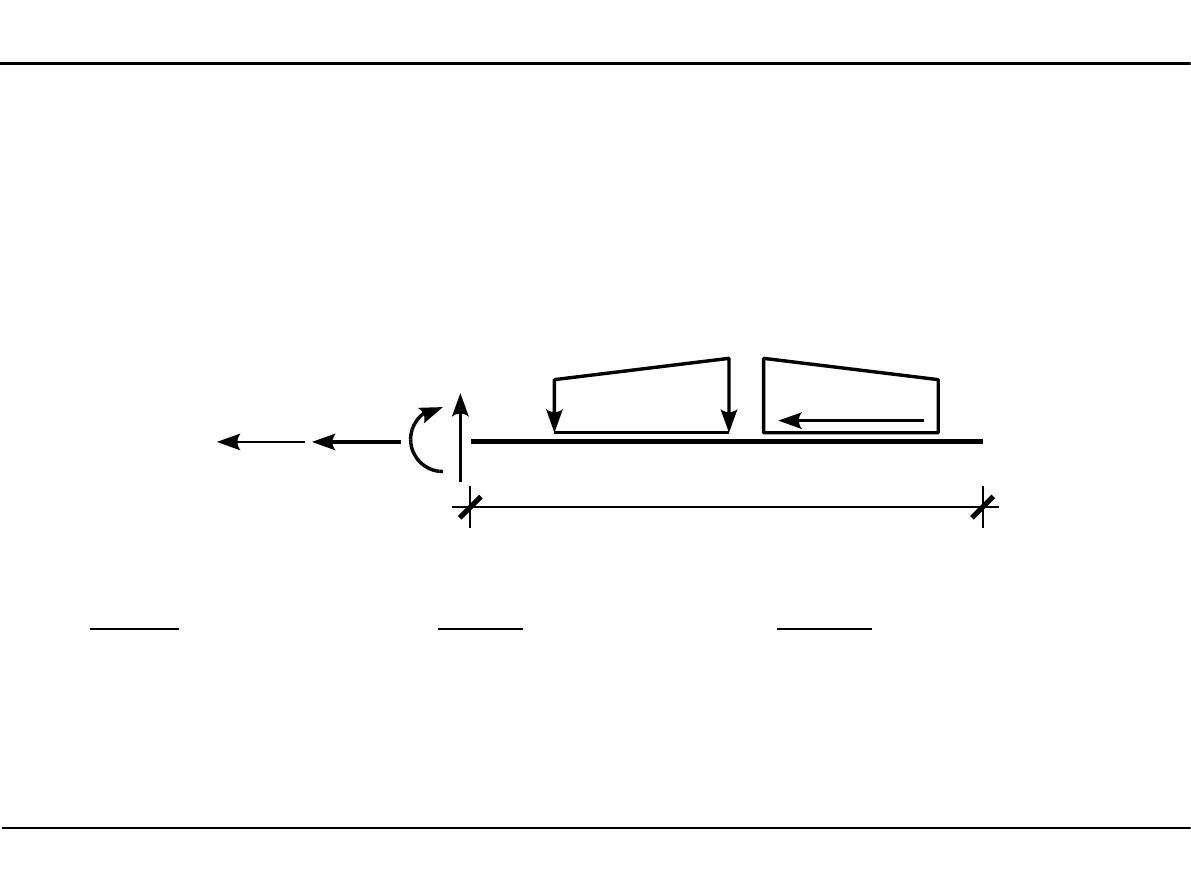
Pomiędzy funkcjami q(x) i h(x), a funkcjami sił przekrojowych istnieją zależności,

które nazywamy równaniami różniczkowymi równowagi.

x

q(x)

h(x)

X

N(x)

T(x)

M(x)

dN



x



dx

=

N '



x



=−

h



x



dT



x



dx

=

T '



x



=−

q



x



dM



x



dx

=

M '



x



=

T



x



Dr inż. Janusz Dębiński

43

5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

Równania różniczkowe równowagi

Równania różniczkowe równowagi dla osi X zwróconej w lewo.

x

q(x)

h(x)

X

N(x)

T(x)

M(x)

dN



x



dx

=

N '



x



=−

h



x



dT



x



dx

=

T '



x



=

q



x



dM



x



dx

=

M '



x



=−

T



x



Dr inż. Janusz Dębiński

44

5. Analiza statyczna płaskich układów prętowych

5.4. Siły przekrojowe

Wykresy sił przekrojowych

Wartości sił przekrojowych zaznaczamy na ich wykresach. Stosujemy wtedy następujące zasady:

w kratownicach na poszczególnych prętach piszemy wartość bezwzględną siły normalnej,

a strzałką rysowaną od węzła zaznaczamy siłę normalną rozciągającą,

strzałką do węzła siłę normalną ściskającą

w belkach i ramach płaskich wykresy rysujemy na ich osiach

na wykresach siły normalnej i poprzecznej oznaczamy ich wartości dodatnie oraz ujemne

dodatnie wartości siły normalnej i poprzecznej w belkach i łukach płaskich rysujemy na górze

w ramach płaskich dodatnie wartości siły normalnej i poprzecznej rysujemy tak,

aby wykresy były czytelnie i jak najmniej nakładały się na siebie

wykres momentu zginającego rysujemy po stronie rozciąganej

i wpisujemy jego wartość bezwzględną.