1 |
S t r o n a
Politechnika Warszawska
Samochody i Maszyny Robocze
Instytut Pojazdów
Dynamika Pojazdów
Grupa 4.4
Rok akademicki 2011/2012
Janusz Skaczkowski
Rafał Skórzyński
Wyznaczanie częstości drgań własnych
samochodu Łada Samara typ 2109
Prowadzący:
prof. dr hab. inż. Wiesław Grzesikiewicz
Warszawa 2012
2 |
S t r o n a
1. Samochód badawczy
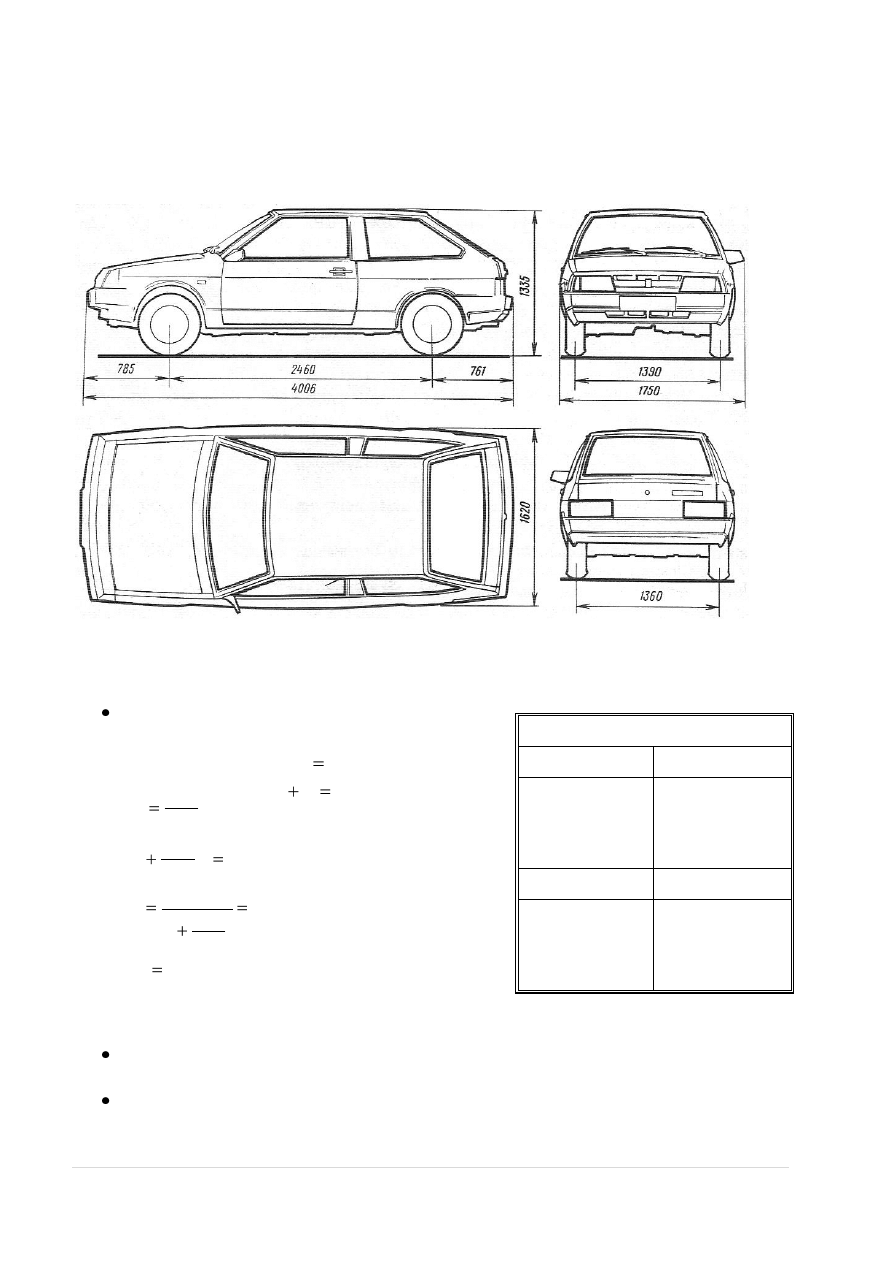
Modelem badań będzie samochód marki Łada
Rys. 1. Podstawowe wymiary obiektu badawczego
położenie środka masy C:
12
2
1
1
2
l
l
l
0,6l
0,4l
2460
l
45
,
0
0,55
l
l
45
,
0
0,55
l
1
1
1
2
]
[
1353
l
]
[
1107
)
45
,
0
55
,
0
1
(
2460
l
2
1
mm
mm
Masa przypadająca na oś przednią:
m
p
= 55% · 920 = 506 [kg]
Masa przypadająca na oś tylną:
m
t
= 45% · 920 = 414[kg]
Dane techniczne:
masa całkowita: m = 920
[kg]
rozkład mas:
- przód
m
p
= 55
[%]
- tył
m
t
= 45
[%]
rozstaw osi:
l
12
= 2460 [mm]
rozstaw kół:
- przód
b
p
= 1390 [mm]
- tył:
b
t
= 1360 [mm]
3 |
S t r o n a
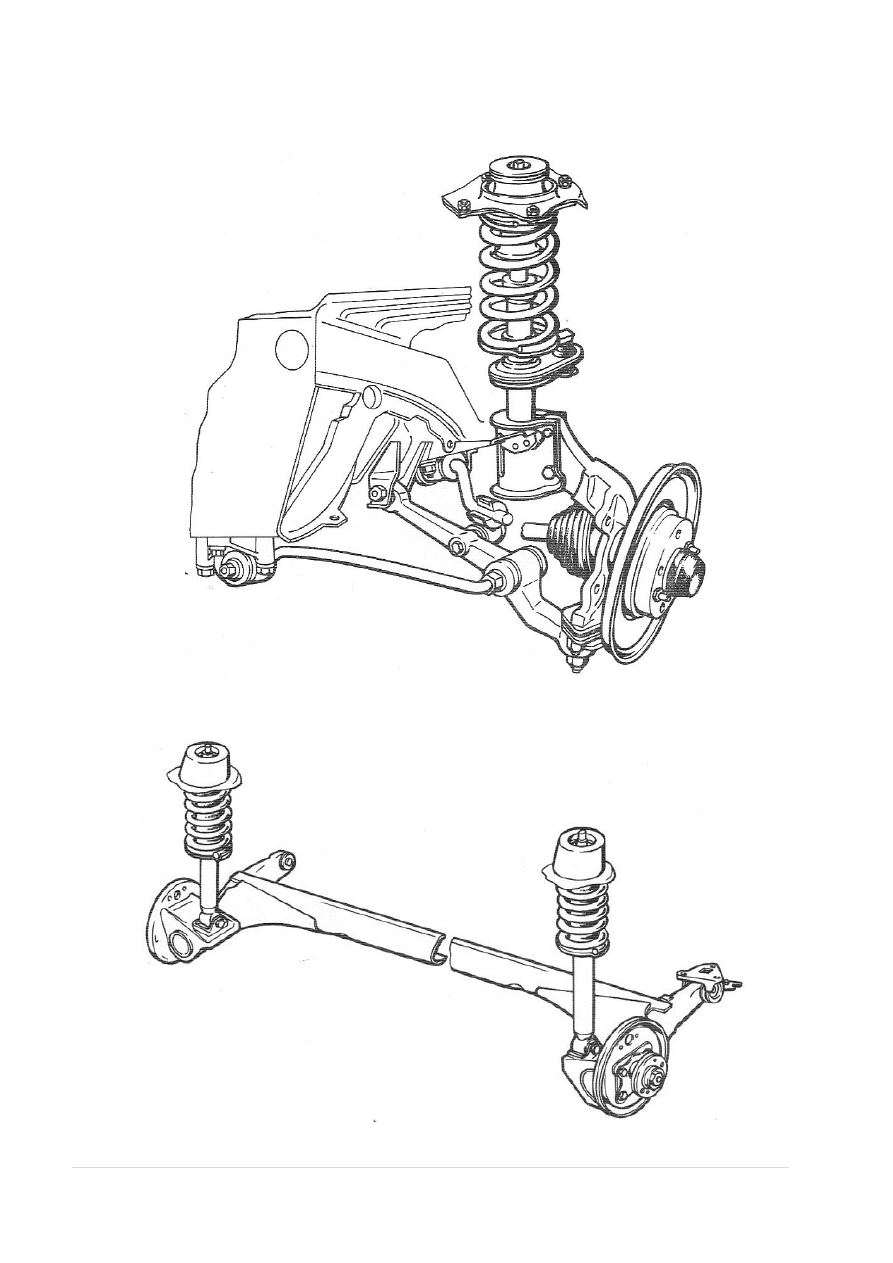
1.1. Zawieszenie przednie
Rys. 2. Zawieszenie przednie
1.2. Zawieszenie tylne
Rys.3. Zawieszenie tylne
4 |
S t r o n a
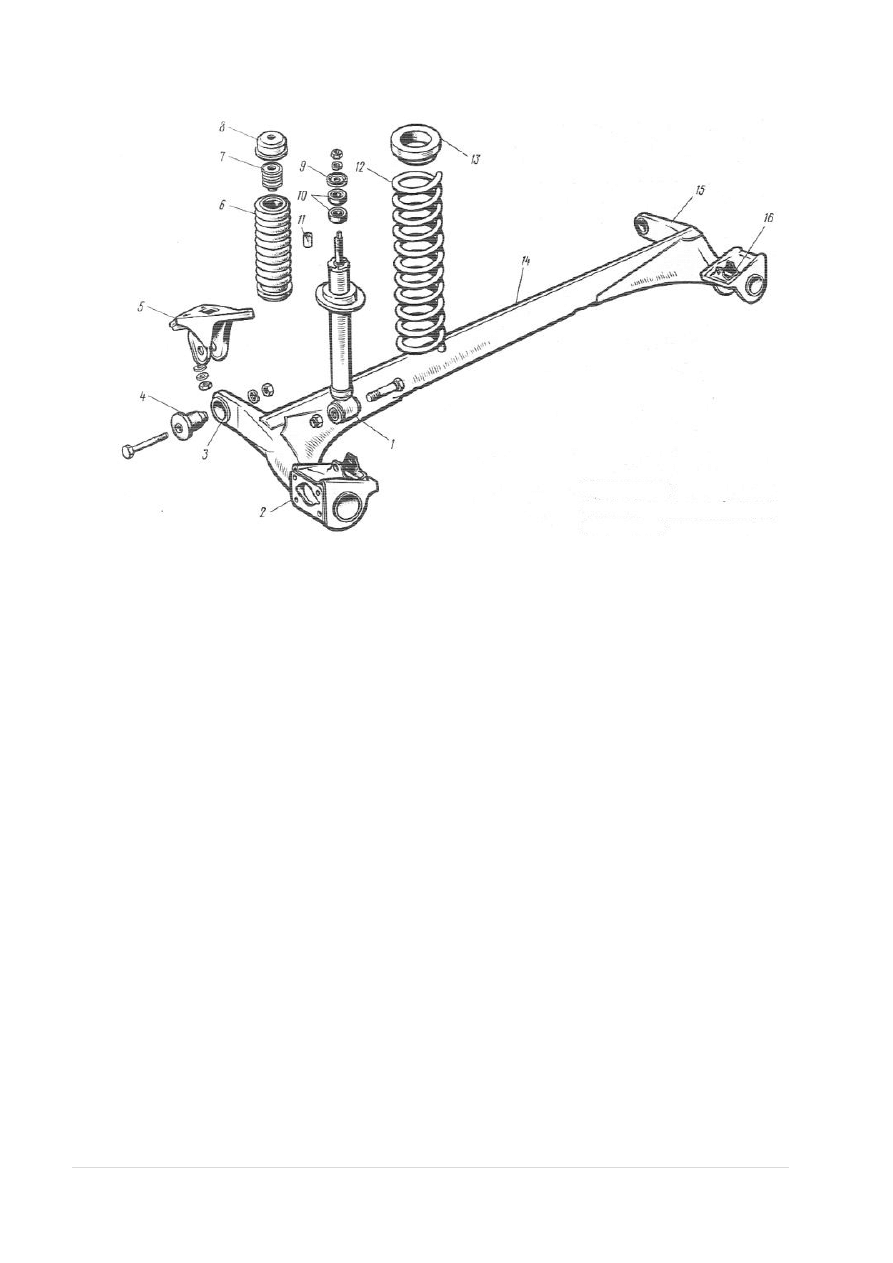
Rys.4. Zawieszenie tylne
5 |
S t r o n a
2. Model obliczeniowy
Jako model obliczeniowy przyjęto płytę prostokątną o masie m i pomijalnie małej grubości
(rys. 4). Zawieszono ją w narożach na czterech sprężynach. Model jest obdarzony trzema
stopniami swobody – przemieszczeniem wzdłuż osi z oraz obrotami wokół osi x i y.
Rys. 5. Model pojazdu o trzech stopniach swobody
6 |
S t r o n a
3. Obliczenia sztywności zawieszenia
Sztywność sprężyn rzeczywistych oblicza się na podstawie porównania ich energii
potencjalnej z energią potencjalną sprężyn teoretycznych. W tym celu wprowadzono w miejsce
koła teoretyczną sprężynę, której sztywność wyliczono z założonej wstępnie częstości drgań
własnych nadwozia f = 1 [Hz] (częstość taka zapewnienia komfort pasażerom podczas jazdy).
3.1. Sztywność zawieszenia kół w modelu teoretycznym
Rys. 6. Schematy do obliczeń sztywności sprężyn
Częstość drgań własnych ciała wyraża się wzorem:
Stąd wynika zależność na sztywność zawieszenia:
gdzie:
m – masa pojazdu przypadająca na jedno koło (odpowiednio osi przedniej lub tylnej)
f – częstotliwość drgań własnych nadwozia (1 [Hz])
Otrzymano:
dla zawieszenia przedniego:
dla zawieszenia tylnego:
7 |
S t r o n a
3.2. Obliczenia sztywności rzeczywistych elementów zawieszenia
3.2.1. Sztywność sprężyn zawieszenia przedniego
długość wahacza:
l
w
= 0,32 [m]
odległość mocowania kolumny od zwrotnicy:
l
a
= 0,20 [m]
kąt odchylenia kolumny:
α = 4 [°]
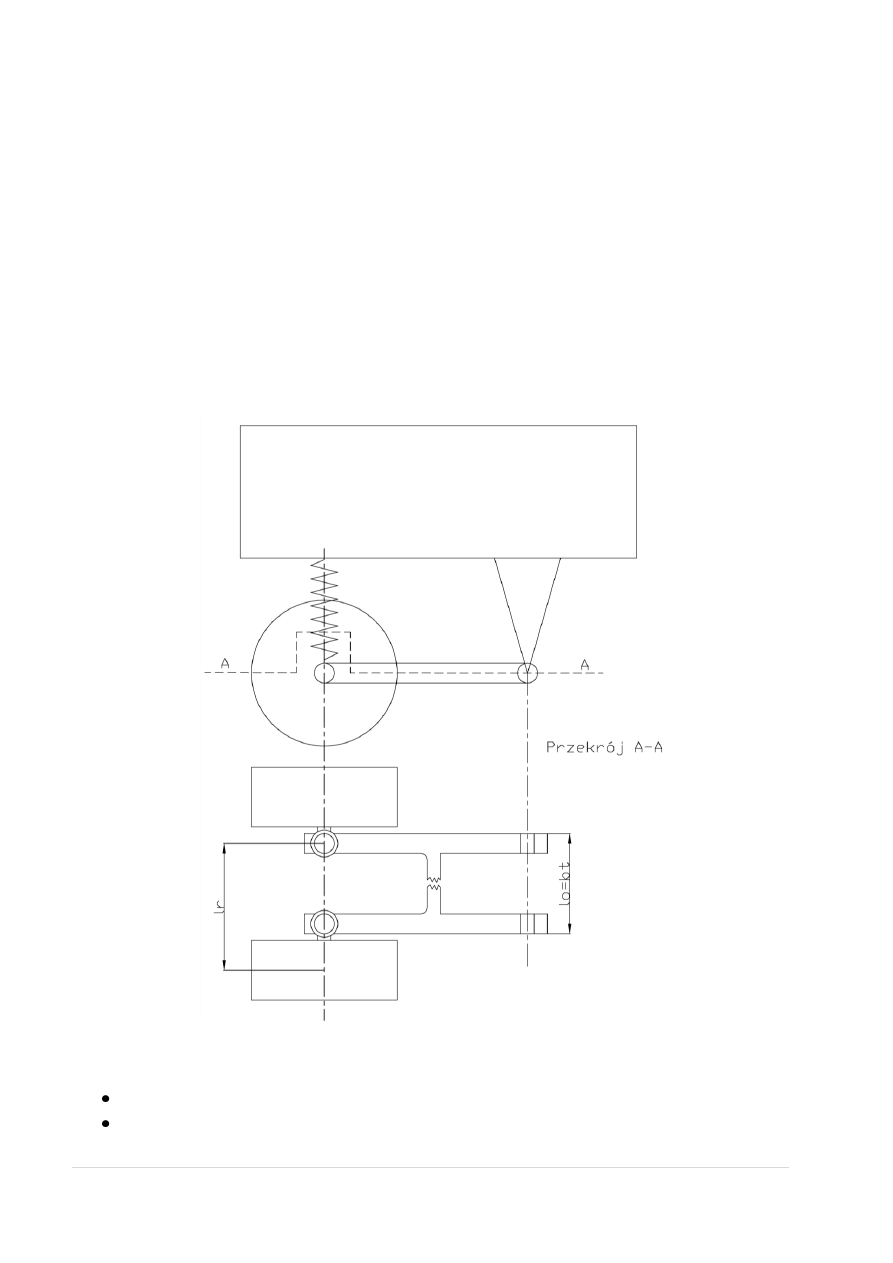
Rys. 7. Schemat kinematyczny zawieszenia osi przedniej samochodu Łada
Kolumna zamocowana jest bezpośrednio do zwrotnicy w punkcie A (rys. 7). Dlatego skok
koła przedniego z
kp
jest równy skokowi punktu A do punktu A’. Ugięcie sprężyny z
sp
jest więc
różnicą odległości AB i A’B.
8 |
S t r o n a
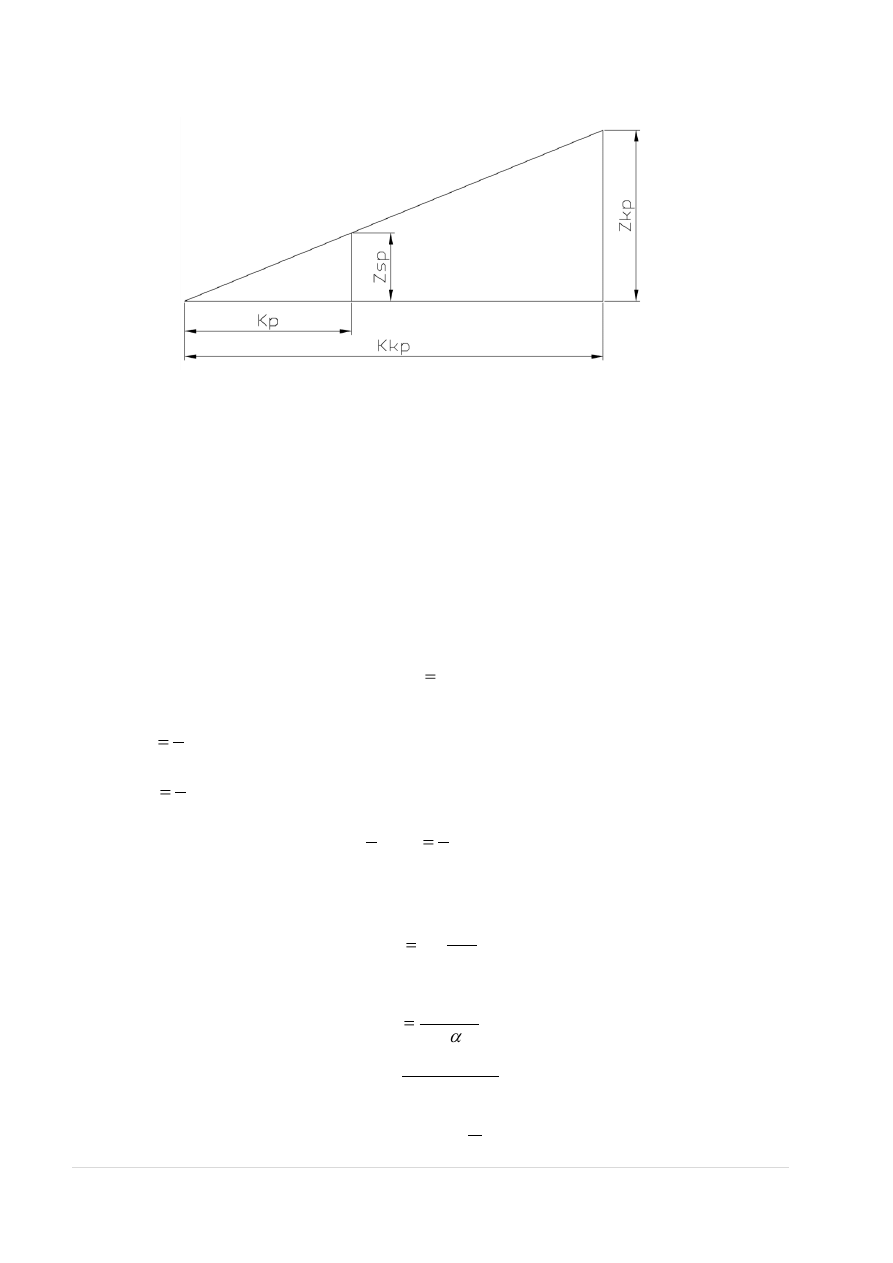
Rys.8. Zależności geometryczne przy ugięciu zawieszenia przedniego
k
p
– ugięcie przedniej sprężyny
k
kp
– ugięcie przedniej sprężyny teoretycznej
z
sp
– ugięcie przedniej sprężyny
z
kp
– ugięcie przedniej sprężyny teoretycznej
Aby obliczyć sztywność sprężyny należy założyć, że energia potencjalna modelu
zawieszenia jest równa energii potencjalnej sprężyny rzeczywistego układu:
kp
sp
E
E
gdzie:
2
sp
p
sp
z
k
2
1
E
- energia potencjalna dla sprężyny przedniej
2
kp
kp
kp
z
k
2
1
E
- energia potencjalna dla teoretycznej sprężyny przedniej
2
kp
kp
2
sp
p
z
k
2
1
z
k
2
1
Stąd sztywność sprężyny rzeczywistej przedniego zawieszenia określa wzór:
2
sp
2
kp
kp
p
z
z
k
k
Ostatecznie:
2
kp
p
)
(
c
k
k
os
9 |
S t r o n a
3.2.2. Sztywność sprężyn zawieszenia tylnego
Badany pojazd ma zawieszenie niezależne tylnej osi w postaci belki skrętnej zawieszonej na
sprężynach śrubowych i tłumikach wiskotycznych (patrz: punkt 1.2). Zespół resorujący jest
zamocowany do nadwozia obrotowo, a do belki skrętnej wahliwie. Aby uprościć analizę, zespół
resorujący został sprowadzony do modelu sprężyny śrubowej. Prowadzenie punktu zamocowania
piasty koła przyjęto jako pionowe, ponieważ odchylenia toru ugięcia zespołu resorującego
zamocowanego wahliwie są niewielkie.
Na rys. 8 przedstawiono schemat kinematyczny tylnego zawieszenia. Zespół resorujący
znajduje się bliżej osi pojazdu niż piasty kół, co zostanie uwzględnione podczas obliczania
przemieszczeń. Przyjęto założenie, że przy niesymetrycznym wymuszeniu (czyli działającym
tylko na jedno koło, np. w wypadku napotkania wyboju) i wystąpieniu skoku jednego z kół, belka
skrętna skręca się wokół własnej osi. Sztywność zespołu resorującego (lewego i prawego)
policzono zakładając równoczesne ugięcie obu kół osi.
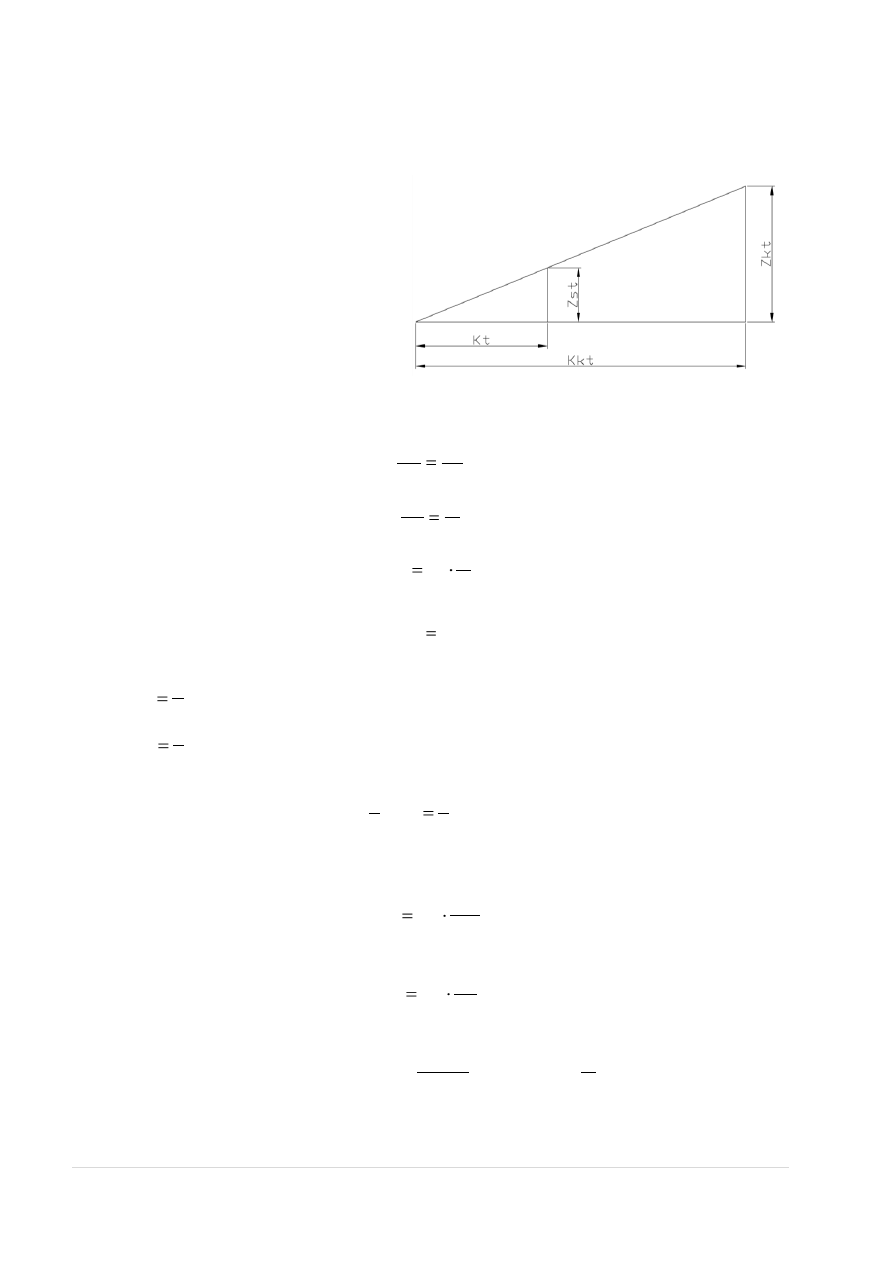
Rys. 9. Schemat kinematyczny tylnego zawieszenia
długość osi :
l
o
= b
t
= 1,360 [m]
odległość mocowania zespołu resorującego od przeciwległego koła: l
r
=1,22 [m]
10 |
S t r o n a
Strzałki ugięć leżą w tej samej płaszczyźnie, dzięki czemu ugięcie z
st
można obliczyć
korzystając z twierdzenia Talesa.
k
t
–ugięcie tylnej sprężyny rzeczywistej
k
kt
– ugięcie tylnej sprężyny teoretycznej
z
st
– ugięcie tylnej sprężyny rzeczywistej
z
kt
– ugięcie tylnej sprężyny teoretycznej
Rys.10. Zależności geometryczne przy ugięciu zawieszenia tylnego
r
l
st
o
kt
z
l
z
r
o
l
l
st
kt
z
z
o
r
kt
st
l
l
z
z
Należy przyrównać energie potencjalne:
kt
st
E
E
gdzie:
2
st
t
st
z
k
2
1
E
- energia potencjalna tylnej sprężyny rzeczywistej
2
kt
kt
kt
z
k
2
1
E
- energia potencjalna tylnej sprężyny teoretycznej
2
kt
kt
2
st
t
z
k
2
1
z
k
2
1
Stąd sztywność sprężyny rzeczywistej określa wzór:
2
st
2
kt
kt
t
z
z
k
k
Ostatecznie:
2
r
2
kt
t
l
l
k
k
o
11 |
S t r o n a
4. Obliczenia przemieszczeń elementów zawieszenia
4.1. Zawieszenie przednie
odległość punktu mocowania kolumny od osi pojazdu:
b
B
= 0,595 [m]
odległość punktu mocowania wahacza od osi pojazdu:
b
C
= 0,49 [m]
odległość osi przedniej od środka ciężkości pojazdu:
l
1
= 1,107 [m]
4.1.1. Prawa strona
Przemieszczenie pionowe charakterystycznych punktów zawieszenia określone jest wzorami:
Stąd skrócenie prawej przedniej sprężyny będzie określone zależnością:
4.1.2. Lewa strona
Skrócenie lewej przedniej sprężyny oblicza się analogicznie, uwzględniając odwrotny
kierunek obrotu nadwozia wokół osi x. Ostatecznie wynosić ono będzie:
12 |
S t r o n a
4.2. Zawieszenie tylne
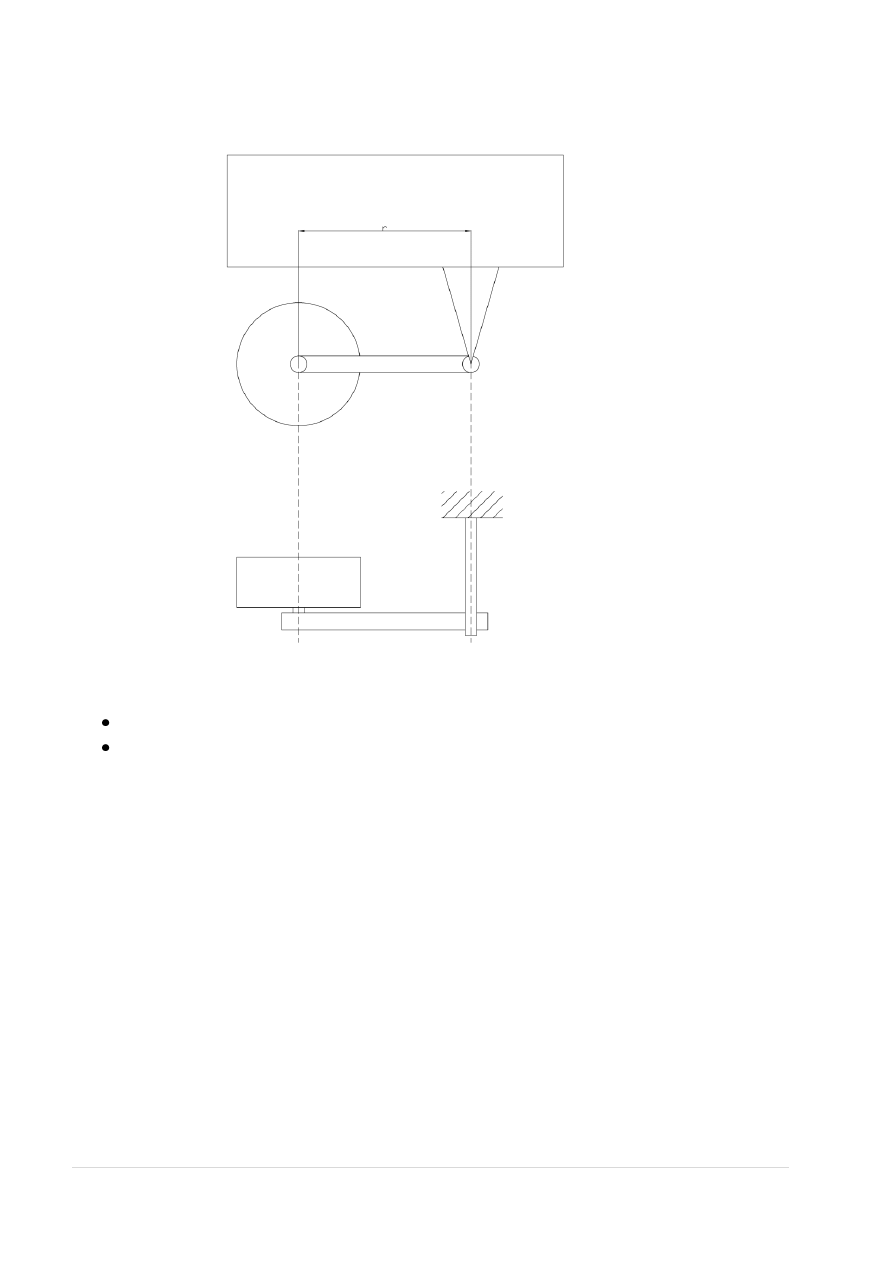
Rys. 9. Oznaczenia wielkości do obliczeń przemieszczeń elementów zawieszenie tylnego
odległość mocowania zespołu resorującego od osi wzdłużnej pojazdu: b
E
= 0,54 [m]
odległość osi tylnej od środka ciężkości pojazdu: l
2
= 1,353 [m]
4.2.1. Prawa strona
Przemieszczenie punktów zawieszenia tylnego pod wpływem ruchów nadwozia:
Stąd ugięcie prawego resoru wyraża zależność:
4.2.2. Lewa strona
Ugięcie lewego zespołu resorujące oblicza się analogicznie:
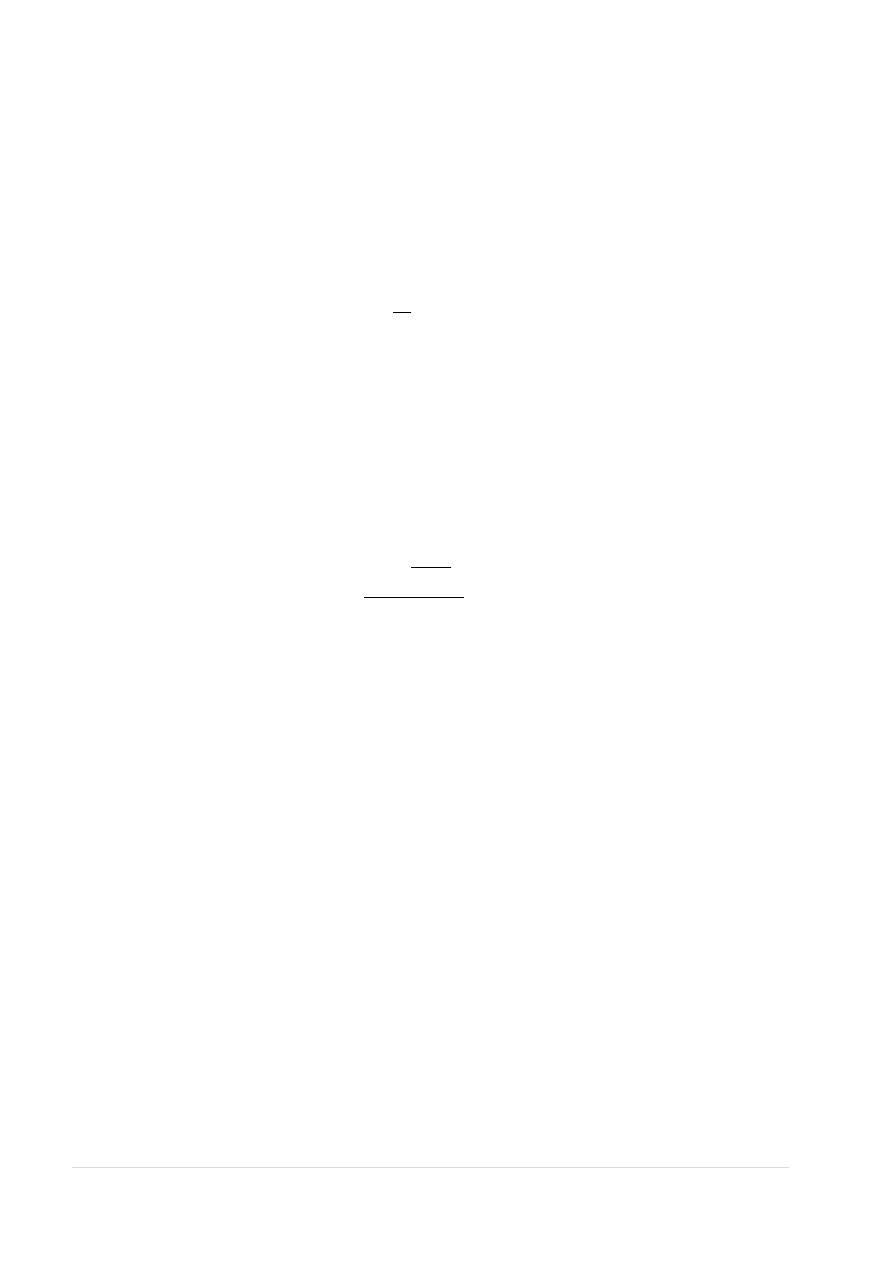
13 |
S t r o n a
5. Obliczenie momentów bezwładności pojazdu
5.1. Moment bezwładności względem osi x (I
x
)
W celu wyznaczenia momentu bezwładności pojazdu względem osi x, samochód
potraktowano jak ciało obrotowe mające promień bezwładności. Ponieważ nie ma możliwości
dokładnego określenia promienia bezwładności (z powodu nieregularności kształtu pojazdu)
przyjęto jego wartość równą 1/3 przedniego rozstawu kół:
Moment bezwładności względem osi x wynosi:
5.2. Moment bezwładności względem osi y
Środek masy pojazdu nie pokrywa się ze środkiem geometrycznym bryły nadwozia. Promień
bezwładności oszacowano przyjmując założenie rozdzielności przedniego i tylnego zawieszenia.
Stąd warunek:
Moment bezwładności względem osi y wynosi:
14 |
S t r o n a
6. Równania ruchu
Model jest obdarzony trzema stopniami swobody – przemieszczeniem wzdłuż osi z oraz
obrotami: wokół osi x – Φ
x
i wokół osi y - Φ
y
(patrz: punkt 2).
6.1. Wzory na energię kinetyczną i energię potencjalną
Energia potencjalna:
Energia kinetyczna:
6.2. Równania Lagrange’a
gdzie
- wektor współrzędnych uogólnionych
Różniczki po współrzędnych uogólnionych:
15 |
S t r o n a
6.3. Równania ruchu
Po podstawieniu wzorów na E
p
i E
k
do równań Lagrange’a otrzymano równania ruchu
względem trzech współrzędnych uogólnionych:
Macierzowy zapis równań:
Macierz bezwładności:
Macierz sztywności:
7. Częstotliwości drgań własnych
Częstotliwości drgań własnych obliczono z wykorzystaniem programu MathCAD.
Zdefiniowano macierze: bezwładności i sztywności:
Utworzono macierz A:
16 |
S t r o n a
Wyznaczono wartości własne macierzy A:
Ich wartości odpowiadają kwadratowi częstości drgań własnych:
Częstości drgań własnych wynoszą:
Częstotliwości drgań własnych:
17 |
S t r o n a
8. Symulacja – wykresy przemieszczenia, prędkości i przyspieszenia
wybranego punktu nadwozia
Wykresy przemieszczenia, prędkości i przyspieszenia wyznaczono dla przedniej lewej lampy
samochodu - punkt A o przybliżonych współrzędnych (1,8; 0,8; 0) [m]. Warunki początkowe:
Granice całkowania: t = 10 [s]