
Matura 2005
Matura 2005
Matura 2005
Matura 2005
Zadania dla poziomu rozszerzonego są wyróżnione kursywą.
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
D
D
O
O
P
P
O
O
W
W
T
T
A
A
R
R
Z
Z
A
A
N
N
I
I
A
A
P
P
R
R
Z
Z
E
E
D
D
M
M
A
A
T
T
U
U
R
R
Ą
Ą
Zestaw IX Rachunek prawdopodobieństwa
Zadanie 1.
Rozwiąż równanie
!
5
2
=
n
Zadanie 2.
Z cyfr 0, 1, 2, …, 9 układamy takie liczby czterocyfrowe, że w każdej z tych liczb cyfra dziesiątek
jest taka sama jak cyfra setek. Ile takich liczb można ułożyć, jeśli cyfry w nich mogą się powtarzać?
Zadanie 3.
Nauczyciel matematyki przygotował zestaw 30 zadań z rachunku prawdopodobieństwa, wśród któ-
rych jest 20 zadań z poziomu podstawowego i 10 z poziomu rozszerzonego. Z tych zadań nauczy-
ciel układa pięciozadaniowe sprawdziany tak, aby w każdym sprawdzianie były 3 zadania z pozio-
mu podstawowego i 2 zadania z rozszerzonego. Ile sprawdzianów nauczyciel może ułożyć, jeśli
dwa sprawdziany różniące się choćby jednym zadaniem są uznawane za różne, a kolejność zadań
w sprawdzianie nie jest istotna?
Zadanie 4.
W urnie są dwie kule białe – mała i duża oraz trzy kule czarne – mała, średnia i duża. Mała kula
biała i mała kula czarna mają taki sam promień i również taki sam promień mają kule: duża biała i
duża czarna. Z urny wyciągamy losowo równocześnie dwie kule. Wymień wszystkie zdarzenia
elementarne
a)
tworzące zbiór
Ω
,
b)
sprzyjające zdarzeniu A: wylosowane dwie kule mają różną wielkość.
Następnie oblicz prawdopodobieństwo zdarzenia A.
Zadanie 5.
Zdarzenia A oraz B są podzbiorami tej samej przestrzeni
Ω
, przy czym P(A) = 0,76; P(B
′
) = 0,38
i
82
,
0
)
(
=
∪
B
A
P
. Oblicz:
a)
)
(
B
A
P
∩
,
b)
)
'
'
(
B
A
P
∪
.
Zadanie 6.
Uzasadnij, że jeśli każdą z trzech danych liczb dodatnich zwiększymy o p%, to otrzymamy trzy
nowe liczby, których średnia jest o p% większa od średniej danych liczb. Jak można uogólnić to
twierdzenie?
Zadanie 8.
Z pełnej talii kart zawierającej 52 karty losujemy kolejno i bez zwracania dwie karty. Oblicz praw-
dopodobieństwo tego, że druga wylosowana karta jest dziesiątką pod warunkiem, że pierwsza wy-
losowana karta jest waletem.
Zadanie 9.
Do pierwszych klas pewnego liceum przyjęto uczniów tylko z trzech gimnazjów:
3
2
1
i
,
G
G
G
. Licz-
by uczniów przyjętych z tych gimnazjów są odpowiednio w stosunku 2 : 3 : 3, a wśród nich dziew-
częta stanowią odpowiednio 62,5%, 75% i 50%. Z listy przyjętych uczniów losujemy jedną osobę.
Oblicz prawdopodobieństwo tego, że wylosowaliśmy dziewczynkę.
Matura 2005
Matura 2005
Matura 2005
Matura 2005
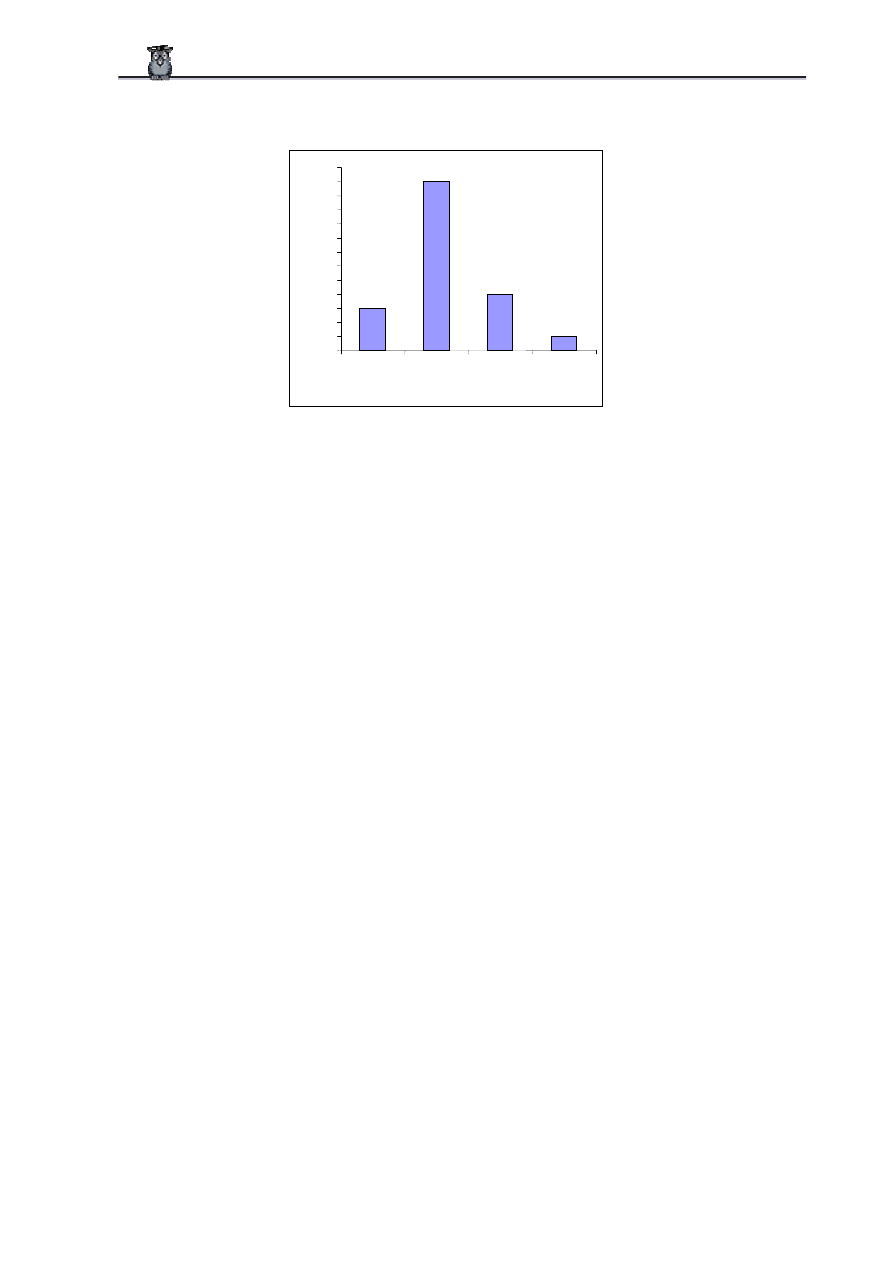
Zadanie 7.
Entuzjasta grzybobrania był, w sezonie 2003 roku, aż 20 razy na grzybach. Poniższy diagram
przedstawia rezultaty tych 20 wypraw na grzyby.
Oblicz:
a)
ś
rednią liczbę kilogramów grzybów przypadającą na jedno grzybobranie,
b)
odchylenie standardowe liczby kilogramów grzybów.
Zadanie 10.
Pewien koszykarz trafia piłką do kosza z prawdopodobieństwem 0,8. Koszykarz ten ma wykonać
trzy rzuty karne. Oblicz prawdopodobieństwo tego, że co najmniej dwa razy trafi piłką do kosza.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
0 kg
1 kg
2 kg
3 kg
Liczba kilogramów
zebranych grzybów
C
z
ę
st
o
ść
(
li
cz
b
a
g
rz
y
b
o
b
ra
ń
)

Matura 2005
Matura 2005
Matura 2005
Matura 2005
Odpowiedzi:
1.
n = 16
2.
900
3.
51300
4.
a) Zbiór
Ω
tworzą wszystkie dwuelementowe podzbiory zbioru pięciu kul. Takich podzbiorów
jest 10
b) Zbiór A tworzą wszystkie dwuelementowe podzbiory kul o różnych promieniach. Takich
podzbiorów jest 8; P(A) =
5
4
5.
a) 0,56 b) 0,44
6.
Twierdzenie jest prawdziwe dla n liczb dodatnich ( n = 2, 3, 4,…)
7.
a) 1,15 b) ok. 0,73
8.
51
4
9.
8
5
10.
0,896
Wyszukiwarka
Podobne podstrony:
Krysicki Rachunek prawdopodobieĹ stwa i statystyka matematyczna cz 1
RACHUNEK PRAWDOPODOBIE STWA, Inne
Kordecki W, Jasiulewicz H Rachunek prawdopodobieństwa i statystyka matematyczna Przykłady i zadania
Matematyka - rachunek prawdopodbieństwa - ściąga, szkoła
7 ELEMENTY RACHUNKU PRAWDOPODOBIEŃSTWA
MATEMATYKA Rachunek prawdopodobieństwa, str tytułowa, Marcin Nowicki
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 01.06.2008
Statystyka dzienne wyklad1, Rachunek prawdopodobie˙stwa
1 zadania z rachunku prawdopodobieństwa, Zad
Zestaw10 rachunek prawdopodobie Nieznany
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 18.05.2008
rachunek prawdopodobieństwa, rachl4
więcej podobnych podstron