Wykład 2 23.10.2003

Def.

Funkcję Fx określoną na zbiorze liczb R wzorem
nazywamy dystrybuantą zmiennej losowej X

Dystrybuanta PA funkcji zmiennej losowej X jest funkcją F:R→ R mającą następujące własności:

1. niemalejąca

b.

c. jest lewostronnie ciągła

Wnioski:

• P(a ≤ x < b) = F(b) - F(a)

• P(X=a) = F(a+0) - F(a) ???
  

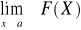
Zmienne losowe

• Typu skokowego (dyskretnego)0000

• Typu ciągłego

Mówimy, że zmienna losowa jest typu skokowego (dyskretnego) jeżeli istnieje skończony {x₁, x₂ , …. x_n} lub przeliczalny {x_1,x_{2 ,}….}zbiór jego wartości , takich że prawdopodobieństwo tego zmienna x przyjmie wartości x_k

P(X = Xk) = Pk ≥ 0 , k
{1,2,…}

(k
N={1,2…})

oraz

Wartość x_n nazywamy punktami skokowymi, prawdopodobnymi Pk - skokami.

Niech x_k będzie punktem skokowym typu skokowego, prawdopodobieństwo tego, że zmienna losowa x przyjmie wartość Xk, nazywamy funkcją prawdopodobieństwa zmiennej losowej x.

Pk = P(x = x_k) , k
{1,2, …n} k
N

Gdzie Pk spełniają warunek .:

Dystrybuanta zmiennej losowej typu skokowego wyraża się wzorem .:

Przykłady.:

1. Rozkład jednopunktowy

X = {X₁}

P(X = X₁) = 1

2. Rozkład dwupunktowy (0,1) z parametrem p

X = {0,1}

P₁ = P(X = 1) = p p₀ = P(X=0 ) = 2 = 1-p

3. Rozkład dwuwymiarowy (Bernouliego) z przestrzeni n,p

X_k = k k = 0,1,…n

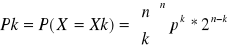
4. Rozkład Poissona

X_k = k k = 0,1,2…

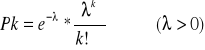
Zmienna losową typu ciągłego nazywamy zmienną losową, dla której istnieje nieujemna funkcja f (x) taka , że dla każdego f(x)

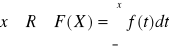
gdzie F(X) nazywamy dystrybuantą zmiennej losowej X , natomiast natomiast gęstością (funkcją gęstości ) zmiennej losowej X. Funkcja gęstości spełnia następującą równość.:

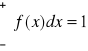
Funkcja jest gęstością zmiennej losowej X jeśli jest funkcją rzeczywistą , nieujemną (
, całkowalną i spełnia następującą równość

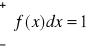
Wnioski

Jeżeli X jest zmienną typu ciągłego, to :

P(X
A) =

Gdzie f jest gęstością zmiennej losowej A

Jeżeli A jest A = {a}

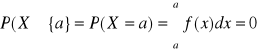
Jeżeli A = <a,b>

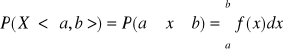
W punktach, w których f jest funkcją ciągłą

F'(X) = f(x)

Przykłady.:

1. rozkład jednostajny(równomierny prostokatny) na odcinku <a,b>

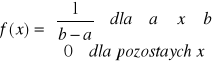
2.rozkłąd wykładniczy z parametrem

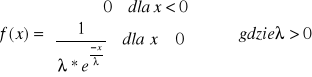
3. rozkład normalny N (m,
) , m - wartość środkowa(m
),
>0 →odchylenie standardowe, x

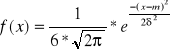
4. rozkład Cauch^'yego z parametrami μ,parametrami

- parametr skali

- parametr przesunięcia

5. rozkład beta

6. rozkład gamma

7. rozkład Rayleigha

8. rozkład Maxwella

9. rozkład Weibulla

10. rozkład Laplace'a

11. rozkład uogólniony gamma

Charakterystyki liczbowe zmiennej losowej.:

a. wartość przeciętna E(x) (wartośc oczekiwana średnia)nadzieja matematyczna

Wartość przeciętna E(x) zmiennej losowej x można określić wzorem
tprzy założeniu , że całka z funkcji X względem miary p ma wartość skończoną .

Jeśli X jest zmienna typu skokowego oraz
.

Jeśli x jest zmienną losową typu ciągłego i
gdzie f jest gęstością zmiennej losowej x.

Twierdzenie .:

Jeżeli zmienna losowa x ma wartość oczekiwaną E(x), to dla dowolnych liczb skończonych a oraz b, E(ax + b) = a* E(x) + b

2. Element zwykły rzędu r zmiennej losowej x wyrażamy wzorem
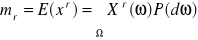
   przy założeniu , że całka z funkcji X względem funkcji P jest skończona .

Jeżeli X jest zmienną typu skokowego i

Jeżeli X jest zmienną losową typu ciągłego ciągłego
, gdzie f jest objętością zmiennej losowej x to

UWAGA

Moment zwykły rzędu I jest to wartość przeciętna. Mnożenie
, gdzie c jest dowolną stałą nazywamy momentem rzędu r względem punktu c.

Def.

Momenty względem wartości przeciętnej nazywamy momentami centralnymi i oznaczamy

Def.

Moment
nazywamy odchyleniem kwadratowym zmiennej losowej x od punktu c.

Def.

Moment centralny rzędu drugiego czyli średnie odchylenei kwadratowe zmiennej losowej x od wartości przeciętnej nazywamy wariancją i oznaczamy
Jeżeli x jest zmienną losową typu skokowego to

Jeżeli x jest zmienną losową typu ciągłego ciągłego gęstości f to
przy założeniu , że odpowiednie szeregi i całki są skończone.

Wariancja z wykorzystaniem momentów zwykłych można wyrażać następującym wzorem.:

Dowód.:

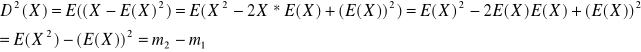
Twierdzenie

Jeżeli dla dowolnej , zmiennej losowej istnieje wariancja
to dla dowolnych skończonych liczb a oraz b wariancja

---