WYKŁAD 3

(by katja``)

Funkcja φ(c) = E((x-c)²) przyjmuje wartość najmniejszą dla c= E(x)

* Miarami rozproszenia (zróżnicowania, zmienności) są:

1. Odchylenie standardowe σ =
(sigma)

2. Współczynnik zmienności V=

* Miarą asymetrii rozkładu jest współczynnik asymetrii (trzeci moment centralny)

*Miarą Koncentracji są:

1. Współczynnik koncentracji (skupienia)

2. Eksces (współczynnik spłaszczenia)

- jest współczynnikiem badającym skupienie rozkładu wokół wartości przeciętnej w stosunku do skupienia odpowiedniego rozkładu normalnego: N(m,
)

Jeżeli
>0 to rozkład jest bardziej skupiony (stromy) niż rozkład normalny

Jeżeli
<0 to rozkład jest mniej skupiony(bardziej spłaszczony) niż rozkład normalny

Standaryzacja zmiennej losowej

Zmienna losowa Y, dla której wartość oczekiwana E(Y)=0 i D²(Y)=1 nazywa się zmienną losową standaryzowaną.

Standaryzacja zmiennej losowej:

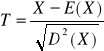
gdzie D²(X)>0

Nierówność Czebyszewa:

1. jeżeli X jest zmienną losową wartości oczekiwanej E(x) i skończonej wariancji D²(x)< ∞, to dla każdego ε>0 zachodzą

2. jeżeli
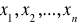
   są niezależnymi zmiennymi losowymi o jednakowych rozkładach oraz

to dla każdego ε>0 teza nierówności Czebyszewa jest następującą:

m- wartość oczekiwana

σ - wariancja zmiennej losowej

Nierówność Kałmogorowa

Niech
są niezależnymi zmiennymi losowymi o skończonej wariancji

U_i = x_i - E(x_i)

Y_k =
dla k = 1,2,…n

Wówczas dla każdego ε>0 zachodzi

np. U₁ = X - E(X)

Y = X - E(X)

dla n=1 otrzymujemy nierówność Czebyszewa

Parametry pozycyjne

Kwantylem rzędu p (gdzie 0<p<1) zmiennej losowej X o dystrybuancie F nazywamy liczbę Xp, dla której zachodzą nierówności:

P(X ≤ Xp) ≥ p i P(X ≥ Xp) ≥ 1 - p ….(1)

nierówności te są równoważne następującemu związkowi:

F(Xp + 0) ≤ p ≤ F(Xp) ….(2)

Wzory (1) i (2) określają kwanty rzędu p dla zmiennej losowej typu skokowego.

Jeżeli X jest zmienną typu ciągłego to kwanty rzędu p wyznacza się z równania

F(Xp) = p

Mediana to kwanty rzędu 0,5

Medianę oznaczamy symbolem x_0,5 lub Me

P(X ≤ x_0,5 ) ≥ 0,5 i P(X ≥ x_0,5 ) ≥ 0,5

Jeżeli X jest zmienna typu skokowego, to mediana jest to wartość, która spełnia podaną wyżej nierówność.

Jeżeli X jest zmienną losową typu ciągłego, to medianę wyznaczamy, jako rozwiązanie równania:

F(x_0,5) = 0,5 - gdy mamy dystrybuantę

Albo z równania równoważnego:

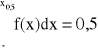
Funkcja charakterystyczna

DEF. Funkcją char. zmiennej losowej X nazywamy funkcję zespoloną φ na zbiorze liczb rzeczywistych następującym wzorem:

gdzie

DEF. Jeżeli X jest zmienną losową typu skokowego to:

dla

DEF. Jeżeli X jest zmienną losową typu ciągłego o gęstości f to:

dla

Mając f char. możemy wyliczyć momenty zwykłe rzędu r.

TW. Jeżeli istnieje moment zwykły rzędu r to funkcja char. jest l-krotnie różniczkowalna oraz

- r-ta pochodna f. char. w punkcie 0

Twierdzenie to pozwala obliczyć momenty rzędu r gdy mamy daną f. char.

TW. Jeżeli f. char. jest bezwzględnie całkowalna to X jest zmienna losową typu ciągłego o gęstości f (którą wyrażamy wzorem:
)

To twierdzenie pozwala nam wyznaczyć f(x), gdy podano φ(t)

Całka bezwzględna znaczy, że istnieje

TW. Jeżeli f. char. jest funkcją okresową w okresie 2π, to X jest zmienną losową typu skokowego mogącą przyjmować tylko wartości całkowite.

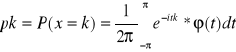
gdzie k jest liczbą całkowitą

Funkcja zmiennych losowych

1. Funkcja zmiennej losowej typu skokowego

Jeżeli X jest zmienna losową typu skokowego o zbiorze Wx punktów skokowych oraz y jest dowolną borelowską funkcją rzeczywistą o wartościach rzeczywistych określonych przynajmniej na zbiorze Wx to równość Y = g(X)

Określona na przestrzeni zdarzeń elementarnych
jest nową skokową zmienną losową Y zwaną funkcją zmiennej skokowej x o punktach skokowych
= g(
) tworzących pewien zbiór Wy;

Gdy g nie jest f. różnowartościową to ten sam punkt skokowy
może być osiągnięty więcej niż dla jednego punktu skokowego
.

Funkcja prawd. zmiennej losowej Y oznaczona przez q jest określona następująco:

2. Funkcja zmiennej losowej typu ciągłego

Niech Y = g(x) jest zmienną losową określoną przynajmniej na zbiorze wartości zmiennej losowej x, g jest funkcją określoną przynajmniej w zbiorze zmiennej X.

TW 1. Niech Y = g(x). Jeżeli X jest zmienna losową o gęstości f_x skoncentrowaną na przedziale (a,b) funkcja Y=g(x) jest funkcją silnie monotoniczną, klasy c¹ o pochodnej
czyli g`(x)
, na przedziale (a,b)

Funkcja x = h(y) jest f. odwrotną do funkcji g, to gęstość zmiennej losowej Y oznacza
wyraża się wzorem:

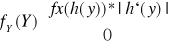
gdzie c = min {c₁,d₁}

d = max {c₁,d₁}

*UWAGA* g jest klasy c¹, jeżeli jest jednokrotnie różniczkowalna i pierwsza pochodna f. jest ciągła.

TW 2. Jeżeli X jest zmienną losową o gęstości fx skoncentrowana na przedziale (a,b) (<-przedział może być niewłaściwy) funkcja Y(x) jest f. silnie monotoniczną przedziałami g(x) = g_i(x) dla i = 1,2…n; g_i są funkcjami silnie monotonicznymi na przedziale (
)

(a,b) =

g_i są klasy c¹, g_i (x)
dla x
(
) i = 1,2…n

Funkcja
jest funkcją odwrotną do g_i dla i = 1,2…n to gęstość zmiennej losowej Y oznacza
wyraża się wzorem:

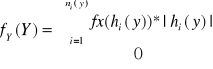
gdzie: c = min c_i d = max c_i

c_i = g (x_i) dla i = 1,2…n

Liczba składników w sumie występująca we wzorze nie jest stałą, zależy od wartości y

Dla ustalonego u należącego do przedziału m(y) jest liczbą rozwiązań równania:

w przedziale (a,b)