1
Prof. Krzysztof Jemielniak
k.jemielniak@wip.pw.edu.pl
http://www.zaoios.pw.edu.pl/kjemiel
ST 107, tel. 22 234 8656
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Wykład 5
Przetwarzanie sygnałów w AUMON – część II
Automatyczne
Monitorowanie i
Nadzór Wytwarzania
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Przetwarzanie
sygnałów
Przetwarzanie sygnałów w DNiPS
miary sygnałów
skorelowane z
monitorowanym
zjawiskiem
sygnały
analogowe
wstępna obróbka
sygnałów
(filtrowanie, A/C)
Transformacja
do dziedziny
częstotliwości
(FFT, STFT,
WT)
wyznaczanie
miar sygnałów
wybór miar
sygnały cyfrowe w
dziedzinie częstotliwości
wszystkie
miary
sygnały cyfrowe w dziedzinie czasu
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Typy sygnałów
stacjonarne
niestacjonarne
deterministyczne
losowe
ciągłe
przejściowe
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Sygnały deterministyczne
Sygnał nazywany jest deterministycznym, ponieważ jego
chwilowa wartość w dowolnej chwili jest przewidywalna.
Da się rozłożyć na sinusoidy
amplituda
amplituda
czas
częstotliwość
drgania
itd.
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Sygnały deterministyczne i ich składowe
czas
częstotliwość
czas
częstotliwość
czas
częstotliwość
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Sygnały losowe
czas
częstotliwość
•
Sygnały losowe nie mają składowych okresowych i ich harmonicznych
•
Charakteryzują się przypadkowymi wartościami, a ich wartość chwilowa
jest nieprzewidywalna
•
Mogą być jednak opisywane statystycznie – wartości podlegają
rozkładowi, mają wartość średnią
•
Stacjonarny sygnał losowy ma widmo bez wyraźnych
maksimów, płaskie w pewnym zakresie
2
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
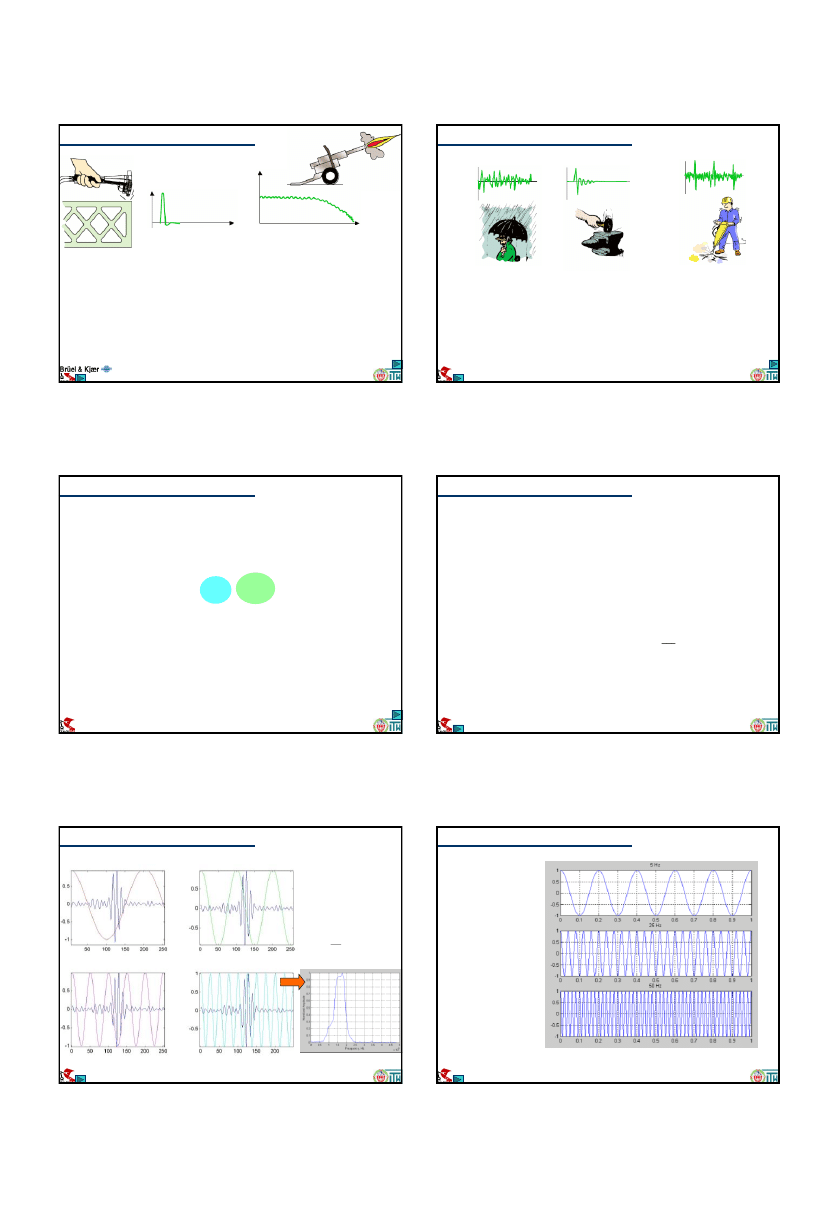
Sygnały przejściowe (impulsowe)
• Impuls mechaniczny jest krótkotrwałym wybuchem energii
• Jego widmo jest w przybliżeniu płaskie do częstotliwości
będącej odwrotnością czasu trwania impulsu
• Impuls nieskończenie krótki miałby widmo nieskończone
czas
częstotliwość
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Sygnały niestacjonarne ciągłe
•
Sygnały niestacjonarne ciągłe mają pewne podobieństwa do
zarówno sygnałów przejściowych jak losowych
•
Można je traktować jako losowe lub rozłożyć na poszczególne impulsy
i traktować jako przejściowe
•
W sygnałach niestacjonarnych składowe widmowe mogą się pojawiać i
zanikać, stąd do ich opisu potrzebna jest charakterystyka
czasowo-częstotliwościowa
losowe
przejściowe
+
=
ciągłe
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Transformata Fouriera
Wyrażenie to odpowiada na pytanie:
“
Czy istnieje nieskończona sinusoida
e
j2
p
ft
w sygnale
x(t)
“
Transformata Fouriera to iloczyn obustronnie
nieskończonych sygnałów
∞
∫
-∞
X(f)=
x(t)
∙
e
-j2
p
ft
dt
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Ale jak to działa?
t
j
t
e
t
j
sin
cos
FT wykorzystuje funkcje Eulera (sinusoidy) jako podstawowe
elementy składowe.
Sinusoida o każdej częstotliwości jest mnożona przez cały
sygnał (porównywana z sygnałem).
p
d
e
F
t
f
dt
e
t
f
F
t
j
t
j
)
(
2
1
)
(
)
(
)
(
Jeśli w sygnale występuje składowa o tej częstotliwości,
korelacja między sinusoidą a sygnałem jest wysoka i wysoki
jest współczynnik FT.
Jeśli w sygnale nie występuje składowa o tej częstotliwości,
korelacja jest niska lub zerowa, a współczynnik FT jest także
niski lub zerowy.
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
FT w działaniu
dt
e
j
X
t
x
dt
e
t
x
j
X
t
j
t
j
p
)
(
2
1
)
(
)
(
)
(
Funkcje Eulera
(sinusoidy) są bazową
funkcją transformaty:
F
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
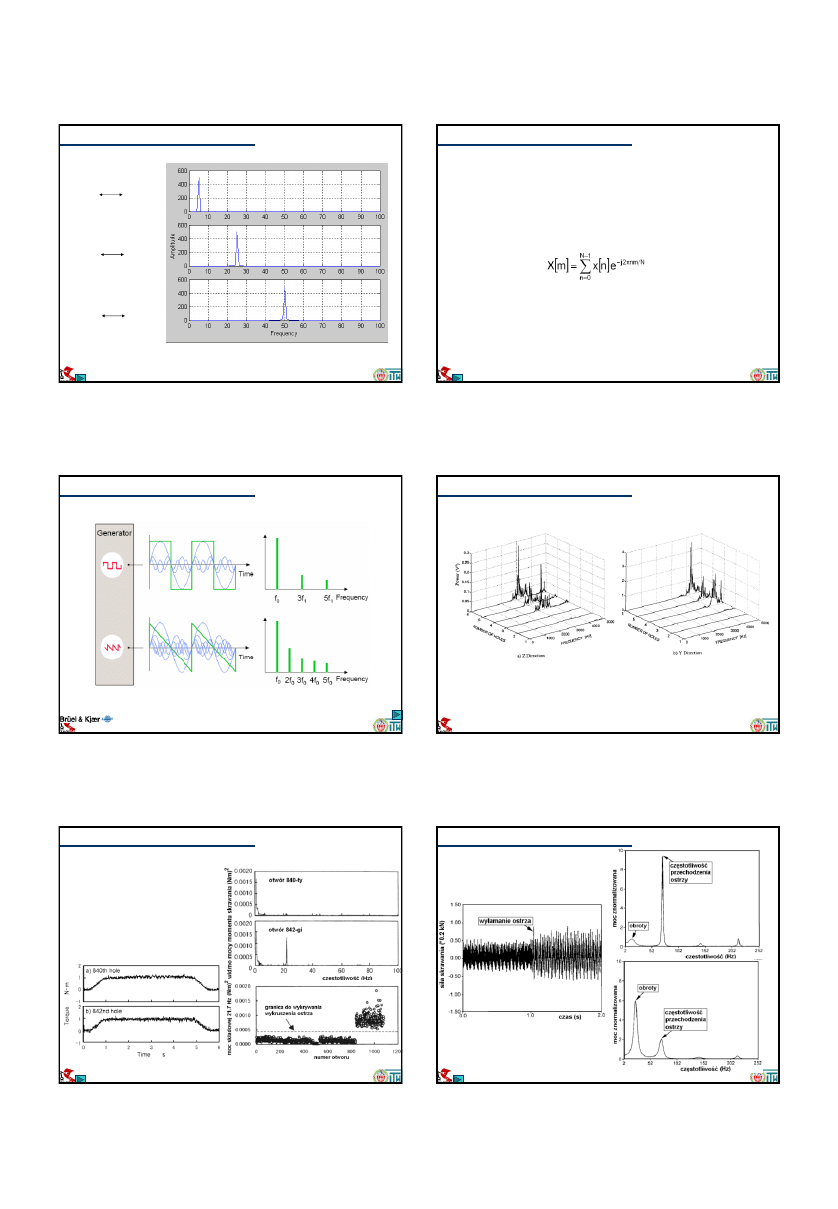
FT w działaniu
)
5
2
cos(
)
(
1
t
t
x
p
)
25
2
cos(
)
(
2
t
t
x
p
)
50
2
cos(
)
(
3
t
t
x
p
3
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
FT w działaniu
)
(
1
X
)
(
2
X
)
(
3
X
F
)
(
1
t
x
F
)
(
2
t
x
F
)
(
3
t
x
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Dyskretne przekształcenie Fouriera
Dyskretne przekształcenie Fouriera (ang.
Discrete Fourier Transform
- DFT)
jest zdefiniowane jako dyskretny ciąg
X[m]
w dziedzinie częstotliwości:
współrzędne biegunowe!
gdzie:
X[m] - m-ta składowa wyjściowa DFT, tj. X[0], X[1], X[2], X[3] itd.,
m - indeks próbek wyjściowych DFT w dziedzinie częstotliwości, m=0,1,2,3....,N-1
x[n] - ciąg próbek wejściowych, x[0], x[1], x[2], x[3] itd.,
n - indeks próbek wejściowych w dziedzinie czasu, n = 0,1,2,3,... ...,N-1,
__
j - √-1 oraz
N - liczba próbek ciągu wejściowego równa liczbie punktów częstotliwości
w ciągu wyjściowym DFT.
Ciągłe przekształcenie Fouriera, zdefiniowane jako:
odpowiada na pytanie:
Czy istnieje nieskończona sinusoida
e
j2
p
ft
w sygnale
x(t)
“
∞
∫
-∞
X(f)=
x(t)
∙
e
-j2
p
ft
dt
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Rozkład sygnału na składowe
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Wpływ zużycia na widmo drgań przy wierceniu
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Wpływ
KSO
na widmo mocy momentu skrawania
przy wierceniu
Wiertło HSS
f
5 mm,
n = 1300 obr/min,
f = 0.1 mm/obr,
mat. obr. stal 45,
l = 10 mm
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
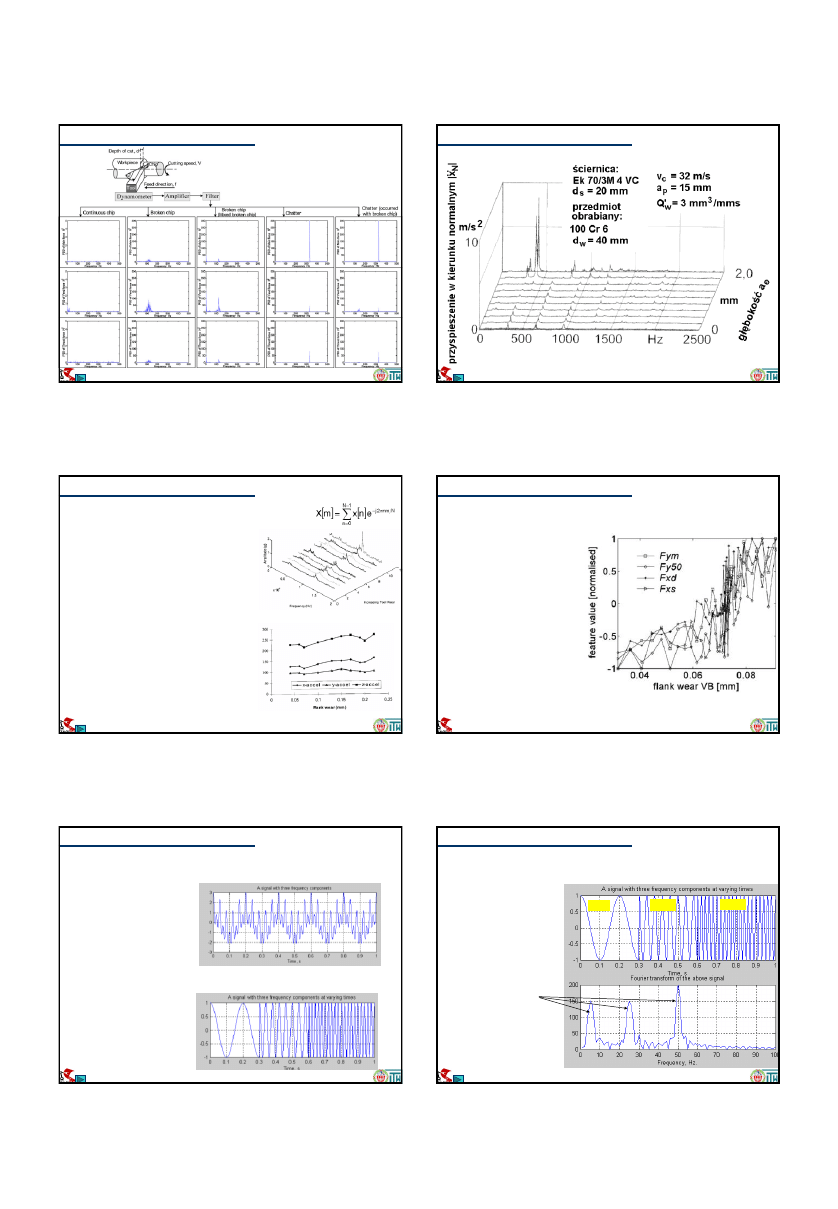
Wpływ
KSO
na przebieg i widmo siły skrawania
przy frezowaniu
4
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Widma siły w różnych stanach procesu
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Wykrywanie nadmiernych drgań
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Miary sygnałów oparte na transformacie Fouriera
•
Bezpośrednie wykorzystanie wartości
współczynników DFT X[m] jest
niepraktyczne – jest ich wiele, energia
przepływa między sąsiednimi prążkami
•
Zwykle stosuje się wyznaczanie miar
widma Fouriera, np.:
•
amplitudy dominujących prążków
•
moc sygnału w wybranych pasmach
•
energia w pasmach
•
miary statystyczne spektrum:
•
średnia częstotliwość
•
wariancja
•
skośność
•
kurtoza
•
częstotliwość najwyższego prążka
zależność widma drgań przy toczeniu od zużycia ostrza
zależność mocy drgań przy toczeniu od zużycia ostrza
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Miary z dziedziny częstotliwości i czasu
stosowane jednocześnie
•
Fym - średnia sygnału siły F
y
,
•
Fy50 - energia sygnału siły F
y
w
pobliżu 50 Hz
•
Fxd – energia pierwszej postaci
sygnału F
x
•
Fxs – odchylenie stardardowe
sygnału F
x
Diagnostyka zużycia ostrza oparta na pomiarach sił skrawania przy toczeniu przerywanym
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Sygnały stacjonarne i niestacjonarne
)
50
2
cos(
)
25
2
cos(
)
5
2
cos(
)
(
4
t
t
t
t
x
p
p
p
Sygnały stacjonarne mają charakterystyki
widmowe (spektrum) stałe w czasie
]
[
)
(
3
2
1
5
x
x
x
t
x
Łączenie szeregowe
Sygnały niestacjonarne mają zmienne spektrum
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
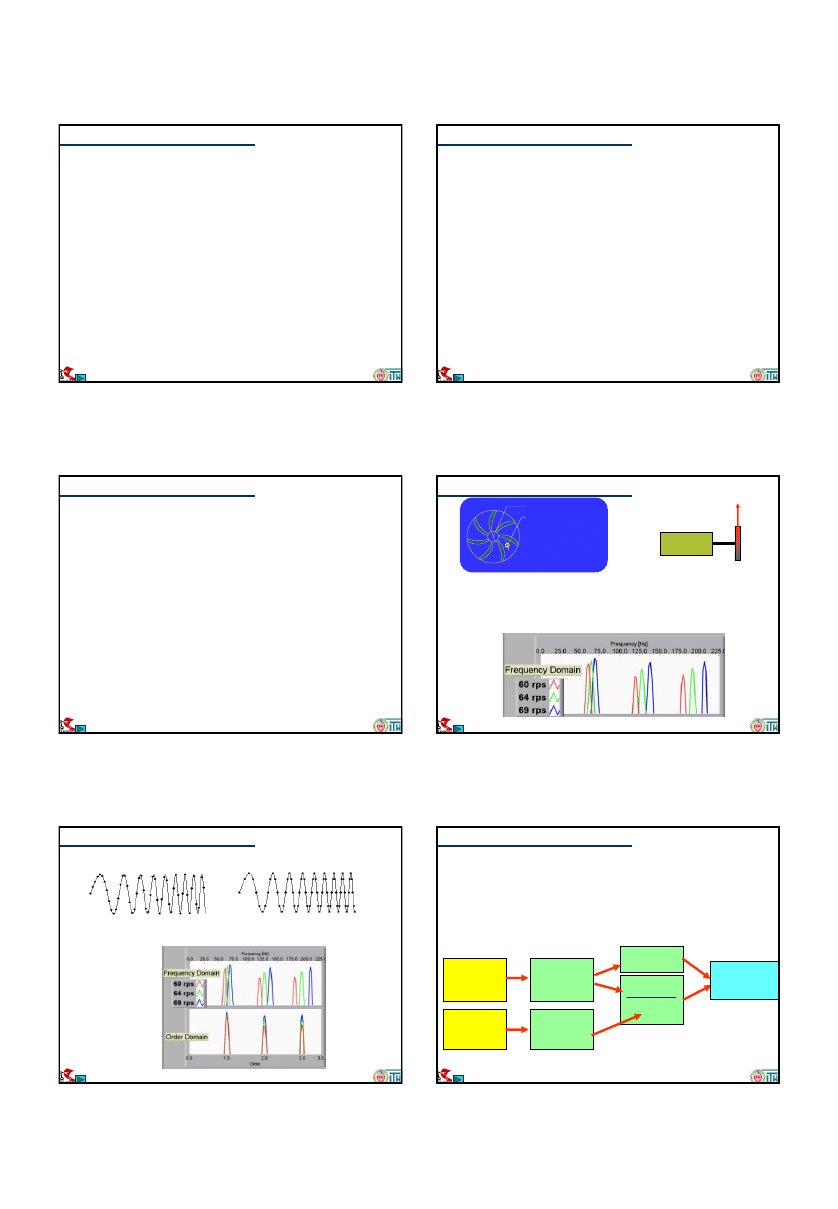
FFT sygnałów niestacjonarnych
5 Hz
25 Hz
50 Hz
Widmo zawiera dokładną
informację o
występowaniu
składowych o określonych
częstotliwościach, ale żadnej
informacji o tym
kiedy
występowały
dt
)=
(j
X
t
x
e
-
t
j
5
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Analiza synchroniczna (analiza rzędów)
Analiza synchroniczna (analiza rzędów, ang.
order analysis, order
tracking
) - zaawansowana metoda diagnostyki maszyn wirujących,
które działają w szerokim zakresie prędkości obrotowych.
Monitorowanie stanu technicznego maszyn wirujących (turbin,
silników, czy pomp) informuje nas o konieczności wykonania napraw
zanim dojdzie do uszkodzenia urządzenia oraz przestoju na linii
produkcyjnej.
Jeśli zostaną odkryte usterki (np. pęknięcia), maszynę można
wycofać z eksploatacji, zanim ulegnie poważnej awarii.
W celu diagnozy stanu maszyny opracowano wiele metod detekcji
uszkodzeń, jednak większość z nich dotyczy ustalonych stanów pracy,
tzn. na stałych obrotach.
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Analiza synchroniczna (analiza rzędów)
Chcąc uzyskać bardziej szczegółowe informacje dotyczące stanu
urządzenia wirującego, należy wykonać pomiary oraz analizę w
stanach nieustalonych, tj. w czasie rozbiegu i wybiegu maszyny.
Analiza synchroniczna umożliwia powiązanie występujących zjawisk z
konkretnymi prędkościami obrotowymi.
Do celów analizy rzędów wykonujemy pomiary hałasu, drgań oraz
prędkości obrotowej.
W razie braku możliwości pomiaru bezpośredniego prędkości
obrotowej, sygnał tachometryczny do analiz pozyskuje się z sygnału
wibracyjnego na podstawie zaawansowanych metod statystycznych.
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Próbkowanie do analizy rzędów
Częstotliwości generowane przez wirujące elementy
maszyny liniowo zależą od prędkości obrotowej.
W przypadku zmian prędkości podczas próbkowania
sygnał pochodzący od jednego elementu będzie generował
sygnał o zmiennej częstotliwości, w wyniku czego jego
widmo zostanie rozmyte.
Składowe pochodzące od różnych elementów mogą na
siebie zachodzić i uniemożliwić analizy częstotliwościowe.
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Niewyrównoważenie
Silna składowa 1go rzędu (zgodna z częstotliwością obrotów)
Częstotliwość i amplituda rośnie z prędkością obrotową
Wyrównoważenie odbywa się dzięki informacji o fazie i dodawaniu mas
Orders
siła
Shaft Centerline
Center of Gravity
oś wirnika
środek ciężkości
Rząd = częstotliwość / prędkość obrotowa
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Stała częstotliwość próbkowania
(próbek na sekundę)
Stała liczba próbek na obrót
Próbkowanie do analizy rzędów
Aby uniknąć tego zjawiska, stosuje się analizę synchroniczną sygnału
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
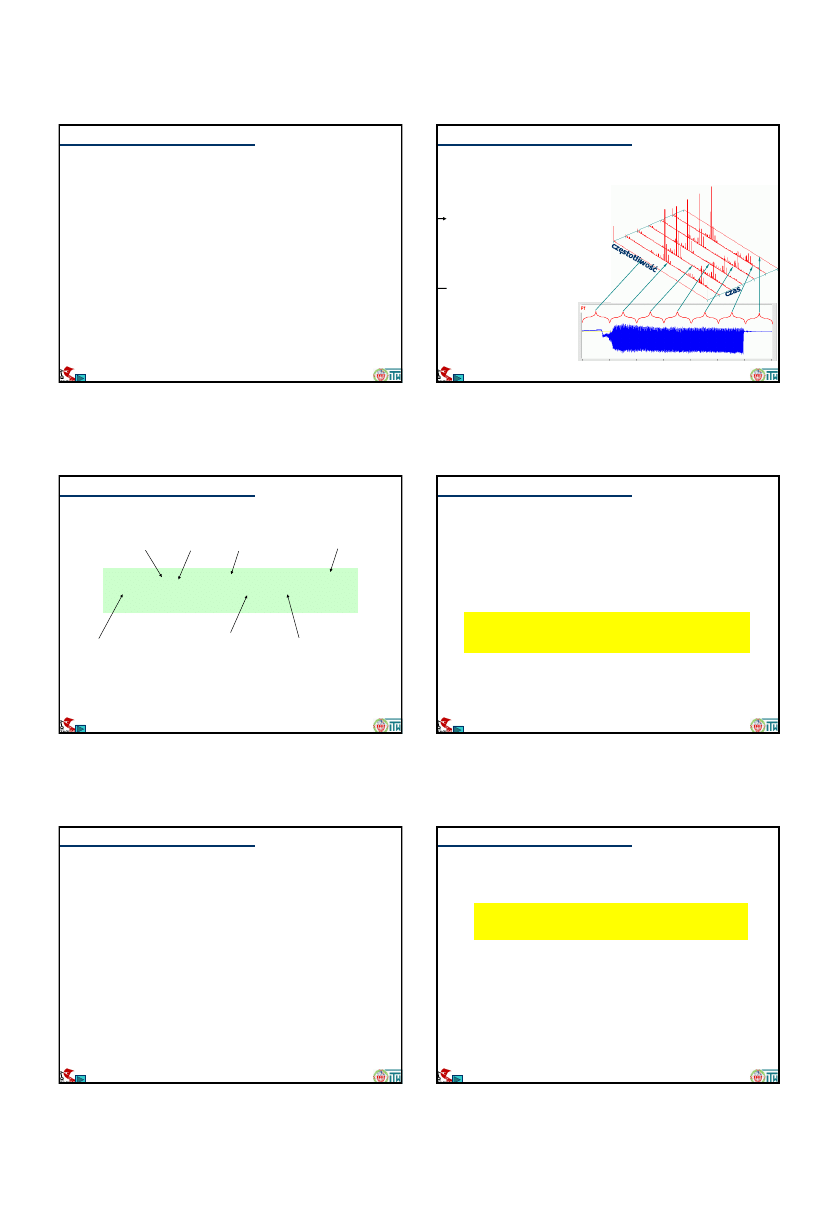
Przetwarzanie sygnałów do analizy rzędów
Alternatywnie – stosując próbkowanie równomierne należy:
1. wyznaczyć widmo mocy z sygnału drgań
2. wyznaczyć chwilową prędkość obrotową przy pomocy
tachografu
3. podzielić oś częstotliwości widma mocy przez chwilową
prędkość obrotową
Sygnał z
tacho
Prędkość
obrotowa
Sygnał
drgań
Widmo
mocy
Oś częstotl.
Prędkość obr.
Faza lub
amplituda
Wykres w
dziedzinie
analizy rzędów
6
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Sygnały stacjonarne i niestacjonarne
FT identyfikuje wszystkie składowe widmowe obecne w sygnale,
jednakże nie daje żadnej informacji na temat ich rozmieszczenia w
czasie. Dlaczego?
Sygnały stacjonarne składają się ze składowych niezmiennych w czasie
wszystkie składniki występują cały czas
nie jest potrzebna informacja o czasie
FT pracuje bardzo dobrze dla stacjonarnych sygnałach
Sygnały niestacjonarne zawierają składowe, których amplituda jest
zmienna w czasie
Jak więc dowiedzieć się kiedy występują poszczególne składowe?
Potrzebny jest jakiś sposób określania
położenia w czasie
składowych
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Krótkookresowa transformata Fouriera
(Short Time Fourier Transform STFT)
1. Wybierz okno o skończonej
długości
2. Umieść je na początku sygnału
(t=0)
3. Obetnij sygnał mnożąc go przez
okno
4. Oblicz FT obciętego sygnału,
zapamiętaj
5. Przesuń okno w prawo o niewielki
odcinek
6. Idź do kroku 3, powtarzaj aż
osiągniesz koniec sygnału
czas
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Znaczenie STFT
t
t
j
x
dt
e
t
t
W
t
x
t
STFT
)
(
)
(
)
,
(
STFT sygnału x(t):
obliczona dla każdego
okna o środku w t=t’
parametr
czasu
parametr
częstotliwości
analizowany
sygnał
Funkcja okna
Funkcja okna dla t=t’
jądro FT
(funkcja bazowa)
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
“Czy i kiedy w sygnale
x(t)
występuje krótka
sinusoida
e
j
t
”
Znaczenie STFT
Oczywiście możliwa jest interpretacja STFT jako zestawu filtrów
Krótkookresowa transformata Fouriera (STFT)
odpowiada na pytanie:
t
t
j
x
dt
e
t
t
W
t
x
t
STFT
)
(
)
(
)
,
(
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Rozważmy dwa skrajne przypadki:
Okno
W(t)
nieskończenie długie STFT staje się FT,
dając dokładną informację o występujących w sygnale
częstotliwościach (dobrą rozdzielczość częstotliwości), ale
żadnej informacji o czasie występowania
Okno
W(t)
nieskończenie krótkie: W(t)=
D
t STFT
zwraca sygnał pierwotny z fazą. Doskonała informacja o
czasie (dobra rozdzielczość czasu), ale brak informacji o
częstotliwości
Wybór długości okna do STFT
t
t
j
x
dt
e
t
t
W
t
x
t
STFT
)
(
)
(
)
,
(
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Zasada nieoznaczoności Heisenberga
Rozdzielczość w czasie (
D
t):
Jak dokładnie można określić
położenie składowej w czasie
Rozdzielczość częstotliwości (
D
f):
Jak dokładnie można określić częstotliwość
składowej
•
Nie możemy dokładnie wiedzieć w której chwili występuje składowa o określonej
częstotliwości.
•
Możemy jedynie wiedzieć, jakie
zakresy częstotliwości
występują w jakich
przedziałach
czasu
.
Rozdzielczość w czasie i częstotliwości nie mogą
jednocześnie być arbitralnie duże!!!
Szerokie okno
zła rozdzielczość w czasie
,
dobra rozdzielczość częstotliwości
Wąskie okno
dobra rozdzielczość w czasie
,
zła rozdzielczość częstotliwości
Po wybraniu szerokości okna, obie rozdzielczości są ustalone.
7
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
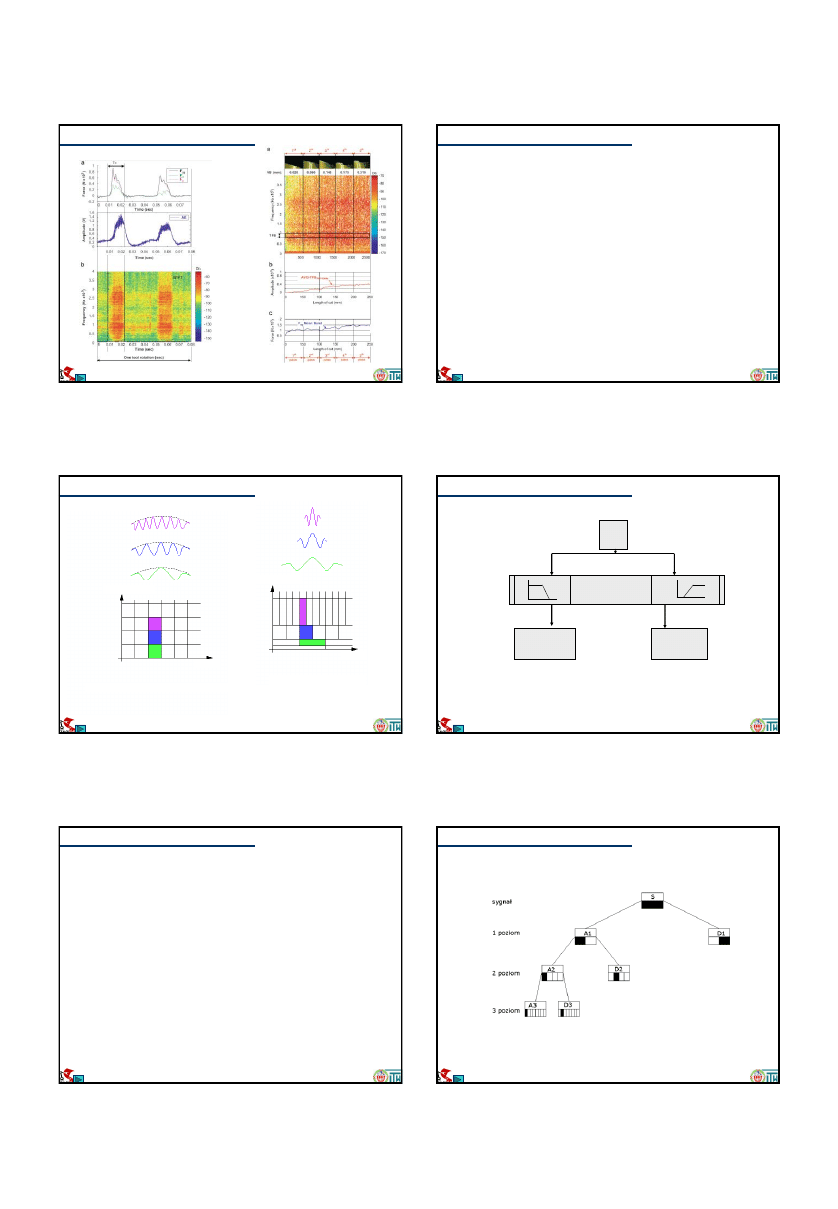
Zastosowanie STFT sygnału AE do wykrywania
skrawania
average of Targeted Frequency Band
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Transformata falkowa
W celu obejścia trudności związanych z rozdzielczością można zastosować okna o różnej
długości dla różnych częstotliwości:
Wyszukiwanie składowych o wysokich częstotliwościach wąskie okno
dla lepszej rozdzielczości w czasie
np.: przy f
próbk
=2000Hz, dla f=900-1000Hz użyjmy
D
t=0.1s, czyli
D
f=10Hz
Wyszukiwanie składowych o niskich częstotliwościach szerokie okno
dla lepszej rozdzielczości częstotliwości
np.: przy f
próbk
=2000Hz, dla f=0-10Hz użyjmy
D
t=1s, czyli
D
f=1Hz
Zasada Heisenberga w dalszym ciągu obowiązuje!
Funkcja okna jaką tu zastosujemy nazywana jest
falką
(
wavelet
)
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
STFT i falki
częstotliwość
czas
krótkookresowa transformata Fouriera
częstotliwość
czas
transformata falkowa
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Dyskretna Transformata Falkowa
(Discrete Wavelet Transform DWT)
DWT – bank filtrów odpowiadający falkom i skalowaniu
Dekompozycję można powtarzać wielokrotnie dla kolejnych
aproksymacji
sygnał
filtry
Aproksymacja
(A)
Detal
(D)
dolno-
przepustowy
górno-
przepustowy
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Dyskretna transformata falkowa
•
Dyskretna transformata falkowa rozkłada sygnał na średnie
(aproksymacje A) i różnice (detale D) przez splot sygnału i
odpowiedzi impulsowej filtru dolno i górnoprzepustowego
•
Odpowiedzi filtrów są decymowane przez 2.
•
Ogólnie aproksymacja A
j+1
i detal D
j+1
na poziomie j+1 opisane są
splotami:
gdzie h – impulsowa filtru dolnoprzepustowego (funkcji skalującej)
g – odpowiedź impulsowa filtru górnoprzepustowego (falki)
A
j+1
[n]= A
j
[k]h[
2
n-k]
∞
k=-∞
S
D
j+1
[n]= A
j
[k]g[
2
n-k]
∞
k=-∞
S
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
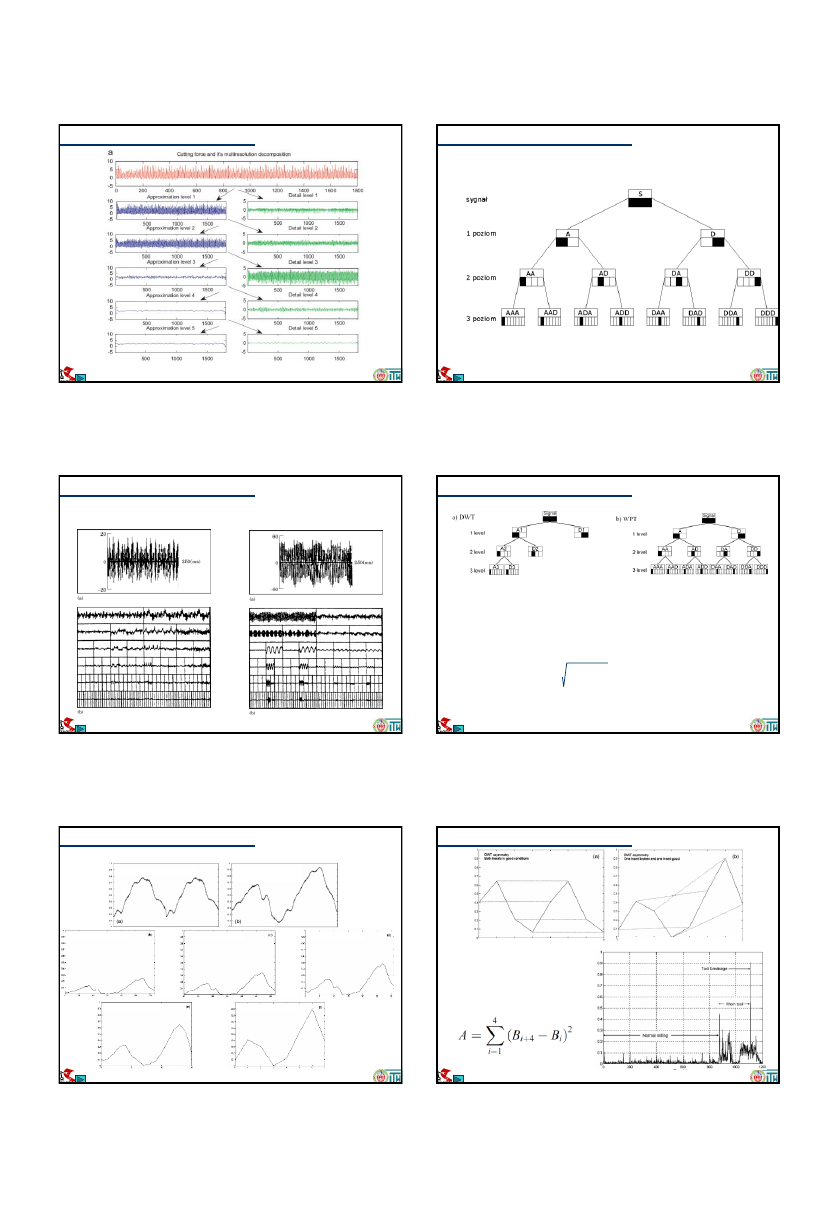
Wielopoziomowa DWT
S= A1+D1 = A2+D2+D1 = A3+D3+D2+D1
8
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
DWT siły skrawania przy frezowaniu
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Pakietowa Transformata Falkowa
WPT (Wavelet Packet Transform)
S= np. A+DA+DDA+DDD
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Zastosowanie WPT do wykrywania drgań
samowzbudnych przy toczeniu
Obróbka stabilna
Obróbka niestabilna
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Miary sygnałów oparta na transformacie falkowej
•
Jak widać współczynniki falkowe są sygnałami pasmowymi w dziedzinie czasu
•
Rzadko stosuje się je bezpośrednio
•
Zwykle są traktowane jak oddzielne sygnały, a z każdego wyznacza się miary,
podobnie jak miary sygnałów oryginalnych w dziedzinie czasu:
•
wartość średnia
•
wartość skuteczna
•
energia
1
x
av
= ̶ |x[i]|
n
n
S
i=1
1
x
RMS
= ̶
x
2
[i]
n
n
S
i=1
p= x
2
[i]
n
S
i=1
(x[i]
–
x
av
)
3
SK= ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶
(n-1)
s
3
n
S
i=1
(x[i]
– x
av
)
4
KU= ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶ ̶
(n-1)
s
4
n
S
i=1
•skośność
•kurtoza
•itd
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Zastosowanie DWT do diagnostyki frezu
Przebieg siły skrawania w czasie jednego obrotu frezu dwuostrzowego:
oba ostrza w dobrym stanie
jedno ostrze wykruszone,
jedno w dobrym stanie
detal, 1szy poziom DWT
detal, 3ci poziom DWT
detal, 2gi poziom DWT
detal, 4ty poziom DWT
detal, 5ty poziom DWT
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
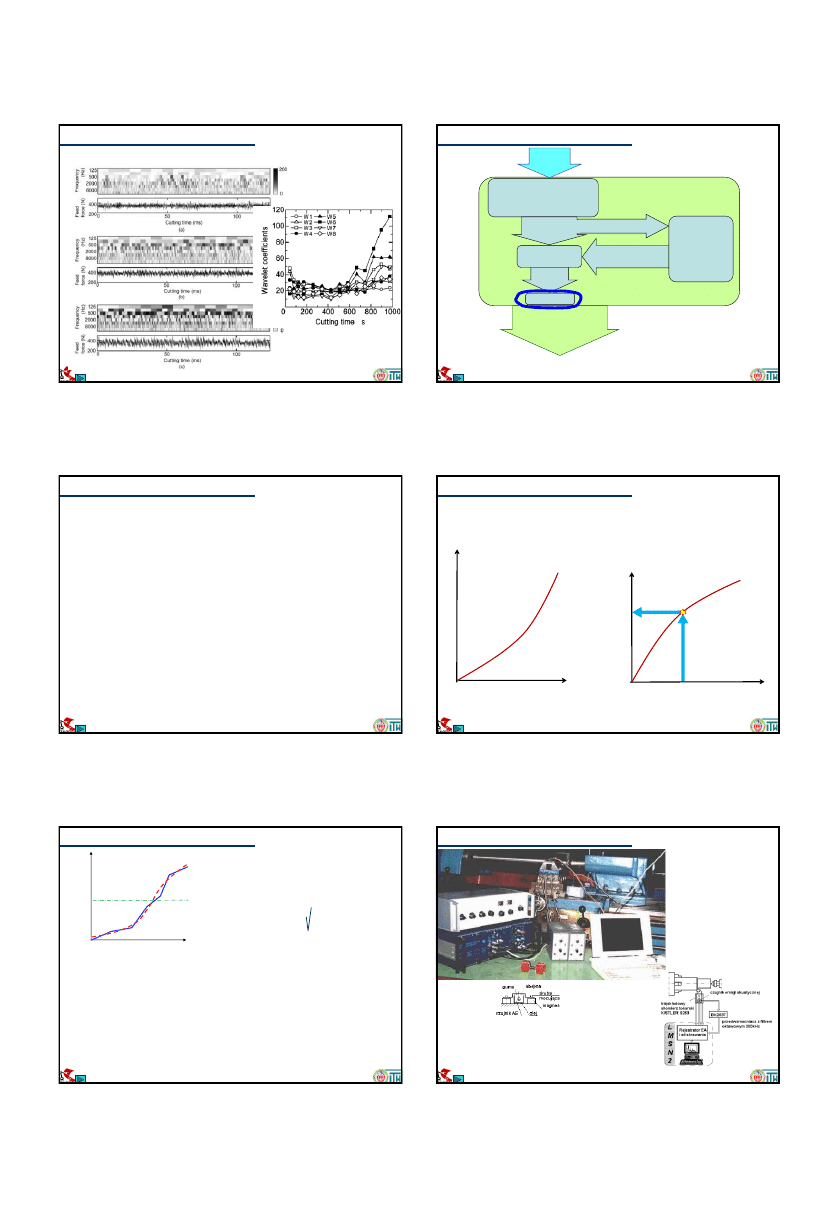
Zastosowanie DWT do diagnostyki frezu
Asymetria – różnica między pojedynczymi
wartościami siły dla kolejnych ostrzy w
czasie pełnego obrotu frezu wyznaczona z
detalu 5 poziomu DWT:
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
9
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Zastosowanie WPT do diagnostyki frezu
VB
=
0.167
mm
VB
=
0.320
mm
VB
=
0.388
mm
Siły skrawania i współczynniki falkowe w trzech stadiach zużycia ostrza (toczenie)
Obikawa T., J.Shinozuka
Int. J. Mach. Tools Manufact. 44 (2004) 1311–1318
Przebiegi wartości średnich
wybranych współczynników
falkowych
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Przetwarzanie
sygnałów
Przetwarzanie sygnałów w DNiPS
miary sygnałów
skorelowane z
monitorowanym
zjawiskiem
sygnały
analogowe
wstępna obróbka
sygnałów
(filtrowanie, A/C)
Transformacja
do dziedziny
częstotliwości
(FFT, STFT,
WT)
wyznaczanie
miar sygnałów
wybór miar
sygnały cyfrowe w
dziedzinie częstotliwości
wszystkie
miary
sygnały cyfrowe w dziedzinie czasu
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Monitorowanie oparte na wielu miarach
•
Zjawiska fizyczne (siły, AE, drgania itd.) związane monitorowaną
wielkością zależą także od wielu innych czynników
•
Związek między np. stanem narzędzia, a miarą sygnału jest złożony,
raczej statystyczny niż zdeterminowany
•
Czasem sygnał z czujnika niedokładnie odzwierciedla mierzoną
wielkość z uwagi na wpływ zakłóceń
•
Przyszłość układów monitorujących należy do układów opartych na
więcej niż jednej tylko mierze sygnału
•
Spośród wielu możliwych do wyznaczenia miar sygnałów należy
wybrać te, które niosą w sobie informacje o monitorowanym zjawisku
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Model zależności miary sygnału od stanu
narzędzia (procesu)
Wykorzystana część okresu trwałości (
D
T)
m
iar
a
syg
nał
u
(S
F)
Nadzorowanie stanu
narzędzia
SF
m
=f(
D
T)
D
T
Miara sygnału (SF)
D
T
=f
-1
(SF
m
)
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Ocena przydatności miary
1.0-
0.8-
0.6-
0.4-
0.2-
0.0-
0 20 40 60 80 100
D
T
SF
Na podstawie pomiarów wartości miary w funkcji
zużycia ostrza (
D
T) określa się model zależności
SF
m
=f(
D
T)
Ocena przydatności miary do diagnostyki stanu
narzędzia to stwierdzenie, na ile miara zależy od
tego stanu oraz ocena jakości modelu, czyli
stwierdzenie, w jakim stopniu model
SF
m
oddaje
rzeczywisty przebieg
SF
współczynnik determinacji
_________
CSK – RSK
R= ––––––––––
CSK
CSK – całkowita suma kwadratów
2
CSK = (SF
i
– SF
śr
)
S
2
RSK = (SF
i
– SF
mi
)
S
RSK – resztowa suma kwadratów
CSK-RSK – zniesiona suma kwadratów
SF
śr
SF
SF
m
Postać modelu nie ma znaczenia
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Badanie emisji akustycznej i sił skrawania przy toczeniu
Program priorytetowy “Patia”, 1996
a) schemat toru pomiarowego
b) mocowanie czujnika AE
10
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
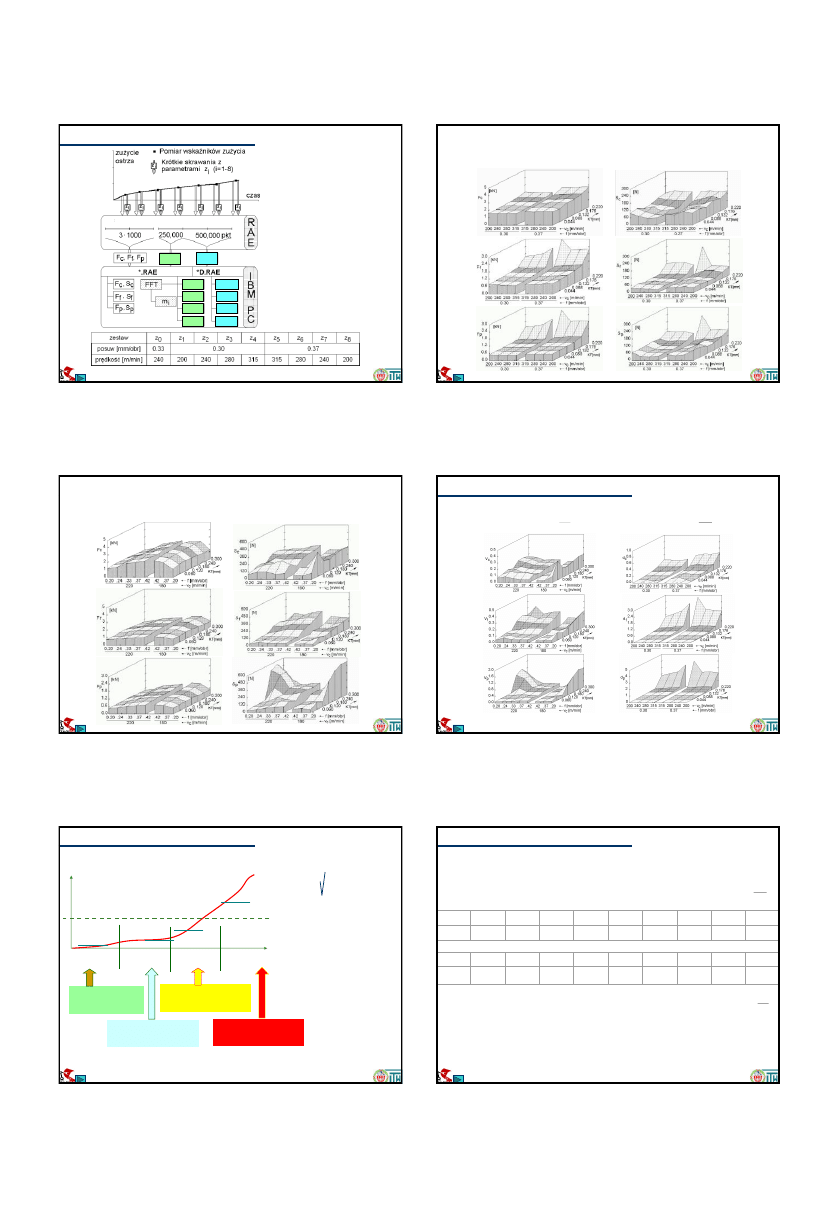
Badanie emisji akustycznej i sił skrawania przy toczeniu
Program priorytetowy “Patia”, 1996
n
i
- wypełnienie impulsów
t
i
– tempo impulsów
wi - wypełnienie wybuchów
li - tempo wybuchów
F
i
, S
i
– wartość średnia i odchylenie
standardowe składowej siły
AE
raw
AE
av
s
AE
n
j
t
j
AE
rms
s
AE,rms
AE
rms,av
l
j
w
j
schemat rejestracji sygnałów sił i AE
sygnały sił oryginalny sygnał AE
raw
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Poszukiwanie najkorzystniejszej miary sił skrawania:
średnie i odchylenia standardowe w funkcji zużycia dla
mat. obrabiany 45 (180 HB), ostrze SNUN
NT35
Program priorytetowy “Patia”, 1996
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Poszukiwanie najkorzystniejszej miary sił skrawania: średnie i
odchylenia standardowe w funkcji zużycia dla mat. obr 45 (180 HB),
ostrze SNUN
S30S
Program priorytetowy “Patia”, 1996
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Miary względne sił skrawania w funkcji zużycia
i
i
i
F
S
V
S
30
S
:
0
i
i
i
F
F
d
35
NT
:
Program priorytetowy “Patia”, 1996
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Ocena powiązania miar sygnału ze zużyciem
SF
w
narzędzie ostre:
KT< ~0.1 dla S30S
KT<~0.05 dla NT35
wyraźne ślady zużycia:
KT
0.1
0.2 dla S30S
KT
0.05
0.1 dla NT35
niebezpieczeństwo KSO
KT >0.25 dla S30S
KT > 0.15 dla NT35
znaczne pogorszenie Rz
KT
0.2
0.25 dla S30S
KT
0.1
0.15 dla NT35
__
SF
^
SF
2
^
SF
1
^
SF
3
^
SF
4
współczynnik determinacji
_________
CSK – RSK
R= ––––––––––
CSK
CSK – całkowita suma kwadratów
__
2
CSK = (SF
i
– SF )
S
^
2
RSK = (SF
i
– SF
i
)
S
RSK – resztowa suma kwadratów
CSK-RSK – zniesiona suma kwadratów
Program priorytetowy “Patia”, 1996
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Współczynniki determinacji między
miarami sił skrawania a KT
NT35
F
c
d
c
S
c
F
f
d
f
S
f
F
p
d
p
S
p
R
0.536
0.511
0.662
0.774
0.757
0.776
0.753
0.789
0.638
S30S
F
c
S
c
V
c
F
f
S
f
V
f
F
p
S
p
V
p
R
0.087
0.797
0.427
0.173
0.727
0.729
0.590
0.598
0.476
i
i
i
F
S
V
S
30
S
:
0
i
i
i
F
F
d
35
NT
:
Program priorytetowy “Patia”, 1996
11
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
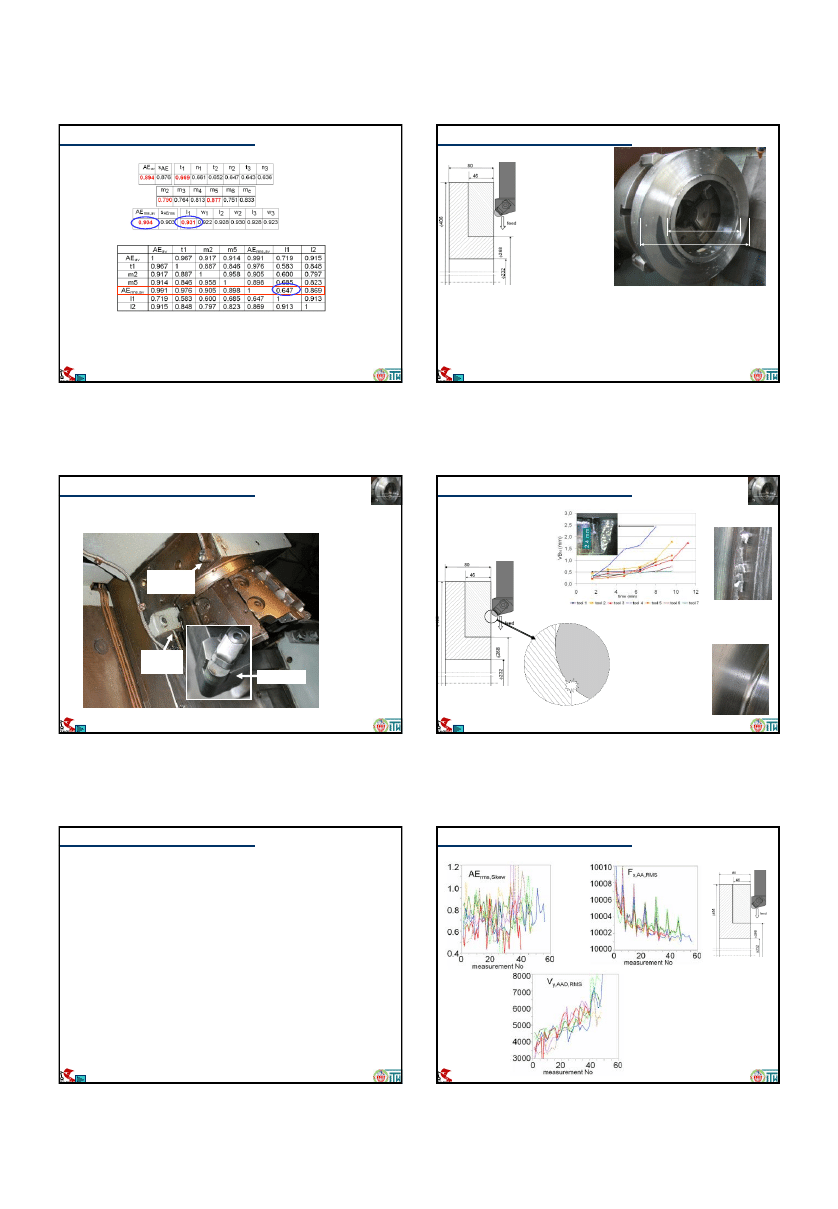
Wybór miar AE (materiał ostrza NT35)
Program priorytetowy “Patia”, 1996
Współczynniki determinacji między miarami AE, a głębokością żłobka
Współczynniki korelacji wzajemnej między najlepszymi miarami sygnału AE
•
Miary AE są w większości bardzo ze sobą skorelowane
•
Przyjmując np. AR
rms,av
nie ma sensu analizować innych miar AE z wyjątkiem
może liczby wybuchów na pierwszym poziomie.
•
Ponieważ wartość skuteczną sygnału AE mierzyć jest z reguły najłatwiej, te
dwie miary przyjęto do dalszej analizy przy użyciu sieci neuronowej.
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
406
268
Diagnostyka zużycia ostrza przy obróbce Inconel 625
Zadanie technologiczne
Parametry skrawania:
a
p
= 2.5mm
f = 0.2mm/rev
v
c
= 220m/min
Czas pojedynczego przejścia – 90s
Na jeden przedmiot kilka okresów trwałości
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Diagnostyka zużycia ostrza przy obróbce Inconel 625
– stanowisko badawcze
Tokarka
TKX 50N
Czujnik
sił F
x
F
z
Czujnik
AE
narzędzie
b)
RNGN 120700T01020
ceramika wiskersowa
CC670
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Diagnostyka zużycia ostrza przy obróbce Inconel 625
Wskaźniki stępienia:
uszkodzenia
powierzchni
zadziory
: zużycie ostrza
rejon zużycia
wrębowego
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Wyznaczane miary sygnałów
Dla każdego sygnału wyznaczano 97 miar:
miary w dziedzinie czasu:
RMS,
odchylenie standardowe, skośność, kurtoza, współczynnik szczytu
miary w dziedzinie częstotliwości (FFT):
częstotliwość dominująca, moc w dominującym paśmie, moc w wybranym
paśmie (6 pasm: 62-125Hz, 125-250Hz, 250-500Hz, 500-1000Hz, 1000-
2000Hz, 2000-4000Hz)
miary w dziedzinie czasowo-
częstotliwościowej (3 poziomowa WPT
oparta na coiflet5
, łącznie 14 pasm):
energia logarytmiczna, RMS, skośność, kurtoza, liczba i szerokość imulsów
Łącznie dla 6 sygnałów wyznaczano 582 miary
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
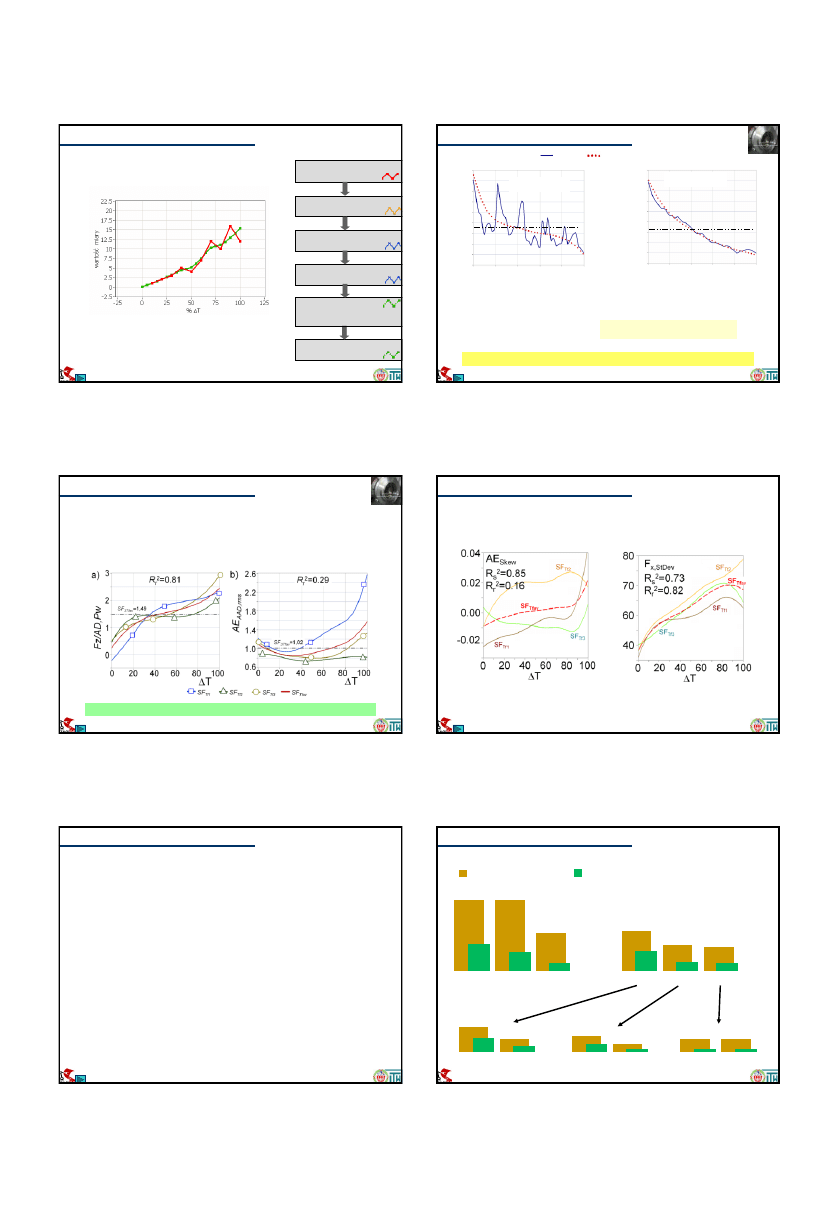
Przykładowe miary
Miara skorelowana ze stanem ostrza, zależna od średnicy
toczenia
Miara skorelowana ze
stanem ostrza, niezależna
od średnicy toczenia
Miara nieskorelowana ze stanem ostrza
12
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Usunięcie zbędnych punktów
na końcu przebiegu, F
n,1
Miara oryginalna w funkcji nr
operacji, SF
Wygładzenie zakłóceń na
końcach przebiegu,
Normalizacja w dziedzinie
czasu:
D
T = 5%, SF
T
Ekstrapolacja na końcach
przebiegu,
Filtrowanie SF
T
SF
Tf
[i] = a SF
T
[i] + b SF
Tf
[i-1]
Badanie korelacji ze stanem ostrza
- wyznaczanie modelu zależności SF
Tf
[
D
T]
Przebieg miary znormalizowany w czasie i
przefiltrowany
SF
Tf
[
D
T]
jest uznawany za model
zależności miary od wykorzystanej części okresu
trwałości ostrza
SF[NrOp]
SF
Tf
[
D
T]
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Badanie korelacji ze stanem ostrza
0
20
40
60
80 100
D
T
6
3
0
-3
R
s
2
=0,98
F
x
/D
D
D
,E
SF
Tav
=0,14
SF
T
SF
Tf
2.5
1.5
0.5
R
s
2
=0,35
AE
AAA,
Sk
SF
Tav
=1,14
0
20
40
60
80 100
D
T
S
i
(SF
Ti
– SF
Tav
)
2
–
S
i
(SF
Ti
– SF
Tfi
)
2
R
s
2
= ––––––––––––––––––––––––––––
S
i
(SF
Ti
– SF
Tav
)
2
Badanie, na ile przyjęty model (przefiltrowany przebieg) oddaje przebieg
znormalizowany w czasie.
Inaczej mówiąc – badanie gładkości miary!
Współczynnik determinacji:
Odrzuca się miary, dla których R
s
2
jest mniejsze od założonego progu
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Wybór miar powtarzalnych
Dysponując kilkoma okresami trwałości ostrza można określić powtarzalność przebiegu miary
Wyznacza się średni przebieg
SF
Tfav
i traktuje jako uśredniony model zależności SF(
D
T)
Współczynnik determinacji R
r
2
pozwala określić, na ile przebiegi są powtarzalne
S
j
S
i
(SF
Tfji
– SF
3Tfav
)
2
–
S
j
S
i
(SF
Tfji
–
SF
Tfavi
)
2
R
r
2
= –––––––––––––––––––––––––––––––––––
S
j
S
i
(SF
Tfji
– SF
3Tfav
)
2
Odrzuca się miary, dla których R
r
2
jest mniejsze od założonego progu
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Wybór miar - przykład
Miara dobrze skorelowana ze
stanem ostrza, słabo powtarzalna
Miara dobrze skorelowana ze
stanem ostrza, dobrze powtarzalna
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Eliminacja miar podobnych
Wśród miar spełniających warunki
•
skorelowania ze stanem ostrza (gładkości)
•
powtarzalności
występują miary skorelowane ze sobą, a więc nie wnoszące nowych informacji
Eliminacja zbędnych miar:
1. uszeregowanie miar pod względem powtarzalności, wybór najlepszej
2. obliczenie współczynnika korelacji między tą miarą SF
0
a kolejno
wszystkimi pozostałymi SF
j
3. odrzucenie tych, dla których współczynnik korelacji jest zbyt duży
4. powtarzanie procedury dla pozostałych miar (od punktu 1) aż nie
pozostanie żadna
S
i
(SF
0,i
– SF
0,av
)(SF
j,i
– SF
j,av
)
2
r
j
2
= –––––––––––––––––––––––––––
S
i
(SF
0,i
– SF
0,av
)
2
S
i
(SF
j,i
– SF
j,av
)
2
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Wyniki selekcji miar
Miary powiązane z
D
T
Miary powiązane z
D
T, powtarzalne
Siły Drgania AE
Siły Drgania AE
F
x
F
z
V
y
V
z
AE
RMS
AE
RAW
52
52
20
14
29
6
27
18
17
15
6
6
18
11
9
12
6
9
8
5
6
3
3
3
Wybrane przydatne miary
Po eliminacji miar podobnych
582 wyznaczone miary
13
Politechnika Warszawska, Wydział Inżynierii Produkcji, Instytut Technik Wytwarzania
Zakład Automatyzacji, Obrabiarek i Obróbki Skrawaniem
Jakieś pytania?