Granica ciągu 

 

1

 

MB 

Nieskończonym  ciągiem  liczbowym  nazywamy  dowolną  funkcję  :

  i  oznaczamy 

  lub 

 lub 

. 

Liczbę 

 nazywamy  ‐tym wyrazem ciągu. 

 
Definicja 1 

Ciąg liczbowy 

 nazywamy ograniczonym z dołu wtedy i tylko wtedy, gdy 

. 

Ciąg liczbowy 

 nazywamy ograniczonym z góry wtedy i tylko wtedy, gdy 

. 

Ciąg, który jest ograniczony z dołu i z góry, nazywamy ciągiem ograniczonym. 

 
Definicja 2 

Ciąg liczbowy 

 nazywamy rosnącym wtedy i tylko wtedy, gdy 

. 

Ciąg liczbowy 

 nazywamy malejącym wtedy i tylko wtedy, gdy 

. 

Ciąg liczbowy 

 nazywamy niemalejącym wtedy i tylko wtedy, gdy 

. 

Ciąg liczbowy 

 nazywamy nierosnącym wtedy i tylko wtedy, gdy 

. 

Ciąg liczbowy 

 nazywamy stałym wtedy i tylko wtedy, gdy 

. 

 
Definicja 3 

Niech 

 będzie ciągiem oraz 

. Mówimy, że   jest granicą ciągu 

, jeśli 

|

|

,  

co zapisujemy 

lim

lub

,

. 

 

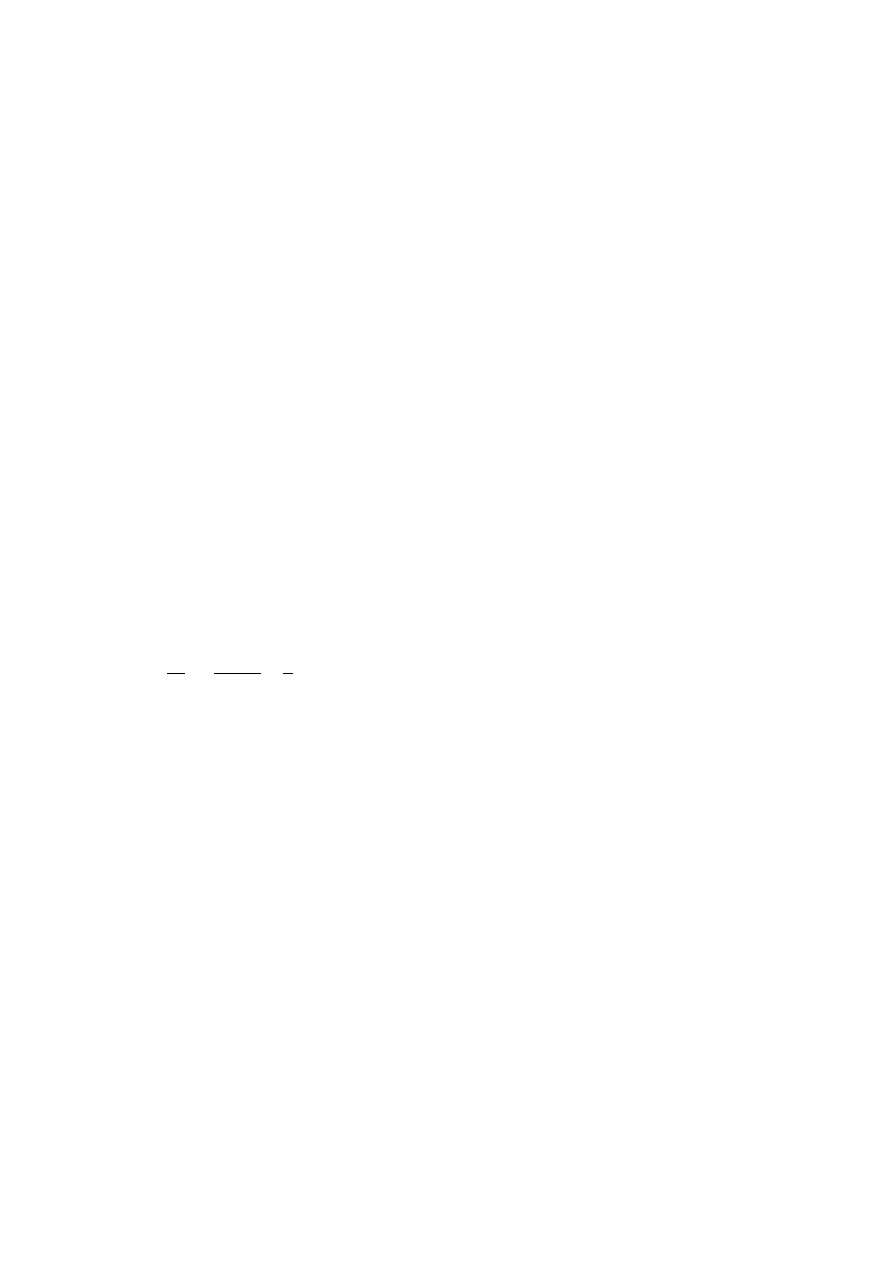
Granica ciągu 

 

2

 

MB 

Definicja 4 

1. Ciąg liczbowy 

 ma granicę niewłaściwą ∞ jeśli  

 

Mówimy wówczas, że ciąg 

 jest rozbieżny do  ∞ i oznaczamy: 

lim

∞. 

2. Ciąg liczbowy 

 ma granicę niewłaściwą  ∞ jeśli  

 

Mówimy wówczas, że ciąg 

 jest rozbieżny do   ∞ i oznaczamy: 

lim

∞. 

 
Ciąg jest zbieżny jeśli ma granicę właściwą. W przeciwnym wypadku ciąg nazywamy rozbieżnym. 

 
Twierdzenie 1 

Jeżeli lim

lim

, to 

a lim

lim

lim

, 

b lim

·

lim

· lim

· , 

c lim

lim
lim

. 

 
Twierdzenie 2 (o trzech ciągach) 

Jeżeli 

, 

, 

 są ciągami liczbowymi spełniającymi warunki: 

1 lim

lim

,  

2

, 

to ciąg 

 jest zbieżny, a ponadto  lim

. 

 
Definicja 5 

Ciąg liczbowy nazywamy ciągiem arytmetycznym, gdy dla każdego 

 zachodzi: 

, 

gdzie   jest stałą nazywaną różnicą ciągu arytmetycznego. 

 
Definicja 6 

Ciąg liczbowy nazywamy ciągiem geometrycznym, gdy dla każdego 

 zachodzi: 

· , 

gdzie   jest stałą nazywaną ilorazem ciągu geometrycznego. 

Granica ciągu 

 

3

 

MB 

Definicja 7 

Jeżeli 

 jest ciągiem liczbowym, to liczbę: 

 

nazywamy sumą   początkowych wyrazów ciągu. 

 
Twierdzenie 3 

Jeżeli 

 jest ciągiem arytmetycznym, to 

2

·

2

1

2

· . 

 
Twierdzenie 4 

Jeżeli 

 jest ciągiem geometrycznym, to 

·

1

1

dla

1

dla

1

. 

 
Twierdzenie 5 

1 lim √

1, 

2 lim √

1, gdzie

0, 

3 lim

1

1

, gdzie :

.