A

B

C

D

V

A

V

B

V

C

V

D

H

A

M

A

C

D

B

D

C

B

A

A

E

F

G

E

F

G

WYTRZYMAŁOŚĆ MATERIAŁÓW

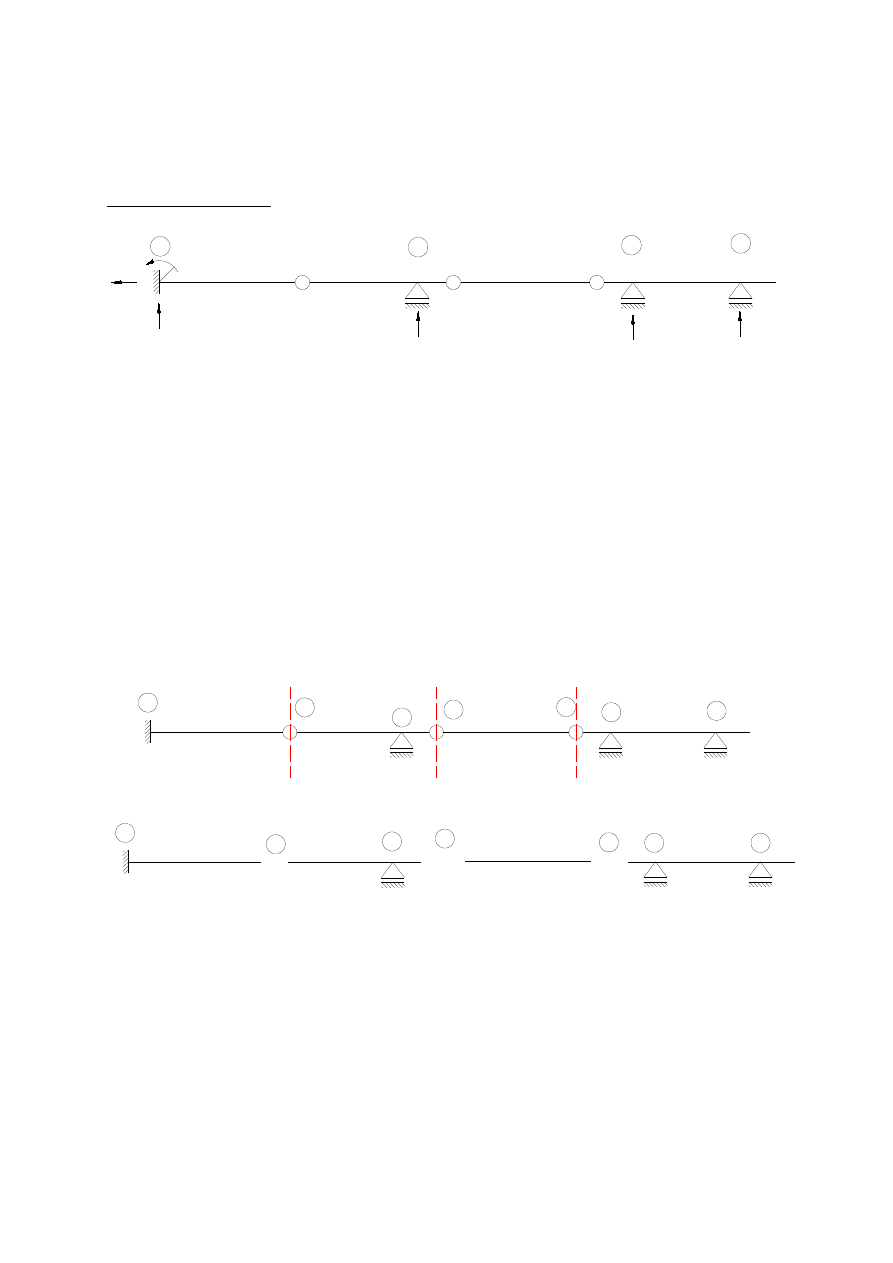
BELKI GERBERA

Są to belki ciągłe przegubowe i należą do układów statycznie wyznaczalnych (zatem

n

s

= 0).

Przykładowy schemat:

Wyznaczenie stopnia statycznej niewyznaczalności układu:

n

s

= R – P – 3

gdzie:
- R – liczba reakcji,
- P – liczba przegubów,
- 3 – liczba równań równowagi na płaszczyźnie.

Dla powyższego schematu: R = 6; P = 3 zatem

n

s

= 6 – 3 – 3 = 0.

Sposób obliczania:

Aby policzyć Belkę Gerbera w najprostszy sposób dzielimy ją w przegubach

uzyskując pojedyncze belki

Aby móc policzyć konstrukcję belki powstałe po podziale muszą być statycznie wyznaczalne
i geometrycznie niezmienne, zatem muszą opierać się na dwóch podporach przegubowych
lub skrajne mogą być utwierdzone. Zatem w powstałych po podziale belkach dokładamy
fikcyjne podpory w przegubach tak aby stały się one geometrycznie niezmienne.
Najniżej znajdują się belki, które bezpośrednio po podziale są statycznie wyznaczalne i nie
potrzebują dodatkowych podpór (utwierdzenie lub belka oparta na dwóch podporach).
Najwyżej umiejscawiamy belkę, która po podziale nie ma żadnego podparcia i potrzebuje
dwóch podpór fikcyjnych (schemat 1.) lub skrajna belka, która po podziale opiera się na
jednej podporze, jeżeli w danym układzie nie ma części nie podpartej żadną podporą
zawierającej się między dwoma przegubami (schemat 2.). Pozostałe belki umiejscawiamy
schodkowo od tej położonej najwyżej do tej położonej najniżej. Jeżeli wyżej ulokowana belka
ma w danym przegubie fikcyjną podporę to druga musi mieć w tym miejscu swobodny
koniec.

mgr inż. Hanna Weber

A

B

C

D

V

A

V

B

V

C

V

D

H

A

M

A

D

C

B

A

E

F

G

D

C

B

A

E

F

G

V

A

H

A

M

A

V

E

V

E

H

E

H

F

V

B

V

F

H

F

V

F

H

G

V

G

H

G

V

G

V

C

V

D

- f ik c y j n a p o d p o r a

WYTRZYMAŁOŚĆ MATERIAŁÓW

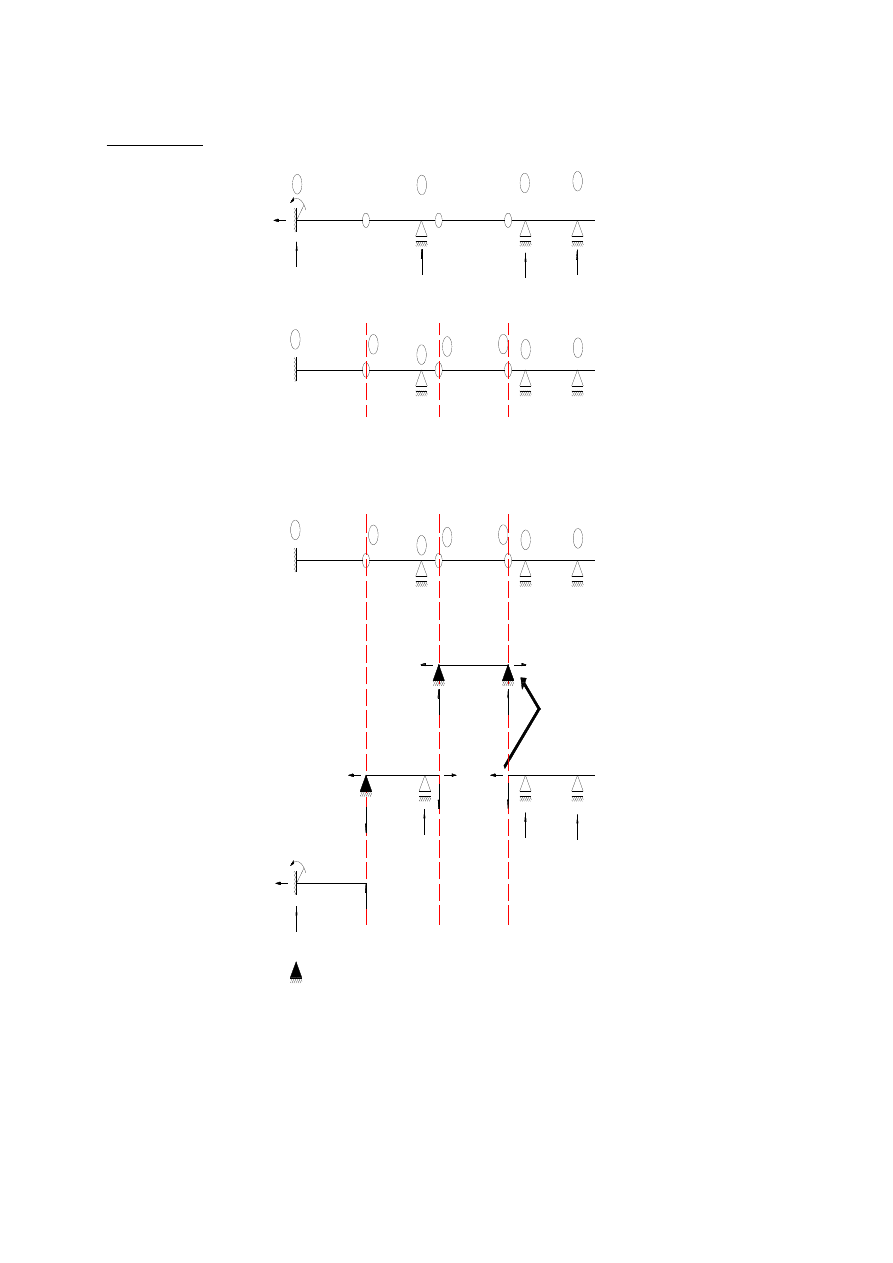
Schemat 1.:

Krok 1.: Dokonujemy podziału belki gerbera w przegubach.

Krok 2.: Wstawiamy podpory fikcyjne tak aby belki powstałe po podziale były geometrycznie
niezmienne i umiejscawiamy je na odpowiedniej wysokości:

Wyznaczamy reakcje dla poszczególnych belek oddzielnie zaczynając od tej położonej
najwyżej i schodzimy stopniowo w dół obciążając belki niżej położone wyliczonymi wcześniej
reakcjami.
W schemacie 1. najpierw liczymy część FG ( część ta jest przypadkiem belki statycznie
niewyznaczalnej, aby policzyć reakcje poziome, należy wyznaczyć H

G

z sumy rzutów na oś x

dla części GD), później części EF lub GD, na końcu zaś AE.

mgr inż. Hanna Weber

A

B

C D

V

A

V

C

V

E

H

A

M

A

E

F

G

A

B

C D

E

F

G

V

A

H

A

M

A

V

B

V

B

H

B

H

B

V

D

V

C

H

D

V

D

H

D

V

E

V

F

H

F

V

F

H

F

V

G

V

G

WYTRZYMAŁOŚĆ MATERIAŁÓW

Schemat 2.:

W schemacie 2. najpierw liczymy część FG, później DF, następnie BD, na końcu zaś AB.

Obciążenie w przegubie:
Jeżeli zdarzy się siła skupiona przyłożona w przegubie to po rozbiciu układu w przegubach
przykładamy ją na belce dolnej ( tylko i wyłącznie!!! – nie wolno jej przyłożyć na obie belki
ponieważ zwiększymy jej wartość dwukrotnie!). Moment zawsze znajduje się po jednej
stronie przegubu (lewa lub prawa), po rozbiciu układu przykładamy go na tej belce, na
której się znajdował przed podziałem bez względu czy jest to belka położona niżej czy wyżej.

mgr inż. Hanna Weber

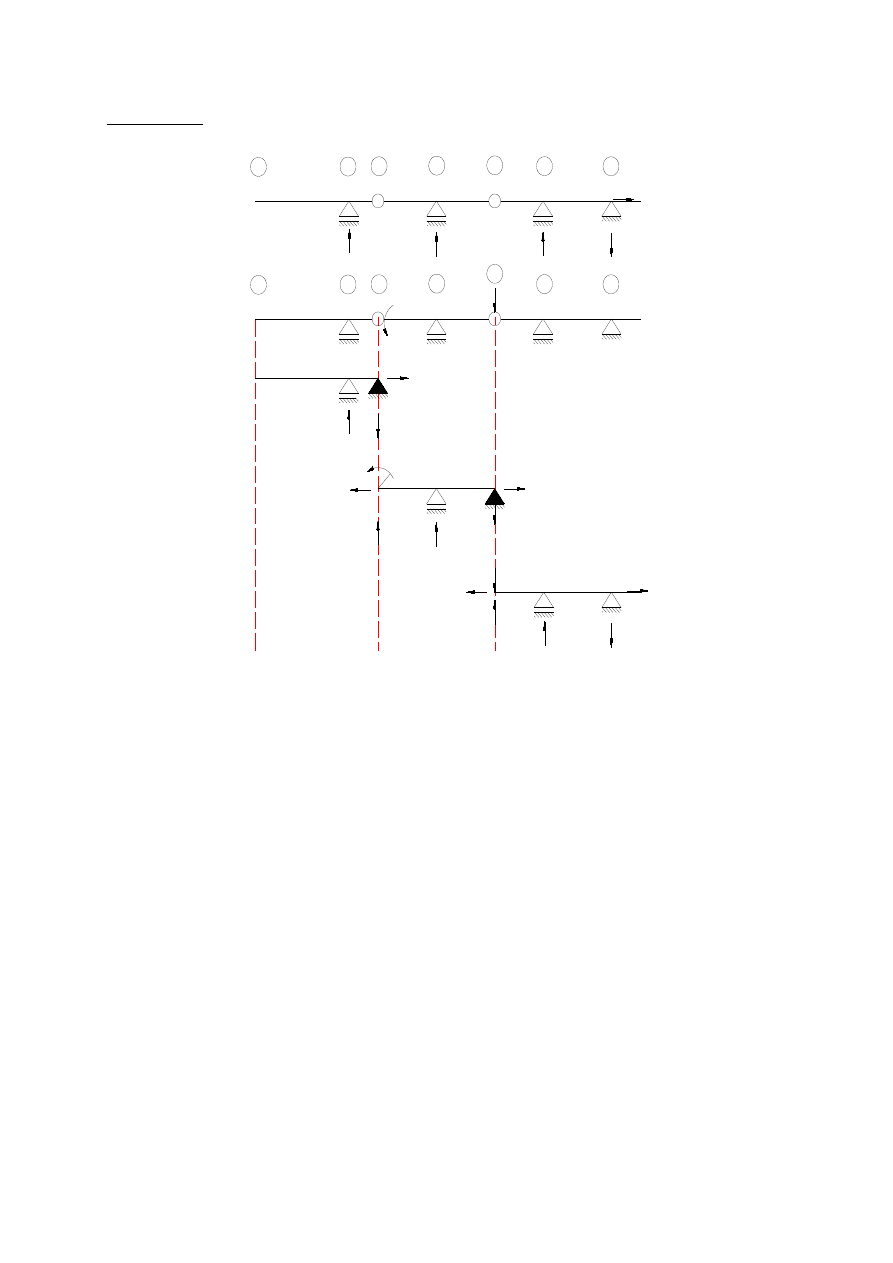
F

A

B

C

V

B

V

D

D

E

G

V

C

V

B

H

C

V

C

H

C

V

D

V

E

H

E

V

E

H

E

V

G

V

G

F

A

B

C

D

E

G

V

F

V

F

M

P

M

P

H

G

H

G

WYTRZYMAŁOŚĆ MATERIAŁÓW

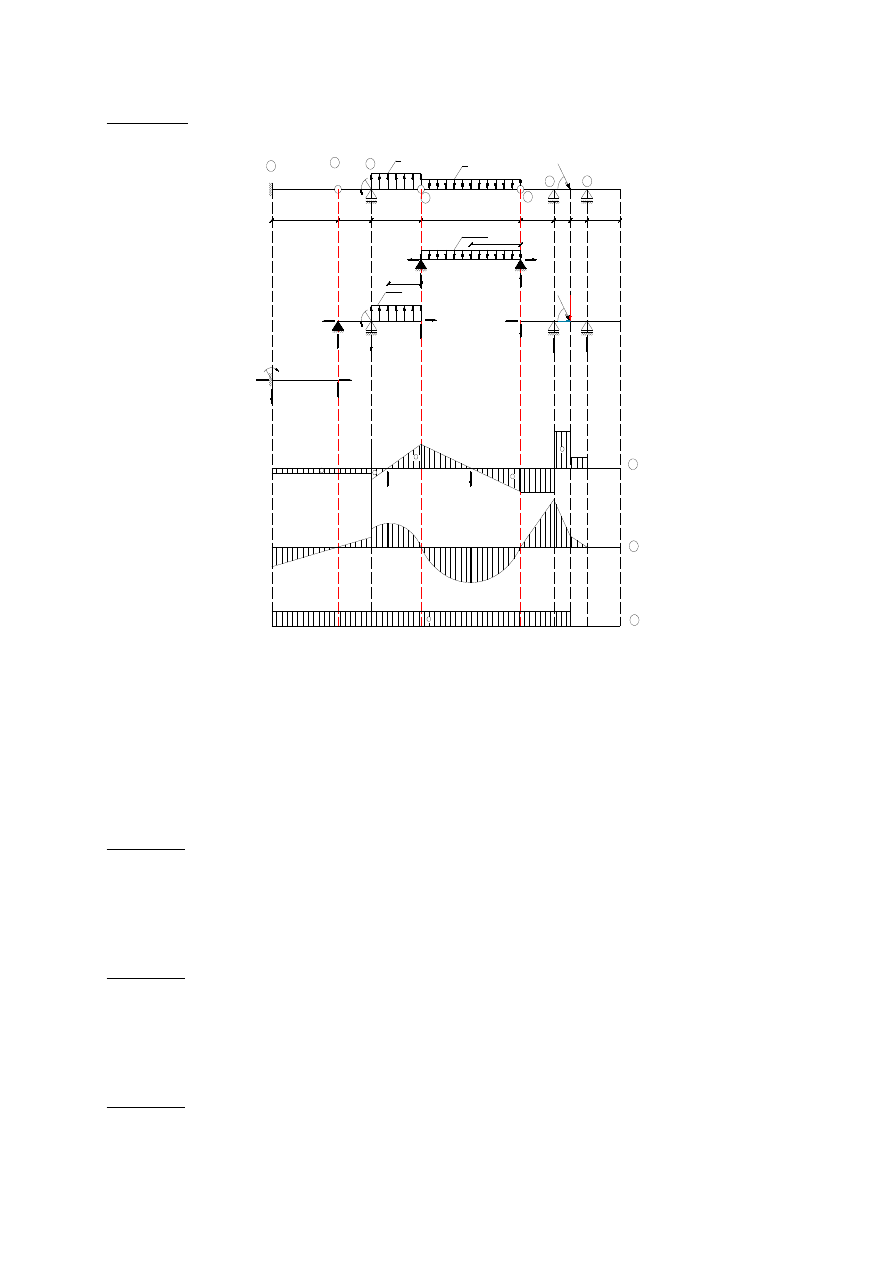
Schemat 3.:

Wykresy:
Wykresy można rysować dla każdej belki osobno i później złożyć je w całość.

mgr inż. Hanna Weber

4

2

3

6

2

1

1

2

q2= 4kN/m

q1=6kN /m

P =1 5kN

6 0

M=4kNm

A

B

C

D

E

F

G

q2= 4kN/m

V = 12kN

E

V = 12kN

D

H = 7,5kN

E

H = 7,5kN

D

P =15 kN

6 0

V = 12kN

E

H = 7,5kN

E

V = 30,495kN

F

P sin60= 12,99kN

P cos60=7,5kN

V = 5,505kN

G

q1= 6kN /m

M=4kNm

V = 12kN

D

V = 3,5kN

C

V = 2,5kN

B

H = 7,5kN

D

H = 7,5kN

B

V = 2,5kN

B

V = 2,5kN

A

H = 7,5kN

B

H = 7,5kN

A

M =10kNm

A

-

-

+

-

+

2,5

6

12

12

18,495

5,505

T

[kN]

10

5

9

12

18

5,505

24

M

[kNm]

7,5

7,5

+

N

[kN]

e

e

2

x= 2,0

x2=3,0

WYTRZYMAŁOŚĆ MATERIAŁÓW

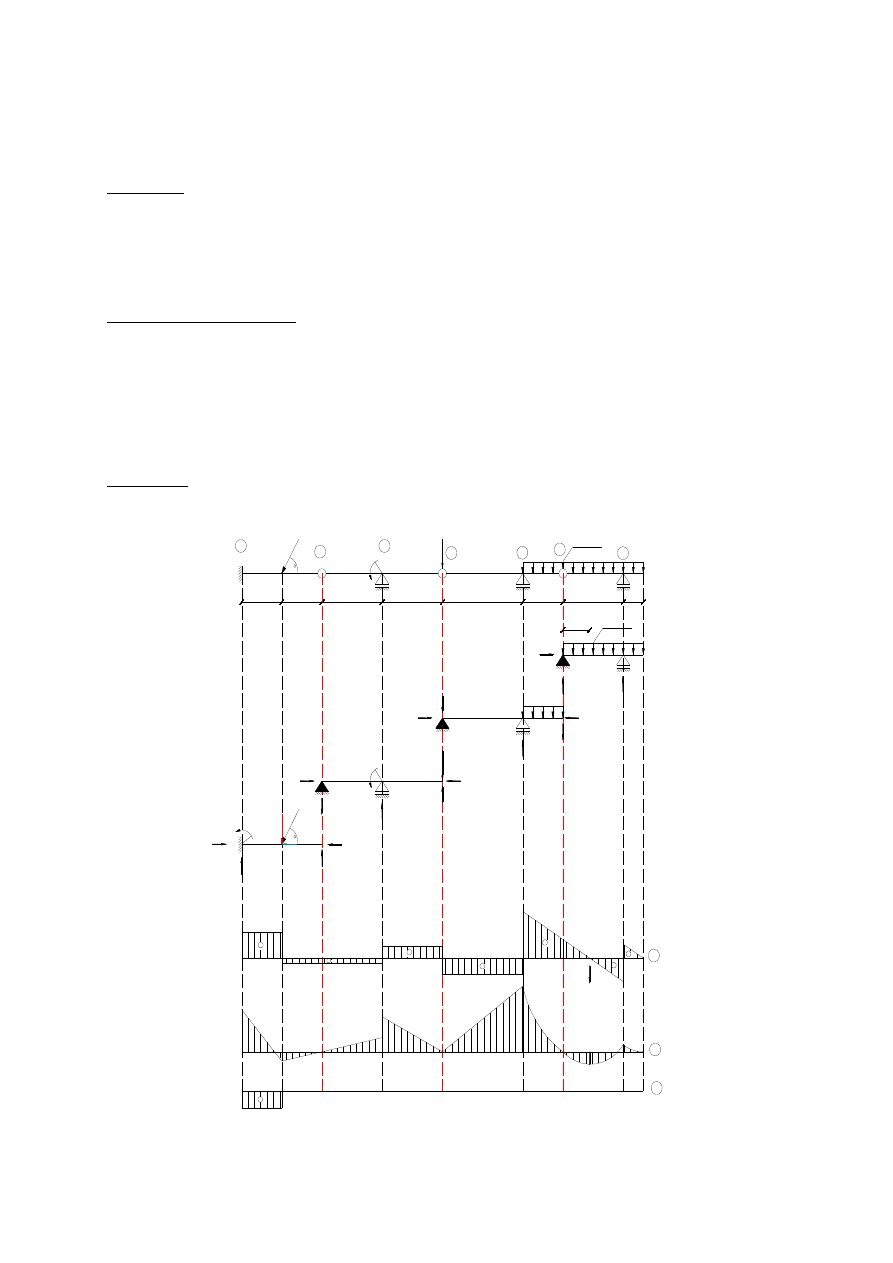
Przykład 1.
Wyznacz reakcje w poniższej belce. Narysuj wykresy sił wewnętrznych. Policz ewentualne
ekstrema.

Wyznaczenie reakcji:

Część DE:

∑F

X

= -H

D

+H

E

=0

∑M

D

= q

2

∙6∙3-V

E

∙6=0 → V

E

=3q

2

=3∙4=12kN

∑M

E

= -q

2

∙6∙3+V

D

∙6=0 → V

D

=3q

2

=3∙4=12kN

Sprawdzenie:

∑F

Y

= V

D

+ V

E

– q

2

∙6 = 12 + 12 - 4∙6 = 0

Część EG:

∑F

X

= -H

E

+ Pcos60°=0 → H

E

= Pcos60°=7,5kN → H

D

= 7,5kN

∑M

F

= - V

E

∙2+Psin60°∙1 +V

G

∙2=0 → V

G

=0,5(2 V

E

- Psin60°∙1) = 0,5(2∙12 – 12,99∙1)=5,505kN

∑M

G

= - V

E

∙4-Psin60°∙1 +V

F

∙2=0 → V

F

=0,5(2 V

E

+ Psin60°∙1) =0,5(2∙12 + 12,99∙1)=30,495kN

Sprawdzenie:

∑F

Y

= V

F

- V

E

– V

G

- Psin60° = 30,495 – 12 - 5,505 - 12,99= 0

Część BD:

∑F

X

= -H

B

+ H

D

= 0 → H

B

= H

D

=7,5kN

∑M

B

= V

C

∙2 - M – q

1

∙3∙3,5 +V

D

∙5=0 → V

C

=0,5∙(M + q

1

∙3∙3,5 - V

D

∙5) = 0,5(4 + 6∙3∙3,5 - 12∙5)=3,5kN

mgr inż. Hanna Weber

A

60

2

2

3

3

4

2

3

1

M =9kNm

P 2= 15kN

P 1=12kN

q=6 kN /m

q=6kN /m

M =9kNm

P 1=12kN

60

P 2= 15kN

Ps in60= 12,99kN

P cos 60=7,5kN

B

C

D

E

F

G

V = 16kN

G

V = 8kN

F

H = 0kN

F

H = 0kN

F

V = 8kN

F

V = 27kN

E

V = 7kN

D

H = 0kN

D

H = 0kN

D

V = 7kN

D

V = 7kN

C

V = 2kN

B

H = 0kN

B

H = 0kN

B

V = 2kN

B

V = 10,99kN

A

H = 7,5kN

A

M =17,98kN m

A

6

10

8

20

7

7

5

5

2

2

10,99

10,99

+

+

+

+

-

-

-

e

T

[kN ]

3

5,33

28

15

6

4

17,98

M

[kNm ]

-

N

[kN]

x =1,33

WYTRZYMAŁOŚĆ MATERIAŁÓW

∑M

C

= -V

B

∙2 - M – q

1

∙3∙1,5 +V

D

∙3=0 → V

B

=0,5∙(-M - q

1

∙3∙1,5 + V

D

∙3) = 0,5(-4 - 6∙3∙1,5 + 12∙3)=2,5kN

Sprawdzenie:

∑F

Y

= -V

B

– V

C

– V

D

+ q

1

∙3= - 2,5 – 3,5 - 12 + 6∙3= 0

Część AB:

∑F

X

= -H

A

+ H

B

= 0 → H

A

= H

B

=7,5kN

∑M

A

= -V

B

∙4 + M

A

=0 → M

A

=4V

B

= 4∙2,5 =10kNm

∑F

Y

= V

A

- V

B

=0 → V

A

= V

B

=2,5kN

Sprawdzenie:

∑M

B

= -V

A

∙4

+ M

A

= - 2,5∙4 + 10 = 0

Wyznaczenie ekstremum:

T[x]= V

D

- q

1

x = 0 → x = V

D

/q

1

= 12/6 = 2m

M[x] = V

D

∙x – q

1

∙x

2

/2

M[x = 2] = 12∙2 - 6∙2

2

/2 = 12kNm

T[x

2

] = V

D

– q

2

x

2

= 0 → x

2

= V

D

/q

2

= 12/4 = 3m

M[x

2

] = V

D

∙x

2

– q

2

∙x

2

2

/2

M[x

2

= 2] = 12∙3 - 4∙3

2

/2 = 18kNm

Przykład 2.
Wyznacz reakcje w poniższej belce. Narysuj wykresy sił wewnętrznych. Policz ewentualne
ekstrema.

mgr inż. Hanna Weber

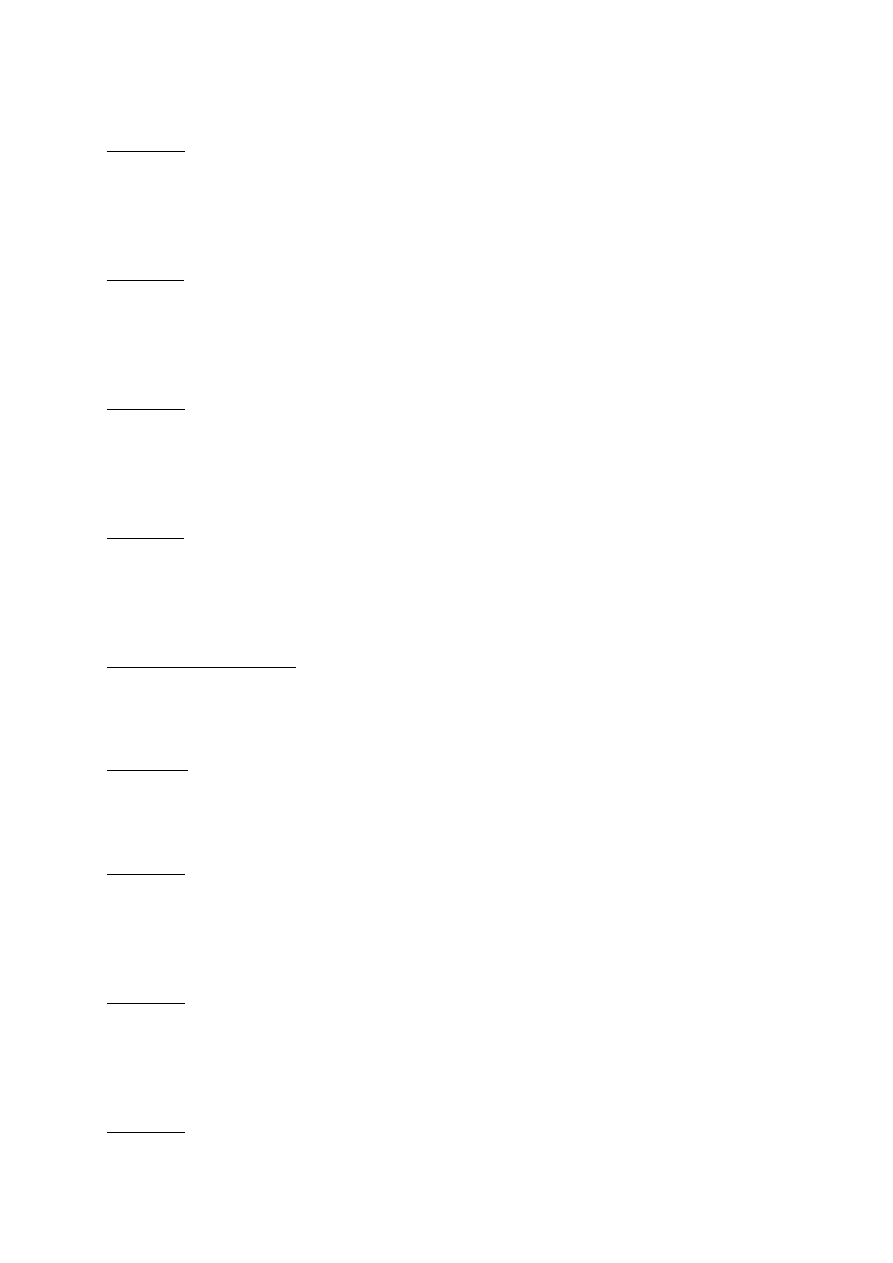
WYTRZYMAŁOŚĆ MATERIAŁÓW

Wyznaczenie reakcji:

Część FG:

∑F

X

= H

F

=0

∑M

F

= q∙4∙2-V

G

∙3=0 → V

G

=1/3(8q)=8/3∙6=16kN

∑M

G

= -q∙4∙1+V

F

∙3=0 → V

F

=4/3q=4/3∙6=8kN

Sprawdzenie:

∑F

Y

= V

F

+ V

G

– q∙4 = 8 + 16 - 4∙6 = 0

Część DF:

∑F

X

= -H

F

+ H

D

=0 → H

D

= H

F

=0kN

∑M

D

= - V

E

∙4+q∙2∙5 +V

F

∙6=0 → V

E

=0,25(6V

F

+ 10q) = 0,25(6∙8 – 10∙6)=27kN

∑M

E

= - V

D

∙4 + q∙2∙1 +V

F

∙2=0 → V

D

=0,25(2V

F

+ 2q) =0,25(2∙8 + 2∙6)=7kN

Sprawdzenie:

∑F

Y

= -V

F

– 2q + V

E

– V

D

= - 8 – 2∙6 +27 - 7= 0

Część BD:

∑F

X

= H

B

- H

D

= 0 → H

B

= H

D

=0kN

∑M

B

= -V

C

∙3 - M +P

1

∙6 - V

D

∙6=0 → V

C

=1/3∙(-M + 6P

1

- 6V

D

) = 1/3∙(- 9 + 6∙12 - 6∙7)=7kN

∑M

C

= -V

B

∙3 - M + P

1

∙3 -V

D

∙3=0 → V

B

=1/3∙(-M + 3P

1

- 3V

D

) = 1/3∙(- 9 + 3∙12 - 3∙7)=2kN

Sprawdzenie:

∑F

Y

= -V

B

+ V

C

+ V

D

- P

1

= - 2 + 7 + 7 – 12 = 0

Część AB:

∑F

X

= H

A

- H

B

– P

2

cos60°= 0 → H

A

= P

2

cos60° + H

B

=7,5 +0 = 7,5kN

∑M

A

= -V

B

∙4 - M

A

+2∙P

2

sin60°=0 → M

A

=- 4V

B

+ 2∙P

2

sin60° = - 4∙2 + 12,99∙2 =17,98kNm

∑F

Y

= V

A

+ V

B

- P

2

sin60° =0 → V

A

= P

2

sin60° - V

B

= 12,99 – 2 = 10,99kN

Sprawdzenie:

∑M

B

= V

A

∙4

- M

A

- 2∙P

2

sin60° = 4∙10,99 – 17,98 - 2∙12,99 = 0

Wyznaczenie ekstremum:

T[x]= V

F

- qx = 0 → x = V

F

/q = 8/6 = 1,33m

M[x] = V

F

∙x – q∙x

2

/2

M[x = 1,33] = 8∙1,33 - 6∙1,33

2

/2 = 5,33kNm

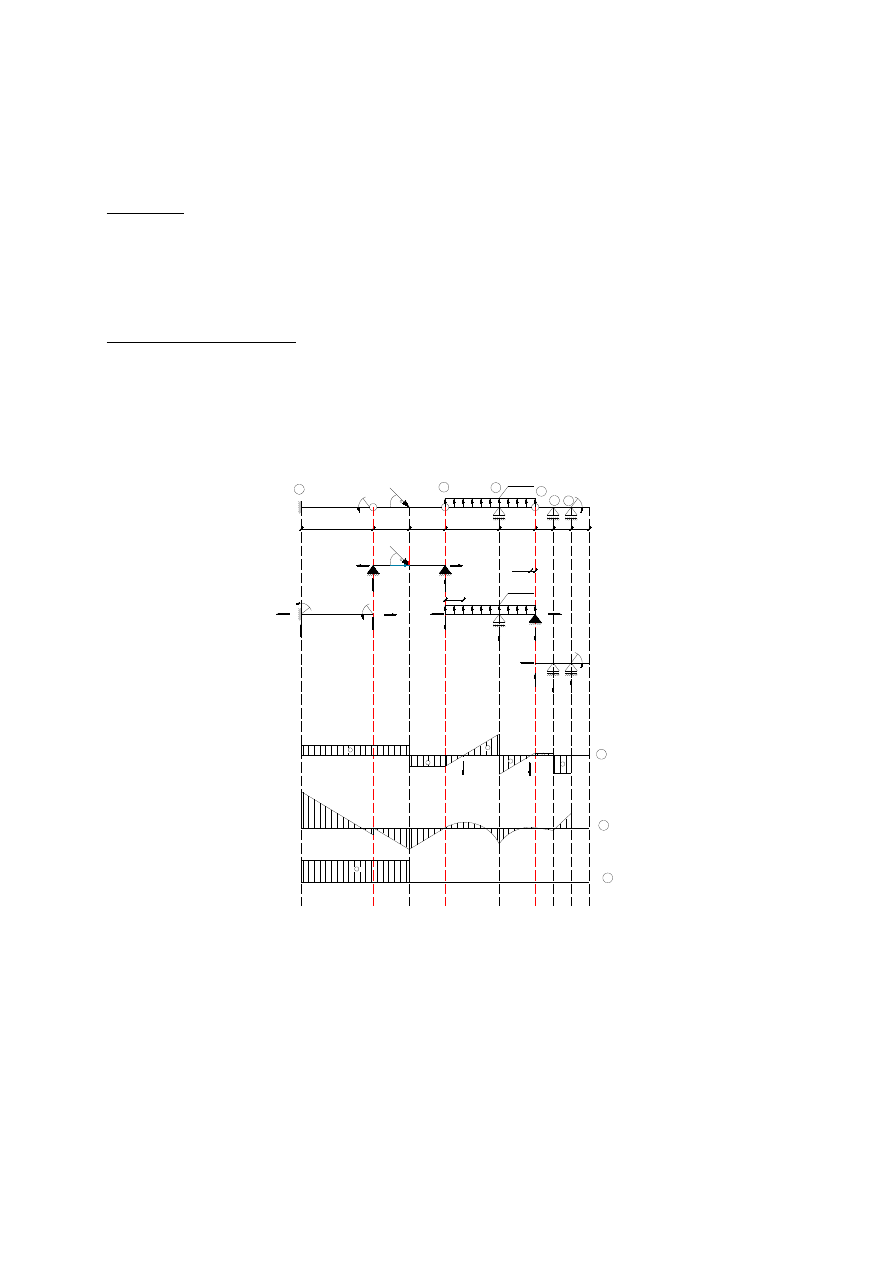
Przykład 3.
Wyznacz reakcje w poniższej belce. Narysuj wykresy sił wewnętrznych. Policz ewentualne
ekstrema.

Wyznaczenie reakcji:

Część BC:

∑F

X

= -H

B

+ H

C

+ P

1

cos45° =0 → H

B

= H

C

+ P

1

cos45°

∑M

B

= -V

C

∙4 + P

1

sin45°∙2=0 → V

C

=0,25∙( 2P

1

sin45°)=0,25∙2∙12,02=6,01kN

∑M

C

= V

B

∙4 - P

1

sin45°∙2=0 = → V

B

=0,25∙( 2P

1

sin45°)=0,25∙2∙12,02=6,01kN

Sprawdzenie:

∑F

Y

= V

B

+ V

C

– P

1

sin45° = 6,01 + 6,01 - 12,02 = 0

Część CE:

∑F

X

= -H

C

+ H

E

=0 → H

C

= H

E

∑M

D

= q∙5∙1 + V

E

∙2 – V

C

∙3=0 → V

E

=0,5(3V

C

- 5q) = 0,5(3∙6,01 – 5∙6)=1,515kN

∑M

E

= - V

D

∙2 + q∙5∙2,5 –V

C

∙5=0 → V

D

=0,5(-5V

C

+ 12,5q) =0,5(- 5∙6,01 + 12,5∙6)=22,475kN

Sprawdzenie:

∑F

Y

= -V

C

+ 5q – V

D

– V

E

= - 6,01 + 5∙12 – 22,475 – 1,515 = 0

Część EG:

∑F

X

= - H

E

= 0 → H

E

= 0kN → H

C

= 0kN → H

B

= 0 + P

1

cos45° = 0 + 12,02 = 12,02kN

mgr inż. Hanna Weber

P1=17kN

45

M =4kNm

M =8kNm

q=6kN/m

4

2

2

3

2

1

1

1

A

C

D

E

F G

P1=17kN

45

M =4kNm

q=6kN/m

M =8kNm

V = 6,01kN

A

H = 12,02kN

A

M =20,04kNm

V = 6,01kN

B

H = 12,02kN

B

H = 12,02kN

B

V = 6,01kN

B

V = 6,01kN

C

H = 0kN

C

H = 0kN

C

V = 6,01kN

C

V = 22,475kN

D

V = 1,515kN

E

H = 0kN

E

H = 0kN

E

V = 1,515kN

E

V = 9,515kN

G

V = 11,03kN

F

Psin45=12,02kN

Pcos45=12,02kN

9,515

1,515

10,485

11,99

6,01

6,01

6,01

6,01

+

+

+

-

-

-

8

1,515

0,19

8,97

3,01

12,02

4

20,04

12,02

12,02

+

T

[kN]

M

[kNm]

N

[kN]

e

e

2

x=1

x2=0,25

A

1

1

2

2

WYTRZYMAŁOŚĆ MATERIAŁÓW

∑M

F

= -V

G

∙1 + M

2

+ V

E

∙1 =0 → V

G

= M

2

+ 1V

E

= 8 + 1∙1,515 = 9,515kN

∑M

G

= -V

F

∙1 + M

2

+ V

E

∙2 =0 → V

F

= M

2

+ 2V

E

= 8 + 2∙1,515 = 11,03kN

Sprawdzenie:

∑F

Y

= -V

F

+ V

E

+ V

G

= - 11,03 + 1,515 + 9,515 = 0

Część AB:

∑F

X

= - H

A

+ H

B

= 0 → H

A

= H

B

= 12,02kN

∑M

A

= V

B

∙4 - M

A

– M

1

=0 → M

A

= 4V

B

– M

1

= 4∙6,01 - 4 =20,04kNm

∑F

Y

= V

A

- V

B

=0 → V

A

= V

B

= 6,01kN

Sprawdzenie:

∑M

B

= V

A

∙4

- M

A

- M

1

= 4∙6,01 – 20,04 - 4 = 0

Wyznaczenie ekstremum:

T[x]= -V

C

+ qx = 0 → x = V

C

/q = 6,01/6 = 1m

M[x] = -V

C

∙x + q∙x

2

/2

M[x = 1] = -6,01∙1 + 6∙1

2

/2 = 3,01kNm

T[x

2

]= V

E

– qx

2

= 0 → x

2

= V

E

/q = 1,515/6 = 0,25m

M[x

2

] = -V

E

∙x

2

+ q∙x

2

2

/2

M[x = 0,998] = -1,515∙0,25 + 6∙0,25

2

/2 = 0,19kNm

mgr inż. Hanna Weber