Ć w i c z e n i e 25

BADANIE ZJAWISKA HALLA

25.1 Wstęp teoretyczny

Zjawisko Halla polega na powstawaniu poprzecznej różnicy potencjałów na płytce półprzewodnika
lub metalu, przez którą przepływa prąd elektryczny, jeżeli jest ona umieszczona w polu magnetycz-
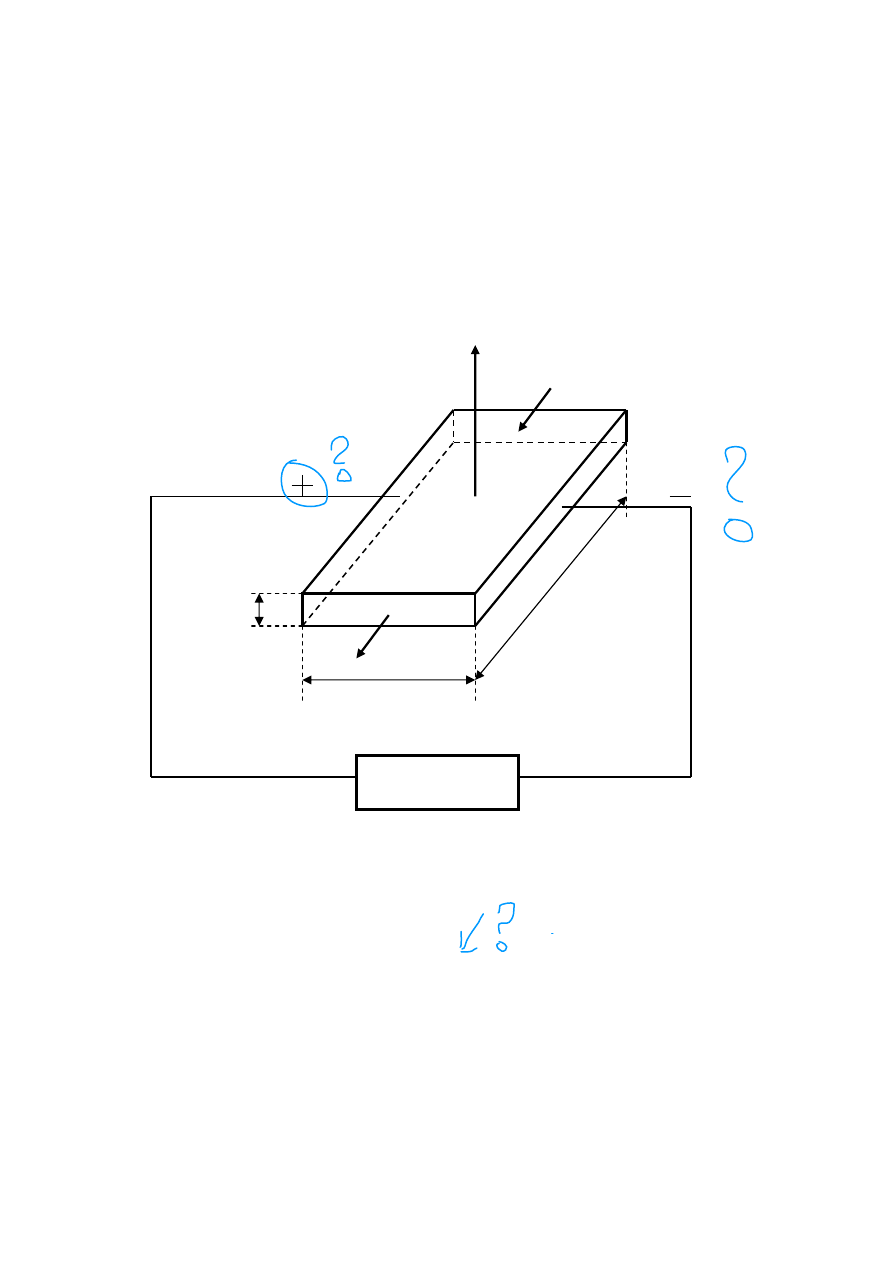
nym prostopadłym do kierunku przepływu prądu (rys. 25.1).

B

I

l

d

b

Napięcie

Halla

Rys. 25.1. Zjawisko Halla.

W przewodzeniu prądu biorą udział elektrony. Na poruszające się z prędkością

vr

elektrony, w polu

magnetycznym o indukcji

B

r

działa siła Lorentza

(

)

B

v

e

F

L

r

r

r

×

=

(25.1)

prostopadła do obu powyższych wektorów (ćw.20). Powoduje ona zakrzywienie torów elektronów
w kierunku jednej ze ścianek płytki półprzewodnika. Gromadzą się one na jednej powierzchni
kryształu, a na przeciwległej występuje ich brak. W przypadku, gdy wektor prędkości

vr

elektronów

jest prostopadły do wektora indukcji

B

r

, możemy napisać następujące wyrażenie na wartość bez-

względną rozpatrywanej siły.

B

v

e

F

L

=

(25.2)

W warunkach równowagi poprzeczne pole elektryczne E

H

wywołane efektem Halla (wynikające z

nagromadzonego na bocznych ściankach ładunku) będzie działało na elektrony siłą e E

H

równą co

do wartości sile Lorentza, przeciwdziałając dalszemu odchylaniu elektronów. A więc zachodzi
wówczas równość

B

v

e

E

e

H

=

(25.3)

Ponieważ gęstość prądu płynącego przez płytkę wynosi j = e n v (gdzie n – koncentracja elektro-

nów) można dokonać podstawienia

n

j

v

e

= do równania (25.3). Po przekształceniu otrzymamy:

B

j

R

n

e

B

j

E

H

=

=

(25.4)

gdzie

n

e

1

R

=

nazywamy stałą Halla.

Przeprowadzając doświadczenie mierzymy nie poprzeczne pole elektryczne (E

H

) i gęstość zasilają-

cego prądu (j), lecz poprzeczną różnicę potencjałów (tzw. napięcie Halla U

H

) oraz natężenie zasila-

jącego prądu (I). Stosując widoczne na rys. 25.1 oznaczenia opisujące geometrię próbki możemy
napisać zależności:

d

b

I

j

=

;

b

U

E

H

H

=

(25.5)

Po podstawieniu ich do związku (25.4) otrzymujemy wyrażenie na napięcie Halla.

d

I

B

R

U

H

=

(25.6)

Widzimy więc, że w doświadczeniu z próbką półprzewodnika o znanej geometrii, wykonując po-
miar napięcia Halla U

H

możemy wyznaczyć stałą Halla R, a z niej koncentrację nośników ładunku

(n) w półprzewodniku.

H

U

d

e

I

B

n

=

(25.7)

Należy pamiętać, że w półprzewodniku istnieją dwa rodzaje nośników ładunku: elektrony i dziury
(ćw.18), w obecności pola magnetycznego są one odchylane w kierunku tej samej ścianki próbki. A
więc odchylenie dziur powoduje zmniejszenie napięcia Halla powstałego w wyniku odchylenia
elektronów. Dlatego też omawiane zjawisko nadaje się do pomiaru koncentracji nośników ładunku
tylko w półprzewodnikach domieszkowanych, w których koncentracja elektronów jest dużo więk-
sza od koncentracji dziur

)

p

n

(

〉〉

lub odwrotnie

)

n

p

(

〉〉

. Doświadczenie pozwala rozróżnić, z

którym z tych przypadków mamy do czynienia, gdyż znak napięcia Halla zależy od rodzaju prze-
wodnictwa płytki półprzewodnikowej. Jeżeli przewodnictwo jest elektronowe

)

p

n

(

〉〉

, to U

H

ujemne. Jeżeli przewodnictwo jest dziurowe

)

n

p

(

〉〉

to U

H

dodatnie. Wyznaczanie napięcia Halla

jest jednym z najdokładniejszych sposobów określenia koncentracji nośników prądu w materiałach
półprzewodnikowych domieszkowanych.

Wyprowadzając równanie (25.6) założono, że w warunkach równowagi siła Lorentza kompensuje
siłę wywołaną hallowskim polem elektrycznym E

H

, czyli że w kierunku poprzecznym w płytce nie

płynie prąd elektryczny. Zatem pomiar napięcia Halla należy przeprowadzić bez przepływu prądu
w tym kierunku. W tym celu zazwyczaj stosuje się kompensacyjne metody pomiaru małych napięć,
woltomierze lampowe i cyfrowe o dużej rezystancji wejściowej lub też elektrometry.

Mierząc dodatkowo konduktywność (

σ) lub rezystywność (ρ) próbki

d

b

V

I

n

e

1

l

n

=

=

=

µ

ρ

σ

(25.8)

gdzie V - napięcie przyłożone z zewnątrz do próbki, można wyznaczyć ruchliwość (

µ) nośników

większościowych (w tym wypadku elektronów):

n

e

d

b

V

I

l

n

=

µ

(25.9)

3

5

4

6

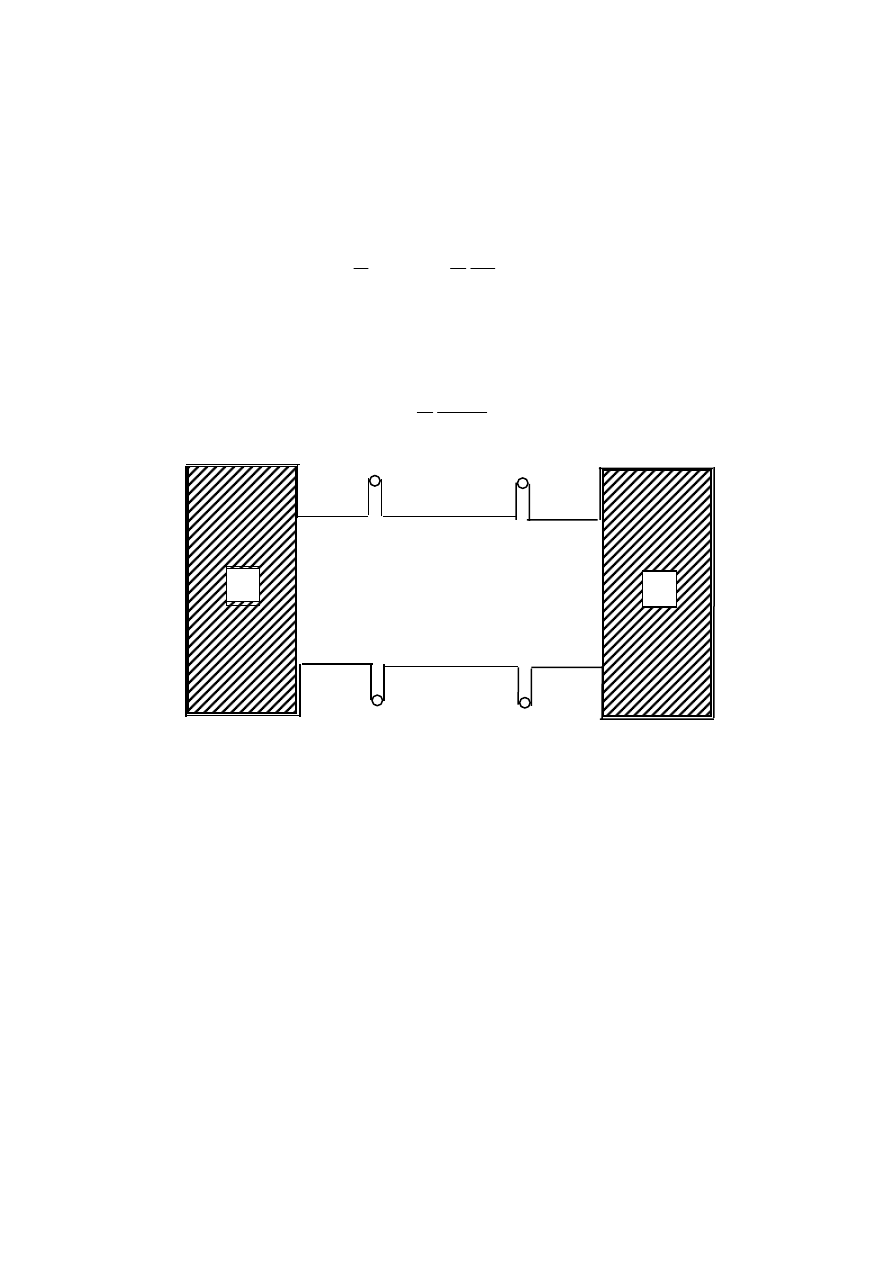
Rys. 25.2. Kształt próbki do pomiarów napięcia Halla.

Próbka do pomiaru napięcia Halla powinna mieć specjalne kontakty, aby wyeliminować ujemne
efekty utrudniające pomiar (wstrzykiwanie nośników, zwieranie próbki, rekombinację nośników).
Przykładowy kształt próbki do pomiaru napięcia Halla przedstawia rys. 25.2. Prąd płynie między
kontaktami (1) i (2), napięcie Halla mierzymy między kontaktami (3-4) lub (5-6).
Zjawisku temu towarzyszy szereg efektów utrudniających pomiar napięcia. Są to:

a) zjawisko Ettingshausena,
b) zjawisko Nerneta
c) zjawisko Righiego-Leduca
d) napięcie asymetrii.

Niemniej wartość napięcia Halla może być znaleziona, jeżeli wykona się cztery niezależne pomiary
napięć (

4

3

2

1

U

,

U

,

U

,

U

) przy dwu przeciwnych kierunkach przepływu prądu I i przy dwu prze-

ciwnych zwrotach indukcji B. Wówczas:

1

2

2

4

U

U

U

U

U

4

3

2

1

H

−

+

−

=

(25.10)

W układzie laboratoryjnym napięcie mierzymy woltomierzem cyfrowym. Próbki półprzewodniko-
we z kontaktami omowymi i z dołączonymi przewodami są na stałe zamocowane do specjalnych
płytek. Końcówkę przewodów próbki dołącza się do układu pomiarowego poprzez gniazdo w pul-
picie. Próbki umieszcza się między biegunami magnesu trwałego wytwarzającego pole magnetycz-
ne o indukcyjności 0,36 T.

25.3. Przebieg pomiarów

1. Pokrętło ustalające napięcie na zasilaczu prądu stałego ustawić w położeniu zerowym (lewe

skrajne położenie).

2. Podłączyć próbkę do gniazdka pomiarowego.
3. Uzyskać od wykładowcy pozwolenie na rozpoczęcie pomiarów.
4. Ustawić prąd płynący przez próbkę I=3 mA za pomocą pokrętła zasilacza prądu stałego.
5. Wykonać cztery następujące pomiary napięcia na zaciskach (3-4) (rys.25.2 ) przy przełączniku

W

1

przełączonym w położenie (1):

U

1

– przełącznik W

2

w położeniu 1, próbka po lewej stronie płytki,

U

2

– przełącznik W

2

w położeniu 2, próbka po lewej stronie płytki,

U

3

– przełącznik W

2

w położeniu 2, próbka po prawej stronie płytki,

U

4

– Przełącznik W

2

w położeniu 1, próbka po prawej stronie płytki.

U w a g a :

Odczyt napięć przeprowadzić razem ze znakiem.

6. Wyjąć próbkę z magnesu i zmierzyć wartość napięcia U

3-5

między kontaktami (3-5) (przełącznik

W

1

w położeniu 2). Pomiaru dokonać dla obu kierunków przepływu prądu (dla dwóch położeń

przełącznika W

2

). Wyznaczyć wartość średnią odczytów bezwzględnych.

7. Czynności wg punktów 4 – 6 powtórzyć dla pozostałych próbek.

25.4. Opracowanie wyników pomiarów.

1. Wyznaczyć napięcie Halla korzystając ze wzoru (25.10).
2. Na podstawie znaku napięcia Halla określić rodzaj przewodnictwa.
3. Wyznaczyć koncentrację nośników ładunku korzystając ze wzoru (27.7). Przyjąć indukcję ma-

gnetyczną B = 0,36 T.

4. Obliczyć ruchliwość nośników korzystając ze wzoru (25.9) – w tym przypadku V = U

3-5

Wy-

miary próbek są podane przy stanowisku.

5. Wyznaczyć graniczne błędy (względne i bezwzględne) koncentracji i ruchliwości nośników

ładunku. W tym celu można posłużyć się zależnością (W.2.14) umieszczoną we wstępie. W ce-
lu oszacowania błędu granicznego należy określić błędy

∆I, ∆U

H

i

∆U

3-5

, przy czym należy

uwzględnić metodę pomiaru, użyty zestaw aparatury, staranność przeprowadzenia pomiarów,
czułość przyrządów itp. Wartości poszczególnych błędów (

∆l, ∆b, ∆d i ∆B) przekonsultować z

prowadzącym ćwiczenie.

6. Czynności wg punktów 1-5 wykonać dla wszystkich próbek.

7. Dokonać oceny otrzymanych wyników. Przedstawić wnioski.

25.5. Pytania kontrolne

1. Omówić zjawisko Halla.
2. Wyprowadzić wzór na napięcie Halla.
3. Omówić zjawiska towarzyszące pomiarowi napięcia Halla.
4. Podać zasadę pomiaru napięcia hallowskiego.
5. Czy zjawisko Halla można wykorzystać do pomiaru indukcji magnetycznej?
6. Wykonano dwie próbki tych samych rozmiarów, lecz z innych materiałów: jedną z metalu, dru-

gą z półprzewodnika. W której z próbek napięcie Halla będzie większe, jeżeli przez każdą z
nich przepływa jednakowy prąd I i obie są umieszczone w tym samym polu magnetycznym o
indukcji B?

L i t e r a t u r a

[1] Boncz-Brujewicz W.L., Kałasznikow S.G.: Fizyka półprzewodników. PWN, Warszawa 1985.
[2] Smith R.A.: Półprzewodniki. PWN, Warszawa 1966.
[3] Szalimowa K.W.: Fizyka półprzewodników. PWN, Warszawa 1974.
[4] Wert Ch.A., Thomson R.M.: Fizyka ciała stałego. PWN, Warszawa 1974.