BADANIE WSPÓŁCZYNNIKA SPĘCZANIA WIÓRA

5-1

5. BADANIE WSPÓŁCZYNNIKA SPĘCZANIA WIÓRA

5.1. Cel ćwiczenia

Celem ćwiczenia jest ustalenie zależności jakościowych i ilościowych dotyczących współ-

czynnika spęczania

Λh i położenia umownej płaszczyzny ścinania. Ponadto zapoznanie się z

metodyka wyznaczania współczynnika spęczania wióra oraz badanie wpływu parametrów

skrawania na ten współczynnik.

5.2. Wstęp

5.2.1. Obszar tworzenia wióra

linia
skrawania

wiór

ostrze

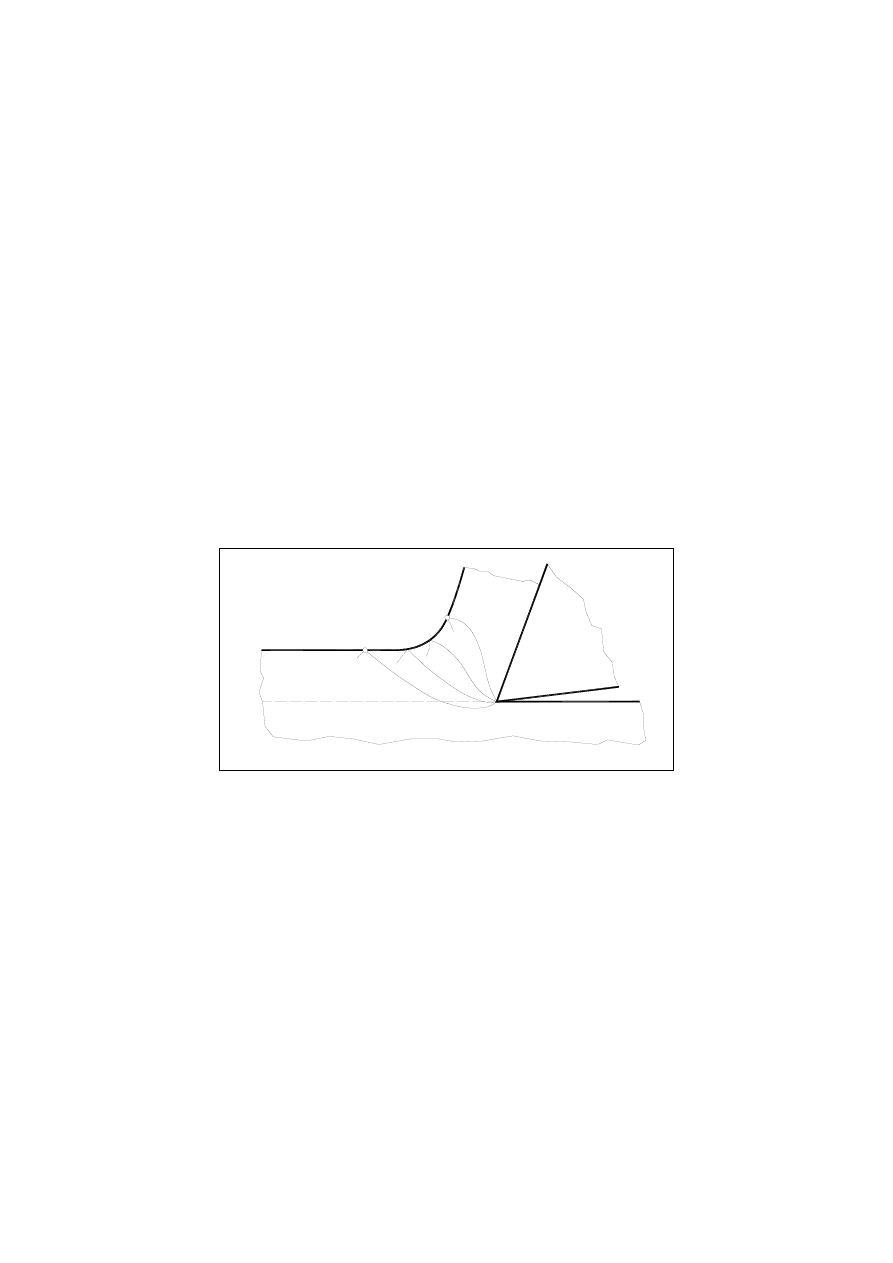
Rys. 5.1 Obszar tworzenia wióra przy skrawaniu swobodnym (ortogonalnym)

Trudności w przedstawieniu rzeczywistego, trójwymiarowego procesu odkształcenia pla-

stycznego w strefie skrawania powoduje, że do jego analizy rozpatruje się przypadek dwu-

wymiarowego (płaskiego) odkształcenia plastycznego, który występuje przy tzw. skrawaniu

prostokątnym (ortogonalnym) swobodnym. Na rys. 5.1 przestawiono zarys obszaru tworzenia

wióra w dowolnym przekroju prostopadłym do krawędzi skrawającej. Obszar ten jest ograni-

czony:

1. początkową granicą odkształcenia plastycznego (linia OP),

2. zewnętrzną granicą odkształcenia plastycznego (linia PK),

3. końcową granicą odkształcenia plastycznego (linia KO).

5-2

W teorii skrawania metali używane są zamiennie trzy wielkości charakteryzujące proces od-

kształcenia plastycznego w strefie tworzenia wióra [1, 2, 4]:

1. względne odkształcenie postaciowe (nie omawiane w tym ćwiczeniu),

2. spęczanie wióra,

3. kąt ścinania (kąt poślizgu, kąt odrywania).

5.2.2. Stopień odkształcenia plastycznego warstwy skrawanej

Rys. 5.2

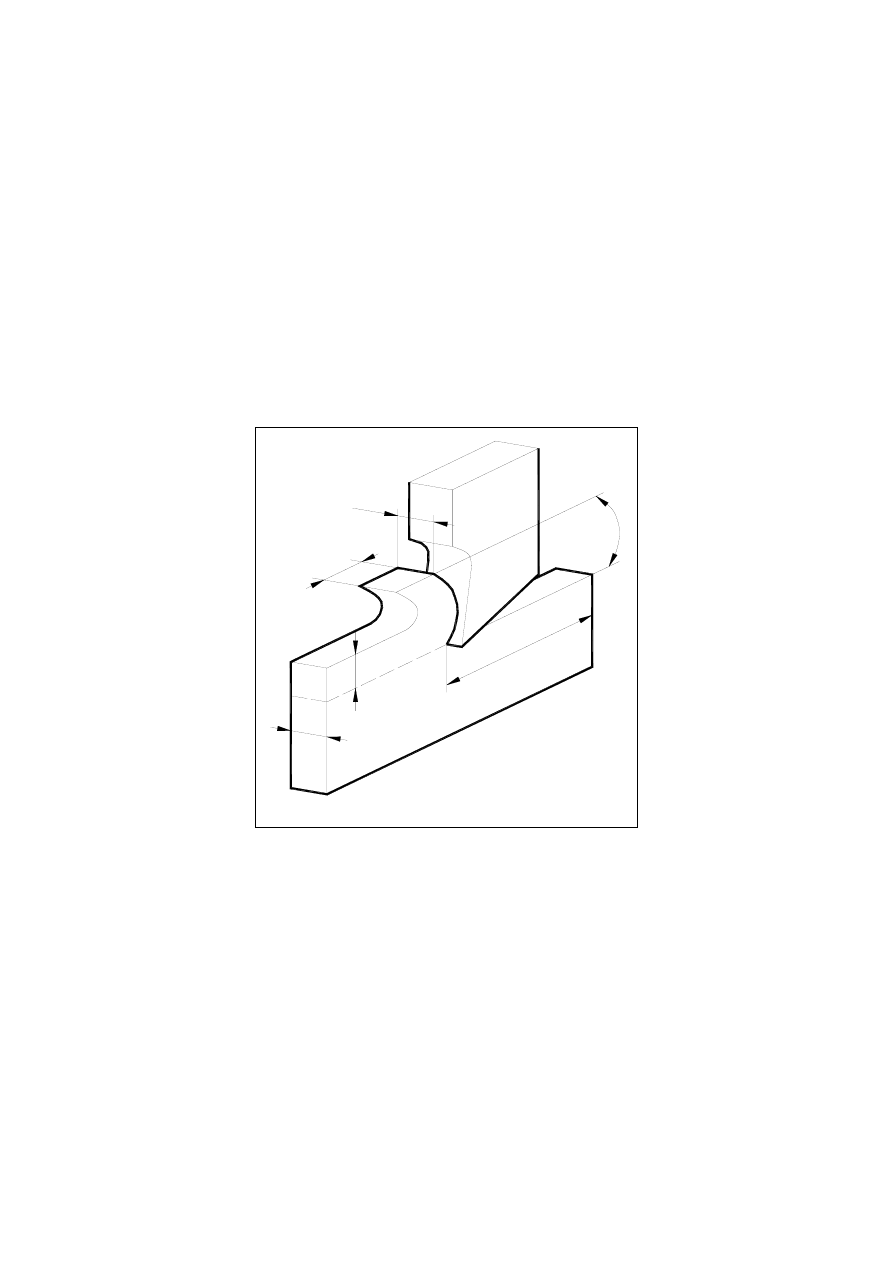
Wymiary warstwy skrawanej i wióra przy skrawaniu swobodnym (ortogonalnym)

Odkształcenie plastyczne w czasie przekształcenia elementu warstwy skrawanej (o wymia-

rach: l, h

i b

) w wiór powoduję zmianę odpowiednich wymiarów (na wymiary: l

, h

). Zakładając brak zmiany gęstości materiału w procesie skrawania objętość materiału nie

ulega zmianie (rys. 5.2):

(5.1)

= h

(5.2)

= l/l

(5.3)

5-3

(5.4)

gdzie:

= h

- współczynnik zgrubienia wióra,

= b

c h

- współczynnik rozszerzenia wióra,

= l/l

- współczynnik skrócenia wióra.

- grubość nominalna warstwy skrawanej, definiowana (PN-92/M-01002/03) jako stosunek

przekroju poprzecznego wióra i szerokości nominalnej warstwy skrawanej:

A
b

(5.5)

Współczynnik zgrubienia wióra

(spęczania poprzecznego) nazywany jest współczynni-

kiem spęczania wióra (PN-92/M-01002/04).

UWAGA: Dotychczas jako współczynnik spęczania wióra (oznaczenie dotych-

czasowe k

) określano współczynnik skrócenia wióra (

= l/l

(5.6)

= l/l

= h

(5.7)

Tak więc dotychczasowy współczynnik spęczania wióra mógł być określony jako

stosunek pól poprzecznego przekroju wióra A

i przekroju warstwy skra-

wanej A

= A

(5.8)

Analizując w literaturze dane dotyczące współczynnika spęczania należy zwrócić

uwagę, czy dotyczą one współczynnika skrócenia wióra.

Badania współczynników spęczania wykazują, że w praktyce przy względnie dużych warto-

ściach b

i w szczególności przy skrawaniu nieswobodnym b

≈

1 stąd też możemy

przyjąć:

(5.9)

Niemniej należy zdawać sobie sprawę z przyjętych uproszczeń i dla badań podstawowych

należy wyznaczać

Współczynnik spęczania wióra jest zwykle większy od jedności i tylko dla niektórych

materiałów obrabianych (np. stopów tytanu, stal hartowana) i warunków skrawania

≤

1 [5].

Uważa się, że spęczanie wióra jako miara odkształcenia może być przyjęta wyłącznie dla do-

datnich kątów natarcia [3]. Znając współczynnik spęczania wióra (dla przypadku

≥

5-4

można określić szybkość spływu wióra v

po ostrzu, która jest mniejsza od szybkości skra-

wania v

zgodnie ze wzorem:

= v

(5.10)

Współczynnik spęczania

jest tzw. fizycznym wskaźnikiem skrawalności materiału okre-

ślającym podatność materiału do odkształceń plastycznych w danych warunkach skrawania

[1, 2, 4] i uważany jest za charakterystykę przybliżoną [3]. Współczynnik spęczania

1 nie musi oznaczać automatycznie braku odkształcenia w strefie tworzenia wióra. Zależy on

od materiału obrabianego, geometrii ostrza, parametrów skrawania, chłodzenia i wielu innych

czynników.

ół

ęc

min

Rys. 5.3

Typowy przebieg zależności współczynnika spęczenia

Λh od prędkości skrawania vc

przy obróbce stali

Typowy przebieg zmian

podczas toczenia stali w zależności od szybkości skrawa-

nia v

przedstawiono na rys. 5.3 [2]. W zakresie 1-2 wartość współczynnika spęczania

zmniejsza się co jest tłumaczone powstaniem narostu, który powoduje zwiększenie rzeczywi-

stego kąta natarcia ostrza. Powoduje to zmniejszenie odkształceń plastycznych wióra. W za-

kresie 2-3 narost zanika, zwiększa się tarcie pomiędzy wiórem a powierzchnią natarcia ostrza.

Powyżej szybkości 3 wartość współczynnika

zmniejsza się (spowodowane jest to zmniej-

szaniem współczynnika tarcia). Zmiany współczynnika spęczenia wióra podczas skrawania

określonych materiałów są podobne do zmian:

• siły i mocy skrawania,

• współczynników tarcia,

5-5

• chropowatości powierzchni obrobionej,

• zgniotu,

• naprężeń w warstwie wierzchniej.

5.3. Wyznaczenie współczynnika spęczenia wióra

Współczynnik spęczenia wióra można wyznaczyć zarówno w przypadku skrawania swobod-

nego jak i nieswobodnego. Aby wyznaczyć współczynnik dla skrawania swobodnego należy

przygotować odpowiednie specjalne próbki (np. dla toczenia wzdłużnego będzie to rura) oraz

narzędzia - nie będzie to omawiane gdyż nie jest to tematem ćwiczenia. W ćwiczeniu współ-

czynnik spęczenia wyznaczany będzie dla skrawania nieswobodnego w przypadku toczenia.

Wzory przytoczone poniżej dotyczą obu przypadków skrawania.

5.3.1. Wyznaczenie współczynnika spęczenia przez pomiar przekroju po-

przecznego wióra

Zgodnie z definicja współczynnika spęczenia możemy wyznaczyć go jako stosunek przekroju

poprzecznego wióra h

i szerokości nominalnej warstwy skrawanej h

. Szerokości nominal-

nej warstwy skrawanej określamy ze wzoru (5.5). Natomiast przekrój poprzeczny wióra okre-

ślamy po zatopieniu wióra w masie i wykonaniu zgładu metalograficznego. Metoda ta jest

stosowana tylko w badaniach podstawowych.

5.3.2. Wyznaczenie współczynnika spęczenia przez pomiar długości wióra

Zgodnie ze wzorem (5.9) i przyjętymi uproszczeniami współczynnik spęczenia można wy-

znaczyć jako stosunek długości warstwy skrawanej która przekształciła się w wiór i długości

wióra:

5-6

= l / l

(5.11)

W przypadku wiórów wstęgowych wyznaczenie długości warstwy skrawanej (dla toczenia

wzdłużnego) wymaga specjalnego przygotowanej próbki. W tym celu na wałku nacina się

rowek wzdłużny o szerokości B, a długość drogi skrawania określa wzór:

l =

(d - a

) - B (5.12)

gdzie:

d - średnica zewnętrzna wałka,

B - szerokość rowka.

Dla

wiórów elementowych określenie długości warstwy skrawanej która przekształciła się w wiór jest

niemożliwe. W tym przypadku w celu określenia współczynnika spęczenia zastosować należy metodę

wagową opartą na pomiarze ciężaru wióra (pkt.. 5.3.3).

5.3.2.1. Pomiar długości wióra za pomocą stanowiska komputerowego

Wykorzystanie komputera do pomiaru długości wióra pozwala na wykonanie pomiaru szyb-

ciej i dokładniej niż innymi metodami graficznymi

Wykorzystanie komputera pozwala uprościć procedurę wyznaczania długości krzywej. Długość krzy-

wej jest wyznaczana automatycznie przez program jako jeden z parametrów krzywej. Nie są potrzeb-

ne żadne dodatkowe obliczenia.

Przed przystąpieniem do pomiarów długości wióra za pomocą tabletu należy przygotować rysunek

wióra na papierze. Określić punkty, które będą wczytywane do komputera. Umieścić rysunek na pul-

picie tabletu u umocować, aby nie przemieszczał się w czasie wczytywania.

5-7

Polilinia

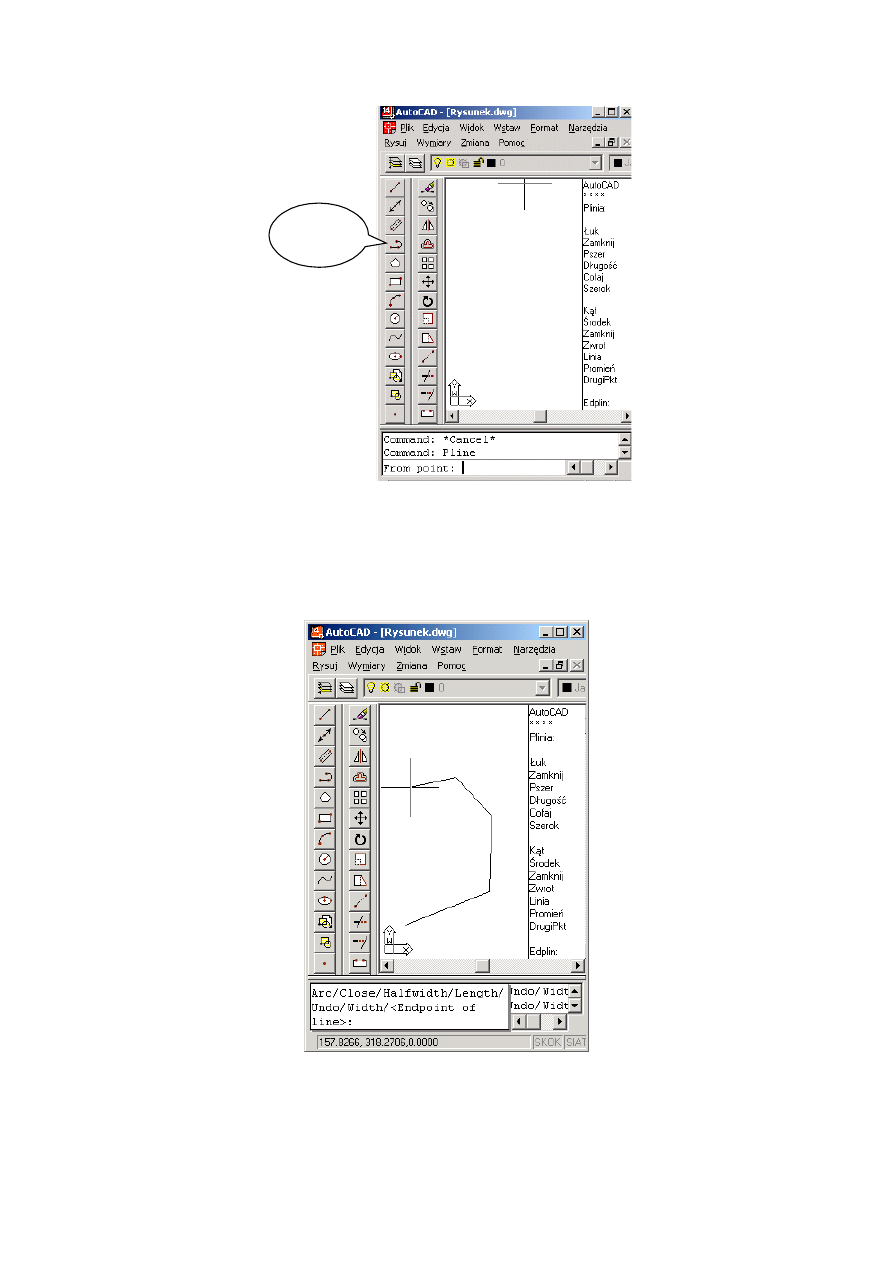
Rys. 5.4 Uruchomienie procedury do wprowadzania polilinii

• Z menu AutoCAD wybrać procedurę rysowania polilinii. Wybrać za pomocą myszy z menu gra-

ficznego lub z menu tekstowego: Rysuj -> Polilinia

Rys. 5.5 Wprowadzanie kolejnych punktów polilinii

• Wprowadzić rysunek do komputera najeżdżając krzyżem goniometrycznym na wybrane punkty i

wprowadzając współrzędne za pomocą przycisku "1"

5-8

• Zakończenie wprowadzania sygnalizujemy naciśnięciem przycisku "Z".

Krzywa aproksymująca
BSPLINE trzeciego stopnia.

Krzywa dopasowująca.
Jest to krzywa BSPLINE
drugiego stopnia

Łamana przechodząca przez
wybrane punkty

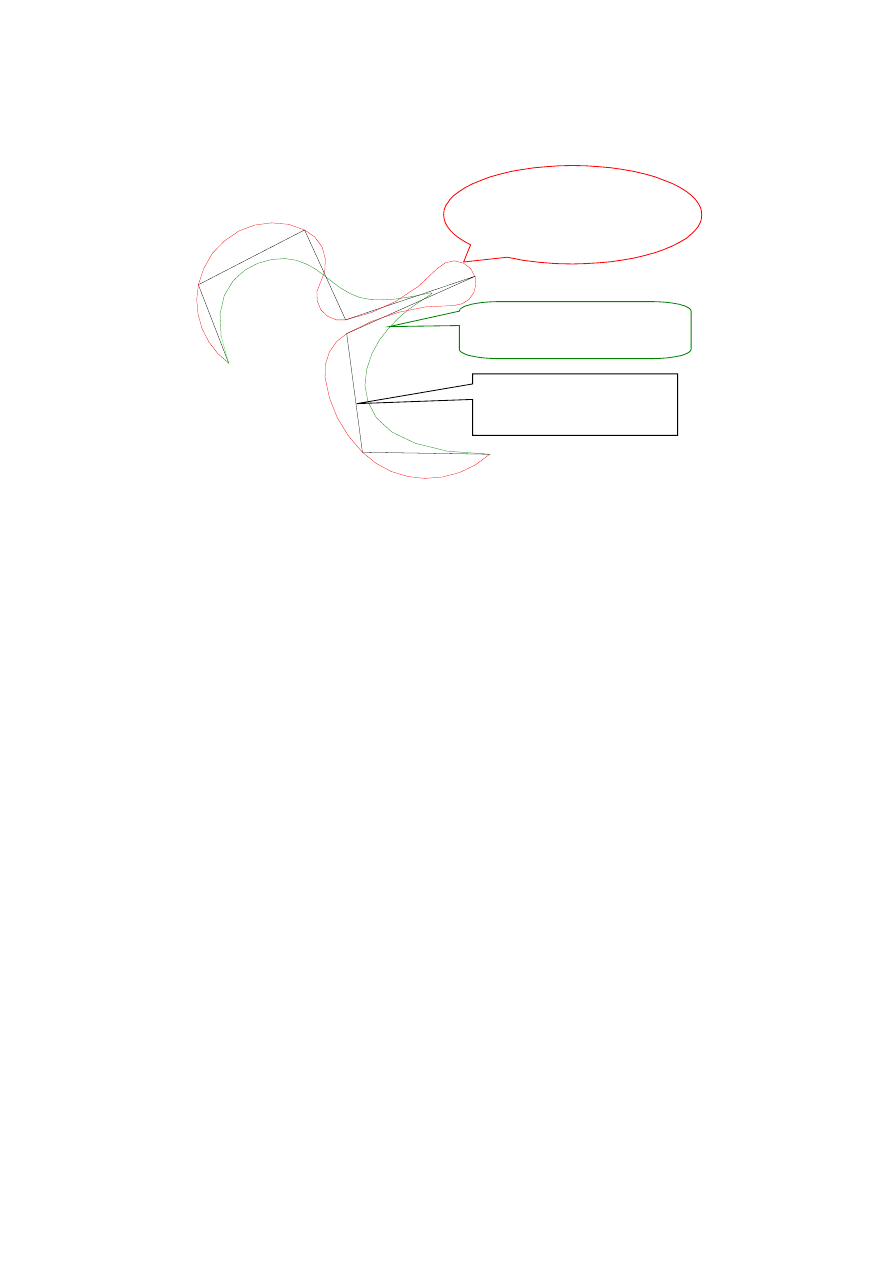
Rys. 5.6 Różne polilinie oparte na tym samy zestawie punktów (węzłów polilinii)

Otrzymana poliinia przez program AutoCAD może być wyświetlana na trzy sposoby:

• linia

łamana przechodząca przez wierzchołki wprowadzonych punktów,

•

krzywa B-SPLINE obliczona w oparciu o wprowadzone punkty

. Ze względu na charakter funkcji

aproksymującej linia B-SPLINE jest zawsze krótsza od łamanej przechodzącej przez punkty, na

podstawie których jest wyznaczana.

•

Jako krzywa ściśle dopasowana przechodząca przez wybrane punkty

. Jest to funkcja B-SPLINE

ale drugiego stopnia. Należy zwrócić uwagę na dopasowanie funkcji - czy nie istnieją miejsca,

gdzie przebieg funkcji różni się znacznie od układu zadanych punktów.

O sposobie wyświetlania decyduje użytkownik. Jeżeli wprowadzonych punktów pomiarowych (wę-

złów) jest mało, należy wybrać jedną z metod aproksymacji. Jeżeli węzłów jest dużo, wystarczy repre-

zentacji polilinii w postaci krzywej łamanej.

Punkty składowe krzywej są wyświetlane za pomocą instrukcji 'LIST'. Wyświetlane są współrzędne

punktów tworzących polilinię, długość polinii, pole powierzchni figury ograniczonej polilinią.

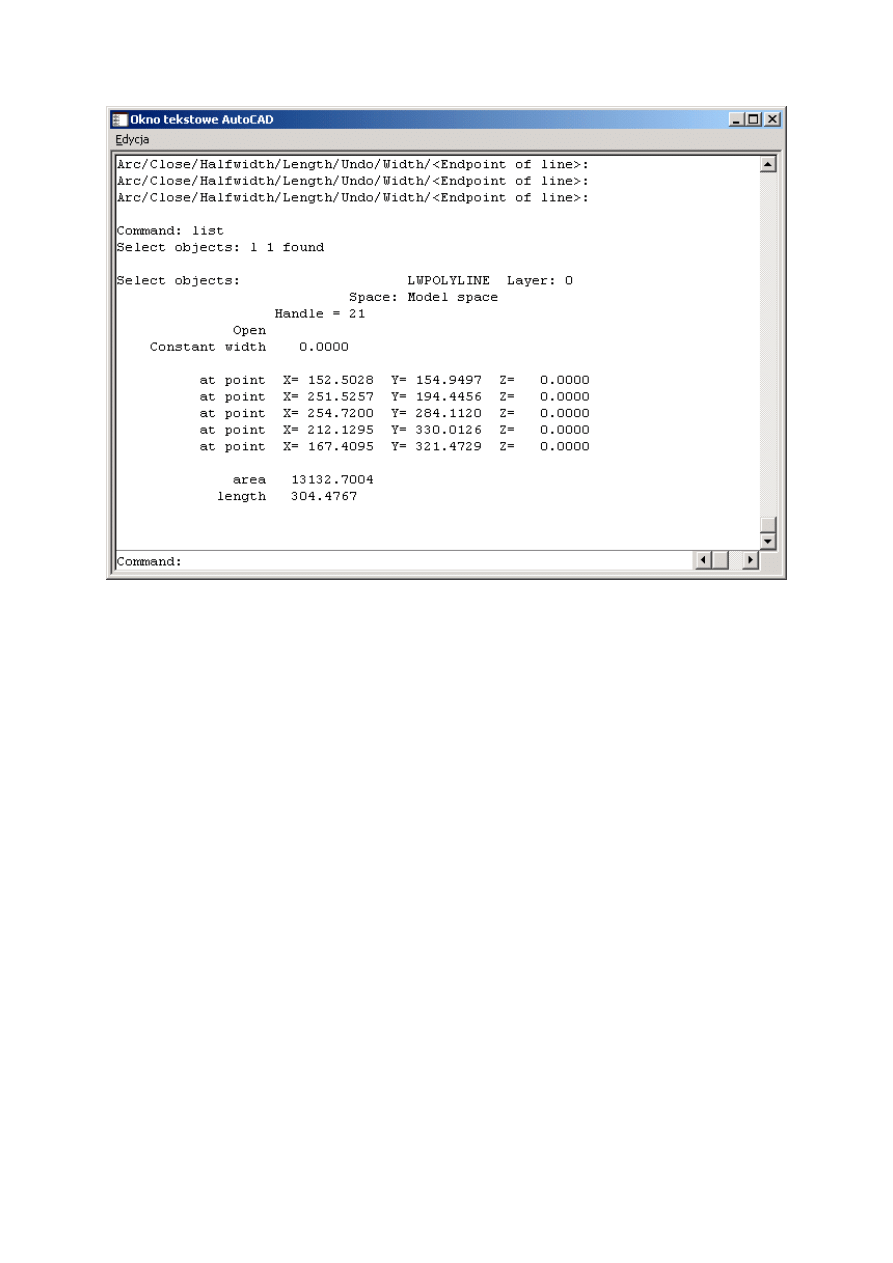
Wyniki wyprowadzane przez instrukcję 'List'

W celu wyprowadzenia wyników przez instrukcję 'List' należy: w linii komend napisać 'List', zaznaczyć

obiekt którego właściwości 'chcemy przeglądać klawiszem '1', naciśnięciem klawisza 'Z' zakończyć

procedurę wyboru. Wyniki są wyprowadzane w oknie tekstowym AutoCADa.

5-9

Rys. 5.7 Okno tekstowe AutoCADa do wyprowadzania wyników.

W zależności od reprezantacji krzywej w oknie są widoczne następujące parametry:

• linia

łamana przechodząca przez wierzchołki wprowadzonych punktów. Widoczne są punkty po-

miarowe o współrzędnych XYZ, obszar ograniczony krzywą, długość krzywej.

at point X= 197.3823 Y= 107.1088 Z= 0.0000

at point X= 115.9576 Y= 107.1088 Z= 0.0000

at point X= 105.0525 Y= 184.0819 Z= 0.0000

at point X= 187.9312 Y= 221.1161 Z= 0.0000

at point X= 104.3255 Y= 193.5220 Z= 0.0000

at point X= 78.8802 Y= 247.9841 Z= 0.0000

at point X= 8.3606 Y= 215.3068 Z= 0.0000

at point X= 28.7168 Y= 164.4756 Z= 0.0000

area 6034.7015

length 530.5767

• krzywa B-SPLINE trzeciego stopnia obliczona w oparciu o wprowadzone punkty. Widoczne są

punkty wprowadzone przez użytkownika,

5-10

VERTEX Layer: 0

Space: Model space

Handle = 5D

at point, X= 105.0525 Y= 184.0819 Z= 0.0000

starting width 0.0000

ending width 0.0000

(Spline control point)

punkty będące wynikiem aproksymacji,

VERTEX Layer: 0

Space: Model space

Handle = 88

at point, X= 31.2689 Y= 217.0088 Z= 0.0000

starting width 0.0000

ending width 0.0000

(Inserted by spline fitting)

długość krzywej i pole powierzchni

area 6888.6476

length 372.2832

• krzywa B-SPLINE drugiego stopnia przechodząca przez wybrane punkty.

Widoczne są punkty wprowadzone przez użytkownika

VERTEX Layer: 0

Space: Model space

Handle = 5B

at point, X= 197.3823 Y= 107.1088 Z= 0.0000

starting width 0.0000

ending width 0.0000

bulge -0.1859

center X= 156.1543 Y= 152.7060 Z= 0.0000

radius 61.4724

start angle 270

end angle 312

punkty będące wynikiem aproksymacji:

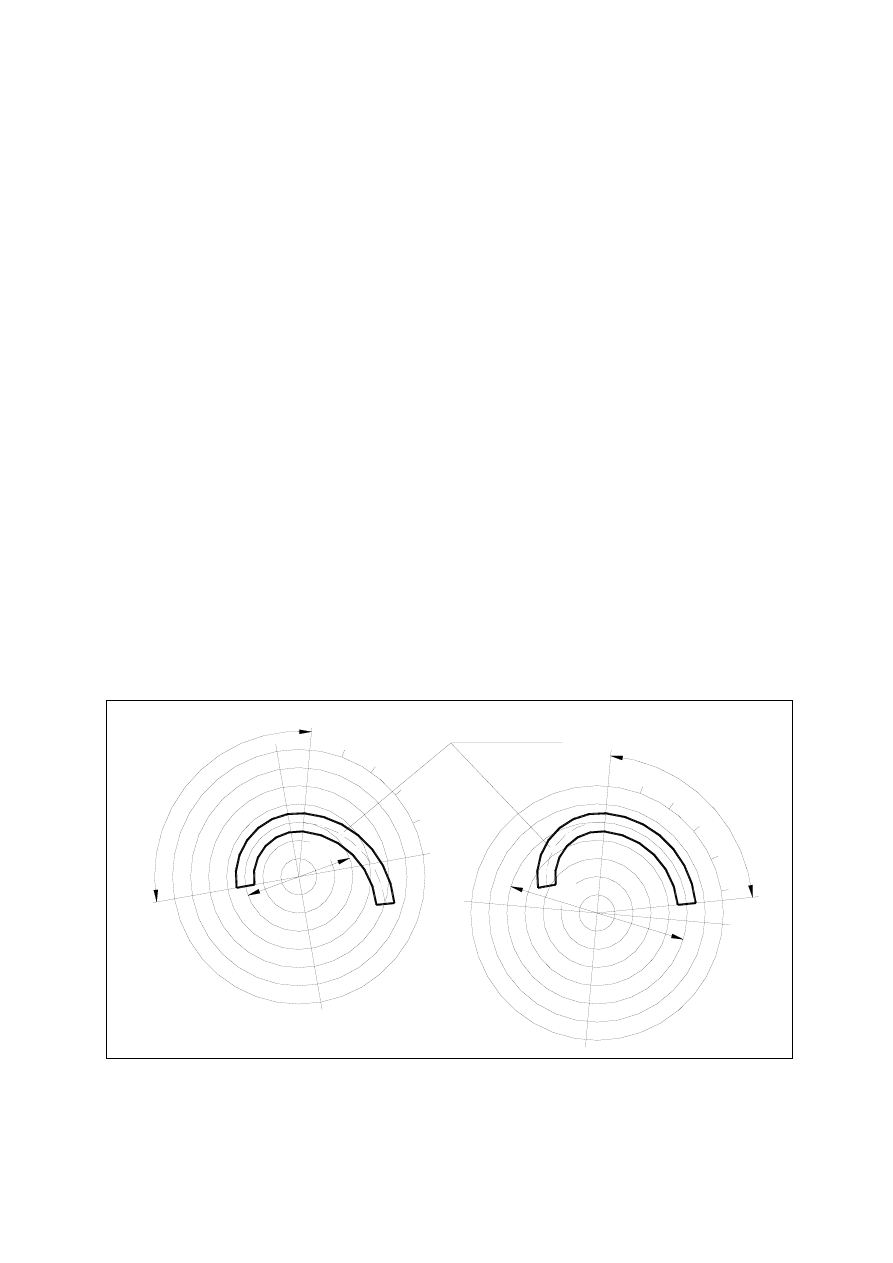
5-11

VERTEX Layer: 0

Space: Model space

Handle = 8F

at point, X= 174.0790 Y= 201.8635 Z= 0.0000

starting width 0.0000

ending width 0.0000

(Inserted by curve fitting)

bulge 0.5294

center X= 174.4612 Y= 216.1981 Z= 0.0000

radius 14.3398

start angle 268

end angle 20

długość krzywej i pole powierzchni:

area 6217.0893

length 597.0637

5.3.2.2. Pomiar długości wióra metodą okręgów współśrodkowych

0°

15°

30°

45°

60°

75°

90°

270°

180°

270°

0°

15°

30°

45°

60°

75°

90°

180°

mierzony wiór

Rys. 5.8

Pomiar długości wióra przy pomocy okręgów współśrodkowych

5-12

Po przerysowaniu wióra z projektora warsztatowego w powiększeniu x-razy i zastosowaniu okręgów

współśrodkowych (rys. 5.4) jego długość liczymy ze wzoru:

i n

∑

180

(5.13)

W przypadku wiórów silnie zniekształconych np. piłokształtnych należy zmierzyć długość po

obydwu stronach wióra i wyznaczyć długość średnią.

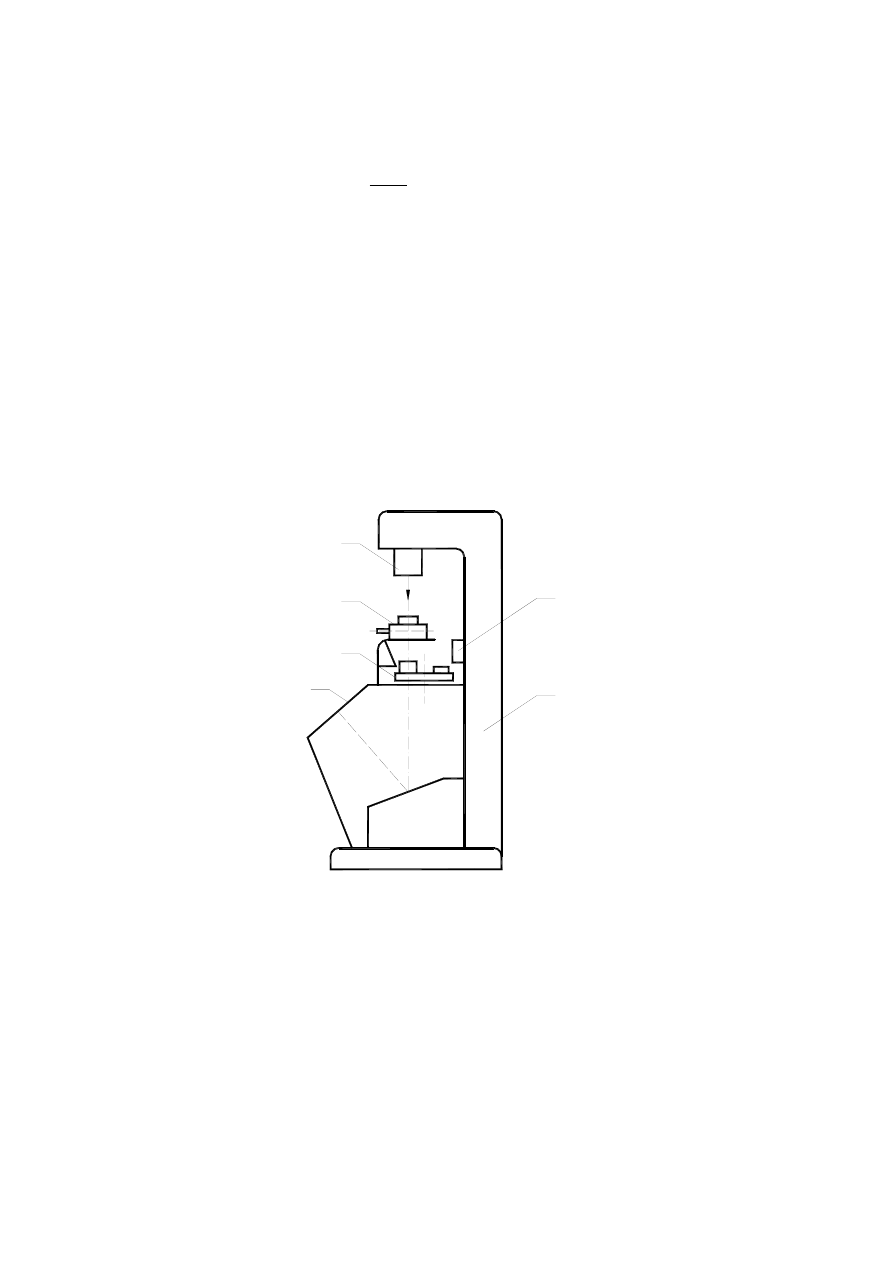
5.3.2.3. Zasada działania projektora warsztatowego Pr-2

Rys. 5.9

Projektor warsztatowy Pr-2

Projektor warsztatowy (rys. 5.5) składa się z korpusu 1, w którym umieszczone są: oświetlacz

2 (dla pomiarów w świetle przechodzącym), oświetlacz 3 (dla pomiarów w świetle odbitym),

krzyżowy stolik pomiarowy 4, rewolwerowa głowica 5 z obiektywami (całkowite powiększe-

nie projektora wynosi x10, x20, x50) oraz ekranu 6. Projektor warsztatowy umożliwia po-

miar i obserwację sprawdzanej części w świetle odbitym i przechodzącym. Pomiar za pomocą

5-13

projektora długości wióra polega na umieszczeniu go na stoliku i przerysowaniu jego powięk-

szenia na kalce technicznej.

5.3.3. Wyznaczenie współczynnika spęczenia przez pomiar ciężaru wióra

Kierunek ruchu
posuwowego

= 0°

Rys. 5.10

Nominalne pole przekroju poprzecznego warstwy skrawanej

Współczynnik spęczenia

można określić w oparciu o znajomość ciężaru wióra G

i jego

średniej długości l

(5.14)

= h

= G

/ A

(5.15)

co prowadzi do zależności

(5.16)

gdzie:

- ciężar wióra,

5-14

- nominalnej grubości warstwy skrawanej,

= h

- przekrój poprzeczny warstwy skrawanej,

- długość wióra określona w pkt. 5.3.2.1,

- średnia szerokość wióra,

= b

= G

/ A

- ciężar właściwy materiału obrabianego.

Badania współczynników spęczenia wykazują, że w praktyce przy względnie dużych warto-

ściach b

i w szczególności przy skrawaniu nieswobodnym

= b

≈

1 stąd też mo-

żemy przyjąć (poza wyjątkami wymienionymi poniżej):

= G

/ A

(5.17)

W praktyce A

oblicza się wg. wzoru:

= a

f sin

(5.18)

gdzie

ϕ jest kątem kierunku ruchu posuwowego (dla toczenia wzdłużnego ϕ = 90o).

= G

/ a

f l

(5.19)

W przypadku bardzo dokładnej obróbki (np. skrawanie materiałami supertwardymi) z

uwagi na niedużą wartość b

należy uwzględnić

= b

oraz dokładnie wyznaczyć

przekrój poprzeczny warstwy skrawanej A

z uwzględnieniem pola resztowego A

(rys. 5.6).

5.3.3.1. Zasada działania wagi analitycznej WA-600 ”TETA 76"

Waga analityczna automatyczna "TETA 76" jest wagą dźwigniową z elektronicznymi ukła-

dami sterowania i odczytu. Obciążenie maksymalne wynosi 199 g, a dokładność odczytu

5x10-4g. W celu uzyskania stabilizacji wskazań wagi przygotowanej do eksploatacji, należy

włączyć układy elektroniczne wagi klawiszem "MAINS" na około 15 minut przed rozpoczę-

ciem pomiarów, sprawdzić ustawienie poziomu wagi oraz wskazanie zerowe. Ważenie odby-

wa się w cyklu automatycznym:

1. otworzyć komorę ważenia,

5-15

2. umieścić wiór ważony pośrodku szalki,

3. włączyć wagę klawiszem "ON",

4. odczytać wynik pomiaru po ustaleniu się wskazań trzeciego zakresu,

5. wyłączyć wagę klawiszem "ON",

6. otworzyć komorę ważenia,

7. zdjąć z szalki zważony wiór,

8. zamknąć komorę ważenia.

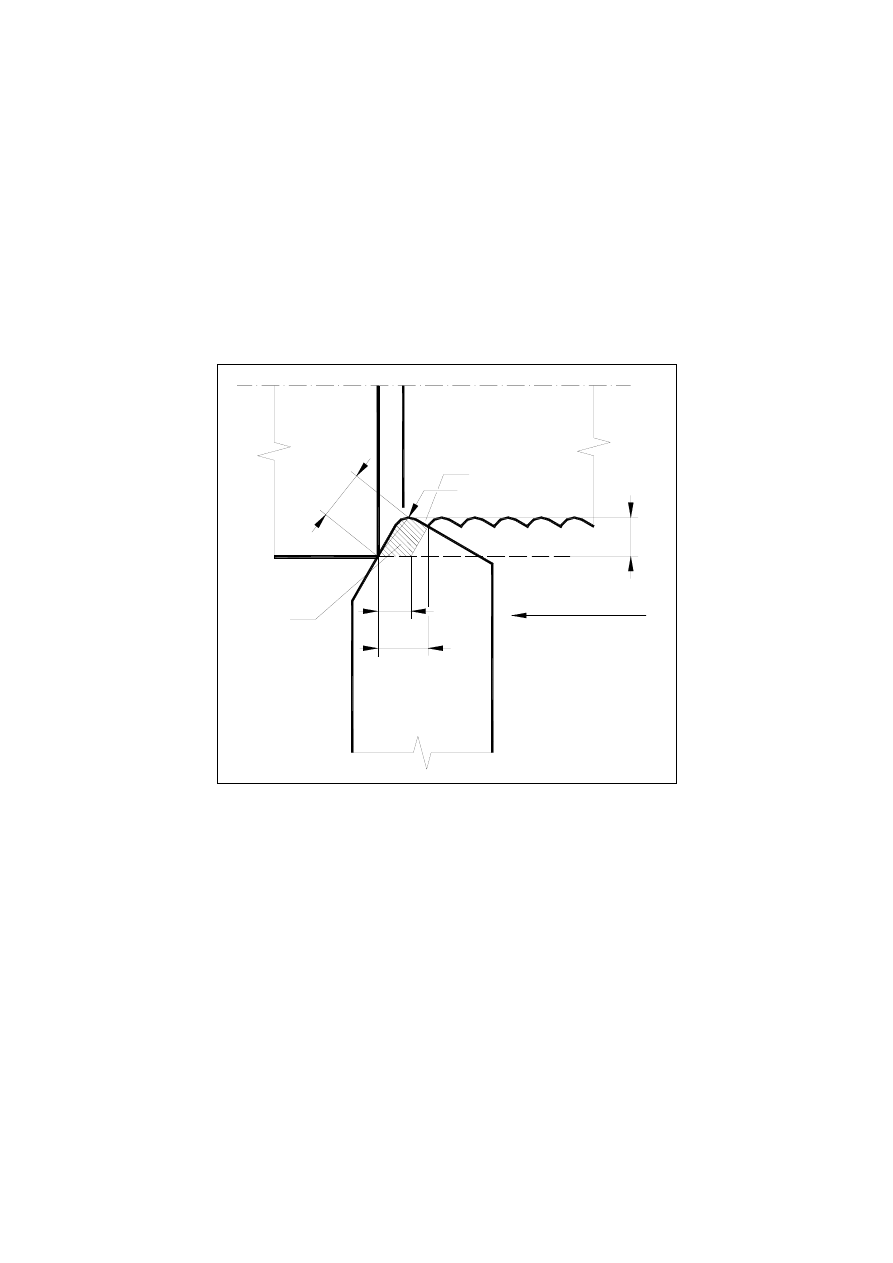
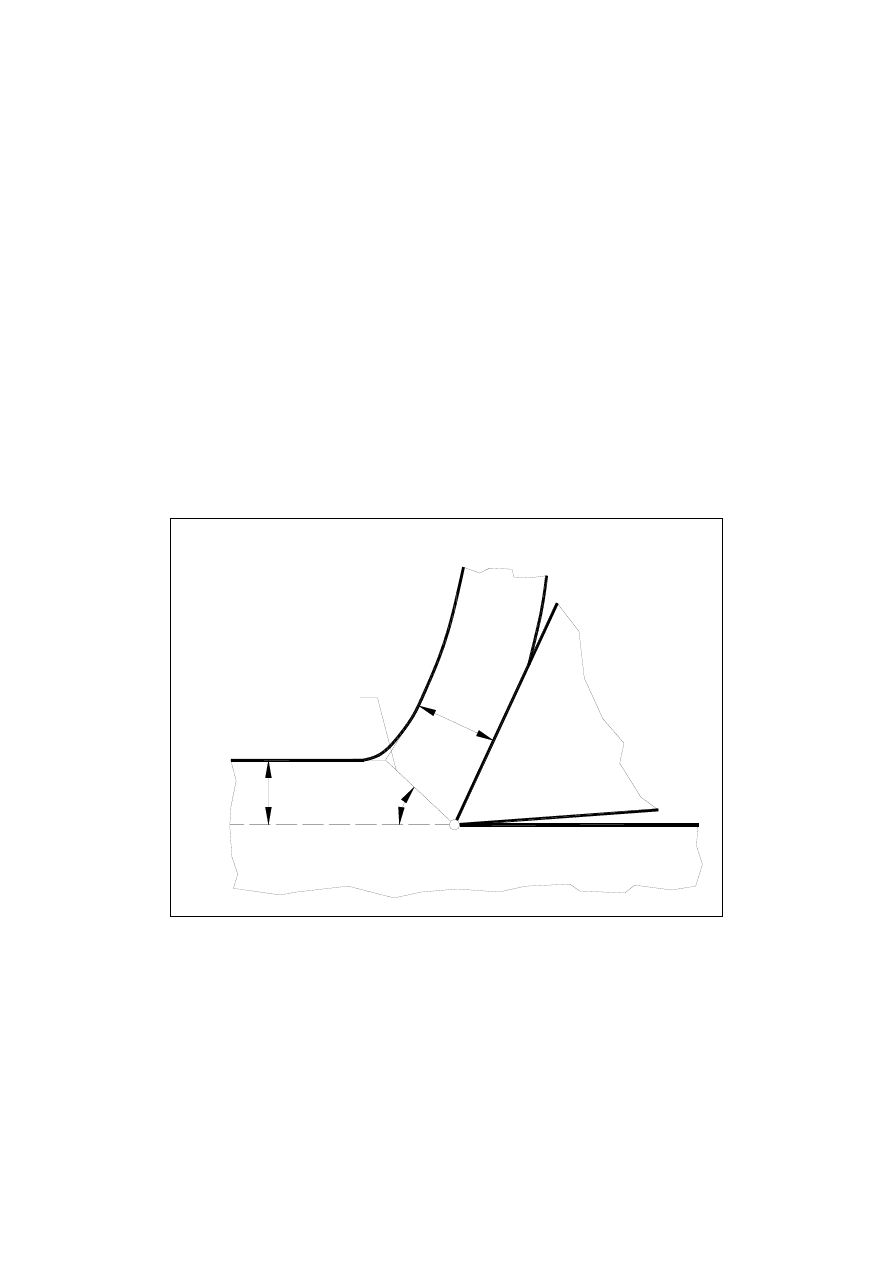
5.4. Wyznaczenie kąta ścinania

Płaszczyzna
ścinania

Rys. 5.11

Model dwuwymiarowy przy skrawaniu swobodnym (ortogonalnym)

Przyjmując uproszczony model strefy ścinania w postaci płaszczyzny zwanej płasz-

czyzną ścinania P

i zakładając, że odkształcenie materiału zachodzi wyłącznie na płasz-

czyźnie ścinania (rys. 5.7) można obliczyć kąt

położenie tej płaszczyzny względem kierun-

5-16

ku skrawania. Wtedy dla określenia kąta ściania

φ na podstawie rys. 5.7 (dla skrawania swo-

bodnego bez narostu) można napisać:

/sin

= h

/ cos(

) (5.20)

= sin

+ cos

/tg

(5.21)

stąd

=cos

-sin

) (5.22)

Kąt ścinania (poślizgu) służy zarówno jako miara stopnia odkształcenia plastycznego jak i

miara średniego kierunku poślizgu w strefie kształtowania wióra. Dane o zmianie kąta ścina-

nia wykorzystuje się ponadto do oceny wpływu różnych czynników na przebieg procesu two-

rzenia wióra.

5.5. Wykonanie ćwiczenia

5.5.1. Stanowisko

Obrabiarka: Tokarka produkcyjna

Materiał obrabiany: Próbki różnych rodzajów stali konstrukcyjnej.

Narzędzia: Noże składane z płytkami z węglików spiekanych.

Aparatura: Waga laboratoryjna, projektor warsztatowy, pomoce warsztatowe.

5.5.2. Wykonanie ćwiczenia

Przeprowadzić próby skrawania dla dwóch różnych (wybranych przez prowadzącego) mate-

riałów obrabianych:

5-17

1. zmieniając szybkość skrawania v

od v

do v

(i ≥ 5) przy pozostałych warunkach

stałych,

2. zmieniają wartość posuwu f od f

do f

≥ 5) przy pozostałych warunkach sta-

łych.

Dokonać pomiaru długości i ciężaru otrzymanych wiórów.

5.5.3. Opracowanie wyników

1. Obliczyć wartości współczynnika spęczenia metodą opisaną w pkt. 5.3.3 i sporzą-

dzić wykresy

= f (v

) oraz

= f (f) dla badanych materiałów obrabianych.

2. Obliczyć kąty ścinania

3. Przedstawić wnioski z przeprowadzonych badań.

LITERATURA:

[1] Biernawski W.: Teoria obróbki metali skrawaniem. Warszawa PWN 1956.

[2] Dmochowski J.: Podstawy skrawania. Warszawa. PWN 1978.

[3] Grzesik W.: Uogólniony model swobodnego skrawania nieortogonalnego. WSI w Opolu -

Studia i Monografie z.18. Opole 1987.

[4] Kaczmarek J.: Podstawy obróbki wiórowej, ściernej i erozyjnej. Warszawa, WNT 1970.

[5] Kawalec M. i inni: Badanie podstaw fizycznych skrawania wiórowego hartowanych stali

ostrzami z CBN. Sprawozdanie z CBPB 0204 1986.

[6] PN-92/M-01002/01- "Podstawowe pojęcia w obróbce wiórowej i ściernej. Geometria czę-

ści roboczej narzędzi skrawających. Terminologia ogólna".

[7] PN-92/M-01002/03- "Podstawowe pojęcia w obróbce wiórowej i ściernej. Wielkości

geometryczne i kinematyczne w obróbce skrawaniem".

[8] PN-92/M-01002/04- "Podstawowe pojęcia w obróbce wiórowej i ściernej. Siły, energia i

moc"