Strona 1

Binboy at Sphere:Problem komiwojażera. Sformuowanie problemu. Rys historyczny. Algorytm Christof...

2007-01-24 21:33:18

http://binboy.sphere.pl/index.php?show=134&drukuj=true

Binboy at Sphere

http://binboy.sphere.pl

Problem komiwojażera. Sformuowanie problemu. Rys
historyczny. Algorytm Christofidesa i jego analiza.

Autor: lahead

Definicja problemu komiwojażera

Problem komiwojażera przedstawia się następująco. Mamy określoną liczbę miast, powiedzmy n, oraz koszt połączenia
pomiędzy każdymi dwoma z nich. Zadaniem komiwojażera jest podróż przez wszystkie miasta (przez każde dokładnie
raz), w taki sposób, aby po jej zakończeniu znalazł się w mieście, z którego startował oraz żeby całkowity koszt podróży
był najmniejszy z możliwych. Zdefiniujmy problem w języku teorii grafów:

Zbiór miast definiujemy jako graf pełny G o n wierzchołkach. Z każdą krawędzią ei,j kojarzymy wagę równą odległości
pomiędzy miastami i i j. Wagę tę oznaczmy wi,j. Problem sprowadza się do wyznaczenia minimalnego cyklu Hamiltona w
grafie G. Jako cykl Hamiltona rozumiemy cykl, do którego należą wszystkie wierzchołki grafu G.

Rozstrzygalność problemu

Problem, choć prosty, jeśli chodzi o zdefiniowanie, okazuje się bardzo trudny do rozwiązania. Jeden z dokładnych
algorytmów polega na kompletnym przeglądzie wszystkich możliwych cykli Hamiltona w grafie G i wybranie najkrótszego.
Ponieważ ilość możliwych cykli rośnie z ilością miast jak (n!)/2 , złożoność problemu wynosi O(n!). Zatem już dla n=20
mamy (20!)/2 (około 1018) cykli. Czas obliczeń tylu cykli Hamiltona dla najszybszych znanych dzisiaj komputerów
wyniósłby około 40tyś lat. Jednak jeśli potrafilibyśmy ,,zgadnąć'' sekwencję kolejnych miast, to w czasie wielomianowym
moglibyśmy udowodnić, że przebyta droga spełnia warunki zadania. Nie znamy jednak deterministycznego algorytmu
znajdowania rozwiązania lub udowadniania, że nie istnieje. Problem ten należy więc do problemów ,,niedeterministycznie
wielomianowych'' -- nondeterministic polynomial, czyli NP. Do tej samej klasy należy m.in. łamanie szyfrów, stosowanych
aktualnie do zabezpieczania transakcji z użyciem kart kredytowych w Internecie. Co ciekawsze, nie udowodniono
dotychczas, ze rozwiązanie problemów klasy NP w czasie wielomianowym nie istnieje.

Krótka historia problemu komiwojażera

Historia problemu komiwojażera sięga wieku XIX. Pierwsze publikacje na temat samego problemu, jak i proponowanych
algorytmów znajdujących rozwiązanie pojawiły się dopiero w latach 20-ych XX wieku. Mianowicie, w tym właśnie okresie
znany matematyk i ekonom Karl Menger opublikował wśród swoich kolegów broszurę poruszającą zagadnienie problemu
komiwojażera. W 1932 natomiast wydał publikację pod tytułem: „Das Botenproblem”, w której definiował on „problem
posłańca” jako: "zadanie znalezienia, dla skończonej liczby punktów, których, parami, odległości są znane, najkrótszej
ścieżki łączącej te punkty… Zasada, wg której dla punktu startowego powinno się wybrać punkt leżący najbliżej niego, itd.,
nie daje w rezultacie najkrótszej ścieżki." W latach 40-tych statystycy: Mahalanobis (w 1940), Jessen (w 1942), Gosh (w
1948) i Marks (w 1948) opracowywali problem w połączeniu z aplikacjami agrokulturalnymi. W roku 1949 Julia Robinson
opublikowała dokument pt. „On the Hamiltonian Game" poruszając tym samym po raz pierwszy znany problem cyklu
Hamiltonowskiego i wynalazła metodę rozwiązywania problemu podobnego do problemu komiwojażera.
W latach 50-tych pojawiła się próba rozwiązania problemu George’a B. Dantzig’a, Fulkerson’a i Johnson’a (1954).
Zaproponowana przez nich metoda przez dziesięciolecia pozostawała jedyną dla liczby miast rzędu kilkuset. G. Morton i
A.H. Land (w 1955) przedstawili algorytm 3-przybliżony (czyli dający conajwyżej 3 razy gorszy wynik od optymalnego), a w
1956 Merill M. Flood w pracy "The travelling-salesman problem" opublikował algorytm 2-przybliżony. W latach 60-tych
opracowano metodę programowania liniowego i z użyciem komputerów testowano metodę George’a B. Dantzig’a,
Fulkerson’a i Johnson’a. Optymalizacje algorytmów w ciągu kolejnych lat (m.in. R. Bellman, M. F. Dacey, R.M. Karp, M.
Held, M. Grötschel) oraz rozwój komputerów doprowadziły w 1998 roku do imponującego, lecz ciągle nie dającego pełnej
satysfakcji, optymalnego rozwiązania zagadnienia dla 13549 amerykańskich miast. W dalszym ciągu nie jest znany
wielomianowy algorytm znajdujący doskonałe rozwiązanie. W 1975 roku jednak N. Christofides w pracy pt. “Worst-case
analysis of a new heuristic for the travelling salesman problem” przedstawił algorytm 1,5-przybliżony oparty na

Strona 2

Binboy at Sphere:Problem komiwojażera. Sformuowanie problemu. Rys historyczny. Algorytm Christof...

2007-01-24 21:33:18

http://binboy.sphere.pl/index.php?show=134&drukuj=true

twierdzeniu o nierówności trójkąta, będący najlepszym dostępnym, tej klasy algorytmem. Istnieją algorytmy dające
dokładniejsze rozwiązania, oparte o sztuczną inteligencję i genetykę; wykorzystujące elementy losowe. Ograniczmy się
jednak do wersji metrycznej i przyjrzyjmy bliżej algorytmowi Christofidesa.

Algorytm Christofidesa (algorytm 1,5-przybliżony)

Zasada nierówności trójkąta, o którą oparty jest algorytm mówi, że: Dla każdych 3 punktów A,B,C odległość od A do C jest
nie większa niż suma odległości A do B i B do C.

Algorytm Christofidesa ma poastać:

procedure

Christofides(G)

begin

1. znajdź minimalne drzewo spinające T0 grafu G;
2. znajdź zbiór Vodd węzłów nieparzystego stopnia w drzewie T0;
3. znajdź w Vodd minimalne skojarzenia dokładne M0odd;
4. znajdź cykl Eulera Ce w podgrafie indukowanym przez T0 + M0odd;
5. przekształć cykl Eulera Ce w cykl Hamiltona Cch w grafie pełnym;

end

Przeanalizujmy działanie algorytmu dla przykładowego grafu G. Dla uproszczenia nie wprowadzam wag połączeń na
rysunkach. Zasada działania algorytmu pozostanie zachowana i jaśniejsza do odczytu.

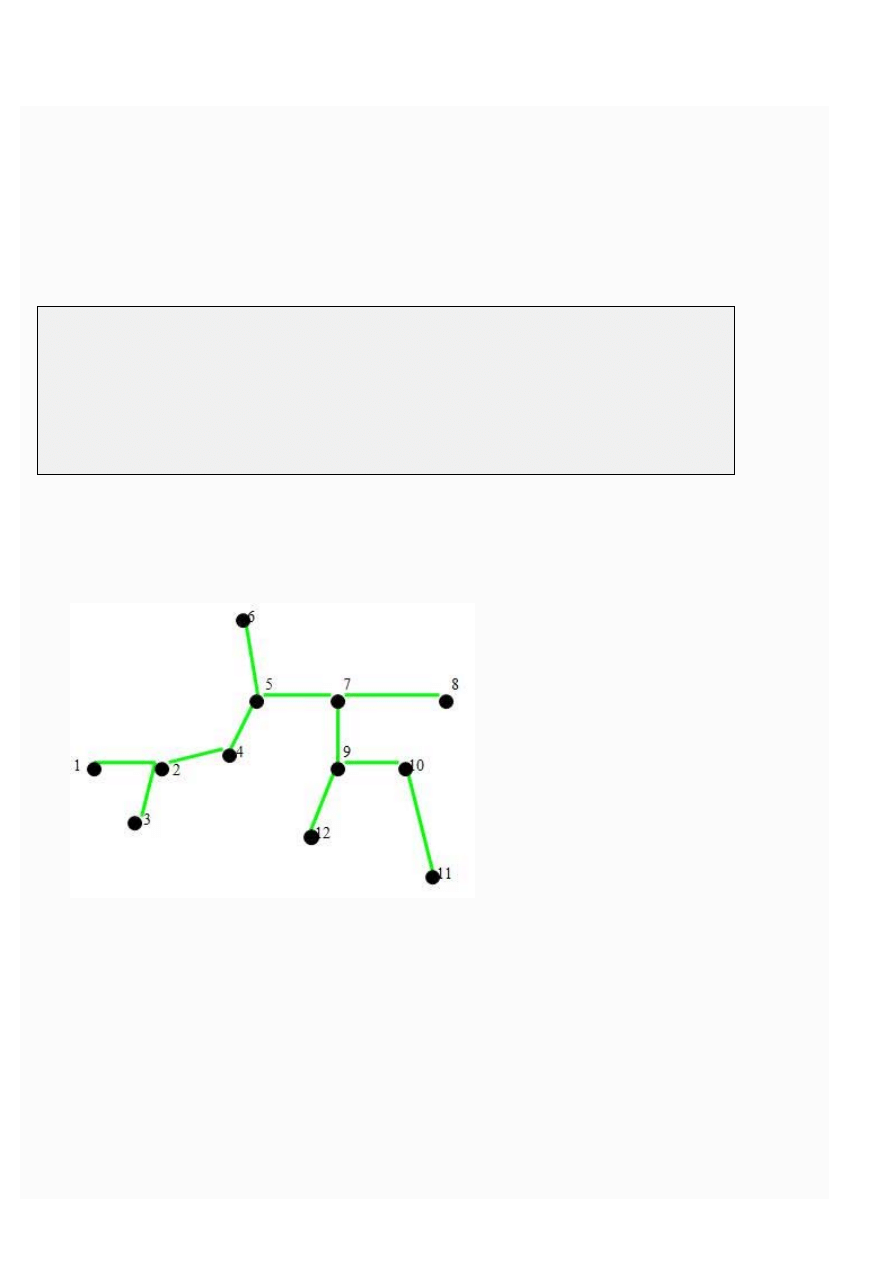
1. znajdź minimalne drzewo spinające T0 grafu G.

Do tego celu możemy posłużyć się znanymi algorytmami (np. algorytm Prima). Po znalezieniu minimalnego
drzewa spinającego nasz graf ma postać:

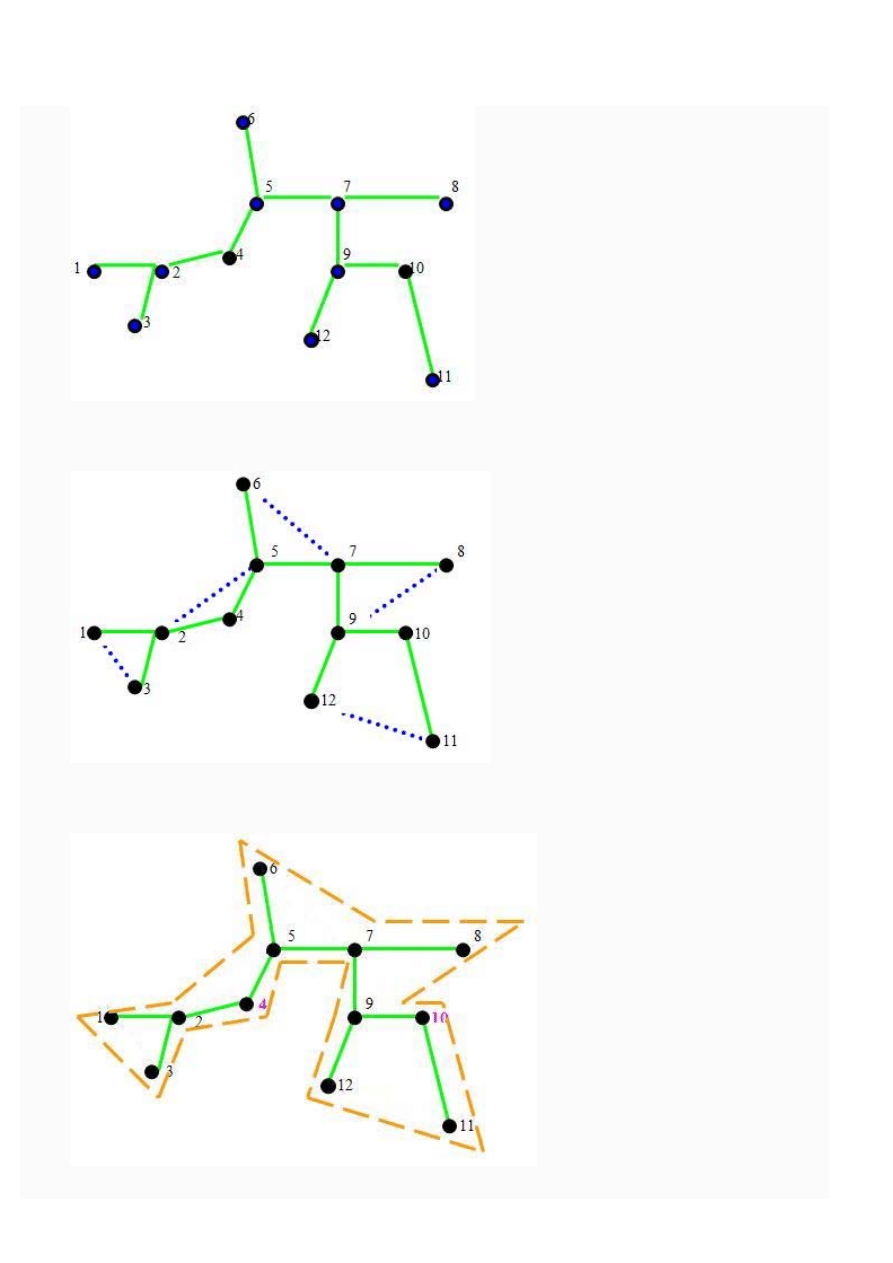
2. znajdź zbiór Vodd węzłów nieparzystego stopnia w drzewie T0;

Wyszukujemy wszystkie węzły nieparzystego stopnia.

Strona 3

Binboy at Sphere:Problem komiwojażera. Sformuowanie problemu. Rys historyczny. Algorytm Christof...

2007-01-24 21:33:18

http://binboy.sphere.pl/index.php?show=134&drukuj=true

3. znajdź w Vodd minimalne skojarzenia dokładne M0odd;

Przeglądamy zbiór węzłów nieparzystego stopnia i wyznaczamy minimalne skojarzenia między nimi:

4. znajdź cykl Eulera Ce w podgrafie indukowanym przez T0 + M0odd;

Korzystamy np. ze znanego algorytmu Fleury’ego:

Strona 4

Binboy at Sphere:Problem komiwojażera. Sformuowanie problemu. Rys historyczny. Algorytm Christof...

2007-01-24 21:33:18

http://binboy.sphere.pl/index.php?show=134&drukuj=true

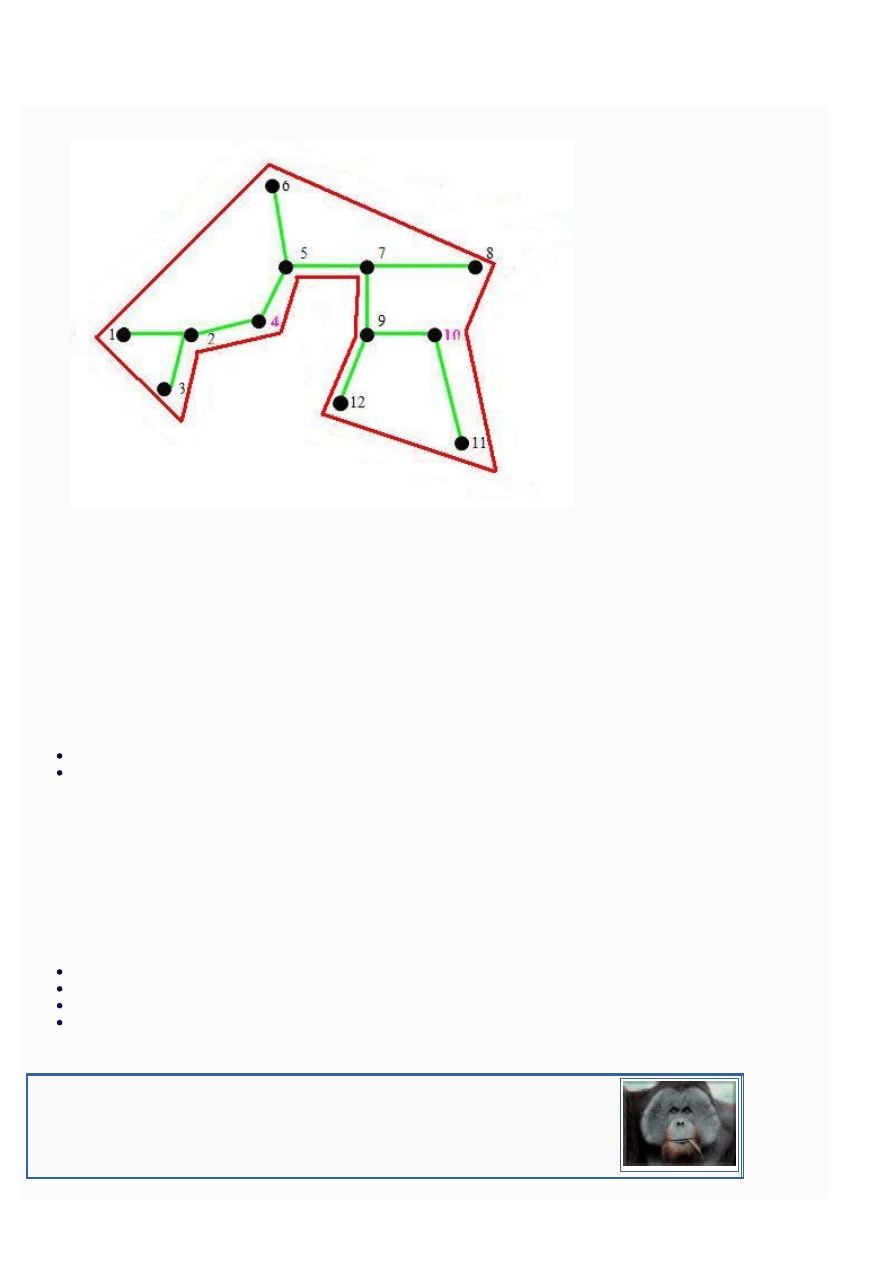
5. przekształć cykl Eulera Ce w cykl Hamiltona Cch w grafie pełnym;

Analiza algorytmu Christofidesa

Na zakończenie udowodnijmy, że algorytm faktycznie jest 1,5-przybliżony. Przyjmując C0 jako optymalne rozwiązanie dla
powyższego grafu, C0odd jako najkrótszy cykl Hamiltona w grafie indukowanym przez V0odd oraz oznaczenia użyte
powyżej udowodnijmy, że:

W(Cch)=3W(C0)/2

gdzie W(H) – suma wag wszystkich połączeń w H (H - podgraf grafu G)

wiemy, że

W(T0)<W(C0)
W(M0odd)<=W(C0odd)/2

Z faktu, że W(C0odd)<=W(C0) wnioskujemy, że W(M0odd)<=W(C0)/2. Natomiast z założenia, że G spełnia nierówność
trójkąta wynika, że W(Cch)<=W(Ce)

Łącząc powyższe nierówności otrzymujemy:

W(Cch)<=W(Ce)= W(T0)+ W(M0odd)< W(C0)+ W(C0)/2=3W(C0)/2

Czas działania algorytmu Christofidesa to O(n^3)

Linki do stron związanych z problemem komiwojażera

http://www.math.princeton.edu/tsp/index.html
http://panda.bg.univ.gda.pl/~sielim/genetic/gen_komi.htm
http://www.wiw.pl/modelowanie/euler.asp
http://www.algebra.com/algebra/about/history/Traveling-salesman-problem.wikipedia

Wyświetleń: 6604

lahead (

O użytkowniku

)

Liczba punktów: 70

Użytkownik przyłączył się: 19.06.2005 i opublikował już: 1 artykuł.

Strona 5

Binboy at Sphere:Problem komiwojażera. Sformuowanie problemu. Rys historyczny. Algorytm Christof...

2007-01-24 21:33:18

http://binboy.sphere.pl/index.php?show=134&drukuj=true

Copyright © 2002-2007 by

Binboy

&

Sphere