MECHANIKA PŁYNÓW - LABORATORIUM
7. PRZEPŁYW PRZEZ UKŁAD HYDRAULICZNY
1. Wstęp teoretyczny.
1.1. Straty ciśnienia w przewodach pojedynczych.
W celu obliczenia strat ciśnienia należy wyprowadzić bilans energetyczny czynnika
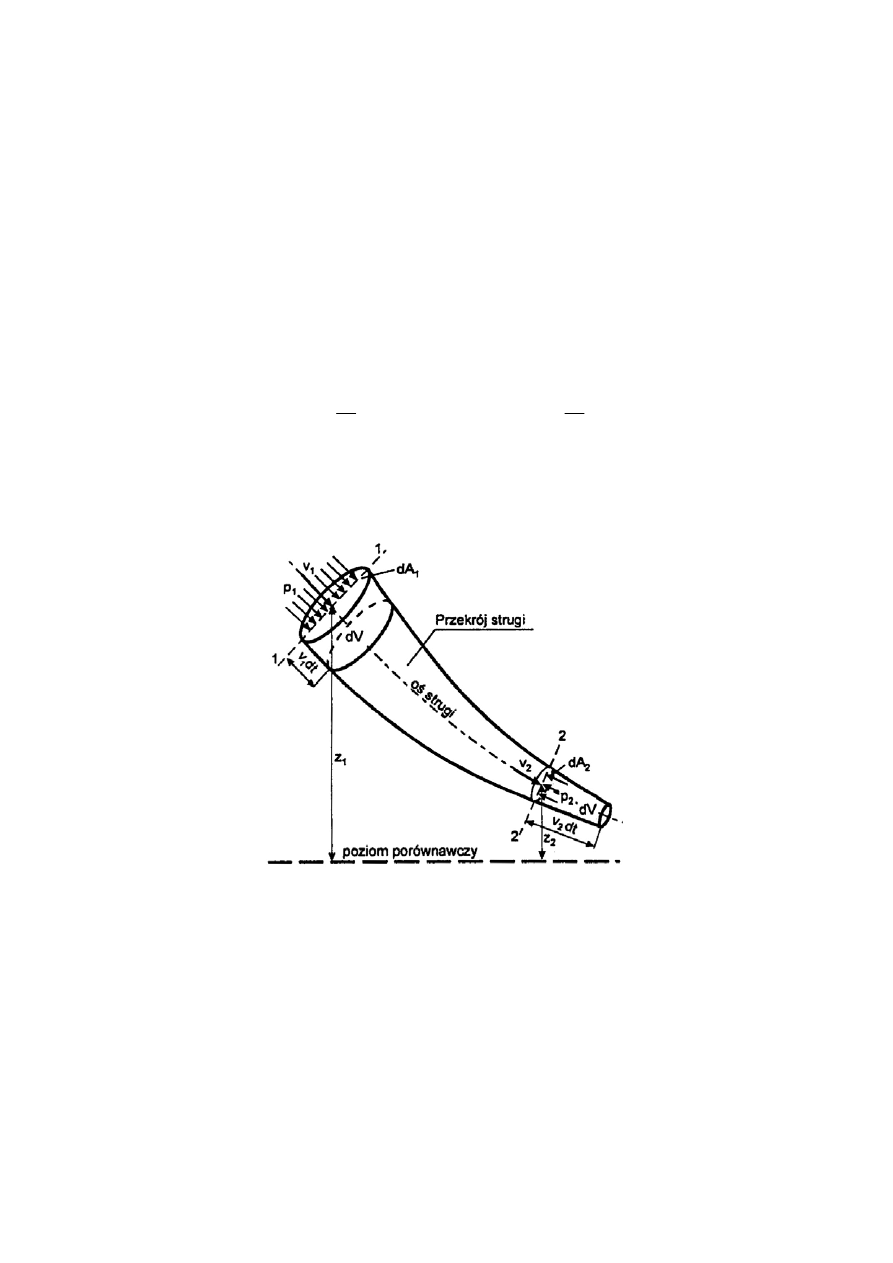
płynącego odcinkiem rurociągu o końcowych przekrojach l i 2 (rys., 1). Gdy przepływ
odbywa się bez wymiany ciepła i masy bilans ten wyraża się wzorem:
2
2
2
2
2
2
2
2
2
1
1
2
1
1
1
1
1
1
2
2
u
v
z
g
p
u
v
z
g
p
ρ
ρ
α
ρ
ρ
ρ
α
ρ
+
+
+
=
+
+
+
,
(1)
gdzie: g – normalne przyśpieszenie ziemskie [m/s
2
], h – wysokość położenia [m], p –
ciśnienie bezwzględne [Pa], u – energia wewnętrzna właściwa [J/kg], v – średnia prędkość
przepływu [m/s], α – współczynnik Coriolisa, ρ – gęstość [kg/m
3
].
Rys. 1.
Przepływ płynów nieściśliwych, należy traktować jako przepływ czynników, dla których
zmiany gęstości ρ
1
=ρ
2
=ρ, bądź ciężaru właściwego nie mają praktycznego wpływu na wyniki
obliczania strat ciśnienia, dlatego dla tych płynów obliczenia należy prowadzić pomijając
ściśliwość. Dodatkowo należy przyjąć u
1
=u
2
=u, przy czym dla osiowometrycznego pola
prędkości czynnika α
1
=α
2
=α. Współczynnik α przyjmuje wartości:
• α=2 – przepływ laminarny,
• α=1 – przepływ turbulentny.
Zakład Inżynierii Procesowej
1
MECHANIKA PŁYNÓW - LABORATORIUM
Po uwzględnieniu wszystkich powyższych warunków otrzymuje się równania dla cieczy
idealnej postaci:
g
v
g
p
z
g
v
g
p
z
2
2
2
2
2
2
2
2
1
1
1
1
+
+
=
+
+
ρ
ρ
,
(2)
.
2
2
const
g
v
g
p
z
E
=
+
+
=
ρ
(3)
gdzie: E – energia całkowita płynu.
Równania (2) i (3) są jedną z form równania Bernoulliego dla cieczy idealnych.
1.2. Spadek ciśnienia.
Spadek ciśnienia w czasie przepływu jest wyznaczany z równania Bernoulliego dla cieczy
rzeczywistych:
∑
+
+
+
=
+
+
str
h
g
v
g
p
z
g
v
g
p
z
2
2
2
2
2
2
2
2
1
1
1
1
ρ
ρ
,
(4)
gdzie h
str.
– to wysokość strat ciśnienia. Suma oporów przepływu
(
)
∑
str
h
, jest różnicą energii
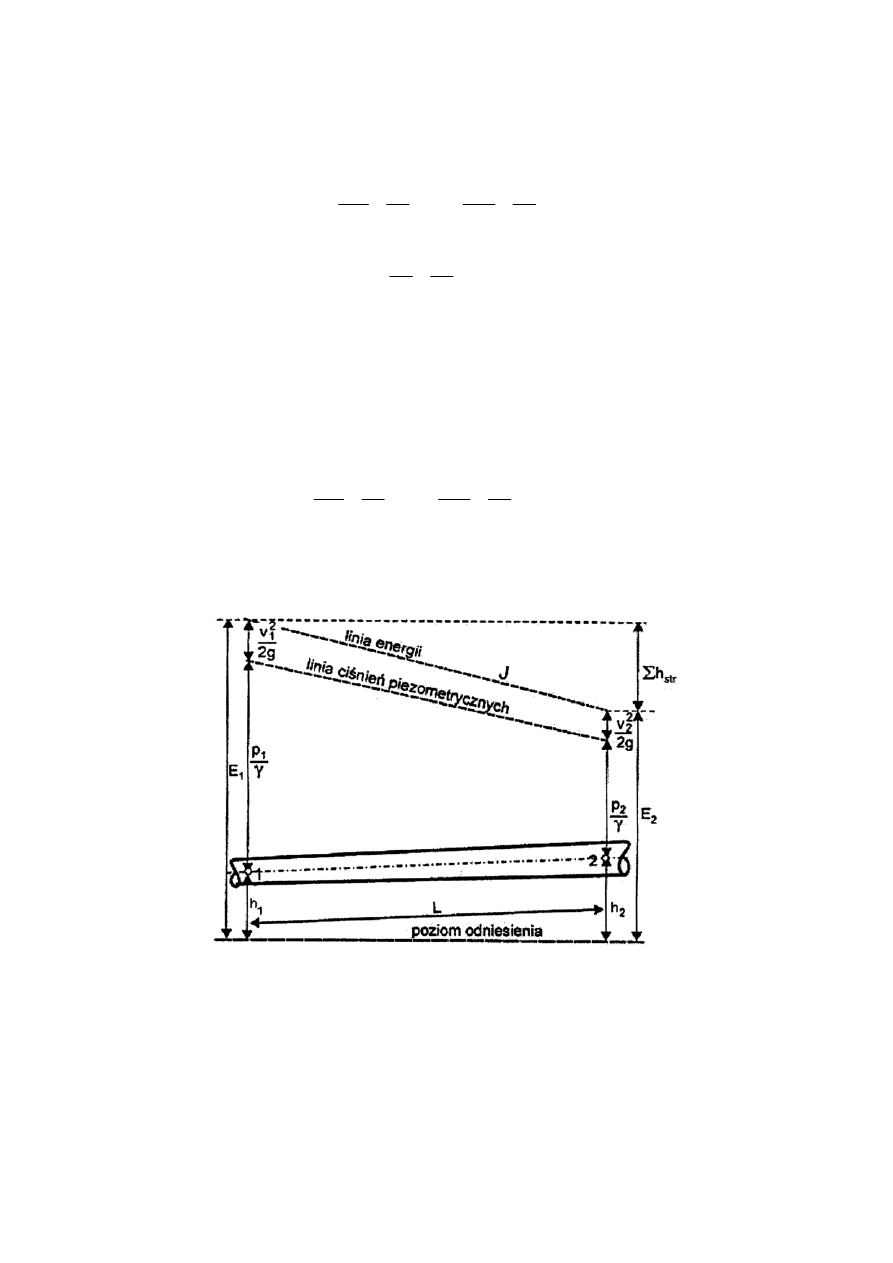
płynu między dwoma przekrojami przewodu (rys. 1 i 2).
Rys. 2. Spadek ciśnienia w przewodzie w czasie przepływu.
Sam spadek ciśnienia oblicza się wychodząc z równania (4), z którego, po odpowiednich
przekształceniach, otrzymujemy:
Zakład Inżynierii Procesowej
2
MECHANIKA PŁYNÓW - LABORATORIUM
2
2
v
Z
p
⋅
⋅
=
Δ
ρ
,
(5)
gdzie Z – całkowity współczynnik strat:
Z = Z
M
+ Z
T
, (6)
gdzie: Z
T
– współczynnik strat liniowych, Z
M
– współczynnik strat miejscowych.
1.2.1. Straty liniowe.
Są wywołane tarciem wewnętrznym płynu oraz w obszarze warstwy przyściennej. W
procesach technologicznych płyny są zwykle transportowane rurociągami, w których efekt
lepkości prowadzi do "tarcia" i rozproszenia pracy użytecznej w ciepło. To tarcie jest zwykle
pokonane zarówno na drodze ciśnienia wygenerowanego przez pompę lub opadania pod
wpływem grawitacji z wyższego poziomu na niższy. W obu przypadkach jest zwykle
niezbędne, aby wiedzieć, z jaką prędkością płynie ciecz i w związku z tym, z jakim
przepływem mamy do czynienia.
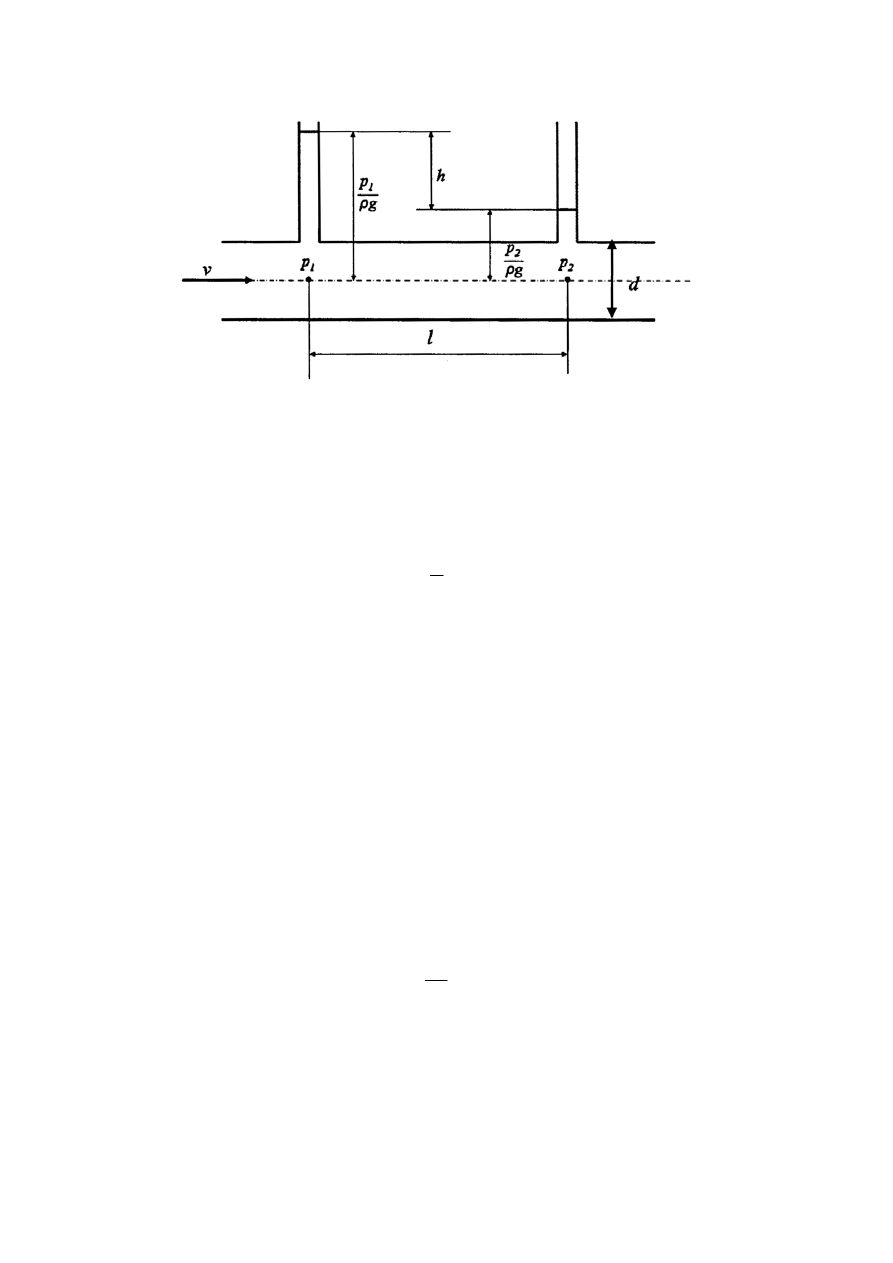
Jeśli ciecz płynie w okrągłym przewodzie o średnicy d ze średnią prędkością przepływu v,
a ciśnienie w dwóch punktach oddalonych od siebie o długość l, wynosi odpowiednio p
1
i p
2
(rys. 3), wówczas związek między prędkością v i stratami liniowymi wynosi:
g
p
g
p
p
h
ρ
ρ
Δ
=
−
=
2
1
.
(7)
Dla przepływu laminarnego straty liniowe h są proporcjonalne do prędkości v. Dla
przepływu turbulentnego zmienia się to do proporcji strat h do v
1,75-2
.
Ogólnie straty liniowe są wyrażone następującym równaniem:
g
v
d
l
h
2
2
⋅
⋅
=
λ
.
(8)
Jest to równanie Darcy-Weisbacha częściej spotykane w postaci:
2
2
v
d
l
p
⋅
⋅
⋅
=
Δ
ρ
λ
(9)
gdzie λ – współczynnik oporów przepływu.
Analizując powyższe równania można zauważyć, że współczynnik strat liniowych jest równy:
d
l
Z
T
λ
=
(10)
Zakład Inżynierii Procesowej
3
MECHANIKA PŁYNÓW - LABORATORIUM
Rys. 3.
Występujący w równaniu współczynnik λ jest nazywany często współczynnikiem tarcia
rur. Często zdarza się w literaturze, zwłaszcza brytyjskiej, że w miejscu λ pojawia się
współczynnik tarcia f (friction factor), który może być definiowany jako:
4
λ
=
f
.
(11)
Dlatego konieczne jest sprawdzenie, do jakiej wartości współczynnika strat dane oznaczenie
się odnosi.
W celu wyznaczenia współczynnika tarcia λ należy ustalić, czy przewód jest hydraulicznie
gładkim, czy szorstkim. Jeżeli jest chropowaty należy ustalić chropowatość względną
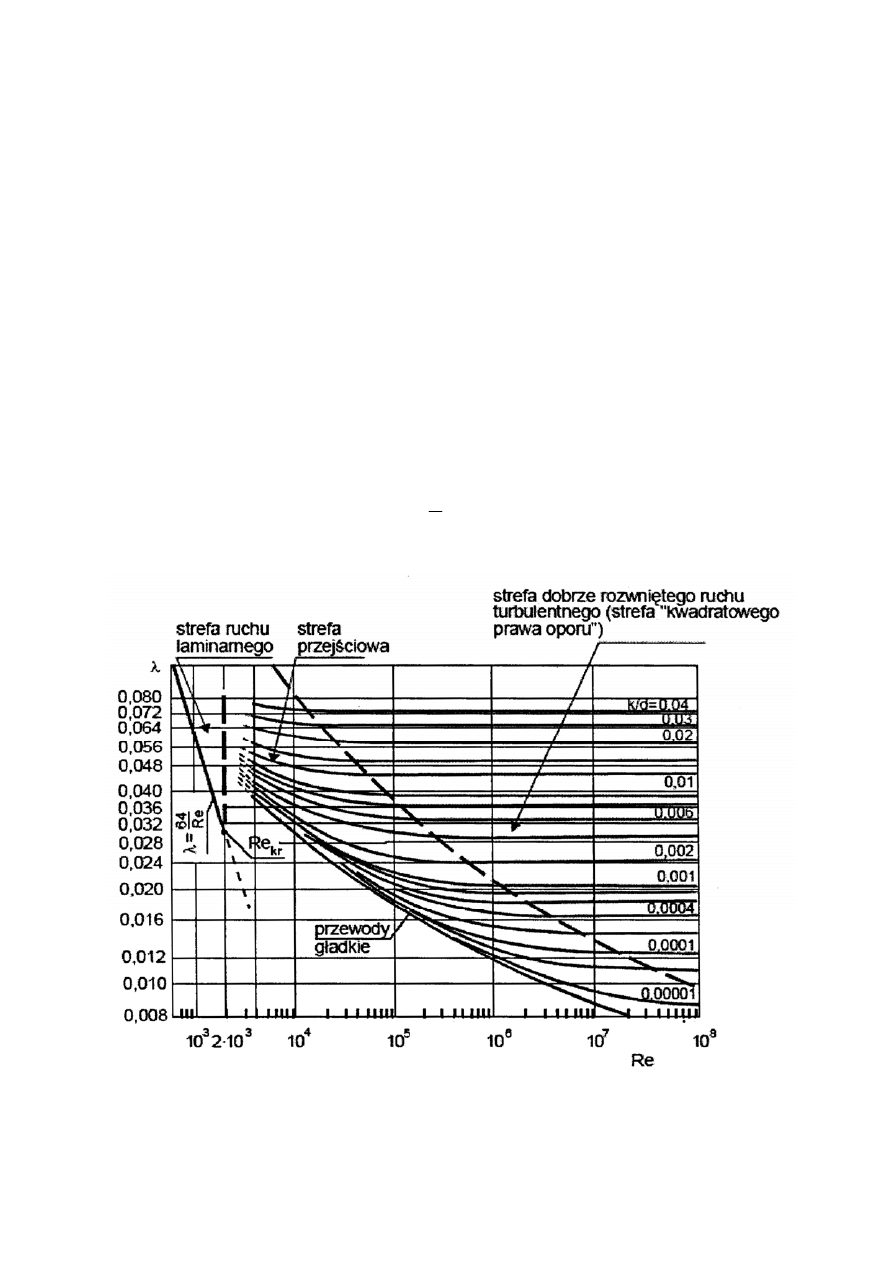
przewodu. Znając jej wartość oraz charakter przepływu (liczbę Reynoldsa) dla danego
czynnika można ustalić w przybliżeniu wielkość współczynnika λ korzystając z wykresu
Colebrooke'a - White'a (rys. 4). Jednak ze względu na możliwość dużej niedokładności
odczytu stosuje się szereg wzorów do obliczenia współczynnika λ.
Chropowatość nie ma wpływu na straty liniowe w zakresie przepływu laminarnego
(Re<2300), dlatego w tym przedziale stosuje się jeden wzór niezależnie od tego, czy przewód
jest hydraulicznie gładki czy szorstki:
Re
64
=
λ
.
(12)
Dla zakresu turbulentnego istnieje kilka wzorów i w tym przypadku są one zależne od
chropowatości przewodów. Z technicznego punktu widzenia każdy materiał, z którego
wykonany jest przewód, wykazuje pewną chropowatość. Zależy ona nie tylko od wysokości
nierówności na ściance, czyli wzniesień i wgłębień na wewnętrznej powierzchni rury, ale
Zakład Inżynierii Procesowej
4
MECHANIKA PŁYNÓW - LABORATORIUM
także od kształtu i rozmieszczenia tych nierówności. Dlatego jest ona związana zarówno z
rodzajem materiału jak i stopniem jego zużycia. Za miarę chropowatości przyjmuje się pewną
wartość k [mm], określającą średnią wysokość nierówności na powierzchni przewodu, z
uwzględnieniem nierównomierności ich rozmieszczenia. Wielkość k nazywana jest
chropowatością bezwzględną. Jednak w przypadku przepływu cieczy praktyka wykazała, ze
chropowatość bezwzględna nie jest wystarczającą miarą, umożliwiającą ocenę wpływu
rodzaju materiału na parametry przepływu. Ta sama wysokość nierówności na powierzchni
wewnętrznej przewodu może mieć istotne znaczenie w przypadku rur o małych średnicach, a
z drugiej strony może być pomijalna przy rurociągach o dużych średnicach. Dlatego za
miarodajną uznaje się chropowatość względną, czyli odniesioną do liniowego wymiaru
charakteryzującego przekrój poprzeczny rurociągu. W przypadku rur kołowych chropowatość
względna ε najczęściej określana jest jako:
d
k
=
ε
.
(13)
Rys. 4. Wykres Colebrooke'a - White'a.
Zakład Inżynierii Procesowej
5
MECHANIKA PŁYNÓW - LABORATORIUM
Dla rur hydraulicznie gładkich współczynnik λ, w zależności od liczby Re, można
wyznaczyć z równań empirycznych:
• Blasiusa dla zakresu
(
)
5
10
Re
3000
<
<
25
,
0
Re
3164
,
0
−
⋅
=
λ
,
(14)
• Nikuradse dla zakresu
(
)
8
5
10
Re
10
<
<
257
,
0
Re
221
,
0
0032
,
0
+
=
λ
.
(15)
1.2.2. Straty miejscowe.
Straty miejscowe odgrywają bardzo ważną rolę w obliczeniach spadku ciśnienia, dlatego
nie mogą być one pominięte w rozważaniach.
Są stratami zwanymi również lokalnymi i zależą przede wszystkim od kształtu i rodzaju
zastosowanych elementów dodatkowych na drodze przepływu, tj. kolanka, zawory, kryzy,
dyfuzory, kontraktory i inne.
Straty lokalne wyznacza się na podstawie współczynnika strat miejscowych. Ich wartości
są bardzo zróżnicowanie, co wynika z budowy odpowiednich elementów. Do ich
wyznaczenia stosuje się przede wszystkim normy np. normę PN-76/M-34034 "Zasady
obliczeń strat ciśnienia. Rurociągi".
W układzie pomiarowym znajdują się następujące elementy:
• Kolanka
Wielkości strat lokalnych wynikają głównie z geometrii samego kolanka. Można to
wytłumaczyć faktem występowania oderwanych stref przepływu w narożnikach oraz zaraz za
ostrymi kantami. Następują tam zawirowania, a powstałe wiry powodują dodatkowe
rozproszenie energii mechanicznej.
Przedstawione na rysunku 5 wartości współczynnika strat lokalnych dotyczą zmian
kierunku przepływu pod kątem 90º. Aby wyznaczyć zakręt pod innym kątem należy
uwzględnić pewien współczynnik proporcjonalności z.
Rys. 5. Współczynnik strat miejscowych dla kolan Z
M
w zależności od ich geometrii.
Zakład Inżynierii Procesowej
6
MECHANIKA PŁYNÓW - LABORATORIUM
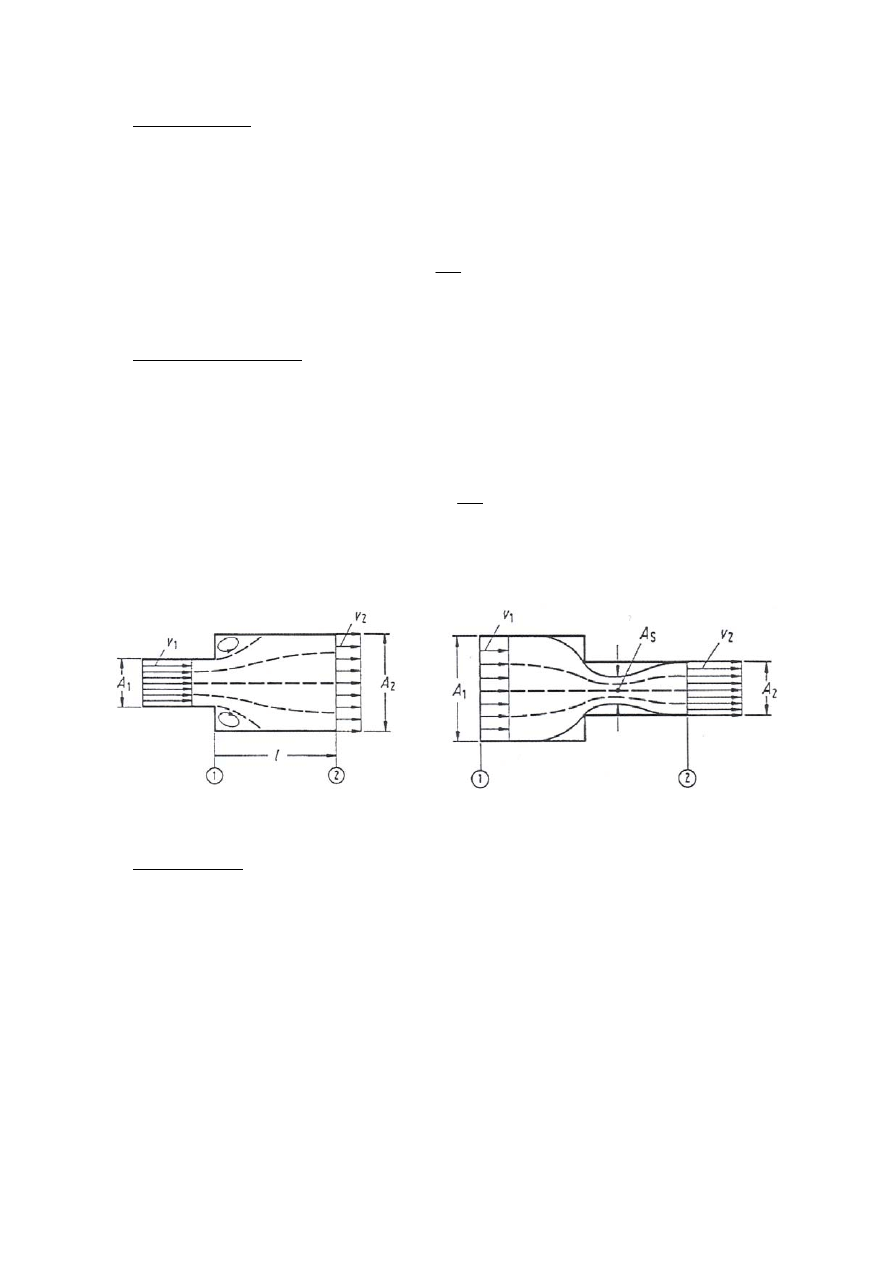
• Dyfuzor Carnot.
Dyfuzor to element rurociągu, w którym dochodzi do rozszerzenia światła przewodu, a
więc zmiany średnicy z mniejszej (d) na większą (D) (rys. 6A). Współczynnik strat lokalnych
dla dyfuzora wyznaczamy ze wzoru:
2
2
2
1
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
D
d
Z
M
,
(16)
gdzie d, D to poszczególne średnice dyfuzora (D>d).
• Zwężka lub kontraktor.
Kontraktor to element rurociągu, w którym dochodzi do zwężenia światła przewodu, a
więc zmiany średnicy z większej (D) na mniejszą (d) (rys. 6B). Współczynnik strat lokalnych
wyznaczamy ze wzoru:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⋅
=
2
2
1
5
,
0
D
d
Z
M
.
(17)
A)
B)
Rys. 6. Schematyczny rysunek: A – dyfuzor Carnot; B – zwężka/kontraktor.
• Zawór kulowy.
Zawory kulowe są jednymi z częściej stosowanych elementów w rurociągach.
Umożliwiają one sterowanie przepływami w poszczególnych gałęziach sieci. W przypadku
zaworu kulowego wielkość strat lokalnych zależy od stopnia zamknięcia zaworu (α).
Zależności te są opisane w normie PN-76/M-34034 dla przykładu:
- Z
M
= 41 dla α = 45º,
- Z
M
= 0 dla α = 0º.
Zakład Inżynierii Procesowej
7
MECHANIKA PŁYNÓW - LABORATORIUM
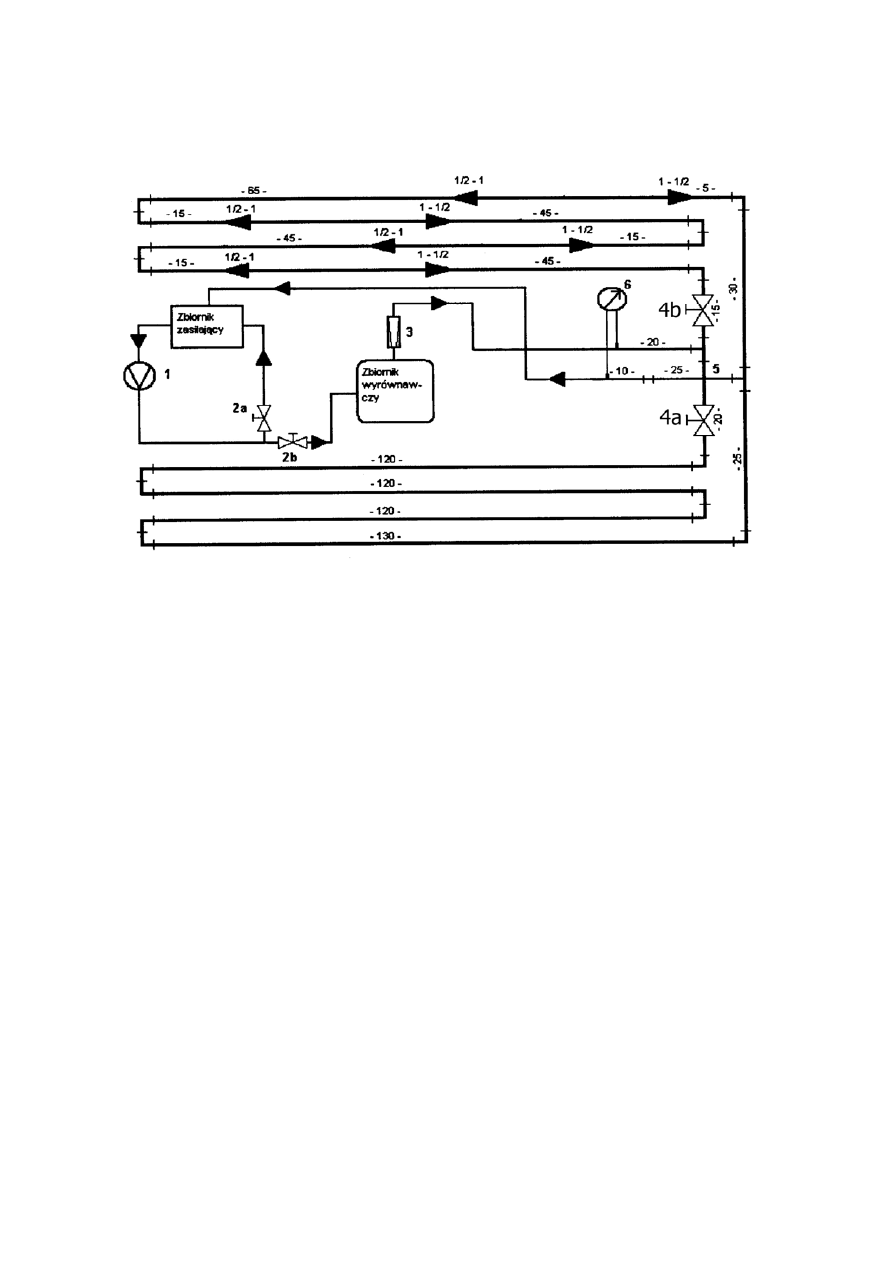
2. Schemat stanowiska pomiarowego.
Rys. 7. Schemat stanowiska pomiarowego: 1 – pompa zalewowa, 2a, b – zawory regulujące, 3
– rotametr, 4a, b – zawory sustemów hydraulicznych, 5 – podwójny uskok o wysokości 5
[cm], 6 – manometr.
Objaśnienia symboli:
◄-►
- zmiana średnicy rury (1”↔1/2”),
┌
- kolano,
-10-
- długość przewodu [cm].
3. Przebieg ćwiczenia.
3.1.
Przygotowanie układu do pracy.
Aby pomiary były poprawne i powtarzalne należy napełnić oba układy rur wodą, żeby
pozbyć się powietrza. W tym celu powinno się otworzyć zawór 2b prowadzący do zbiornika
wyrównawczego i zamknąć kurek powrotny 2a do zbiornika zasilającego. Dzięki temu woda
o maksymalnym możliwym natężeniu przepływu zostanie puszczona do układu. Po
dokonaniu tych czynności należy otworzyć zawór kurka na dole zbiornika i następnie
otworzyć zawór 4 jednego z systemów. O otwarciu zaworu świadczy ustawienie kurka
wzdłuż osi rury. Pozycja poprzeczna oznacza, że zawór jest zamknięty.
Po upewnieniu się, że powyższe czynności zostały wykonane można wlać wodę do
Zakład Inżynierii Procesowej
8
MECHANIKA PŁYNÓW - LABORATORIUM
zbiornika zasilającego i uruchomić pompę 1. Na początku następuje wypełnianie wodą
zbiornika wyrównawczego, dlatego też, gdy woda w zbiorniku zasilającym zacznie się
wyczerpywać, należy wlać kolejną porcję. Czynność powtarzać do momentu, aż wężem
powrotnym z układu przestaną płynąć pęcherze powietrza. Gdy to nastąpi trzeba wyłączyć
pompę i zamknąć kurek układu wypełnionego już wodą i otworzyć zawór systemu "suchego"
i następnie włączyć pompę ponownie. W przypadku, gdyby zaczęło brakować znowu wody w
zbiorniku zasilającym, należy dolać jej niewielką ilość, aby poziom utrzymywał się wokoło
połowie wysokości pojemnika. Należy czekać, aż wężem powrotnym przestaną płynąć
pęcherze powietrza.
Gdy te czynności zostaną wykonane, można przystąpić do pomiarów. Ważne jest, aby
podczas pracy pompa była zawsze zalana wodą!!!
3.2.
Wykonanie pomiarów.
3.2.1. Upewnić się, że oba systemy są zalane wodą, oraz czy w zbiorniku zasilającym i
wyrównawczym jest odpowiednia ilość cieczy.
3.2.2. Otworzyć zawór 4a dla systemu o stałej średnicy przewodu.
3.2.3. Otworzyć zawór 2a i włączyć pompę. Regulując zaworami 2a i 2b ustawić natężenie
przepływu na najwyższą możliwą wartość przepływu.
3.2.4. Włączyć manometr i ustawić jednostkę wskazań na milimetry słupa wody (mmH
2
0).
3.2.5. Odczekać, aż wartość się ustabilizuje i następnie spisywać wskazania manometru w
ustalonych odstępach czasowych, np. co 5 sekund, tak by uzyskać 10 pomiarów.
3.2.6. Następnie regulując zaworami 2a i 2b zmniejszyć wartości przepływu o 0,02 [m
3
/h] i
ponownie dokonać pomiaru (punkt 3.2.5).
3.2.7. Po osiągnięciu najniższej możliwej wartości natężenia przepływu, zwiększyć je znów
do wartości maksymalnej.
3.2.8. Otworzyć zawór 4b dla systemu o zmiennej średnicy przewodu, a następnie zamknąć
zawór 4a dla systemu o stałej średnicy przewodu.
3.2.9. Wykonać analogiczne pomiary jak dla układu o stałej średnicy przewodu.
3.2.10. Po osiągnięciu najniższej możliwej wartości natężenia przepływu, zwiększyć je znów
do wartości maksymalnej.
3.2.11. Otworzyć zawór 4a dla systemu o stałej średnicy przewodu (oba systemy otwarte).
Wykonać analogiczne pomiary jak dla układu o stałej i zmiennej średnicy przewodu.
3.2.12. Po zakończeniu ćwiczenia zamknąć zawór 2b, a następnie 4a i 4b, wyłączyć pompę i
dopiero zamknąć zawór 2a.
Zakład Inżynierii Procesowej
9
MECHANIKA PŁYNÓW - LABORATORIUM
3.2.13. Do celów obliczeniowych należy zmierzyć temperaturę wody w zbiorniku
zasilającym, oraz spisać liczbę poszczególnych elementów generujących opór miejscowy
Z
m
(tab. 1) dla obu systemów.
4. Opracowanie wyników.
Dla każdego systemu hydraulicznego:
4.1.
Wyznaczyć teoretyczną prędkość przepływu cieczy:
x
x
A
V
v
•
=
,
(18)
gdzie:
– objętościowe natężenie przepływu [m
•
V
3
/s], v
x
– prędkość liniowa płynu [m/s] w
przewodzie x, A
x
– powierzchnia przewodu x [m
2
]. Dla układu o stałej średnicy przewodu x=
½”=const., dla układu o zmiennej średnicy przewodu x=½” i x=1” (wyznaczamy dwie
prędkości dla systemu). Wewnętrzne średnice przewodów wynoszą odpowiednio:
0122
,
0
"
2
/
1
=
d
[m],
0226
,
0
"
1
=
d
[m].
4.2.
Wyznaczyć liczbę Reynoldsa:
η
ρ
⋅
⋅
=
x
x
x
d
v
Re
,
(19)
gdzie: ρ – gęstość [kg/m
3
], η – lepkość
s]
[Pa
⋅
wody w zmierzonej temperaturze wyznaczone z
zależności:
• dla T = 0 ÷ 40 [
o
C]
]
[kg/m
)
2
,
67
(
57
,
503
)
283
(
)
4
(
1000
3
2
+
⋅
+
⋅
−
−
=
T
T
T
ρ
,
(20)
• dla T = 25 ÷ 100 [
o
C]
]
[kg/m
)
67
(
7
,
466
)
273
(
)
4
(
1000
3
2
+
⋅
+
⋅
−
−
=
T
T
T
ρ
,
(21)
2
)
0
(
)
(
000221
,
0
0337
,
0
1
T
T
T
⋅
+
⋅
+
=
η
η
,
(22)
gdzie: T – temperatura [ºC], η
(0)
– lepkość wody w T=0 [ºC] (η
(0)
=0,00179
).
]
s
Pa
[
⋅
4.3.
Na podstawie wyznaczonej liczby Reynoldsa, dobrać odpowiednie równanie (12, 14,
15) i wyznaczyć współczynnik oporu przepływu λ
x
.
Zakład Inżynierii Procesowej
10
MECHANIKA PŁYNÓW - LABORATORIUM
4.4.
Wyznaczyć współczynnik strat liniowych Z
Tx
:
x
x
x
Tx
d
l
Z
∑
=
λ
.
(23)
Długości poszczególnych odcinków przewodu x w danym systemie odczytać z schematu
stanowiska (rys. 7).
4.5.
Wyznaczyć współczynnik strat miejscowych Z
M
:
∑
⋅
=
Mel
M
Z
n
Z
,
(24)
gdzie: n – liczba elementów o danym współczynniku, Z
Mel
– współczynnik start miejscowych
dla danego elementu. Elementy wykorzystane w układzie zostały wyszczególnione w tabeli 1.
Tab.
1.
Współczynniki strat miejscowych dla poszczególnych elementów.
l.p. Element Z
Mel
1 kolano
90º
0,2
2 zawrót
180º
2
3 uskok
rurowy
2,8
4 zawór
otwarty
0
5 dyfuzor
0,5
6 konfuzor
0,354
4.6.
Wyznaczyć całkowity współczynnik strat:
Z
x
= Z
Mx
+ Z
Tx
. (25)
4.7.
Wyznaczyć teoretyczny spadek ciśnienia dla poszczególnych systemów:
• dla systemu o stałej średnicy:
2
2
"
2
/
1
"
2
/
1
v
Z
p
stT
⋅
⋅
=
Δ
ρ
,
(26)
• dla systemu o zmiennej średnicy:
(
)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
+
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
=
Δ
2
2
2
2
2
"
1
")
1
(
2
"
2
/
1
")
2
/
1
(
")
2
/
1
(
2
"
1
"
1
2
"
2
/
1
"
2
/
1
v
Z
v
Z
Z
v
Z
v
Z
p
T
T
M
zmT
ρ
ρ
ρ
ρ
(27)
4.8.
Otrzymane wyniki teoretycznego spadku ciśnienia porównać z wynikami odczytanymi
z manometru.
4.9.
Wykreślić wykres zależności
)
(
•
=
Δ
V
f
p
D
dla każdego z pomiarów.
Zakład Inżynierii Procesowej
11
MECHANIKA PŁYNÓW - LABORATORIUM
Zakład Inżynierii Procesowej
12
4.10. Sformułować wnioski.
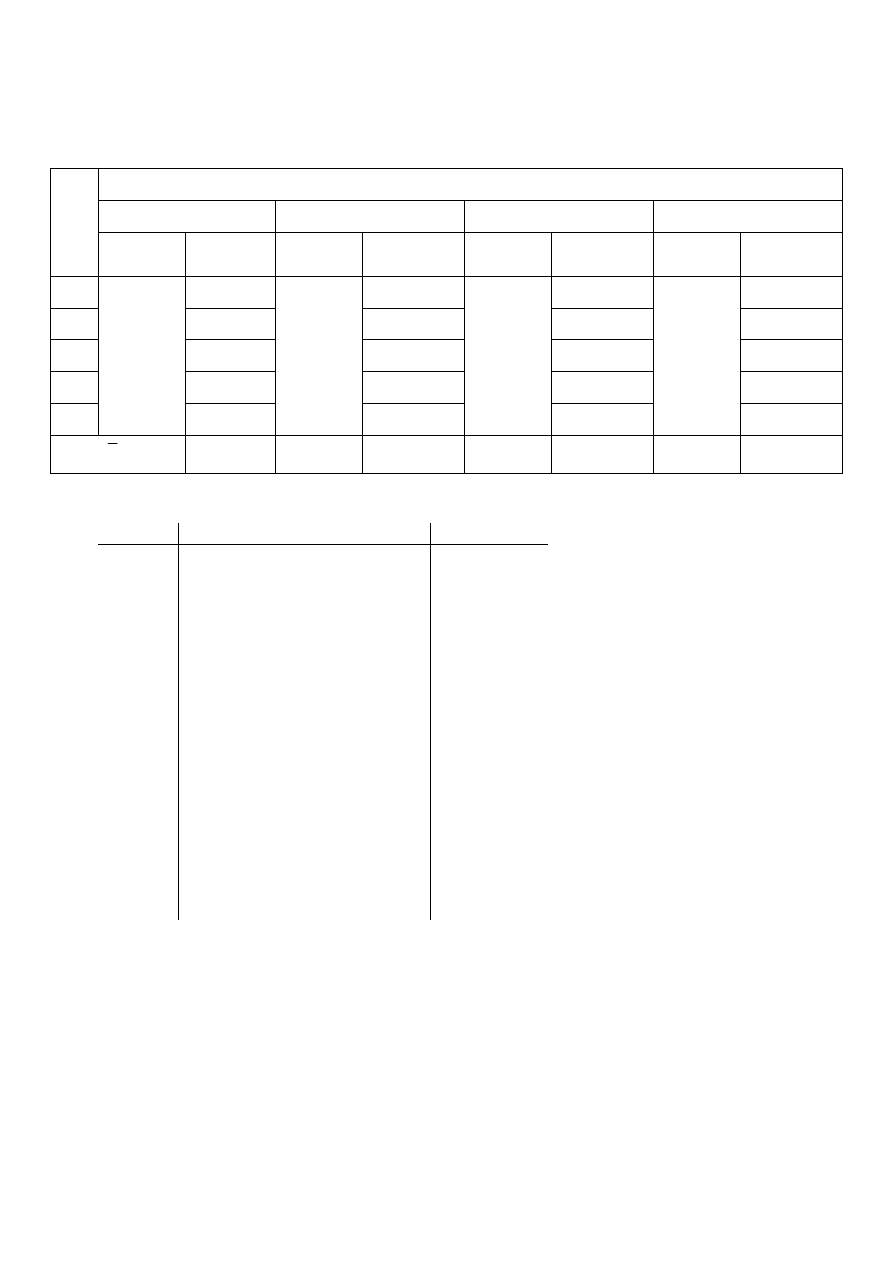
Tab.2 Tabela pomiarowa (wzór).
System .........................................................................................
Seria I
Seria II
Seria III
Seria IV
l.p.
•
V
D
p
Δ
•
V
D
p
[m
3
/h]
[Pa]
[m
3
/h]
Δ [Pa]
•
V
D
p
[m
3
/h]
Δ [Pa]
•
V
D
p
[m
3
/h]
Δ [Pa]
1
2
3
...
10
(
)
D
p
Δ
=
- - -
5. Wykaz stosowanych oznaczeń.
Symbol: Opis:
Wymiar:
•
V
objętościowe natężenie
przepływu
[m
3
/s]
A
powierzchnia [m
2
]
d, D
średnica [m]
E
energia całkowita [J]
g
przyśpieszenie grawitacyjne
[m/s
2
]
l
długość [m]
p
ciśnienie
[Pa]
T
temperatura [ºC]
u
energia właściwa
[J/kg]
v
prędkość liniowa
[m/s]
Z
współczynnik strat
[-]
z, h
wysokość [m]
α
współczynnik Coriolisa
[-]
ε
chropowatość [-]
η
lepkość dynamiczna
• „Laboratorium z mechaniki płynów”, praca zbiorowa pod red. Weinerowskiej K.,
Wydawnictwo Politechniki Gdańskiej, Gdańsk 2004 r.
• „Mechanika płynów w inżynierii środowiska”, Orzechowski Z., Prywer J., Zarzycki R.
WNT, Warszawa 2001 r.
• „Mechanika płynów z hydrauliką”, Gryboś R., Wyd. VIII, Politechnika Śląska, Skrypty
uczelniane Nr 1610, Gliwice 1990 r.
6. Literatura uzupełniająca.
s]
[Pa
⋅
λ
współczynnik oporu
[-]
ρ
gęstość [kg/m
3
]
MECHANIKA PŁYNÓW - LABORATORIUM
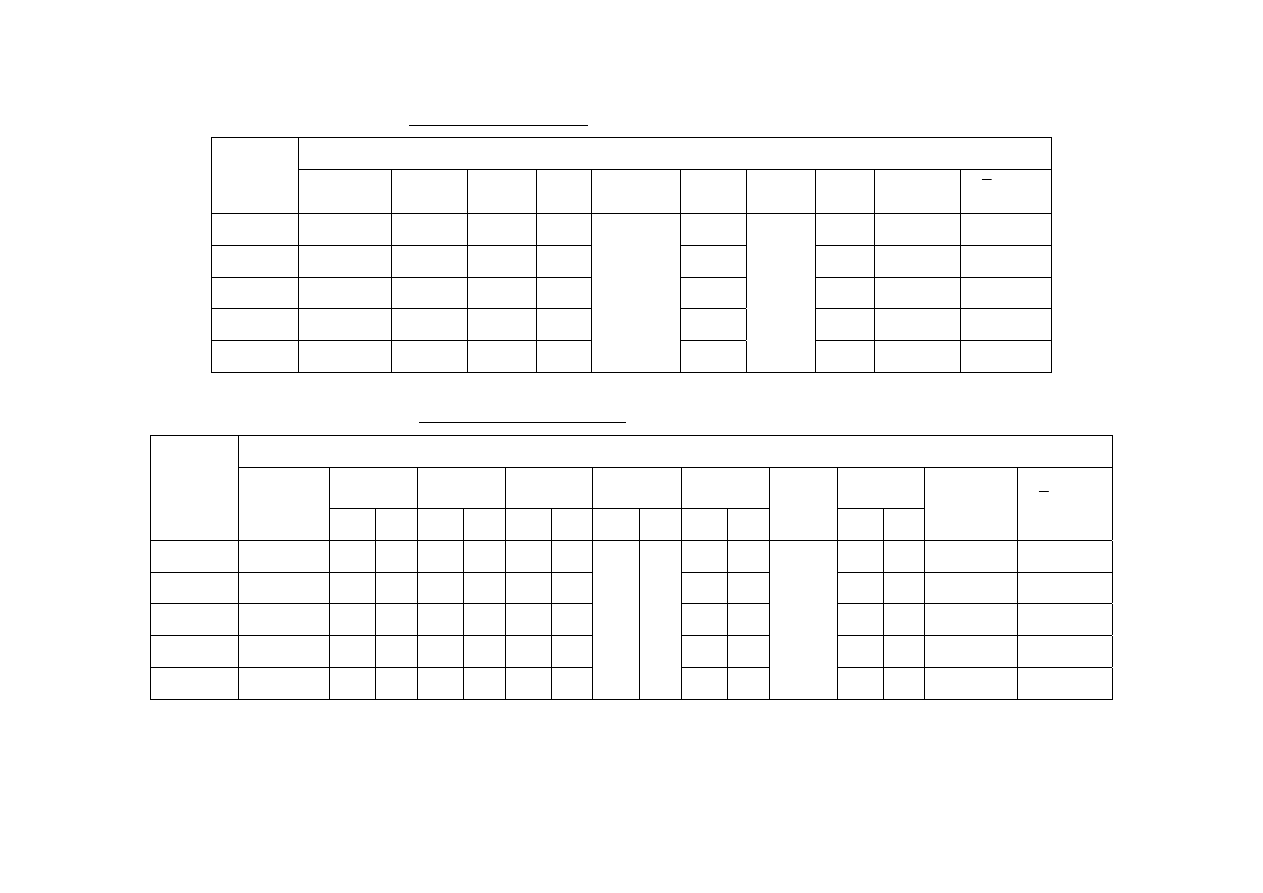
Tab. 3. Tabela obliczeniowa dla układu o stałej średnicy przewodu (wzór).
System o stałej średnicy przewodu.
Seria nr
•
V
[m
3
/s]
v [m/s] Re [-] λ [-]
∑
l [m] Z
T
[-]
Z
M
[-]
Z [-]
stT
p
Δ
[Pa]
D
st
p
Δ
[Pa]
I
II
III
IV
n
Tab. 4. Tabela obliczeniowa dla systemu o zmiennej średnicy przewodu (wzór).
System o zmiennej średnicy przewodu.
v [m/s] Re [-]
λ [-]
∑
l [m]
Z
T
[-]
Z [-]
Seria nr
•
V
[m
3
/s]
½” 1” ½” 1” ½” 1” ½” 1” ½” 1”
Z
M
[-]
½” 1”
zmT
p
Δ
[Pa]
D
zm
p
Δ
[Pa]
I
II
III
I
V
n
Zakład Inżynierii Procesowej
13
Document Outline