Fizyka relatywistyczna

Zadania z rozwiązaniami

Zadanie 1

Na spoczywającą cząstkę zaczyna działać stała siła. Jaką prędkość uzyska cząstka, gdy siła wykona pracę W?

Porównaj rozwiązanie klasyczne i relatywistyczne.

Rozwiązanie klasyczne:

Energię kinetyczną przyrównujemy do wykonanej pracy

Rozwiązanie relatywistyczne:

Energia kinetyczna wynosi : , czyli:

0

2

0

2

2

m

W

v

W

v

m

klas

klas







2

0

2

c

m

mc



W

c

m

mc





2

0

2

2

0

2

0

2

0

2

0

0

2

0

2

2

2

0

1

2

1

1

2

1

2

1

c

m

W

c

m

W

v

c

m

W

c

m

W

m

W

v

W

c

m

c

v

c

m

klas

.

relat

























Z porównania rozwiązań wynika, że wzór relatywistyczny przechodzi we wzór klasyczny, gdy spełniony jest warunek

, a zatem gdy praca wykonywana przez siłę przyspieszającą jest znacznie mniejsza od energii spoczynkowej

przyspieszanej cząstki. Wynika stąd, że obok znanego kryterium stosowania mechaniki relatywistycznej, gdy prędkość
ciała jest bliska prędkości światła w próżni c, można sformułować drugie kryterium, które mówi, że mechanikę
relatywistyczną stosujemy wtedy, gdy energia dostarczona ciału jest, co najmniej bliska jego energii spoczynkowej.

2

0

c

m

W



Przypomnijmy, że używana w fizyce atomowej, relatywistycznej i jądrowej wygodna jednostka energii elektronowolt [eV] jest
zdefiniowana jako energia, którą uzyskuje ładunek elementarny przebywając różnicę potencjałów U = 1 V,
czyli . Wskutek przebycia drogi, dla której różnica potencjałów wynosi U elektron uzyskuje energię
kinetyczną równą pracy wykonanej przez pole elektryczne W = eU. Rozważmy dwa przypadki:

1.

Elektron przyspieszany w lampie kineskopowej w różnicy potencjałów U

1

= 25 kV uzyskuje energię ,

zatem

gdzie

Różnica między wartością prędkości końcowej obliczoną klasycznie i relatywistycznie jest niewielka.

2.

Elektron przyspieszany w akceleratorze van de Graaffa w różnicy potencjałów U

2

= 25 MV uzyskuje energię

, więc

stąd:

C

,

e

19

10

6

1







J

,

eV

19

10

6

1

1







keV

eU

W

25

1

1





05

0

2

0

1

,

c

m

W



96

0

05

0

1

025

0

1

1

,

v

,

,

v

v

klas

klas













c

,

v

klas

31

0



MeV

eU

W

25

2

2





50

2

0

2



c

m

W

1

0

50

1

250

1

2

,

v

v

v

klas

klas













c

,

v

klas

9

9



kg

,

m

31

0

10

1

9







C

,

e

19

10

6

1







MeV

,

eV

,

J

,

s

m

kg

,

c

m

E

51

0

10

51

0

10

19

8

10

9

10

1

9

6

14

2

2

16

31

2

0

0

























Przykład: Weźmy jako cząstkę elektron o masie spoczynkowej i ładunku przyspieszany
w polu elektrycznym (stałą siłą). Energię spoczynkową elektronu można obliczyć ze wzoru:

,

W tym przypadku wartość prędkości końcowej obliczona ze wzoru klasycznego jest oczywiście nonsensowna.

gdzie

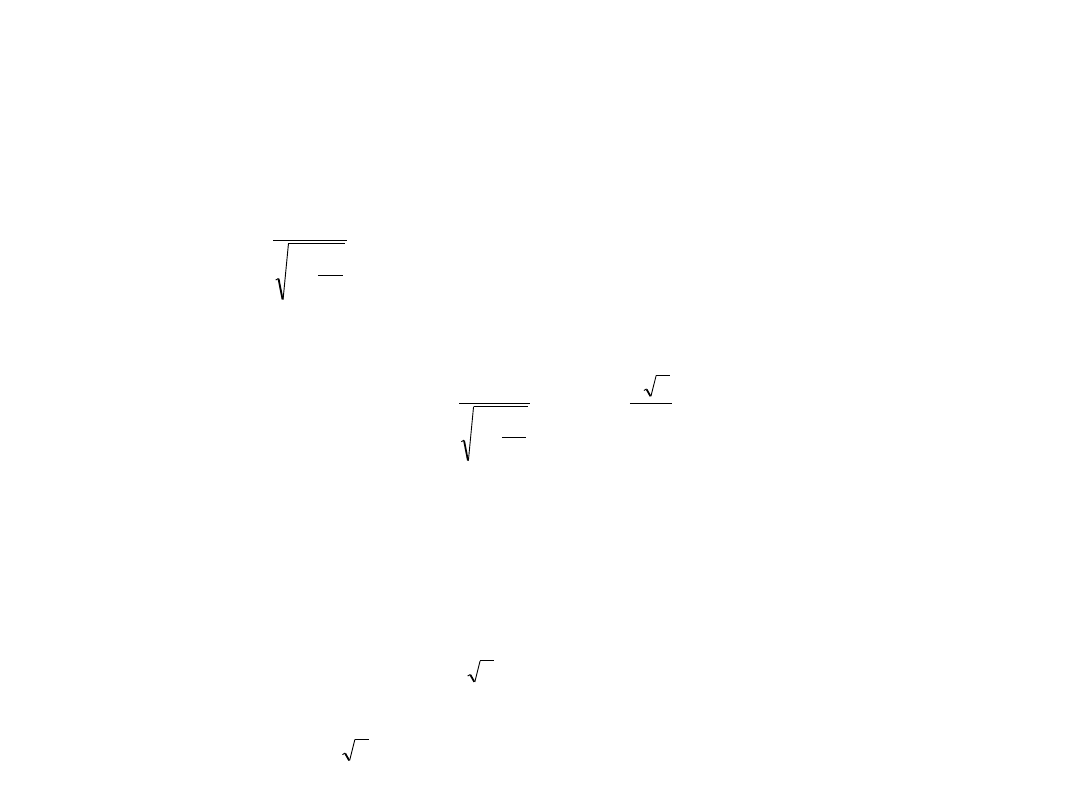
Zadanie 2

Cząstka o masie spoczynkowej m

0

porusza się z taką prędkością, że jej czas życia obserwowany w układzie

laboratorium jest trzy razy dłuższy niż średni czas życia tej cząstki zmierzony wtedy, gdy cząstka jest w

spoczynku. Oblicz energię kinetyczną i prędkość tej cząstki oraz jej pęd.

2

2

1

c

v

t











Zależność między czasem własnym



a czasem mierzonym w laboratorium t:

3

3











t

Energia kinetyczna wynosi:





2

0

2

0

2

0

2

2

1

c

m

c

m

c

m

mc

E

k













Pęd można obliczyć na dwa sposoby

1.

z zależności między energią całkowitą, pędem i energią spoczynkową:

2.

Z definicji pędu:









1

2

4

2

0

4

2

0

2

2

0

4

2

0

2

2

2

















c

m

c

m

c

m

c

m

E

c

p





2

2

0

2

2

c

m

c

p

E





c

m

p

0

2

2



Aby obliczyć prędkość skorzystamy ze wzoru:

c

v

c

v

3

2

2

3

1

1

2

2









c

m

v

m

mv

p

0

0

2

2









Rozwiązanie

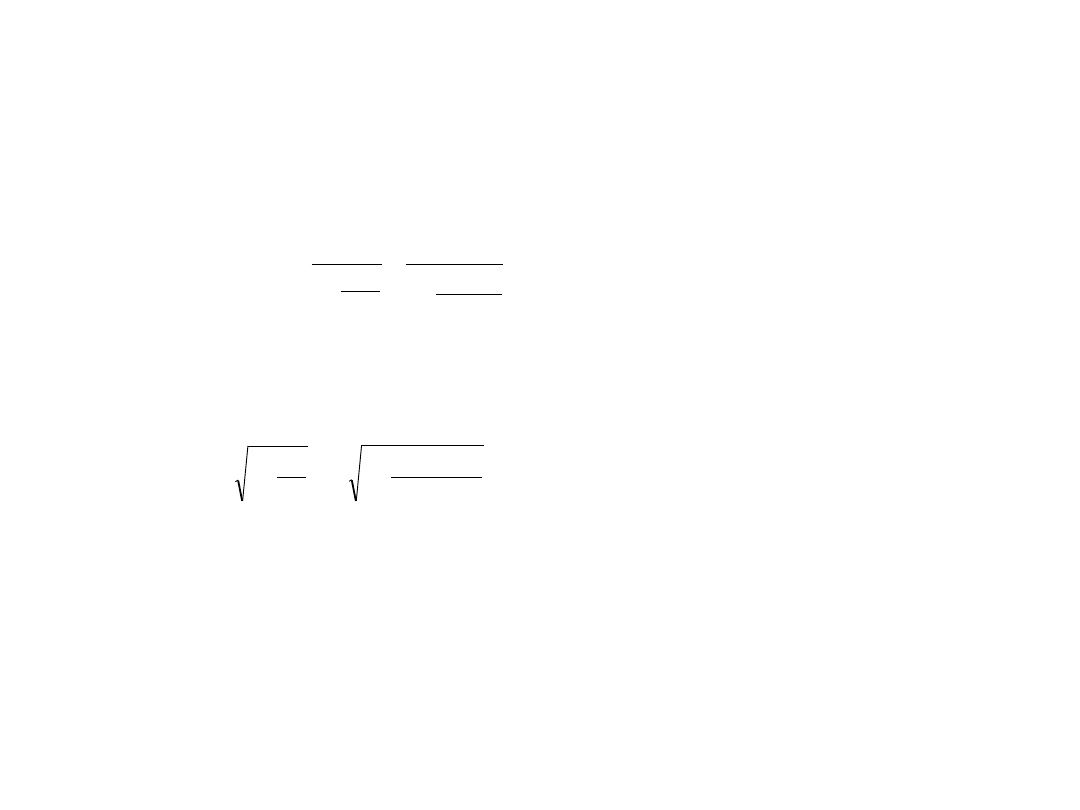
Zadanie 3

Obserwator O

widzi dwa identyczne statki kosmiczne zbliżające się do niego z dwóch stron z prędkością .

Długość własna statku wynosi d = 10 m. Jaką długość jednego z pojazdów obserwuje pilot drugiego pojazdu?

c

,

v

8

0



Rozwiązanie

Trzeba obliczyć prędkość jednego ze statków względem drugiego.

c

,

c

c

,

c

,

c

v

v

v

v

'

v

976

0

64

0

1

6

1

1

2

2

2

2

1

2

1













Długość jednego pojazdu w układzie drugiego:





m

,

d

,

c

c

,

d

c

'

v

d

'

d

2

2

22

0

976

0

1

1

2

2

2

2













Odp.: Pilot widzi drugi pojazd o długości 2,2 m.

Zadanie 4

Zdarzenie A

ma w układzie O współrzędne czasoprzestrzenne x

A

, ct

A

, zdarzenie B -

współrzędne

czasoprzestrzenne x

B

, ct

B

. Czy może istnieć związek przyczynowy między tymi zdarzeniami? Wartości

współrzędnych:

a) x

A

= 1, ct

A

= 2, x

B

= 5, ct

B

= 5, b) x

A

= 2, ct

A

= 0, x

B

= 3, ct

B

= 6

Rozwiązanie a)

Kwadrat interwału czasoprzestrzennego między zdarzeniami A i B w układzie O wynosi:

   



 



7

16

9

2

2

2

2

2



























B

A

B

A

x

x

ct

ct

x

t

c

S

Interwał czasoprzestrzenny jest urojony:

x

t

c







Oznacza to, że między zdarzeniami nie może być związku przyczynowego – zdarzenia są tak daleko od siebie

(duże ), że światło nie zdąży dotrzeć od zdarzenia A do B w czasie

x



t



Rozwiązanie b)

Kwadrat interwału czasoprzestrzennego między zdarzeniami A i B w układzie O wynosi:

   



 



35

1

36

2

2

2

2

2

























B

A

B

A

x

x

ct

ct

x

t

c

S

Interwał czasoprzestrzenny jest rzeczywisty:

Oznacza to, że zdarzenia mogą być powiązane przyczynowo – zdarzenia są na tyle bliskie przestrzennie (małe ),

że światło zdąży dotrzeć od zdarzenia A do B w czasie

x



t



x

t

c







Zadanie 5

Zdarzenie A

ma w układzie O współrzędne czasoprzestrzenne x

A

, ct

A

, zdarzenie B -

współrzędne

czasoprzestrzenne x

B

, ct

B

. Jaka jest ich kolejność czasowa w układzie współrzędnych O’ poruszającym się

wzdłuż osi x z prędkością v = 0,8c? Wartości współrzędnych:

a) x

A

= 1, ct

A

= 2, x

B

= 5, ct

B

= 5, b) x

A

= 2, ct

A

= 0, x

B

= 3, ct

B

= 6

x

ct

A

B

O

x’

ct’

O’

v

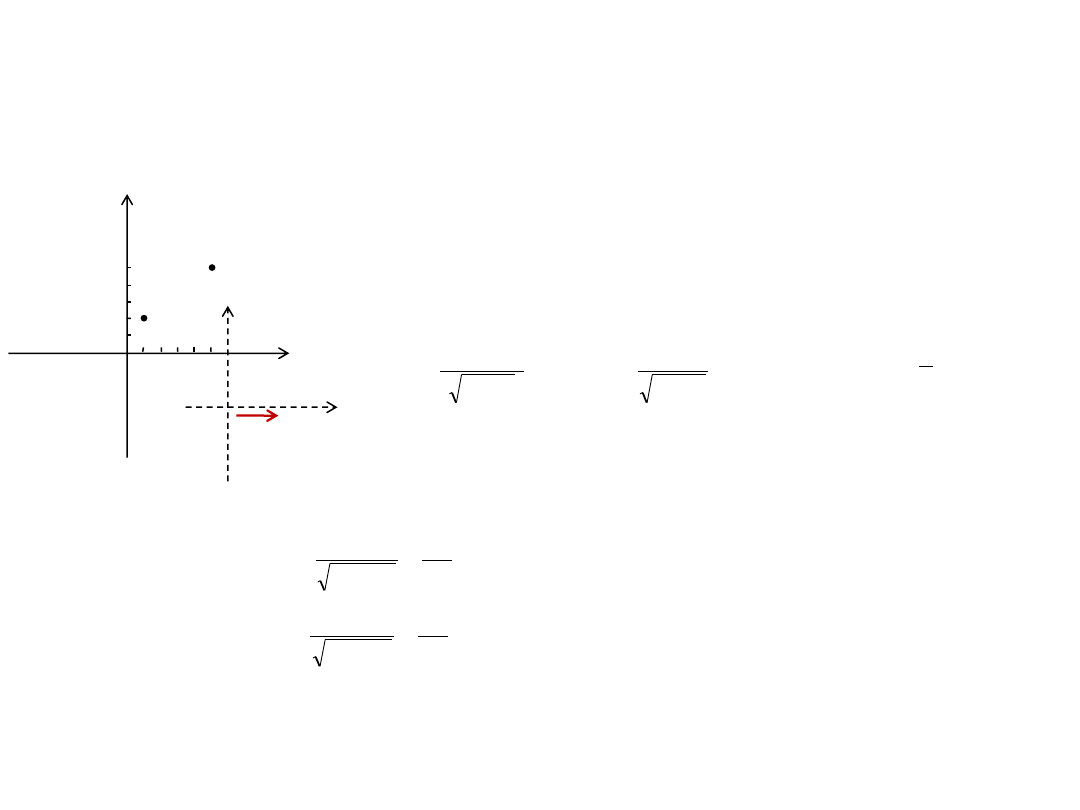
Aby zbadać, jaka jest ich kolejność czasowa w układzie O’, należy znaleźć

współrzędne czasowe zdarzeń w tym układzie (wykonać transformację

Lorentza)

 

2

1











ct

x

'

x

2

1











x

ct

'

ct

gdzie

c

v





2

6

0

2

1

8

0

1

1

8

0

2

2













,

,

,

,

'

ct

A

6667

1

6

0

1

8

0

1

5

8

0

5

2

,

,

,

,

'

ct

B













Rozwiązanie a)

O ile w układzie O najpierw zaszło zdarzenie A, a potem B (ct

A

< ct

B

), to w układzie O’ kolejność zdarzeń jest

odwrotna (

ct’

A

>

ct’

B

).

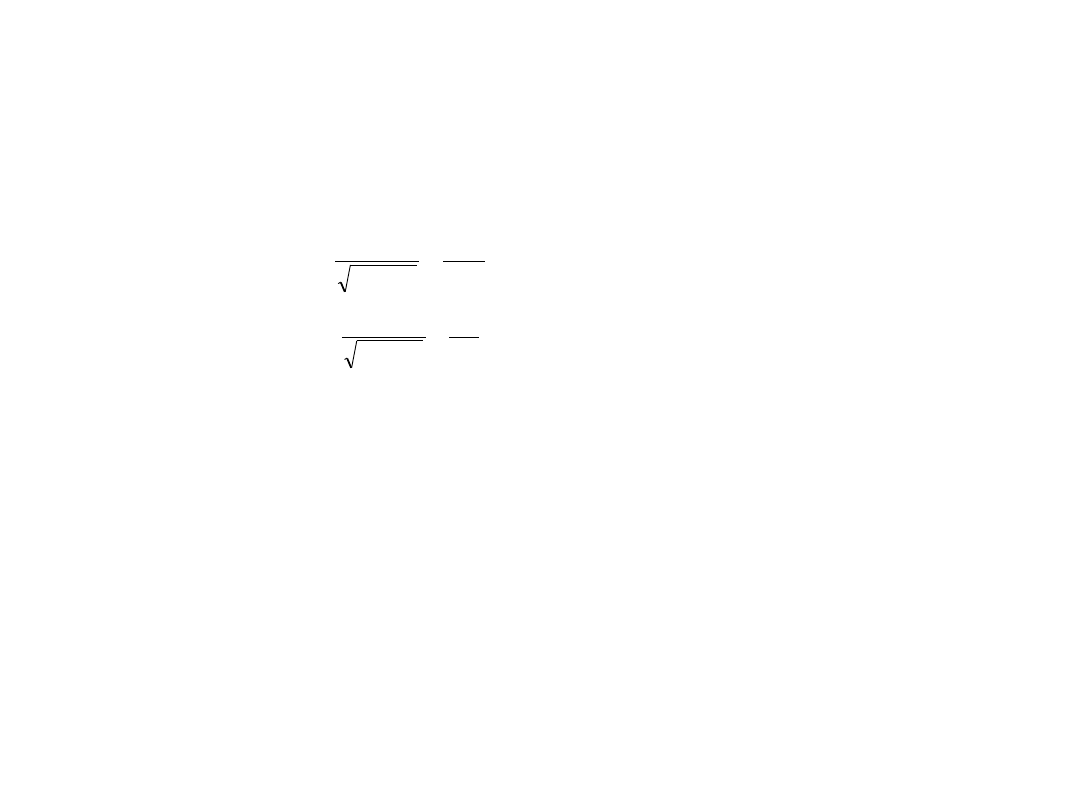
Współrzędne zdarzeń w układzie O’ wynoszą:

667

2

6

0

6

1

8

0

1

2

8

0

0

2

,

,

,

,

,

'

ct

A















6

6

0

6

3

8

0

1

3

8

0

6

2













,

,

,

,

'

ct

B

Kolejność zdarzeń w układzie O i w układzie O’ jest jednakowa: najpierw zaszło zdarzenie A, a potem B

(ct

A

< ct

B

) i (

ct’

A

<

ct’

B

).

Rozwiązanie b)

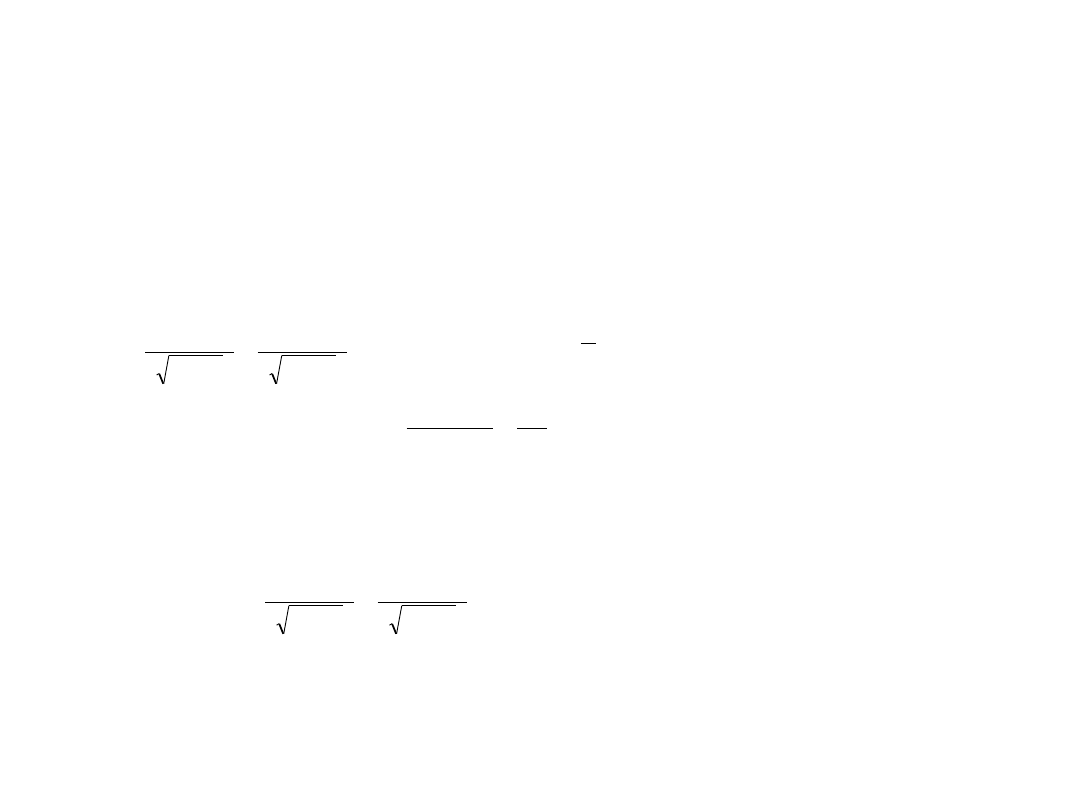
Zadanie 6

Zdarzenie A

ma w układzie O współrzędne czasoprzestrzenne x

A

, ct

A

, zdarzenie B -

współrzędne

czasoprzestrzenne x

B

, ct

B

. Z jaką prędkością porusza się układ O’, w którym zdarzenia zajdą jednocześnie? Jaki

warunek musi spełniać prędkość układu O’, aby kolejność zdarzeń była odwrócona? Wartości współrzędnych:

a) x

A

= 1, ct

A

= 2, x

B

= 5, ct

B

= 5, b) x

A

= 2, ct

A

= 0, x

B

= 3, ct

B

= 6

Aby znaleźć prędkość takiego układu, w którym zdarzenia są równoczesne, należy przyrównać wyrażenia na

współrzędne czasowe w układzie poruszającym się z szukaną prędkością u.

2

2

1

1



















B

B

A

A

x

ct

x

ct

gdzie

c

u













75

0

4

3

,

x

x

ct

ct

x

x

ct

ct

B

A

B

A

B

A

B

A



























czyli u = 0,75c (dodatni znak prędkości oznacza, prędkość u skierowana jest zgodnie z osią x)

B

A

'

ct

'

ct



Rozwiązanie a)

Odp.: Układ, w którym zdarzenia A i B są równoczesne porusza się w kierunku dodatnim osi x z prędkością u = 0,75c,

jeśli prędkość układu będzie większa niż 0,75c, to kolejność zdarzeń będzie odwrócona.

Kolejność zdarzeń będzie odwrócona w układzie poruszającym się z prędkością u, w którym zachodzi nierówność:

2

2

1

1



















B

B

A

A

x

ct

x

ct

B

A

'

ct

'

ct







B

A

B

A

x

x

ct

ct









wstawiamy dane liczbowe i otrzymujemy:

75

0

4

3

,















Rozwiązanie b)

Czy istnieje układ, w którym zdarzenia są równoczesne? Spróbujmy znaleźć prędkość takiego układu u.









6

1

6























B

A

B

A

B

A

B

A

x

x

ct

ct

x

x

ct

ct





Otrzymaliśmy absurdalny wynik, ponieważ prędkość układu nie może być większa od prędkości światła.

Musi być spełniona nierówność:

Odp.: Nie ma takiego układu, w którym zdarzenia są równoczesne, jak również w żadnym układzie nie

zachodzą w odwrotnej kolejności. Jest to słuszne dla każdych dwóch zdarzeń, które mogą być

powiązane przyczynowo

Uwalnia nas to od dylematów filozoficznych, gdybyśmy mogli w jakimś układzie obserwować najpierw skutek (np.

narodziny syna), a potem przyczynę (narodziny jego ojca).

1





Kolejność zdarzeń byłaby odwrócona w układzie poruszającym się z prędkością u, w którym zachodzi nierówność:

B

A

'

ct

'

ct



Prowadzi to to nierówności:

6





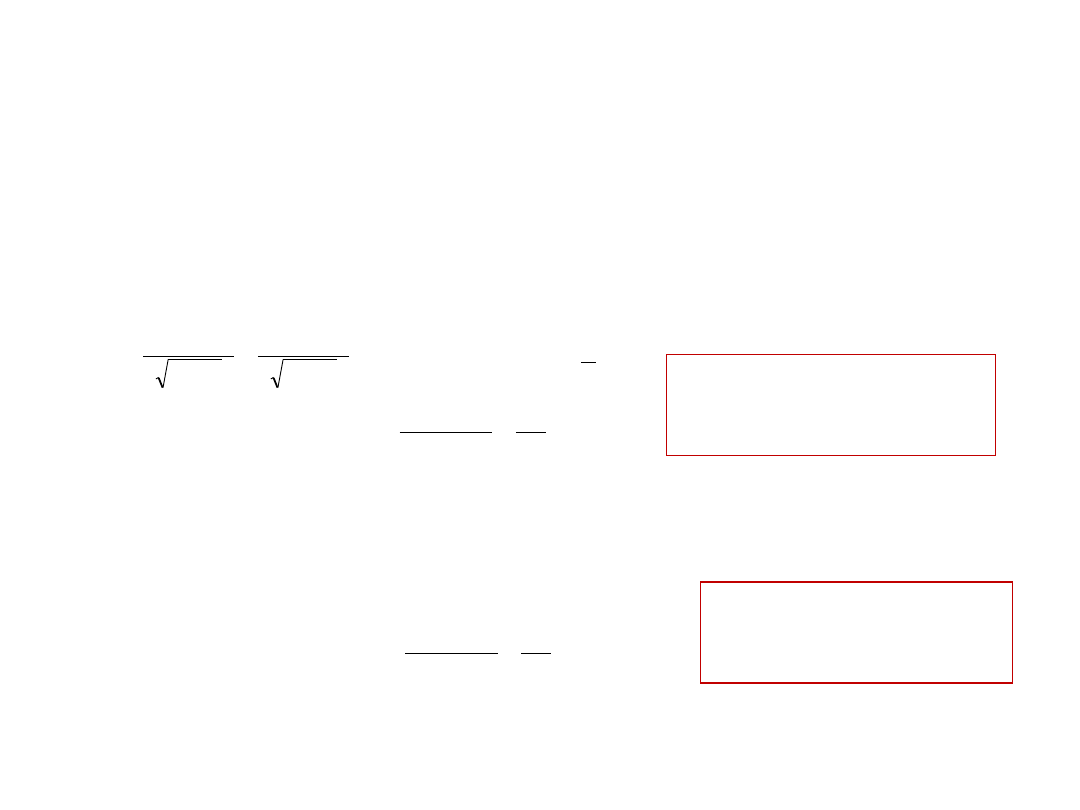
Zadanie 7

Zdarzenie A

ma w układzie O współrzędne czasoprzestrzenne x

A

, ct

A

, zdarzenie B -

współrzędne

czasoprzestrzenne x

B

, ct

B

. Z jaką prędkością porusza się układ O’, w którym zdarzenia zajdą w tym samym

miejscu? Wartości współrzędnych:

a) x

A

= 1, ct

A

= 2, x

B

= 5, ct

B

= 5, b) x

A

= 2, ct

A

= 0, x

B

= 3, ct

B

= 6

Żaden układ nie może poruszać się z prędkością większą od prędkości światła. Wynika z tego, że nie ma

takiego układu, w którym zdarzenia A i B zajdą w tym samym miejscu.

Aby znaleźć prędkość takiego układu, w którym zdarzenia zajdą w tym samym miejscu, należy przyrównać

wyrażenia na współrzędne przestrzenne w układzie poruszającym się z szukaną prędkością u’.

2

2

1

1



















B

B

A

A

ct

x

ct

x

gdzie

c

u

















333

1

3

4

,

ct

ct

x

x

ct

ct

x

x

B

A

B

A

B

A

B

A



























B

A

'

x

'

x



Rozwiązanie a)













667

0

6

1

,

ct

ct

x

x

ct

ct

x

x

B

A

B

A

B

A

B

A



























B

A

'

x

'

x



Rozwiązanie b)

Odp.: Układ, w którym zdarzenia A i B zajdą w tym samym miejscu porusza się w kierunku dodatnim osi x z prędkością

u = 0,667c.

Nie

istnieje układ, w którym zdarzenia

zachodzą w tym samym miejscu, nie mogą

więc byd powiązane przyczynowo.

I

stnieje układ, w którym zdarzenia

zachodzą w tym samym miejscu, mogą

więc byd powiązane przyczynowo.

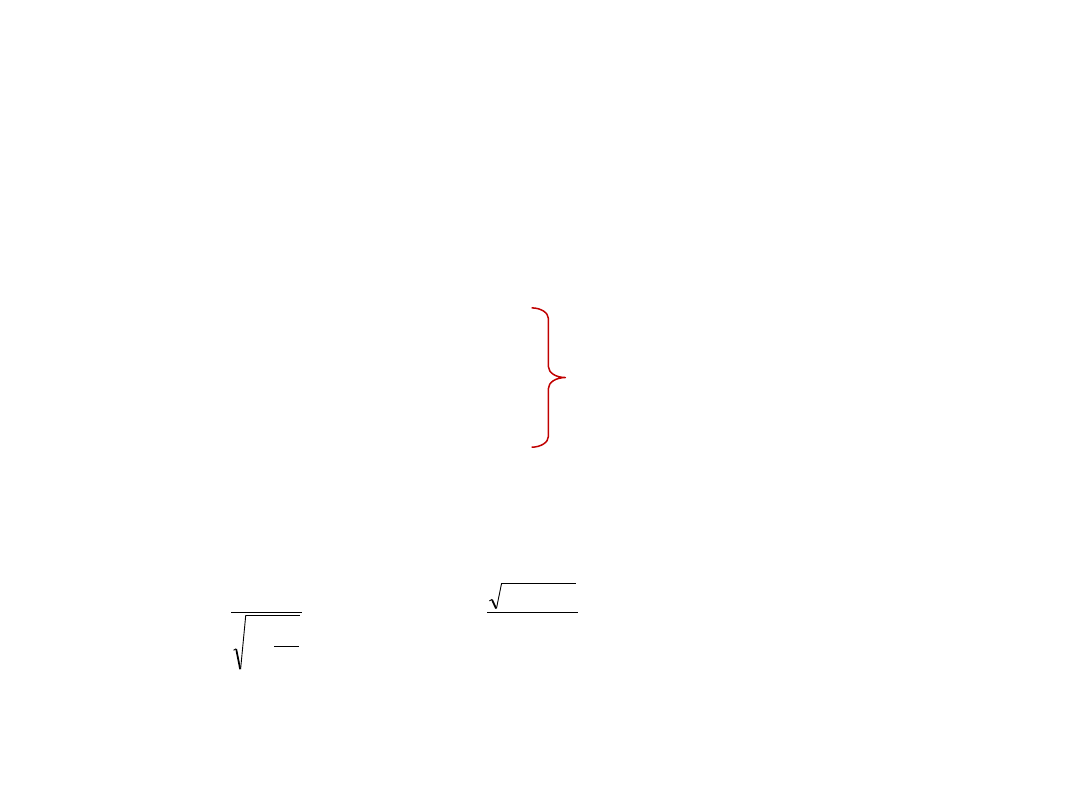
Zadanie 8

Na nieruchomą cząstkę o masie spoczynkowej m

0

zaczyna działać stała siła F. Po jakim czasie energia

kinetyczna cząstki w laboratoryjnym układzie odniesienia stanie się k razy większa od energii spoczynkowej

cząstki. Ile razy wzrośnie w tym czasie masa cząstki? Jaką drogę przebędzie cząstka w tym czasie w układzie

laboratoryjnym?

Rozwiązanie

Energia początkowa:

2

0

1

c

m

E



Energia końcowa:





2

0

2

0

2

0

2

1

c

m

k

c

km

c

m

E









2

2

2

c

m

E







0

2

1

m

k

m





Z wyrażenia na masę końcową m

2

obliczamy prędkość końcową v:









1

2

1

1

0

2

2

0















k

k

k

c

v

m

k

c

v

m

Aby obliczyć drogę przebytą x

L

przez cząstkę w układzie laboratoryjnym, przyrównujemy pracę wykonaną

przez siłę do nabytej przez cząstkę energii kinetycznej.

F

c

km

x

c

km

Fx

L

L

2

0

2

0







F

dt

dp



Z II zasady dynamiki:

Fdt

dp



Ft

p

Fdt

dp

t

p

p











2

0

2

1









1

2

1

0

2

2











k

k

k

c

m

k

v

m

p













2

1

2

1

0

0















k

k

F

c

m

t

Ft

k

k

k

c

m

k

szukany czas

Odp.: masa cząstki wzrośnie k+1 razy w czasie , w układzie laboratoryjnym cząstka przebędzie

drogę





2

0





k

k

F

c

m

t

F

c

km

x

L

2

0



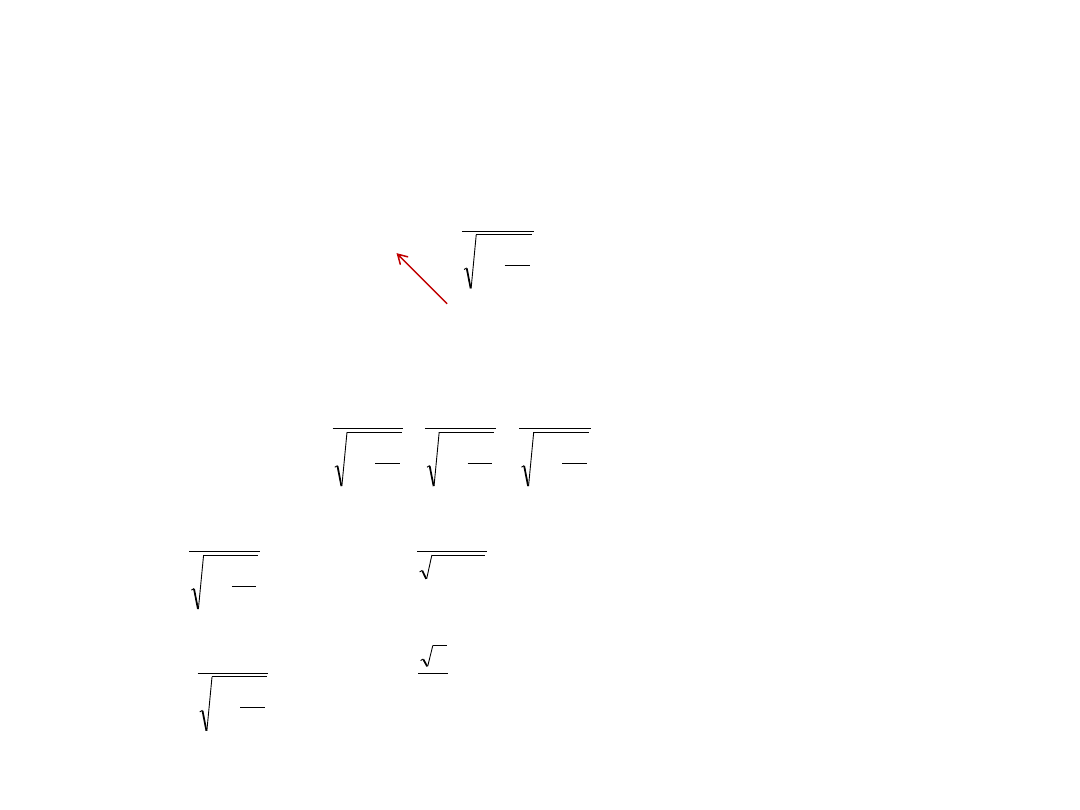
Zadanie 9

Cząstka o masie spoczynkowej m

0

i pędzie zderza się z identyczną cząstką o pędzie .

Obie cząstki poruszają się wzdłuż jednej prostej. Obliczyć masę spoczynkową M

0

i prędkość u powstałej w

wyniku zderzenia cząstki złożonej.

Rozwiązanie

Z prawa zachowania energii:

c

km

p

0

1



c

m

p

0

2



2

2

0

0

0

1

c

u

u

M

c

m

c

km







Z prawa zachowania pędu:

plus

– prędkości cząstek mają jednakowe zwroty,

minus -

prędkości cząstek mają przeciwne zwroty

2

2

2

0

2

2

2

2

0

2

2

1

2

0

1

1

1

c

u

c

M

c

v

c

m

c

v

c

m











1

1

2

1

0

2

2

1

1

0











k

k

c

v

c

km

c

v

v

m

2

2

1

2

0

2

2

2

2

0

c

v

c

m

c

v

v

m









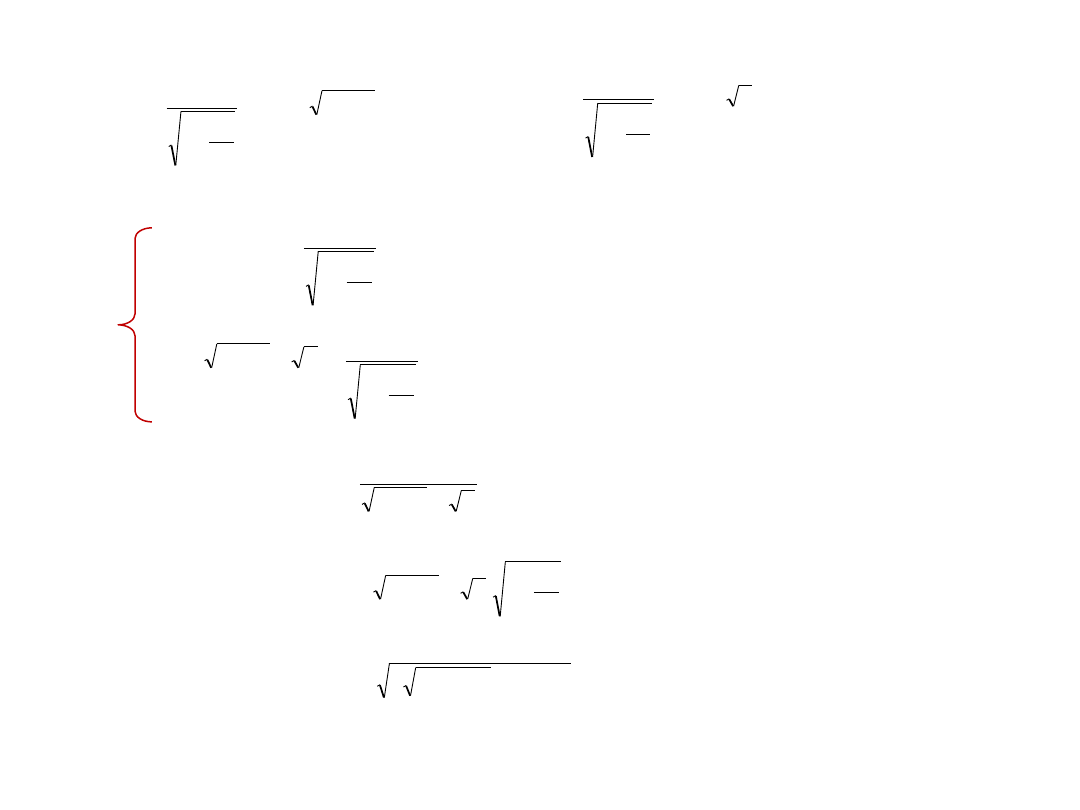
1

1

2

2

0

2

2

1

2

0

1









k

c

m

c

v

c

m

E

2

1

2

0

2

2

2

2

0

2

c

m

c

v

c

m

E











2

2

0

0

1

1

c

u

u

M

k

c

m











2

2

2

0

2

2

0

1

2

1

c

u

c

M

k

c

m









Dzielimy równania stronami





2

1

1

2









k

k

c

u





2

2

2

0

0

1

2

1

c

u

k

m

M













k

k

m

M

2

2

1

2

2

2

0

0









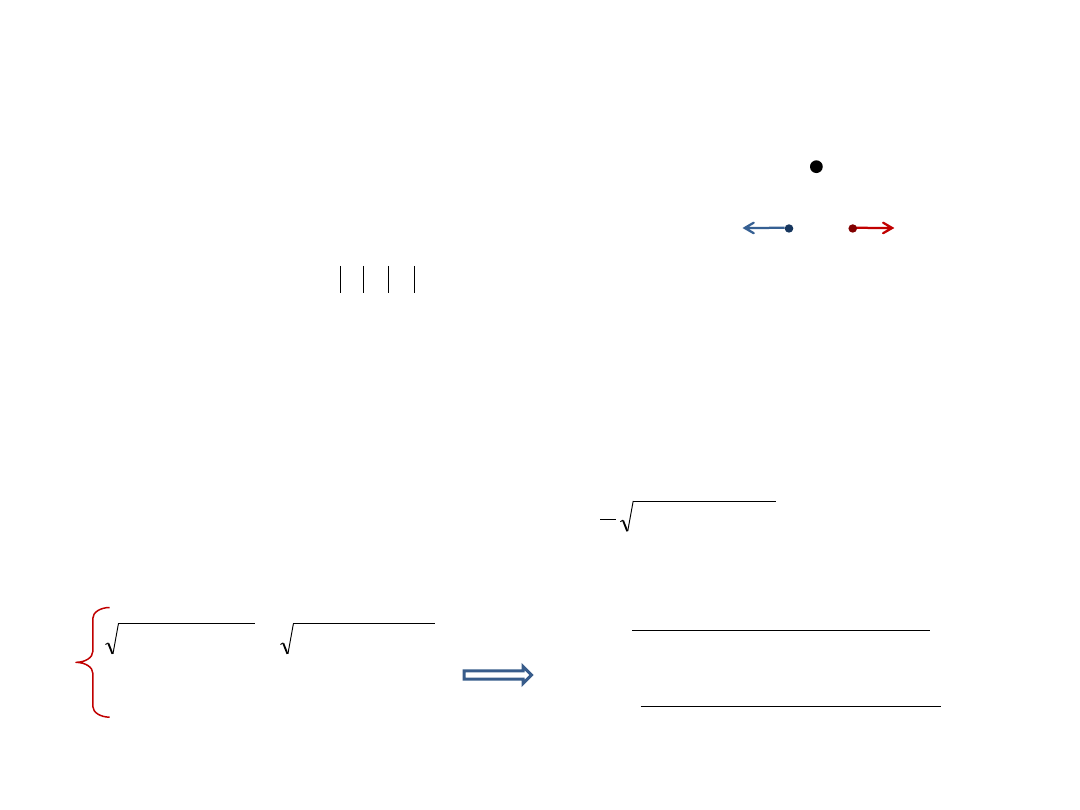
m

2

p

2

p

1

Zadanie 10

Spoczywająca cząstka o masie spoczynkowej M rozpada się na dwie cząstki o masach spoczynkowych m

1

i m

2

.

Wyznaczyć energie kinetyczne powstałych cząstek E

1

i E

2

.

Rozwiązanie

prawo zachowania energii:

 

1

2

1

p

p







prawo zachowania pędu:



 



 

2

2

2

2

2

1

2

1

Mc

E

c

m

E

c

m









m

1

M

0

2

1





p

p





Pęd cząstki należy wyrazić przez jego energię kinetyczną





2

2

0

2

2

c

m

c

p

E









4

2

0

2

2

0

4

2

0

2

2

2

c

m

E

c

m

c

m

E

c

p

k











2

0

2

2

1

c

m

E

E

c

p

k

k





równanie (1) i (2) tworzą układ równań z 2 niewiadomymi

2

2

2

2

2

2

1

1

2

1

2

2

c

m

E

E

c

m

E

E









 



2

2

2

2

1

2

1

Mc

E

c

m

E

c

m









M

Mc

m

c

m

c

m

c

M

E

2

2

2

1

2

2

2

2

2

1

2

2

1









M

Mc

m

c

m

c

m

c

M

E

2

2

2

2

2

2

1

2

2

2

2

2

2









Zadania do samodzielnego rozwiązania

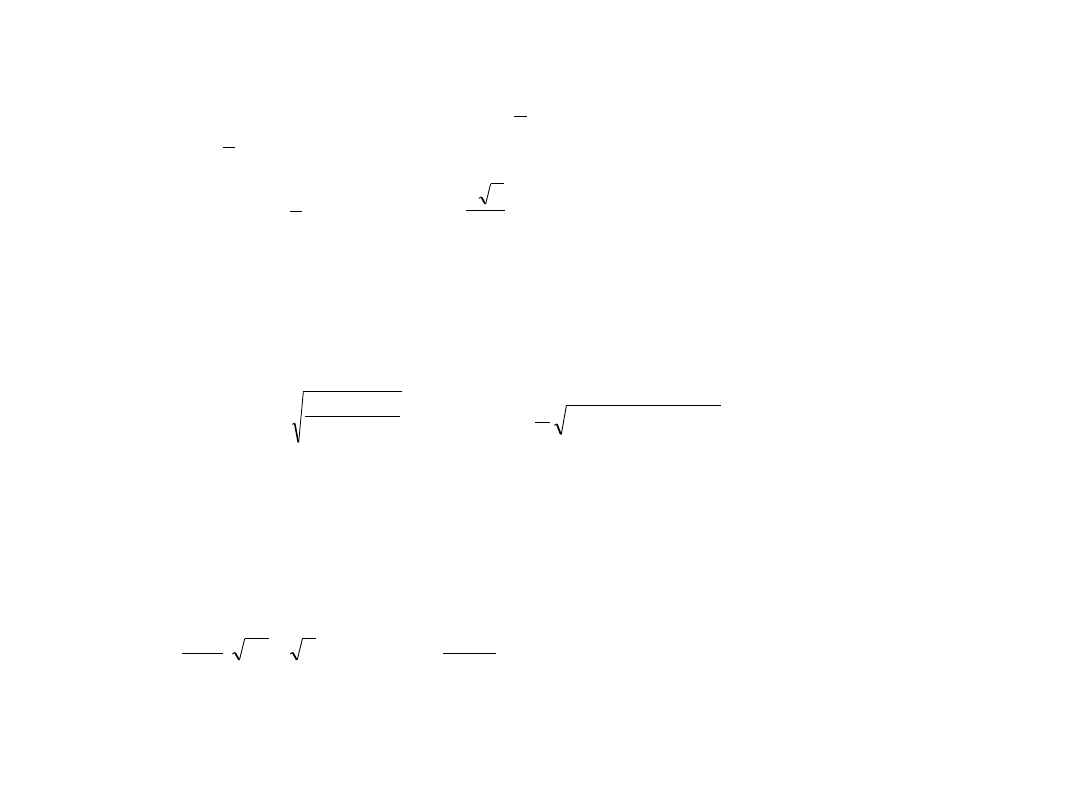
Zadanie 1

Cząstka o masie spoczynkowej m

0

i prędkości dogania identyczną cząstką poruszającą się z

prędkością . Obliczyć masę spoczynkową M

0

i prędkość u powstałej w wyniku zderzenia cząstki

złożonej.

Odp:

c

v

5

4

1



c

u

7

5



c

v

5

3

1



0

0

0

04

2

6

6

5

m

,

m

M





Zadanie 2

Cząstka o masie spoczynkowej m

0

i energii kinetycznej E

1

zderza się z nieruchomą cząstką o tej samej masie

spoczynkowej. Obliczyć masę spoczynkową M

0

i prędkość u powstałej w wyniku zderzenia cząstki złożonej.

Odp:

2

0

1

1

2

c

m

E

E

c

u









2

0

1

0

0

2

2

1

c

m

E

m

c

M





Zadanie 3

Na poruszającą się cząstkę o masie spoczynkowej m

0

zaczyna działać stała siła F. Po jakim czasie masa

cząstki wzrośnie od 2m

0

do 4m

0

Ile razy wzrośnie w tym czasie masa cząstki? Jaką drogę przebędzie cząstka w

tym czasie w układzie laboratoryjnym?

Odp:





3

15

0





F

c

m

t

F

c

m

S

0

2



Zadanie 4

Znaleźć własny czas życia cząstki, jeśli porusza się ona z prędkością i do momentu rozpadu przebyła

odległość 20 km.

Odp:

s

6

10

35

,

8









c

,

v

97

0



Zadanie 5

Znaleźć układ odniesienia, w którym chrzest Polski i bitwa pod Grunwaldem odbyły się

a) w tym samym miejscu,

b) w tym samym czasie.

c)

Czy te zdarzenia mogą być w związku przyczynowo-skutkowym?

Przyjąć, że w układzie Ziemi odległość między Gnieznem a Grunwaldem wynosi 200 km, a czas między tymi

wydarzeniami wynosi 400 lat.

Odp

: a) układ poruszający się od Gniezna do Grunwaldu z prędkością

b) taki układ nie istnieje

c) tak

s

m

v

5

10

59

,

1







Zadanie 6

Sprawdzić, czy zdarzenia A i B mogą być powiązane przyczynowo. Z jaką prędkością porusza się układ O’, w

którym zdarzenia zajdą jednocześnie? Jaki warunek musi spełniać prędkość układu O’, aby kolejność zdarzeń

była odwrócona? Wartości współrzędnych:

a) x

A

= 4, ct

A

= 2, x

B

= 6, ct

B

= 3, b) x

A

= 5, ct

A

= 3, x

B

= 1, ct

B

= 0

Odp: a)

zdarzenia zajdą jednocześnie w układzie poruszającym z prędkością, , kolejność zdarzeń

będzie odwrócona w układzie poruszającym z prędkością,

b) taki układ nie istnieje

c

,

v

5

0



c

,

v

5

0



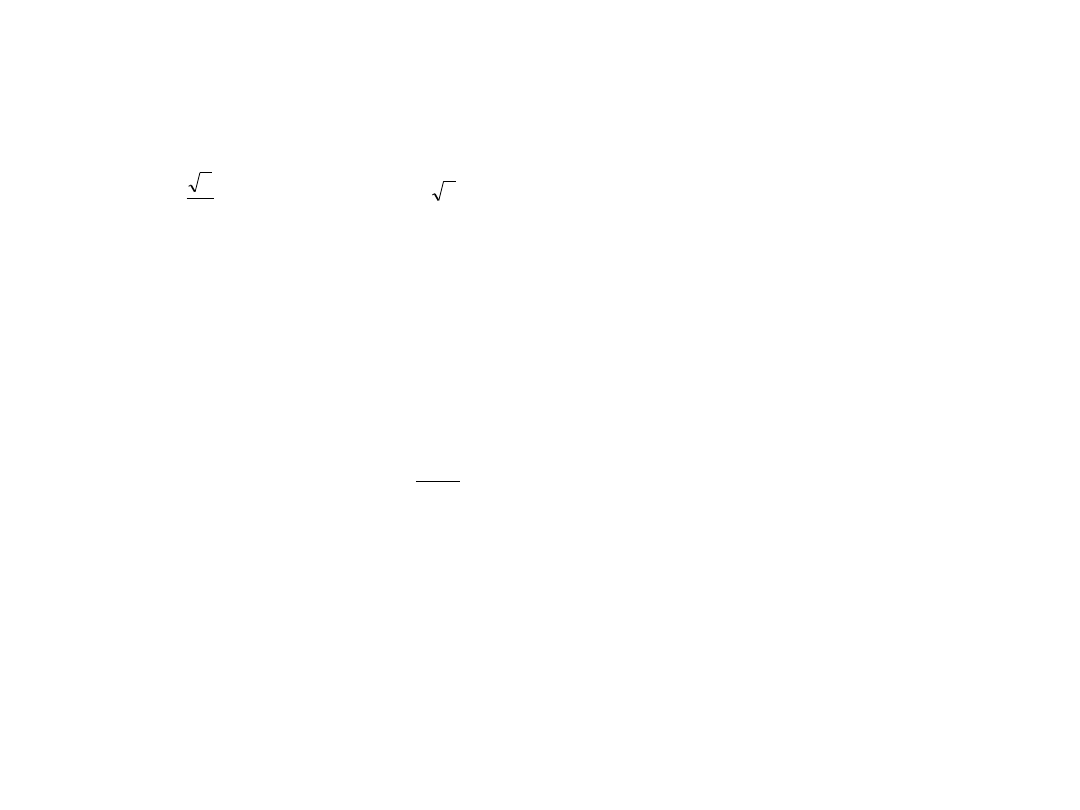
Zadanie 7

Pręt o masie spoczynkowej m

0

porusza się z taką prędkością, że jego długość obserwowana w układzie

laboratorium jest dwa razy krótsza niż zmierzona wtedy, gdy pręt jest w spoczynku. Oblicz energię kinetyczną i

prędkość pręta oraz jego pęd.

Odp:

c

v

2

3



2

0

c

m

E

k



c

m

p

0

3



Zadanie 8

Mezon porusza się z energią całkowitą . Jego energia spoczynkowa wynosi , a

własny czas życia równy jest Oblicz:

a)

Czas życia w laboratorium

b)

Pęd

c)

Energię kinetyczną

Odp:

Zadanie 9

Ze statku kosmicznego poruszającego się względem Ziemi z prędkością wystrzelono w kierunku

ruchu pocisk z prędkością . Z jaką prędkością u porusza się pocisk względem Ziemi? Jakie wymiary

pocisku widzi obserwator na Ziemi, jeśli w układzie własnym pocisk jest kulą o średnicy d = 10 cm?

Odp: Pocisk ma kształt spłaszczonej kuli o grubości 3,2 cm.

c

,

v

6

0



c

,

v

8

0



c

,

u

946

0



Gev

E

10



MeV

c

m

200

2

0



s

6

10







s

t

4

10

2







c

GeV

,

p

999979

9



GeV

,

E

k

8

9

