ENERGIA RELATYWISTYCZNA

Energia relatywistyczna wiąże się z Ogólną Teorią Względności Alberta Einsteina. Zdefiniowana jest jako energia całkowita ciała izolowanego od otoczenia, a więc nie znajdującego się pod wpływem żadnych potencjałów zewnętrznych. Einstein odkrył, że nawet ciało znajdujące się w idealnym spoczynku ma pewien zasób energii. Dla takiego nieruchomego ciała energia relatywistyczna jest nazywana energią spoczynkową i definiuje ją słynny wzór na równoważność masy i energii:

E = mc²

gdzie m jest masą ciała a stała c wartością prędkości fal elektromagnetycznych w próżni; c @ 299 000 km/s)

Inaczej wygląda równanie dla ciała poruszającego się z dowolna prędkością v < c. Wówczas jednak, co jest intuicyjnie łatwe do zrozumienia, całkowita energia stanowi sumę energii kinetycznej ruchu oraz energii spoczynkowej ze wzoru Einsteina. Dla cząstki materialnej można zapisać sumę jako:

E = mgc² - mc²

Współczynnik g wynosi tu 1/[1-(v/c)²], jest wartością występująca bardzo często w mechanice relatywistycznej, a pochodzi bezpośrednio z teorii eteru, poprzedzającej powstanie Teorii Względności. W przypadku nie relatywistycznym, czyli gdy v << c, powyższe równanie upraszcza się:

E = mc² +1/2mv²

Pierwszy człon (mc²) odpowiada tu energii wewnętrznej ciała, podczas gdy drugi jest energia kinetyczną znaną z mechaniki klasycznej. Ponieważ współczynnik g wzrasta wraz ze zwiększaniem się prędkości ciała przy założeniu niezmienności stałej c, energia relatywistyczna punktu materialnego także rośnie przy wzroście prędkości, osiągając teoretycznie maksymalną wartość dla v = c.

Pozostaje wyjaśnić, skąd właściwie bierze się energia spoczynkowa cząstki nieruchomej. Badania wykazały, że jest ona suma wielu składników: energii kinetycznej elementów jądra atomowego, energii potencjalnej wynikającej ze wzajemnych oddziaływań pomiędzy częściami jądra, ruchów termicznych itd. Bezpośrednim rezultatem jest nierównoważność masy całej cząstki złożonej i sumy jej tworzących ją składników. Energię spoczynkową można rozumieć jako pewien rodzaj energii wewnętrznej ciała.

W próżni nic nie może poruszać się szybciej niż światło

Przy bardzo dużej prędkości, zbliżonej do c, mianownik wyrażenia na γ zaczyna dążyć do 0, a sama wartość γ dąży do nieskończoności. Wynika z tego, że przy prędkości światła energia ciała posiadającego niezerową masę spoczynkową powinna być nieskończona, czyli praktycznie nie istnieje możliwość rozpędzenia go do tej prędkości. Oznacza to, że absolutnie nic nie może poruszać się szybciej od prędkości światła, a prędkość tę mogą osiągnąć tylko cząstki, które same posiadają zerową masę spoczynkową, takie jak fotony.

Tachiony to hipotetyczne cząstki, które mogłyby się poruszać z prędkością większą od światła, ale jak dotąd, nikt nie posiada żadnych dowodów eksperymentalnych na istnienie tych cząstek, choć istnieją teorie postulujące ich istnienie.

Wrażenie symultaniczności zdarzeń zależy od układu odniesienia

W teorii względności istnieją pojęcia "ścieżki czasowej" i "ścieżki przestrzennej" w czasoprzestrzeni. Gdy jakiś obiekt porusza się ze stałą prędkością razem z obserwatorem, to wówczas obserwator w swoim układzie odniesienia odczuwa tylko upływ czasu a nie ma możności zaobserwowania ruchu obiektu. Trasa jaką pokonuje taki obiekt definiuje pojęcie "ścieżki czasowej". Można też sobie wyobrazić trasę w czasoprzestrzeni, wzdłuż której obserwator nie odczuwa upływu czasu a jedynie przemieszczanie się w przestrzeni. To właśnie jest ścieżka przestrzenna. Biorąc pod uwagę, że maksymalna prędkość jaką można osiągnąć to prędkość światła, można łatwo dowieść, że każdy prosty odcinek między takimi dwoma punktami w czasoprzestrzeni, którego nie można przebyć w skończonym czasie jest ścieżką przestrzenną. Obiekty połączone taką ścieżką nie mogą na siebie w żaden sposób oddziaływać fizycznie, ani siebie wzajemnie obserwować. Stosując szczególną teorię względności można też łatwo dowieść, że dla obserwatorów z dwóch różnych układów odniesienia, między którymi istnieje ścieżka czasowa, dwa zdarzenia między którymi istnieje tylko ścieżka przestrzenna, a nie ma czasowej, mogą następować w różnej kolejności czasowej! Obserwator A może widzieć zdarzenie 1 jako pierwsze, zaś obserwator B może widzieć zdarzenie 2 jako pierwsze.

OGÓLNA TEORIA WZGLĘDNOŚCI EINSTEINA

Podstawową ideą teorii względności jest to, że nie możemy mówić o wielkościach fizycznych takich jak prędkość czy przyspieszenie, nie określając wcześniej układu odniesienia, oraz że układ odniesienia definiuje się poprzez wybór pewnego punktu w czasoprzestrzeni, z którym jest on związany. Oznacza to, że wszelki ruch określa się i mierzy względem innych określonych układów odniesienia. W ramach tej teorii, inaczej niż w szczególnej teorii względności, która podawała opis ruchu w inercjalnych (nie posiadających przyspieszenia) układach odniesienia, opis ruchu prowadzony jest w dowolnych układach odniesienia, inercjalnych lub nieinercjalnych. Podstawowym założeniem jest takie sformułowanie praw fizycznych i opisu ruchu aby miały one identyczną postać matematyczną bez względu na używany do opisu układ odniesienia, stąd konieczność zastosowania rachunku tensorowego.

OTW mówi, że z daną dokładnością można definiować jedynie lokalne układy odniesienia, dla skończonych okresów czasu i ograniczonych obszarów w przestrzeni. Jest to analogia z rysowaniem map fragmentów powierzchni Ziemi - nie można sporządzić mapy obejmującej całą powierzchnię Ziemi bez deformacji. Zasady dynamiki Newtona są w ogólnej teorii względności zachowane w lokalnych układach odniesienia.

W szczególności cząstki, na które nie działa żadna siła, poruszają się po liniach prostych w lokalnych inercjalnych układach odniesienia. Jednak jeżeli linie te się przedłuży, to nie otrzymujemy linii prostych, lecz krzywe zwane geodezyjnymi. Dlatego też pierwsza zasada dynamiki Newtona zostaje zastąpiona przez zasadę poruszania się po geodezyjnej.

Odróżniamy inercjalne układy odniesienia, w których ciała fizyczne nie zmieniają swojego stanu ruchu, jeżeli nie oddziałują z żadnym innym ciałem fizycznym, od nieinercjalnych układów odniesienia, w których poruszające się ciała mają przyspieszenie pochodzące od układu odniesienia. W tych drugich pojawia się pozorna siła wynikająca z przyspieszenia samego układu odniesienia, a nie z oddziaływania z innym ciałem fizycznym. W związku z tym np. odczuwamy siłę odśrodkową wtedy, gdy samochód, będący naszym układem odniesienia, skręca. Podobnie obserwujemy siłę Coriolisa i siłę odśrodkową wtedy, gdy układem odniesienia jest ciało będące w ruchu obrotowym (na przykład bąk-zabawka lub Ziemia). Zasada równoważności w ogólnej teorii względności mówi, że w układzie lokalnym nie można przeprowadzić doświadczenia, dzięki któremu dałoby się odróżnić spadek swobodny w polu grawitacyjnym od ruchu jednostajnego przy braku pola grawitacyjnego. Mówiąc w skrócie, w układzie odniesienia związanym z ciałem spadającym swobodnie nie ma grawitacji. Oznacza to, że obserwowana na powierzchni Ziemi grawitacja jest siłą obserwowaną w układzie odniesienia związanym z materią na powierzchni, która nie jest "wolna", lecz na którą oddziałuje materia z wnętrza Ziemi i sytuacja ta jest analogiczna do sytuacji w skręcającym samochodzie.

Matematycznie, Einstein modeluje czasoprzestrzeń przy pomocy czterowymiarowej pseudo-riemannowskiej rozmaitości, a jego równanie pola mówi, że krzywizna rozmaitości w punkcie jest bezpośrednio związana z tensorem napięć-energii w tym punkcie; tensor ten jest miarą gęstości materii i energii. Krzywizna określa sposób, w jaki materia się porusza, a materia określa sposób, w jaki przestrzeń się zakrzywia. Równanie pola nie jest dowiedzione w sposób jednoznaczny i istnieje możliwość zaproponowania innych modeli, pod warunkiem, że nie będą stały w sprzeczności z obserwacjami.

Ogólna teoria względności wyróżnia się spośród innych teorii grawitacji swoją prostotą powiązania materii i krzywizny, chociaż wciąż nie istnieje teoria unifikacji pomiędzy ogólną teorią względności, a mechaniką kwantową i nie umiemy zastąpić równania pola bardziej ogólnym prawem kwantowym. Niewielu fizyków wątpi w to, że taka teoria wszystkiego będzie zawierała w sobie ogólną teorię względności, tak jak ogólna teoria względności zawiera w sobie prawo powszechnego ciążenia Newtona w zakresie nierelatywistycznym.

Równanie pola Einsteina zawiera parametr zwany stałą kosmologiczną Λ, która została wprowadzona przez Einsteina po to, aby Wszechświat pozostał statyczny (tzn. nierozszerzający i niezapadający się). Ta próba zakończyła się niepowodzeniem z dwóch powodów: statyczny Wszechświat opisywany przez tę teorię byłby niestabilny, co więcej, obserwacje prowadzone przez Hubble'a dekadę później pokazały, ze nasz Wszechświat nie jest statyczny, lecz się rozszerza. Dlatego też zrezygnowano ze stałej Λ, lecz ostatnie obserwacje supernowych typu Ia wskazują na to, że być może należy ją ponownie wprowadzić do równań.

PARADOKS BLIŹNIĄT

Załóżmy, że jest dwóch braci bliźniaków. Jeden z nich wyrusza w podróż statkiem kosmicznym z prędkością bliską prędkości światła, drugi natomiast zostaje na Ziemi.
Po pewnym czasie brat podróżnik zawraca rakietę i wraca na Ziemię. Okazuje się, że gdy bracia ponownie się spotykają ten, który wrócił z podróży jest młodszy od tego, który pozostał na Ziemi. Jest to skutkiem „rozszerzenia” czasu w jego pojeździe kosmicznym.
Z zasady względności wynika, że opis zdarzenia we wszystkich układach inercjalnych powinien być taki sam. Szybsze starzenie się bliźniaka z układu laboratoryjnego wydaje się temu przeczyć. Paradoks jest jednak tylko pozorny, gdyż w rozważanym przypadku układ poruszającego się bliźniaka nie jest układem inercjalnym: zarówno na początku swego ruchu jak i przy zmianie kierunku ruchu układ porusza się z przyspieszeniem. Bliźniak poruszający się nie ogląda swego brata na początku i przy końcu swej wycieczki z tego samego inercjalnego układu, a zatem opis zdarzeń w ujęciu obu bliźniaków musi być różny.
Różnice w upływie czasu, jakie obserwujemy są chyba najbardziej fascynującym elementem całej szczególnej teorii względności. Dlaczego jest to takie ciekawe? Otóż, dlatego, że jak wiele innych zjawisk opisywanych przez szczególną teorię względności jest to całkowicie niezgodne z naszym Ziemskim zdrowym rozsądkiem a jednocześnie wielokrotnie sprawdzone i udowodnione w różnego rodzaju eksperymentach. Poznanie całej teorii potrzebne do zrozumienia tych zjawisk nie jest łatwe, czego powodem jest właśnie owa niezgodność pomiędzy tym, o czym traktuje STW a naszymi doświadczeniami życia codziennego.
A wszystko, dlatego, że efekty, które grają tu kluczową rolę występują tylko dla bardzo dużych prędkości, które są dla nas nieosiągalne. Dla prędkości, z którymi spotykamy się, na co dzień zjawiska te są niezauważalne i nie grają żadnej roli.

PODSUMOWANIE

-

ENERGIA RELATYWISTYCZNA

Tożsamość masy i energii

Prawdopodobnie najsłynniejszą implikacją szczególnej teorii względności jest wniosek, że energia i masa, które jak wcześniej uważano, są całkowicie odseparowanymi od siebie wielkościami, są w pewnym sensie tożsame, gdyż można je przekształcać jedne w drugie zgodnie ze słynnym równaniem:

E = m₀c²

gdzie E jest energią ciała w spoczynku, m₀ jest jego masą spoczynkową, a c to prędkość światła w próżni. Jeśli ciało porusza się z prędkością v w stosunku do obserwatora to całkowita jego energia wynosi:

E = m(v)c² = m₀γc²,

gdzie

.

(Termin γ pojawia się często w teorii względności, i pochodzi jeszcze z teorii eteru Lorentza), zwany jest czynnikiem Lorentza, m(v)=γm jest masą relatywistyczną. Gdy v jest dużo mniejsze od c równanie można uprościć do:

i przyjmując, że pierwszy człon (mc²), odpowiada energii wewnętrznej ciała, dochodzi się do "zwykłego" równania na całkowitą energię ciała w ruchu. (Drugi człon jest równy, "normalnej" energii kinetycznej wynikającej z mechaniki klasycznej.)

• Podana definicja pędu w przypadku prędkości dużo mniejszych od prędkości światła przechodzi w definicję klasyczną:

• Energia zdefiniowana przez Einsteina też powinna ulec takiej transformacji, a więc:

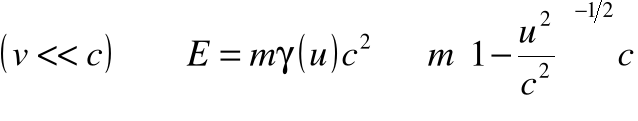
• Dla małych prędkości możemy jeszcze skorzystać z rozwinięcia w szereg wyrażenia na energię. Otrzymamy wtedy:

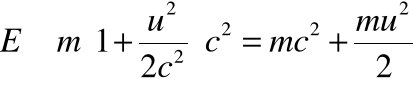
• Przypomnijmy wzór na rozwinięcie „nowej” definicji energii:

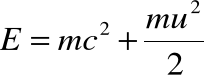
• Drugi człon jest klasyczną energią kinetyczną - energią cząstki swobodnej o prędkości
. Pierwszy człon jest natomiast pewną stałą, którą według praw mechaniki klasycznej można dodać jako dowolną wartość do całkowitej energii ciała (por. pojęcie energii potencjalnej!).

• Według Einsteina ten drugi człon:

ma sens energii spoczynkowej ciała - wielkości, której istnieniu zawdzięczamy m.in. bombę atomową...

---