2.Transformacja Lorentza: Weźmy pod uwagę dwa układy inercjalne S i S`, których osie x i x` są do siebie równoległe, a początki O i O` pokrywają się w układzie S ze stałą prędkością v , zwróconą zgodnie ze zwrotem osi x. Gdy pewne zdarzenie zaobserwowane w układzie S ma współrzędne x,y,z,t, to odpowiednie jego współrzędne w układzie S` wynoszą x`,y`,z` ,t`. Układy odniesienia wybieramy w taki sposób, żeby zawsze y` = y i z` = z i tymi współrzędnymi nie będziemy się zajmować. Mamy więc w każdym układzie jedną współrzędną przestrzenną (x lub x`) i jedna współrzędną czasową (t lub t`).
Równanie czoła fali kulistej :
x2+y2+z2=c2t2
x'2+y'2+z'2=c2t'2
stosuję podstawienia
x' = x - v t
y' = y
z' = z
t' = t + f x
c't' - promień kuli
podstawiam wartości i rozwiązuję układ równań , przy czym 2c2f + 2v = 0 ⇒
f = -(v / c2) , współczynnik
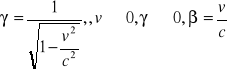
x' = γ( x - v t) x = γ( x' +vt')
y' = y y = y'
z' = z z = z'
t' = γ( t - (v/c2)x) t = γ( t'- (v/c2)x')
3.SKŁADANIE PRĘDKOŚCI
DYLATACJA CZASU
Z założeń teorii względności Einsteina wynika nierównoczesność zdarzeń w różnych nieinercjalnych układach odniesienia.
Najprostszym przykładem dylatacji jest paradoks bliźniąt. Astronauta wystrzelony w kosmos po powrocie będzie młodszy od swojego brata bliźniaka, ponieważ w poruszającym się układzie "czas płynie wolniej".
SKRÓCENIE DŁUGOŚCI
Długość odcinka z punktu widzenia obserwatora znajdującego się względem niego w spoczynku jest mniejsza niż z punktu widzenia obserwatora będącego względem tego odcinka w stanie ruchu.
Zjawisko skrócenia długości można wytłumaczyć na następującym przykładzie: Antek znajduje się w poruszającym się pociągu twierdzi, ż jego linijka ma 1m. Benek będąc w układzie spoczywającym (stoi na peronie) stwierdza, że linijka Antka ma mniej niż 1m. Antek tego nie zauważa, gdyż znajduje się w poruszającym się układzie odniesienia.
4.Masa, pęd relatywistyczny
• Można sformułować definicję pędu relatywistycznego cząstki na sposób „klasyczny” jako:
![]()
jeśli wprowadzimy pojęcie masy relatywistycznej:
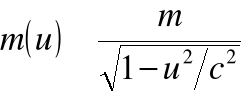
gdzie ![]()
jest masą spoczynkową cząstki.
• Masa relatywistyczna to inaczej energia relatywistyczna podzielona przez stałą ![]()
- masa relatywistyczna układu odosobnionego jest zachowana, podczas gdy masa spoczynkowa, zawarta w indywidualnych cząstkach, może się zmieniać (zasada zachowania energii).
Pęd relatywistyczny
• Klasyczna definicja pędu:
![]()
Taka definicja pędu, w połączeniu z transformacją Einsteina dla prędkości nie zapewni nam jednak spełnienia zasady zachowania pędu! ![]()
jest prędkością cząstki).
• Nowa definicja pędu (która zapewni prawdziwość zasady zachowania pędu przy transformacji do dowolnego układu współrzędnych) podana przez Einsteina:
![]()
gdzie: 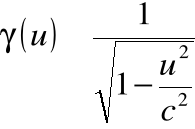
(uwaga! Podobieństwo oznaczeń, ale TO ![]()
zależy od prędkości cząstki ![]()
, a nie od prędkości ![]()
poruszania się układu współrzędnych!).
5. Energia relatywistyczna
• Podana definicja pędu w przypadku prędkości dużo mniejszych od prędkości światła przechodzi w definicję klasyczną:
![]()
• Energia zdefiniowana przez Einsteina też powinna ulec takiej transformacji, a więc:
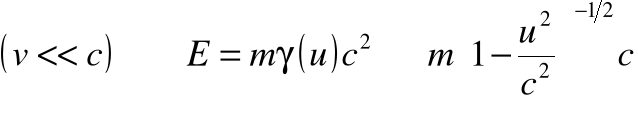
• Dla małych prędkości możemy jeszcze skorzystać z rozwinięcia w szereg wyrażenia na energię. Otrzymamy wtedy:
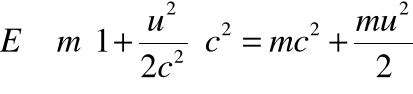
Energia relatywistyczna - c.d.
• Przypomnijmy wzór na rozwinięcie „nowej” definicji energii:
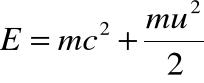
• Drugi człon jest klasyczną energią kinetyczną - energią cząstki swobodnej o prędkości ![]()
. Pierwszy człon jest natomiast pewną stałą, którą według praw mechaniki klasycznej można dodać jako dowolną wartość do całkowitej energii ciała (por. pojęcie energii potencjalnej!).
• Według Einsteina ten drugi człon:
![]()
ma sens energii spoczynkowej ciała - wielkości, której istnieniu zawdzięczamy m.in. bombę atomową...
7. Fizyka rozszczepienia jądrowego
Rozszczepienie jądrowe zachodzi, gdy jądra pewnych izotopów bardzo ciężkich pierwiastków, na przykład uranu czy plutonu, pochłaniają neutrony. Jądra tych izotopów są ledwo stabilne i dodanie małej ilości energii (np. pochodzącej z neutronu) spowoduje nagłe rozszczepienie na dwa jądra, czemu towarzyszy uwolnienie ogromnej ilości energii (180 MeV natychmiastowo dostępnej energii) i kilku nowych neutronów (średnio 2.52 dla U-235, i 2.95 dla Pu-239). Jeżeli średnio jeden neutron z każdego rozszczepienia jest pochłaniany i powoduje reakcję rozszczepienia kolejnego jądra dochodzi do samo podtrzymywania, zwanego reakcją łańcuchową. Gdy natomiast średnio więcej niż jeden neutron z każdego rozpadu wywołuje rozszczepienie kolejnego jądra liczba neutronów i ilość wydzielonej energii rośnie wykładniczo do czasu.
Aby reakcja rozszczepienia mogła być użyta do wytworzenia potężnej eksplozji muszą być spełnione dwa warunki: 1) liczba neutronów nie biorących udziału w rozszczepieniu musi być możliwie najmniejsza, i 2) prędkość, z jaką zachodzi reakcja łańcuchowa musi być bardzo szybka. Niezwykle ważne jest bowiem, aby zakończyć rozszczepienie większości materiału zanim bomba wybuchnie. Stopień, w jakim bomba tego dokonuje określa jej skuteczność. Niepoprawne zaprojektowanie lub złe funkcjonowanie bomby może spowodować wydzielenie tylko drobnej części energii.
8.Reakcje fuzji
Najbardziej wydatne reakcje syntezy termojądrowej to:
1. D + T -> He-4 + n + 17.6 MeV
2. D + D -> He-3 + n + 3.27 MeV
3. D + D -> T + p + 4.03 MeV
4. He-3 + D -> He-4 + p + 18.4 MeV
5. Li-6 + n -> T + He-4 + 4.78 MeV
6. Li-7 + n -> T + He-4 + n - 2.47 MeV
[gdzie D to deuter (H-2), a T - tryt (H-3)]
W temperaturze uzyskiwanej w bombie opartej o rozszczepienie reakcja 1 przebiega 100 razy szybciej niż reakcje następne (2 i 3), które z kolei są 10 krotnie szybsze niż reakcja 4. Szybkość reakcji 1-4 wzrasta szybko (wykładniczo) z temperaturą, ale nie w takich samych proporcjach. W wyższych temperaturach uzyskanych przez fuzję, reakcja 4 przekracza szybkością reakcje 2 i 3.
Kilka dodatkowych faktów na temat tych reakcji:
Neutron wyprodukowany w reakcji 1 jest nadzwyczaj energetyczny, odbiera 14.1 MeV energii całej reakcji. Natomiast neutron wyprodukowany w reakcji 2 ma energię tylko 2.45 MeV, zbliżoną do energii szybkich neutronów powstających przy reakcji rozszczepienia. Dwie reakcje pomiędzy deuterem (D+D) są równie prawdopodobne i każda zabiera połowę czasu.
Reakcje 5 i 6 nie są reakcjami termojądrowymi w dosłownym znaczeniu. Są reakcjami neutronowymi, jak rozszczepienie, i nie wymagają szczególnej temperatury czy ciśnienia - niezbędnej energii dostarczają neutrony. Ta różnica jest zazwyczaj lekceważona w literaturze dotyczącej broni nuklearnej. Reakcja Li-6+n wymaga neutronu o małej energii (zbliżonej do MeV lub mniejszej). Reakcja Li-7+n jest znacząca tylko gdy energia jest mniejsza niż 4 MeV.
Wyszukiwarka
Podobne podstrony:
fizyka-egzam, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
Energia relatywistyczna, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
elektrycznosć i magnetyzm nr 13, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
zagadnienia z fizyki na egzamin-1, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
zagadnienia z fizyki na egzamin, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
mechanika, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
217, STUDIA, Polibuda - semestr I, Fizyka, laborki, 217
Fala to zaburzenie, STUDIA, Polibuda - semestr I, Fizyka, laborki, 217
215--, STUDIA, Polibuda - semestr I, Fizyka, laborki, 215
tresyta, STUDIA, Polibuda - semestr I, Fizyka
217 - instrukcje, STUDIA, Polibuda - semestr I, Fizyka, laborki, 217
PYTANIA skoczek, STUDIA, Polibuda - semestr IV, Organizacja Produkcji Budowlanej, obp zaliczenie
opbskoczek, STUDIA, Polibuda - semestr IV, Organizacja Produkcji Budowlanej, obp zaliczenie
opb opracowanie ok łabud, STUDIA, Polibuda - semestr IV, Organizacja Produkcji Budowlanej, obp zalic
Cwiczenie zabawowe, STUDIA, Polibuda - semestr II, Hydraulika i hydrologia, laborki z hydro
linia cisnien, STUDIA, Polibuda - semestr II, Hydraulika i hydrologia, laborki z hydro, laborki
więcej podobnych podstron