Systemy Dialogowe

Sprawozdanie z ćwiczenia laboratoryjnego nr 2

Temat laboratorium:
Analiza sygnału mowy.
Ekstrakcja charakterystyk w środowisku MATLAB
(wersja poprawiona)

Prowadzący:

Dr inż Andrzej Wiśniewski

Wykonała

Anna Grzeszyk

I0I1S1

10.12.2012r.

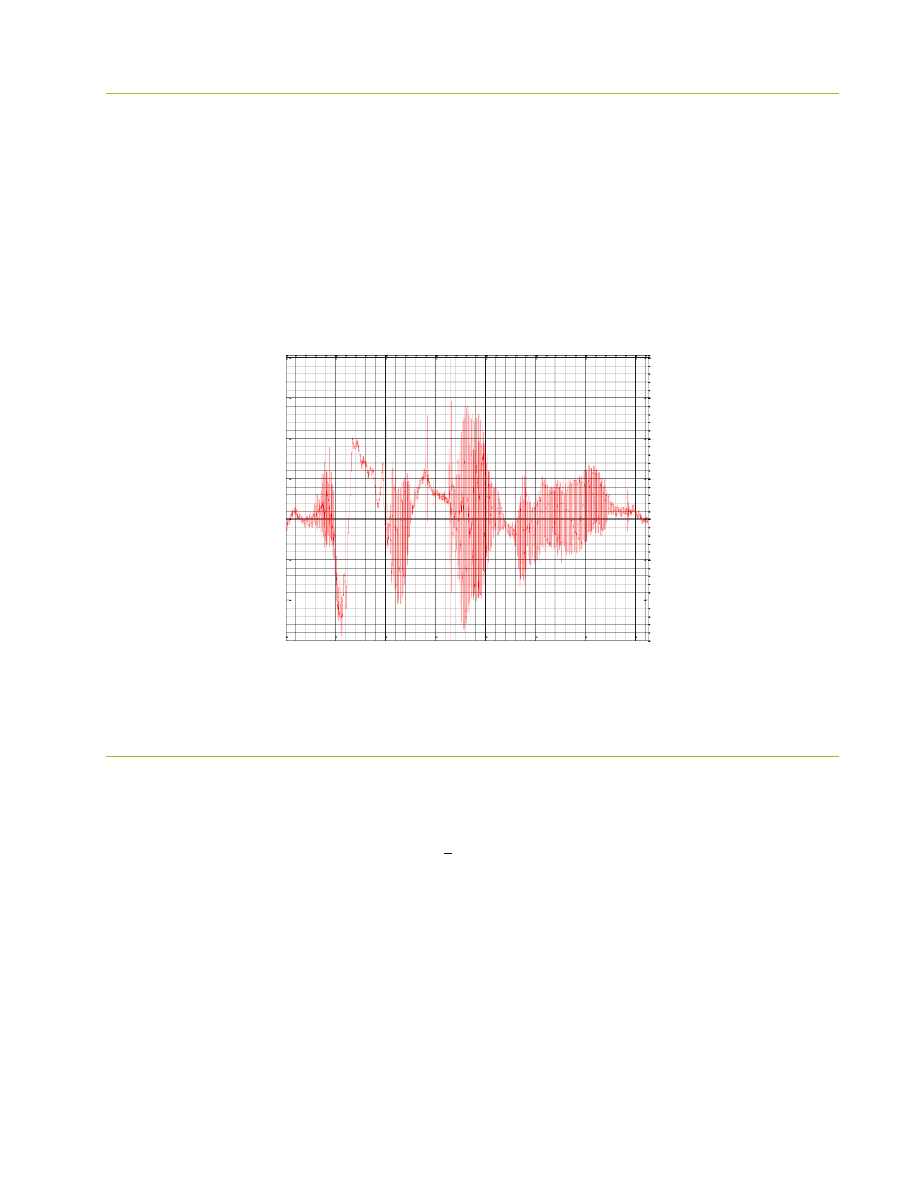
0. Rejestracja badanego słowa

Zarejestrowano słowo „sztukowań” według zadanych kryteriów: dźwięk mono, o częstotliwości

próbkowania f

s

= 22050 Hz i przy 16 bitach na jedną próbkę. Dźwięk zapisano w formacie .wav, a następnie

odczytano w programie MATLAB za pomocą następującego fragmentu kodu:

% Wczytanie i wyświetlenie sygnału

[d,fs, nbits]= wavread(

'grzeszyk.wav'

);

Dźwięk zapisano w wektorze d, częstotliwość próbkowania pobrano do zmiennej fs, odczytano również

dla sprawdzenia poprawności liczbę bitów na próbkę. Ciszę usunięto przed zaimportowaniem pliku
dźwiękowego za pomocą programu do edycji plików audio Audacity. Pobrany dźwięk przedstawiono na wykresie
w funkcji czasu.

1. Przetwarzanie wstępne

Kolejnym krokiem na drodze analizy sygnału mowy jest utworzenie sygnału z(i) o zerowej wartości

średniej. Aby to uczynić, należy policzyć wartość średnią (µ) dla wszystkich próbek pobranego dźwięku (s(i)), a
następnie policzyć różnicę pomiędzy wartością każdej z próbek i wartością średnią. Potrzebne wzory:

∑

0

0.2

0.4

0.6

0.8

1

1.2

1.4

-0.1

-0.05

0

0.05

0.1

0.15

0.2

Sygnał wejściowy (czas trwania)

W

ie

lk

oś

ć

pr

ób

ek

Wykres sygnału w funkcji czasu

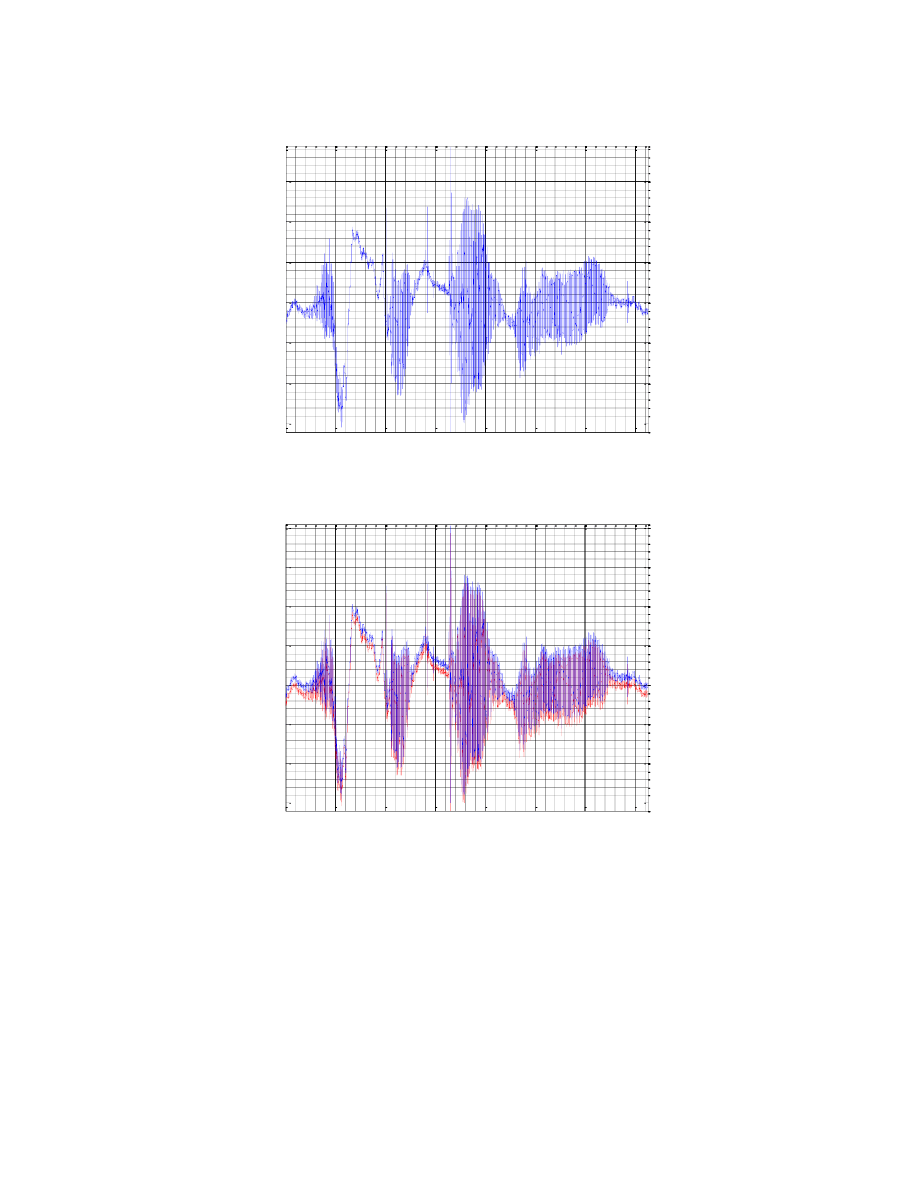
Otrzymany sygnał:

Porównanie sygnału przed i po obróbce:

Widać, iż uzyskany w wyniku operacji sygnał nie różni się znacząco od sygnału oryginalnego, przez co

możemy wnioskować, że został nagrany w dosyć dobrych warunkach, jeśli chodzi o szumy. Nie jest ich jednak
pozbawiony, na co wskazuje niezerowa wartość średnia, równa w przypadku zarejestrowanego słowa
0.009727762222290.

0

0.2

0.4

0.6

0.8

1

1.2

1.4

-0.15

-0.1

-0.05

0

0.05

0.1

0.15

0.2

Sygnał wejściowy

W

ie

lk

oś

ć

pr

ób

ek

Wykres różnic pomiędzy sygnałem oryginalnym a sygnałem o zerowej wartości średniej w funkcji czasu

0

0.2

0.4

0.6

0.8

1

1.2

1.4

-0.15

-0.1

-0.05

0

0.05

0.1

0.15

Sygnał wejściowy (czas trwania)

W

ie

lk

oś

ć

pr

ób

ek

Wykres sygnału o zerowej wartości średniej w funkcji czasu

20

40

60

80

100

120

0

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

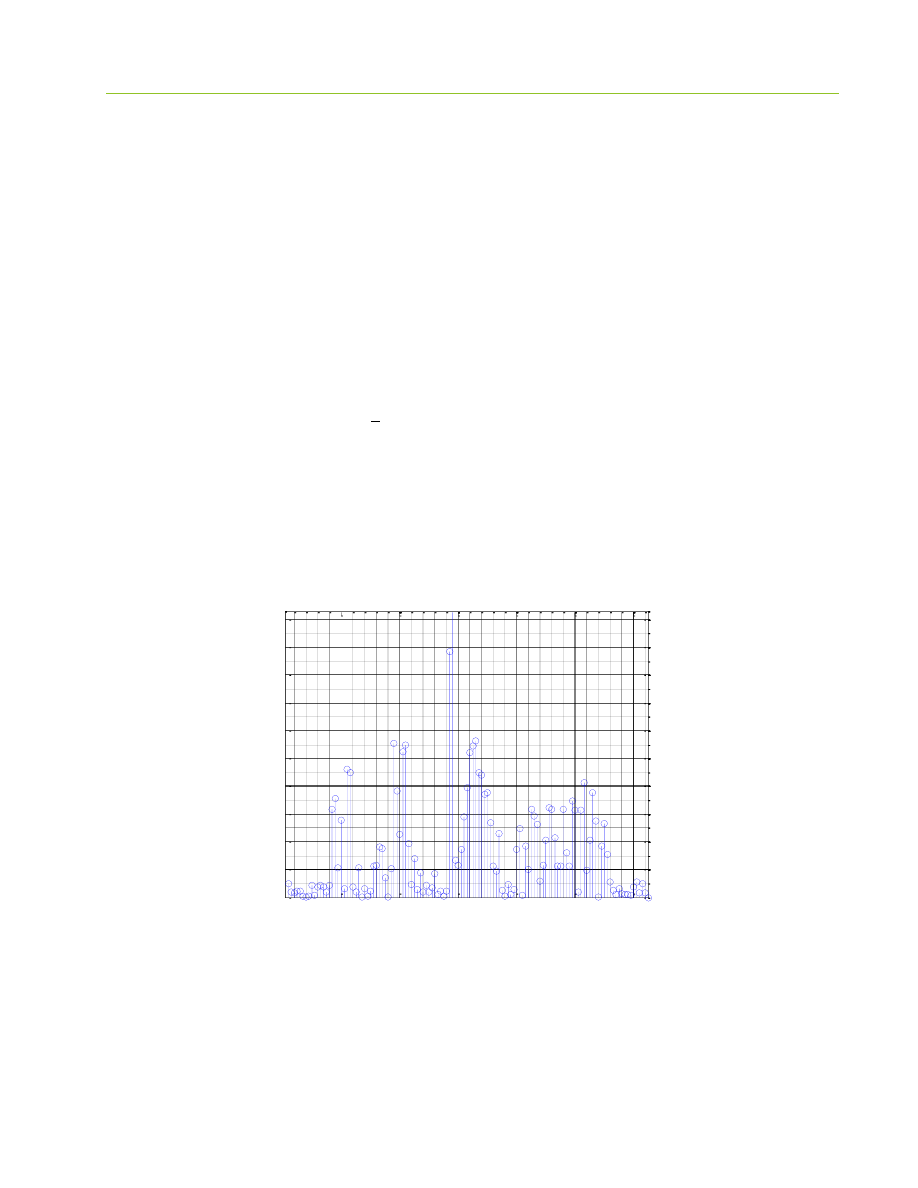
Wykres maksymalnych wartości w poszczególnych ramkach

Numer ramki

W

ar

to

ść

m

ak

sy

m

al

na

2. Analiza sygnału podzielonego na ramki

Odtąd wszystkie operacje zostaną przeprowadzone w oparciu o sygnał z(i). Podzielono go na segmenty o

długości 256, czyli mieszczące po 256 próbek dźwięku. Dla każdej ramki należało wyznaczyć następujące
cechy:



wartość największą



energię sygnału

∑



współczynnik LPC (parametr p=12)



liczba przejść przez zero PPZ

∑ [ ] [ ]

gdzie:

{

[ ]

[ ]

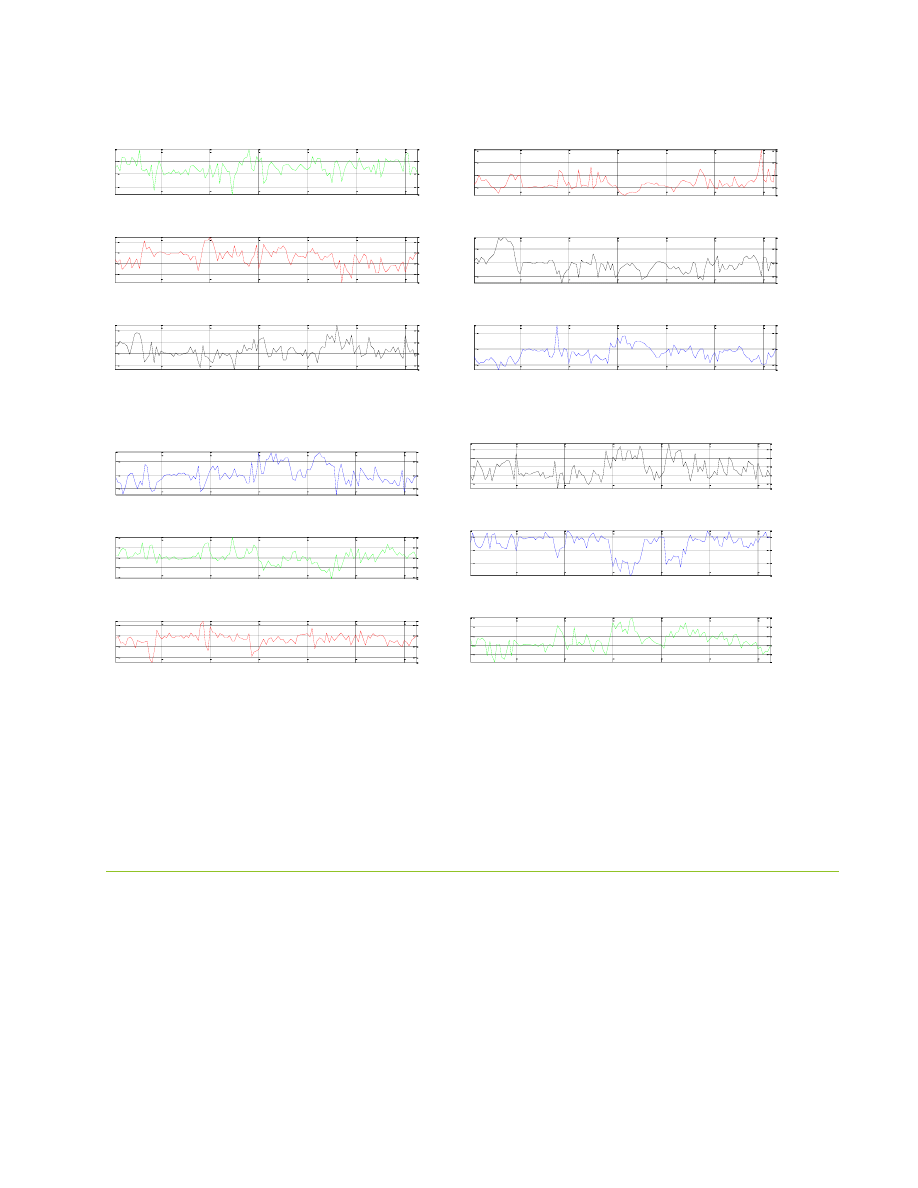
Następnie wykonano odpowiednie wykresy ilustrujące otrzymane wyniki:

Dzięki wykresowy maksymalnych wartości w poszczególnych ramkach możemy dostrzec granice pomiędzy

kolejnymi fonemami słowa oraz zauważyć, gdzie mamy głoski dźwięczne, a gdzie bezdźwięczne. Na początku
wykresu obserwujemy chwilę nieusuniętej ciszy, natomiast ramki o dużo wyższych wartościach reprezentują
już dźwięki mowy. Możemy zaobserwować, że największe wartości notujemy w okolicach fonemu „k”,
natomiast lokalne maksima o mniej więcej takim samym poziomie reprezentują samogłoski.

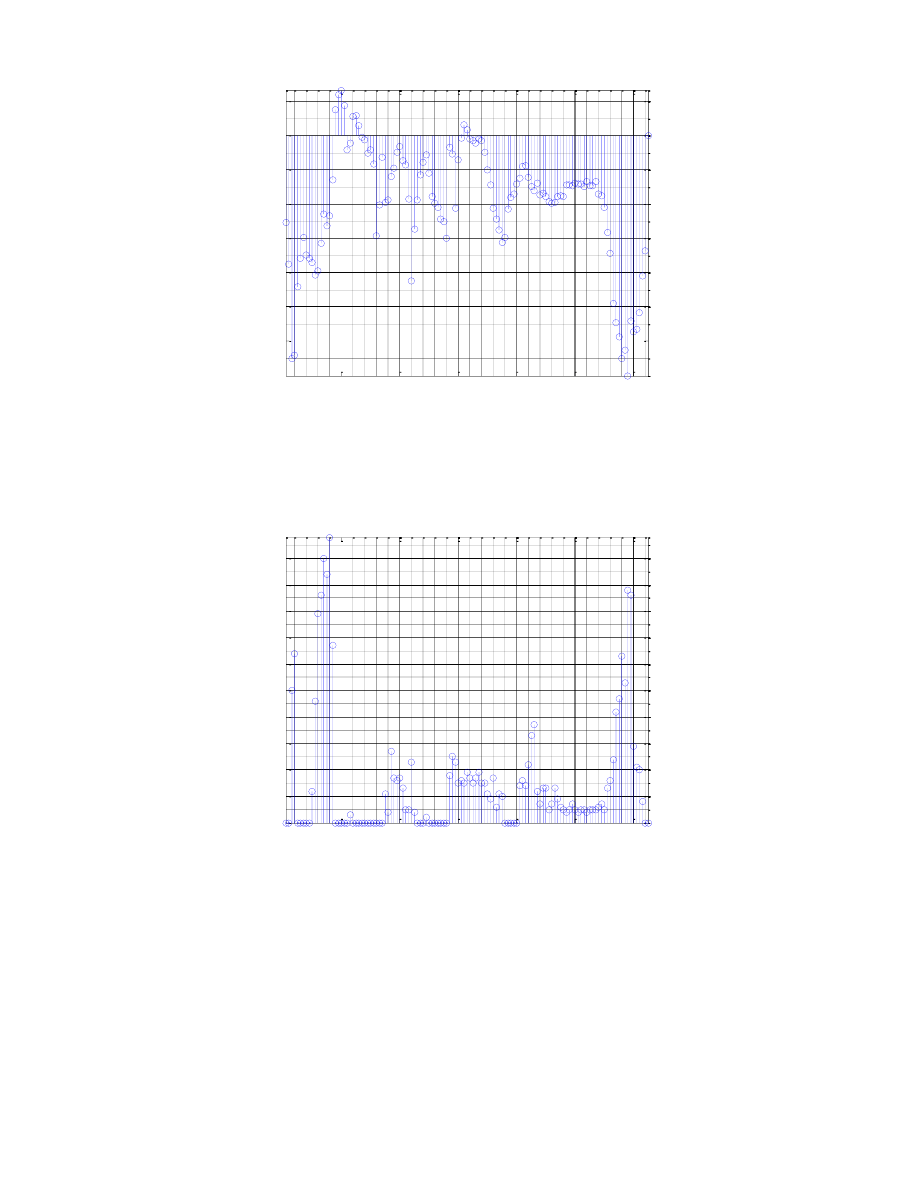
Wykres wartości energii jest również miarą pomocną w rozpoznawaniu dźwięków. Informuje nas, w

których miejscach rozmieszczone są dźwięczne i bezdźwięczne fonemy. Chwila ciszy posiada bardzo dużą
energię ujemną, natomiast w momencie rozpoczęcia artykulacji słowa widzimy nagłą zmianę energii, która
znów przechodzi w dziedzinę ujemną, a znaczne spadki notujemy w okolicach wybrzmiewania samogłosek.

Wykres liczby przejść przez 0 daje nam informację o położeniu dźwięków szeleszczących i dźwięcznych

jak i również pokazuje miejsca ciszy – tam mamy dużą ilość zmian sygnału. Przy głoskach dźwięcznych drganie
krtani powoduje powstanie sygnałów okresowych, które oscylują wokół zera, dając zarówno wartości ujemne,
jak i dodatnie. Toteż nie dziwi fakt, że największe ilości przejść notujemy właśnie w tych rejonach. Dla
porównania warto spojrzeć na takie głoski w słowie jak „t”, „k” czy „w” – widzimy, iż tam drgań nie
obserwujemy wcale.

20

40

60

80

100

120

-6

-5

-4

-3

-2

-1

0

1

Wykres wartości energii dla poszczególnych ramek

Numer ramki

E

n

e

rg

ia

20

40

60

80

100

120

0

10

20

30

40

50

60

70

80

90

100

Wykres PPZ dla ramek

Numer ramki

Li

cz

ba

p

rz

ej

ść

p

rz

ez

z

er

o

Wykresy LPC, inaczej liniowego kodowania predykcyjnego informuje nas, jaka jest odpowiedź filtru

biegunowego na pobudzenie, próbowane jest przybliżenie przyszłych próbek na podstawie kombinacji
poprzednich. Rząd filtra został ustalony na 12, wobec tego w predykcji jest branych pod uwagę 12 próbek. W
efekcie otrzymano 13 współczynników opisujących sygnał mowy, przy czym pierwszy jest zawsze równy jeden,
a więc został pominęty.

3. Wyznaczenie spektrogramów sygnału z(i)

Zasada wyznaczania spektrogramu sygnału polega na pokazaniu częstotliwości sygnału w funkcji czasu.

Uzyskuje się go na podstawie obliczonych amplitud harmonicznych opisujących dany sygnał. W metodzie
najważniejsze jest odpowiedni dobór okna i przekrycia. Można wobec tego uzyskać albo wierne odwzorowanie
czasowe albo częstotliwościowe sygnału w zależności od wielkości okna. Przekrycie zaś jest to wartość, o jaką
ramki zachodzą na siebie. W poniższych przykładach używano przykładowych przekryć o wartościach 25, 50 i
75%. Im większe przekrycie, tym wierniejsze odwzorowanie, jednakże zwiększa się nadmiarowość obliczeń.
Przeprowadziłam test w ramach którego dobierałam wielkość okna oraz podane wyżej przekrycie i najlepsze
rezultaty, największą widoczność uzyskałam w przypadku okna o wielkości 256 próbek. Zwyczajowo wykresy
spektrogramu przedstawia się jako funkcję czasu w dziedzinie częstotliwości (podawanej w Hz). Niestety nie
jest to standard w użytej bibliotece programu Matlab, toteż do generacji wykresów musiałam posłużyć się
niestandardową składnią.

20

40

60

80

100

120

-0.2

0

0.2

Wykres LPC dla współczynnika5

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.4

-0.2

0

0.2

Wykres LPC dla współczynnika6

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.2

0

0.2

0.4

Wykres LPC dla współczynnika7

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-1

-0.5

0

0.5

Wykres LPC dla współczynnika2

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.5

0

0.5

Wykres LPC dla współczynnika3

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.5

0

0.5

Wykres LPC dla współczynnika4

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.2

0

0.2

Wykres LPC dla współczynnika8

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.4

-0.2

0

0.2

0.4

Wykres LPC dla współczynnika9

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.4

-0.2

0

0.2

Wykres LPC dla współczynnika10

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.1

0

0.1

0.2

0.3

Wykres LPC dla współczynnika11

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.4

-0.2

0

Wykres LPC dla współczynnika12

Numer ramki

W

a

rt

o

s

c

L

P

C

20

40

60

80

100

120

-0.1

0

0.1

0.2

0.3

Wykres LPC dla współczynnika13

Numer ramki

W

a

rt

o

s

c

L

P

C

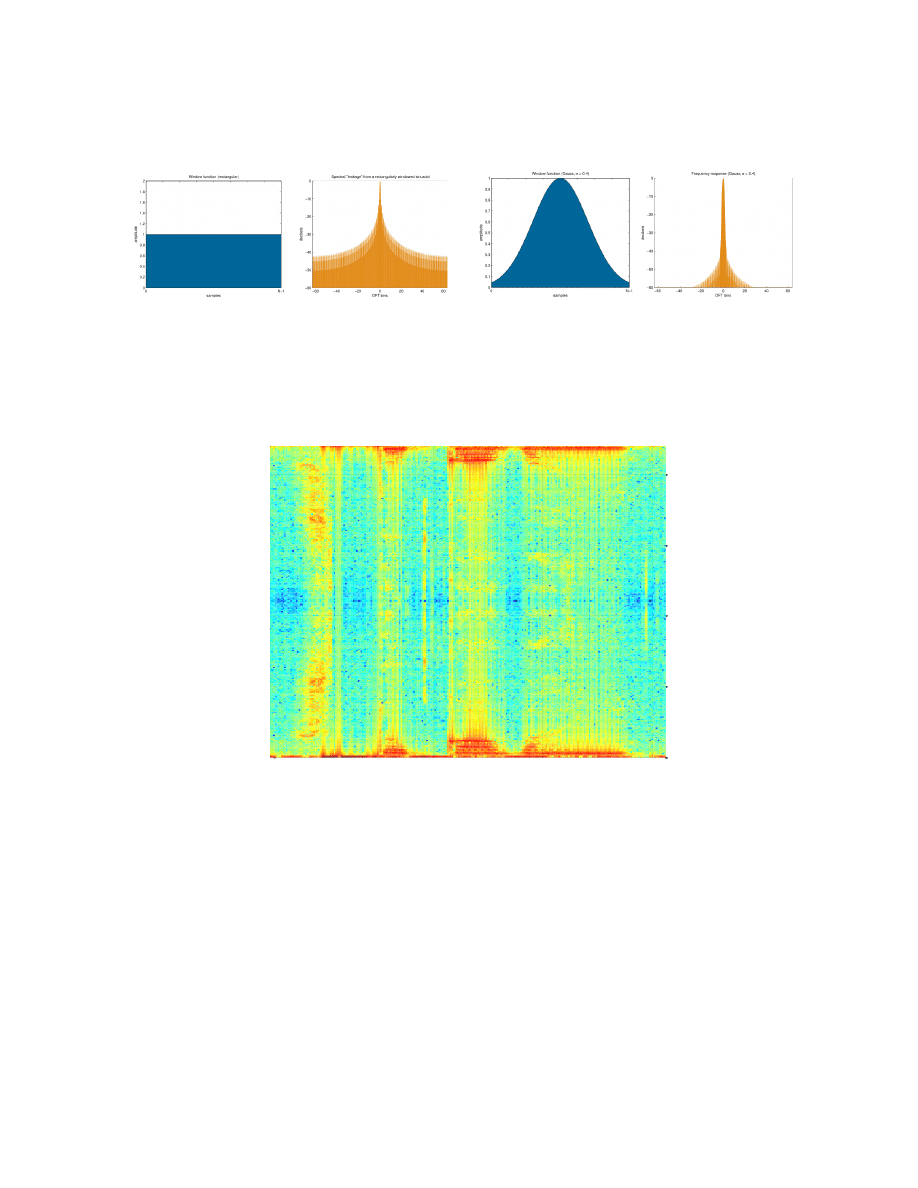
Należy również wspomnieć o rodzajach okien stosowanych w spektrogramach. Jest ono stosowane, aby

pozbyć się szumów występujących w sygnałach. Z racji różnych kształtów, okna przydają się w różnych
zastosowaniach. Dla potrzeb rozpoznawania mowy zostało użyte okno prostokątne i Hamminga. Poniżej
zamieszczam obrazek ilustrujący różnice pomiędzy tymi dwoma oknami (zaczerpnięty z polskiej Wikipedii –
hasło okno czasowe):

Okno prostokątne charakteryzuje się mniejszym tłumieniem na końcach przedziału czasowego, natomiast

okno Hamminga stosuje stopniowe wygładzanie krawędzi, toteż przy usuwaniu szumów jest efektywniejsze, co
zostało docenione przez funkcję wbudowaną, bowiem okno te jest standardowo stosowane przy uzyskiwaniu
spektrogramów.

Wykresy uzyskanych spektrogramów:

Okno prostokątne daje nam obraz rozłożenia fonemów w mowie, jednakże nie jest on wyraźny, wszystkie

dźwięczne fonemy wyglądają podobnie. Spójrzmy wobec tego na okno Hamminga:

0.2

0.4

0.6

0.8

1

1.2

1.4

0

0.5

1

1.5

2

x 10

4

Time

Spektrogram okno prostokątne szerokość 256, przekrycie 50%

F

re

q

u

e

n

c

y

(

H

z

)

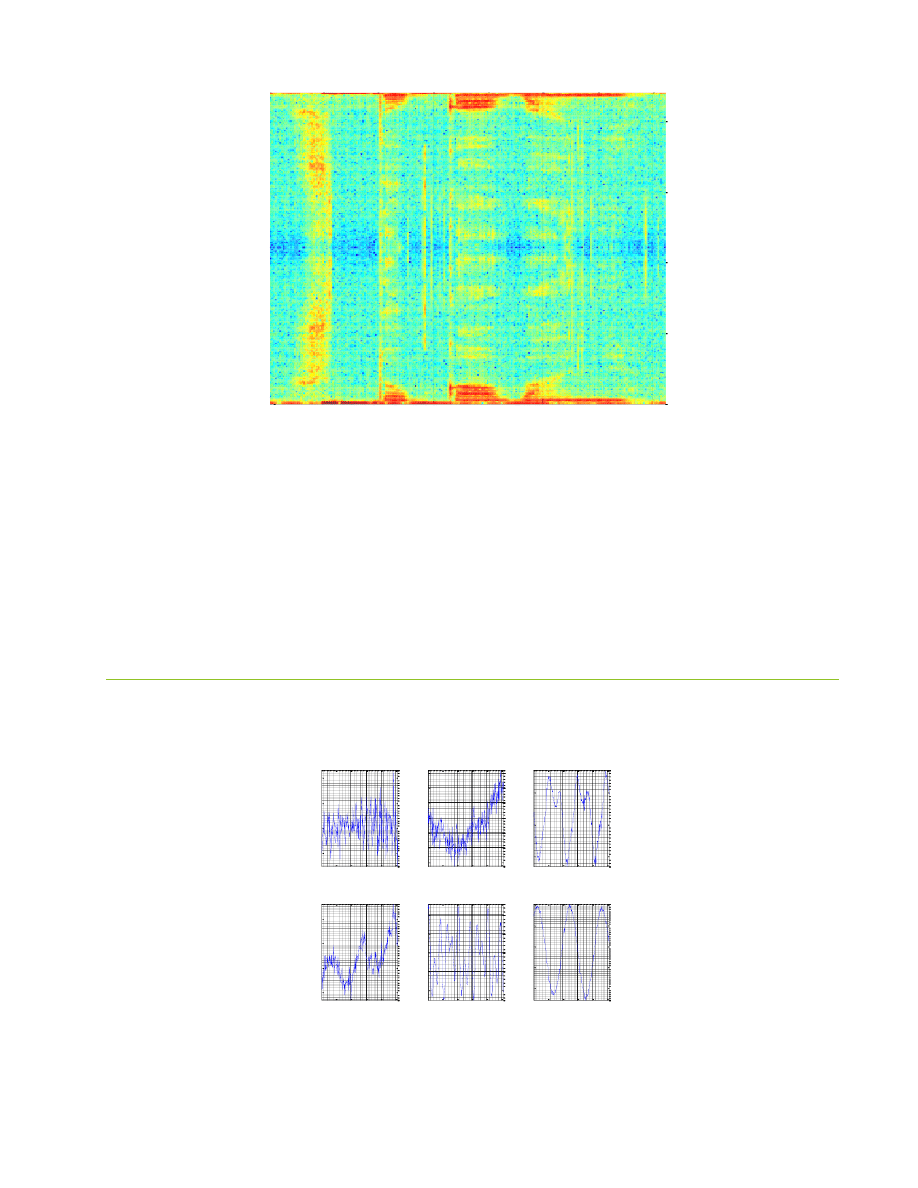
Zmiana jest zauważalna, zniknęły długie, żółte pasy poprzez całą dziedzinę częstotliwości, stąd można

poznać różnicę pomiędzy wydźwiękiem głosek.

Widać wyraźnie, iż rozmiar okna ma wpływ na uzyskane wyniki, duży rozmiar powoduje, iż można

dostrzec formanty, jednak wyniki w dziedzinie czasowej zostały uśrednione. Zauważono, iż okno o rozmiarze
256 bądź 512 daje najlepsze rezultaty, gdyż zależy nam na dostrzeżeniu częstotliwości wyżej wspomnianych
formantów. Na obrazach widać również, iż dźwięki szeleszczące tworzą długą linię, ciągnąca się przez całą
długość osi częstotliwości. Głoski takie jak t,k czy w w zarejestrowanym słowie w dziedzinie częstotliwości
niemal nie występują. Jeśli chodzi o przekrycie, najlepsze rezultaty daje nadmiarowość rzędu 50 bądź 75%.

4. Analiza wybranych ramek dla fonemów

Wybrano 6 ramek, zawierających dwie samogłoski, spółgłoskę nosową, spółgłoskę trącą

bezdźwięczną oraz spółgłoskę zwartą. Każda z ramek posiada 256 próbek, wybranych ze środka zakresu danego
fonemu. Poniżej przedstawiono zbiorczy wykres wartości próbek dla wszystkich ramek

Wynikiem wykonania funkcji xcorr() jest wektor zawierający 511 wartości (2n-1, gdzie n jest

liczbą próbek). Autokorelacja jest funkcją z dziedziny statystyki, która informuje nas, jaka jest zależność
danej próbki od próbek sąsiednich. Wartości z otrzymanego wektora są bardzo różne i zależne od badanej
ramki. Wynikać to może z niedoskonałości nagrania, zawierającego mimo redukcji zakłóceń otoczenia wciąż

0.2

0.4

0.6

0.8

1

1.2

1.4

0

0.5

1

1.5

2

x 10

4

Time

Spektrogram okno Hamminga szerokość 256, przekrycie 50%

F

re

q

u

e

n

c

y

(

H

z

)

50 100 150200250

-0.02

0

0.02

0.04

50 100150200250

0.076

0.078

0.08

0.082

0.084

0.086

0.088

50 100150200250

-0.1

-0.05

0

50 100 150200250

0.035

0.04

0.045

0.05

50 100150200250

-0.1

-0.05

0

0.05

0.1

50 100150200250

-0.04

-0.02

0

0.02

0.04

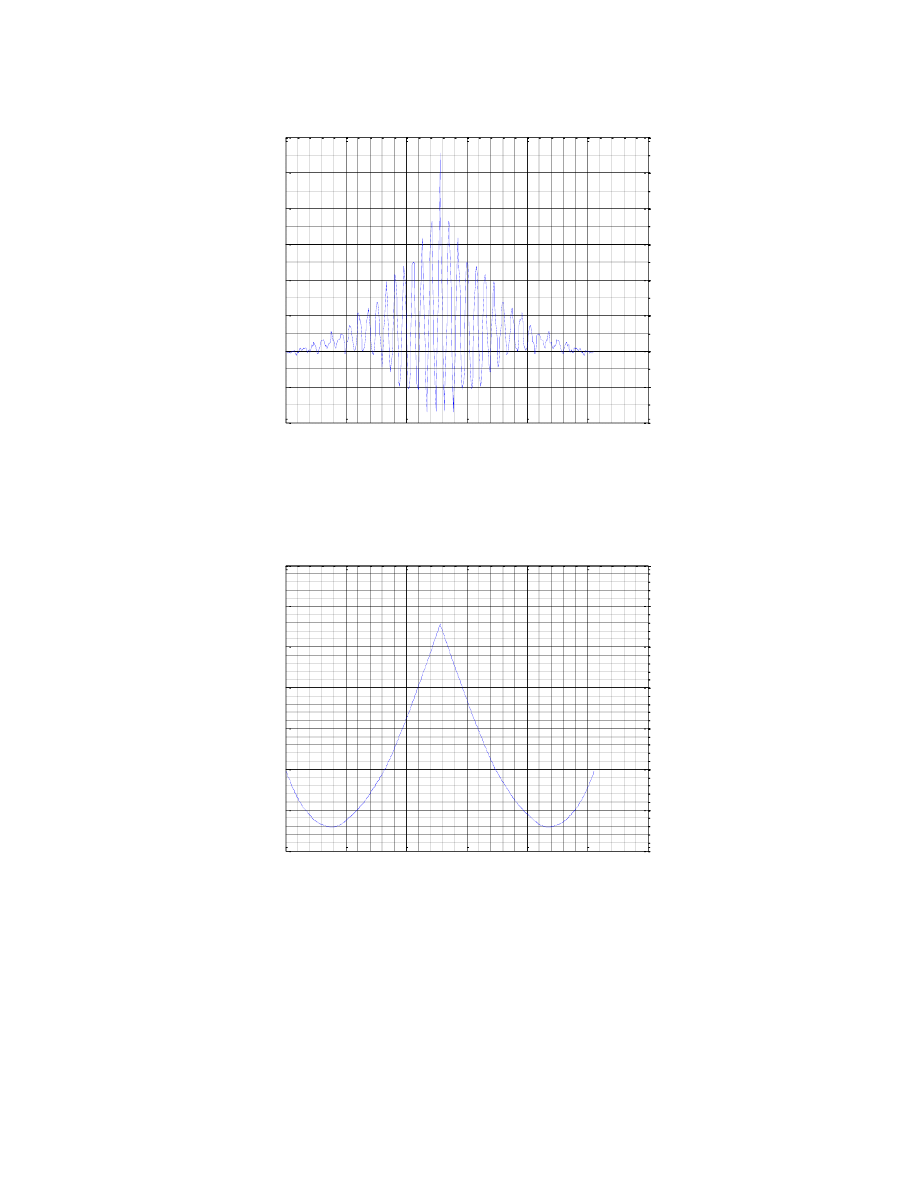
wiele czynników zniekształcających pobrany sygnał. Poniższe wykresy prezentują wartości otrzymanych
autokorelacji dla wszystkich 6 ramek:

W przypadku fonemu sz mamy potwierdzenie, iż jest on typem dźwięcznym, toteż obserwujemy sygnał

okresowy, o wyraźnie zaznaczonym szczycie, symetryczny. Świadczy on o dobrym dopasowaniu ramki do
dalszej analizy.

Fonem t, z racji swojej bezdźwięczności, nie posiada harmonicznego wykresu, natomiast i tutaj

dostrzegamy wysoką zależność w ramce, odpowiednią dla głosek bezdźwięcznych. Należy zauważyć, iż w
poprzednim przypadku dobierałam ramki ze środka fonemu, gdzie napotkałam się w przypadku fonemów
bezdźwięcznych na ciszę, toteż niniejsze wykresy są otrzymane z początków fonemów, co zaowocowało
otrzymaniem innych wyników, jeśli chodzi o nieprawidłowe wykresy korelacyjne.

0

100

200

300

400

500

600

-4

-2

0

2

4

6

8

10

12

x 10

-3

Autkorelacja dla fonemu sz

0

100

200

300

400

500

600

-0.1

-0.05

0

0.05

0.1

0.15

0.2

0.25

Autkorelacja dla fonemu t

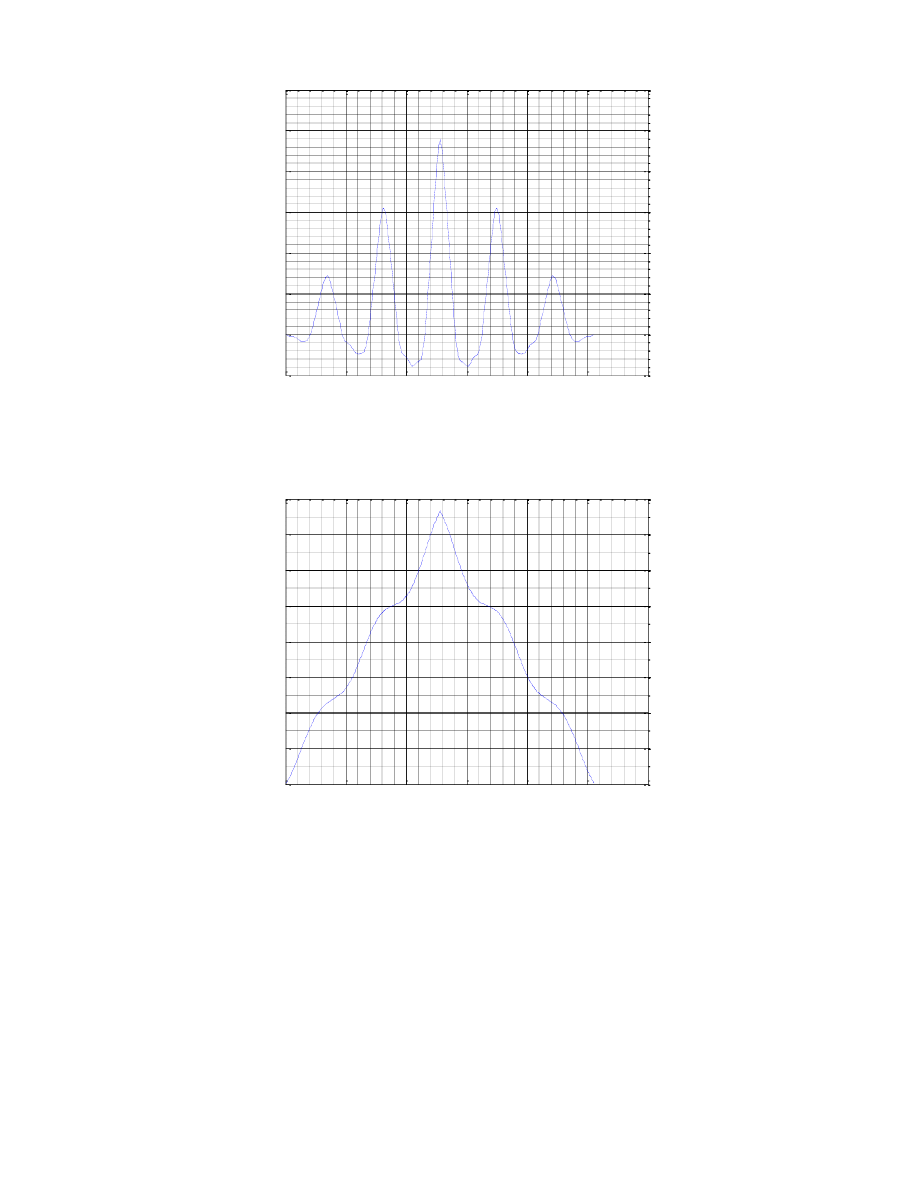
Fonem u z kolei jest samogłoską, toteż na wykresie autokorelacji widzimy wyraźny harmoniczny przebieg,

charakterystyczny dla innych samogłosek.

Dla fonemu k uzyskaliśmy dosyć nietypowy przebieg, tutaj wnioskować możemy o złym dopasowaniu

ramki, gdyż wykres autokorelacji podobny jest do wykresu autokorelacji ciszy.

0

100

200

300

400

500

600

-0.1

0

0.1

0.2

0.3

0.4

0.5

0.6

Autkorelacja dla fonemu u

0

100

200

300

400

500

600

0

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

Autkorelacja dla fonemu k

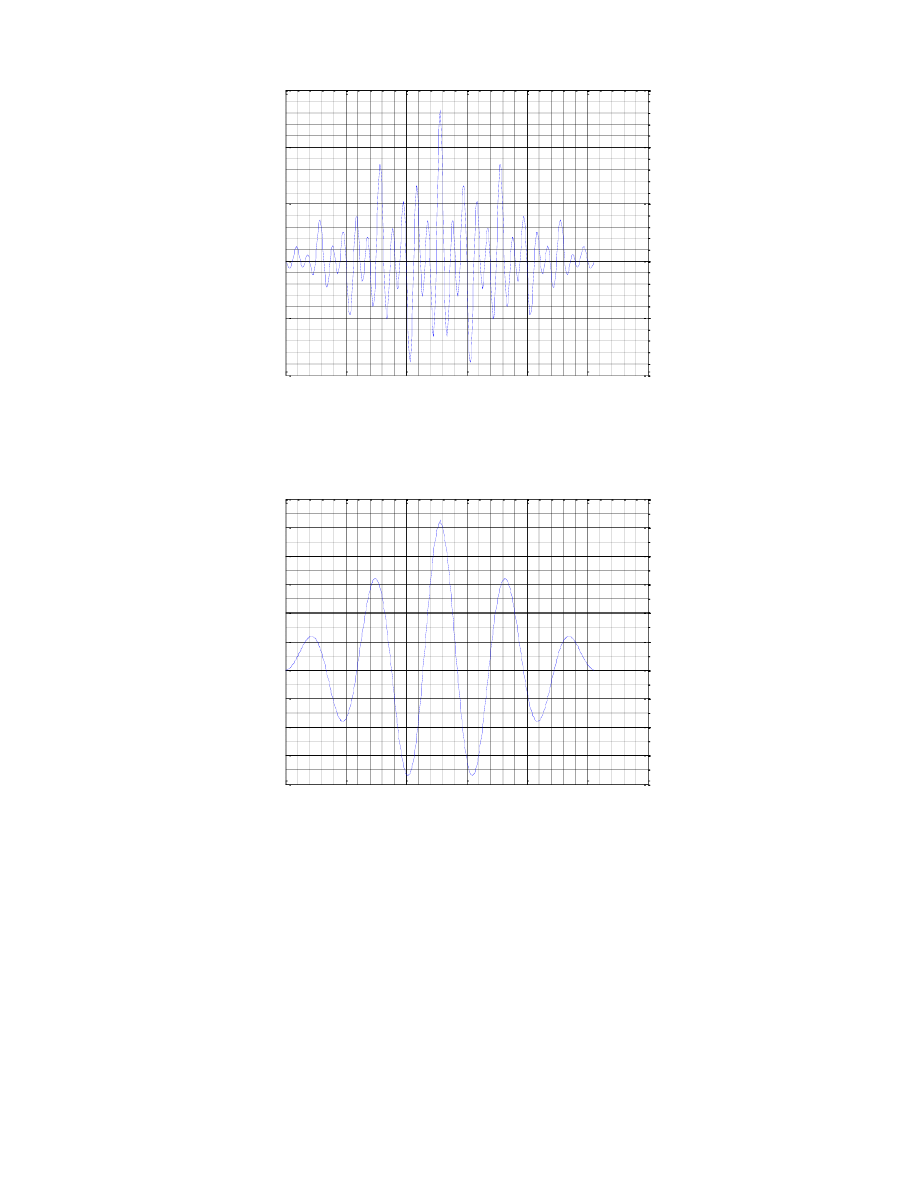
Fonem o to kolejna samogłoska, której dźwięczność możemy zaobserwować na wykresie autokorelacji,

charakteryzuje się znacznie bardziej dynamicznym przebiegiem niż u.

Fonem ń również przy artykulacji pobudza struny głosowe do drgania, toteż wykres autokorelacji jest

podobny do innych głosek dźwięcznych.

Kolejnym krokiem w analizie sygnału jest wyznaczenie 256-punktowej szybkiej transformaty Fouriera z

oknem Hamminga oraz narysowanie widma amplitudowego w zakresie połowy częstotliwości nagrania. Dzięki
zobrazowaniu widma amplitudowego otrzymujemy wartości częstotliwości w dziedzinie czasu. Wspomniane
ograniczenie połowy częstotliwości (w wypadku nagrania będzie to zakres [0 11025]) jest stosowane, gdyż
uzyskane widmo jest symetryczne względem fs/2. Spowodowane jest to faktem, iż powstałe widma po
osiągnięciu tego progu zaczynają się na siebie nakładać, a przez to zadanego sygnału nie dałoby się odtworzyć.
Należy również wspomnieć, iż z każdego otrzymanego widma dałoby się odtworzyć cały sygnał. Kod
odpowiedzialny za utworzenie widma amplitudowego wygląda następująco:

0

100

200

300

400

500

600

-1

-0.5

0

0.5

1

1.5

Autkorelacja dla fonemu o

0

100

200

300

400

500

600

-0.2

-0.15

-0.1

-0.05

0

0.05

0.1

0.15

0.2

0.25

0.3

Autkorelacja dla fonemu ni

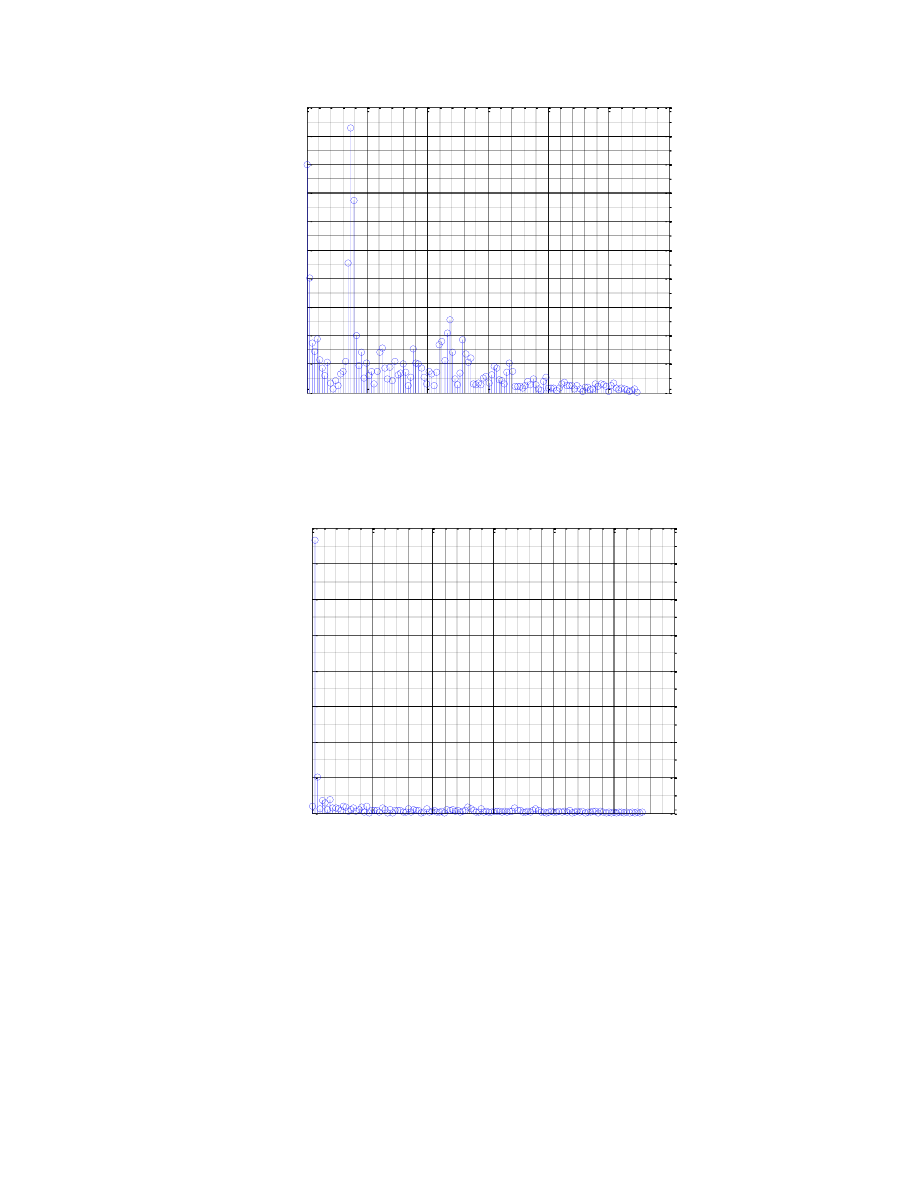
Otrzymane wykresy przedstawiają się następująco:

Widmo amplitudowe jest szczególnie pomocne w analizie dźwięków mowy, gdyż pozwala ono na

dostrzeżenie częstotliwości formantowych ramek. Wyznacza się je poprzez odnalezienie lokalnych maksimów w
dźwięku, które w przypadku szeleszczącej zgłoski sz można odnaleźć na poziomie około 1400Hz oraz w
okolicach 5kHz.

Widmo amplitudowe dla fonemu t nie pozwala nam odnaleźć żadnych charakteryzujących ten dźwięk

miejsc, z racji jego bezdźwięczności.

0

2000

4000

6000

8000

10000

12000

0

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] sz

Częstotliwość [Hz]

A

m

p

lit

u

d

a

0

2000

4000

6000

8000

10000

12000

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] t

Częstotliwość [Hz]

A

m

p

lit

u

d

a

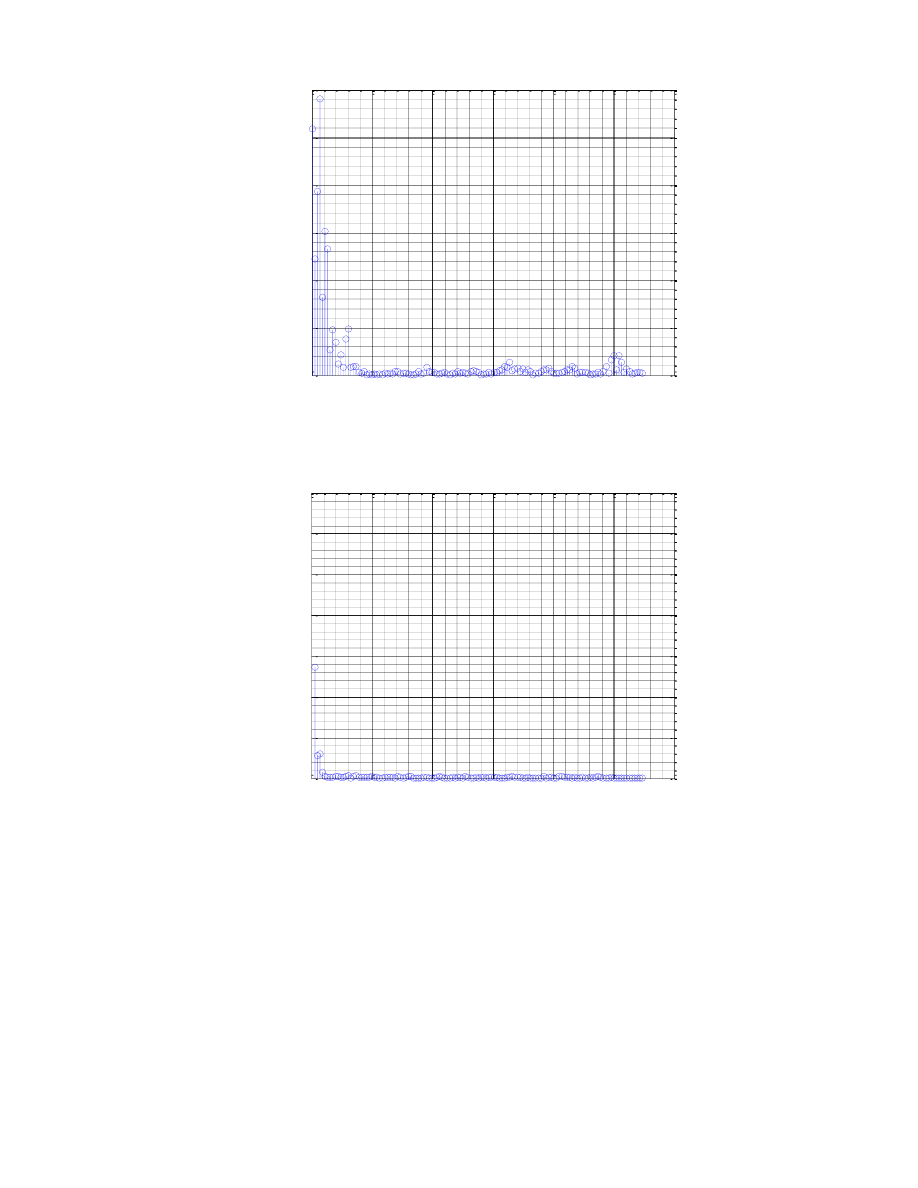
Spółgłoska u należy do dźwięcznych, stąd też należałoby szukać jej maksimów lokalnych, choć

specyficznych dla każdego rozmówcy, to jednak bezsprzecznie istniejących. Dla „u” odnaleźć można
częstotliwości formantowe w okolicach około 200Hz jak i 1500Hz.

Dla fonemu t sytuacja jest podobna, jak w przypadku k – częstotliwości formantowych po prostu nie ma.

0

2000

4000

6000

8000

10000

12000

0

0.5

1

1.5

2

2.5

3

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] u

Częstotliwość [Hz]

A

m

p

lit

u

d

a

0

2000

4000

6000

8000

10000

12000

0

0.5

1

1.5

2

2.5

3

3.5

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] k

Częstotliwość [Hz]

A

m

p

lit

u

d

a

Dla fonemu o najwięcej informacji dostarcza pasmo do 2kHz. Obserwujemy tam wszystkie lokalne

maksima na poziomie około 300Hz, 700Hz oraz 1400Hz. Oczywiście wszystkie podawane przeze mnie wartości
są tylko próbą przybliżenia miejsc występowania maksimum lokalnego, dlatego nie są one dokładne, a jedynie
odczytane z wykresu. Dokładne wyznaczenie częstotliwości formantowych odbywać się będzie w dalszych
punktach niniejszego sprawozdania.

Widmo amplitudowe dla fonemu ń jest dosyć jednostajne poza fragmentem spotkanym około 300Hz –

tam mamy wyraźne maksimum lokalne.

Następnie dokonano analizy formantów dla fonemów za pomocą poniższych metod:

Metoda I:



wyznaczono widmo amplitudowe za pomocą polecenia:

[abs(fft(sig)];



wyznaczono widmo amplitudowe za pomocą polecenia:

[abs(fft(hamming(256).*sig))];



wyznaczono widmo mocy za pomocą polecenia:

[10 log10(abs(fft([a zeros(1,256-17)))];

Metoda II:



wyznaczyć widmo predykcji liniowej:

a = lpc(hamming(256).*sig,16);
h = abs(1./fft([a zeros(1,256-17)]));

0

2000

4000

6000

8000

10000

12000

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

5

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] o

Częstotliwość [Hz]

A

m

p

lit

u

d

a

0

2000

4000

6000

8000

10000

12000

0

0.5

1

1.5

2

2.5

3

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] ń

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

Wykonano wykresy widm zgodnie z podanym w instrukcji laboratoryjnej wzorami. Na rysunkach

podobnie jak w przypadku widm wyznaczanych powyżej ujęto skalę częstotliwościową w zakresie od 0 do
połowy fs sygnału. Poniżej przedstawiono wszystkie otrzymane wykresy z podziałem na wybrane ramki
fonemów:

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Widmo amplitudowe dla ramki fonemu sz

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

-25

-20

-15

-10

-5

0

Widmo mocy dla ramki fonemu sz

Częstotliwość [Hz]

M

o

c

[

d

B

]

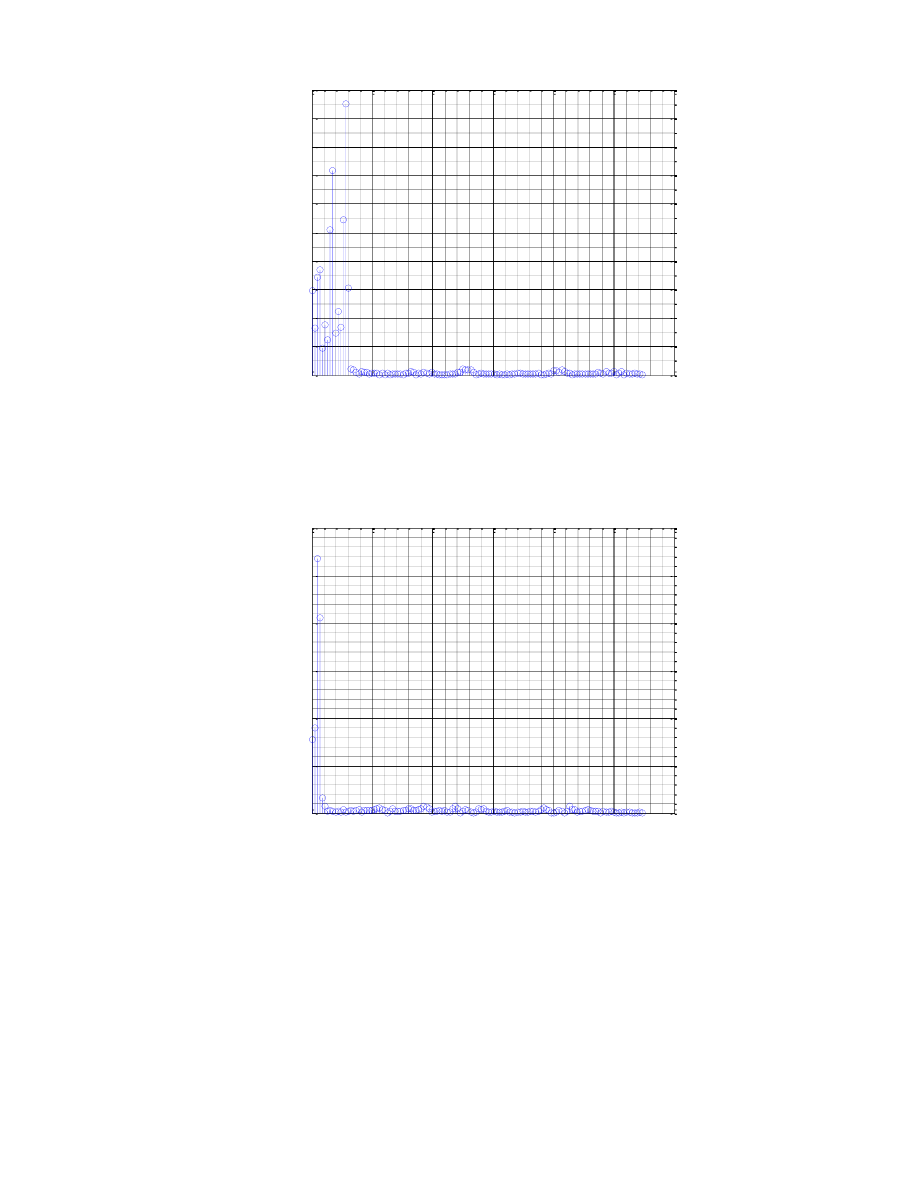
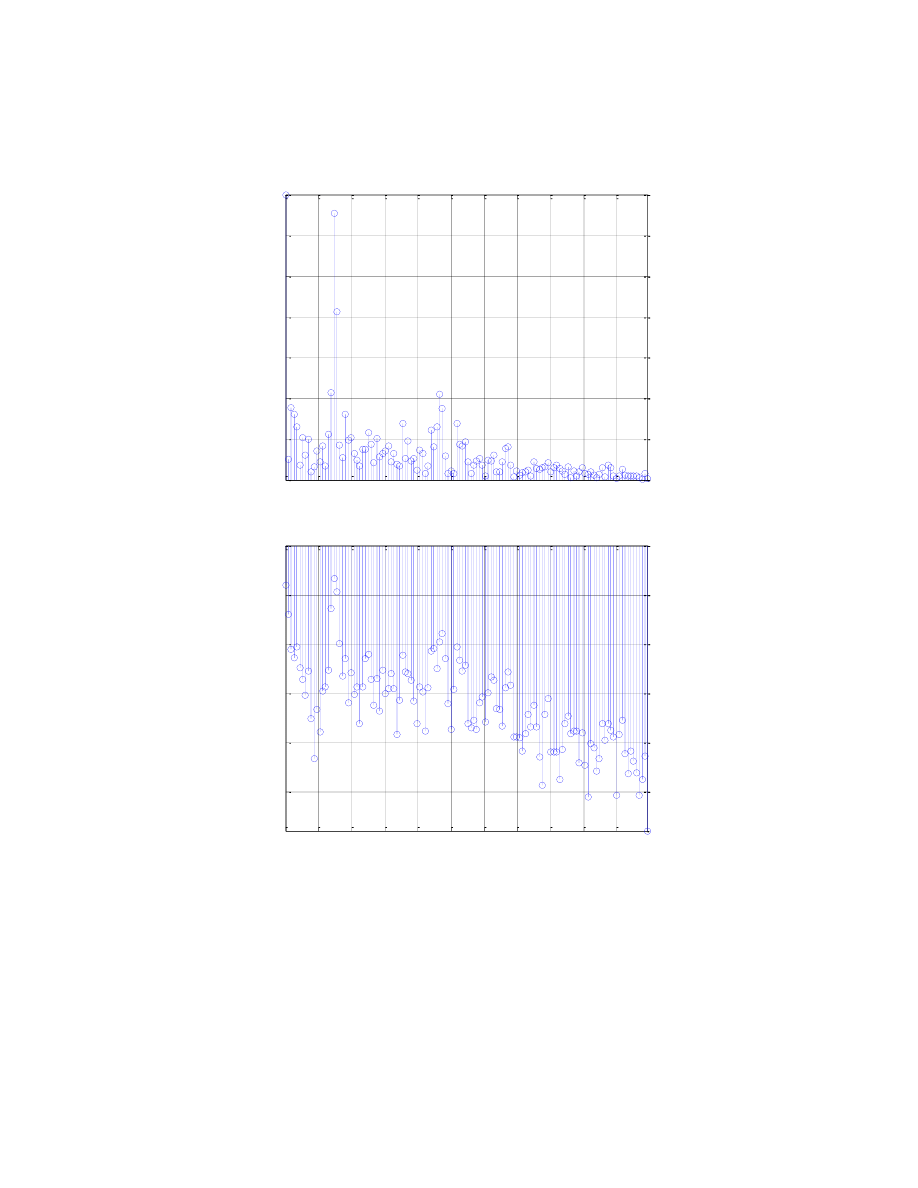
Widmo amplitudowe informuje nas, iż w sygnale największe amplitudy mają harmoniczne z przedziału

od 1 do 6kHz. W dźwięku „sz” występują bardzo duże spadki mocy, co może świadczyć o jego dużej zmienności.
Widmo predykcji liniowej doskonale nakreśla nam lokalne maksima w dźwięku – piki pokrywają się z
odnalezionymi w widmie amplitudowym.

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

2

4

6

8

10

12

14

16

Widmo predykcji liniowej dla ramki fonemu sz

Częstotliwość [Hz]

H

(f

s

)

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

0.5

1

1.5

2

2.5

3

3.5

Widmo amplitudowe dla ramki fonemu t

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

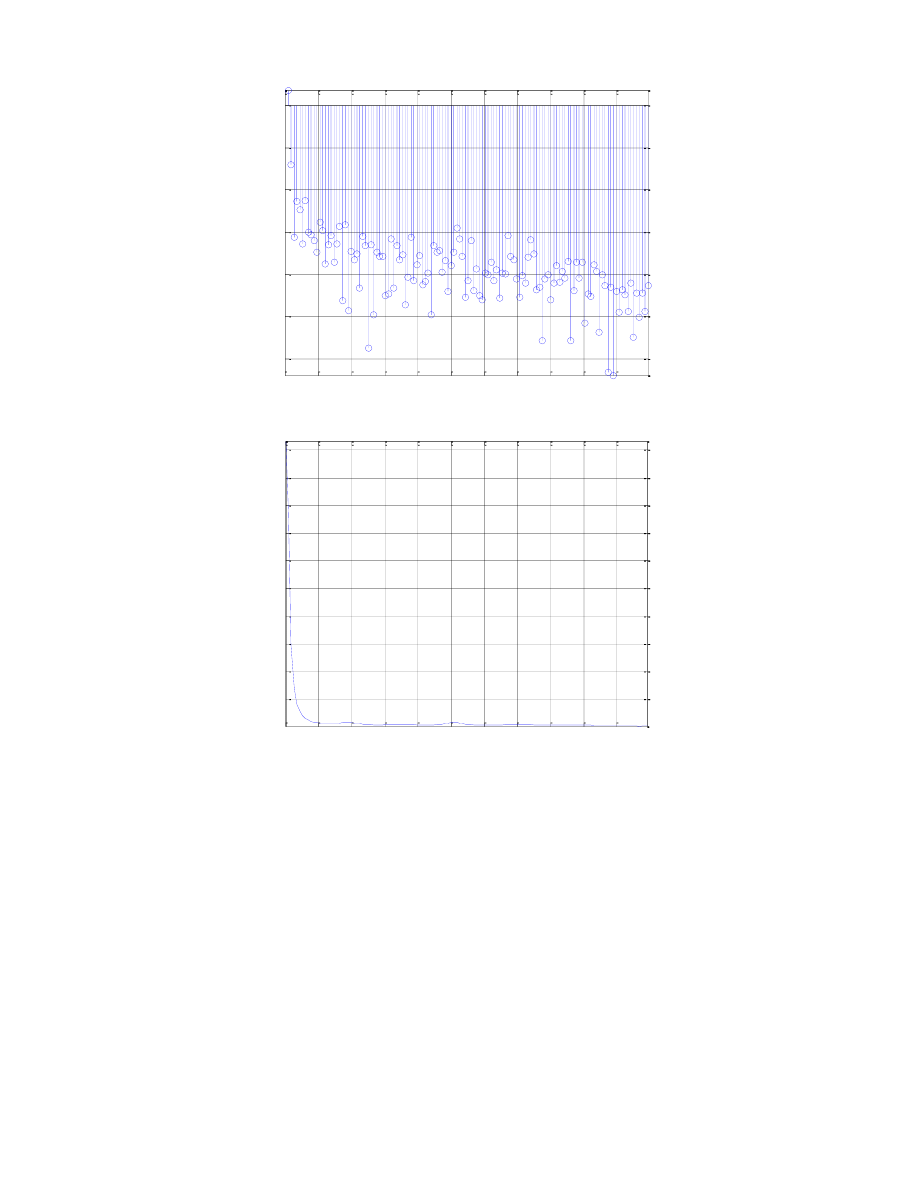
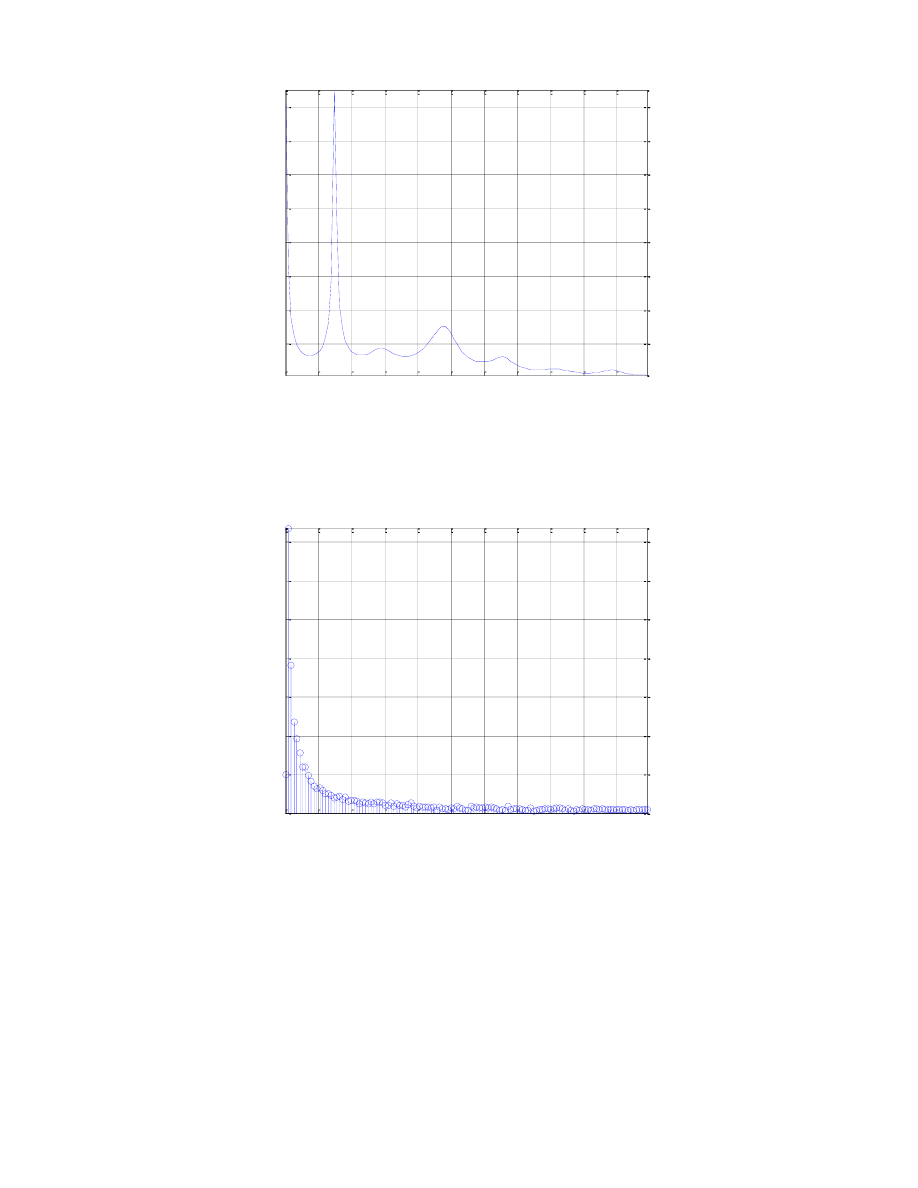
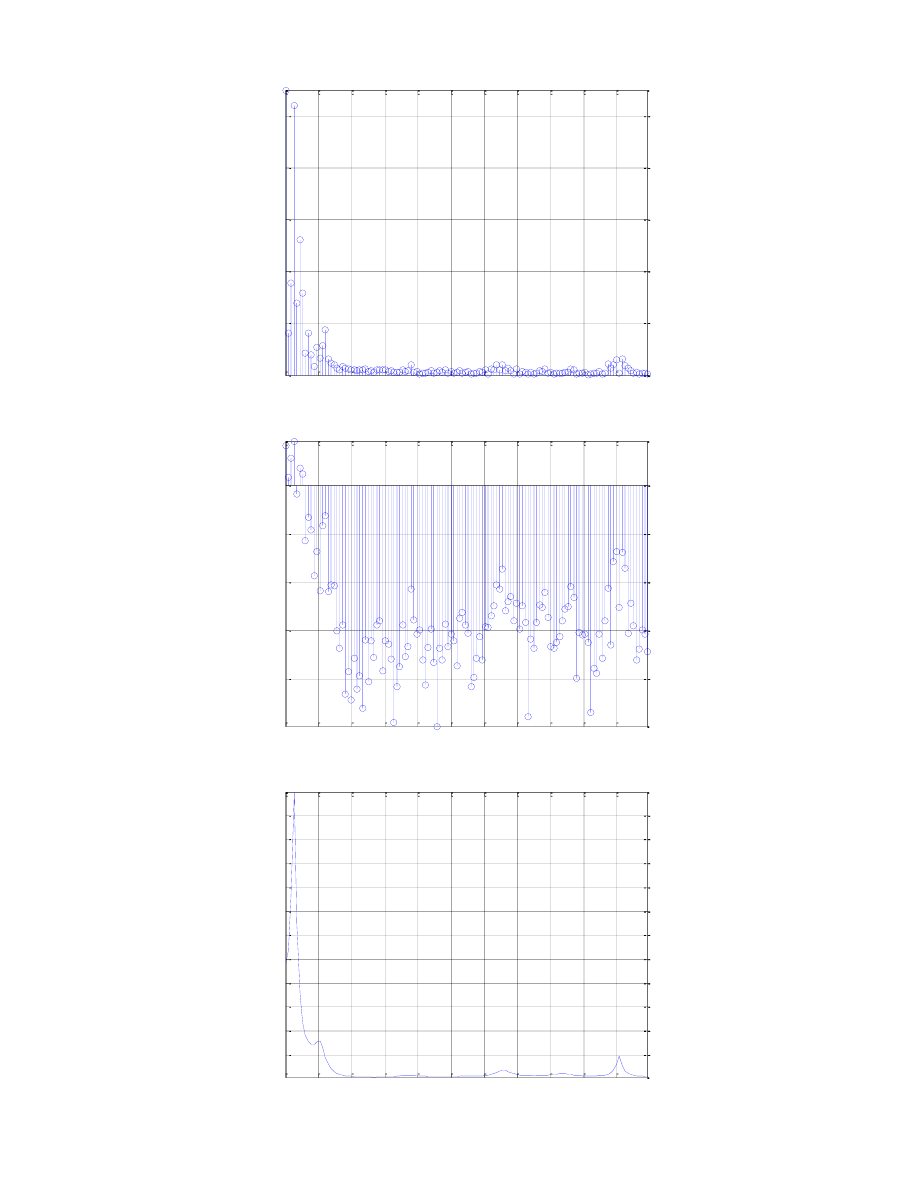
Dźwięk „t” to spółgłoska bezdźwięczna toteż obserwowane widmo amplitudowe jest znikome, zerowe.

Moc sygnału jest również dosyć duża, a predykcja z racji zerowych wartości widma amplitudowego również
równa 0, poza wartością początkową, którą z racji możliwości wystąpienia błędu należy pominąć.

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

-30

-25

-20

-15

-10

-5

0

Widmo mocy dla ramki fonemu t

Częstotliwość [Hz]

M

o

c

[

d

B

]

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

10

20

30

40

50

60

70

80

90

100

Widmo predykcji liniowej dla ramki fonemu t

Częstotliwość [Hz]

H

(f

s

)

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

1

2

3

4

5

Widmo amplitudowe dla ramki fonemu u

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

-20

-15

-10

-5

0

Widmo mocy dla ramki fonemu u

Częstotliwość [Hz]

M

o

c

[

d

B

]

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

5

10

15

20

25

30

35

40

45

50

55

Widmo predykcji liniowej dla ramki fonemu u

Częstotliwość [Hz]

H

(f

s

)

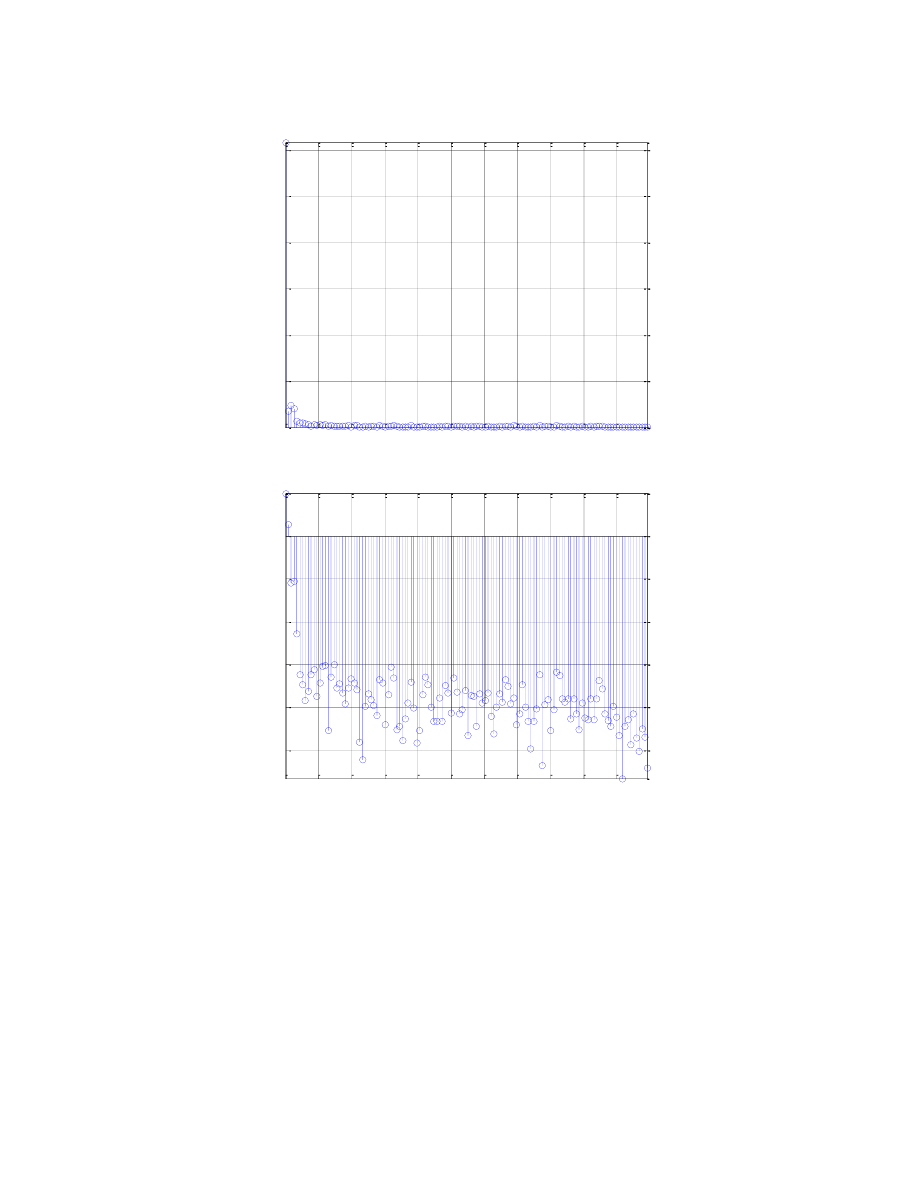
Samogłoska dźwięczna „u” charakteryzuje się dużą wartością widma amplitudowego w niskich

częstotliwościach (zbliżonych do częstotliwości formantowych), dla tego przedziału jest również
zaobserwowana moc dodatnia sygnału, jak i silna predykcja.

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

1

2

3

4

5

6

Widmo amplitudowe dla ramki fonemu k

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

-25

-20

-15

-10

-5

0

5

Widmo mocy dla ramki fonemu k

Częstotliwość [Hz]

M

o

c

[

d

B

]

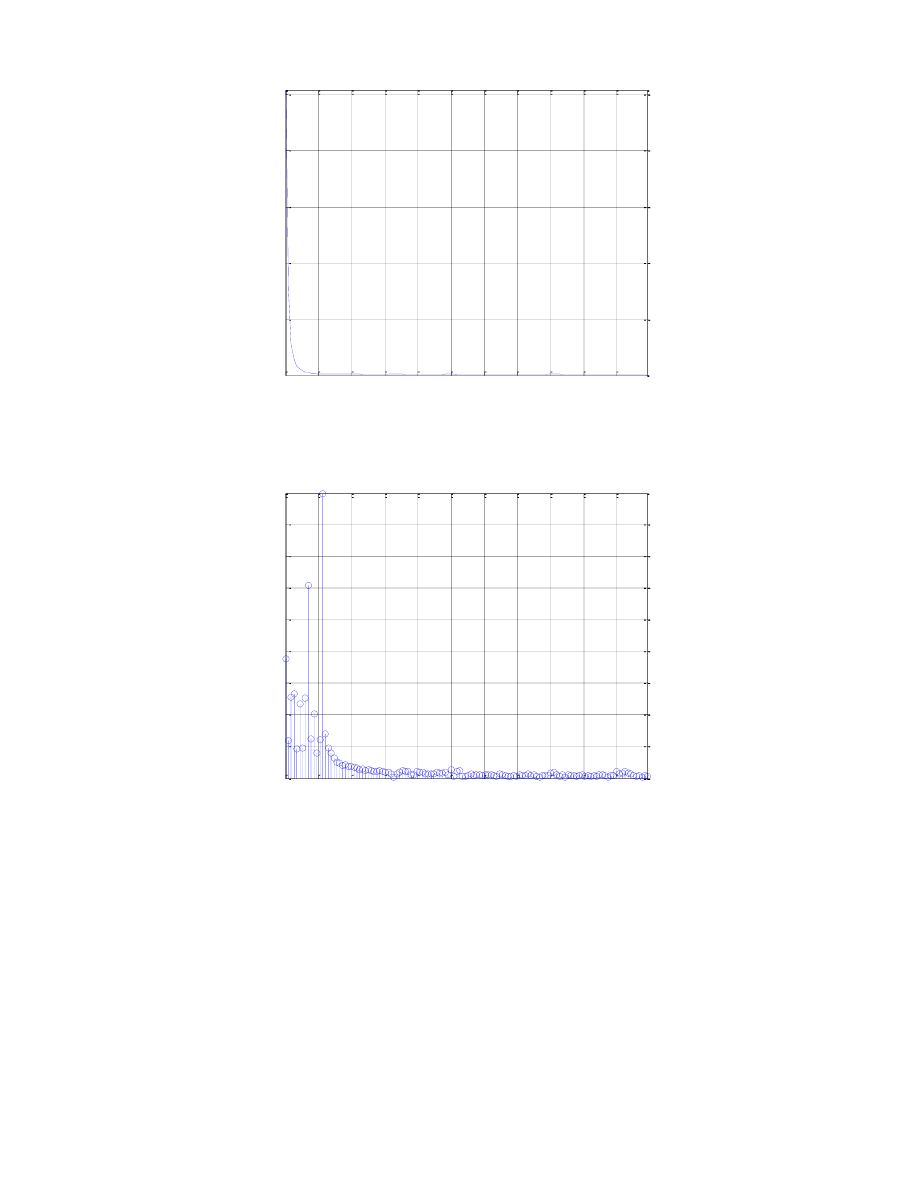
Dźwięk „k” daje podobne wyniki co „t” – obserwujemy niską wartość widma amplitudowego, bardzo duże moce
ujemne sygnału oraz zerowe wartości widma predykcji.

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

50

100

150

200

250

Widmo predykcji liniowej dla ramki fonemu k

Częstotliwość [Hz]

H

(f

s

)

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

1

2

3

4

5

6

7

8

Widmo amplitudowe dla ramki fonemu o

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

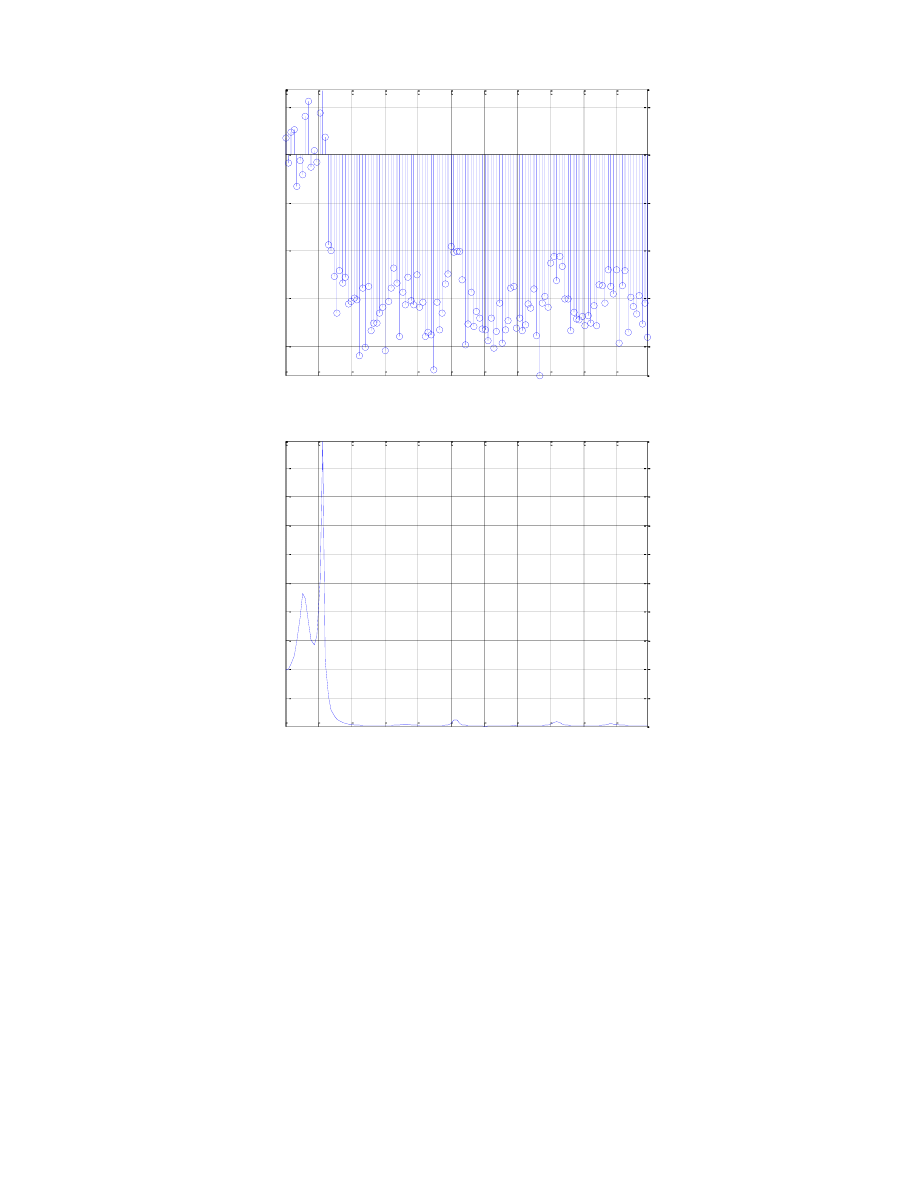
W widmie amplitudowym ramki zawierającej fragment fonemu o największe wartości możemy

zaobserwować w przedziale do 2kHz oraz nagły skok przy 3kHz, możemy się więc domyślać, iż tam
umiejscowione są częstotliwości formantowe. Zauważono również, iż są to miejsca o największej mocy
dodatniej bądź najmniejszej ujemnej wartości.

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

-20

-15

-10

-5

0

5

Widmo mocy dla ramki fonemu o

Częstotliwość [Hz]

M

o

c

[

d

B

]

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

10

20

30

40

50

60

70

80

90

Widmo predykcji liniowej dla ramki fonemu o

Częstotliwość [Hz]

H

(f

s

)

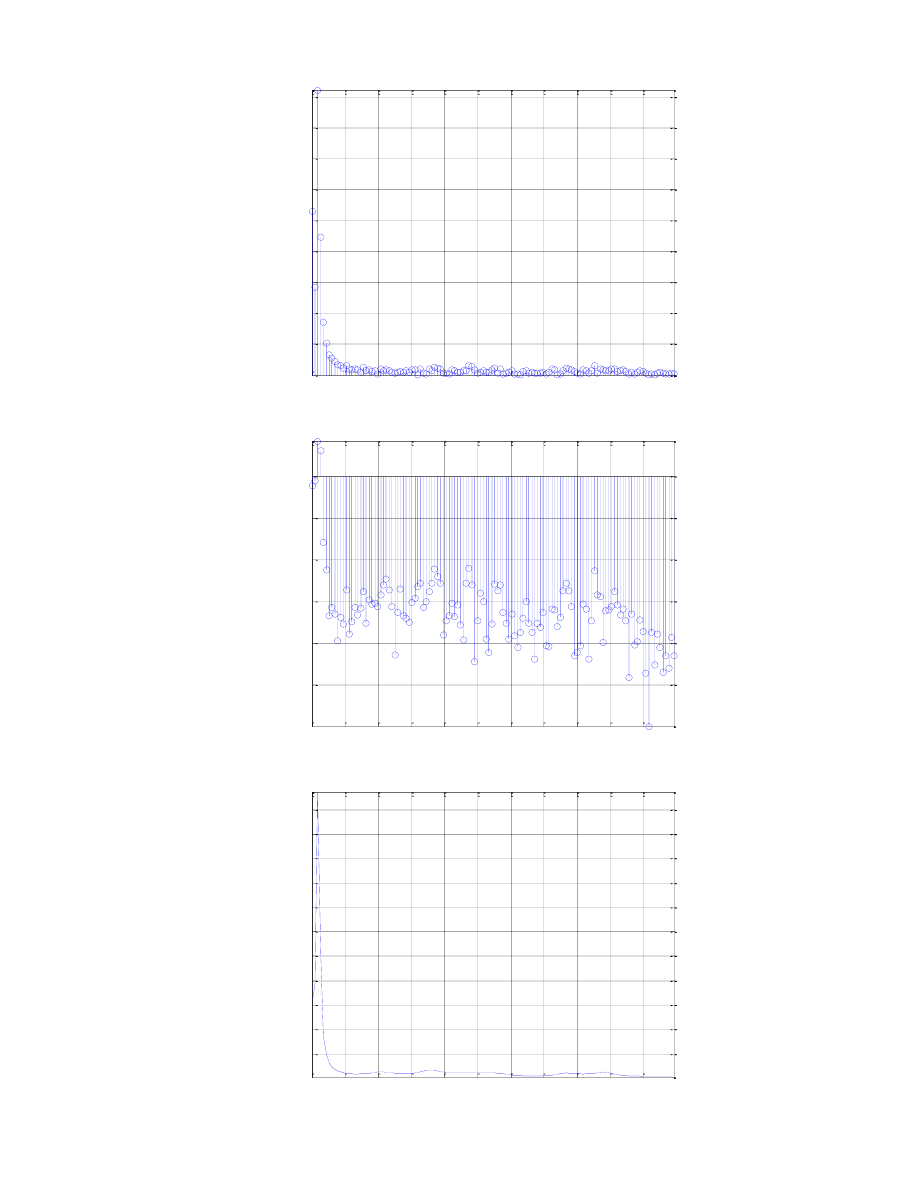
0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

Widmo amplitudowe dla ramki fonemu ń

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

-25

-20

-15

-10

-5

0

Widmo mocy dla ramki fonemu ń

Częstotliwość [Hz]

M

o

c

[

d

B

]

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

5

10

15

20

25

30

35

40

45

50

55

Widmo predykcji liniowej dla ramki fonemu ń

Częstotliwość [Hz]

H

(f

s

)

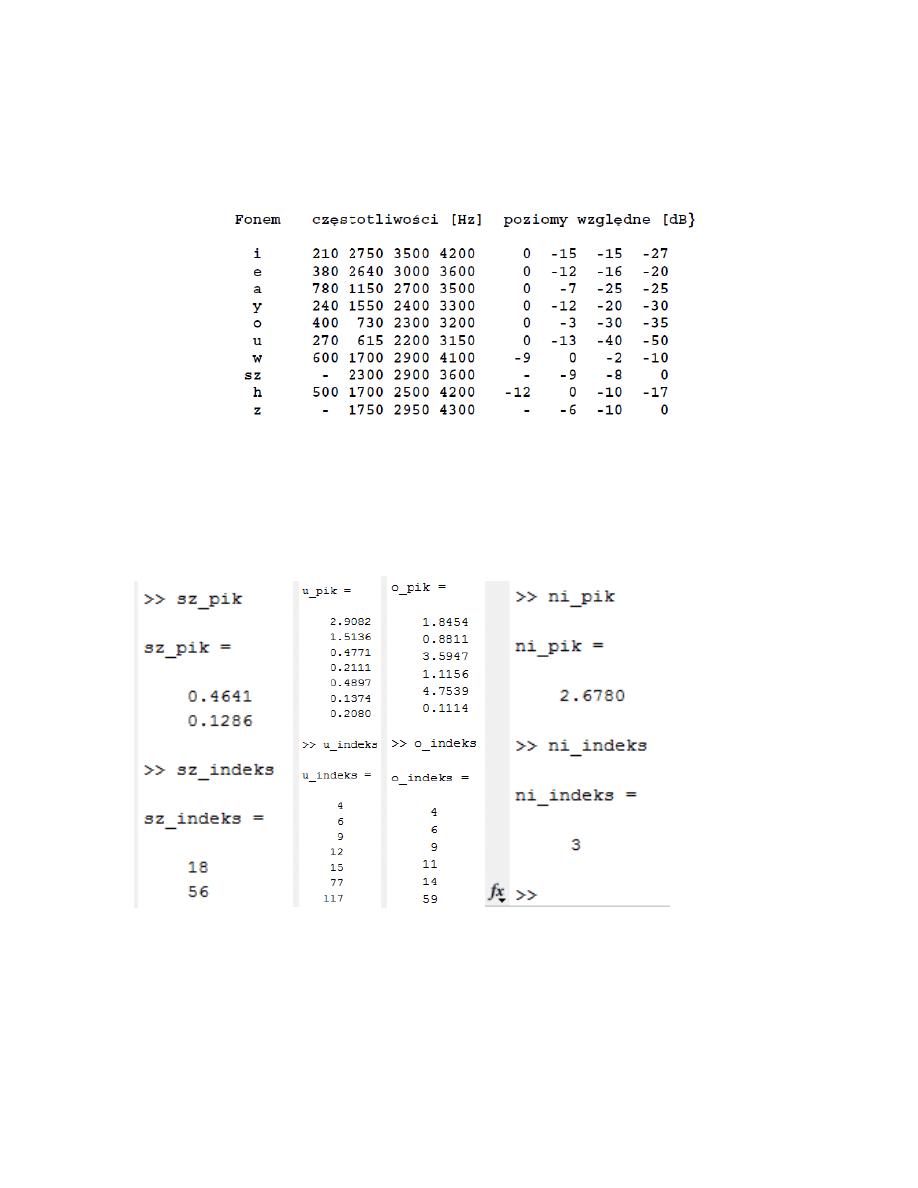
Ramka dla fragmentu fonemu „ń” charakteryzuje się najwyższymi wartościami widma amplitudowego w

przedziale do 1kHz, obserwujemy względne poziomy na mocy na stopie ok. -20dB oraz bardzo duże wyniki dla
widma predykcji liniowej we wspomnianym przedziale 1kHz.

Wyznaczenie częstotliwości formantowych opiera się na wyznaczeniu maksimów lokalnych dla obwiedni

widma amplitudowego i odpowiadających im częstotliwości. Głoski polskie posiadają 7 formantów, zaś w
praktyce ogranicza się do poszukiwania od 3 do 5. Oto tablica zawierająca informacje odnośnie częstotliwości,
na jakich występują formanty:

Zostały wyznaczone przedziały częstotliwości, w których mogą formanty występować, jednakże ich

pasma zachodzą na siebie, co dodatkowo utrudnia ich odszukanie. Jako że wcześniejsze wykresy potwierdziły,
iż nie wszystkie głoski posiadają częstotliwości formantowe, swoje poszukiwania ograniczyłam tylko do głosek
sz, u, o, ń. Wykorzystałam w tym celu wbudowaną funkcję programu Matlab, w której poszukuję w ramce
widma (właściwie w jego użytecznej połowie) wartości maksimów lokalnych, przy zastrzeżeniu odnośnie
wartości minimalnych pików i ich oddaleniu od siebie. Pobieram do dwóch wektorów wartość pierwszych 6
pików oraz ich indeksy.

Numer indeksu odnalezionego piku naleźy teraz przemnożyć przez skalę częstotliwościową, aby uzyskać

odnalezione piki (w przypadku branego pod uwagę widma jest to fs/256):

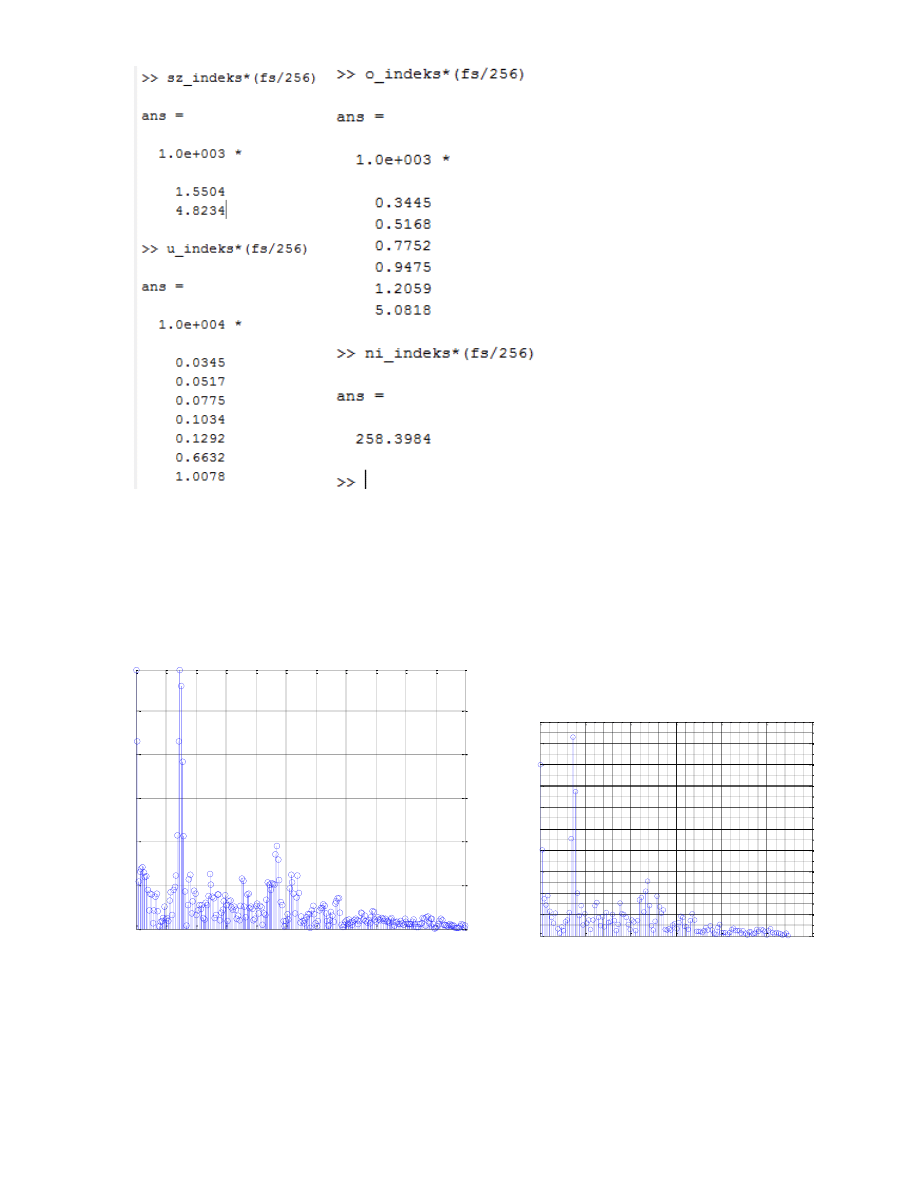
Dla uzyskanych wyników porównanie z wartościami odczytanymi z wykresów daje dosyć dobre

rezultaty, gdyż mimo nieznalezienia wszsystkich pików poprawnie, to dla prawidłowych dopasowań możemy
określić dokładną wartość. Należy nadmienić, iż ze względu na skalowanie częstotliwości, przedział pomyłki
wynosi +/- 40 Hz. Otrzymane wyniki obarczone są dosyć dużym prawdopodobieństwem złego dopasowania, gdyż
nie jest zapewniona dobra rozdzielczość ramki w dziedzinie częstotliwości. Dlatego też w kolejnym poleceniu
okno zostało rozszerzone do 512 próbek, przy czym 128 próbek o zerowej wartości zostaje umieszczonych
przed i po właściwym sygnale ramki. Należy zaznaczyć, iż formanty dobrze opisują głoski dźwięczne. Do
rozpoznawania np. głosek szeleszczących służą momenty widmowe.

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

0.1

0.2

0.3

0.4

0.5

Widmo amplitudowe dla ramki fonemu sz z oknem Hamminga równym 512

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

2000

4000

6000

8000

10000

12000

0

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] sz

Częstotliwość [Hz]

A

m

p

lit

u

d

a

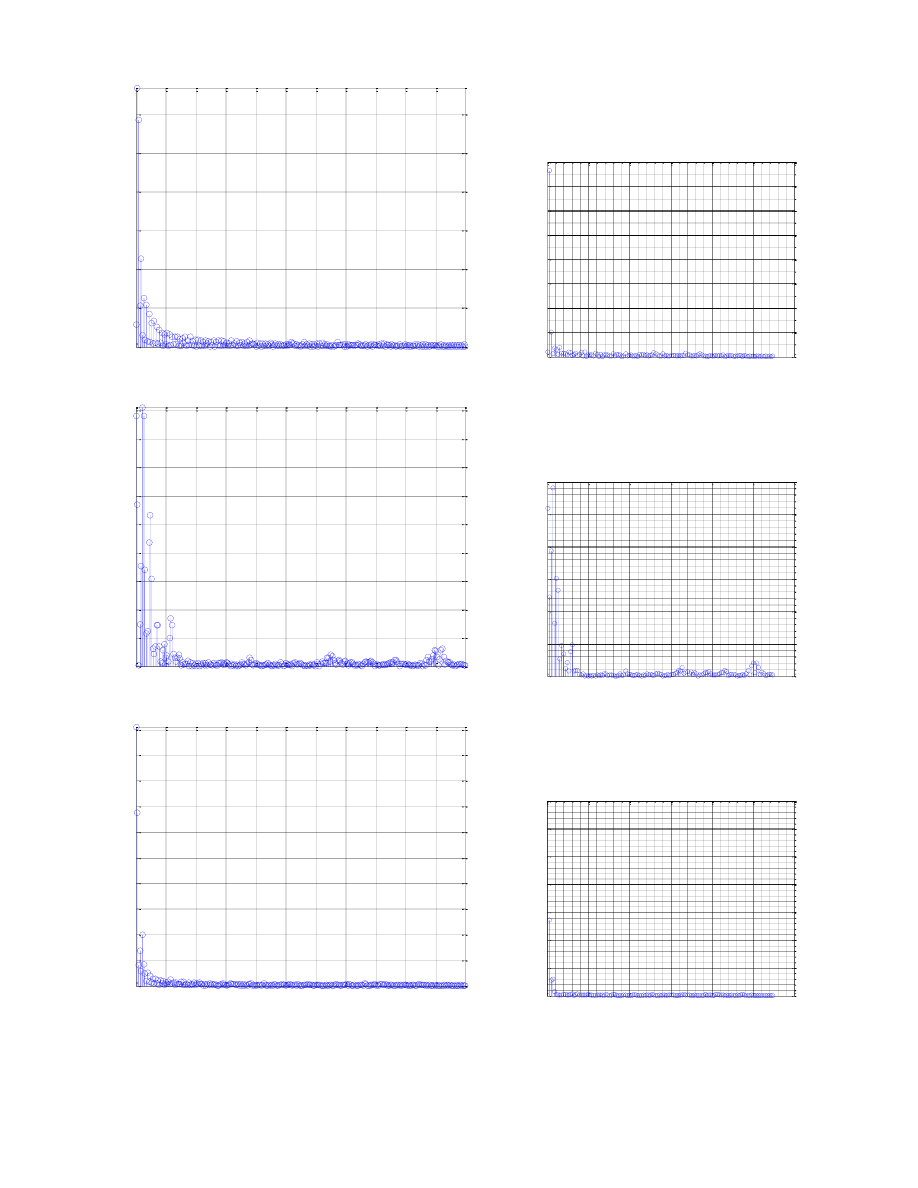
0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

0.5

1

1.5

2

2.5

3

Widmo amplitudowe dla ramki fonemu t z oknem Hamminga równym 512

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

2000

4000

6000

8000

10000

12000

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] t

Częstotliwość [Hz]

A

m

p

lit

u

d

a

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

Widmo amplitudowe dla ramki fonemu u z oknem Hamminga równym 512

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

2000

4000

6000

8000

10000

12000

0

0.5

1

1.5

2

2.5

3

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] u

Częstotliwość [Hz]

A

m

p

lit

u

d

a

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

5

Widmo amplitudowe dla ramki fonemu k z oknem Hamminga równym 512

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

2000

4000

6000

8000

10000

12000

0

0.5

1

1.5

2

2.5

3

3.5

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] k

Częstotliwość [Hz]

A

m

p

lit

u

d

a

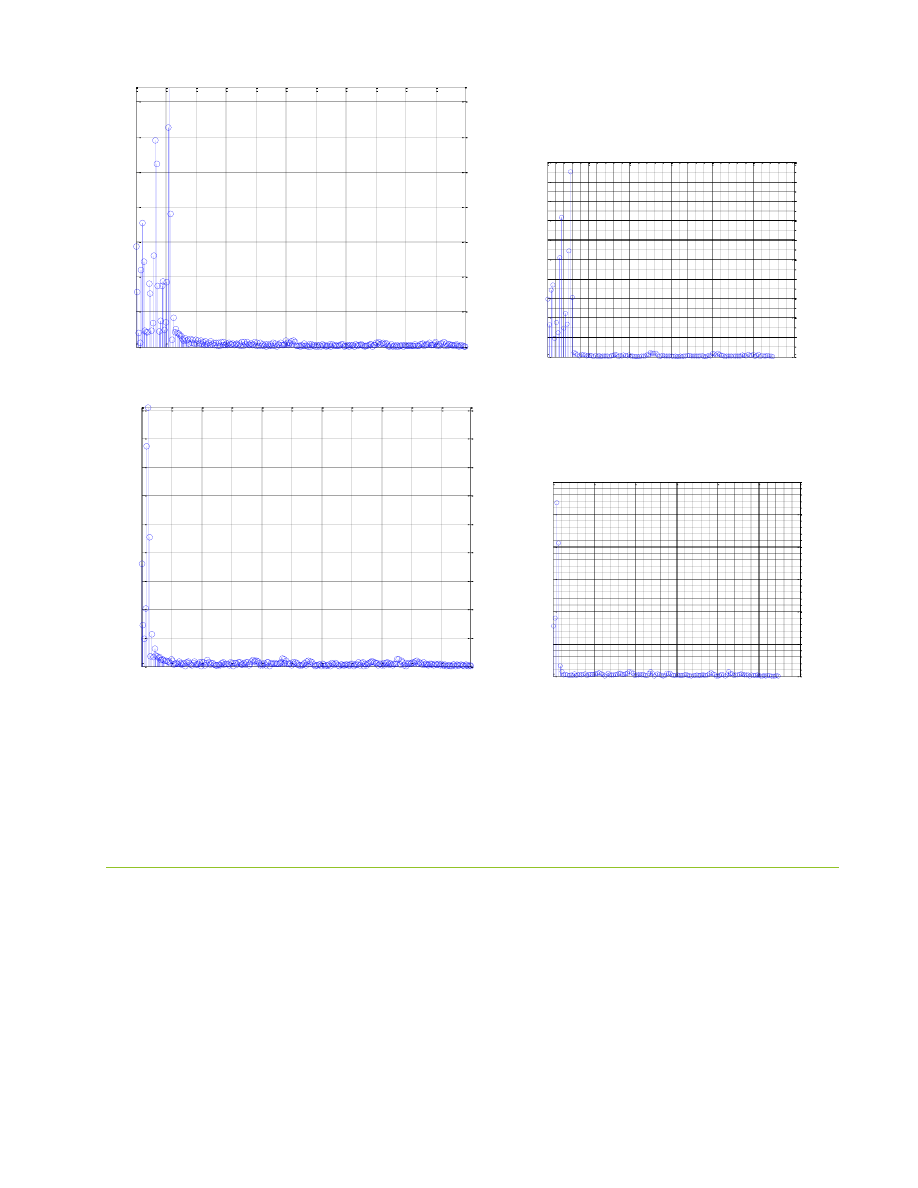
Po dodaniu 256 próbek zerowych na pierwszy rzut oka wykresy nie zmieniły się, jednak po dokładnym

przyjrzeniu można zauważyć, iż amplituda wzrosła dwukrotnie, niektóre z prążków już nie osiągają tak
wysokich wartości. Świadczyć to może o wpływie zakłóceń na badany sygnał, ponieważ praktyka dodawania
nadmiarowych próbek jest prowadzona właśnie po to, aby zapewnić lepszą rozdzielczość wykresów w
dziedzinie częstotliwości, a tym samym umożliwić bardziej dokładne określenie częstotliwości formantowych.

5. PODSUMOWANIE

Drugie ćwiczenie laboratoryjne miało za zadanie zaznajomienie przeprowadzających z technikami

stosowanymi w analizie mowy a także trudnościach, jakie napotyka się w drodze do prawidłowych odczytów.
Nagranie jest bowiem niezwykle podatne na wszelkiego rodzaju zniekształcenia płynące z otaczających
nagrywającego dźwięk szumów otoczenia. O ile odszukanie częstotliwości formantowych dla samogłosek
powiodło się, o tyle inne formanty nie były już na tyle czytelne do zdiagnozowania.

Ogromnym problemem w rozpoznawaniu mowy jest również fakt, iż ten sam dźwięk wypowiedziany

dwa razy może dawać zupełnie inne rezultaty. Parametry wyliczone w tym ćwiczeniu są specyficzne dla każdej
osoby, i aby osiągnąć dobre wyniki w rozpoznawaniu mówcy, nie należy ich wyliczać tylko na podstawie jednej
próbki dźwiękowej.

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

1

2

3

4

5

6

7

Widmo amplitudowe dla ramki fonemu o z oknem Hamminga równym 512

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

2000

4000

6000

8000

10000

12000

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

5

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] o

Częstotliwość [Hz]

A

m

p

lit

u

d

a

0

1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

Widmo amplitudowe dla ramki fonemu ń z oknem Hamminga równym 512

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]

0

2000

4000

6000

8000

10000

12000

0

0.5

1

1.5

2

2.5

3

Widmo amplitudowe dla częstotliwości z zakresu [0;fs/2] ń

Częstotliwość [Hz]

A

m

p

lit

u

d

a

[

V

]