METODY PORÓWNANIA WIELKOSCI MIERZONEJ

Z WZORCEM

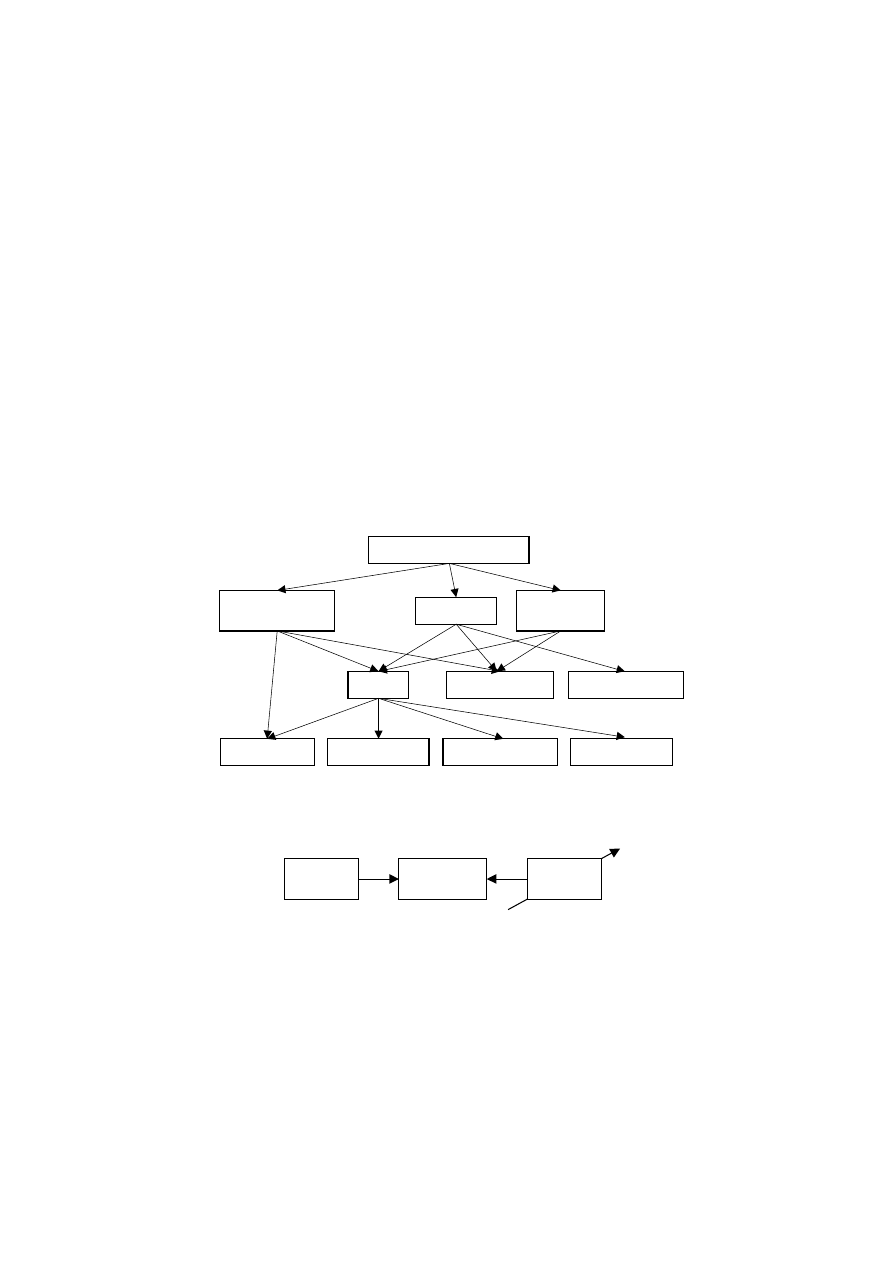
Klasyfikacja ze względu na zasadę pomiaru (rys. 2.1)

Metoda pomiarowa bezpośredniego porównania

Metoda pomiarowa bezpośredniego porównania polega na porówna-

niu wartości wielkości mierzonej z wartością znaną tej samej wielkości,
która w postaci wzorca wchodzi bezpośrednio do pomiaru. Zasadę tę
przedstawiono na rys.2.2.

Podstawienia

Przestawienia

Kompensacyjna

Komparacyjna

Zerowa

Wychyleniowa

Koincydencyjna

Bezpośredniego

porównania

Różnicowa

Pośredniego

porównania

Metody porównawcze

Rys.2.1. Klasyfikacja metod pomiarowych

Wielkość

mierzona

Układ

porównania

Wzorzec

nastawny

X

m

X

W

Rys.2.2. Zasada porównania bezpośredniego

Nastawę wartości wzorca prowadzi się do momentu, w którym układ po-
równania wskaże równość wartości mierzonej i wzorcowej, czyli

2

X

m

= X

WO

(2.1)

gdzie:

X

WO

- wartość wzorca X

W

, dla której układ porównania wskaże

równość X

m

i X

WO

.

Przyjmując, że wzorzec X

W

jest regulowany w sposób ciągły oraz, że

układ porównania wskaże dokładnie równość X

m

i X

WO

, błąd pomiaru

jest wówczas równy

∆X

m

=

∆X

W

+

∆X

S

(2.2)

gdzie:

∆X

W

- błąd wykonania wzorca,

∆X

s

- błąd niesymetrii układu porównania wyznaczony w metodzie

przestawienia.

Zależność (2.2) jest słuszna dla idealnego układu pomiarowego. W

rzeczywistym układzie pomiarowym wzorzec jest nastawiany w sposób
skokowy. Minimalną zmianę

∆Z wartości nastawianego wzorca nazywa

się rozdzielczością wzorca. Rozdzielczość wzorca

∆Z powoduje, że w

zasadzie nie jest możliwe otrzymanie dokładnej równości X

m

= X

WO

. Za

wartość mierzoną X

m

przyjmuje się więc te wartość X

WO

, dla której war-

tość bezwzględna różnicy |X

m

- X

W

| przyjmuje wartość najmniejszą ze

wszystkich możliwych nastawień wzorca X

W

. Przyjęcie, że X

m

= X

WO

mimo, że X

m

≠ X

WO

jest przyczyną powstawania błędu systematycznego

granicznego rozdzielczości, który jest równy

2

Z

X

Wr

∆

=

∆

(2.3)

W rzeczywistym układzie pomiarowym układ porównania może

wskazać zero już przy pewnej różnicy X

m

- X

WO

≠ 0. Maksymalna war-

tość tej różnicy, dla której układ porównania wskaże zero, jest nazywana
błędem pobudliwości (

∆X

pob

) (dawniej błędem nieczułości). Stąd całkowi-

ty błąd pomiaru w rzeczywistym układzie pomiarowym jest równy

∆X

m

=

∆X

W

+

∆X

S

+

∆X

Wr

+

∆X

pob

(2.4)

W większości przypadków dla żadnej wartości X

W

wzorca nastawne-

go układ porównania nie wskaże zero. Można wówczas przyjąć za war-
tość mierzoną X

m

taką wartość wzorca X

WO

, dla której różnica |X

m

- X

WO

|

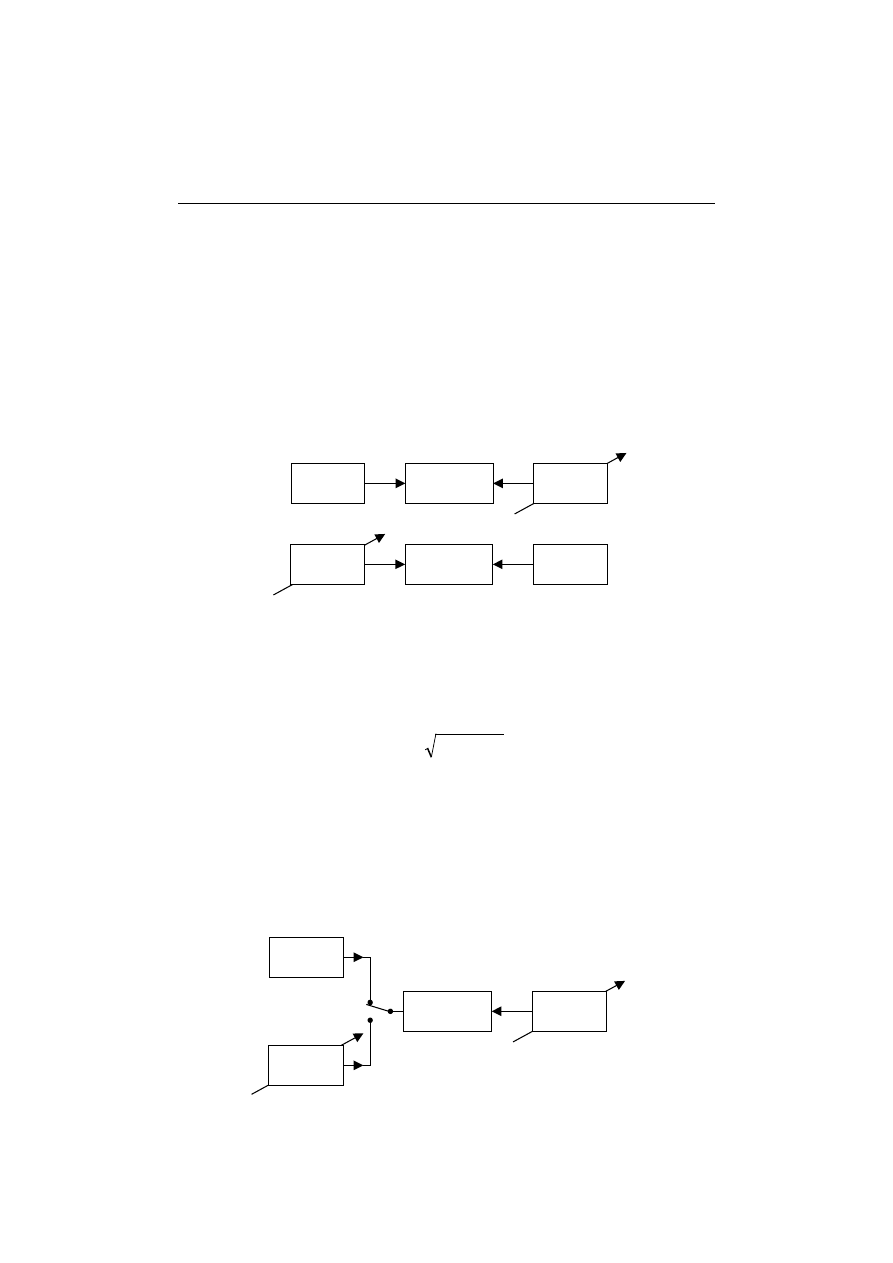
3

jest najmniejsza. Błąd pomiaru X

m

oblicza się wówczas z zależności

(2.4).

Występujący w metodzie pomiarowej bezpośredniego porówna-

nia błąd niesymetrii układu porównania (

∆X

S

) można zmniejszyć

stosując metodę przestawienia lub metodę podstawienia.

Metoda przestawienia (rys.2.3) polega na zrównoważeniu wartości

wielkości mierzonej najpierw za pomocą znanej wartości X

W1

tej wielko-

ści, następnie na przestawieniu wielkości mierzonej X

m

w miejsce wzor-

ca X

W

i ponownym zrównoważeniu jej znaną wartością X

W2

tej samej

wielkości.

Wielkość

mierzona

Układ

porównania

Wzorzec

nastawny

X

m

X

W

Wielkość

mierzona

Układ

porównania

Wzorzec

nastawny

X

W

X

m

Rys.2.3. Zasada pomiaru metodą przestawienia

Jeżeli układ porównania jest symetryczny (

∆X

S

= 0) to X

m

= X

W1

= X

W2

.

Natomiast jeżeli układ porównania jest niesymetryczny (X

W1

≠ X

W2

), to

wynik pomiaru wielkości X

m

jest średnią geometryczną z obu pomiarów

2

1

W

W

m

X

X

X

=

(2.7)

Metoda podstawienia polega na zastąpieniu wartości wielkości mie-
rzonej wartością znaną tej samej wielkości, wybraną w ten sposób, aby
skutki wywołane przez te dwie wartości były takie same. Na rys.2.4
przedstawiono zasadę pomiaru metodą podstawienia z wzorcem taro-
wym. W pierwszym etapie pomiaru do wejścia układu porównania

Wielkość

mierzona

Układ

porównania

Wzorzec

tarowy

X

m

X

T

Wzorzec

nastawny X

W

P

1

2

4

Rys.2.4. Zasada pomiaru metodą podstawienia z wzorcem tarowym

przyłącza się wielkość mierzoną X

m

(przełącznik P w pozycji 1). Wzo-

rzec tarowy nastawia się tak, aby otrzymać równowagę układu porów-
nania (X

m

= X

T1

). W drugim etapie pomiaru do wejścia układu porówna-

nia przyłącza się wzorzec nastawny X

W

(przełącznik P w pozycji 2) i na-

stawia się go na wartość X

WO

, dla której układ porównania wskazuje

stan równowagi. Wtedy X

WO

= X

T1

.

Jeżeli w obu fazach pomiaru wartość wzorca tarowego była stała, to

wartość zmierzona X

m

jest równa

X

m

= X

T1

= X

WO

(2.11)

a jej błąd pomiaru można wyznaczyć z zależności

∆X

m

=

∆X

W

+

∆X

Tr

+

∆X

Wr

+ 2

∆X

pob

(2.12)

gdzie

∆X

Tr

jest błędem rozdzielczości wzorca tarowego.

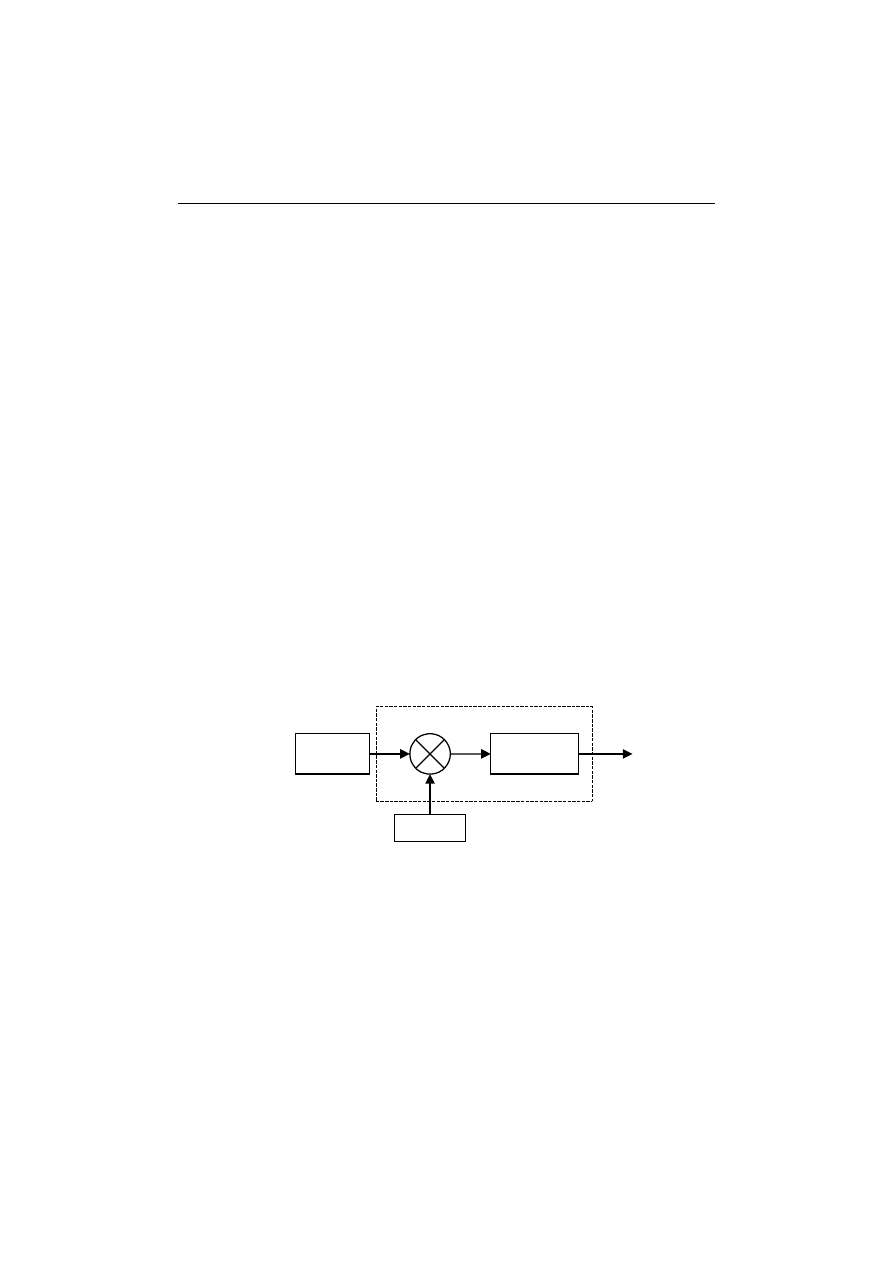
Metoda różnicowa

Metoda pomiarowa różnicowa polega na porównaniu wartości wielko-

ści mierzonej X

m

z niewiele różniąca się od niej znaną wartością tej sa-

mej wielkości X

W

i pomiarze różnicy r tych wartości (najczęściej metodą

wychyleniową). Zasadę tej metody przedstawiono na rys.2.5.

Wielkość

mierzona

Przyrząd

pomiarowy

X

m

X

W

Wzorzec

r=X

m

-X

W

y=f(r)

Układ porównania

Rys.2.5. Zasada pomiaru metodą różnicową

Wartość mierzona X

m

jest wówczas równa

X

m

= X

W

+ r (2.13)

a błąd bezwzględny jej pomiaru jest określony zależnością

∆X

m

=

∆X

W

+

∆r + ∆X

S

(2.14)

5

gdzie:

∆r - błąd pomiaru różnicy r.

Przyjmując, że błąd niesymetrii układu porównania jest równy zero, a
wartość wielkości mierzonej X

m

jest bliska wartości wielkości wzorcowej

X

W

(czyli IrI << X

W

) oraz wartość różnicy r jest mierzona przyrządem

wskazówkowym to błąd systematyczny pomiaru wielkości X

m

jest równy

r

m

Xw

Xm

X

r

δ

δ

δ

+

=

(2.15)

gdzie:

δ

Xw

- błąd względny wzorca,

δ

r

- błąd przyrządu do pomiaru różnicy r

Z zależności (2.15) wynika, że błąd przyrządu pomiarowego będzie

nieznacznie wpływał na błąd pomiaru X

m

, jeżeli stosunek.

1

〈〈

m

X

r

. Przy

spełnieniu tego warunku przyrząd pomiarowy może być znacznie mniej
dokładny niż wzorzec.

Metody różnicowe, umożliwiające uzyskanie dokładnych wyników,

znajdują zastosowanie w różnych gałęziach techniki, zwłaszcza w po-
miarach wielkości nieelektrycznych sposobami elektrycznymi. Przyrzą-
dami mierzącymi metodą różnicowa mogą być: waga odważnikowo-
uchylna, mostki niezrównoważone itp.

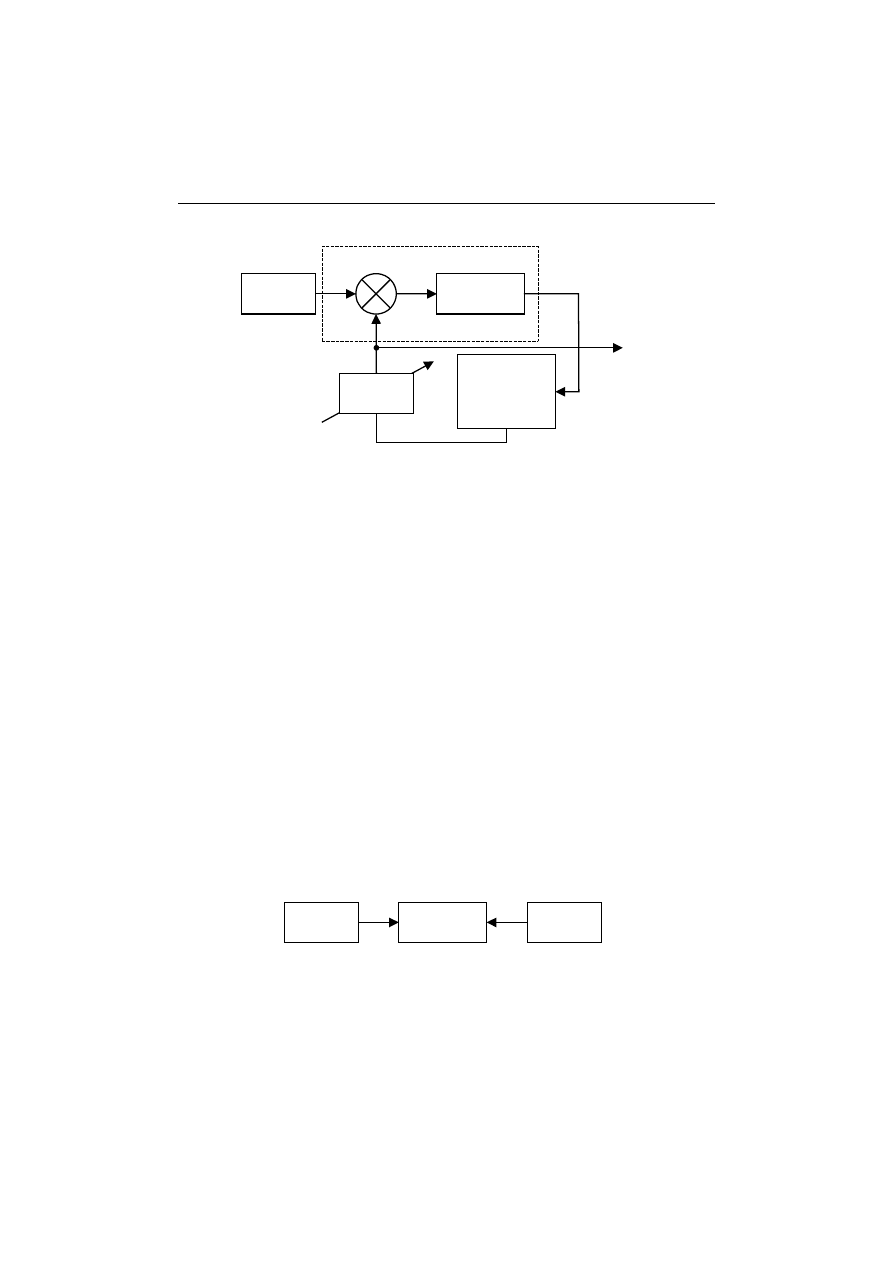
Metoda zerowa.

Metoda zerowa stanowi przypadek szczególny metody różnicowej.

Polega ona na sprowadzeniu do zera różnicy r między wartością wielko-
ści mierzonej X

m

, a znaną, nastawianą wartością wzorca X

W

tej samej

wielkości z nią porównywanej (rys.2.6). Nastawy wzorca X

W

ustalane są

ręcznie przez obserwatora lub automatycznie przez urządzenie wyko-
nawcze na podstawie wskazań wskaźnika zera. W chwili, gdy wskaźnik
zera wskaże zero (r = 0) wówczas wartość wielkości mierzonej X

m

jest

równa nastawionej wartości wzorca X

W.

6

Wielkość

mierzona

Wskaźnik

zera

X

m

X

W

r=X

m

-X

W

y=X

W

Obserwator

lub

urządzenie

wykonawcze

r

Wzorzec

nastawny

Układ porównania

Rys.2.6. Zasada pomiaru metodą zerową

Czynności związane ze sprowadzeniem do zera różnicy r = X

m

- X

W

nazywane są równoważeniem układu. Dokładność pomiaru wykonanego
metodą zerową zależy głównie od dokładności wielkości wzorcowej i od
właściwości układu pomiarowego.

Metoda zerowa jest metodą najczęściej stosowaną w metodach bez-

pośredniego porównania. Stąd przedstawione w pkt.2.2 rozważania od-
nośnie dokładności pomiaru dotyczą również metody zerowej. Metody
zerowe należą do tej grupy metod pomiarowych, w których można osią-
gnąć największe dokładności pomiaru wielkości mierzonej X

m

. W mier-

nictwie elektrycznym typowym przykładem metody zerowej są mostki
zrównoważone. Metoda zerowa oraz przedstawiona wcześniej metoda
różnicowa są przykładami porównania jednoczesnego wielkości mierzo-
nej z wzorcem.

Metoda kompensacyjna

Kompensacyjna metoda pomiaru wielkości fizycznych należy do me-

tod zerowych i polega na skompensowaniu skutków działania wielkości
mierzonej X

m

wielkością wzorcowa X

W

równą co do wartości i przeciwną

co do znaku; X

m

= X

W

(rys.2.7).

Wielkość
mierzona

Wskaźnik

zera

Wielkość

wzorcowa

X

m

X

W

Rys.2.7. Zasada pomiaru metodą kompensacyjną.

7

Metodami kompensacyjnymi można mierzyć wielkości fizyczne tego

samego rodzaju, będące nośnikami energii i mające charakter wektoro-
wy, np.: siły, napięcia. W metodzie kompensacyjnej wyróżnia się nastę-
pujące stany:
• X

m

= X

W

lub X

m

- X

W

= 0 - równowaga kompensacyjna, w stanie

kompensacji przyrząd (kompensator) nie pobiera energii z ukła-
du badanego, co jest zaletą tej metody,

• X

m

> X

W

- niedokompensowanie, przyrząd pobiera energię z układu

badanego,

•

X

m

< X

W

- przekompensowanie, przyrząd pobiera energię z układu

wzorcowego.

W

metodzie komparacyjnej porównuje się bezpośrednio wiel-

kość mierzoną X

m

ze znaną krotnością k wielkości wzorcowej X

w

.

Badając różnicę X

m

- kX

w

sprowadza się ją do zera przez regula-

cję współczynnika k. Dla stanu równowagi wartość wielkości mie-
rzonej oblicza się ze wzoru X

m

= kX

w

. Praktyczne znaczenie tej

metody polega na zastosowaniu wzorca odtwarzającego tylko
jedną wartość X

w

( wzorca jednomiarowego), a więc wzorca o

większej dokładności niż wzorce odtwarzające wiele wartości
(wzorce wielomiarowe).

Metoda wychyleniowa - polega na przetworzeniu wielkości mie-
rzonej na przesunięcie wskazówki względem podziałki.


Metoda pośredniego porównania

Dla wielu wielkości fizycznych nie ma układów porównań reagu-
jących na wartość lub różnicę wartości. Przetwarza się wówczas
wielkość mierzoną X

m

i wzorcową X

w

na inną wielkość, dla której

są takie układy.
Np. nie ma układów bezpośrednio reagujących na różnicę mas
(masę). Masa jednak w sposób naturalny jest przetwarzana w polu
grawitacyjnym Ziemi na siłę, którą mierzymy.

8

Wielkość

mierzona

Y=f(X

M

)

Układ

porównania

X

m

Y

m

Y

w

Wzorzec

nastawny

Rys. 2.8. Zasada porównania pośredniego: X

m

, X

w

- takie

same

wielkości, Y = f(X

w

) , Y = f(X

m

) - takie same przetworniki

wielkości

Ponieważ f( ) jest funkcją monotoniczną, z równania Y

m

=Y

w

otrzy-

muje się X

m

=X

w

.

Błąd pomiaru – jak w metodzie porównania bezpośredniego do-
datkowo powiększony o błędy wynikające z przetwarzania wielko-
ści.

Przykład: Pomiar masy za pomocą wagi dwuszalkowej na pod-
stawie zależności M=F

⋅l = m⋅g⋅l (M – moment siły)