1

Ćwiczenia 7

W. Chemii, semestr 1, 2009/10

1. Energia kinetyczna. Energia potencjalna. Zasada zachowania energii mechanicznej.

Uważnie przeczytaj wykład 5. Przypomnij sobie wzory całek podanych funkcji – będą Ci potrzebne do
rozwiązania zadao. Spróbuj samodzielnie zrobid przykłady z wykładu, a następnie przystąp do rozwiązy-
wania poniższych zadao.

1. Znajdź energię potencjalną w: a. polu elektrostatycznym, w którym na ładunek punktowy działa siła pocho-

dząca od ładunku punktowego dana wzorem Coulomba

stała; b. w polu grawitacyjnym we-

wnątrz tunelu przechodzącego przez środek planety X o masie i promieniu , gdzie na masę w odległości

od środka planety działa siła

( energię licz względem powierzchni planety i przyjmij

); c. w polu sił quasi sprężystych

.

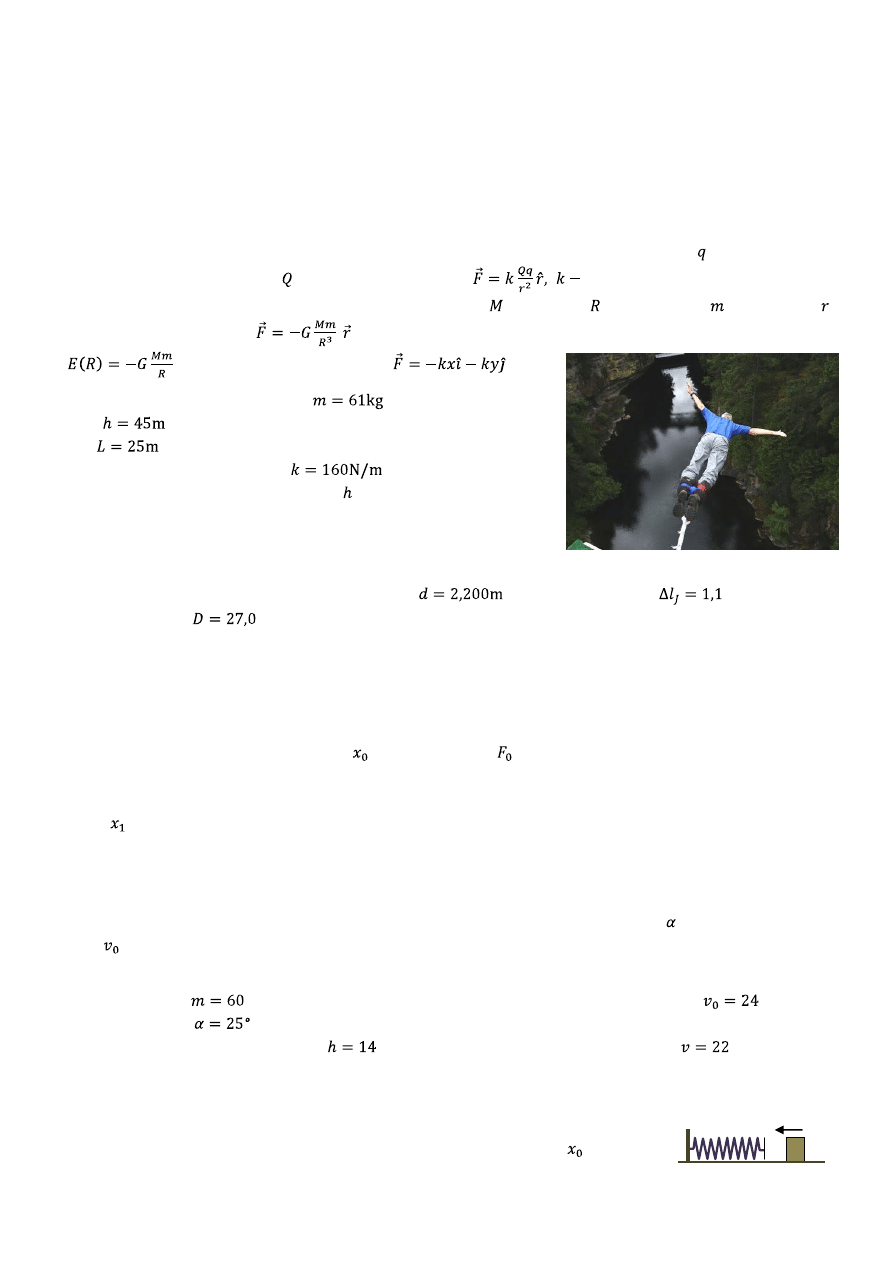
2. Skoczek na linie bungee ma masę

i stoi na moście o wyso-

kości

nad wodą. Długośd nieodkształconej sprężystej liny wy-

nosi

. Przyjmij, że odkształcenie liny spełnia prawo Hooke’a, a

stała sprężystości liny jest równa

. W czasie skoku skoczek

nie wpada do wody. Wyznacz wysokośd stóp skoczka nad wodą, gdy
znajduje się on najbliżej wody.

3. Dwoje dzieci bawi się w ten sposób, że starają się trafid kulką kamien-
ną w małe pudełko leżące na podłodze. Kulka jest wystrzeliwana a ustawionej na stole wyrzutni sprężynowej.
Pudełko jest odległe w poziomie od krawędzi stołu o

. Jaś ścisnął sprężynę o

cm, lecz kulka

upadła na podłogę

cm przed środkiem pudełka. O jaki odcinek musi ścisnąd sprężynę Małgosia, aby trafid

w środek pudełka? Wszelkie opory ruchu zaniedbaj.

4. Jaś wylądował na równiku nieznanej planety, której promieo wynosił R=3560 km. Kiedy podskoczył w górę z
szybkością v

0

=3,00m/s, wzniósł się na wysokośd h=0,570m. (a) Ile wynosiła masa planety? (b) Gdyby uwzględnid

ruch planety wokół własnej osi i to, że doba planetarna trwa 10,0h, to na jaka wysokośd wzniósłby się Jaś?

5. Nieważka sprężyna może byd ściśnięta o pod wpływem siły . Ta sama sprężyna została umieszczona przy
podstawie doskonale gładkiej równi pochyłej, o kącie nachylenia



. Ciało o masie M, pozostające początkowo w

spoczynku na szczycie równi, zaczyna ześlizgiwad się w dół. Ciało to zatrzymuje się natychmiast po ściśnięciu sprę-
żyny o . (a) Jaką odległośd przebywa ciało do chwili zatrzymania się? (b) Jaką prędkośd ma to ciało bezpośrednio
przed zetknięciem ze sprężyną?

2. Energia mechaniczna, praca sił niezachowawczych

1. Ciało o masie m pchnięto w górę po równi pochyłej, nachylonej do poziomu pod kątem , z szybkością począt-
kową . Okazało się, ze ciało przebyło drogę s, zatrzymało się i ześliznęło w dół. Obliczyd współczynnik tarcia f
oraz szybkośd ciała przy podstawie równi.

2. Małysz (o masie

kg) ma przy odbiciu z progu skoczni narciarskiej prędkośd o wartości

m/s, skie-

rowaną pod kątem

w górę od poziomu. Na skoczka działa siłą oporu powietrza, w wyniku czego w chwili

lądowania w punkcie leżącym w pionie

m niżej od progu, ma on prędkośd o wartości

m/s. O ile

zmniejszyła się pod wpływem oporu powietrza energia mechaniczna układu narciarz-Ziemia w czasie jego lotu, od
wybicia z progu do lądowania na zeskoku?

3. Sprężyna o współczynniku sprężystości k, której masę pomijamy, umocowana jest po-
ziomo. Ze sprężyną tą zderza się ciało o masie m powodując jej ściśnięcie o , licząc od

2

położenia równowagi. Obliczyd prędkośd ciała w chwili zderzenia, jeśli współczynnik tarcia kinetycznego między
ciałem a poziomą powierzchnią, równy jest f.

3. Zasada zachowania pędu i energii mechanicznej

1. Kula drewniana o masie M ułożona została na metalowym pierścieniu zamocowanym w statywie. Z dołu w kulę
trafia pocisk o masie m lecący pionowo do góry i przebija ją. W wyniku tego zderzenia kula podnosi się na wyso-
kośd h. Na jaką wysokośd H podniesie się pocisk, jeśli jego szybkośd przed zde-
rzeniem wynosiła .

2. Rysunek przedstawia wahadło balistyczne służące do pomiaru prędkości
pocisków. Kula o masie m

k

wystrzelona poziomo uderza z szybkością v

0

w

drewniany blok o masie M. Zderzenie jest całkowicie niesprężyste, a blok wy-
chyla się na wysokośd h. Znając wartości: m

k

, M, h oblicz energię kinetyczną

kuli i porównaj ją z energią kinetyczną układu po zderzeniu. Czy w czasie zde-
rzenia energia kinetyczna, ew. mechaniczna jest zachowana?

3

.

Doskonały karateka łamie drewnianą deskę o masie

kg uderzając w nią z góry pięścią o masie

kg. Stała sprężystości deski wynosi

N/m. Deska pęka przy jej wygięciu o

mm. a.Ile

wynosi energia zgromadzona w desce tuż przed jej złamaniem? b. Ile wynosi najmniejsza prędkośd pięści potrzeb-
na do złamania deski? Załóż, że zderzenie jest niesprężyste, biorą w nim udział jedynie pięśd i deska, zginanie de-
ski zaczyna się tuż po zderzeniu, podczas zginania przedmiotu zachowywana jest energia mechaniczna, a gdy
przedmiot zaczyna pękad, prędkości pięści i deski są praktycznie równe zeru.

4. W przestrzeni kosmicznej doszło do niesprężystego zderzenia meteorytu
o masie

=20,0kg z satelitą o masie

=500kg . Znajdź wektor prędkości

satelity , jeśli wartośd prędkości meteorytu wynosiła 1000m/s, a po
zderzeniu (meteoryt ugrzązł w satelicie) wrak satelity poruszał się z szybko-
ścią 66,6m/s pod kątem 30

o

do kierunku początkowego ruchu meteorytu.

Na następne zajęcia proszę zrobić powyższe zadania oraz nauczyć się materiału z wykładu 5.

Literatura

D.Halliday,R.Resnick,J.Walker: Podstawy fizyki, t.1.
(podręcznik polecany – z niego są zaczerpnięte niektóre tematy zadao)
B.Oleś: Wykłady z fizyki , Wydawnictwo PK

A.Januszajtis: Fizyka dla politechnik, t.1

Pytania i zagadnienia, które mogą pojawić się na egzaminie pisemnym

1. Zasada zachowania energii mechanicznej. a. Wyprowadź wzór na energię kinetyczną ciała.(2p) b. Zdefiniuj ener-
gię potencjalną. Podaj wyrażenie na energię potencjalną. (2p) c. Wyprowadź i sformułuj zasadę zachowania energii
mechanicznej.(3p) d. Oblicz energię potencjalną meteorytu o masie m znajdującego się w odległości 3R od środka
Ziemi. Jeśli meteoryt w odległości 3R od środka Ziemi posiada prędkość , to ile wyniesie wartość jego prędkości w
momencie uderzenia o Ziemię? (3p

)

2. Zasada zachowania energii mechanicznej. a. Zdefiniuj energię mechaniczną (podaj wyrażenie na energię kine-
tyczną i energię potencjalną). (2p) b. Wyprowadź i sformułuj zasadę zachowania energii mechanicznej.(3p) c. Znajdź

m

2

m

1

3

wyrażenie na sprężystą energię potencjalną. Rozważ oscylator harmoniczny i wykaż, że przy zaniedbaniu tłumienia
jego energia mechaniczna jest zachowana. (4p) e. Narysuj wykresy funkcji

,

i

dla przypadku oscy-

latora harmonicznego. (1p)

3. Zasada zachowania pędu. a. Zdefiniuj pęd i wyraź drugą zasadę dynamiki poprzez zmianę pędu. Uzasadnij, że ta
postać jest bardziej ogólna od poznanej wcześniej. (3p) b. Wyprowadź i sformułuj zasadę zachowania pędu (1) poje-
dynczej cząstki i (2) układu cząstek. (4p) c. Zapisz zasadę zachowania pędu dla sprężystego, niecentralnego zde-
rzenia dwóch kul: kula o masie m

1

i prędkości uderza w spoczywającą kulę o masie m

2

. Po zderzeniu kule po-

ruszają się odpowiednio z prędkościami i , tworzącymi kąty



i



z początkowym kierunkiem ruchu kuli nr 1

(Zapisz równanie najpierw w postaci wektorowej, potem równania skalarne dla współrzędnych wektorów pędu). (3p)