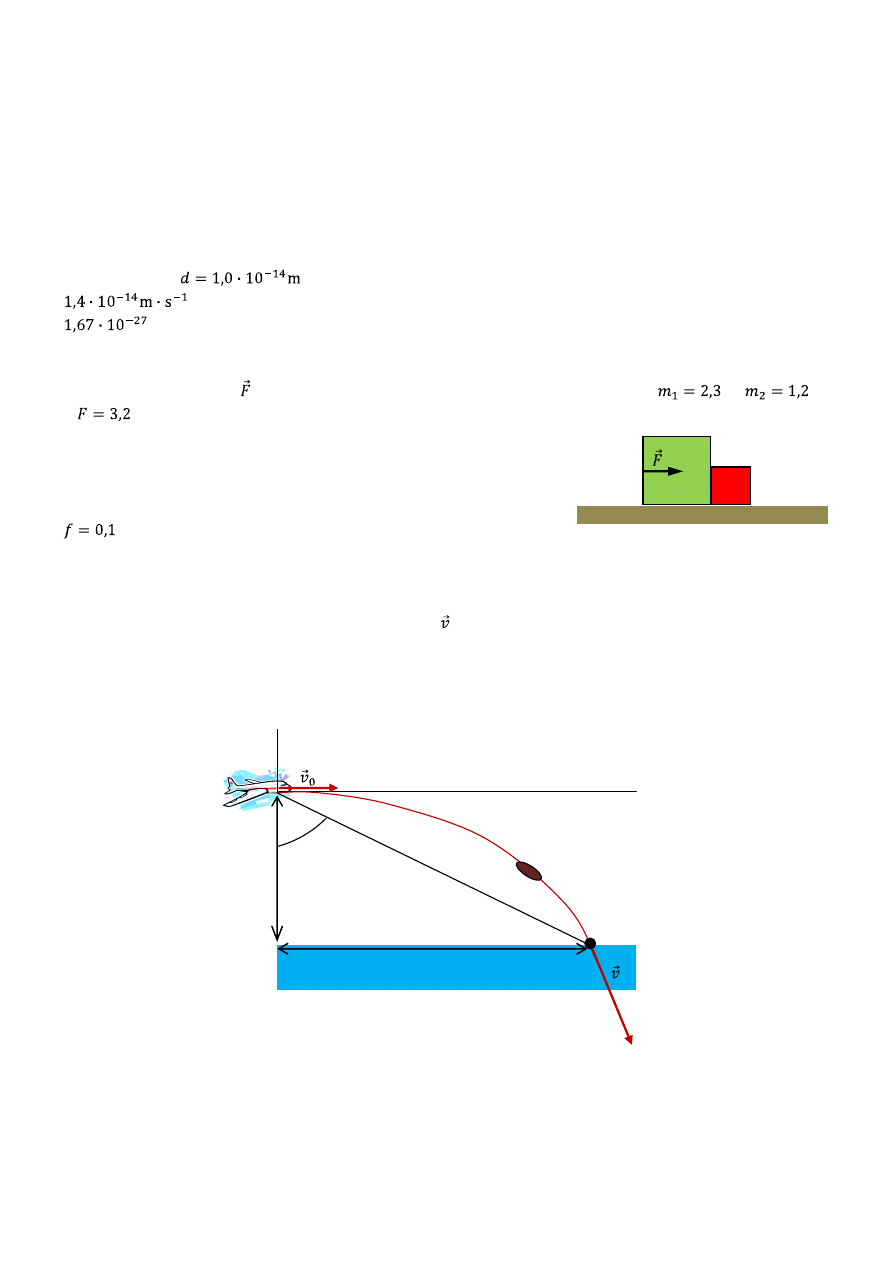
1
Ćwiczenia 3
W. Chemii, semestr 1, 2009/10
1. Zasady dynamiki Newtona
Uważnie przeczytaj wykład 2. Spróbuj samodzielnie zrobid przykłady z wykładu, a następnie przystąp do
rozwiązywania poniższych zadao.
1. Gdy jądro wychwytuje rozproszony neutron, musi go zatrzymad na drodze równej średnicy jądra. Siła, jaką dzia-
ła ono wówczas na neutron, a która skleja ze sobą cząstki w jądrze, jest poza nim praktycznie równa zeru. Załóż, że
jądro o średnicy
może wychwycid neutron o początkowej wartości prędkości nie większej niż
. Wyznacz wartośd siły, zakładając, że jest ona stała w obszarze jądra. Masa neutronu wynosi
kg.
2. Dwa stykające się ze sobą klocki leżą na stole, po którym mogą się poruszad bez tarcia. Do większego klocka
przykładamy siłę poziomą . (a) Wyznacz wartośd siły, jaka działają na siebie klocki, jeśli
kg,
kg,
a
N. (b) Wykaż, ze jeśli siłę o takiej samej wartości, lecz prze-
ciwnym zwrocie przyłożymy do mniejszego klocka, to siła, jaką będą na
siebie działad klocki będzie miała wartośd 2,1 N, różną od otrzymanej w
punkcie (a). Wyjaśnij, dlaczego! (c) Jak zmieniłby się wynik, gdyby
uwzględnid siłę tarcia i przyjąd współczynnik tarcia kinetycznego
?
3. Samolot ratowniczy lecący z prędkością 198,0m/h na stałej wysokości 500m, ku punktowi znajdującemu się
bezpośrednio nad rozbitkiem, zmagającym się z falami, musi wypuścid kapsułę ratowniczą tak, aby wpadła do
wody możliwie blisko rozbitka. (a) ) Wyznacz prędkośd kapsuły w chwili, gdy wpada ona do wody; wyraź ją za
pomocą wektorów jednostkowych oraz przez długośd i kierunek. (b) Wyznacz kąt, pod jakim pilot widzi rozbitka w
chwili najbardziej odpowiedniej do zwolnienia kapsuły. (c) Znajdź równanie toru kapsuły.
m
1
m
2
h
tor kapsuły
kierunek obserwacji
x
y
x
k
2
4. Do kooca nieważkiej i nierozciągliwej liny przerzuconej przez nieruchomy bloczek umocowany jest klocek o
masie m
1
. Drugi koniec liny przywiązano do klocka o masie m
2
, znajdującego się na równi pochyłej o kącie nachy-
lenia
. Przyjmij, że w czasie ruchu drugiego klocka w górę równi współczynnik tarcia wynosi f. (a). Zaznacz wekto-
ry sił działających na każdy z klocków oraz zapisz dla każdego z nich równanie ruchu (drugie prawo Newtona). (b).
Oblicz przyspieszenie klocka o masie m
1
oraz czas, po jakim przemieści się on o odcinek d. (Patrz: zad.2, str.74 w
[1])
Metoda rozwiązywania zadań:
1.Uważnie przeczytaj temat i zastanów się, jakie wielkości są podane a jakie musisz wyznaczyd.
2. Sporządź rysunek układu, wyizoluj ciała, których ruch będziesz badał. Zastanów się, jakim oddziaływa-
niom one podlegają i zaznacz wektory sił. Zapisz dla każdego z nich równanie ruchu Newtona oraz warunki
początkowe. Jeśli ciała tworzą układ, jak w powyższym zadaniu to pamiętaj, że przyspieszenia ich mają tę
samą wartośd (inny kierunek, zwrot!)
3. Wybierz najdogodniejszy do opisu ruchu układ współrzędnych kartezjaoskich i rozłóż wektory sił na skła-
dowe równoległe do osi.
4. Oblicz wartości wypadkowych sił dla każdego kierunku:
,
, a następnie zastąp rów-
nanie ruchu w postaci wektorowej równaniami skalarnymi.
5. Zastanów się jaki charakter będzie miał ruch w kierunku każdej z osi (jednostajny prostoliniowy, jedno-
stajnie przyspieszony, etc.). Wykorzystaj odpowiednie wzory w celu wyznaczenia
.
4. Znajdź x(t) oraz y(t).
5. Sprawdź, czy otrzymane wzory na składowe prędkości i położenia mają poprawny wymiar.
6. Zastanów się, czy otrzymane wyniki są sensowne (np. jeśli z tematu zadania wynika, że ciało zwalnia to
jego prędkośd powinna maled a nie rosnąd).
7. W niektórych zadaniach można podad równanie toru, zasięg, czas trwania ruchu, itd.
Metoda rozwiązywania zadania:
Patrząc na rysunek widzimy, że
, gdzie
współrzędną rozbitka w kierunku pozio-
mym i jednocześnie współrzędną kapsuły, gdy uderzy w wodę. Musimy zatem znaleźd zależnośd
oraz
rozwiązując równanie ruchu kapsuły.
1. Zastanów się, jakie siły działają na kapsułę i zapisz równanie ruchu (drugie prawo Newtona) oraz
warunki początkowe, czyli prędkośd i położenie w chwili początkowej.
2. Zastąp równanie ruchu wektorowe równaniami skalarnymi, znajdź składowe przyspieszenia i za-
stanów się, jaki charakter będzie miał ruch wzdłuż każdej osi.
3. Korzystając ze wzorów podanych na wykładzie znajdź składowe wektora prędkości, a następnie
położenia.
4. Rozważ ruch kapsuły w kierunku pionowym; wiedząc, że znajduje się na wysokości h nad rozbit-
kiem możesz wyznaczyd czas jej spadania z równania
.
5. Znaleziony czas po podstawieniu do
pozwoli znaleźd odległośd rozbitka od samolotu w
kierunku poziomym, czyli
.
6. Teraz mamy już wszystkie wielkości potrzebne do wyznaczenia kąta! Sprawdź, czy dostałeś
.
3
5. Na jednym koocu liny przerzuconej przez nieruchomy bloczek umocowana jest skrzynia
z bananami mogąca przesuwad się po stole. Małpa chwyta drugi koniec liny i zaczyna się
po niej wspinad z prędkością
. Współczynnik tarcia w czasie ruchu skrzyni przyjmij rów-
ny f, jej masę M, a masę małpy m. (a) Z jakimi oddziaływaniami masz do czynienia w po-
wyższym zadaniu? (b) Znajdź wypadkowe sił działających na skrzynię oraz na małpę, zapisz
równania ruchu i oblicz przyspieszenia oraz prędkości. (c) Oblicz czas, po którym skrzynia
przesunie się na skraj stołu, jeśli początkowo znajdowała się w odległości D od niego.
(Wskazówka: patrz rozwiązanie zad.4)
6
. Kuleczka o masie m
0
i dodatnim ładunku q wpada w punkcie P(x
0
, 0 , z
0
) z prędkością
w jed-
norodne, stałe pole elektryczne o natężeniu
. Opory ruchu kuleczki zaniedbujemy, ale uwzględnia-
my siłę ciężkości skierowaną wzdłuż osi . (a) Zaznacz wektory sił działających na kuleczkę, napisz dla niej drugą
zasadę Newtona (równanie ruchu) oraz warunki początkowe. (b) Zastąp wektorowe równanie ruchu równaniami
skalarnymi i przeanalizuj ruch kuleczki w wzdłuż każdej osi. (c) Znajdź składowe wektora prędkości i położenia
kuleczki i zapisz te wektory za pomocą sumy iloczynów współrzędnych i wektorów jednostkowych.
.
Na następne zajęcia proszę zrobić powyższe zadania oraz nauczyć się materiału z wykładu 1
oraz zapoznać się z wykładem 2.
Literatura
D.Halliday,R.Resnick,J.Walker: Podstawy fizyki, t.1.
(podręcznik polecany – z niego są zaczerpnięte niektóre tematy zadao)
B.Oleś: Wykłady z fizyki , Wydawnictwo PK.
A.Januszajtis: Fizyka dla politechnik, t.1.
Pytania i zagadnienia, które mogą pojawić się na egzaminie pisemnym
1. a.
Wymień zasady dynamiki klasycznej.
(3p)
b. Rozważ klocek o masie m ciągnięty w górę równi pochyłej o kącie
nachylenia
siłą . Współczynnik tarcia wynosi f. Narysuj wektory sił działających na klocek (starannie, z zacho-
waniem odpowiednich proporcji!). Kiedy do ruchu klocka zastosujesz pierwsze prawo dynamiki, drugie? Napisz od-
powiednie równania.
(2p
) c. Podaj wektory sił akcji- reakcji i zaznacz na rysunku w przypadku klocka spoczywają-
cego na stole
(1p)
c.
Jak rozumiesz stwierdzenie: Świat mechaniki klasycznej jest deterministyczny? Podaj przykła-
dy.
(2p)
Podaj ograniczenia w stosowaniu praw dynamiki klasycznej.
(2p)
2. a. W oparciu o pierwszą zasadę dynamiki zdefiniuj inercjalny układ odniesienia. Podaj przykłady takich układów i
uzasadnij swój wybór. Zastanów się, czy w warunkach ziemskich możesz podać taki układ, który byłby układem iner-
cjalnym.
(3p
)
b. Wyprowadź wzory transformacji Galileusza – czego ona dotyczy?
(2p)
c. Omów zasadę względno-
ści Galileusza. (2p) d. Kiedy transformacji Galileusza nie można stosować? Zastosuj transformację Galileusza do
obliczenia szybkości światła , którą zmierzy obserwator na Ziemi, jeśli zostało ono wysłane ze statku kosmicznego
poruszającego się z szybkością 1,5
10
8
m/s. Jakie nasuwają się wnioski?
(2p)