1

Ćwiczenia 2

WChemii, semestr 1, 2009/10

1. Położenie, prędkośd, przyspieszenie

Uważnie przeczytaj wykład 1. Skorzystaj z podanych definicji prędkości i przyspieszenia chwilowego do
rozwiązania podanych zadao.

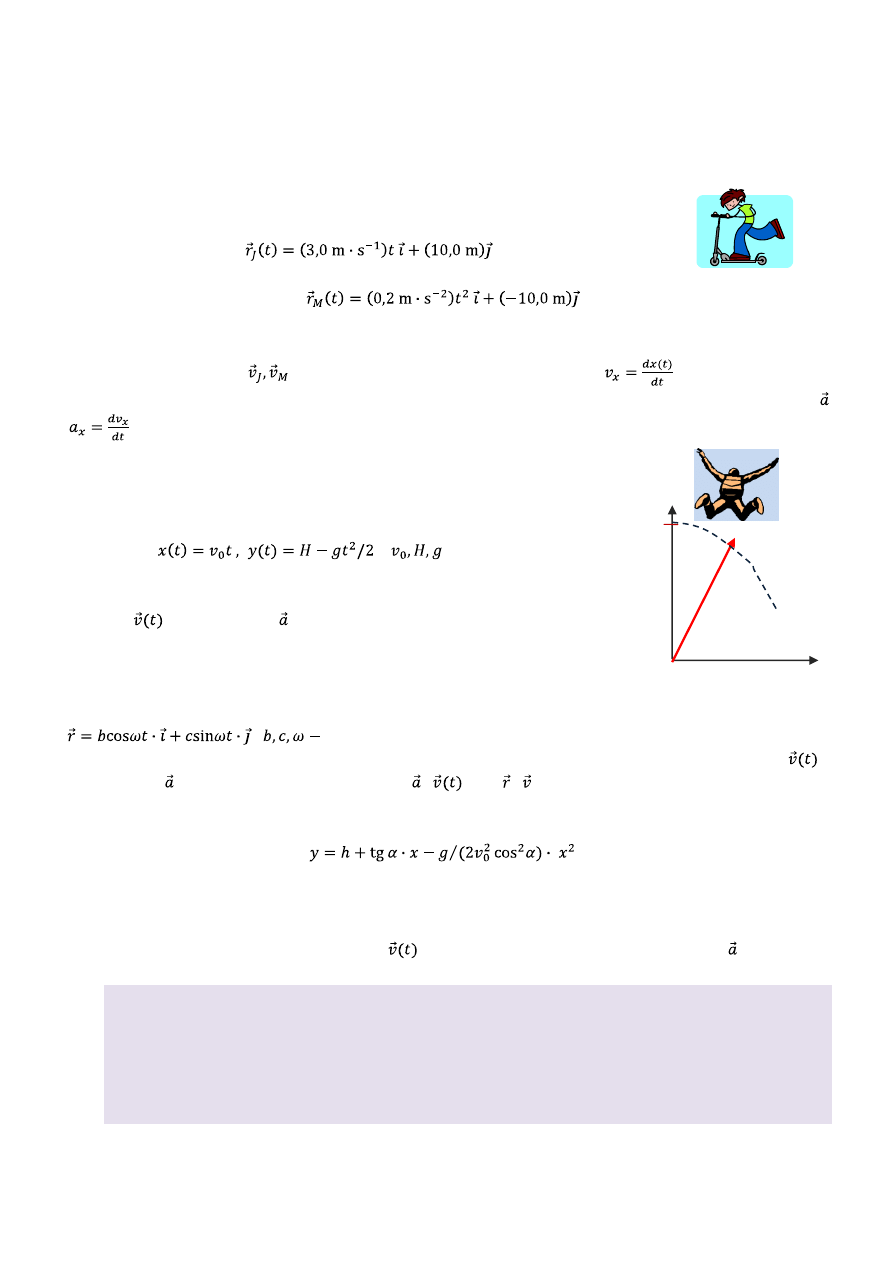
1. Położenie Jasia jadącego na hulajnodze dane jest wektorem położenia:

,

a Małgosi

.

(a) Znajdź wektor przemieszczenia Małgosi względem Jasia oraz Jasia względem Małgosi. Co zauważyłeś? Oblicz
odległośd między nimi (wartośd wektora przemieszczenia po czasie t =1min. (b) Znajdź wektory prędkości

chwilowych Jasia i Małgosi

(znajdź najpierw składowe wektora prędkości

, itd.). Jakie są wartości

prędkości (szybkości) każdego z nich po czasie 2min? Które z nich porusza się szybciej? (c) Znajdź przyspieszenie

(

, itd.) każdego z bohaterów zadania. Na podstawie uzyskanych wyników scharakteryzuj ruchy Jasia i

Małgosi.

2. Jaś skacze z samolotu lecącego z prędkością v

0

na wysokości H, ale spadochron

mu się nie otwiera! Jego położenie w czasie skoku określone jest przez
współrzędne:

, (

– stałe dodatnie).

(a) Znajdź równanie toru Jasia i naszkicuj go (wskazówka: wyraź t przez x i podstaw
do wyrażenia na y(t) - dostaniesz równanie znanej ci krzywej). (b) Znajdź wektory:
prędkości

i przyspieszenia . (c) Oblicz czas spadku Jasia (wskazówka: po tym

czasie Jaś dotknie ziemi – zastanów się, jaka będzie wówczas wartośd współrzędnej
y).

3. Sonda Cassini, zanim odłączył się od niej próbnik Huyghens, okrążyła Saturna po torze danym równaniem:

(

stałe dodatnie). (a) Po jakiej krzywej poruszała się sonda? Jej równanie

znajdziesz, jeśli zastosujesz metodę podaną na wykładzie 1. (b) Znajdź wektory: prędkości chwilowej

i

przyspieszenia . (c) Oblicz kąty między: wektorami i

oraz i . Naszkicuj tor sondy i wymienione wektory.

4*.

Kamieo porusza się w powietrzu po torze danym równaniem:

,

gdzie h, g, α ,

v

0

– stałe dodatnie (odpowiednio: wysokośd, wartośd przyspieszenia ziemskiego, kąt, pod którym

rzucono kamieo, wartośd wektora prędkości początkowej), a współrzędne jego położenia przyjmują tylko wartości
dodatnie. Wiadomo, że pozioma składowa prędkości

v

x

= const . (a) Naszkicuj tor kamienia i znajdź zależnośd x(t)

oraz y(t). (b) Znajdź wektor prędkości chwilowej

. (a) Znajdź przyspieszenie chwilowe kamienia .

Metoda rozwiązywania zadania:

1. Uważnie przeczytaj temat i zastanów się, jakie wielkości są podane a jakie musisz wyznaczyd.
2. Sporządź rysunek, w tym przypadku możesz naszkicowad tor kamienia w odpowiednio wybranym
układzie współrzędnych xy.
3. Przeanalizuj ruch kamienia porównując ze znanymi ci przykładami z życia (możesz wykonad
doświadczenie np. rzucając kamieo pod różnymi kątami).

H

x

O

y

2

4. Znajdź x(t) oraz y(t). Jak wykorzystad informację, że v

x

= const? (wskazówka: wzdłuż osi x ruch jednostajny

prostoliniowy:

, a jeśli podstawimy to wyrażenie do wzoru na y, to co dostaniemy?)

5. Wykonaj obliczenia składowych prędkości korzystając z podanych na wykładzie wzorów:

, itd.

6. Sprawdź, czy otrzymane wzory na składowe prędkości dają poprawny wymiar tej wielkości.
7. Zastanów się, jaki wpływ na ruch kamienia mają graniczne wartości kąta α.

8. Oblicz przyspieszenie kamienia (

, itd.)

Na następne zajęcia proszę zrobić powyższe zadania oraz nauczyć się materiału z wykładu 1
oraz wykładu 2.

Literatura

D.Halliday,R.Resnick,J.Walker: Podstawy fizyki, t.1.
B.Oleś: Wykłady z fizyki , Wydawnictwo PK.
A.Januszajtis: Fizyka dla politechnik, t.1.

Pytania na egzamin pisemny

1. Kinematyka punktu materialnego. Na czym polega względność położenia i ruchu?(

1p)

Jak określamy położenie

ciała?

(1p

) Zdefiniuj przemieszczenie, prędkość chwilową i przyspieszenie chwilowe.

(2p

) Podaj różnice między

torem i drogą.

(1p)

Oblicz przemieszczenie, prędkość i przyspieszenie ciała, jeśli podane są funkcje

(5p)