Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
1
ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW TARCZ SZTYWNYCH
1. Rodzaje wi
ę
zów i reakcje wi
ę
zów
Ka
ż
da konstrukcja budowlana, stanowi
ą
ca przedmiot analizy nauki wytrzymało
ś
ci
materiałów, jest w jaki
ś
sposób posadowiona, b
ę
d
ą
c po
ś
rednio lub bezpo
ś
rednio zwi
ą
zana z
podło
ż
em, na które przekazuje siły pochodz
ą
ce od jej ci
ęż
aru i przyło
ż
onego obci
ąż
enia
u
ż
ytkowego.
Od konstrukcji budowlanej wymaga si
ę
, aby była ona geometrycznie niezmienna. Aby tak
było nale
ż
y konstrukcji odebra
ć
wszystkie stopnie swobody. (Stopniem swobody nazywamy
niezale
ż
ny parametr słu
żą
cy do opisu poło
ż
enia obiektu w przestrzeni lub na płaszczy
ź
nie.) Aby
odebra
ć
konstrukcji wszystkie stopnie swobody nale
ż
y j
ą
unieruchomi
ć
za pomoc
ą
wi
ę
zów,
stanow
ą
je wszelkie poł
ą
czenia konstrukcji z podło
ż
em lub inn
ą
konstrukcj
ą
. Takie poł
ą
czenia
nazywa
ć
b
ę
dziemy tak
ż
e podporami. Siły, z którymi podpory oddziaływuj
ą
na rozpatrywan
ą
brył
ę
w miejscach zetkni
ę
cia, nazywamy reakcjami podpór.
Na poni
ż
szych rysunkach zaczerpni
ę
tych ze skryptu Stefana Piechnika „Wytrzymało
ść
Materiałów dla wydziałów budowlanych” przedstawione s
ą
wi
ę
zy płaskie, tzn. takie gdzie siły
reakcji le
żą
w jednej płaszczy
ź
nie. Oczywi
ś
cie istniej
ą
te
ż
wi
ę
zy przestrzenne, analogiczne do
płaskich i siły je zast
ę
puj
ą
ce. Podpory mo
ż
emy sklasyfikowa
ć
w dwóch grupach: pierwszy rodzaj
to podpory kierunkowe, których reakcje le
żą
na znanej linii działania l, za
ś
drugi rodzaj to
podpory przegubowe, których reakcje przechodz
ą
przez znany punkt A. Rozró
ż
niamy
nast
ę
puj
ą
ce podpory płaskie:
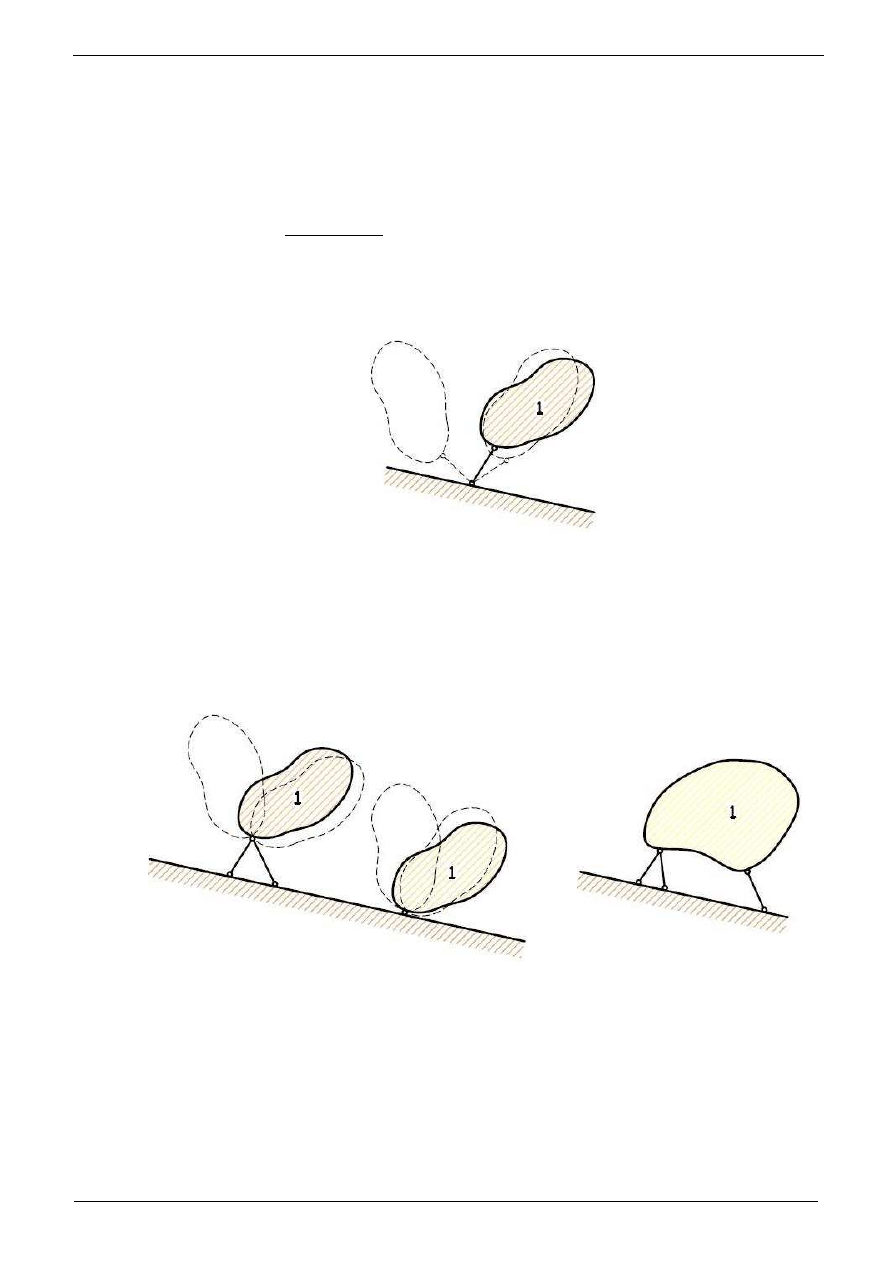
Styk gładki, czyli poł
ą
czenie „na styk”, gdy jedna tarcza dotyka innej, a mi
ę
dzy nimi
nie wyst
ę
puje tarcie. W takim przypadku linia działania reakcji jest prostopadła do
płaszczyzny styku.
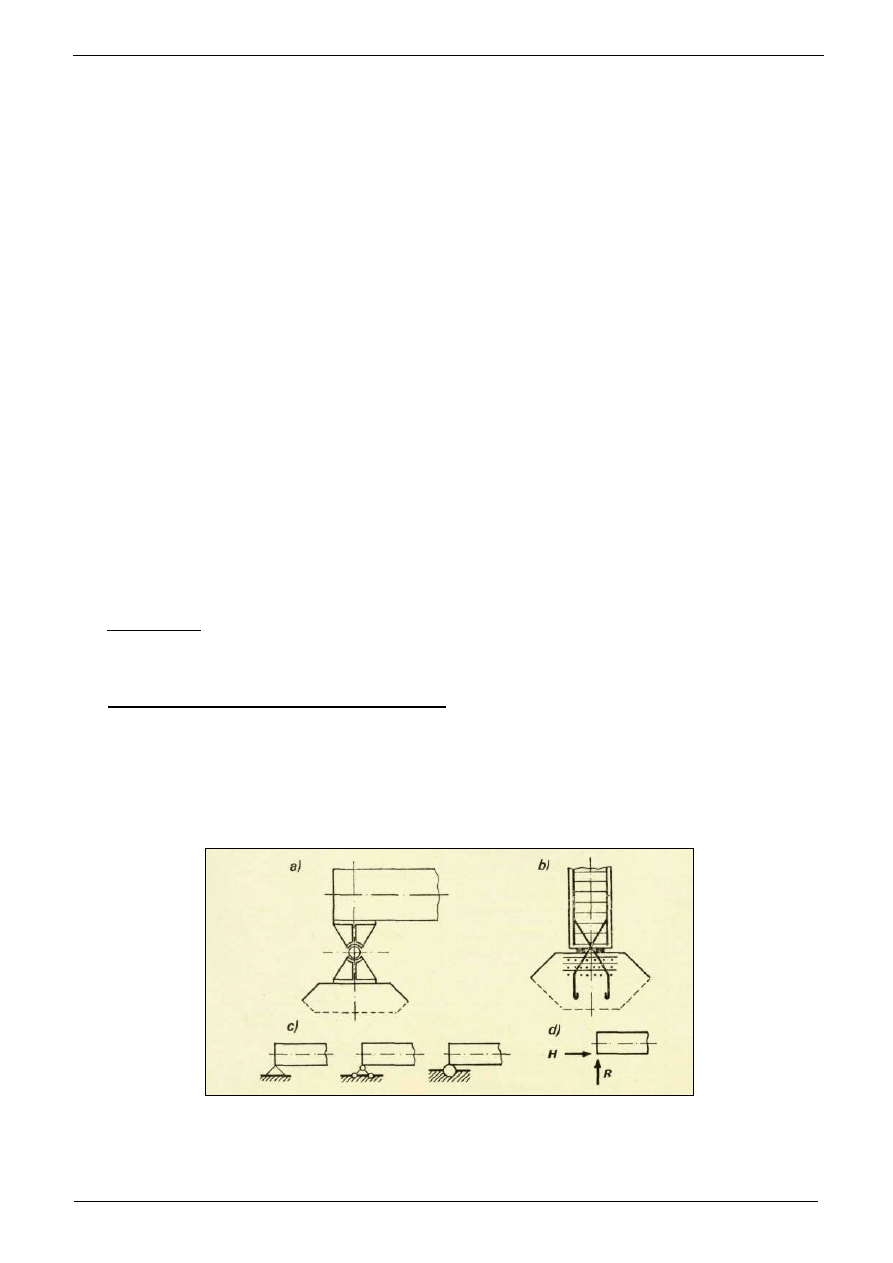
Podparcie przegubowo-nieprzesuwne. Na poni
ż
szym rysunku przedstawiono
podparcie przegubowo-nieprzesuwne w konstrukcji stalowej i
ż
elbetowej (rys.1a i 1b),
schematy takiego podparcia (rys.1c) i siły zast
ę
puj
ą
ce działanie tych wi
ę
zów, czyli reakcje
(rys.1d). Jak wiemy przy takim sposobie podparcia mo
ż
liwy jest tylko obrót, niemo
ż
liwy jest
natomiast przesuw w
ż
adnym kierunku. Musi wyst
ą
pi
ć
wi
ę
c reakcja, któr
ą
najcz
ęś
ciej rozkładamy
na dwie składowe (pionow
ą
R i poziom
ą
H).
Rys. 1
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
2
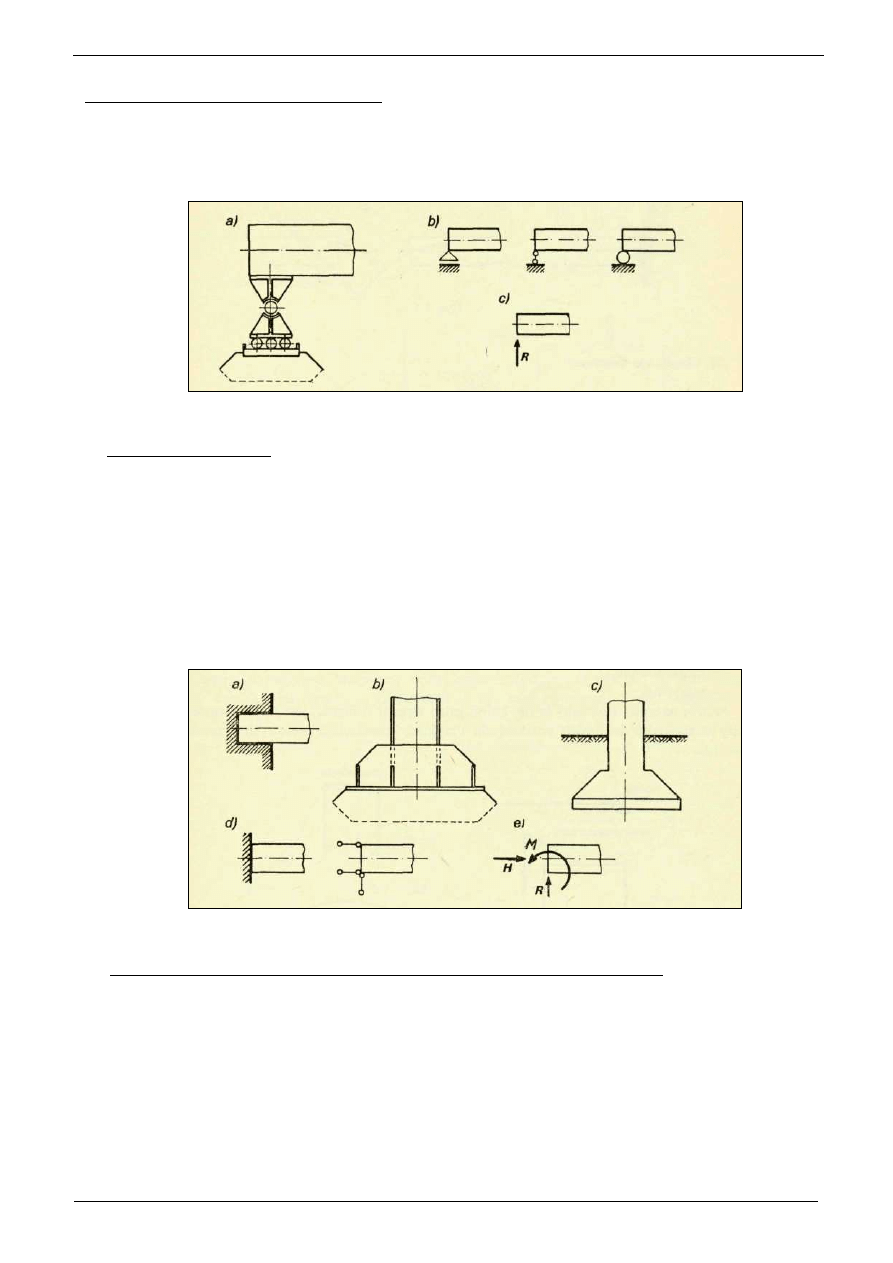
Podparcie przegubowo-przesuwne. Na poni
ż
szym rysunku przedstawiono tego typu
podpor
ę
wykonan
ą
w konstrukcji stalowej, na rys.2b schematy takiego podparcia i na
rys.2c reakcje. Poniewa
ż
w takiej podporze mo
ż
liwy jest przesuw i obrót, wyst
ę
puje tylko
reakcja R o kierunku działania prostopadłym do mo
ż
liwego kierunku przesuwu podpory.
Rys. 2
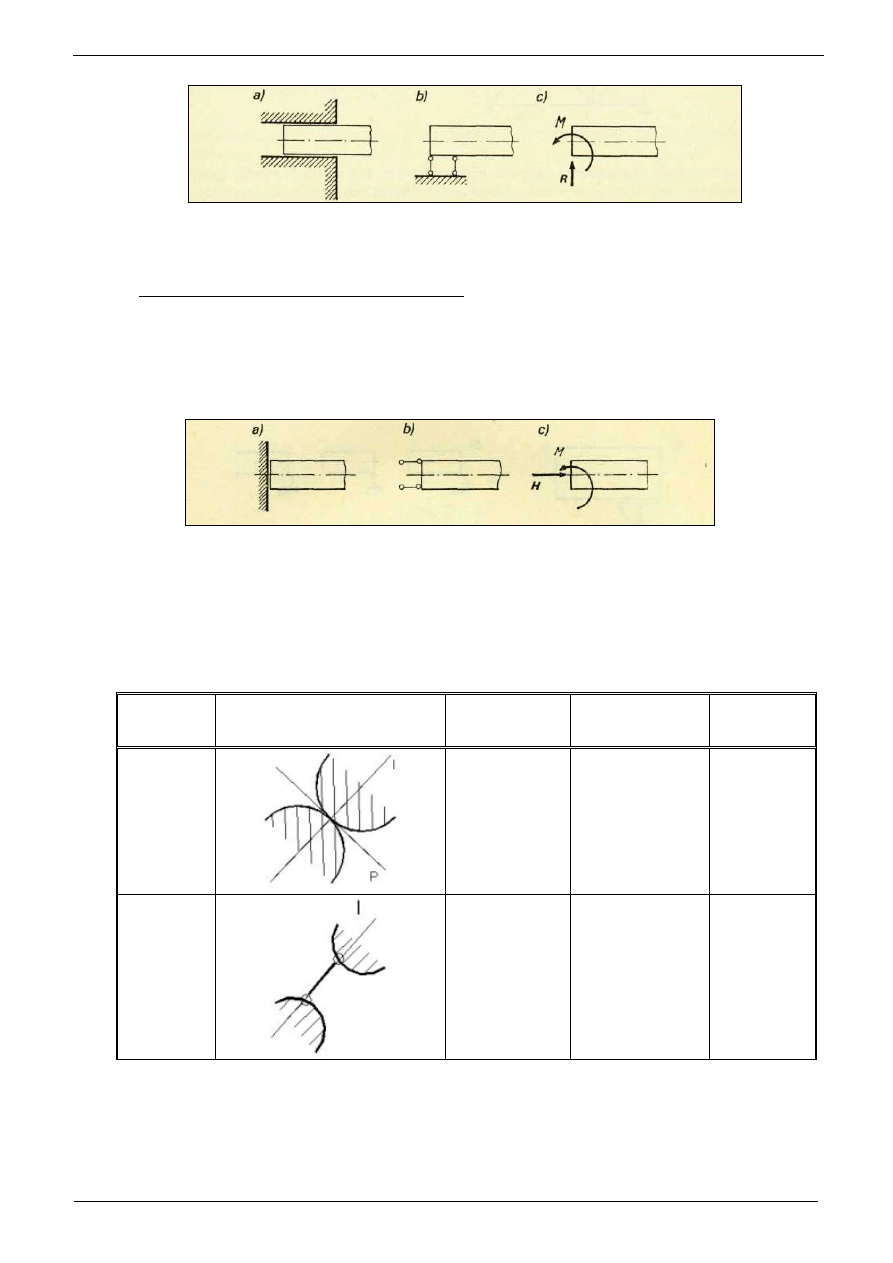
Pełne utwierdzenie. Przykłady wi
ę
zów, które przyjmowa
ć
b
ę
dziemy jako pełne
utwierdzenie, przedstawiono na poni
ż
szych schematach; na rys.a utwierdzenie w
ś
cianie belki
drewnianej, na rys.3b pełne utwierdzenie słupa stalowego, za
ś
na rys. 3c utwierdzenie słupa
ż
elbetowego; schematy tego typu wi
ę
zów przedstawiono na rys. 3d, a na rys.e pokazano siły
zast
ę
puj
ą
ce działanie wi
ę
zów, czyli reakcje.
Utwierdzenie odbiera trzy stopnie swobody, czyli nakłada trzy wi
ę
zy na pr
ę
t. Blokuje ono
przesuwy w obu kierunkach oraz obrót wokół podpory. W przypadku pełnego utwierdzenia
wyst
ę
puj
ą
trzy reakcje: pionowa, pozioma oraz moment zginaj
ą
cy.
Rys. 3
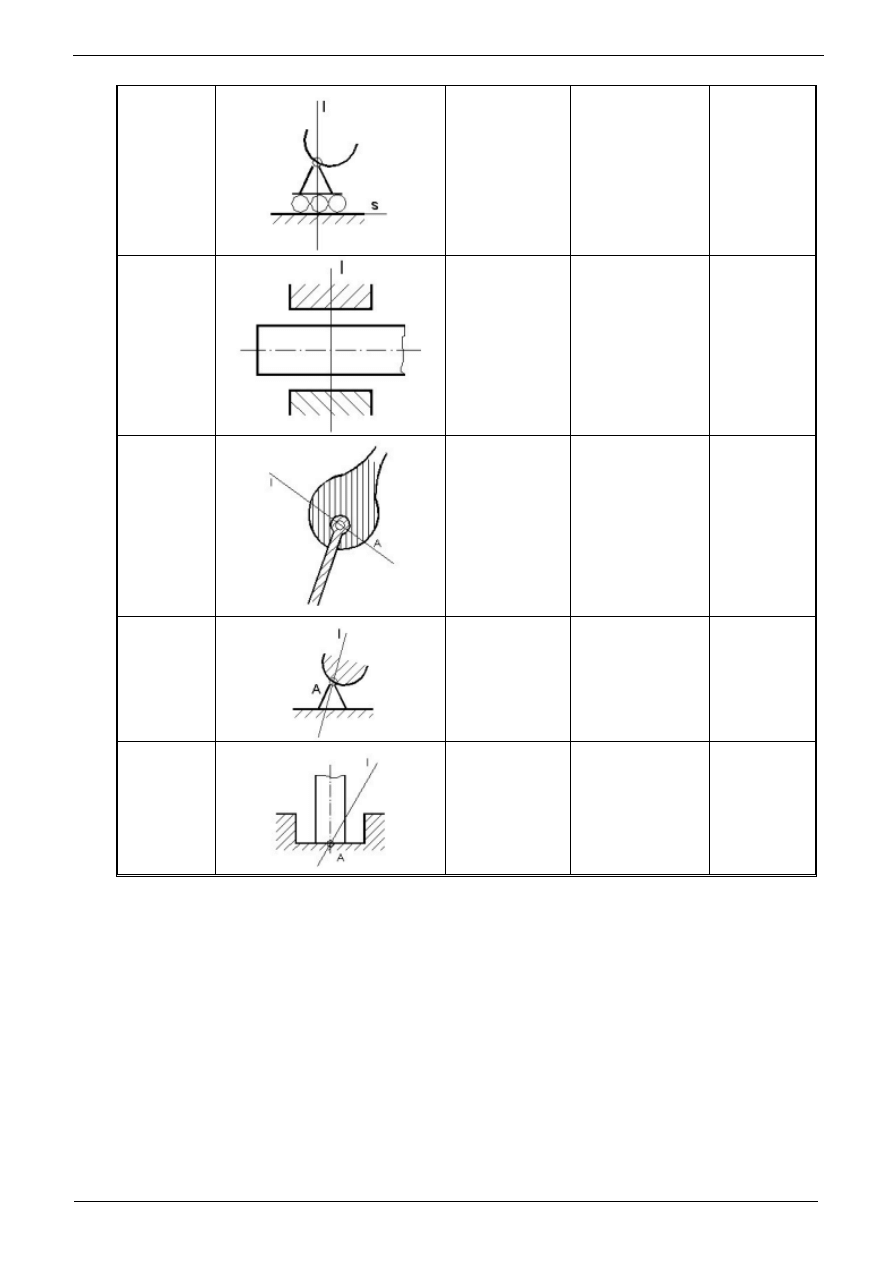
Utwierdzenie z poziomym przesuwem (poł
ą
czenie teleskopowe). Nazwa tego typu
pochodzi st
ą
d,
ż
e wi
ę
zy uniemo
ż
liwiaj
ą
obrót i przemieszczenie pionowe, natomiast
umo
ż
liwiaj
ą
przemieszczenie poziome (rys.4a); schemat i reakcje przedstawiono na rys.4.
Podpora taka odbiera dwa stopnie swobody, czyli nakłada dwa wi
ę
zy na pr
ę
t.
Zablokowane zostan
ą
: przesuw w jednym kierunku oraz obrót wokół podpory, mo
ż
liwy jest
natomiast przesuw w drugim kierunku. Odpowiada ona dwóm równoległym podporom
przegubowo-przesuwnym (rys.4b).
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
3
Rys. 4
Utwierdzenie z pionowym przesuwem. Utwierdzenie z mo
ż
liwo
ś
ci
ą
pionowego
przesuwu przedstawia rys.5a, schemat wi
ę
zów rys.5b, reakcje rys.5c. W literaturze taki
typ podpory cz
ę
sto okre
ś
lany jest jako podpora
ś
lizgowa, potocznie natomiast cz
ę
sto
takie poł
ą
czenie nazywamy ły
ż
w
ą
.
Rys. 5
W poni
ż
szej tabeli przedstawi
ę
krótkie zestawienie rodzajów podpór, uzupełniaj
ą
c
podstawowe informacje i cechy:
Rodzaj
podpory
Schemat podpory
Nazwa
podpory
Opis linii
działania reakcji
podpory
Niewiadome
podpory
kierunkowe
styk
gładki
linia I jest
prostopadła
do pł. styku p
warto
ść
reakcji
podpory
kierunkowe
pr
ę
t z dwoma
przegubami
kulistymi
linia l pokrywa si
ę
z osi
ą
pr
ę
ta
warto
ść
reakcji
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
4
podpory
kierunkowe
przgub
przesuwny
linia l jest
prostopadła
do mo
ż
liwego
kierunku
przesuwu podpory
warto
ść
reakcji
podpory
kierunkowe
ło
ż
ysko
poziome
linia l jest
prostopadła
do osi pr
ę
ta
warto
ść
reakcji
podpory
przegubowe
przegub
kulisty
linia l przechodzi
przez znany punkt
A
warto
ść
i
kierunek
reakcji
podpory
przegubowe
przegub
nieprzesuwny
linia l przechodzi
przez znany punkt
A
warto
ść
i
kierunek
reakcji
podpory
przegubowe
ło
ż
ysko
pionowe
linia l przechodzi
przez znany punkt
A
warto
ść
i
kierunek
reakcji
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
5
2. Klasyfikacja i analiza płaskich układów tarcz sztywnych
Rozwa
ż
my układ powstały w wyniku poł
ą
czenia pewnej tarczy z tarcz
ą
podporow
ą
, czyli
pewn
ą
nieruchom
ą
tarcz
ą
odniesienia (rysunki poni
ż
ej). W zale
ż
no
ś
ci od liczby wi
ę
zów, które
ł
ą
cz
ą
obie tarcze, oraz od sposobu uło
ż
enia tych wi
ę
zów wyró
ż
ni
ć
mo
ż
emy kilka przypadków:
Najpierw przeanalizujmy jedn
ą
tarcz
ę
i zastanówmy si
ę
, jaki sposób rozmieszczenia wi
ę
zów,
oraz jaka ich liczba gwarantuje geometryczn
ą
niezmienno
ść
.
a)
Tarcza oznaczona jako „1” doł
ą
czona jest do tarczy podporowej za pomoc
ą
jednego
wi
ę
zu. Wi
ę
z ten nie jest w stanie unieruchomi
ć
tarczy. Odbiera jej tylko jeden stopie
ń
swobody.
Rys. 2.1 a
b)
Tarcza „1” poł
ą
czona jest z tarcza podporow
ą
za pomoc
ą
dwóch wi
ę
zów, które
odbieraj
ą
dwa stopnie swobody, pozostawiaj
ą
c jej jeszcze jeden stopie
ń
swobody
(obrót). Tarcza z prawej poł
ą
czona jest za pomoc
ą
przegubu z tarcz
ą
podporow
ą
,
natomiast ta po lewej stronie rysunku, poł
ą
czona jest z tarcz
ą
podporow
ą
za pomoc
ą
dwóch pr
ę
tów sztywnych. Oba wi
ę
zy s
ą
jednakowe pod wzgl
ę
dem „zdolno
ś
ci
poł
ą
czenia”.
Rys. 2.1b
Rys. 2.1c
c)
Tarcza „1” poł
ą
czona jest z tarcz
ą
podporow
ą
za po
ś
rednictwem trzech wi
ę
zów
(zauwa
ż
my dodatkowo – wi
ę
zów – pr
ę
tów o kierunkach NIE przecinaj
ą
cych si
ę
w
jednym punkcie), które odbieraj
ą
tarczy wszystkie stopnie swobody, a wi
ę
c
unieruchamiaj
ą
całkowicie tarcz
ę
„1” wzgl
ę
dem tarczy podporowej.
Nale
ż
y zauwa
ż
y
ć
,
ż
e bardzo istotny jest warunek, aby kierunki pr
ę
tów nie przecinały
si
ę
w jednym punkcie (jest to warunek dostateczny dla tego typu układów). Tylko
wtedy mo
ż
emy mówi
ć
o układzie geometrycznie niezmiennym. (Układy chwilowo
geometrycznie zmienne zostan
ą
omówione pó
ź
niej.)
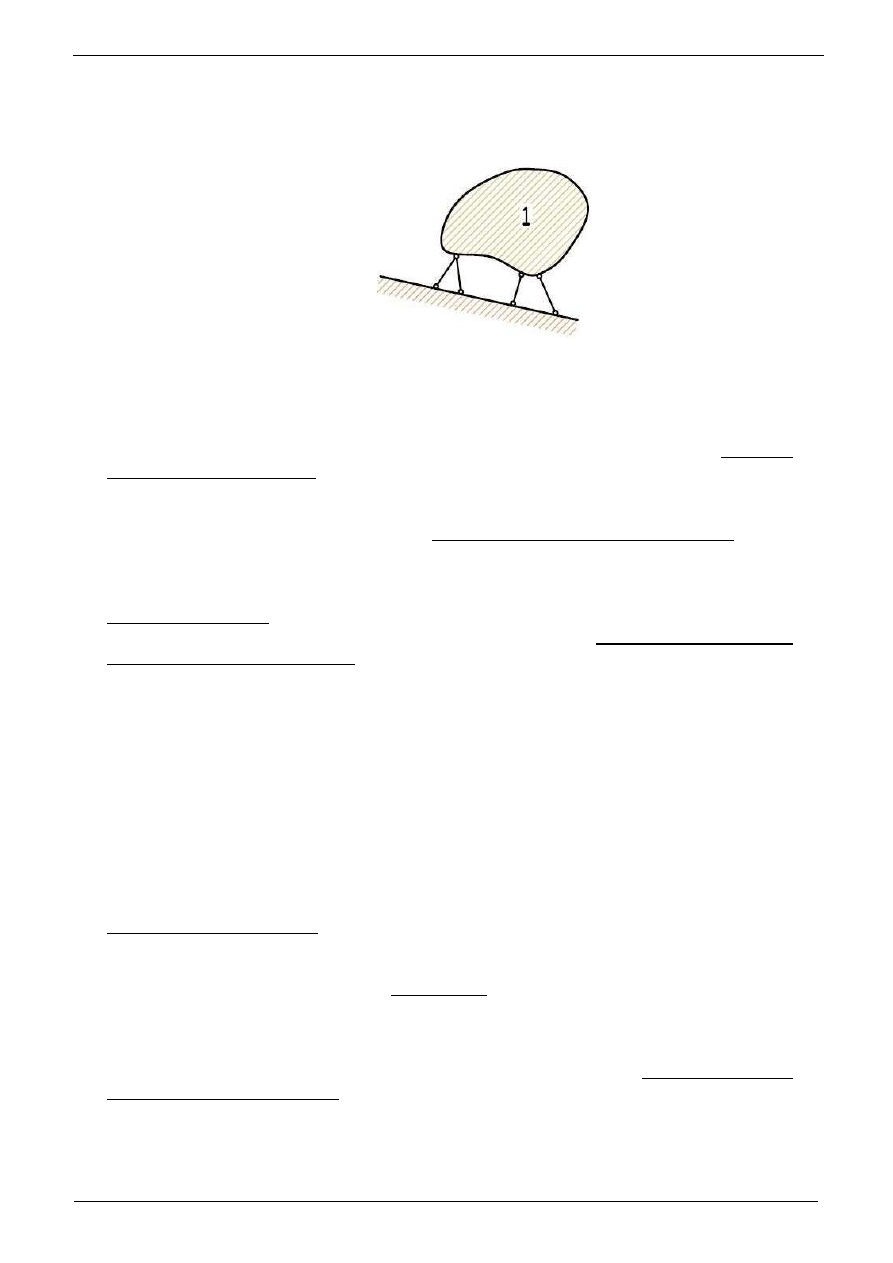
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
6
d)
Tarcza „1” poł
ą
czona jest czterema pr
ę
tami. Wyst
ę
puje tutaj wi
ę
c nadmiar wi
ę
zów,
tzn. ich liczba wi
ę
ksza jest od liczy stopni swobody układu.
Rys. 2.1d
Tarcza sztywna ma na płaszczy
ź
nie trzy stopnie swobody, co oznacza,
ż
e dla
unieruchomienia tarczy sztywnej na płaszczy
ź
nie potrzebne jest wprowadzenie trzech
wi
ę
zów.
Układy tarcz przedstawione w podpunktach a) i b) nazywali b
ę
dziemy układami
geometrycznie zmiennymi, co zwi
ą
zane jest bezpo
ś
rednio z faktem, ze tarcza „1” ma
odpowiednio 1 (podpunkt b) i 2 (podpunkt a) stopnie swobody.
Układ z podpunktu c) nazywany b
ę
dzie układem geometrycznie niezmiennym, co ma
podkre
ś
la
ć
, ze tarczy „1” odebrano 3 (wszystkie) stopnie swobody, a wi
ę
c liczba
stopni swobody tarczy 1 wynosi 0. Nale
ż
y jednak pami
ę
ta
ć
,
ż
e liczba stopni swobody
równa zeru nie gwarantuje jeszcze geometrycznej niezmienno
ś
ci. Jest to tylko
warunek konieczny, nie jest natomiast warunkiem dostatecznym. Oprócz tego
warunku
układ
pr
ę
towy
powinien
tak
ż
e
spełnia
ć
warunki
wystarczaj
ą
ce
geometrycznej niezmienno
ś
ci. Je
ż
eli tarcza podparta jest trzema podporami
przegubowo-przesuwnymi (ka
ż
da z podpór nakłada po jednym wi
ę
zie na tarcz
ę
) to,
aby tarcza była geometrycznie niezmienna “kierunki” trzech podpór nie mog
ą
przecina
ć
si
ę
w jednym punkcie. Gdyby taka sytuacja zaistniała, mo
ż
liwy byłby obrót
wzgl
ę
dem przegubu wirtualnego, le
żą
cego wła
ś
nie w miejscu przeci
ę
cia kierunków
pr
ę
tów. Je
ż
eli tarcza jest podparta podpor
ą
przegubowo-przesuwn
ą
i przegubowo-
nieprzesuwn
ą
to, aby był geometrycznie niezmienny podpora przegubowo-
nieprzesuwna nie mo
ż
e le
ż
e
ć
na “kierunku” podpory przegubowo-przesuwnej.
Układ pokazany w podpunkcie d) to przykład, w którym zaanga
ż
owana jest czynnie
wi
ę
ksza liczba wi
ę
zów ni
ż
to konieczne dla odebrania tarczy „1” wszystkich stopni
swobody. Układ ten jest oczywi
ś
cie tak
ż
e układem geometrycznie niezmiennym. Z
uwagi jednak
ż
e na wyst
ą
pienie nadmiaru wi
ę
zów układ taki nazywali b
ę
dziemy
układem przesztywnionym.
Przejd
ź
my do układów zło
ż
onych z dwóch tarcz (nie wliczaj
ą
c „podło
ż
a”)
Dodanie do układu tarcz (tarcza „1” i tarcza podporowa) kolejnej tarczy wymaga
dodania kolejnych trzech wi
ę
zów, o ile oczywi
ś
cie chcemy nadal zachowa
ć
geometryczn
ą
niezmienno
ść
. Mo
ż
emy w tym miejscu sformułowa
ć
warunek konieczny
geometrycznej niezmienno
ś
ci układu w nast
ę
puj
ą
cy sposób:
p
t
≤
⋅
3
gdzie
t
oznacza liczb
ę
tarcz nale
żą
cych do układu, nie licz
ą
c tarczy podporowej,
p
natomiast jest liczb
ą
wszystkich wi
ę
zów wyst
ę
puj
ą
cych w układzie.
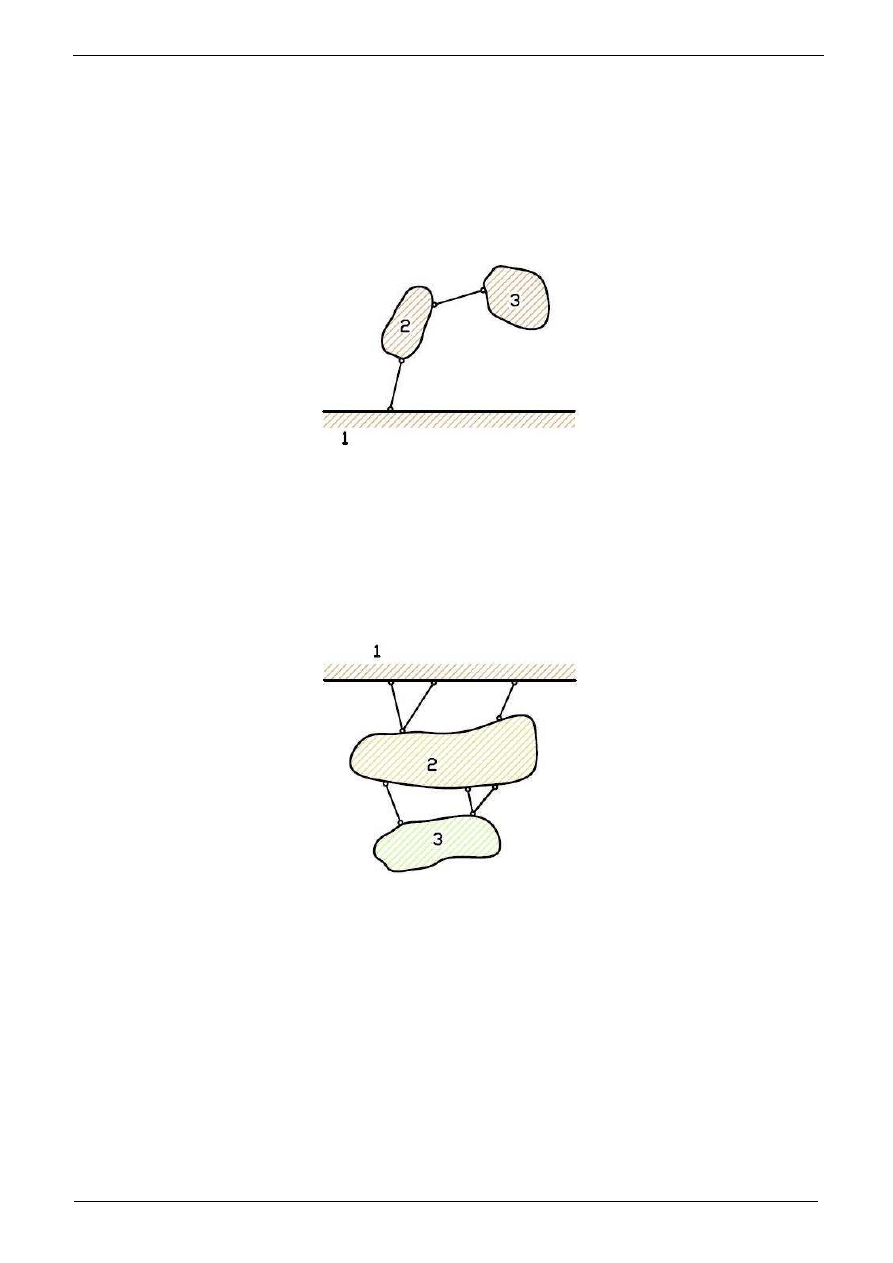
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
7
Wprowadzone dla jednej tarczy okre
ś
lenia b
ę
dziemy odnosili równie
ż
dla układów
zbudowanych z wi
ę
kszej liczby tarcz. Na poni
ż
szych rysunkach przedstawiono układy
dwóch tarcz, stanowi
ą
ce kolejno przykłady układów: geometrycznie zmiennego,
geometrycznie niezmiennego i przesztywnionego.
- układ geometrycznie zmienny:
Rys. 2.2 a
Na rysunku 2.2a sytuacja jest jednoznaczna. Tarcza „2” jest poł
ą
czona z podło
ż
em
tylko jednym pr
ę
tem; nie jest wi
ę
c spełniony nawet warunek konieczny
geometrycznej niezmienno
ś
ci. Tarcza „3” poł
ą
czona jest z geometrycznie zmienn
ą
tarcz
ą
„2” równie
ż
tylko jednym pr
ę
tem, a wi
ę
c cało
ść
jest geometrycznie zmienna.
- układ geometrycznie niezmienny:
Rys. 2.2 b
Rysunek 2.2b to typowy przykład układu geometrycznie niezmiennego. Tarcza „2”
jest geometrycznie niezmienna, poniewa
ż
ł
ą
czy si
ę
z podło
ż
em (tarcz
ą
„1”) za
pomoc
ą
trzech pr
ę
tów, których kierunki nie przecinaj
ą
si
ę
w jednym punkcie.
Spełnione s
ą
wi
ę
c oba warunki geometrycznej niezmienno
ś
ci: konieczny i
dostateczny. Tarcz
ę
„2” w takiej sytuacji traktowa
ć
mo
ż
na jako podło
ż
e dla tarczy
„3”. Analiza geometrycznej niezmienno
ś
ci tarczy „3” jest analogiczna jak tarczy „2”.
Tarcza „3” równie
ż
ł
ą
czy si
ę
z cz
ęś
ci
ą
geometrycznie niezmienn
ą
trzema pr
ę
tami,
których kierunki nie przecinaj
ą
si
ę
w jednym punkcie. Spełniony jest wi
ę
c warunek
konieczny i wystarczaj
ą
cy, a wi
ę
c cało
ść
pozostaje geometrycznie niezmienna.
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
8
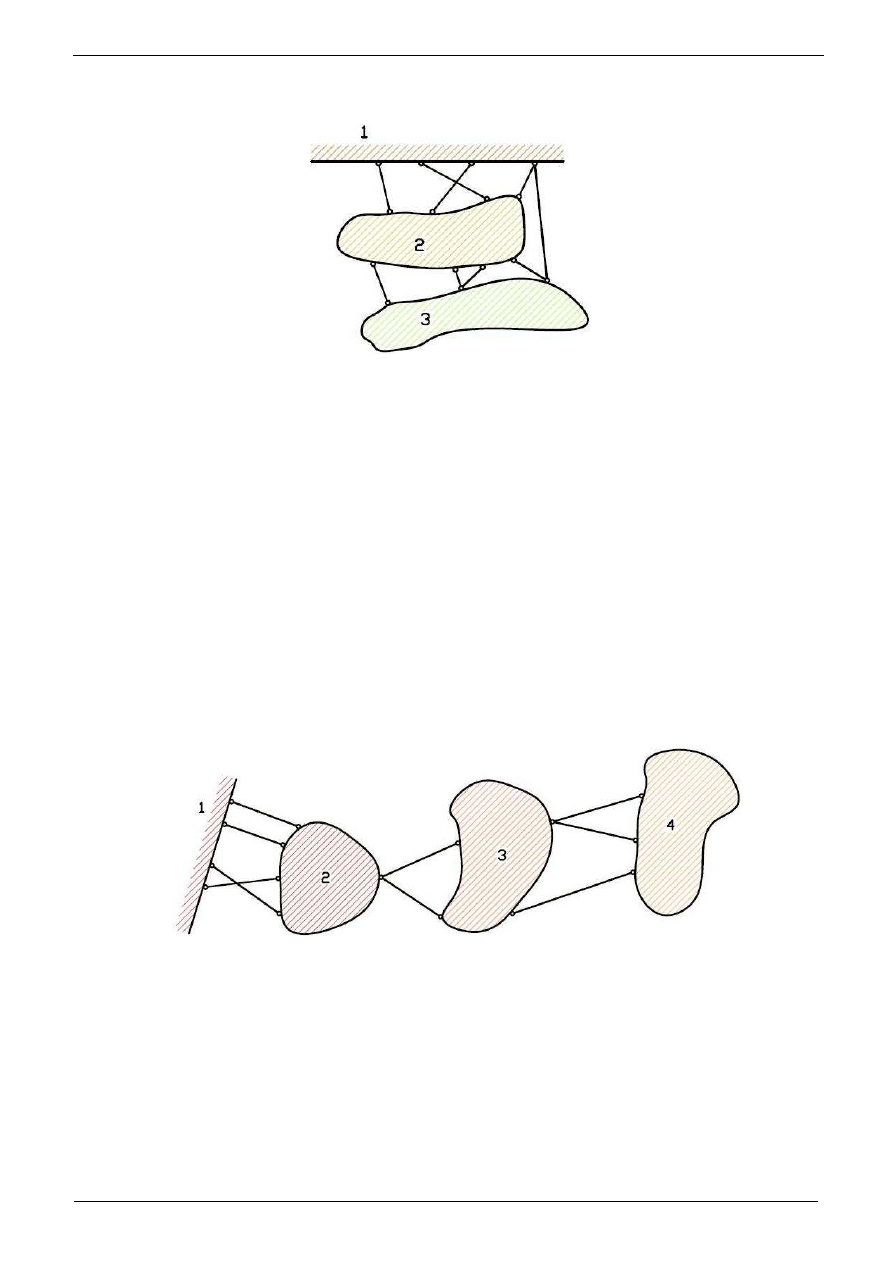
- układ przesztywniony:
Rys. 2.2 c
Rysunek 2.2c przedstawia przykład układu przesztywnionego. Tarcz
ę
„2” do podło
ż
a
„1” przytwierdzaj
ą
a
ż
cztery pr
ę
ty, których kierunki nie przecinaj
ą
si
ę
w jednym
punkcie. Mogliby
ś
my wi
ę
c usun
ąć
jeden, dowolny z tych pr
ę
tów, aby układ nadal
pozostawał geometrycznie niezmienny. Podobnie, gdy rozpatrujemy tarcz
ę
„3”.
Tarcza ta poł
ą
czona jest z cz
ęś
ci
ą
„nieruchom
ą
” a
ż
pi
ę
cioma pr
ę
tami.
ś
adne trzy z
nich nie przecinaj
ą
si
ę
w jednym punkcie, a wi
ę
c mogliby
ś
my usun
ąć
dowolne dwa z
tych pr
ę
tów bez szkody na stateczno
ść
układu.
Nawet w układach pozornie przesztywnionych (jak wskazuje na to warunek
konieczny) nale
ż
y koniecznie sprawdzi
ć
warunek dostateczny geometrycznej
niezmienno
ś
ci. Nawet cztery i wi
ę
cej pr
ę
tów mo
ż
e nie gwarantowa
ć
sztywno
ś
ci.
Zachodzi to w sytuacji, gdy ich kierunki przecinaj
ą
si
ę
w jednym punkcie.
Mo
ż
na równie
ż
wyobrazi
ć
sobie układ zło
ż
ony, którego poszczególne fragmenty
stanowi
ą
układy wyró
ż
nionych typów. Poni
ż
ej pokazany jest układ, który – jako cało
ść
– nazywaliby
ś
my geometrycznie zmiennym, mimo
ż
e poszczególne fragmenty
poł
ą
czone s
ą
ze sob
ą
za pomoc
ą
dwóch i wi
ę
kszej liczby pr
ę
tów.
Rys. 2.3
Tarcza „2” poł
ą
czona jest z tarcza podporow
ą
czterema pr
ę
tami, a wi
ę
c te dwie tarcze
tworz
ą
układ przesztywniony. Tarcze „3” oraz „4” poł
ą
czone s
ą
ze sob
ą
za pomoc
ą
trzech pr
ę
tów, których kierunki nie przecinaj
ą
si
ę
w jednym punkcie, a wi
ę
c wzgl
ę
dem
siebie s
ą
geometrycznie niezmienne. Zauwa
ż
my jednak,
ż
e poł
ą
czenie tarcz „2” i „3”
ze sob
ą
odbiera jedynie dwa stopnie swobody, co nie wystarcza do całkowitego
usztywnienia układu. Wła
ś
nie poł
ą
czenie mi
ę
dzy tarczami „2” i „3” decyduje o tym, ze
układ jako cało
ść
nazywamy układem geometrycznie zmiennym.
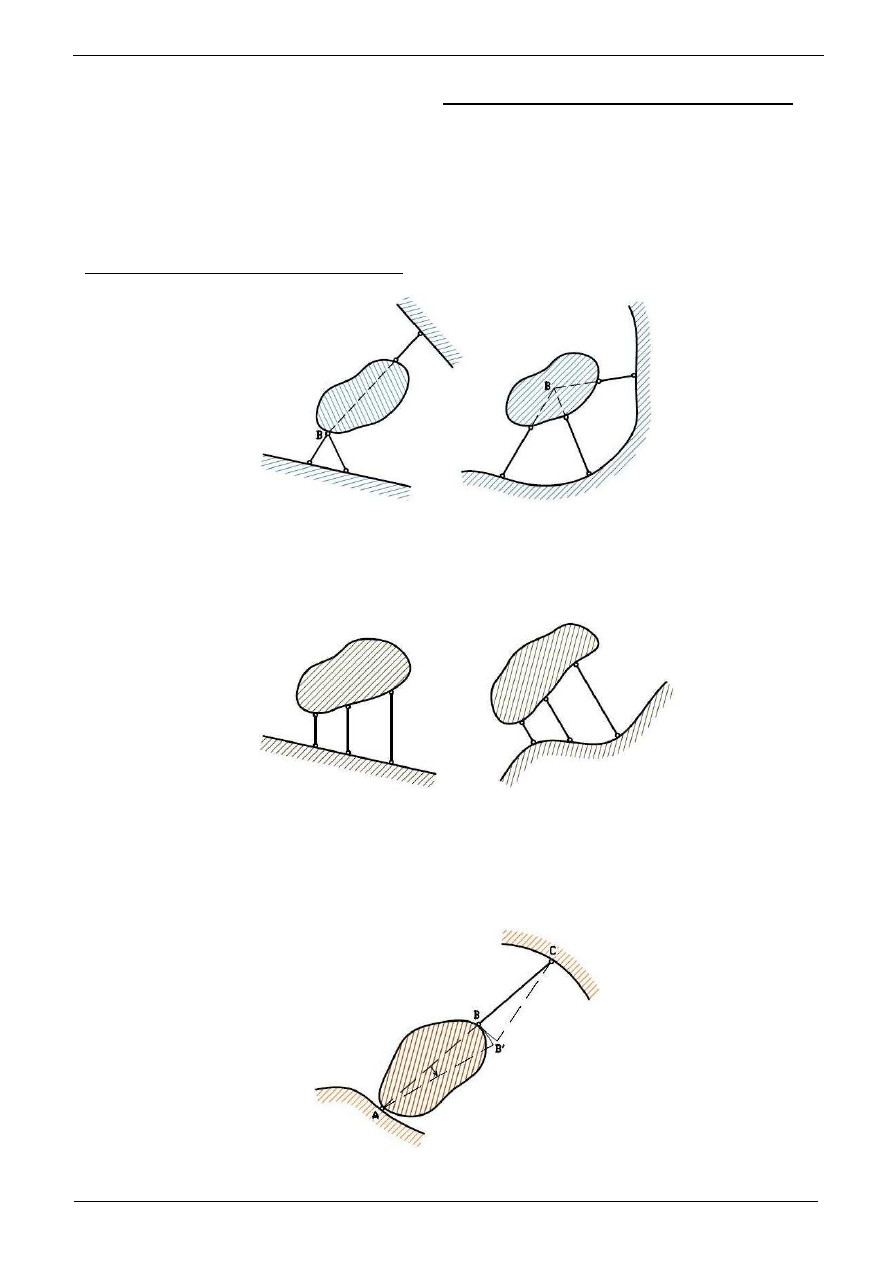
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
9
Zajmijmy
si
ę
dokładniejsz
ą
analiz
ą
warunku
dostatecznego
geometrycznej
niezmienno
ś
ci. Warunek ten jest niezwykle istotny, poniewa
ż
cz
ę
sto to on rozstrzyga czy
układ jest geometrycznie zmienny, niezmienny, czy nale
ż
y do trzeciej grupy: układów
chwilowo geometrycznie zmiennych.
Przeanalizujmy tarcz
ę
poł
ą
czon
ą
z podło
ż
em za pomoc
ą
trzech wi
ę
zów, których kierunki
przecinaj
ą
si
ę
w jednym punkcie (rys. 3.1a). Tarcza ta ma mo
ż
liwo
ść
wykonania niesko
ń
czenie
małego obrotu wokół punktu przeci
ę
cia si
ę
kierunków wi
ę
zów. Punkt taki nazywali b
ę
dziemy
biegunem (
ś
rodkiem) chwilowego obrotu.
Rys. 3.1a
Podobna sytuacja zachodzi na poni
ż
szym przykładzie (rys. 3.1b). Tutaj równie
ż
kierunki
wi
ę
zów (tutaj pr
ę
tów) przecinaj
ą
si
ę
w jednym punkcie. Punkt ten w przypadku pr
ę
tów
równoległych znajduje si
ę
w niesko
ń
czono
ś
ci. Jest to tak zwany biegun niewła
ś
ciwy.
Rys. 3.1b
Równie
ż
tarcza przedstawiona na rys. 3.1c mo
ż
e obróci
ć
si
ę
o pewien bardzo mały k
ą
t, co
wynika z faktu,
ż
e łuki, zakre
ś
lone promieniami BC i AC, maj
ą
wspóln
ą
styczn
ą
, a zatem maj
ą
niesko
ń
czenie mały wspólny odcinek BB’, o który wła
ś
nie mo
ż
e przemie
ś
ci
ć
si
ę
punkt C. Na
poni
ż
szym schemacie przedstawiono t
ą
sytuacj
ę
w znacznym wyolbrzymieniu.
Rys. 3.1c
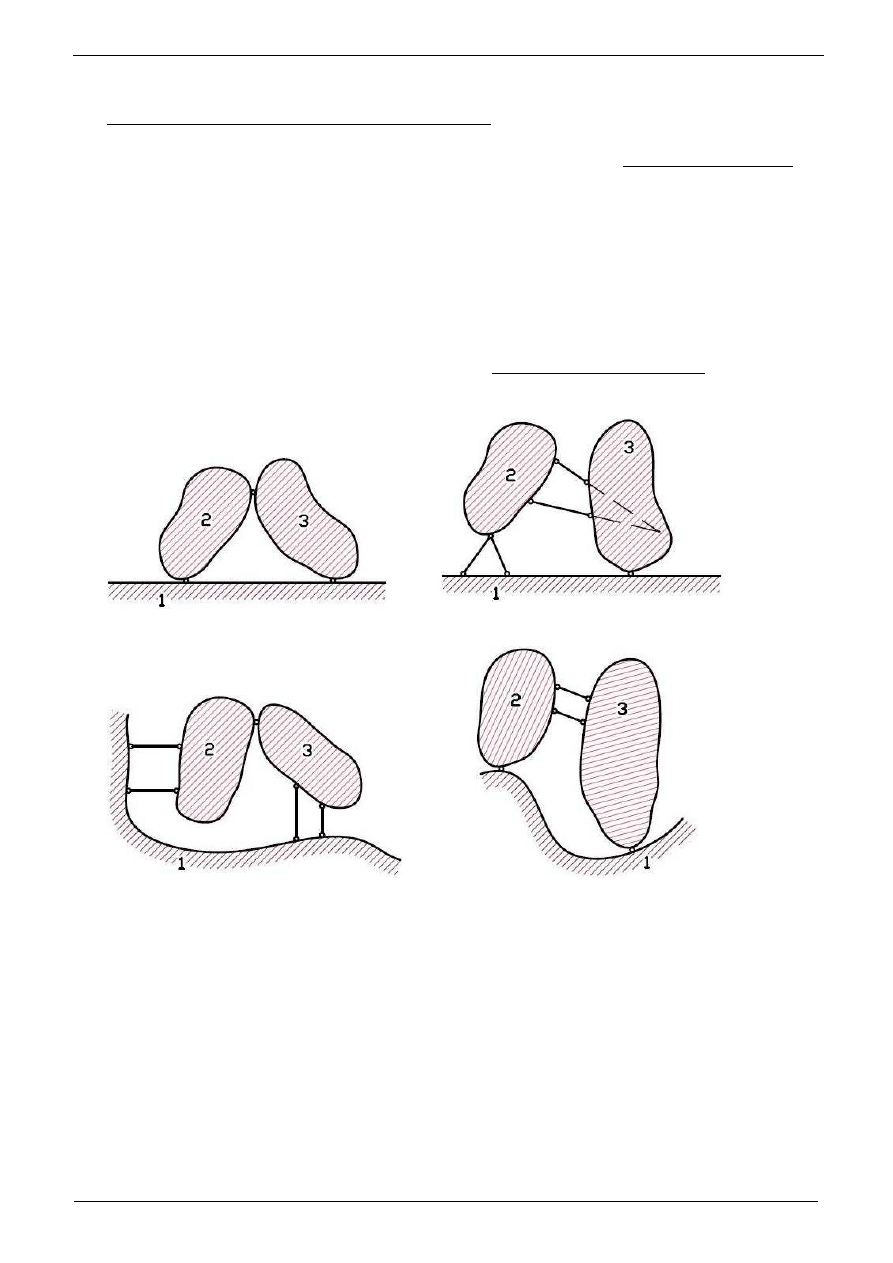
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
10
Typ układów przedstawionych na rysunkach 3.1a i 3.1c okre
ś
lali b
ę
dziemy mianem
układów chwilowo geometrycznie zmiennych (chwilowo, bo ka
ż
de najmniejsze
przemieszczenie spowoduje,
ż
e kierunki wi
ę
zów nie b
ę
d
ą
przecinały si
ę
w jednym
punkcie). W
ś
wietle powy
ż
szych rozwa
ż
a
ń
sformułowa
ć
mo
ż
na warunek dostateczny
geometrycznej niezmienno
ś
ci układu tarcz, ł
ą
cz
ą
c ze sob
ą
warunki dotycz
ą
ce
zarówno liczby jak i kierunków wi
ę
zów:
Układ dwóch tarcz sztywnych jest układem geometrycznie niezmiennym, gdy
tarcze składowe poł
ą
czone s
ą
za pomoc
ą
trzech wi
ę
zów, których kierunki nie
przecinaj
ą
si
ę
w jednym punkcie (rzeczywistym lub niewła
ś
ciwym).
Spróbujmy sformułowa
ć
podobne kryterium dla układów zbudowanych z trzech tarcz
poł
ą
czonych mi
ę
dzy sob
ą
w sposób przedstawiony na rysunkach 3.2 a-d, gdzie
ka
ż
da tarcza poł
ą
czona jest z pozostałymi za pomoc
ą
dwóch (i tylko dwóch) wi
ę
zów.
Układy tarcz o podanej strukturze nosz
ą
nazw
ę
układów trójprzegubowych. Przykłady
takich układów przedstawiaj
ą
poni
ż
sze rysunki:
Rys. 3.2 a Rys. 3.2 b
Rys. 3.2 c Rys. 3.2 d
Dla ka
ż
dego układu trójprzegubowego spełniony jest warunek konieczny
geometrycznej niezmienno
ś
ci – potrojona liczba tarcz (nie licz
ą
c tarczy podporowej)
równa jest liczbie zastosowanych wi
ę
zów. Nie ka
ż
dy jednak układ trójprzegubowy jest
układem geometrycznie niezmiennym, tzn. nie dla ka
ż
dego układu trójprzegubowego
spełniony jest warunek dostateczny geometrycznej niezmienno
ś
ci. Na rysunku 3.3a
przedstawiony jest jeden z takich układów. Punkt B w tym układzie mo
ż
e dozna
ć
niesko
ń
czenie małego przemieszczenia w kierunku prostopadłym do linii, na której
le
żą
przeguby A, B i C, a zatem układ ten jest chwilowo geometrycznie zmienny.
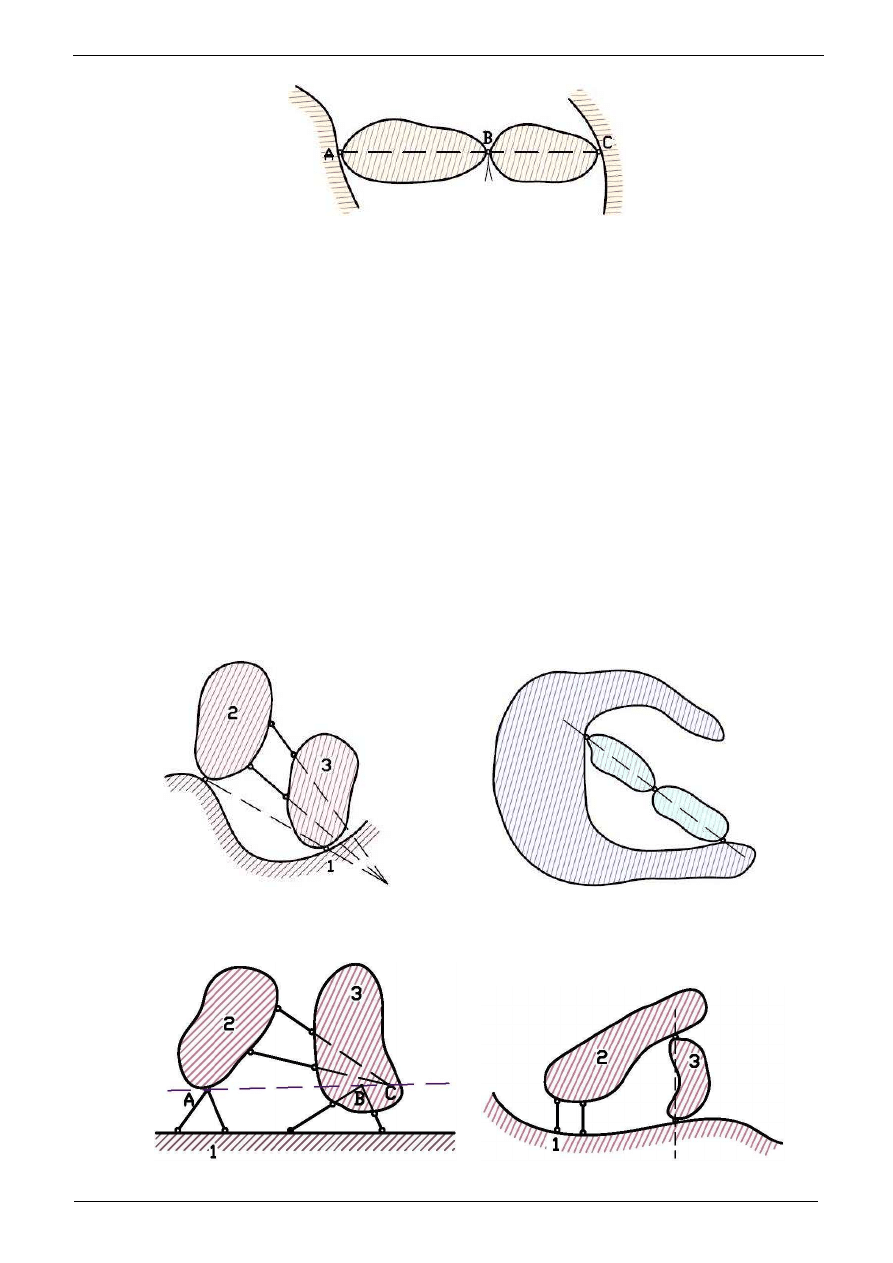
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
11
Rys. 3.3a
Wystarczyłoby jednak, aby jeden z przegubów nie le
ż
ał na prostej przechodz
ą
cej
przez dwa pozostałe przeguby. Układ taki byłby geometrycznie niezmienny. Tak wi
ę
c
sformułujmy
warunek
dostateczny
geometrycznej
niezmienno
ś
ci
układu
trójprzegubowego:
Układ trójprzegrzegubowy jest układem geometrycznie niezmiennym, gdy trzy
przeguby (rzeczywiste lub fikcyjne – przez które rozumiemy punkty przeci
ę
cia si
ę
wi
ę
zów
nie maj
ą
cych w rzeczywisto
ś
ci punktów wspólnych) ł
ą
cz
ą
ce tarcze sztywne tego układu ze
sob
ą
nie le
żą
na jednej prostej.
Wszystkie układy trójprzegubowe przedstawione na rysunkach 3.2a-d s
ą
układami
geometrycznie niezmiennymi. Rysunki 3.3a-f przedstawiaj
ą
układy trójprzegubowe
chwilowo geometrycznie zmienne. Warto zwróci
ć
uwag
ę
,
ż
e o klasyfikacji układu decyduje
warunek dostateczny, poniewa
ż
w ka
ż
dym z poni
ż
szych przypadków warunek konieczny
geometrycznej niezmienno
ś
ci jest spełniony. Nale
ż
y zauwa
ż
y
ć
,
ż
e w przypadku, gdy jeden
z przegubów znajduje si
ę
w niesko
ń
czono
ś
ci (rys. 3.3e oraz 3.3f), aby układ był
geometrycznie niezmienny dwa pozostałe przeguby nie mog
ą
le
ż
e
ć
na prostej równoległej
do kierunku pr
ę
tów tworz
ą
cych ów przegub fikcyjny.
Rys. 3.3 b Rys. 3.3c
Rys. 3.3d Rys. 3.3e
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
12
Rys. 3.3f
Na koniec zajmijmy si
ę
układami zło
ż
onymi:
Analiz
ę
kinematyczn
ą
układu zło
ż
onego z wielu tarcz rozpoczynamy od sprawdzenia
warunku koniecznego, je
ś
li jest spełniony – sprawdzamy warunek dostateczny
geometrycznej niezmienno
ś
ci, wyodr
ę
bniaj
ą
c z układu zło
ż
onego fragmenty o budowie
opisanej powy
ż
ej, a wi
ę
c dwie tarcze poł
ą
czone ze sob
ą
trzema pr
ę
tami, układy
trójprzegubowe, lub ich kombinacje, pami
ę
taj
ą
c o istotnym warunku niewspóliniowo
ś
ci
przegubów
układu
trójprzegubowego
i
warunku
dostatecznym
geometrycznej
niezmienno
ś
ci tarcz sztywnych poł
ą
czonych trzema pr
ę
tami.
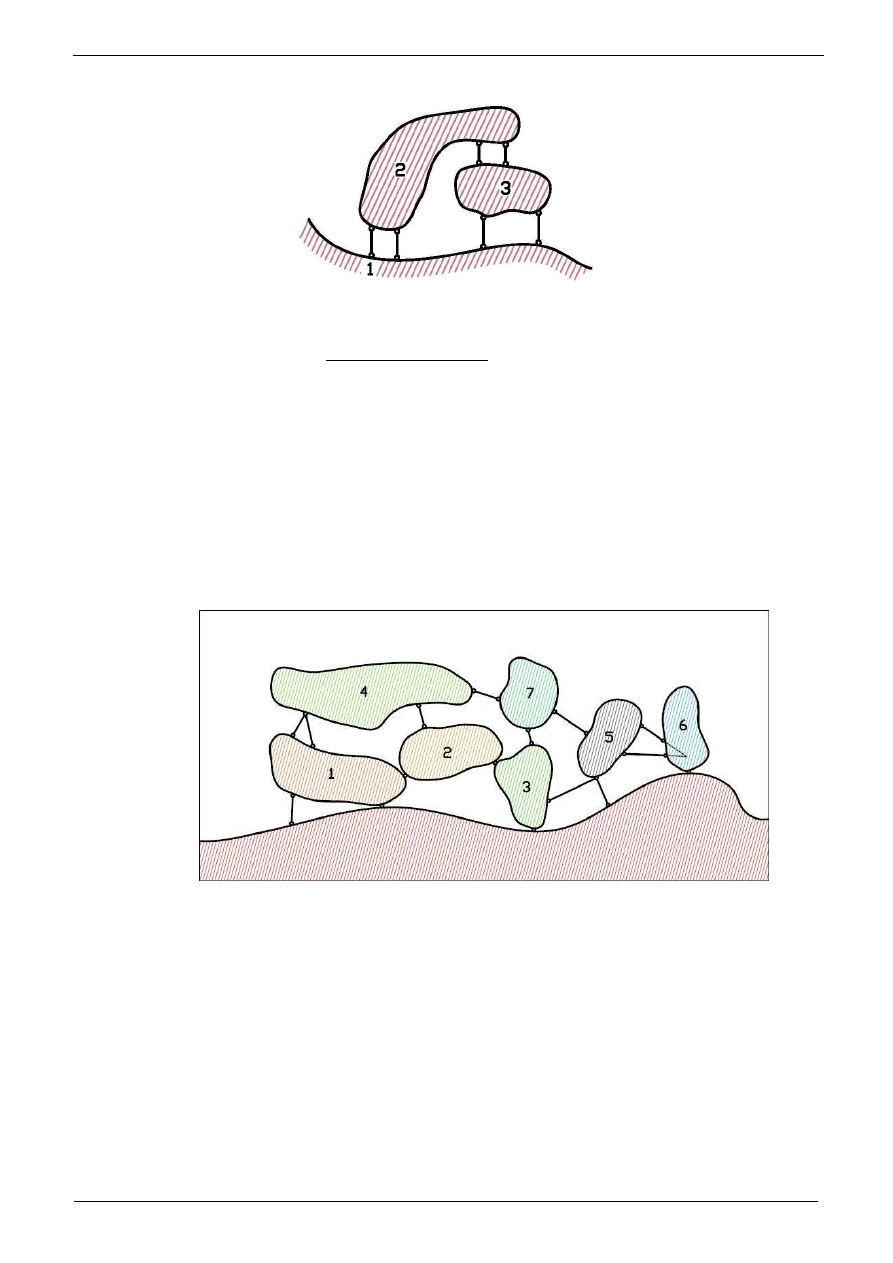
Przeanalizujmy dla przykładu poni
ż
szy układ składaj
ą
cy si
ę
z 7 tarcz sztywnych i
tarczy podporowej.
Sprawd
ź
my najpierw warunek konieczny geometrycznej niezmienno
ś
ci tego układu:
p
t
≤
⋅
3
U nas:
7
=
t
(liczba tarcz, nie licz
ą
c tarczy podporowej)
21
2
5
1
11
=
⋅
+
⋅
=
p
(11 pr
ę
tów odbieraj
ą
cych po jednym stopniu swobody ka
ż
dy,
i 5 przegubów, ka
ż
dy odbieraj
ą
cy dwa stopnie swobody)
21
21
21
7
3
≤
≤
⋅
Otrzymali
ś
my to
ż
samo
ść
, a wi
ę
c spełniony jest warunek konieczny.
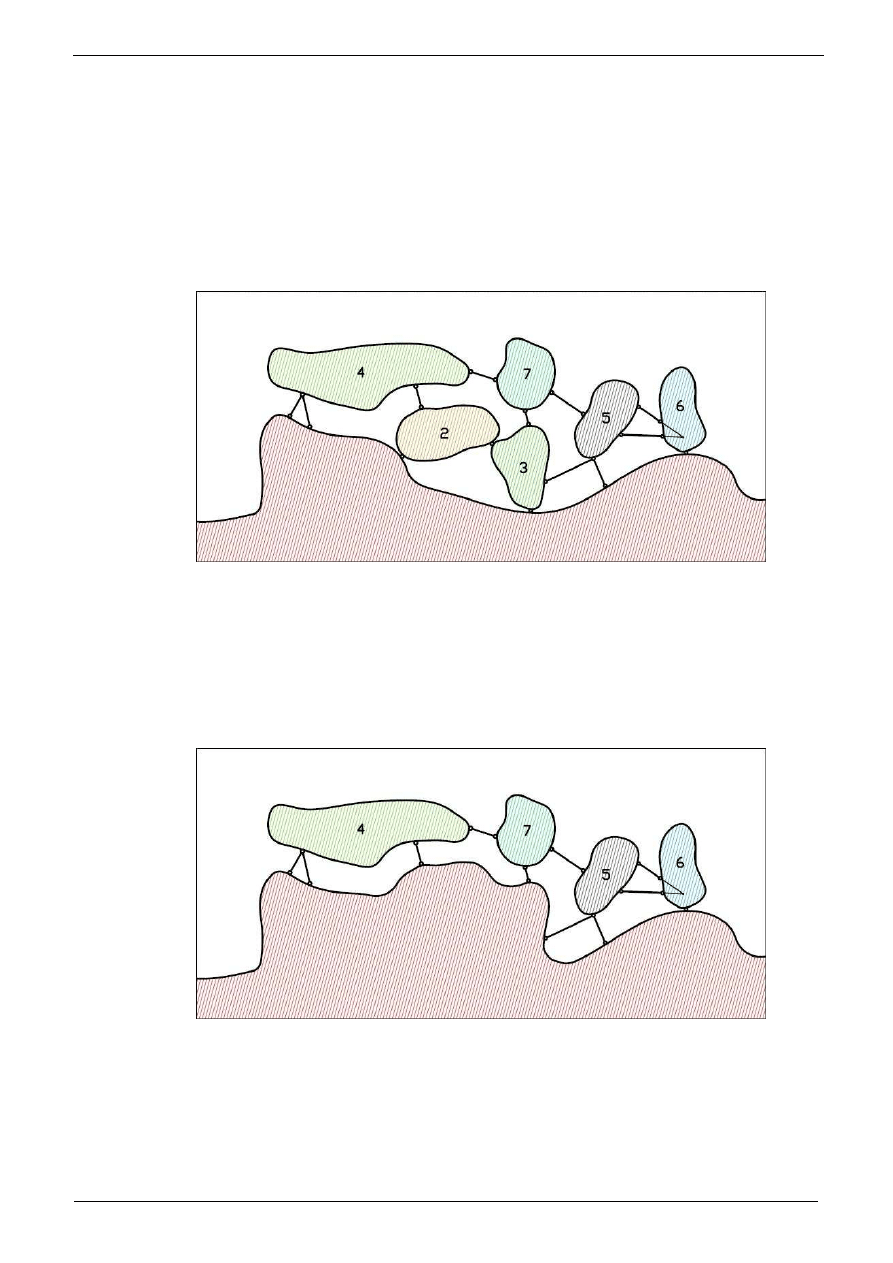
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
13
Rozpatrzymy na pocz
ą
tku poł
ą
czenie tarczy „1” z tarcz
ą
podporow
ą
. Tarcze te
zwi
ą
zane s
ą
ze sob
ą
za pomoc
ą
trzech wi
ę
zów – jednego przegubu i jednego pr
ę
ta,
przy czym przegub nie le
ż
y na kierunku pr
ę
ta. Tarczy „1” wi
ę
zy odbieraj
ą
wi
ę
c trzy
stopnie swobody. Tarcze „1” i tarcza podporowa stanowi
ą
zatem zespół geometrycznie
niezmienny zwany tarcz
ą
zast
ę
pcz
ą
. Po takiej analizie poł
ą
czenie tarcz: podporowej i
tarczy „1” uznajemy za sztywne i tarcz
ę
„1” traktujemy wraz z tarcz
ą
podporow
ą
jako
„cało
ść
”. Tarcza „1” mo
ż
e wi
ę
c stanowi
ć
podpor
ę
dla innych, dalszych tarcz. Na
rysunku zaznaczymy to schematycznie zespalaj
ą
c tarcz
ę
„1” z tarcz
ą
podporow
ą
:
Do takiego układu doł
ą
czone s
ą
tarcze „2” oraz „3”, tworz
ą
ce razem z nim układ
trójprzegubowy. Ka
ż
da z tarcz („1” i „2”) poł
ą
czona jest z tarcz
ą
podporow
ą
jednym
przegubem, a drugim przegubem ł
ą
czy si
ę
z tarcz
ą
tworz
ą
c
ą
układ. Poniewa
ż
przeguby nie le
żą
na jednej prostej, to równie
ż
układ tarcz: tarcza podporowa (p’), 2 i 3
mo
ż
emy traktowa
ć
w naszej analizie kinematycznej jako układ geometrycznie
niezmienny. Znów schematycznie zaznaczymy to jako „powi
ę
kszenie” tarczy
podporowej o geometrycznie niezmienny układ trójprzegubowy:
Kolejno do tej niezmiennej cz
ęś
ci przył
ą
czona jest za pomoc
ą
trzech pr
ę
tów tarcza
„4”. Poniewa
ż
kierunki pr
ę
tów nie przecinaj
ą
si
ę
w jednym punkcie, równie
ż
ta tarcza
pozostaje niezmienna geometrycznie.
Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
14
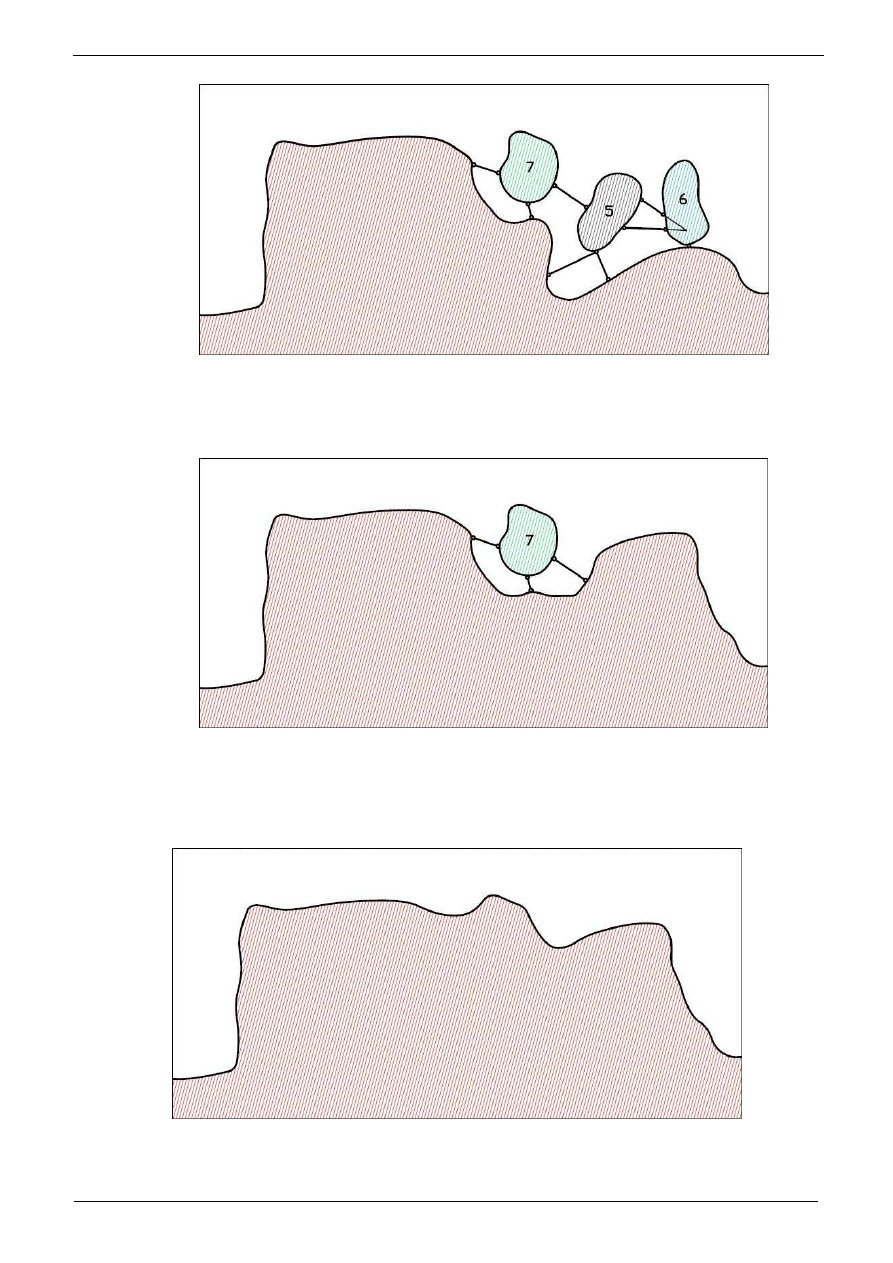
Id
ą
c dalej zauwa
ż
amy układ trójprzegubowy. Tworz
ą
go tarcza podporowa i tarcze „5”
oraz „6”. Przeguby (rzeczywiste i fikcyjne) nie le
żą
na jednej prostej, a wi
ę
c układ ten
jest geometrycznie niezmienny. Mamy wi
ę
c:
Pozostała tarcza „7”, która poł
ą
czona jest z tarcza podporow
ą
za pomoc
ą
trzech pr
ę
tów,
których kierunki nie przecinaj
ą
si
ę
w jednym punkcie. Tarcza ta jest wi
ę
c nieruchoma
wzgl
ę
dem tarczy podporowej. Zaznaczmy to schematycznie zespalaj
ą
c i t
ą
tarcz
ę
z
tarcza podporow
ą
.
W ten sposób pokazali
ś
my,
ż
e cały układ jest geometrycznie niezmienny. Na tym
ko
ń
czymy analiz
ę
kinematyczn
ą
układu tarcz sztywnych.

Politechnika Pozna
ń
ska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2004/2005
www.ikb.poznan.pl/anita.kaczor
wykonał Dariusz Włochal
15
Opracowano na podstawie:
•
„Wytrzymało
ść
materiałów – zarys teorii, przykłady, zadania. Cz
ęść
I” Praca
zbiorowa pod redakcj
ą
K. Wrzesniowskiego. Wyd. PP, 1985 r.
•
„Wytrzymało
ść
materiałów dla wydziałów budowlanych” – Stefan Piechnik,
PWN, Warszawa – Kraków, 1978 r.
•
„Mechanika materiałów i konstrukcji pr
ę
towych” – Andrzej Gaw
ę
cki, Wyd. PP,
1998 r.
•
Materiałów zamieszczonych na stronie:
http://student.uci.agh.edu.pl/
Wyszukiwarka
Podobne podstrony:
Analiza kinetyczna belki, ramy i kratownice płaskie
Analiza kinetyczna i statyczna płaskich układów tarcz sztywnych
analiza cieplna, sprawozdanie1, Dariusz Winiarski
Projekt 1 (Dariusza Włochata)
zagadnienia-opr, Pedagogika studia magisterskie, zintegrowany paradygmat analizy działania w polu pr
Analiza mikrofalowego suszenia selera korzeniowego w warunkach obniżonego ciśnienia Kinetyka suszeni
Analiza mikrofalowego suszenia pietruszki w warunkach obniżonego ciśnienia Cz 1 Kinetyka suszenia pi
analiza złożonych aktów ruchowych w sytuacjach patologicznych
Prezentacja 2 analiza akcji zadania dla studentow
Wypadkoznawstwo analiza wypadków
Zarz[1] finan przeds 11 analiza wskaz
Analiza czynnikowa II
4 ANALIZA WSKAŹNIKOWA Rachunkowość
analiza finansowa ppt
więcej podobnych podstron