6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________

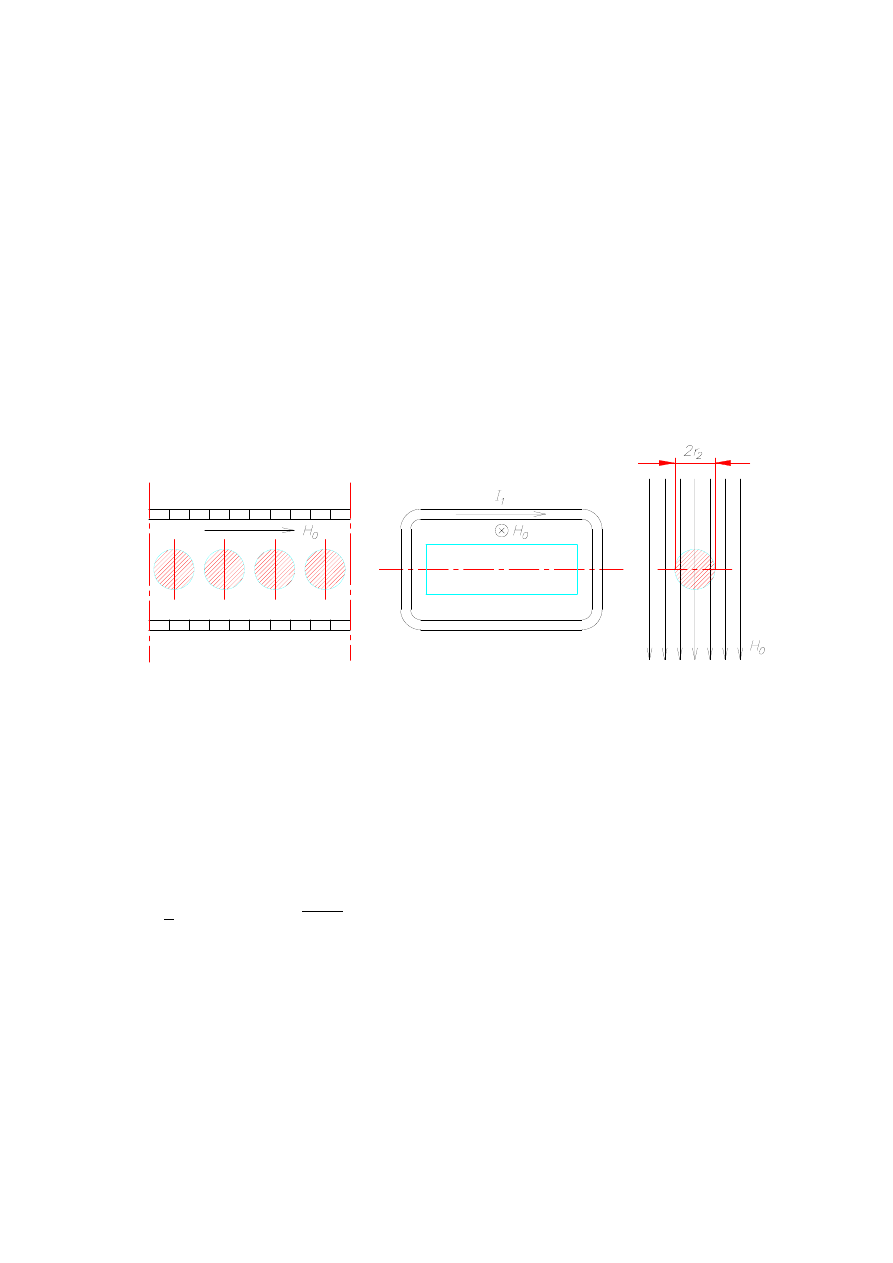
6.1.2.10. Wsady w poprzecznym polu elektromagnetycznym

We wszystkich dotąd rozpatrzonych przypadkach z polem podłużnym znane było natężenie
pola magnetycznego na granicy rozważanych obszarów, co znacznie ułatwiało wyznaczanie
stałych w rozwiązaniach równania różniczkowego opisującego pole we wnętrzu tych
obszarów. Układy grzejne o polu poprzecznym, czyli o kierunkach linii pola nie będących
stycznymi do powierzchni wsadu nie mają tej cechy i dlatego obliczenie rozkładu
podstawowych wielkości elektromagnetycznych jest trudniejsze. Pole na granicy obszaru, w
którym poszukuje się rozwiązania, np. na powierzchni wsadu, ma dwie składowe. Ich
wyznaczenie nie jest także łatwe i dlatego rozwiązania analityczne o dużej dokładności istnieją
dla nielicznych przypadków. Jeden z nich zostanie w dalszym ciągu przedstawiony.

Rys. 6.23. Wsad walcowy w polu poprzecznym, wg [352]

Cylinder w polu poprzecznym jest przypadkiem mającym duże znaczenie praktyczne,

zwłaszcza przy potokowej obróbce elementów o niewielkich średnicach. Jeśli cylinder o
promieniu r

2

jest umieszczony w jednorodnym sinusoidalnie zmiennym polu magnetycznym o

pulsacji ω (rys. 6.23), to w układzie współrzędnych cylindrycznych dla r= r

2

muszą być

spełnione warunki (6.18) i (6.20). Przyjmując, że wsad jest niemagnetyczny i ma stałe
parametr materiałowe, średnią gęstość powierzchniową mocy pozornej wnikającej do wsadu
określa się z zależności

)

jF

F

(

δ

γ

H

jq

p

S

x

r

2

2

2

0

m

2

20

20

20

+

=

+

=

(6.133)

przy czym współczynniki kształtu F

r

i F

x

przyjmują wartości charakterystyczne dla wsadu

walcowego w polu podłużnym.

Dwukrotnie większą moc we wsadzie w porównaniu z nagrzewaniem w polu

podłużnym tłumaczy się lokalnie większym natężeniem pola magnetycznego na powierzchni
wsadu. W przypadku wsadu magnetycznego moc we wsadzie w polu poprzecznym może być
mniejsza (gdy 2r

2

<δ

2

) lub większa (gdy 2r

2

>>δ

2

) aniżeli w polu podłużnym. Rozkład mocy na

powierzchni wsadu jest zawsze nierównomierny [514], [558].
51

6. Nagrzewanie indukcyjne
____________________________________________________________________________

Układy z polem poprzecznym są często stosowane przy nagrzewaniu płyt, blach, taśm

oraz przy międzyoperacyjnym lokalnym dogrzewaniu taśm [383], [481], [558]. Spośród
wymienionych w p. 6.1.2.3 metod obliczeń i analizy takich przypadków, współcześnie
najczęściej korzysta się z metod numerycznych.

6.1.2.11. Wsady ferromagnetyczne o nieliniowej charakterystyce magnesowania w polu

elektromagnetycznym

Przedstawione dotąd modele dotyczyły układów z wsadami charakteryzującymi się stałością
przenikalności magnetycznej, a więc dobrze opisywały zjawiska występujące przy propagacji
pola we wsadach niemagnetycznych. Istnieją wsady znamienne tym, że ich przenikalność
magnetyczna zależna jest od natężenia pola magnetycznego, a także od temperatury w stopniu
wykluczającym posługiwanie się modelami charakteryzującymi się µ

2

= const. Do wsadów

takich należy wiele gatunków stali, zwłaszcza gdy są nagrzewane powyżej punktu Curie (punkt
przemiany magnetycznej). Analiza pola dla takich przypadków przy użyciu metod
analitycznych jest trudna.

Jedna z metod analizy polega na oddzielnym rozważeniu propagacji pola w trzech

charakterystycznych fazach procesu nagrzewania, a mianowicie: od początku procesu do
osiągnięcia przez powierzchnię wsadu punktu przemiany magnetycznej określonej temperaturą
Curie t

C

, w fazie przejściowej, podczas której tylko część wsadu przekroczyła t

C

, w fazie

końcowej kiedy to cały wsad ma temperaturę t > t

C

.

W dalszym ciągu omówione zostanie padanie fali płaskiej na półprzestrzeń

przewodzącą, a w zakończeniu przeprowadzona zostanie analiza możliwości wykorzystania
uzyskanych wyników w zadaniach dotyczących układów cylindrycznych.

Pierwsza faza procesu przebiega przy

)

τ

,

H

(

f

µ

2

2

=

, a więc w czasie zmian

przenikalności magnetycznej określonej funkcją

)

τ

,

x

(

f

2

µ

=

, ponieważ

. Biorąc

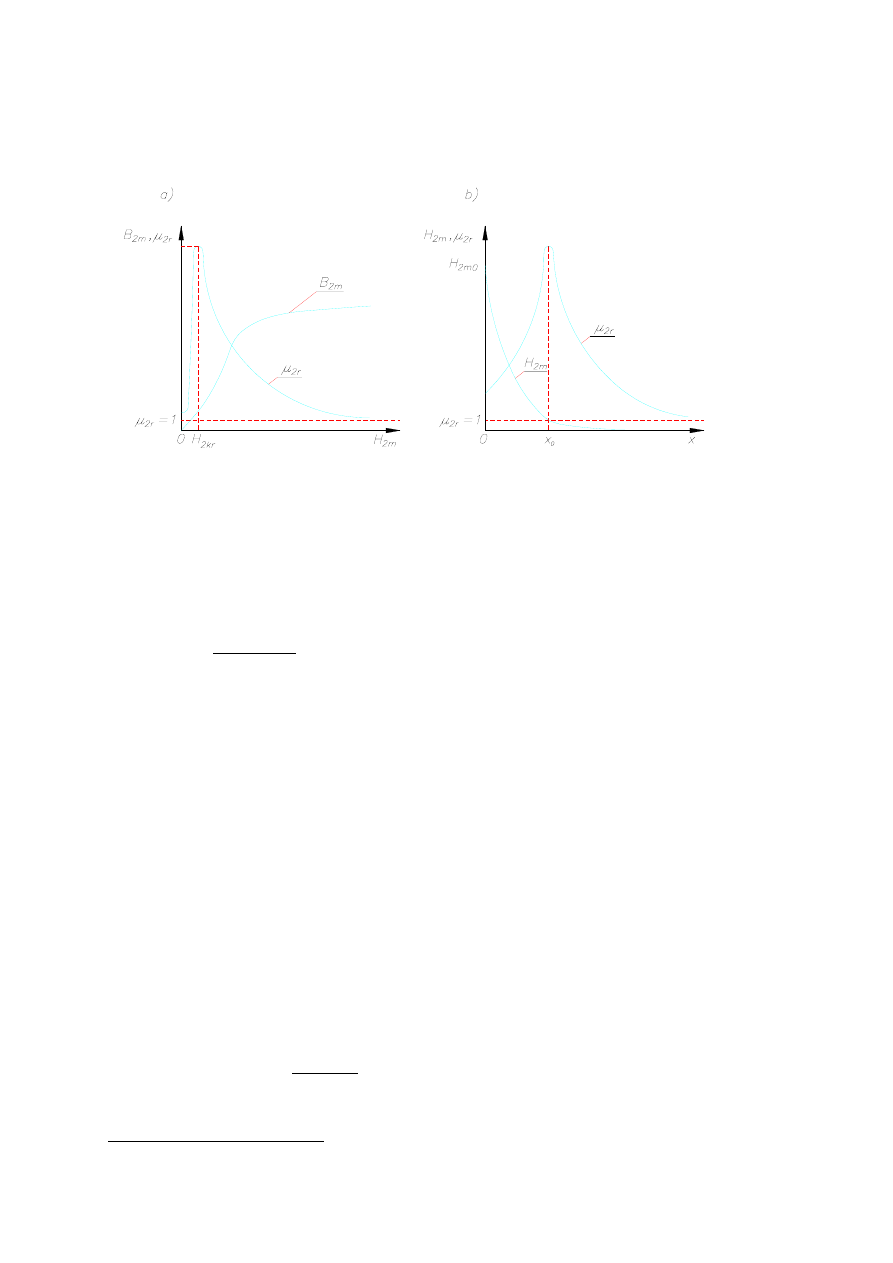
pod uwagę, iż istnieje krytyczna wartość natężenia pola magnetycznego

, przy której

przenikalność magnetyczna względna

osiąga wartość największą

(rys. 6.24a), zmiana

przenikalności magnetycznej w funkcji odległości od powierzchni wsadu daje się przedstawić
tak jak to pokazano na rys. 6.24b. Dla większości stopów żelaza krytyczna wartość natężenia
pola magnetycznego

zawiera się w przedziale 50÷2000 A/m. Przy nagrzewaniu

indukcyjnym natężenie pola magnetycznego

i zwykle ma wartość większą niż

50 000 A/m [652].

)

x

(

f

H

2

=

kr

2

H

r

2

µ

rm

2

µ

kr

2

H

kr

2

H

>>

mo

2

H

Przebiegi funkcji

daje się w przybliżeniu przewidzieć na podstawie

znajomości

i charakterystyki magnesowania wsadu (krzywa

na rys. 6.24a).

Według dość rozpowszechnionej aproksymacji Nejmana

)

x

(

f

µ

r

2

=

)

x

(

f

H

m

2

=

m

2

B

n

/

1

m

2

H

m

2

H

C

B

=

(

6.134)

przy czym

C

- stałe (dla

n

,

H

20

n

4

,

H

H

kr

2

m

2

<

<

>

zaś dla

1

n

,

H

H

kr

2

m

2

≤

<

).

Biorąc pod uwagę fakt, że

jest zależnością nieliniową, wielkości

są niesinusoidalnymi funkcjami czasu. Stąd też

i

zastępuje się ich pierwszymi

harmonicznymi i wówczas przenikalność magnetyczna przestaje zależeć od czasu.

)

H

(

B

2

2

2

2

2

B

,

H

,

E

)

τ

(

B

2

)

τ

(

H

2

52

6.1. Zasady nagrzewania indukcyjnego
___________________________________________________________________________

Rys. 6.24. Charakterystyki magnetyczne ferromagnetyka, wg [652]: a) indukcja magnetyczna

i

przenikalność magnetyczna względna

w funkcji natężenia pola magnetycznego

b) zależność

natężenia pola magnetycznego oraz przenikalności względnej od odległości od powierzchni wsadu x

m

2

B

2

H

r

2

µ

m

Dla pierwszych harmonicznych

)

x

(

f

µ

r

2

=

aproksymuje się wyrażeniem

1

)

x

/

x

1

(

µ

µ

0

0

r

2

1

m

2

1

−

=

(6.135)

przy czym

jest przenikalnością magnetyczną względną (indeks r) wsadu (indeks 2) dla

pierwszej harmonicznej (indeks l) w miejscu

0

r

2

1

µ

0

x

=

, czyli na powierzchni wsadu (indeks 0), zaś

jest wartością

x, przy której występuje optimum przenikalności magnetycznej.

0

x

Z zależności (6.135) wynika, że przy

,

0

x

x

→

∞

→

r

2

1

µ

0

m

zaś

. W rze-

czywistości

osiąga wtedy

(rys. 6.24). Takie uproszczenie jest dlatego dopuszczalne,

ponieważ przy nagrzewaniu indukcyjnym

0

H

m

2

→

m

2

H

kr

2

H

2

H

kr

2

H

<<

, czyli dla

fala elekt-

romagnetyczna praktycznie zanika.

0

x

=

x

Według Nejmana

powinno się wyznaczać z pierwotnej krzywej magnesowania

przy wartości natężenia pola magnetycznego równej wartości skutecznej

1

na

powierzchni wsadu [593]. Według Turowskiego dostateczną dokładność uzyskuje się
przyjmując

1

dla wartości maksymalnej

1

[701].

0

r

2

1

µ

0

m

2

H

0

r

2

µ

0

m

H

W przypadku padania fali płaskiej na półprzestrzeń przewodzącą i aproksymacji wg

[593] dla pierwszej harmonicznej

2

s

2

0

m

2

1

m

2

1

δ

457

.

1

x

1

H

H













−

=

(6.136)

1

Indeks po lewej stronie wielkości oznacza numer harmonicznej

6. Nagrzewanie indukcyjne
____________________________________________________________________________













−

=

s

2

s

2

2

0

m

2

1

m

2

δ

457

.

1

x

1

δ

γ

1

H

68

.

1

E

1

(6.137)

przy czym:

1

jest natężeniem pierwszej harmonicznej pola magnetycznego na powie-

rzchni półprzestrzeni, zaś

0

m

2

H

0

2

0

r

2

1

s

2

ωµ

γ

µ

2

δ

=

(6.138)

Porównując wzory (6.137) i (6.57) można wykazać, że natężenie pola elektrycznego i

gęstość prądu indukowanego na powierzchni wsadu ferromagnetycznego o

są

19% większe niż przy

)

H

(

f

µ

m

2

r

2

1

=

const

µ

µ

0

r

2

r

2

1

=

=

, o ile w obu przypadkach przenikalność

magnetyczna na powierzchni jest jednakowa.

Ponadto

2

0

r

2

1

2

0

m

2

1

3

s

2

2

2

0

m

2

1

20

γ

/

f

µ

H

10

37

.

1

δ

γ

2

H

37

.

1

p

−

⋅

≈

=

(6.139)

s

2

2

21

δ

γ

2

1

37

.

1

R

=

(6.140)

s

2

2

21

δ

γ

2

1

972

.

0

X

=

(6.141)

816

.

0

φ

cos

=

(6.142)

przy czym

l

1

0

m

2

1

w

I

2

H

=

W porównaniu z półprzestrzenią o

const

µ

2

=

, wartość

oraz

są w rozważanym

przypadku większe o 37%,

o ok. 14%, natomiast wartość

jest mniejsza o ok. 3%.

20

p

21

X

21

R

φ

cos

Efektywną głębokość wnikania prądu przy zmiennej przenikalności magnetycznej

można określić przyrównując rezystancję określoną przy stałej wartości

(n=1 w

zależności (6.134)) z rezystancją przy zmianie wartości

(tzn. gdy

n > 1 w tejże

zależności). Porównanie to wymaga przyjęcia tej samej częstotliwości i przenikalności
magnetycznej na powierzchni. W przypadku gdy

r

2

1

µ

r

2

1

µ

∞

→

n

wg [670]

372

.

1

δ

δ

s

2

z

2

=

(6.143)

gdzie

δ jest głębokością wnikania dla

.

s

2

0

r

2

1

µ

Gdy przenikalność magnetyczna wsadu

1

const

µ

r

2

=

, to moc fali maleje wykładniczo,

zaś wartość

jest osiągana w odległości

20

p

05

.

0

s

2

05

.

0

δ

498

.

1

x

=

. Dla przenikalności

54

6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________

magnetycznej wsadu

1

gdy

var

µ

r

2

=

2

05

.

0

δ

498

.

1

x

,

n

≈

∞

→

, a więc efekt naskórkowości jest

większy.

Zasadnicza trudność w korzystaniu z zależności (6.134), (6.137), (6.139) polega na

konieczności określenia wartości

oraz

0

m

2

1

H

)

µ

H

/(

B

µ

20

0

m

2

1

0

m

2

1

0

r

2

1

=

, a więc dla nieznanych

pierwszych harmonicznych pola. W obliczeniach przybliżonych (z błędem nie
przekraczającym kilku procent) można je określić za pomocą pierwotnej krzywej mag-
nesowania dla wartości skutecznych

i

1

[652]. Procedura postępowania opiera się przy

tym na założeniu, że zadana jest gęstość powierzchniowa mocy czynnej

, a także

konduktywność wsadu i częstotliwość. W takim przypadku

2

1

B

2

H

20

p

2

20

0

r

2

1

2

20

1

γ

/

f

p

367

µ

H

=

(6.144)

Z krzywych magnesowania stali sporządza się uśrednione charakterystyki

1

,

)

H

(

f

B

2

1

2

=

)

H

(

f

µ

H

20

1

0

r

2

1

2

20

1

=

i

jak na rys.6.25. Dla danych

i

f z (6.144)

oblicza się iloczyn

)

H

(

f

µ

20

1

0

r

2

1

=

2

γ

,

20

p

0

r

2

1

µ

2

20

1

H

i z odpowiedniej krzywej

)

H

(

f

20

1

µ

H

r

2

1

2

20

1

20

1

H

0

=

na rys.

6.25, odczytuje się wartość

1

. Następnie dla znanego

na podstawie podanych

krzywych wyznacza się

1

i

1

(652], [670].

20

H

2

B

0

r

2

µ

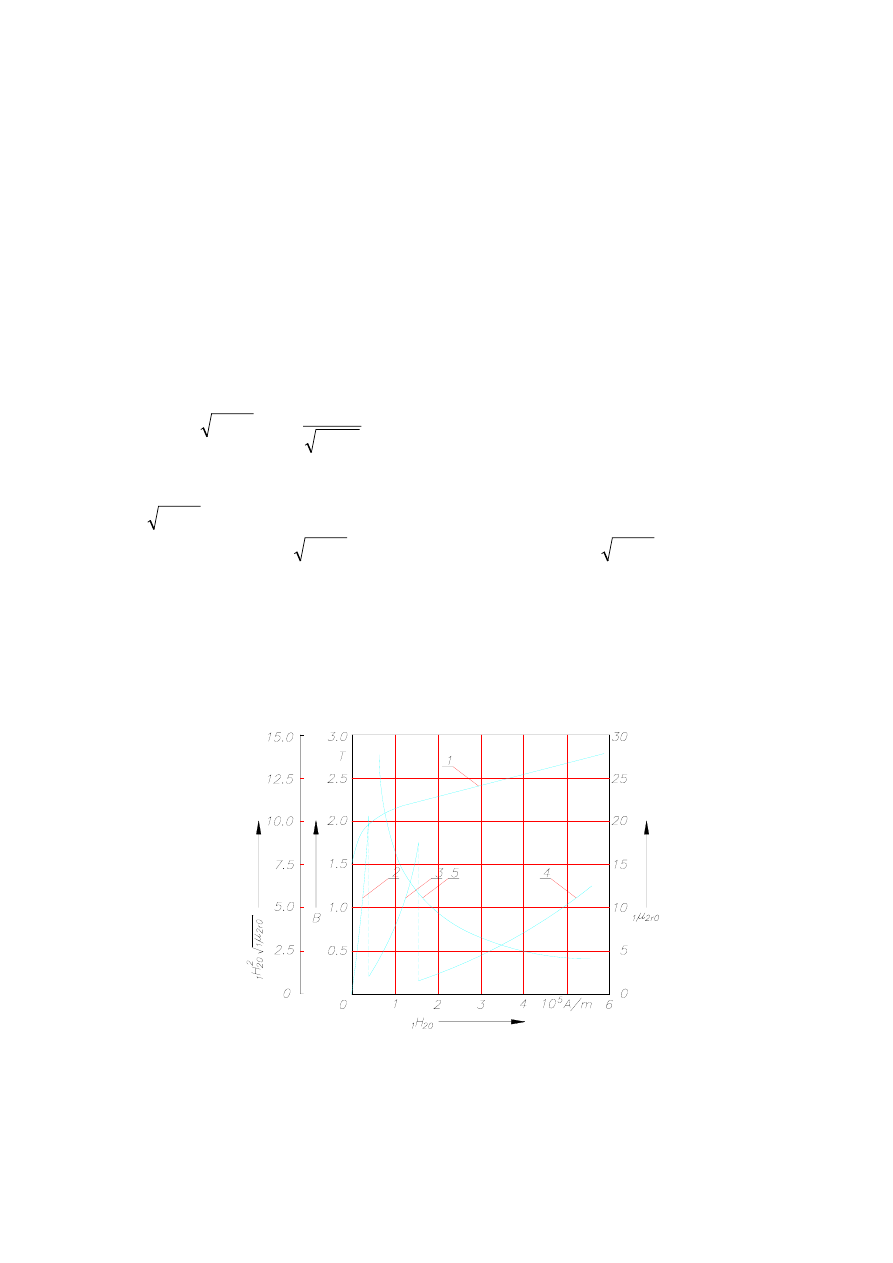
Dla tych gatunków stali, w których zawartość węgla zawiera się w przedziale od 0,23÷ 0,99%,
można korzystać ze średnich wartości przenikalności magnetycznych. Błąd przy tym
uproszczeniu nie powinien przekroczyć 6,7% przy

A/m oraz 2,5%

przy

1

. Przy jeszcze większych natężeniach, błąd maleje do ok. 1%.

3

2

1

10

4

H

⋅

=

4

2

10

4

H

⋅

=

Rys. 6.25. Uśrednione charakterystyki właściwości magnetycznych stali, wg [670]

1 -

1

; 2, 3, 4 -

1

(wartości odczytane z kolejnych krzywych na

wykresie należy pomnożyć odpowiednio przez 10

)

H

(

f

B

20

1

2

=

)

H

(

f

H

20

1

2

20

=

9

, 10

10

, 10

11

); 5 –

1

)

H

(

f

µ

20

1

0

r

2

=

55

6. Nagrzewanie indukcyjne
____________________________________________________________________________

Biorąc pod uwagę, że we wszystkich zależnościach przenikalność magnetyczna występuje pod
pierwiastkiem kwadratowym, błąd maleje dwukrotnie i jego wartość zrównuje się z wartością
błędu pomiaru tej wielkości [670].

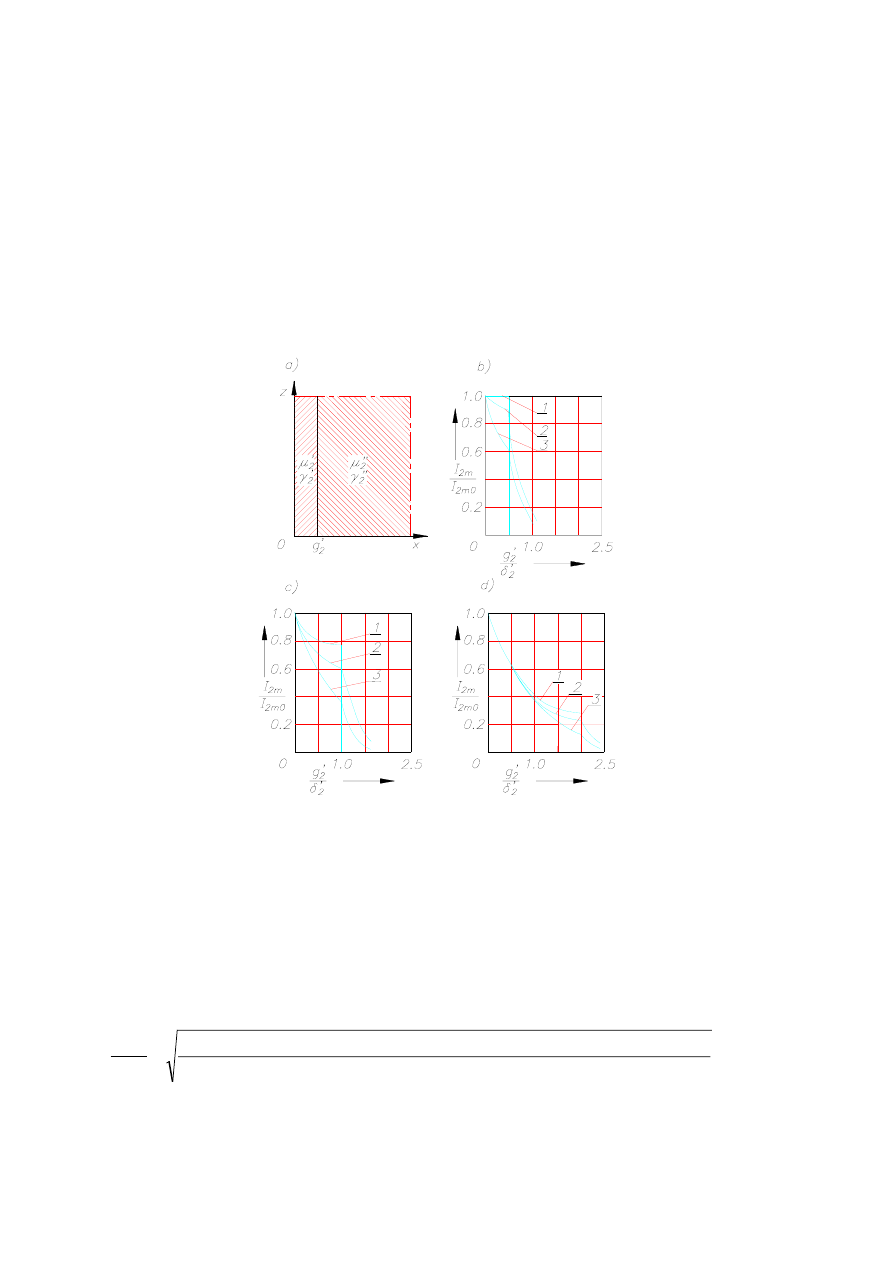
Druga faza procesu charakteryzuje się skokową zmianą przenikalności

a więc

wsad należy traktować jako dwuwarstwowy, przy czym warstwa pierwsza o parametrach

ma grubość

. Druga warstwa jest w rozważanym przypadku półprzestrzenią o

parametrach

. Rozkłady gęstości prądów w tej fazie pokazano na rys. 6.26.

2

µ

2

0

2

γ

,

µ

µ

′

=

′

2

g′

2

2

γ

,

µ

′′

′′

Rys. 6.26. Wsad o skokowo zmieniających się właściwościach magnetycznych, wg [670]: a) półprzestrzeń

przewodząca z warstwą niemagnetyczną o grubości

2

g

x

0

′

<

≤

oraz obszar o właściwościach

magnetycznych dla

; b) rozkłady względnej gęstości przy

2

g

x

′

≥

5

.

0

δ

/

g

2

2

=

′

′

; c) - przy

1

δ

/

g

2

2

=

′

′

;

d) - przy

2

δ

/

g

2

2

=

′

′

1 – przy

∞

=

′′

2

µ

2

g

x

, 2 – przy

, 3 - bez uwzględnienia wpływu właściwości magnetycznych

obszaru

16

µ

2

=

′′

′

≥

Rozkład względnej gęstości prądów w warstwie pierwszej określa związek [670]

)

δ

/

g

2

cos(

m

2

)

δ

/

g

2

exp(

m

)

δ

/

g

2

exp(

]

δ

/

)

x

g

(

2

cos[

m

2

]

δ

/

)

x

g

(

2

exp[

m

]

δ

/

)

x

g

(

2

exp[

J

J

2

2

2

2

2

2

2

2

2

2

2

2

2

2

0

m

2

m

2

′

′

−

′

′

−

+

′

′

′

−

′

−

′

−

′

−

+

′

−

′

=

′

′

(6.145)
56

6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________
przy czym

r

2

r

2

µ

1

µ

1

m

′′

+

′′

−

=

(6.146)

2

0

2

γ

ωµ

2

δ

′

=

′

(6.147)

Przy

m = -1, a więc dla dużych wartości

2

r

µ

2

2

2

2

2

2

2

2

0

m

2

m

2

)

δ

/

g

2

cos(

)

δ

/

g

2

(

ch

]

δ

/

)

x

g

(

2

cos[

]

δ

/

)

x

g

(

2

[

ch

J

J

′

′

+

′

′

′

−

′

+

′

−

′

=

′

′

(6.148)

Rozkład względnej gęstości prądów w warstwie drugiej określa zależność

]

δ

/

)

g

x

(

exp[

J

J

2

2

mg

2

m

2

′′

′

−

−

=

′′

′′

(6.149)

przy czym wartość

mg

2

J ′′

otrzymuje się z (6.145) dla

2

g

x

′

=

, natomiast

2

r

2

2

γ

µ

ω

2

δ

′′

′′

=

′′

(6.150)

Krzywe rozkładu w warstwie drugiej przedstawione są przy założeniu, że

,

const

µ

2

=

′′

const

γ

γ

2

2

=

′

=

′′

.

Z rysunku 6.26 wynika, że obecność drugiego ośrodka o

1

µ

r

2

>

′′

ma poważny wpływ

na rozkład gęstości prądu. Im większa jest wartość

r

2

µ ′′ , tym bardziej równomierna jest gęstość

prądu w warstwie pierwszej i w konsekwencji tym większa równomierność mocy grzejnej.
Przy malejącej głębokości nagrzania, rozkład gęstości prądu w funkcji

jest coraz

bardziej stromy, co w konsekwencji sprzyja jednorodności temperatury w warstwie nagrzanej.
Przy

, wpływ drugiej warstwy na rozkład gęstości prądu w warstwie pierwszej

maleje zbliżając się do przebiegu wykładniczego. Nagrzewanie przybiera charakter
powierzchniowy [670].

2

δ

/

x

′

1

δ

/

g

2

2

>

′

′

Impedancja jednostkowa wsadu

21

21

21

jX

R

Z

+

=

, przy czym

2

21

21

φ

cos

Z

R

=

(6.151)

(6.152)

2

21

21

φ

sin

Z

X

=

2

2

21

δ

γ

K

2

Z

′

′

=

(6.153)

57

6. Nagrzewanie indukcyjne
____________________________________________________________________________

Kąt przesunięcia fazowego między wektorami natężenia pola magnetycznego i elektrycznego

)

δ

/

g

4

exp(

m

1

)

δ

/

g

2

sin(

)

δ

/

g

2

exp(

m

2

arctg

4

π

φ

2

2

2

2

2

2

2

2

′

′

−

−

′

′

′

′

−

+

=

(6.154)

Współczynnik

K oblicza się ze wzoru [670]

)

δ

/

g

2

cos(

)

δ

/

g

2

exp(

m

2

)]

δ

/

g

4

exp(

m

1

)

δ

/

g

2

(

sin

)

δ

/

g

4

exp(

m

4

)]

δ

/

g

4

exp(

m

1

[

K

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

′

′

′

′

−

+

′

′

−

+

′

′

′

′

−

+

′

′

−

−

=

(6.155)

Gęstość powierzchniową mocy czynnej, w W/m

2

określa się także za pomocą współczynnika

K

i

cos

[670]

φ

2

2

2

0

m

2

3

20

φ

cos

γ

/

f

K

H

10

405

.

1

p

−

⋅

=

(6.156)

przy czym:

wyrażone jest w A/m,

f w Hz zaś

0

m

2

H

2

γ′ w 1/(Ω • m).

Korzystanie z podanych wzorów wymaga znajomości względnej przenikalności

magnetycznej

oraz . Problem istnieje ze znalezieniem jedynie

r

2

µ ′′

2

δ′

r

2

µ ′′ ponieważ określa

się wprost ze wzoru (6.147). Wartość

2

δ′

r

2

µ ′′ wyznaczana jest metodą iteracyjną poprzez

poszukiwanie natężenia

)

g

x

(

H

2

m

2

′

=

′′

, od którego jest ona zależna (rys.6.25). Biorąc pod

uwagę, że natężenie pola magnetycznego na granicy warstwy niemagnetycznej i magnetycznej,
tzn. dla

jest zależne od natężenia tegoż pola na powierzchni zewnętrznej

(x = 0),

najwygodniej posłużyć się związkiem [670]

2

′

g

x

=

(

)

)

δ

/

g

2

cos(

m

2

)

δ

/

g

2

exp(

m

)

δ

/

g

2

exp(

µ

1

2

1

N

H

H

2

2

2

2

2

2

2

r

2

m

2

0

m

2

′

′

+

′

′

−

+

′

′

′′

+

=

=

′′

(6.157)

Algorytm wyznaczania poszukiwanej wartości

r

2

µ ′′ przy znanej mocy

jest

następujący:

20

p

— założenie pierwszego przybliżenia wartości

i obliczenie

m ze wzoru (6.146),

)

1

(

r

2

µ ′′

— obliczenie

z (6.154), a zatem także

cos ,

)

1

(
2

φ

)

1

(

2

— obliczenie

)

1

(

K

z (6.155),

— obliczenie

z (6.156),

)

1

(

0

m

2

H

— obliczenie

z (6.157),

)

1

(

N

— obliczenie

,

)

1

(

)

1

(

0

m

2

)

1

(

m

2

N

/

H

H

=

′′

— określenie z rys. 6.25 dla

wartości

,

)

1

(

m

2

H ′′

)

2

(

r

2

µ ′′

— obliczenie

.

)

1

(

)

2

(

r

2

)

1

(

r

2

ε

µ

µ

=

′′

−

′′

58

6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________

Obliczenia kończą się po

n iteracjach, gdy

, czyli po osiągnięciu założonej

dokładności obliczeń. Można także posłużyć się metodą wykreślną oraz tablicami pomo-
cniczymi zawartymi m.in. w pracach [652], [670]. Znajomość

max

)

n

(

ε

ε

≤

r

2

µ ′′

,a więc

K pozwala obliczyć

wszystkie interesujące parametry, a m.in.

R

21

oraz X

21.

W celu ułatwienia obliczeń termokinetycznych dla drugiej fazy procesu wygodnie jest
posłużyć się równoważną głębokością wnikania

. Definiuje się ją w odniesieniu do

głębokości wnikania

δ osiąganej po przekroczeniu punktu Curie w całym wsadzie

r

2

δ

g

2

g

2

21

21

r

2

δ

R

R

δ

′

=

(6.158)

przy czym

jest rezystancją jednostkową półprzestrzeni po przekroczeniu punktu Curie, zaś

- rezystancją jednostkową wsadu dwuwarstwowego. Stosunek ich wartości jest określony

zależnością

21

R′

21

R

2

g

2

g

2

2

2

21

21

φ

cos

K

δ

γ

δ

γ

R

R

′

′

=

′

(6.159)

w której

jest konduktywnością wsadu nagrzanego powyżej . Mając na uwadze, że wzór

(6.150) został wyprowadzony przy założeniu

g

2

γ

C

t

const

γ

γ

2

2

=

′

=

′′

, wobec tego

,

2

g

2

γ

γ

′

=

2

g

2

δ

δ

′

= i

ostatecznie

2

2

r

2

φ

cos

K

2

1

δ

δ

′

=

(6.160)

Przy

2

r

2

2

2

δ

δ

,

δ

g

′

≈

′

≥

′

, ponieważ

1

φ

cos

K

2

2

≈ .

Trzecia faza procesu to stan, w którym w całej objętości wsadu temperatura

przekroczyła punkt Curie. Wsad staje się jednorodny magnetycznie o przenikalności

0

2

µ

µ

=

.

Obowiązują wtedy zależności podane w p. 6.1.2.4.
Uzyskane rezultaty, mimo że słuszne dla półprzestrzeni, mogą być w dużym zakresie
wykorzystywane w rozważaniach dotyczących układów cylindrycznych. Wynika to stąd, że w
odległości

od powierzchni wsadu gęstość prądu osiąga wartości bardzo małe, zaś

gęstość objętościowa mocy dla

praktycznie jest równa zeru. W związku z tym

wpływ krzywizny powierzchni wsadu, a tym samym wartość jej wymiaru charakterystycznego
(np. promienia), nie ma praktycznie wpływu na dokładność rezultatów. Pewnym
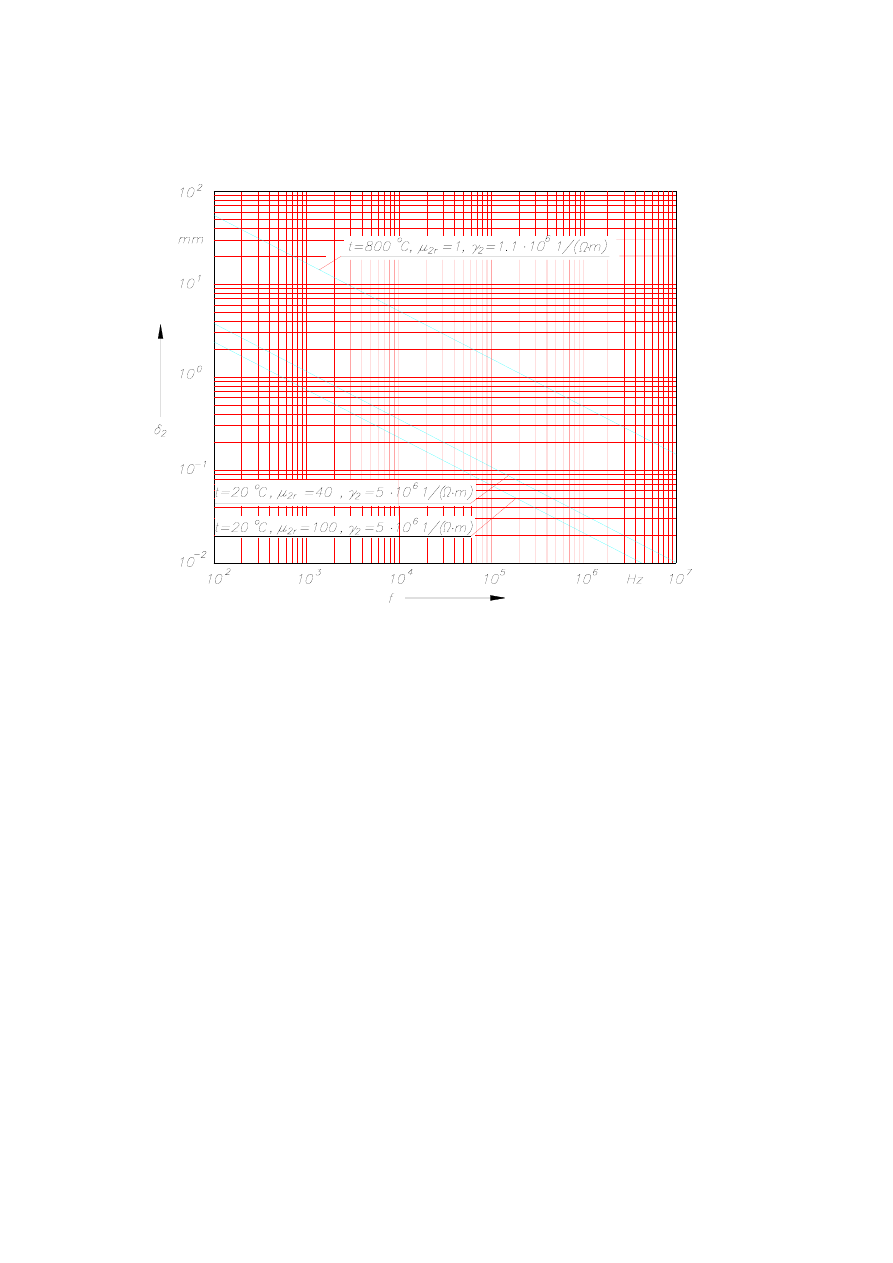
odzwierciedleniem tej tezy jest rys. 6.27. Należy przy tym zaznaczyć, że małe częstotliwości
stosuje się zwykle do nagrzewania wsadów „grubych", a więc nawet przy 50 Hz podane w
niniejszym punkcie wzory w większości przypadków znajdują zastosowanie.

2

δ

)

3

2

( K

2

δ

)

3

2

(

x

K

>

59

6.Nagrzewanie indukcyjne
____________________________________________________________________________

Rys. 6.27. Zależność głębokości wnikania od częstotliwości dla stali

6.1.3. Schematy zastępcze indukcyjnych układów grzejnych
i ich parametry elektryczne

6.1.3.1. Parametry schematu zastępczego w stanie jałowym

Zarówno dla konstruktora, jak i użytkownika indukcyjnych urządzeń grzejnych niezbędna jest
informacja o jego parametrach elektrycznych w stanie pracy bez obciążenia, czyli bez
umieszczenia wsadu we wzbudniku (stan jałowy) jak i w stanie pracy z obciążeniem.
Parametry te najczęściej określa się korzystając ze schematów zastępczych. Zasada ich
tworzenia - stosowana powszechnie w elektrotechnice - wynika z zastępowania struktur
rzeczywistych, będących układami o parametrach rozłożonych, strukturami dyskretnymi,
opisanymi przez parametry skupione. Bez względu na to jaką metodą dochodzi się do
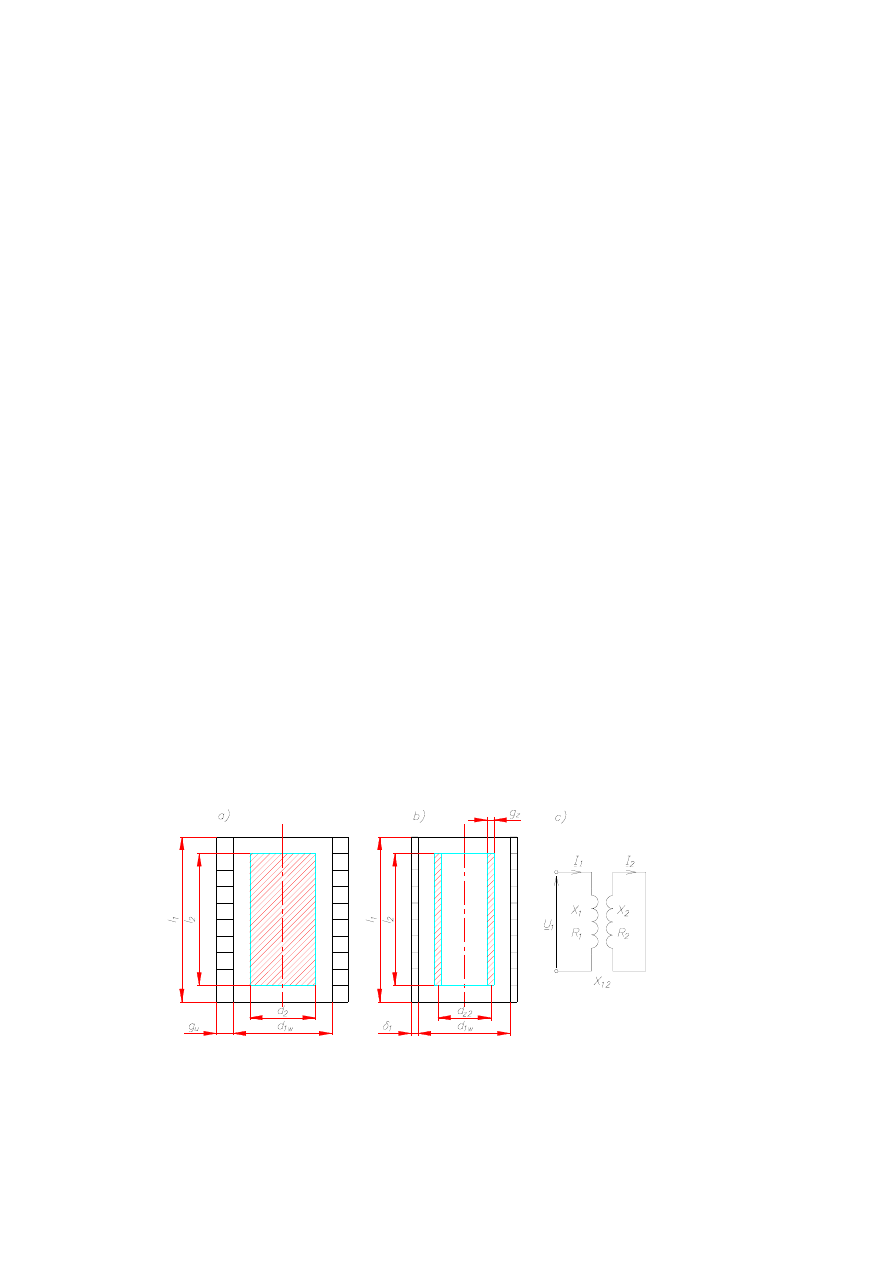
określenia schematu zastępczego (dwa najczęściej spotykane rozwiązania przedstawione są na
rys. 6.28a, b), determinują go: rezystancja

, oraz reaktancja indukcyjna

, w przypadku

schematu szeregowego lub

- w przypadku schematu równoległego. Podstawową regułą

obowiązującą przy określaniu tych parametrów jest równość mocy czynnej i biernej pobieranej
ze źródła w układzie rzeczywistym i zastępczym.

z

R

z

X

z

z

X

,

R

′

′

60

6.1. Zasady nagrzewania indukcyjnego
___________________________________________________________________________

Rys. 6.28. Schematy zastępcze indukcyjnych układów grzejnych: a) szeregowy, b) równoległy, c) szeregowy
w stanie jałowym

Jeśli chodzi o najprostszy układ jakim jest wzbudnik bez magnetowodu (rdzenia lub

koncentratora) w stanie jałowym, to najwygodniej odwzorowuje się go schematem szerego-
wym o oznaczeniach jak na rys. 6.28c. Załóżmy w dalszym ciągu, że jednowarstwowy
wzbudnik cylindryczny jest nieskończenie długi, ma gęstość zwojów

wykonany

jest z przewodnika o przekroju prostokątnym, którego grubość

1

l

l

/

n

w

=

w

1

z

1

r

−

u

r

g

=

(rys. 6.18). W

modelu tym odstępy izolacyjne między zwojami są bliskie zeru

(

)

0

z

l

∆

≈

.

Amplituda natężenia pola magnetycznego we wnętrzu nieskończenie długiego

wzbudnika ma wartość stałą i równą

m

3

H

co wynika z (6.121). Na zewnątrz wzbudnika jest

ono równe zeru. Prąd we wzbudniku o amplitudzie

mj

1

I

wywołuje strumień magnetyczny

mj

3

mj

1

mj

Φ

Φ

Φ

+

=

, którego składowa

mj

1

Φ

przenika obszar

z

1

w

1

r

r

r

<

<

zaś składowa

mj

3

Φ

obszar

. Obie te składowe strumienia wywołują spadki napięć na reaktancjach

wzbudnika

oraz rezystancji

. Wielkość

w

1

r

r

0

<

<

j

1

X

,

X ′

j

1

′′

j

1

R

j

1

X ′ określa się mianem reaktancji we-

wnętrznej wzbudnika. Jest ona związana ze strumieniem

mj

3

Φ

.

Reaktancję

j

1

X ′ oraz rezystancję

określa się wprost na podstawie wyznaczonych

w p. 6.1.2.8 reaktancji i rezystancji jednostkowych wzbudnika

, których wartości na-

leży pomnożyć przez

w

.

j

1

R

11

11

R

,

X

n

r

π

2

w

1

l

n

r

π

2

w

F

δ

γ

1

n

r

π

2

w

R

R

w

1

l

r

1

1

w

1

l

11

j

1

=

=

(6.161)

n

r

π

2

w

F

δ

γ

1

n

r

π

2

w

X

X

w

1

l

x

1

1

w

1

l

11

j

1

=

=

′

(6.162)

przy czym wartości

oraz

są zgodne z zależnościami (6.85) i (6.86) przy uwzględnieniu

odpowiedniości

,

Reaktancja zewnętrzna

r

F

g

≡

x

F

δ

2

u

2

g

.

δ

1

≡

j

1

X ′′ jest równa impedancji

zewnętrznej

. Oznaczając przez

U

j

1

Z ′′

mj

1

′′ wartość maksymalną składowej napięcia na n zwo-

jach wzbudnika w stanie jałowym wywołaną strumieniem

mj

3

Φ

otrzymuje się

mj

1

0

m

1

3

2

w

1

mj

1

mj

3

''

j

1

mj

1

''

mj

1

''

j

1

I

H

µ

r

π

n

ω

j

I

Φ

n

ω

j

jX

I

U

Z

=

=

=

=

(6.163)

61

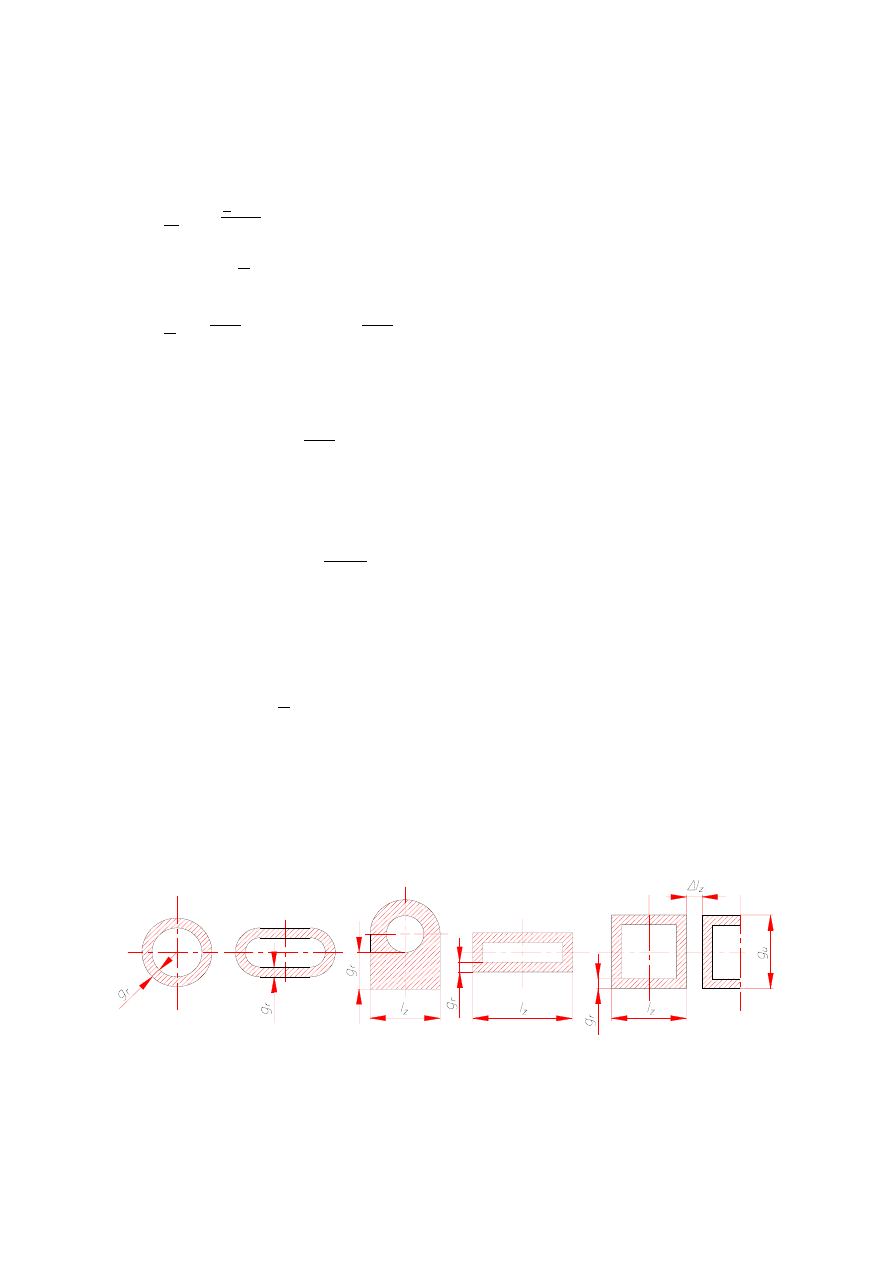
6.Nagrzewanie indukcyjne
____________________________________________________________________________

Ponieważ

1

mj

1

0

m

1

l

n

I

H

=

(6.164)

oraz

, to

0

3

µ

µ

=

0

2

w

1

l

''

j

1

µ

r

ωπ

n

w

Z

=

, wobec tego impedancja zastępcza wzbudnika w stanie

jałowym













+

+

=

0

2

w

1

l

w

1

l

x

1

1

w

1

l

r

1

1

j

1

µ

r

ωπ

n

w

n

r

π

2

w

F

δ

γ

1

j

n

r

π

2

w

F

δ

γ

1

Z

(6.165)

Rezystancję wzbudnika w stanie jałowym określa więc wzór (6.161) zaś reaktancję zależność

0

2

w

1

l

w

1

l

x

1

1

j

1

j

1

j

1

µ

r

ωπ

n

w

n

r

π

2

w

F

δ

γ

1

X

X

X

+

=

′′

+

′

=

(6.166)

Straty mocy czynnej we wzbudniku w stanie jałowym przy

1

l

l

/

n

w

=

r

1

1

1

w

1

2

10

j

1

2

10

s

F

l

δ

γ

r

π

2

)

n

I

(

R

I

P

=

=

(6.167)

Rozważając związek między

, i grubością uzwojenia

s

P

w

1

z

1

u

r

r

g

−

=

łatwo wykazać, że

najmniejsze straty występują przy minimalnej wartości

min

,

r

F

917

r

.

0

F

=

=

co ma miejsce gdy

1

w

1

z

1

u

δ

2

π

r

r

g

=

−

=

(6.168)

Z przebiegu współczynnika kształtu

, przedstawionego na rys. 6.9 wynika, że w

obszarze

, zmiany strat są już niewielkie, co powinno być uwzględnione przy

konstrukcji wzbudników. Gdy warunek ten jest spełniony, w praktycznych obliczeniach
rezystancji wzbudnika można przyjmować

r

F

r

1

u

δ

g

>

.

1

F

=

Rys. 6.29. Przekroje przewodów wzbudników wykonanych z przewodów profilowanych

62

6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________

Znaczna część wzbudników nie jest wykonywana z pełnych przewodów o przekroju

prostokątnym, tak jak to pokazuje rys. 6.18 i jak przyjęto w przeprowadzonej analizie, lecz z
rurek miedzianych o przekrojach jak na rys. 6.29. Wzór (6.161), określający rezystancję
wzbudnika przy takich rozwiązaniach, obowiązuje nadal przy założeniu

.

r

u

g

g

≡

W celu skorygowania wcześniejszego założenia o zerowej grubości międzyzwojowej

izolacji elektrycznej

wprowadzony został współczynnik wypełnienia uzwojenia

z

l

∆

z

z

z

w

l

∆

l

l

k

+

=

(6.169)

przy czym

l

jest długością przewodu wzbudnika w kierunku jego osi. Współczynnik

modyfikuje (6.161) następująco:

z

w

k

r

w

1

1

1

w

1

2

j

1

F

k

l

δ

γ

r

π

2

n

R

=

(6.170)

Zależność tę można uogólnić na wzbudniki o innym przekroju niż kołowy

r

1

1

1

w

1

2

j

1

F

l

δ

γ

L

n

R

=

(6.171)

przy czym

jest obwodem wewnętrznym wzbudnika, zaś

- współczynnikiem kształtu dla

danej geometrii i ma wartość inną aniżeli wynikająca z (6.170).

w

1

L

r

F

Reaktancja wewnętrzna wzbudnika

j

1

X ′ przy częstotliwościach wyższych niż sieciowa

jest znacznie mniejsza aniżeli reaktancja zewnętrzna i dlatego można przyjmować

j

1

j

1

X

X

′′

≈

.

Dla częstotliwości sieciowej,

może jednak mieć wartość nawet

0

.

j

1

X ′

j

1

X

2

.

′′

Wprowadzone wzory są ścisłe dla wzbudników nieskończenie długich. Bez ryzyka

popełnienia znaczącego błędu można je stosować gdy

, przy czym dla tzw.

wzbudników krótkich, charakteryzujących się małymi wartościami

, największe błędy

popełnia się przy wyznaczaniu reaktancji

. Korekta wartości tej wielkości możliwa jest

przy użyciu tzw. współczynnika Nagaoki

.

w

1

1

d

5

l

>

1

l

w

1

d

/

j

1

X

1

N

k

1

N

1

3

0

2

j

1

j

1

k

l

F

ω

µ

n

X

X

=

′′

≈

(6.172)

przy czym

jest powierzchnią przekroju obszaru, przez który przenika składowa strumienia

3

F

mj

3

Φ

3

F

=

(dla wzbudnika cylindrycznego

, dla wzbudnika o przekroju prostokątnym

). Wartości współczynnika

podane są na rys. 6.30.

2

B

A

k

w

1

3

r

π

F

=

1

1

1

N

63

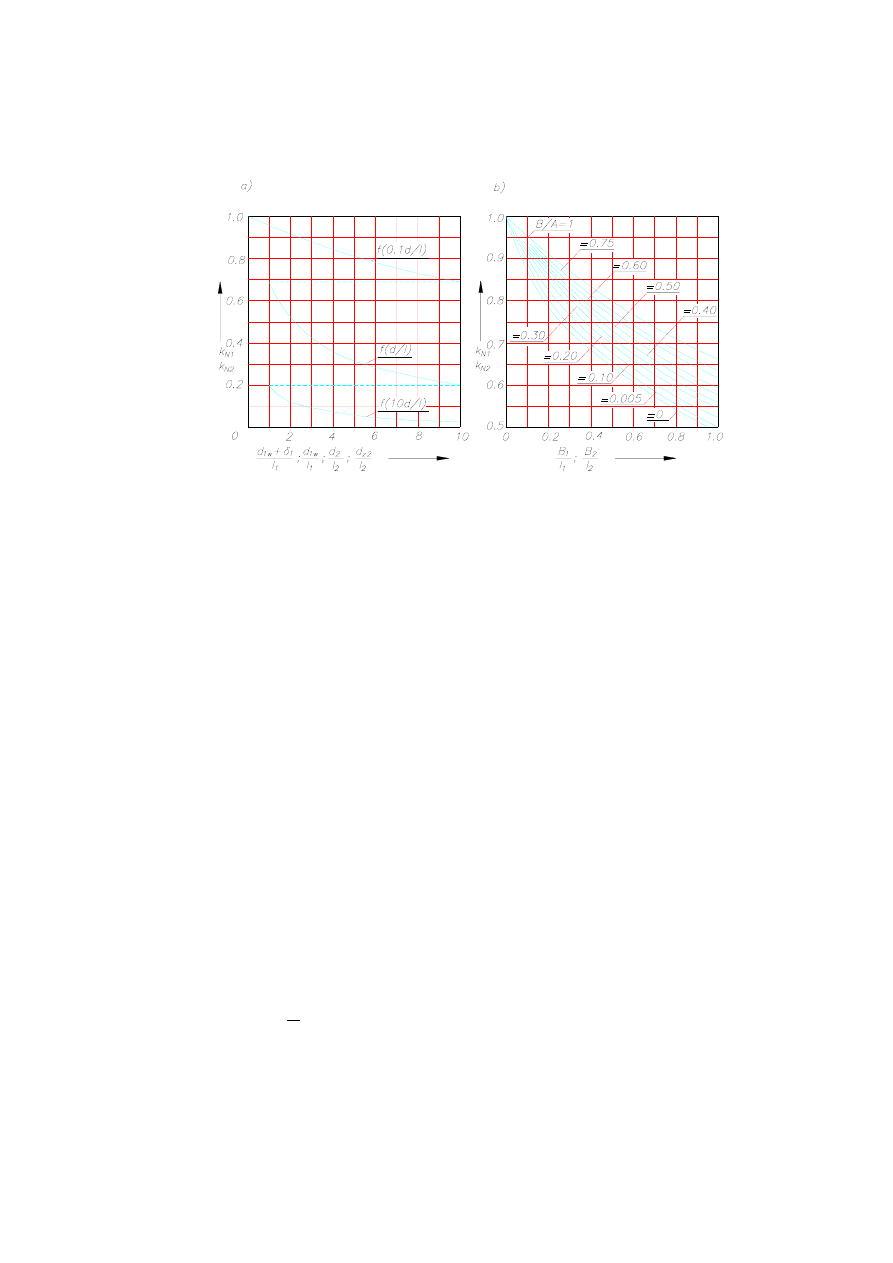
6.Nagrzewanie indukcyjne
_________________________________________________________________________

Rys. 6.30. Współczynniki Nagaoki: a) dla układu o przekroju kołowym, b) dla układu o przekroju prostokątnym

k

N1

- współczynnik dla wzbudnika krótkiego,

k

N2

- współczynnik dla wsadu krótkiego, d = d

1w

-

średnica wewnętrzna wzbudnika,

d = d

2

- średnica wsadu, δ

1

- głębokość wnikania,

l = l

1

- wysokość

wzbudnika,

l = l

2

- wysokość wsadu, B = B

1

- szerokość wewnętrzna wzbudnika,

A = A

1

, - długość

wewnętrzna wzbudnika,

B = B

2

,- szerokość wsadu,

A = A

2

- długość wsadu

6.1.3.2. Parametry schematów zastępczych układów długich dla stanu obciążenia

Na podstawie reguły obowiązującej przy określaniu parametrów schematów zastępczych
(równość mocy czynnej i biernej pobieranej ze źródła w układzie rzeczywistym i zastępczym)
można zapisać

(6.173)

2

1

2

1

2

1

P

R

I

P

P

P

+

=

+

=

przy czym:

P

1

- straty mocy we wzbudniku;

P

2

- moc wydzielana we wsadzie,

R

1

- rezystancja

uzwojenia wzbudnika równa rezystancji określonej dla stanu jałowego, czyli

R

1

= R

1j

;

I

1

- prąd

wzbudnika.

I dalej

2

1

1

2

1

2

1

Q

)

X

X

(

I

Q

Q

Q

+

′′

+

′

=

+

=

(6.174)

gdzie:

- reaktancja wewnętrzna w stanie obciążenia,

1

X ′

1

X ′′

- reaktancja zewnętrzna w stanie

obciążenia,

Q

2

– moc bierna wsadu. Wartość

j

1

X

1

X

′

=

′

, natomiast

, ponieważ

związany z

strumień

j

1

1

X

X

≠ ′′

′′

1

X ′′

m

3

Φ

przenika nie przez powierzchnię

jak w stanie jałowym, lecz

przez szczelinę między wzbudnikiem i wsadem o powierzchni przekroju

π

, gdzie

r

2

w

1

r

π

)

r

r

(

2

2

2

w

1

−

2

jest promieniem wsadu pełnego (rys.6.31).

64

6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________

Rys. 6.31. Fragment długiego układu
cylindrycznego wzbudnik - wsad

Prąd indukowany we wsadzie

I

2

ma kierunek przeciwny do prądu

I

1

. Strumień

magnetyczny wywołany we wsadzie niemagnetycznym przez prąd

I

2

powoduje zmniejszenie

strumienia magnetycznego we wzbudniku. W efekcie reaktancja

. W przypadku

wsadu ferromagnetycznego strumień skojarzony ze wzbudnikiem

j

1

1

X

X

<

j

1

1

Φ

≤

Φ

lub

j

1

1

Φ

>

Φ

.

Zależy to od tego jak wielkie jest oddziaływanie na wartość

1

Φ

prądów indukowanych we

wsadzie (przy ich wzroście zmniejsza się strumień) w porównaniu z wpływem przenikalności
magnetycznej (przy jej wzroście strumień także rośnie). W efekcie przy

wartość

reaktancji zastępczej układu w stanie obciążenia

1

r

2

>

µ

2

1

z

X

X

X

+

=

może być mniejsza, równa lub

większa niż wartość w stanie jałowym

j

1

z

X

X

=

.

Jeśli chodzi o

, to jest oczywiste, że w stanie obciążenia wartość tej wielkości musi

być większa niż

z uwagi na dodatkowe straty od prądów wirowych we wsadzie co

prowadzi do wzrostu mocy czynnej pobieranej przez układ. Impedancja zastępcza w stanie
obciążenia na ogół jest mniejsza od

z

R

j

1

R

j

1

Z jedynie przy częstotliwościach

Hz

przewyższa ona tę wartość.

150

f

≤

Uogólnienie metody wyznaczania parametrów schematu zastępczego układów długich

dla stanu obciążenia na układy krótkie jest trudniejsze niż dla stanu jałowego. Stąd też do
obliczeń układów krótkich wykorzystuje się wiele różnych metod, z których do najbardziej
popularnych zalicza się metodę transformatora powietrznego i metodę oporów magnetycznych.

Dla układu jednowymiarowego o przekroju kołowym, nieskończenie rozciągłego w

kierunku osi

z przy współczynniku wypełnienia uzwojenia

1

k

w

≠ , zgodnie z rys. 6.31

otrzymuje się

65

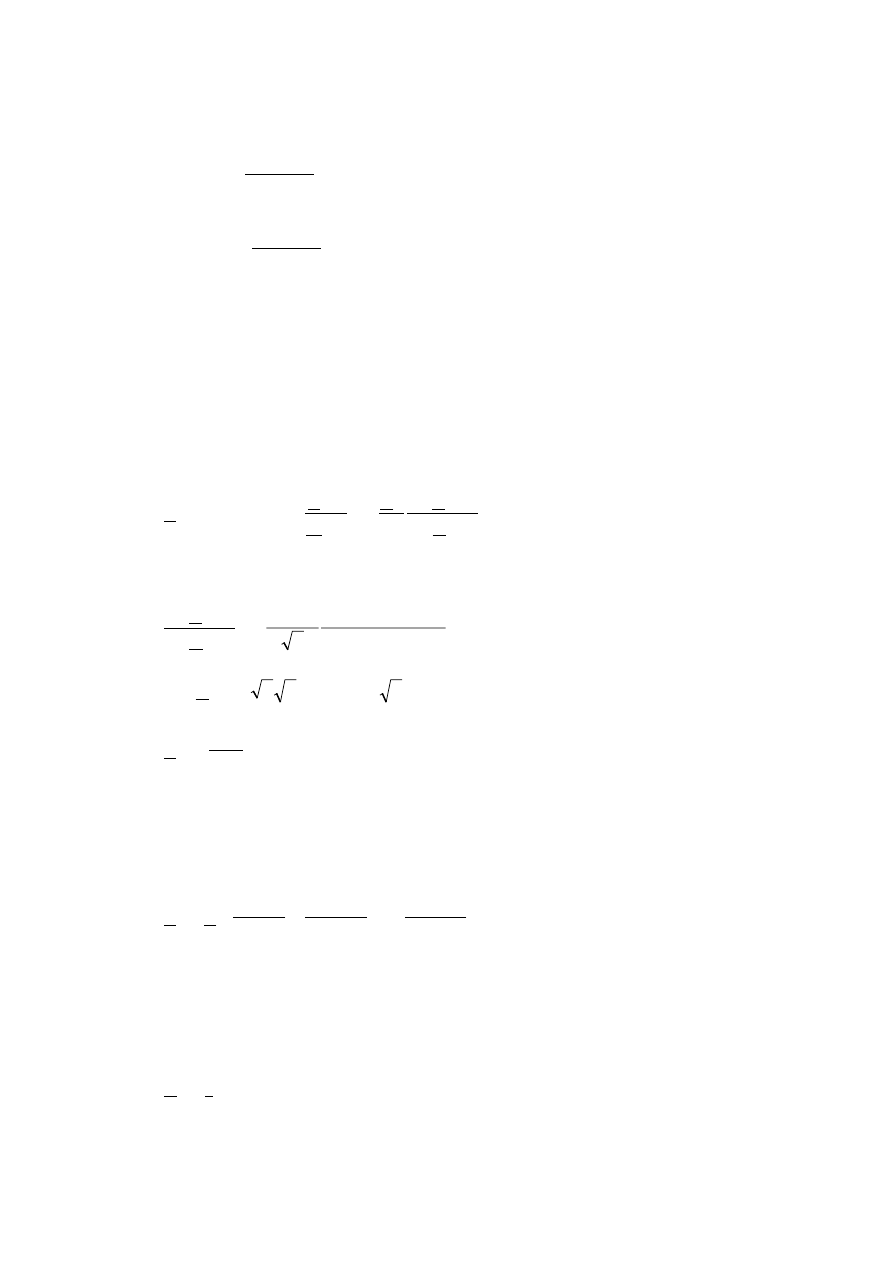
6. Nagrzewanie indukcyjne
____________________________________________________________________________

r

w

1

1

w

1

l

j

1

1

F

k

δ

γ

n

r

π

2

w

R

R

=

=

(6.175)

x

w

1

1

w

1

l

j

1

1

F

k

δ

γ

n

r

π

2

w

X

X

=

′

=

′

(6.176)

Ponieważ

, wobec tego

2

w

1

2

2

2

w

1

j

1

1

π

:

)

r

r

(

π

X

:

X

−

=

′′

′′

(6.177)

n

µ

)

r

r

(

ωπ

w

X

0

2

2

2

w

1

l

1

−

=

′′

Podobnie jak dla stanu jałowego

1

1

X

X

′′

≈

.

W celu wyznaczenia parametrów wsadu

R

2

,

X

2

wychodzi się z zależności pozwalającej

wyznaczyć impedancję jednostkową wsadu. Na podstawie (6.102) i (6.103), gdy

r

2

r

=

)

r

Γ

(

I

)

r

Γ

(

I

γ

Γ

H

E

jX

R

Z

2

2

0

2

2

1

2

2

0

m

2

0

m

2

21

21

21

−

=

=

+

=

(6.178)

Ponieważ

2

2

2

2

2

2

0

2

2

1

jbeiC

berC

C

i

jbe

C

r

be

2

)

j

1

(

)

r

Γ

(

I

)

r

Γ

(

I

+

′

+

′

−

−

=

(6.179)

przy czym:

j

C

δ

/

r

j

2

r

Γ

2

2

2

2

2

=

=

, to

)

jF

F

(

δ

γ

1

Z

x

r

2

2

21

+

=

(6.180)

gdzie:

F

r

,

F

x

– współczynniki kształtu wsadu cylindrycznego pełnego (zależność (6.114)); są

one przedstawione w funkcji argumentu

na rys.6.14.

2

2

δ

/

r

Impedancja wsadu cylindrycznego o średnicy

i wysokości

2

r

2

1

2

l

l

=

2

2

x

2

2

2

l

r

2

2

2

l

2

2

2

21

2

jX

R

F

δ

γ

n

r

π

2

w

F

δ

γ

n

r

π

2

w

l

n

r

π

2

Z

Z

+

=

+

=

=

(6.181)

przy czym

jest gęstością zwojów we wzbudniku.

1

l

l

/

n

w

=

Znajomość

R

2

oraz

X

2

pozwala określić parametry schematu zastępczego dla stanu obciążenia

(rys. 6.32).
Napięcie zasilające wzbudnik

)]

X

X

X

(

j

R

R

[

I

U

2

1

1

2

1

1

1

+

′′

+

′

+

+

=

(6.182)

66

6.1. Zasady nagr

z

ewania indukcyjnego

___________________________________________________________________________

Rys. 6.32. Schemat zastępczy indukcyjnego układu grzejnego w stanie obciążenia

R

1

- rezystancja wzbudnika,

X

1

’

- reaktancja wewnętrzna wzbudnika, X

1

’’

- reaktancja zewnętrzna

wzbudnika,

R

2

- rezystancja wsadu,

X

2

- reaktancja wsadu

Wielkości

R

2

,

X

2

związane z mocami P

2

,

Q

2

wydzielanymi we wsadzie określa się

często mianem oporów wniesionych. Wielkość

1

1

1

X

X

X

′′

+

′

=

nazywa się reaktancja

rozproszenia zaś przedstawioną metodę wyznaczania tych parametrów - metodą oporów
wniesionych.

Wyznaczone w ten sposób parametry zastępcze są wystarczająco dokładne dla układów

długich, tzn. takich, których długości są co najmniej 10-krotnie większe niż ich promienie

w przypadku gdy wsady są niemagnetykami i 20-krotnie większe w

przypadku magnetyków [558].

2

2

w

1

1

r

10

l

,

r

10

l

(

>

>

Podobnie jak w przypadku stanu jałowego, wyznaczone parametry dają się w przybliżeniu
uogólnić na układy o innych kształtach niż cylindryczne

1

r

w

1

1

w

1

l

1

F

k

δ

γ

nL

w

R

=

(6.183)

1

x

w

1

1

w

1

l

1

F

k

δ

γ

nL

w

X

=

′

(6.184)

(6.185)

3

0

l

1

F

ωµ

n

w

X

=

′′

2

r

2

2

z

2

l

2

F

δ

γ

nL

w

R

=

(6.186)

2

x

2

2

z

2

l

2

F

δ

γ

nL

w

X

=

(6.187)

przy czym:

F

r

, F

x

- współczynniki kształtu dla danej geometrii wzbudnika (wskaźnik l) i wsadu

(wskaźnik 2),

L

1w

- obwód wewnętrzny wzbudnika, L

2z

- obwód wsadu,

F

3

- przekrój szczeliny

między wsadem i wzbudnikiem,

k

w

- współczynnik wypełnienia uzwojenia.

Parametry schematów zastępczych układów z wsadami ferromagnetycznymi określa się

analogicznie tzn. biorąc za podstawę zależności określające rezystancję i reaktancję
jednostkową wsadu i uwzględniając rzeczywiste wymiary układu, a także liczbę

67

6. Nagrzewanie indukcyjne
____________________________________________________________________________

przewodników we wzbudniku (w układzie cylindrycznym - liczbę zwojów wzbudnika lub
gęstość zwojowa). Dla półprzestrzeni oraz układów cylindrycznych charakteryzujących się

będą to wzory: (6.140) i (6.141) dla pierwszej fazy procesu, wzory (6.151) i (6.152)

dla drugiej fazy procesu oraz wzór (6.64) dla fazy trzeciej, czyli po przekroczeniu

t

3

δ

/

r

>

2

′

2

2

C

. W

przypadku geometrii cylindrycznej, wyznaczone dla każdej fazy wartości

R

21

,

X

21

należy

pomnożyć przez

n

przy czym

2

2

l

/

r

π

2

r′

jest promieniem zastępczym wsadu. Dla pierwszej i

drugiej fazy procesu, gdy grubość warstwy nagrzanej jest znacznie mniejsza niż średnica
wsadu można przyjmować

. Dla trzeciej fazy procesu wg [670] zaleca się, aby

2

2

r

=

′

r

(6.188)

g

2

r

2

2

2

δ

2

/

δ

r

r

−

=

′

Parametry zastępcze wzbudnika

R

1

, X

1

wyznacza się z zależności obowiązujących dla

wsadów niemagnetycznych.

6.1.3.3. Parametry schematów zastępczych układów krótkich dla stanu obciążenia

Spośród najczęściej stosowanych metod wyznaczania parametrów zastępczych dwie są
preferowane szczególnie: metoda transformatora powietrznego i metoda oporów mag-
netycznych. Jest to rezultat niewielkiego stopnia ich komplikacji przy zadowalającej
dokładności, zwłaszcza w przypadku układów o geometrii regularnej. Metody oporów
wniesionych, odnoszącej się do układów długich i przedstawionej w punkcie poprzednim, nie
można polecać do obliczeń układów o skończonych wymiarach nawet przy korzystaniu z
zalecanych współczynników korekcyjnych. Uzyskiwane przy ich użyciu rezultaty są poprawne
tylko w pewnym wąskim zakresie zmienności parametrów.

Metoda transformatora powietrznego pozwala uzyskać poprawne rezultaty w

obliczaniu parametrów schematów zastępczych układów z wsadami niemagnetycz-

Rys. 6.33. Krótki indukcyjny układ grzejny i jego modele: a) układ rzeczywisty, b) model strukturalny, c) model

elektryczny

68

6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________

nymi. W użyciu są dwie jej wersje. Otrzymany model strukturalny jest transformatorem
powietrznym ze wzbudnikiem o wysokości

l

1

, średnicy zastępczej

i grubości

uzwojenia

(uzwojenie pierwotne) i z uzwojeniem wtórnym w postaci jednego zwoju

zwartego o wysokości

l

1

w

1

1

z

δ

d

d

+

=

1

δ

2

, średnicy zewnętrznej

d

z2

i grubości

g

z

(rys. 6.33b).

Zgodnie z II prawem Kirchhoffa (rys. 6.33c)

2

12

1

1

1

1

I

X

I

)

jX

R

(

U

+

+

=

(6.189)

2

12

2

1

12

I

)

jX

R

(

I

jX

0

+

+

=

(6.190)

przy czym:

X

12

jest reaktancją sprzężenia wzbudnika i wsadu.

Stąd

1

z

z

1

2

2

12

1

2

2

12

1

1

I

)

jX

R

(

I

)]

X

p

X

(

j

R

p

R

[

U

+

=

−

+

+

=

(6.191)

zaś kwadrat współczynnika transformacji

2

2

2

2

2

12

2

2

2

2

2

12

2

12

X

R

1

1

X

X

X

R

X

p













+













=

+

=

(6.192)

Według Langera [185]

w

1

1

1

1

2

1

k

l

δ

γ

L

n

R

=

(6.193)

1

N

1

z

1

0

2

1

k

l

F

ωµ

n

X

=

(6.194)

2

d

2

r

2

2

2

2

2

d

2

r

2

2

2

2

g

2

2

2

d

2

z

2

2

2

z

2

Y

F

l

δ

γ

L

Y

F

l

δ

γ

r

π

2

K

l

δ

γ

K

r

π

2

g

l

γ

d

π

R

=

=

=

=

(6.195)

2

d

2

N

2

z

2

0

2

K

k

l

F

ω

µ

X

=

(6.196)

2

2

2

2

2

N

m

2

2

12

X

R

1

1

k

k

n

p













+













=

(6.197)

2

2

x

2

2

2

r

2

d

F

δ

r

F

δ

1

Y













−

+

=

(6.198)

2

2

x

2

d

d

r

F

δ

1

Y

K

−

=

(6.199)

69

6. Nagrzewanie indukcyjne
___________________________________________________________________________

przy czym:

- obwód wzbudnika o średnicy zastępczej

d

;

)

δ

r

2

(

π

L

1

w

1

1

+

=

1

z

2

2

r

π

2

L

=

- obwód wsadu rzeczywistego;

- powierzchnia zastępcza wzbudnika;

- powierzchnia zastępcza przekroju wsadu;

4

/

d

π

F

2

1

z

z

1

=

4

/

d

π

F

2

2

z

z

2

=

9

.

0

8

.

0

k

w

÷

=

- współczynnik

wypełnienia uzwojenia;

- współczynnik Nagaoki dla wzbudnika (rys. 6.30a);

- współczynnik Nagaoki dla wsadu (rys. 6.30a); F

)

l

/

1

k

m

d

(

f

k

w

1

1

N

=

)

l

/

d

(

f

2

k

2

2

z

=

r2

,

F

x2

- współczynniki

kształtu dla wsadu cylindrycznego (rys. 6.14);

)

l

/

l

,

l

/

d

2

1

2

2

z

,

l

/

d

(

f

1

1

z

=

- współczynnik o

wartościach liczbowych podanych m.in. w [92], [652].

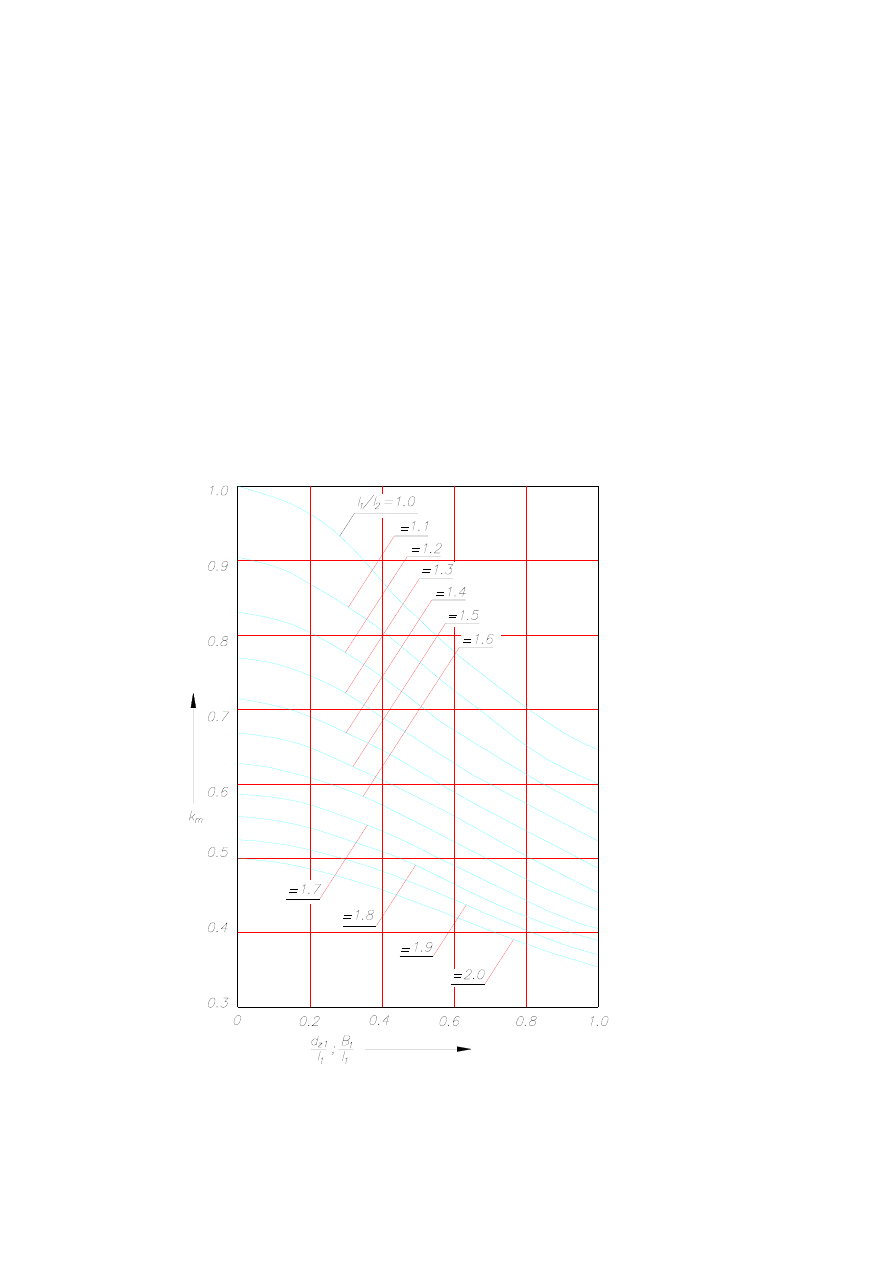
Zmiany

k

m

w funkcji

są niewielkie. W zakresie zmienności

2

2

z

l

/

d

0

.

1

2

.

0

l

/

d

1

1

z

÷

=

2

2

l

/

;

, maksymalny błąd wynikający z nieuwzględnienia wpływu

na wartość

k

2

1

l

/

l

2

1

÷

=

/

d

(

f

k

1

z

m

=

z

d

m

równy jest ok.

8% zaś na R

2

, oraz

X

2

około

6%. Wartość współczynnika

przedstawia rys. 6.34.

)

l

/

l

,

l

2

1

1

Rys. 6.34. Współczynnik

k

m

dla wzbudnika cylindrycznego i prostopadłościennego

70

6.1. Zasady nagrzewania indukcyjnego
___________________________________________________________________________
Dla układu prostopadłościennego (wsad prostopadłościenny o wymiarach

2

2

2

l

B

A

×

×

,

wzbudnik o przekroju prostokątnym o wymiarach

1

1

l

B

A

×

×

- patrz rys. 6.21), parametry

schematu zastępczego wyznacza się także wg wzorów (6.193)

÷ (6.199), przy czym:

;

)

δ

2

B

A

(

2

L

1

1

1

1

+

+

=

)

δ

2

2

B

A

(

2

L

2

2

2

−

+

=

;

)

δ

B

)(

1

1

1

δ

A

(

1

F

z

1

+

+

=

;

;

)

2

δ

B

)(

δ

A

(

F

2

2

2

z

2

+

+

=

9

.

0

8

.

0

k

w

÷

=

;

;

;

;

)

A

/

B

,

l

1

1

1

/

B

(

f

1

1

=

k

N

)

2

A

/

B

,

l

/

B

(

f

k

2

2

2

2

N

=

1

F

r

=

1

F

x

= ;Y

1

d

= ;

1

d

K

= ;

)

l

/

l

),

l

B

2

1

1

/

1

(

f

k

m

=

. Podobnie

jak dla wsadu cylindrycznego przyjęto, że współczynnik

k

m

nie zależy od

(błędy wyni-

kające z tego założenia są takie same jak dla układu cylindrycznego) (rys. 6.34).

2

2

l

/

B

Z przedstawionych rozważań wynika zasadność ograniczenia stosowania metody

transformatora powietrznego do wsadów niemagnetycznych. Bierze się to z pominięcia w
obliczeniach parametrów zastępczych składowej normalnej natężenia pola magnetycznego na
powierzchni wsadu, która dla wsadów magnetycznych krótkich - charakteryzujących się
małymi wartościami

l

- może być większa niż składowa styczna [558].

2

1

l

/

Rys. 6.35. Schematy zastępcze indukcyjnego układu grzejnego o skończonych wymiarach: a) pełny schemat

zastępczy, b) zredukowany schemat zastępczy

Metoda oporów magnetycznych polega na analizie rozpływu strumieni mag-

netycznych w układzie wzbudnik - wsad. Istnieje wiele jej wariantów, a ich wyróżnikiem jest
sposób podejścia do obliczania oporu magnetycznego przestrzeni poza obszarem wzbudnik -
wsad. Przegląd możliwych rozwiązań w tym zakresie przedstawił Reiß [640], preferując
następujące zależności odnoszące się do schematu zastępczego jak z rys. 6.35:

1

r

w

1

1

1

1

2

1

F

k

l

δ

γ

L

n

R

=

(6.200)

1

x

w

1

1

1

1

2

1

F

k

l

δ

γ

L

n

X

=

(6.201)

71

6. Nagrzewanie indukcyjne
___________________________________________________________________________

przy czym współczynniki kształtu

F

r1

,

F

x1

będące funkcjami

(w przypadku uzwojeń z

przewodów pełnych) lub

(dla uzwojeń z przewodów jak na rys. 6.29) są zawarte w

zależności (6.88) i przedstawione na rys. 6.9

1

u

δ

/

g

/

g

δ

r

2

1

r

δ

/

g

)

δ

/

g

δ

/

g

(

1

2

1

u

≡

≡

; dalej

2

r

2

2

2

2

2

2

F

l

δ

γ

L

n

R

=

(6.202)

2

x

2

2

2

2

2

2

F

l

δ

γ

L

n

X

=

(6.203)

przy czym

F

r2

i

F

x2

określa się z (6.114) lub z rys.6.14, oraz

2

3

0

2

3

l

F

ω

µ

n

X

=

′

(6.204)

1

N

2

1

1

N

z

1

0

2

s

z

1

0

2

3

k

l

l

k

F

ω

µ

n

k

F

ω

µ

n

X

−

=

=

′′

(6.205)

przy czym:

L

1

,

L

2

,

F

1z

zarówno dla układu cylindrycznego jak i prostopadłościennego są

określane tak samo jak w metodzie transformatora powietrznego;

.

)

r

r

(

π

F

2

w

1

3

−

=

2

2

Wyrażenie określające

w postaci wzoru (6.205) podają m.in. A. Sluchockij i S.

Ryskin [670]. Podobne wartości

3

X ′′

3

X ′′ otrzymuje się przy stosowaniu często cytowanej

zależności podanej przez Siegerta, odnoszącej się do układu cylindrycznego [457]. Siegert
zaleca przyjmowanie ,

)

Kr

1

k

w

1

s

l

2

l

/(

1

+

−

=

46

.

0

≈

przy czym

K = 0,9 w przypadku układu bez

magnetowodu oraz

w przypadku, gdy strumień magnetyczny na zewnątrz

wzbudnika zamyka się nie przez powietrze lecz przez magnetowód (np. przez bocznik
magnetyczny).

K

Parametry zastępcze schematu (rys. 6.35)

(6.206)

2

2

12

1

z

R

p

R

R

+

=













′′

+

′

+

+

′

+

+

=

3

2

2

2

3

2

3

2

2

12

1

z

X

R

)

X

X

(

X

X

p

X

X

(6.207)

2

3

3

2

2

2

3

2

12

)

X

X

X

(

R

X

p

′′

+

′

+

+

′′

=

(6.208)

Wartości parametrów zastępczych układów krótkich przy obciążeniu, określone na

podstawie podanych zależności, różnią się od wartości wyznaczonych empirycznie nie więcej
niż 20% [528].

Metoda oporów magnetycznych jest przydatna także do obliczania parametrów

układów zastępczych innych niż wyżej przedstawione. Dotyczy to w szczególności ukła-

72

6.1. Zasady nagrzewania indukcyjnego
___________________________________________________________________________

dów o innej geometrii, z magnetowodami [528], [558], [670], a także układów ze wzbudnikami
wielowarstwowymi [457 ], [668]. Te ostatnie są szczególnie przydatne przy nagrzewaniu
materiałów niemagnetycznych.

6.1.3.4. Sprawność elektryczna układu

Sprawnością elektryczną układu grzejnego jest iloraz mocy czynnej wydzielanej we wsadzie
P

2

i całkowitej mocy czynnej pobieranej przez indukcyjny układ grzejny P

2

+P

1

,

przy czym

P

1

, jest mocą czynną traconą we wzbudniku.

2

1

2

e

P

P

P

η

+

=

(6.209)

Szczegółowe wzory na obliczenie sprawności

zależne są od rodzaju schematu

zastępczego, na podstawie którego określane są składniki (6.209). Ażeby określić wpływ na
sprawność podstawowych wielkości charakteryzujących układ, posłużymy się schematem
zastępczym przedstawionym na rys. 6.35 oraz parametrami elektrycznymi wyznaczonymi dla
tego schematu metodą oporów magnetycznych i odnoszących się do układu cylindrycznego
długiego. Z (6.200) oraz (6.202) wynika, że

e

η

=

+

=

+

=

+

=

2

r

2

2

2

2

2

w

1

1

1

1

r

1

2

2

1

2

2

1

1

2

1

2

2

1

e

F

L

n

l

δ

γ

k

l

δ

γ

F

L

n

1

1

R

R

1

1

R

I

R

I

R

I

η

2

1

1

2

2

1

w

2

w

1

2

r

1

r

µ

γ

µ

γ

l

l

k

r

r

F

F

1

1

+

=

(6.210)

Przyjęto przy tym, że średnica zastępcza wzbudnika równa jest jego średnicy wewnętrznej

w

1

r

2

.

Jest rzeczą oczywistą, że sprawność elektryczna będzie tym większa im większy będzie

współczynnik wypełnienia uzwojenia

k

w

czyli im mniejsza grubość międzyzwojowej izolacji

elektrycznej

(patrz wzór (6.169)). Sprawność będzie tym większa, im mniejsza będzie

szczelina między wzbudnikiem i wsadem, a więc przy

. Ponieważ wzbudnik

wykonywany jest zwykle z Cu, wobec tego

z

l

∆

w

1

2

r

r

→

0

1

µ

µ

=

czyli jest tym większa, im

konduktywność wsadu mniejsza i im większa jego przenikalność magnetyczna.

e

η

Analizując rys. 6.9 oraz 6.14 łatwo dostrzec, że iloraz

wartość minimalną

osiąga przy dla dużych wartości ilorazu

r

. Oznacza to, że ze względu na sprawność

elektryczną, korzystnie jest eksploatować układ przy wielkich częstotliwościach, czyli przy
małych głębokościach wnikania. Wzrost częstotliwości pociąga za sobą także ujemne skutki,
np. zmniejszenie sprawności cieplnej (przy wydzielaniu się ciepła

2

r

1

r

F

/

F

2

2

δ

/

73

6. Nagrzewanie indukcyjne
___________________________________________________________________________

głównie w warstwie przypowierzchniowej straty są większe w porównaniu ze stratami przy
bardziej równomiernym rozkładzie źródeł ciepła). Koszt źródeł energii na ogół rośnie także w
miarę wzrostu częstotliwości roboczej. Z tych względów przyjmuje się ograniczenia
częstotliwości

f od góry, lecz ze względu na sprawność elektryczną

nie jest to konieczne.

Konieczne jest natomiast ograniczenie jej od dołu, ponieważ przy zbyt du

ż

ych głębokościach

wnikania pola, wsadów o małych średnicach nie można nagrzewać z zadowalającą
sprawnością. Na rysunku 6.36, przedstawiono charakterystyki sprawności elektrycznej dla
różnych metali przy przyjęciu

e

η

1

k

,

1

l

/

l

,

1

r

/

r

w

2

1

2

w

1

=

=

=

oraz przy za

ł

ożeniu, że chłodzony

wodą o temperaturze 60°C wzbudnik wykonany jest w sposób poprawny, co wymaga
spełnienia warunku

i w konsekwencji pozwala przyjąć

. Z krzywych

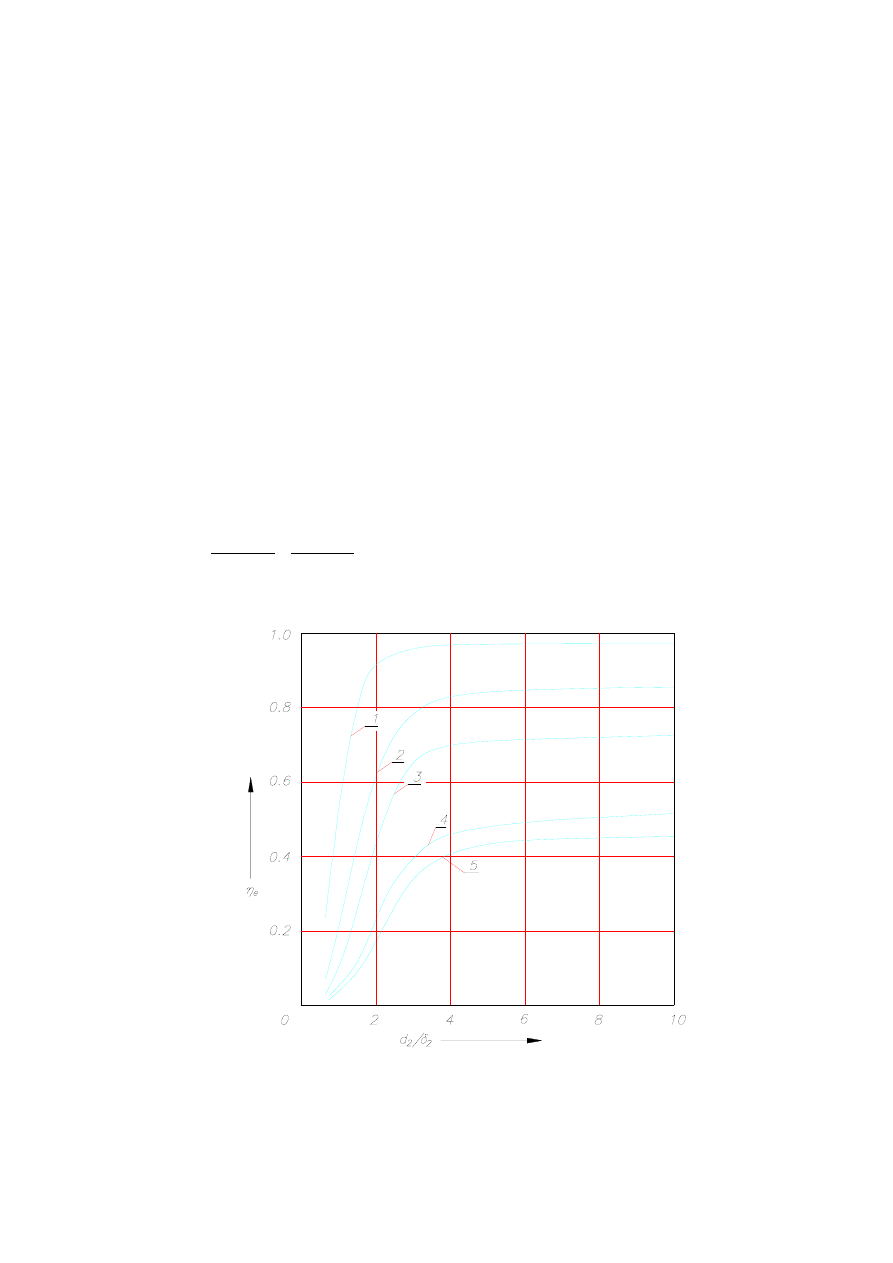
przedstawionych na rys. 6.36 wynika, że dla określonego materiału istnieje pewna najmniejsza
wartość ilorazu

i odpowiadająca jej częstotliwość

f

1

u

δ

g

>

2

δ

1

F

1

r

≈

r

2

2

2

/

r

2

min

.

Jeżeli

f<f

min

, to następuje

gwałtowny spadek sprawności. Ma to miejsce przy wartościach ilorazu

4

2

δ

/

2

÷

=

, co

odpowiada

2

2

2

2

2

2

2

2

min

µ

γ

r

π

4

µ

γ

r

π

1

f

÷

=

(6.211)

Rys. 6.36. Sprawność elektryczna indukcyjnego układu grzejnego przy nagrzewaniu

l - stali węglowej w temp. 600°C przy µ

2

= 40, 2 - stali nierdzewnej w temp. 800°C przy µ

2

= 1,

3 -miedzi w temp. 1100°C, 4 - aluminium w temp. 20°C, 5 - miedzi w temp. 20°C

74

6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________

Sprawność elektryczna określona zależnością (6.210) dotyczy wyłącznie układu wzbudnik -
wsad. Układy rzeczywiste mają wyposażenie dodatkowe, a w szczególności przewody
doprowadzające prąd ze źródła do wzbudnika, często - transformator, rdzenie, boczniki
magnetyczne, koncentratory, a także baterie kondensatorów do kompensacji mocy biernej. W
obliczeniach sprawności całkowitej należy te elementy uwzględniać.

Przy posługiwaniu się metodą transformatora powietrznego oraz metodą oporów

magnetycznych zależność (6.210) na pozostaje ważna, przy czym w miejsce parametru

R

e

η

2

należy wprowadzić czynnik

, w którym

p

2

2

12

R

p

12

określony jest odpowiednio wzorami (6.192)

oraz (6.208).

6.1.3.5. Współczynnik mocy układu i jego poprawa

Współczynnik mocy układu wzbudnik - wsad bez wyposażenia określona jest zależnością

z

2

z

2

z

z

Q

1

X

R

R

φ

cos

≈

+

=

(6.212)

przy czym

R

z

, X

z

są parametrami zastępczymi układu sprowadzonymi zwykle do napięcia

U

1

zaś

Q

dobrocią układu.

z

z

z

R

/

X

=

Jest prawie regułą, że

i stąd

indukcyjnych urządzeń grzejnych bez

kompensacji ma małe wartości. I tak, np. przy

f = 50 ÷ 150 Hz,

z

z

R

X

>>

φ

cos

6

.

0

2

.

0

φ

cos

÷

=

, z wyjątkiem

indukcyjnych pieców kanałowych, dla których wzrasta on do 0,9. Przy częstotliwościach

,

zaś przy

,

kHz

10

5

.

0

f

÷

=

5

.

0

1

.

0

÷

φ

cos

=

kHz

60

f

>

1

.

0

01

.

0

φ

÷

cos

=

[652]. Wartość

w czasie nagrzewania wsadu ulega zmianom, głównie wskutek zmiany przenikalności

magnetycznej (dotyczy wsadów ferromagnetycznych) oraz wskutek zmian konduktywności
wsadu. Przy wzroście temperatury powyżej punktu Curie i zmniejszeniu przenikalności

do

jedności, wartość

cos φ także gwałtownie maleje, a zmiany tej nie kompensuje równoczesne

zmniejszenie się konduktywności wsadu. Możliwości polepszenia

cos φ bez kompensacji są

ograniczone i jak łatwo wykazać, po podstawieniu szczegółowych wartości do wzoru (6.212),
sprowadzają się one do zmniejszenia szczeliny między wzbudnikiem i wsadem. Z różnych
względów nie może być ona jednak zbyt mała.

φ

cos

2

µ

W celu zwiększenia

cos φ do wartości bliskiej jedności stosuje się kompensację mocy

biernej przy użyciu kondensatorów statycznych włączanych do układu indukcyjnego w trojaki
sposób: szeregowo (6.37a), równolegle (6.37b) lub szeregowo-równolegle. Przy połączeniu
szeregowym pojemność kondensatora dobiera się do rezonansu napięć, zgodnie ze wzorem

z

X

ω

1

C

=

(6.213)

Tego rodzaju rozwiązanie jest stosowane przy zasilaniu układów niskim napięciem przy
dużych prądach znamionowych, co ma miejsce zwłaszcza w małych piecach do wytopu stali.

75

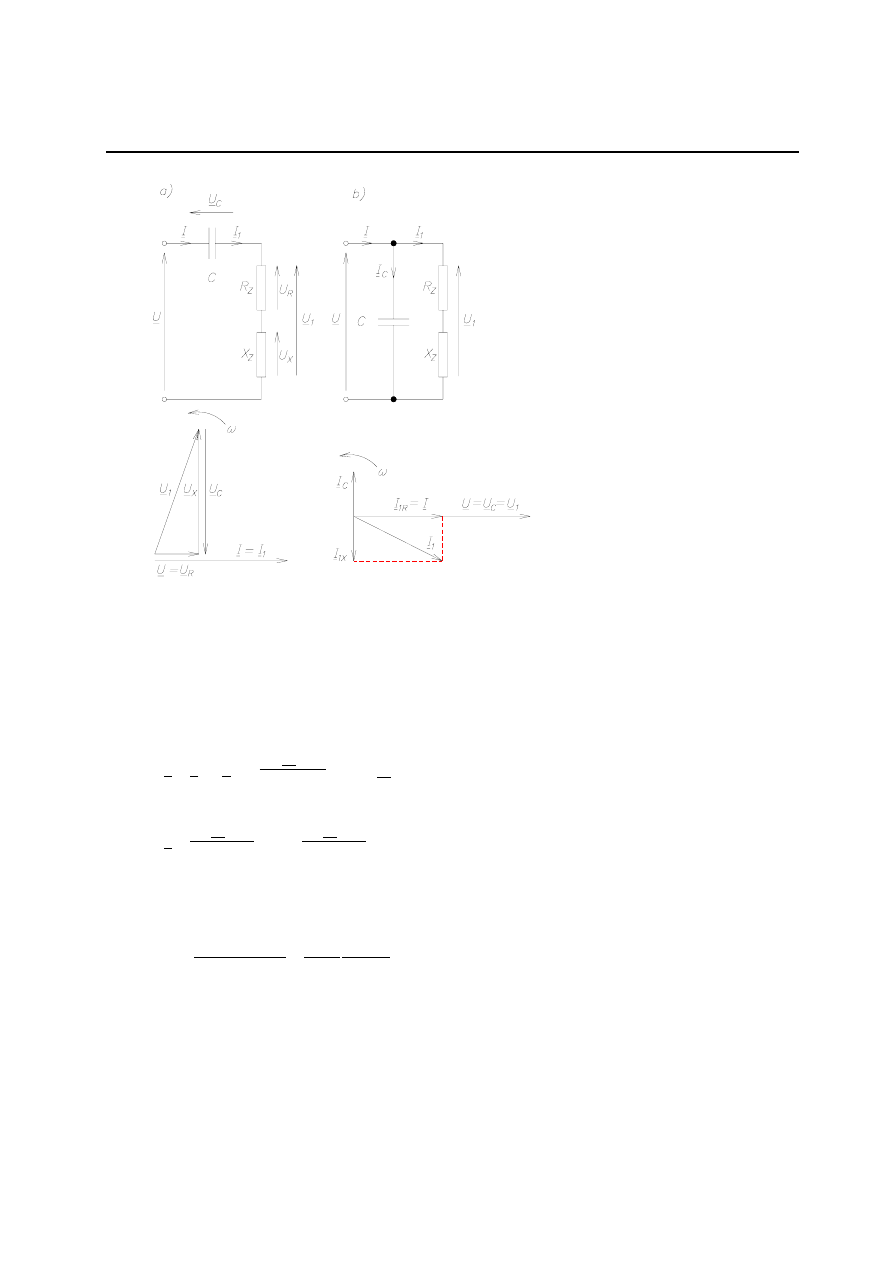
6. Nagrzewanie indukcyjne

Rys. 6.37. Kompensacja mocy biernej indukcyjnego układu grzejnego i wykresy wektorowe: a) szeregowy; b)

równoległy

Częściej jest stosowany układ równoległy (rys.6.37b), pracujący przy rezonansie
prądów. Wtedy

1

z

z

1

C

1

U

C

ω

j

jX

R

U

I

I

I

+

+

=

+

=

(6.214)

lub

)

X

CX

ω

CR

ω

(

X

R

U

j

R

X

R

U

I

z

2

z

2

z

2

z

2

z

1

z

2

z

2

z

1

−

+

+

+

+

=

(6.215)

W warunkach rezonansu napięć cześć urojona prądu powinna być równa zeru, stąd

1

Q

Q

X

ω

1

)

X

R

(

ω

X

C

2

z

2

z

z

2

z

2

z

z

+

=

+

=

(6.216)

Pojemność

C zależy więc od parametrów zastępczych R

z,

X

z

, które ulegają podczas procesu

nagrzewania zmianom w rezultacie zmian temperatury wsadu. Z tego względu podczas
procesu nagrzewania pojemność

C musi być zmieniana, co realizuje się przez przyłączanie i

odłączanie kondensatorów. Związek (6.216) określa zależność pojemno-

76

6.1. Zasady nagrzewania indukcyjnego
___________________________________________________________________________

ści

C od dobroci układu Q

z

. Zwykle

, czyli

Q

. Oznacza to, że

można

pominąć i dla obwodu rezonansowego otrzymuje się

2

z

2

z

Z

R

<<

1

2

z

>>

2

z

R

C

L

1

ω

z

2

=

(6.217)

przy czym

L

z

jest indukcyjnością zastępczą obwodu.

W przypadku, gdy pojemność

C ma wartość określoną zależnością (6.216), obwód

prądowy jest dopasowany do częstotliwości pracy generatora, który jest obciążony wyłącznie
składową czynną prądu o wartości wynikającej z (6.215), czyli

2

z

z

1

z

z

z

z

z

1

z

2

z

2

z

1

Q

1

jQ

1

I

jX

R

R

jX

R

U

R

X

R

U

I

+

+

=

+

+

=

+

=

(6.218)

Stąd

z

1

2

z

1

Q

I

Q

1

I

I

≈

+

=

(6.219)

Analogicznie otrzymuje się

1

2

z

z

1

C

I

Q

1

Q

I

I

≈

+

=

(6.220)

Fakt, że

wykorzystuje się przy eksploatacji indukcyjnych urządzeń grzejnych, a w

szczególności pieców. Utrzymywanie

1

C

I

I

≈

1

C

I

I

≈ przez zmianę pojemności baterii kondensatorów

C pozwala na pracę w warunkach zbliżonych do rezonansu, czyli przy minimalnej wartości
prądu

I. Prąd

osiąga duże wartości i np. dla

Q

1

I

≈

C

I

z

=

10,

1

C

I

995

.

0

I

≈

, przy

1

I

1

.

0

I

=

.

Wymaga to odpowiednich połączeń między wzbudnikiem i baterią kondensatorów

C,

gwarantujących małe straty mocy (optymalny przekrój połączeń o profilu prostokątnym równy
jest

- wzór (6.168)). Podobnie powinno się ograniczać reaktancję tych połączeń.

2

/

πδ

1

Konstruując indukcyjne urządzenia grzejne, a zwłaszcza piece, oblicza się największą
niezbędną w procesie wartość pojemności baterii kondensatorów

C

max

i połowę jej włącza się

na stałe do obwodu. Reszta podzielona na stopnie jest przyłączana lub odłączana w trakcie
procesu w celu utrzymania punktu pracy w pobliżu rezonansu [92], [652].
Jeżeli indukcyjny układ grzejny jest eksploatowany przy częstotliwości sieciowej i jest
odbiornikiem jednofazowym, to oprócz baterii kondensatorów do kompensacji mocy biernej
wyposaża się go zwykle w układ symetryzujący. Wynika to z niedopuszczalności przyłączania
do sieci trójfazowej odbiorników jednofazowych o dużych mocach, znamionujących
większość indukcyjnych urządzeń grzejnych. W użyciu są przeważnie układy Steinmetza i
Scotta [461].

77

6. Nagrzewanie indukcyjne
___________________________________________________________________________

6.1.4. Charakterystyka problemów termokinetycznych

Podstawowa problematyka wymiany ciepła w indukcyjnych urządzeniach grzejnych należy do
zagadnień złożonych, m.in. z uwagi na specyficzne powiązania pól temperatury i pól
elektromagnetycznych, a niekiedy także pól przepływowych i naprężeń cieplnych. W tej
sytuacji w niniejszej książce można jedynie zasygnalizować sposób podejścia do tych zadań,
których efektywne rozwiązanie wymaga wiadomości specjalistycznych, przynajmniej z
zakresu wymiany ciepła.

Obliczeniom cieplnym indukcyjnych urządzeń grzejnych poświęcona jest bardzo duża

liczba prac, przy czym w większości przypadków dotyczą one zagadnień jednostkowych lub co
najwyżej pewnej kategorii zadań [618]. Jednym z podstawowych warunków uzyskania
rozwiązań termokinetycznych jest oczywiście poprawnie określony rozkład źródeł ciepła, co
było przedmiotem dotychczas prowadzonych rozważań. Spośród książek wydanych w Polsce,
które mogą być w tym pomocne polecić można m.in. następujące pozycje: [13], [471 ], [634],
[663], [676], [684], [724].

Charakteryzując podstawowe procesy termokinetyczne w indukcyjnych układach

grzejnych należy - generalnie rzecz biorąc - wyróżnić dwa sposoby podejścia do ich
rozwiązywania: matematyczne i empiryczne. Podejście matematyczne wymaga sfor-
malizowania opisu wymiany ciepła i dochodzenia do wyniku metodą analityczną, numeryczną,
analogową bądź hybrydową. Punktem wyjścia jest przy tym zwykle równanie Fouriera-
Kirchhoffa lub układ takich równań

)]

t

λ

(

[

ρ

c

1

ρ

c

p

t

)

(

τ

t

V

∇

∇

∇

+

=

⋅

+

∂

∂

w

(6.221)

gdzie:

t - temperatura, τ - czas, w - wektor prędkości nagrzewanego czynnika (np. metalu), p

V

-

jednostkowa objętościowa moc źródeł ciepła,

c - ciepło właściwe, ρ - gęstość masy, λ-

przewodność cieplna właściwa.

W ogólnym przypadku jest to zagadnienie trójwymiarowe. Gdy ośrodki są stałe,

sprowadza się ono do równania lub układu równań Poissona [131]. Oczywiście równania te
muszą być uzupełnione warunkami początkowymi i brzegowymi, przy czym złożoność tych
drugich, w połączeniu z nie zawsze elementarną geometrią układu oraz zależnością
parametrów materiałowych od temperatury, bardzo komplikuje zadanie. Stopień komplikacji
tych zadań wyklucza często przydatność metod analitycznych, stąd też podstawowym
narzędziem stają się metody numeryczne.

Jedną z głównych trudności analizy oraz syntezy problemów termokinetycznych jest

brak możliwości ich separacji od zagadnień elektromagnetycznych. Wielkością, która wiąże
pole temperatury z polem elektromagnetycznym jest jednostkowa moc objętościowa

p

V

. Jak to

wynika z dotychczasowych rozważań, na jej wartość ma wpływ m.in. konduktywność wsadu i
jego przenikalność magnetyczna, czyli wielkości zależne od temperatury.

Podejście empiryczne opiera się najczęściej na badaniach modelowych, prototypowych

lub wykorzystaniu danych statystycznych odnoszących się do podobnych za-

78

6.1. Zasady nagr

z

ewania indukcyjnego

___________________________________________________________________________

gadnień. Dane statystyczne dotyczą zużycia właściwego energii, mocy urządzeń, czasu
nagrzewania. Niekiedy tego rodzaju informacje są wystarczające, zwłaszcza jeśli chodzi o
topienie i o tzw. nagrzewanie objętościowe, czyli bez wymagań dotyczących znajomości
dokładnego rozkładu temperatury. Znajomość takiego rozkładu ma znaczenie w procesach
nagrzewania selektywnego, związanego np. z hartowaniem powierzchniowym.

Nagrzewanie indukcyjne nie zawsze wykorzystywane jest jako bezpośrednie i wtedy

modelem matematycznym ustalonego pola temperatury we wsadzie jest równanie lub układ
równań Laplace'a. Trzeba też tu wspomnieć o wielu innych zadaniach, znacznie mniej
złożonych, zwłaszcza stacjonarnych, związanych z obliczeniami o charakterze bilansowym.
Tego rodzaju zagadnienia nie wchodzą oczywiście w zakres problematyki podstawowej i
rozwiązywane są elementarnymi metodami termokinetyki.
W celu przybliżenia Czytelnikowi istoty i skutków powiązań zjawisk elektromagnetycznych i
cieplnych przedstawione zostanie przykładowe rozwiązanie zadania, które dotyczy
nagrzewania wsadu ferromagnetycznego [598]. Uzyskane ono zostało metodą numeryczną
bilansów elementarnych przy zoptymalizowanej, a więc nierównomiernej dyskretyzacji
przestrzeni. Nagrzewany wsad, w postaci pełnego długiego walca ze stali St45o średnicy

d =

0,1 m, umieszczony był we wzbudniku o średnicy wewnętrznej

i gęstości

zwojowej

w

m

11

.

0

d

w

1

=

l

= 100 m

-1

. Częstotliwość napięcia zasilającego

f =2500 Hz. Przy napięciu U

2

=

220 V (patrz rys. 6.32) uzyskane zostały rezultaty przedstawione na rys. 6.38 ÷ 6.42. Zostały
one odniesione do następujących wartości maksymalnych:

t

max

= 1200°C, τ

max

=

360 s, δ

2max

=

14,4 mm, R

2max

= 0.5 mΩ/m.

Rys. 6.38

.

Rozkład temperatur w

ferromagnetycznym wsadzie
cylindrycznym przy częstotliwo-
ści napięcia zasilającego 2.5 kHz
oraz nagrzewaniu prądem o stałej
wartości (lewa część rysunku) i
napięciem o stałej wartości
(prawa część rysunku)

79

6. Nagrzewanie indukcyjne
____________________________________________________________________________

Rys.6.39. Zmiana w czasie
głębokości wnikania pola
przy nagrzewaniu ferroma-
gnetyka (długi cylinder
pełny)

Rys. 6.40. Charakterystyki
dynamiczne temperatury
wsadu (długi cylinder pełny)

80

6.1. Zasady nagrzewania indukcyjnego
____________________________________________________________________________

Na prawej części rys. 6.38 przedstawiono rozkłady temperatur we wsadzie przy

U

2

=

const (natężenie pola magnetycznego na powierzchni wsadu ulega zmianom), na lewej części
tegoż rysunku dodatkowo przedstawiono rozkłady temperatur we wsadzie przy

I

1

= const, co

odpowiada stałej wartości natężenia pola magnetycznego na powierzchni wsadu. Poszczególne
krzywe obrazują rozkłady temperatur po czasach względnych

tak dobranych, że

temperatury na powierzchni wsadu przy

U

max

τ

/

τ

const

2

=

oraz

const

I

1

=

są sobie równe. Z

kolejnego rys. 6.39 wynika, że głębokość wnikania pola magnetycznego, zdefiniowana jako
grubość warstwy przypowierzchniowej, w której wydziela się 86,5% całkowitej mocy czynnej
generowanej we wsadzie, wzrasta w wyniku zmian temperatury prawie 15 razy.
Charakterystyki dynamiczne nagrzewania wsadu dla trzech wartości promienia pokazane są na
rys. 6.40. Zmiany w czasie nagrzewania wartości podstawowych wielkości elektrycznych,
uwidocznione na rys. 6.41, dowodzą bardzo dużego wpływu temperatury na te przebiegi, co w
konsekwencji powoduje konieczność odpowiedniego sterowania procesem. Potwierdzają to
również krzywe na rys. 6.42, stanowiące relacje między napięciem

prądem

I

2

U

1

oraz mocą

wydzielaną we wsadzie

P

2

, bez kompensacji mocy biernej i przy utrzymywaniu jednej z tych

wielkości na stałym poziomie, co jest jednym ze sposobów eksploatacji indukcyjnych urządzeń
grzejnych.

Rys. 6.41. Zmiany podstawowych wielkości elektrycznych w czasie nagrzewania ferromagnetyka (długi cylinder

pełny) powyżej

t

C

81

6. Nagrzewanie indukcyjne
____________________________________________________________________________

Rys.6.42. Przebiegi parametrów zasila-
nia indukcyjnego układu grzejnego (z
długim cylindrem pełnym) przy stałej
wartości prądu

I

1

, stałej wartości napię-

cia

U

2

i stałej mocy

P

2

82

6.2. Urządzenia indukcyjne i ich zastosowania
____________________________________________________________________________

6.2. Urządzenia indukcyjne i ich zastosowania

6.2.1. Klasyfikacja

Urządzenia indukcyjne należą do najbardziej zróżnicowanych urządzeń elektrotermicznych.
Jeśli wykorzystać przyjęte we wstępie kryteria klasyfikacyjne, to okazuje się, że trudno znaleźć
konstrukcję urządzenia do nagrzewanie indukcyjnego, która nie odpowiada jednej z możliwych
kombinacji cech wynikających z tych kryteriów. I tak wyodrębnić można urządzenia do
nagrzewania bezpośredniego i jest to grupa dominująca, ale w użyciu są także urządzenia
wykorzystujące nagrzewanie pośrednie, np. przeznaczone do topienia materiałów
nieprzewodzących w tyglach przewodzących, do nagrzewania indukcyjnego mediów
transportowanych rurociągami na wielkie odległości itd.

Według kryterium cyklu nagrzewania urządzenia dzieli się na przeznaczone do pracy

przerywanej, okresowej i ciągłej. Główną domeną ich zastosowań jest przemysł, ale bywają
one także stosowane w gospodarce komunalno-bytowej (np. kuchnie indukcyjne). Kryterium
technologii, które było podstawą wyodrębnienia dwunastu głównych kategorii zastosowań
urządzeń, wykorzystujących wszystkie metody elektrotermiczne (p. 1.2, w część I książki), jest
przyjmowane często za wyjściowe przy charakteryzowaniu urządzeń indukcyjnych [56], [274],
[373]. Posługując się nim, rozróżnić należy urządzenia indukcyjne wykorzystywane do:
obróbki plastycznej, obróbki cieplnej, topienia, suszenia, lutowania, zgrzewania, ogrzewania.
Wykaz ten można uzupełnić obszerną listą urządzeń przeznaczonych do celów
specjalistycznych i stanowiących jedynie elementy wyposażenia takich obiektów
technologicznych jak kotły, kadzie, reaktory, autoklawy, kolumny absorpcyjne.

Wychodząc z kryterium konstrukcji, stosuje się podział na nagrzewnice i piece

indukcyjne. Często utożsamia się te pojęcia odpowiednio z urządzeniami indukcyjnymi
bezkomorowymi i komorowymi [254], [439], [652]. Ta praktyka językowa w odniesieniu do
tej kategorii urządzeń jest zbyt popularna, by można było oczekiwać jej zarzucenia. Wynikają
z niej też pewne trudności klasyfikacyjne ponieważ, np. topienie indukcyjne jest realizowane
nie tylko w piecach, lecz także w układach beztyglowych (topienie lewitacyjne, topienie
strefowe). Ponadto niektóre człony główne urządzeń do nagrzewania wsadów bez zmiany ich
stanu skupienia, bardziej przypominają piece mimo, że pod pojęciem pieca rozumie się
najczęściej człon główny urządzenia komorowego przeznaczonego wyłącznie do topienia.
Według kryterium częstotliwości wyróżnia się urządzenia częstotliwości zmniejszonej w
stosunku do częstotliwości sieciowej, przy czym dolną granicą jest na ogół wartość 16 2/3 Hz,
urządzenia częstotliwości sieciowej (50 lub 60 Hz), zwiększonej (50 Hz

l0 kHz) i

wielkiej (10 kHz

≤

< f

≤

< f 27,12 MHz)

1

. Ostatnie dwa kryteria,

1)

Zamiast pojęcia „zmniejszona" używa się też terminu „mała" lub „obniżona", zaś zamiast „zwiększona"

„średnia" lub „podwyższona". Ponieważ we wszystkich przypadkach odniesieniem jest częstotliwość sieciowa, za
podstawowy przyjęto ciąg określeń: zmniejszona, sieciowa, zwiększona, wielka. Ciąg ten znamionuje pożądana
spójność językowa.

83

6. Na

g

rzewanie indukcyjne

____________________________________________________________________________

spośród wymienionych w p. 1.2, też mają zastosowanie do omawianej grupy urządzeń. Chodzi
tu o kryterium środowiska wsadu (zgodnie z nim wyodrębnia się urządzenia indukcyjne z
atmosferą naturalną, sztuczną i próżniowe) oraz o kryterium kinetyki wsadu, prowadzące do
podziału na urządzenia nieprzelotowe i przelotowe.

Dalsza, bardziej szczegółowa, charakterystyka urządzeń indukcyjnych i ich zastosowań

przedstawiona zostanie w dwóch grupach, wyodrębnionych wg kryterium konstrukcji, czyli w
sposób przyjęty przez większość autorów różnego rodzaju publikacji z zakresu nagrzewania
indukcyjnego.

W odrębnym punkcie omówione będą źródła zasilania, ponieważ ich podobne

rozwiązania stosowane są zarówno do pieców, jak i nagrzewnic. Inne człony wyposażenia
urządzeń indukcyjnych mają przeważnie charakter specjalizowany i dlatego najważniejsze z
nich są scharakteryzowane przy omawianiu nagrzewnic, pieców i ich zastosowań.

6.2.2. Źródła zasilania

6.2.2.1. Charakterystyka ogólna

Procesy nagrzewania indukcyjnego są oczywiście możliwe do zrealizowania wyłącznie przy
zasilaniu wzbudnika prądem zmiennym. Jak wynika z dotychczas przeprowadzanych
rozważań, istotny wpływ na sprawność tych procesów ma częstotliwość prądu indukowanego
we wsadzie. Musi być ona dobrana przy uwzględnieniu właściwości i wymiarów wsadu, a
także technologicznego celu nagrzewania. Jak powiedziano, zakres częstotliwości
wykorzystywanych w tej technice zawiera się w przedziale od 16 2/3 Hz do 27,12 MHz [314],
[463], [486]. Przy tak szerokim zakresie częstotliwości trudno mówić o jednym rodzaju źródeł
zasilania zwłaszcza, że moce jednostkowe urządzeń indukcyjnych wynoszą od kilku watów do
kilkudziesięciu megawatów i nie ma przeszkód by obszar ten rozszerzyć.

Możliwości precyzyjnego doboru częstotliwości w procesie nagrzewania indukcyjnego

powstały z chwilą wprowadzenia do przemysłu przyrządów półprzewodnikowych. Źródła
zasilania budowane z ich wykorzystaniem, uzupełnione niektórymi klasycznymi już
rozwiązaniami, pokrywają obecnie całkowicie obszar częstotliwości niezbędnych do realizacji
różnych technologii związanych z nagrzewaniem w procesach obróbki cieplnej, cieplno-
chemicznej, plastycznej, topieniem, lutowaniem, spawaniem i w wielu innych dziedzinach. W
niektórych obszarach częstotliwości do dyspozycji są źródła różnego rodzaju, a o ich wyborze
decydować musi szczegółowa analiza techniczno - ekonomiczna.

Jeśli przyjąć za podstawę podziału źródeł zasilania zasadę ich działania (rozumianą

bardzo ogólnie), wyróżnić można: przemienniki statyczne budowane z wykorzystaniem
tyrystorów bądź tranzystorów, generatory lampowe i tranzystorowe, generatory maszynowe,
przekształtniki transformatorowe i magnetyczne mnożniki częstotliwości.


84

6.2. Urządzenia indukcyjne i ich zastosowania
___________________________________________________________________________

Przy pracy z częstotliwościami mniejszymi niż 50 Hz stosuje się tyrystorowe

przemienniki statyczne. Trzeba tu dodać, że urządzenia na częstotliwości mniejsze od
sieciowej budowane są rzadko, ponieważ częstotliwość 50 Hz jest z reguły wartością
wystarczająco małą by zrealizować proces przy dobrej sprawności [456]. Jeśli istnieje taka
potrzeba to zwykle wybiera się

f = 16 2/3 Hz.

Urządzenia o częstotliwości roboczej 50 Hz bardzo rzadko zasila się wprost z sieci, bez

pośrednictwa elementów dopasowujących. Wynika to z potrzeby regulacji wielkości
elektrycznych znamionujących urządzenie (moc, napięcie, prąd), często także z konieczności
przyłączenia odbiorników jednofazowych do sieci trójfazowej. Elementami pośredniczącymi
między siecią i piecem względnie nagrzewnicą są różne rodzaje transformatorów
regulowanych (z odczepami, autotransformatory, regulatory indukcyjne, transduktory). Przy
większych mocach stosuje się kaskadę transformator obniżający - transformator regulacyjny.
W użyciu są tyrystorowe regulatory prądu zmiennego [460].

W obszarze częstotliwości 150 ÷ 450 Hz w dalszym ciągu z powodzeniem są

stosowane magnetyczne mnożniki częstotliwości. Znane są rozwiązania umożliwiające
zwielokrotnienie częstotliwości sieciowej 2 ÷ 35 razy, a także niecałkowitą liczbę razy.
Spotyka się układy hybrydowe magnetyczno - półprzewodnikowe. W technice nagrzewania
indukcyjnego konkurencyjne są jednak mnożniki pracujące przy 3 ÷ 9 krotnym zwielo-
krotnieniu częstotliwości sieciowej. Ich moce sięgają 7 MW przy sprawności 95% [508].

Częstotliwości większe niż 150 Hz mogą być osiągane jeszcze dwoma innymi

sposobami. Pierwszy z nich polega na użyciu przetwornic maszynowych, przy czym ich
częstotliwości maksymalne nie są większe niż 10 kHz [566]. Przed wprowadzeniem
przyrządów półprzewodnikowych były to praktycznie jedyne urządzenia pozwalające na pracę
do 10 kHz. Ich wady (malejąca sprawność przy niepełnym obciążeniu - rys. 6.43), konieczność
osadzenia na specjalnych fundamentach, hałaśliwa praca) sprawiły, że nie wytrzymują one
konkurencji z przekształtnikami statycznymi. W drugim sposobie generacji częstotliwości
większych niż 150 Hz są stosowane przekształtniki tyrystorowe [546]. Interesująca jest przy
tym górna granica możliwych do uzyskania częstotliwości. Tyrystory konwencjonalne SCR
umożliwiają uzyskiwanie częstotliwości o wartości 10 kHz, tyrystory o strukturze
wielokatodowej GTO wyłączane prądem bramki - 30 kHz

1

, tyrystory RCT przewodzące

wstecznie, zawierające scaloną monolitycznie diodę przeciwrównoległą (w literaturze
niemieckojęzycznej oznaczane - RLT) - 50 kHz, tyrystory ZTO (odmiana niewyłączalna
tyrystora GTO) - powyżej 50 kHz, zaś tyrystory elektrostatyczne SITh - 200 kHz. Stosowanie
tych ostatnich uważa się za kłopotliwe ze względu na niebezpieczeństwo zwarcia obwodu
głównego w przypadku utraty sterowania bramkowego spowodowanego zanikiem sygnału
[510]. Już na przełomie lat 80-tych i 90-tych uzyskiwane przy użyciu przekształtników
tyrystorowych największe moce jednostkowe urządzeń sięgały 15 MW. W roku 1997
doniesiono o opracowaniu tyrystora

85

1)

Są to wartości maksymalne, uzyskiwane przy mniejszych mocach i w specjalnych układach. Za górną granicę

częstotliwości w elektrotermicznych zastosowaniach tyrystorów SCR przyjmuje się najczęściej wartość 4 kHz
oraz 10 kHz dla tyrystorów GTO [408].

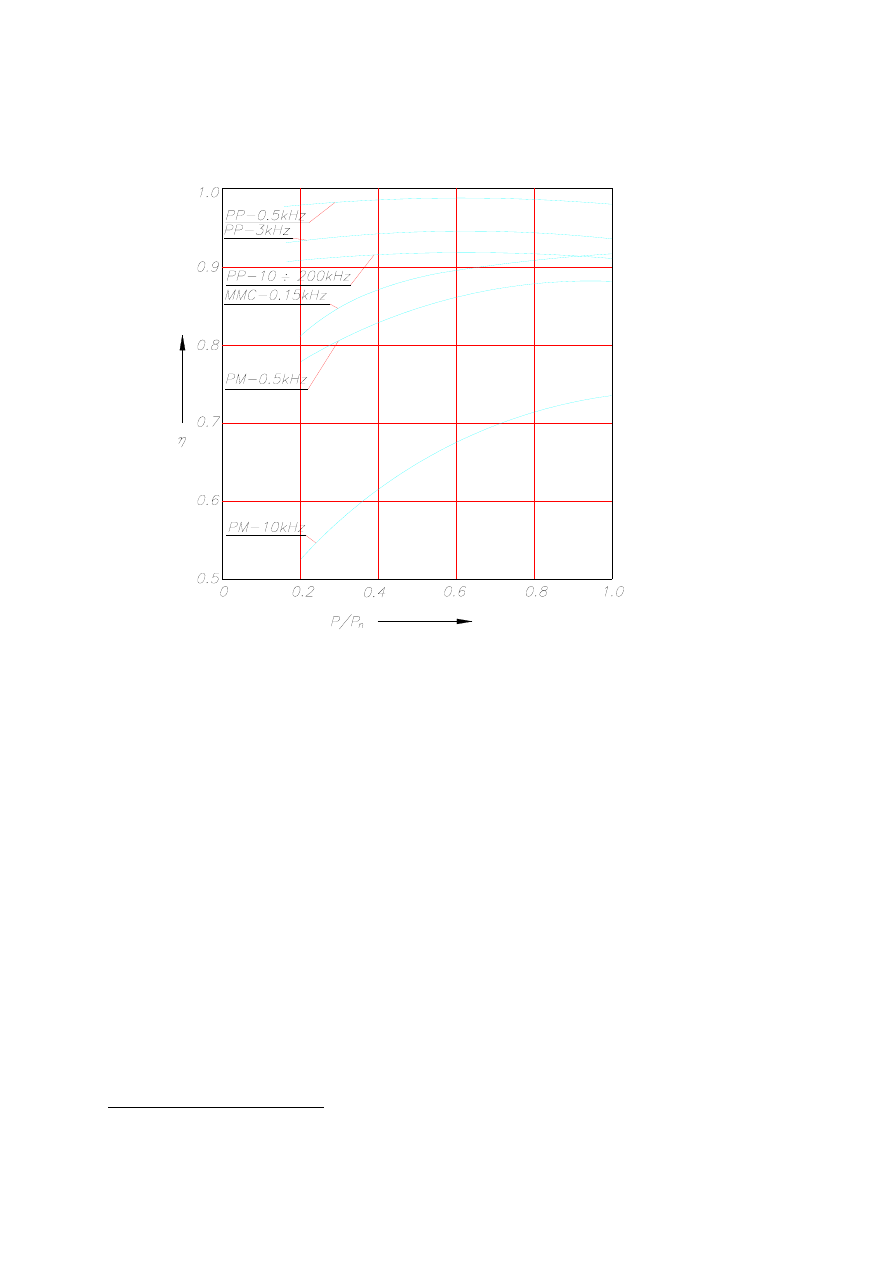
6. Nagrzewanie indukcyjne
___________________________________________________________________________

Rys. 6.43. Sprawność przetwornic maszynowych (PM) przekształtników półprzewodnikowych (PP) oraz mag-

netycznego mnożnika częstotliwości (MMC) w funkcji ich względnego obciążenia przy różnych
częstotliwościach roboczych (P. - obciążenie znamionowe)

IGCTs, przy użyciu którego możliwe jest budowanie jednostek o mocy do 100 MW, co przy
korzystaniu z innych przyrządów wymaga stosowania szeregowo-równoległego łączenia
zaworów. Jako górny zakres częstotliwości podawana jest dla tego tyrystora wartość l kHz
[680]. Oczywiście im większe częstotliwości, tym możliwe do uzyskania graniczne moce
urządzeń są mniejsze. Trzeba też wspomnieć o możliwościach zwiększenia częstotliwości
pracy przemienników tyrystorowych przez stosowanie specjalnych rozwiązań układowych
[400], [677]. Przy większych mocach mogą być one w pewnych przypadkach konkurencyjne z
przekształtnikami zbudowanymi z użyciem tranzystorów mocy w zakresie częstotliwości

f =

10 ÷ 150 kHz.

Znacznie szerszy zakres częstotliwości możliwy jest do uzyskania przy użyciu

przemienników tranzystorowych (4÷1000 kHz) [400], [409], [477]. Są one budowane głównie
przy wykorzystaniu tranzystorów unipolarnych o strukturze wieloemiterowej MOSFET
(

600 kHz), tranzystorów bipolarnych z izolowaną bramką IGBT (

150 kHz) oraz

tranzystorów elektrostatycznych SIT (

≤

f

≤

f

≤

f

l MHz

1)

). Już w końcu lat

86

1)

Tranzystory złączowe bipolarne BJT zostały w elektrotermii praktycznie zastąpione przez tranzystory MOSFET

i IGBT.

6.2. Urządzenia indukcyjne i ich zastosowania
____________________________________________________________________________

80-tych, budowane w technice tranzystorowej SIT urządzenia osiągnęły moce o wartościach
0,6 MW przy 100 kHz oraz 0,4 MW przy 200 kHz [498], [503], [505]. Lampowe generatory
mocy pokrywają najszersze pasmo częstotliwości wykorzystywanych w urządzeniach
indukcyjnych (4 kHz ÷27 MHz), przy mocach przekraczających l MW. Ze względu na ich
znacznie mniejszą sprawność w porównaniu z przemiennikami półprzewodnikowymi nie
można wykluczyć faktu, że będą one systematycznie traciły na znaczeniu.

Buduje się także generatory tranzystorowe o mocach nie przekraczających kilku

kilowatów i częstotliwościach wykorzystywanych zwykle w technice nagrzewania poje-
mnościowego, np. 27,12 MHz [374], [465], [475], [493], [494].

6.2.2.2. Źródła częstotliwości zmniejszonej (małej)

Istnieją przypadki, w których zmniejszenie częstotliwości w stosunku do sieciowej jest
korzystne. Chodzi tu o nagrzewanie skrośne wsadów o dużych przekrojach, co występuje w
szczególności w dziedzinie obróbki plastycznej, podczas której optymalne warunki
temperaturowe występują przy maksymalnej jednorodności pola temperatury. Zmniejszenie
częstotliwości może się także przyczynić do ograniczenia tworzenia się zgorzeliny oraz
odwęglenia warstw przypowierzchniowych, ponieważ nie są one nadmiernie przegrzewane.
Trzeba" tu również wspomnieć o indukcyjnym mieszaniu metalu, a więc technice silnie
zintegrowanej z zastosowaniami elektrotermicznymi, wymagającej częstotliwości od ułamka
herca do kilku herców. We wszystkich tych przypadkach źródłami energii są tyrystorowe
bezpośrednie przemienniki częstotliwości, czyli cyklokonwertory przekształcające przemienne
napięcie wejściowe o częstotliwości sieciowej na napięcie o regulowanej wartości i
częstotliwości zmniejszonej, bez pośrednictwa obwodu prądu lub napięcia stałego [322].

Podstawowym elementem klasycznego bezpośredniego przemiennika częstotliwości

jest przekształtnik rewersyjny zbudowany z zespołów tyrystorowych połączonych
przeciwsobnie i sterowanych na przemian. Schemat bardziej rozpowszechnionego prze-
miennika bezpośredniego o wyjściu jednofazowym, złożonego z dwóch zespołów trój-
fazowych tyrystorowych mostków sterowanych, połączonych odwrotnie równolegle
przedstawia rys. 6.44. Napięcie

U

2

ma okres trzy razy większy niż okres napięcia zasilania,

czyli częstotliwość roboczą równą 1/3 częstotliwości sieciowej. Nie jest to napięcie
sinusoidalnie zmienne, ale w przypadku nagrzewania lub mieszania nie ma to znaczenia.
Pewną wadą przekształtnika jest dość znaczny pobór mocy biernej z sieci. Dławiki w układzie
służą do ograniczenia amplitud prądu wyrównawczego.

6.2.2.3. Źródła częstotliwości sieciowej
Na wybór częstotliwości sieciowej, oprócz parametrów geometrycznych i materiałowych
wsadu, wpływ mają inne czynniki techniczne np. zależność intensywności mieszania wsadu
płynnego w piecu od częstotliwości źródła zasilania, pojemność wsadowa,

87

6. Nagrzewanie indukcyjne
___________________________________________________________________________

Rys. 6.44. Bezpośredni tyrystorowy przemiennik
częstotliwości (cyklokonwerter)
U

1

– na pięcie o częstotliwości sieciowej,

U

2

– napięcie o częstotliwości roboczej

(zmniejszonej)

dopuszczalne zmiany obciążenia sieci. Wpływ mają także czynniki ekonomiczne, zwłaszcza że
wiele procesów jest możliwych do zrealizowania zarówno przy częstotliwości 50 Hz, jak i przy
częstotliwościach większych, bez istotnego wpływu na rezultaty technologiczne. Dotyczy to w
szczególności procesów topienia metali [421].

Częstotliwość sieciowa jest stosowana w technologiach nagrzewania skrośnego,

nagrzewania powierzchniowego mającego na celu uzyskanie dużych głębokości hartowania
oraz małych gradientów twardości na przejściu od warstwy utwardzonej do nieutwardzonego
wnętrza wsadu (nagrzewanie dwuczęstotliwościowe przy 50 Hz i np. 1000 Hz) oraz w
technologiach topienia do zasilania pieców kanałowych oraz znacznej grupy pieców tyglowych
[614]. Nagrzewnice budowane są jako układy jedno- bądź trójfazowe. Te drugie są trudniejsze
w realizacji i bywają używane raczej w układach przelotowych. Napięcie zasilania
wzbudników zawiera się w przedziale od kilkudziesięciu do kilkuset woltów. W niektórych
rozwiązaniach układów przelotowych stosuje się napięcie przekraczające 1000 V, ale ma to
miejsce przy zasilaniu zespołu szeregowo połączonych wzbudników zasilanych z jednej fazy
(rys. 6.45). Wymagane napięcia zasilania pojedynczych wzbudników lub ich zespołów
szeregowo połączonych uzyskuje się bezpośrednio

88

6.2. Urządzenia indukcyjne i ich zastosowania
____________________________________________________________________________

Rys. 6.45. Zasilanie 20 - wzbudnikowej trójfazowej nagrzewnicy częstotliwości sieciowej

T - transformator, RI - regulator indukcyjny, C - baterie kondensatorów do kompensacji mocy biernej

z sieci lub za pośrednictwem transformatorowych bądź tyrystorowych układów dopaso-
wujących. Bezpośrednio z sieci zasila się niektóre rodzaje nagrzewnic mniejszej mocy z
magnetowodami (o rdzeniu zamkniętym oraz otwartym) [568].

Piece indukcyjne zarówno tyglowe, jak i kanałowe budowane są jako jedno-, dwu- i

trójfazowe. Napięcia zasilania pieców kanałowych: kilkaset do tysiąca kilkuset woltów,
tyglowych - kilkaset do około 3000 V. Typowymi elementami pośredniczącymi między siecią i
piecami są różnego rodzaju transformatory. Stosuje się także sterowniki tyrystorowe pracujące
w układzie odwrotnie równoległym ze sterowaniem fazowym. Transformatory jednostek o
mocy większej niż l MW są przyłączane do sieci wysokiego napięcia. Rysunek 6.46
przedstawia typowe rozwiązania układów zasilania urządzeń indukcyjnych częstotliwości
sieciowej [254] [657], rys. 6.47 zaś przykład zasilania pieca tyglowego dużej mocy.

Układy symetryzujące obciążenie sieci trójfazowej są stosowane bardzo często,

ponieważ większość nagrzewnic i pieców to odbiorniki jednofazowe. Są one dopasowywane
do sieci za pośrednictwem układu Steinmetza. Do kategorii odbiorników

89

6. Nagrzewanie indukcyjne
____________________________________________________________________________

Rys. 6.46. Elementy najbardziej rozpowszechnionych układów zasilania nagrzewnic i pieców indukcyjnych o

częstotliwości sieciowej

A) transformator regulacyjny jednofazowy; B) autotransformator regulacyjny jednofazowy; C)
transformator trójfazowy; D) autotransformator regulacyjny trójfazowy; E) regulator indukcyjny
jednofazowy; P) transformator trójfazowy w układzie V; G) dwa transformatory jednofazowe w
układzie Scotta; H) autotransformator regulacyjny trójfazowy w układzie V; I) regulator indukcyjny
trójfazowy; a) ÷ f) układy połączeń wzbudników z kondensatorami do kompensacji mocy biernej, przy
czym wzbudniki pieca kanałowego w eksploatowane w układzie V wg rys. d) mogą być przełączane
także na pracę w układach jak na rysunkach a), b), c)

90

6.2. Urządzenia indukcyjne i ich zastosowania
___________________________________________________________________________

Rys. 6.47. Układ zasilania jednofazowego pieca tyglowego częstotliwości sieciowej

l - rozłącznik, 2 - transformator, 3 - wyłącznik piecowy, 4 - układ symetryzacji, 5 - autotransformator,
6 - rezystor rozruchowy z wyłącznikiem, 7 - baterie kondensatorów do kompensacji mocy biernej,
8 - piec

wymagających symetryzacji należą także dwufazowe piece kanałowe. Najczęściej stosuje się
do tego celu układ Scotta [566].
W nowoczesnych rozwiązaniach zarówno symetryzacja, jak i kompensacja realizowane są
automatycznie i coraz częściej z wykorzystaniem techniki mikroprocesorowej [515].
Korzystne jest stosowanie do tego celu łączników tyrystorowych, ponieważ umożliwia to
bezproblemowe przełączanie zaczepów transformatora regulacyjnego pod obciążeniem, a
ponadto wyeliminowanie udarów prądu przy przełączaniu baterii kondensatorów [614].

6.2.2.4. Źródła częstotliwości zwiększonej (średniej) i wielkiej
Magnetyczne mnożniki częstotliwości. Istnieje wiele odmian magnetycznych mnożników
częstotliwości (MMC), przy czym wszystkie one zaliczane są do klasy magnetycznych
przemienników mocy służących do przetwarzania parametrów energii elektrycznej przy
wykorzystaniu nieliniowości krzywej magnesowania i zjawisk nasyceniowych [591].
Do MMC mających największe znaczenie w elektrotermii zalicza się mnożniki typu
transformatorowego oraz typu dławikowego, przy czym te drugie stosowane są do zasilania
urządzeń o mocy nie przekraczającej 350 kV•A, co wynika z braku możliwości ich
bezpośredniego zasilania z sieci wysokiego napięcia [553]. Mnożniki typu transformatorowego
pozbawione są tej wady. Tym nie mniej, w przypadku odbiorników największych mocy,
stosuje się elementy dopasowujące do sieci w postaci autotransformatorów (przy napięciach do
10 kV) lub transformatorów regulacyjnych (przy napięciach większych niż 10 kV). Daje to
możliwość zmiany w pewnych granicach napięcia zasilającego MMC, a tym samym stopnia
nasycenia rdzenia oraz ogranicza oddziaływanie na sieć [662].


91

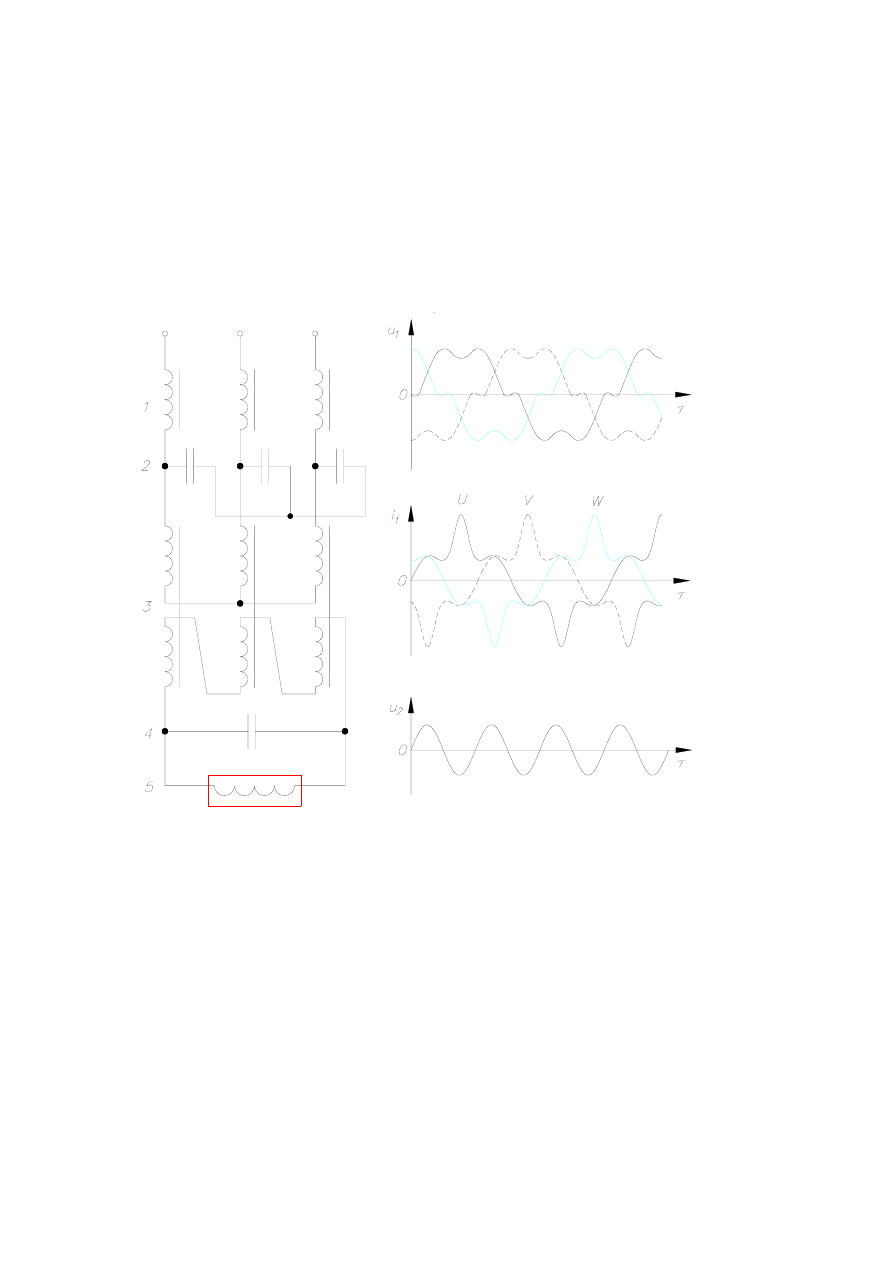
6. Nagrzewanie indukcyjne
___________________________________________________________________________

Spośród MMC typu transformatorowego najbardziej rozpowszechniony jest układ

złożony z jednofazowych transformatorów dwukolumnowych o jednakowych cha-
rakterystykach magnesowania i uzwojeniach połączonych w taki sposób, że przy symet-
rycznym trójfazowym zasilaniu z częstotliwością

f uzyskuje się symetryczny n-fazowy układ

pierwszych harmonicznych napięcia. Na duże moce buduje się najczęściej potrajacze, ale także
pięciokrotniki i dziewięciokrotniki częstotliwości sieciowej.

Rys. 6.48. Zasilanie urządzeń indukcyjnych za pośrednictwem magnetycznego potrajacza częstotliwości:

a) schemat układu zasilania; b) przebieg chwilowych wartości prądów i napięć

l - dławiki

wygładzające, 2 - kondensatory tłumiące,

3 - magnetyczny potrajacz częstotliwości, 4 - kondensatory

kompensacji i regulacji napięcia, 5 - wzbudnik odbiornika,

u

1

,

i

1

, - napięcie i prąd po strome pierwotnej

potrajacza,

u

2

- napięcie wypadkowe po stronie wtórnej

Potrajacze częstotliwości tworzą trzy dwukolumnowe transformatory, których uzwojenia
pierwotne są połączone w gwiazdę zaś uzwojenia wtórne tworzą trójkąt z włączonym w jego
obwód wzbudnikiem nagrzewnicy lub pieca (rys. 6.48a). Transformatory pracują w zakresie
nasycenia magnetycznego ich rdzeni, wskutek czego zniekształceniu ulegają napięcia fazowe
oraz prądy fazowe po strome pierwotnej. W przypadku potrajacza chwilowe wartości wtórnych
napięć fazowych są określone zależnością [613]

92

6.2. Urządzenia indukcyjne i ich zastosowania
___________________________________________________________________________

∑

=





















+

−

+

−

+

=





















7

,

5

,

3

,

1

k

k

o

k

o

k

k

2

m

W

2

V

2

U

2

)

φ

240

ωτ

(

k

sin

)

φ

120

ωτ

(

k

sin

)

φ

ωτ

(

k

sin

U

u

u

u

(6.222)

przy czym

U

jest wartością maksymalną

k-tej harmonicznej napięcia.

k

2

m

Napięcie wtórne

)

φ

ωτ

(

k

sin

U

3

u

k

k

2

m

2

+

=

∑

(6.223)

przy czym

k = 3, 9, 15, 21.

Udział harmonicznych 9, 15, 21... jest niewielki i wobec tego można uznać, że napięcie

na zaciskach wyjściowych potrajacza ma częstotliwość

3f. O wartości napięcia strony wtórnej

decyduje trzecia harmoniczna indukcji w rdzeniu zależna od kształtu charakterystyki
magnesowania i stopnia nasycenia obwodu. Na rysunku 6.48b pokazano przebiegi wartości
chwilowych napięć i prądów w potrajaczu.

Prąd pobierany z sieci przez nieskompensowany MMC zawiera wyższe harmoniczne

nieparzyste, a ponadto charakteryzuje się małym współczynnikiem mocy

. W

celu zmniejszenia oddziaływania na sieć i poprawy

, po stronie pierwotnej instaluje się

dławiki szeregowe i baterie kondensatorów.

5

.

0

3

.

0

φ

cos

÷

=

φ

cos

Oczywiście niezależnie od tego stosuje się kompensację mocy biernej pieca lub

nagrzewnicy po stronie wtórnej. Bateria kondensatorów przeznaczona do tego celu jest
przełączana pod obciążeniem i umożliwia regulację napięcia na wzbudniku, a tym samym
regulację pobieranej mocy [509], [662]. Sprawność MMC maleje przy mniejszych
obciążeniach (rys. 6.43) oraz przy rosnących częstotliwościach. Według niektórych źródeł dla
jednostek dużej mocy przy obciążeniach znamionowych sięga ona 95% [314], [508]. Mało
kłopotliwa eksploatacja, duża niezawodność, poprawna współpraca z siecią oraz możliwość
uzyskania pożądanej charakterystyki zewnętrznej (zależność napięcia wyjściowego od prądu
obciążenia) sprawiają, że MMC w zakresie częstotliwości do 450 Hz stanowią alternatywne
źródła zasilania w stosunku do maszynowych i półprzewodnikowych przemienników
częstotliwości.

Przetwornice maszynowe. Są to jednofazowe prądnice synchroniczne napędzane

silnikami trójfazowymi. Używa się ich w zakresie częstotliwości 150÷10000 Hz, przy czym
nowo uruchamiane indukcyjne urządzenia grzejne na ten zakres częstotliwości wyposaża się
już w przemienniki półprzewodnikowe. Przetwornice maszynowe są często wykorzystywane
jako źródła zasilania w sieciach zwiększonej częstotliwości. W zakresie do około 1000 Hz
stosuje się generatory synchroniczne z wystającymi biegunami, czyli takiego samego typu, jak
generatory częstotliwości sieciowej. Przy

f >1000 Hz w użyciu są maszyny reluktancyjne z

nieuzwojonym wirnikiem (dla

f < 4000 Hz generatory Lorenza-Schmidta, dla f < 10 000 Hz

generatory Guy'a). Generatory Guy'a są szczególnie przydatne do nagrzewania indukcyjnego z
uwagi na małe elektromagnetyczne stałe czasowe. Przetwornice małej mocy (do 200 kV·A) to
przeważnie konstrukcje o wale pionowym, charakteryzujące się mniejszymi drganiami.

93

6. Nagrzewanie indukcyjne
___________________________________________________________________________

Do napędu generatorów, których moce sięgają 10 MV·A, używa się najczęściej

silników indukcyjnych zwartych, przy większych mocach - także pierścieniowych. Jednostki o
mocy l MV bywają zasilane silnikami synchronicznymi. Generatory są chłodzone wodą,
powietrzem, a także wodorem [405].

≥

Z uwagi na silną zależność sprawności przetwornicy od jej obciążenia (rys. 6.43),

korzystna jest eksploatacja mniejszych jednostek przy pracy na wspólne szyny, z których zasila
się wiele indukcyjnych urządzeń grzejnych. Przy zmieniającym się obciążeniu istnieje
wówczas możliwość optymalnego wyboru liczby równocześnie pracujących generatorów. O
ile zachodzi potrzeba regulacji ich mocy wyjściowej, to można tego dokonać przez zmianę
prądu wzbudnika. W niektórych przypadkach (np. nagrzewanie w procesach obróbki
powierzchniowej, lutowanie) stosuje się na wyjściu transformatory dopasowujące średniej
częstotliwości. W użyciu są także autotransformatory.

Tyrystorowe przemienniki częstotliwości. Zakres częstotliwości możliwych do

uzyskania przy użyciu tyrystorowych przemienników częstotliwości, dzięki ogromnemu
postępowi w dziedzinie wytwarzania nowych odmian tyrystorów oraz dzięki nowym
rozwiązaniom układowym, stale się poszerza. Już do roku 1989 wdrożono przemienniki
tyrystorowe o częstotliwości roboczej sięgającej 100 kHz [454], [573], [620]. Moce
uzyskiwane w zakresie największych częstotliwości są przy tym duże, np. przy 60 kHz -100
kW (przemiennik zrealizowany w technice SITh o sprawności większej niż 90% [498]). W tej
samej technice moc 20 kW osiągnięto przy 80 kHz oraz 50 kW przy 100 kHz [465], [620]. Na
bazie już istniejących środków technicznych, granica ta może być przekroczona. Równoległy
rozwój tranzystorów mocy sprawił jednak, że zakres powyżej 50 kHz zaczyna być domeną
przekształtników tranzystorowych i dlatego wartość tę można z dużym prawdopodobieństwem
uznać za ekonomicznie uzasadnioną granicę zastosowań przemienników tyrystorowych,
przynajmniej w perspektywie do roku 2000.

Spośród spotykanych rozwiązań przemienników najwięcej z nich zbudowanych jest na

bazie falowników przedstawionych na rys. 6.49. Przy użyciu tyrystorów konwencjonalnych
falownik napięciowy z szeregowym obwodem rezonansowym (rys. 6.49a) jest stosowany jest
w zakresie do 3 kHz, falownik prądowy z równoległym obwodem rezonansowym (rys. 6.49b) -
10 kHz, falowniki prądowe z szeregowym obwodem rezonansowym o podwójnej
częstotliwości (6.49c) - 20 kHz, i o potrójnej częstotliwości (6.49d) - 30 kHz. Falowniki
napięciowe szeregowo-równoległe (jedno z rozwiązań przedstawia rys. 6.49e) są stosowane
nawet do 50 kHz [399], podobnie jak falowniki napięciowe drgań tłumionych (6.49f) oraz
falowniki napięciowe z szeregowym obwodem rezonansowym i tyrystorami RCT
przewodzącymi wstecznie. Wszystkie wymienione przemienniki wykonuje się z obwodem
pośredniczącym prądu lub napięcia stałego. Dowiedziono także przydatności - w dziedzinie
nagrzewania indukcyjnego - przemienników bezpośrednich, a więc nie mających obwodu
pośredniczącego. Przemienniki te pozwalają przekształcać energię o częstotliwości sieciowej
na energię o częstotliwości zwiększonej sięgającej 10 kHz [476].

94

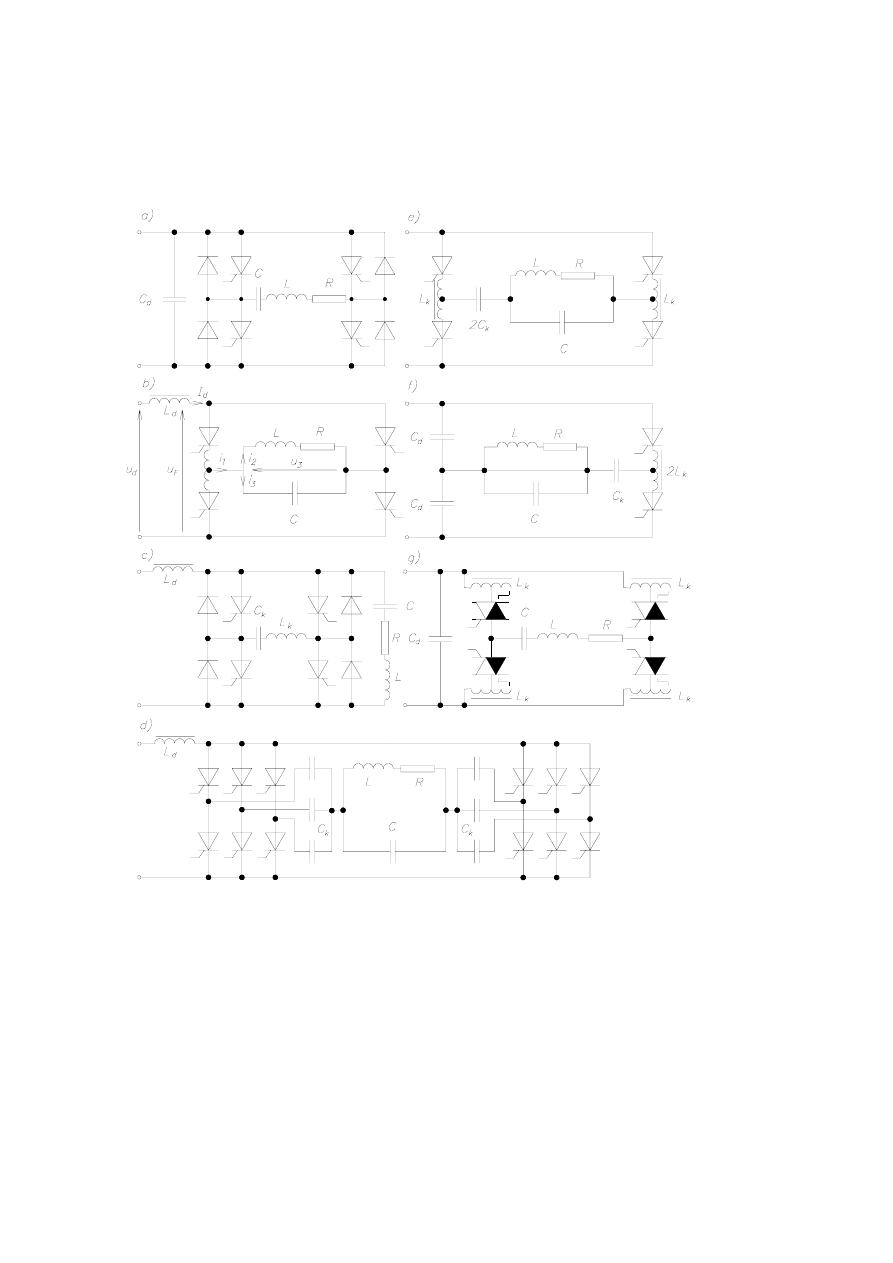
6.2. Urządzenia indukcyjne i ich zastosowania
_________________________________________________________________________

Rys. 6.49. Schematy falowników tyrystorowych stosowanych do zasilania indukcyjnych urządzeń grzejnych:

a) falownik napięciowy z szeregowym obwodem rezonansowym; b) falownik prądowy z równoległym
obwodem rezonansowym; c) falownik prądowy z szeregowym obwodem rezonansowym o podwójnej
częstotliwości; d) falownik prądowy z szeregowym obwodem rezonansowym o potrójnej
częstotliwości; e) falownik prądowy szeregowo - równoległy; f) falownik napięciowy drgań
tłumionych; g) falownik napięciowy z szeregowym obwodem rezonansowym i tyrystorami
przewodzącymi wstecznie RCT
C - pojemność obwodu rezonansowego. C

d

, - pojemność obwodu pośredniczącego,

C

k

, - pojemność

obwodu komutacyjnego,

L - indukcyjność obwodu rezonansowego, L

d

- indukcyjność dławika w

obwodzie prądu wyprostowanego,

L

k

,

- indukcyjność obwodu komutacyjnego, R - rezystancja

obciążenia

95

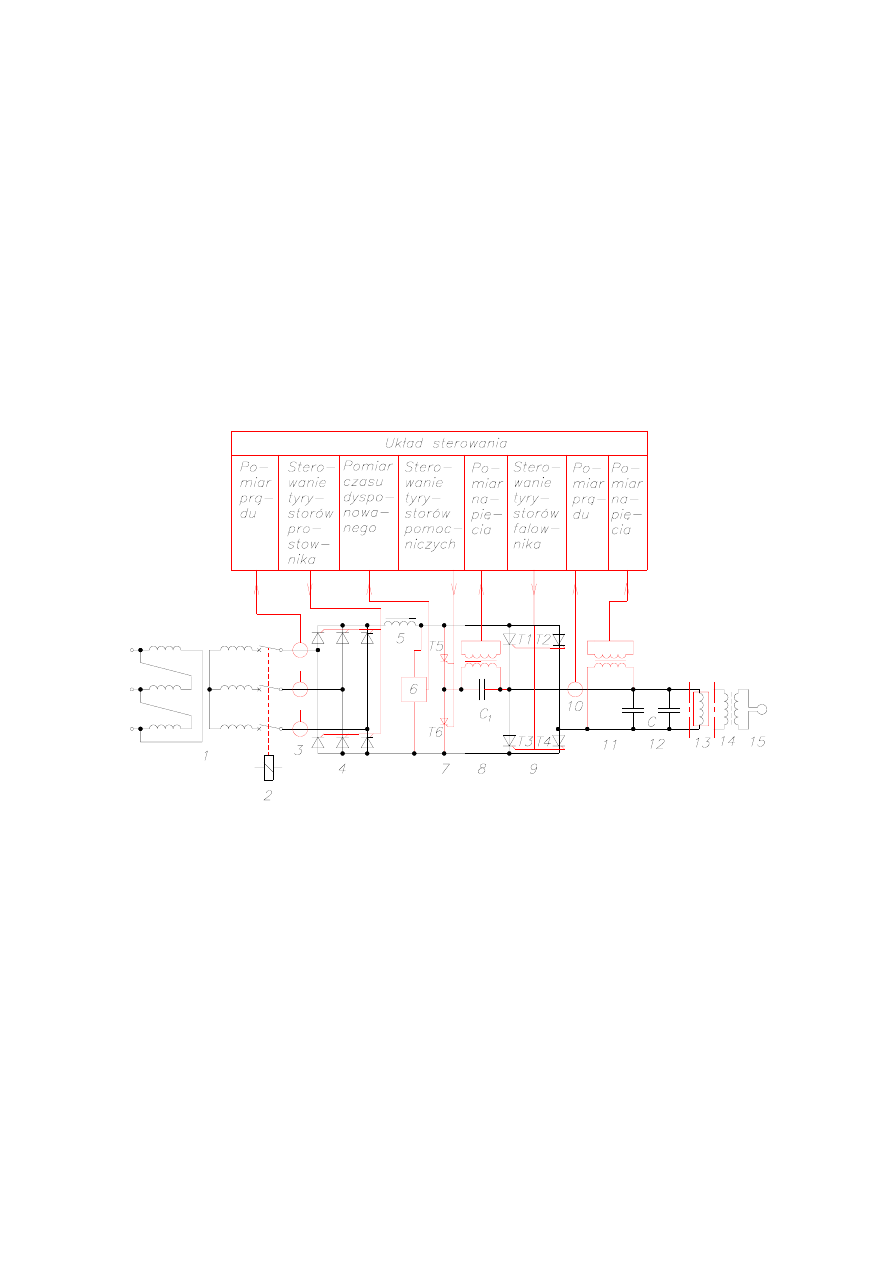
6. Nagrzewanie indukcyjne
____________________________________________________________________________

Poszczególne rozwiązania przekształtników znamionują dość istotne różnice związane

nie tylko z częstotliwością, lecz także z takimi ich cechami jak niezawodność, cena, złożoność
układów sterowania i zabezpieczeń, możliwości regulacyjne i inne. Przy uwzględnieniu
wszystkich tych czynników pierwszeństwo daje się przemiennikom z równoległymi obwodami
rezonansowymi i falownikami prądu, które są najczęściej stosowane. Przy użyciu tyrystorów o
czasach wyłączenia

(jeden z najważniejszych parametrów tyrystora), a więc np.

typu GTO, powiększa się zakres stosowanych częstotliwości w stosunku do znamionujących
falowniki wyposażone w tyrystory konwencjonalne. Zasada działania falowników z
tyrystorami szybkimi pozostaje taka sama, tym nie mniej kompletne przemienniki znamionują
dość istotne różnice, zwłaszcza w obwodach pomocniczych.

s

µ

10

τ

q

<

Rys. 6.50. Schemat przemiennika z tyrystorami klasycznymi, równoległym obwodem rezonansowym i falo-

wnikiem prądu
l - transformator zasilający, 2 - wyłącznik główny, 3 - przekładniki prądowe, 4 - prostownik, 5 -
dławik,

6 - nastawnik czasu dysponowanego, 7 - tyrystory układu rozruchowego, 8 - kondensator

układu rozruchowego,

9 - tyrystory falownika, 10 - przekładnik prądowy, 11 - przekładnik

napięciowy,

12 - bateria kondensatorów do kompensacji mocy biernej, 13 - wzbudnik, 14 -

transformator dopasowujący,

15 - wzbudnik, (elementy 14 i 15 są alternatywą 13)

Z uwagi na największe znaczenie przemienników tyrystorowych z równoległymi

obwodami rezonansowymi i falownikami prądu, zostaną one bliżej scharakteryzowane.
Zwrócona też będzie uwaga na najważniejsze różnice między rozwiązaniami z użyciem
tyrystorów SCR i tyrystorów GTO. Schemat przemiennika tego typu z tyrystorami
konwencjonalnymi SCR przedstawia rys. 6.50.

96

6.2. Urządzenia indukcyjne i ich zastosowania
____________________________________________________________________________

Przemiennik zasilany jest z transformatora

l lub bezpośrednio z sieci. Jeśli jest

stosowany transformator, to prawie zawsze służy do obniżenia napięcia sieci do wartości
wymaganej na wejściu prostownika. Galwaniczna separacja od sieci nie w każdym przypadku
jest konieczna. Ponadto transformator, dzięki swojej indukcyjności rozproszenia, gwarantuje
wymaganą reaktancję obwodu komutacji prostownika.

W skład przemiennika wchodzi prostownik w postaci pełnosterowanego 6-pulsowego

mostka tyrystorowego

4. W układach dużej mocy lub przy szczególnych wymaganiach

dotyczących ograniczenia oddziaływania na sieć stosuje się prostowniki 12-pulsowe.
Kolejnym elementem jest dławik

5, który służy do wygładzenia prądu. Pełni on także rolę

filtru separującego obwód zwiększonej częstotliwości od prostownika ograniczając
jednocześnie przetężenia [711].

Jednofazowy falownik

9 o komutacji zewnętrznej, czyli wymuszonej obciążeniem

tworzą: tyrystory

T1, T2, T3, T4 w układzie mostkowym, włączona w przekątną mostka bateria

kondensatorów

12 wraz z przyłączonym równolegle wzbudnikiem 13 lub układem

transformator obniżający

14 - wzbudnik 15. Transformator umożliwia dopasowanie źródła do

wsadu w przypadku wzbudników jedno - lub małozwojowych, a ze względu na fakt
przenoszenia energii zwiększonej częstotliwości wyposażony musi być w rdzeń o małej
stratności. Doskonale do tego nadają się rdzenie z magnetycznych materiałów amorficznych
[313], [561].

W wyniku wprowadzania w stan przewodzenia na przemian par tyrystorów

T1, T4 i T2,

T3, skompensowany obwód obciążenia jest zasilany prądem przemiennym trapezoidalnym.
Prąd wzbudnika oraz napięcie wyjściowe falownika mają w przybliżeniu kształt sinusoidalny.
Układ sterowania automatycznie utrzymuje częstotliwość pracy falownika na poziomie bliskim
częstotliwości rezonansowej obwodu obciążenia, bez potrzeby zmiany pojemności baterii
kondensatorów

12. Układ regulacji prądu wejściowego falownika wpływa na kąt wysterowania

tyrystorów prostownika. Tyrystory falownika są sterowane w taki sposób, by prąd wyjściowy
falownika

i

1

wyprzedzał napięcie wyjściowe falownika

u

3

(rys. 6.51), a więc tak, aby

obciążenie miało zawsze charakter pojemnościowy. Wyprzedzenie pierwszej harmonicznej
tego prądu

i

11

w stosunku do napięcia

u

3

jest sumą połowy czasu komutacji, czyli

0

oraz

czasu dysponowanego

czyli czasu jakim się rozporządza w celu umożliwienia odzyskania

przez aktualnie wyłączaną parę tyrystorów zdolności zaworowych. Czas

zależy od wartości

zastępczych parametrów

R i C obwodu wyjściowego falownika (rys. 6.49b). Musi być on

oczywiście dłuższy od charakteryzującego każdy tyrystor czasu wyłączenia

. A więc

teoretycznie wyprzedzenie (

i

k

τ

5

.

d

τ

d

τ

τ

5

.

0

5

.

q

τ

d

τ

11

w stosunku do

u

3

mogłoby wynosić

, jednakże z

uwagi na możliwe różnice

dla poszczególnych egzemplarzy tyrystorów, przyjmuje się

pewną rezerwę czasu. Według [437]

, czyli wyprzedzenie pierwszej harmonicznej

prądu

i

q

k

t

+

k

τ

+

q

τ

q

d

τ

3

.

1

τ

>

11

w stosunku do napięcia

u

3

wynosić musi co najmniej

0

. Stąd też

współczynnik mocy układu obciążenia jest równy

)]

τ

5

.

0

τ

(

f

π

2

cos[

φ

cos

k

d

+

=

(6.224)

97

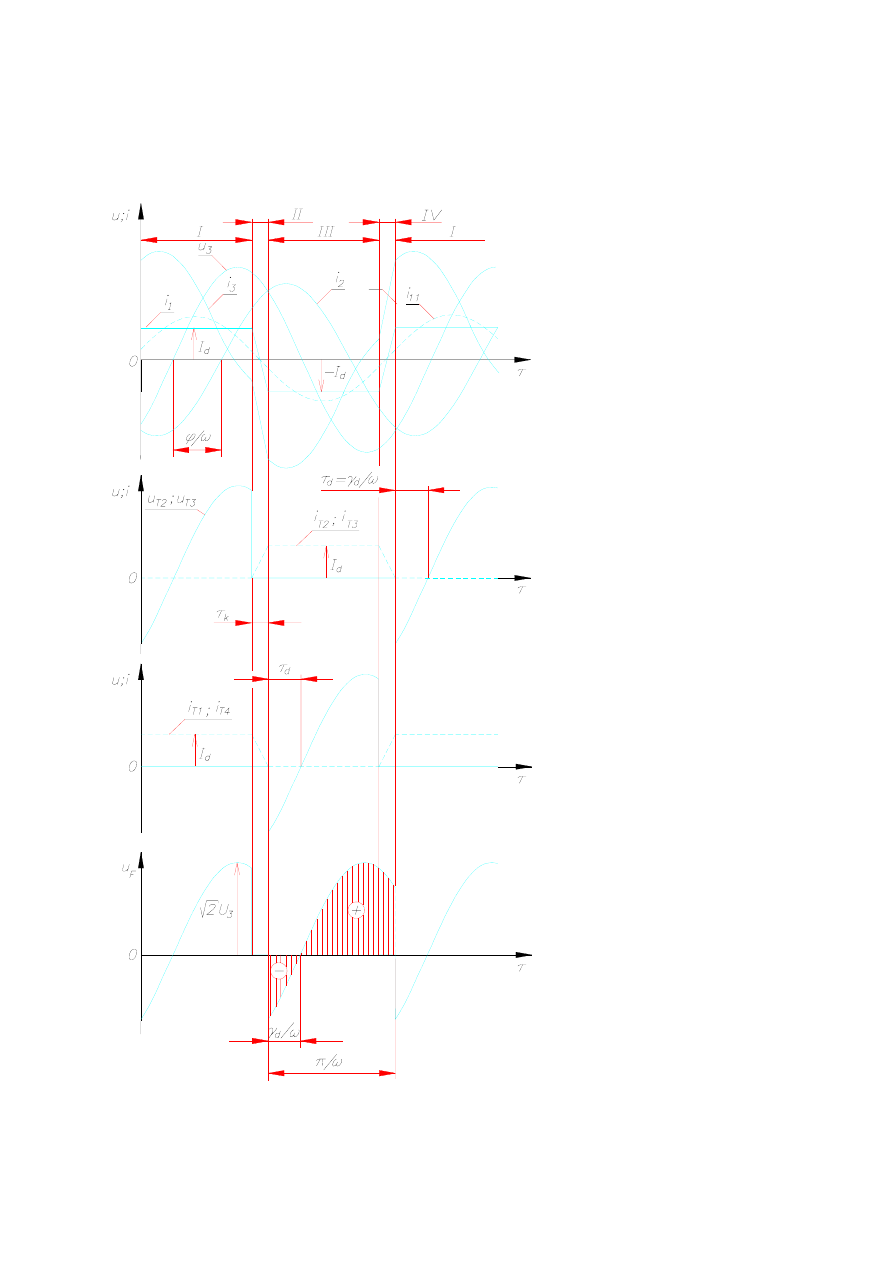
6.Nagrzewanie indukcyjne
___________________________________________________________________________

Rys.6.51. Przebiegi czasowe napięć
i prądów równoległego falownika
prądu w stanie ustalonym, wg [322]
I - przewodzenie tyrystorów T1, T4;
II - komutacja prądu wyprostowa-
nego

I

d

- przewodzenie tyrystorów

T2, T3; IV - komutacja prądu wy-
prostowanego

I

d

;

i

1

- prąd wyj-

ściowy falownika;

i

2

- prąd

odbiornika (patrz rys. 6.4 9b);
i

3

- prąd w gałęzi kondensatora C;

i

11

- pierwsza harmoniczna prądu

wyjściowego falownika;

i

T1

,

i

T2

,

i

T3

,

i

T4

, -prądy

przewodzenia tyrysto-

rów;

u

3

- napięcie na odbiorniku;

u

T1

, u

T2

, u

T3

, u

T4

- napięcia przewo-

dzenia tyrystorów;

u

F

- napięcie na

zaciskach wejściowych falownika;
U

3

, - wartość skuteczna napięcia

odbiornika; γ

d

- kąt

dysponowany na

wyłączenie tyrystora;

τ - czas; τ

d

-

czas dysponowany;

τ

k

- czas komuta-

cji;

φ - kąt przesunięcia fazowego

między prądem i napięciem odbior-
nika;

ω - pulsacja

98

6.2. Urządzenia indukcyjne i ich zastosowania
____________________________________________________________________________
Uzależniając

od parametrów

RLC obwodu wyjściowego, otrzymuje się

d

τ













−

−

=

=

RC

ω

R

C

L

ω

R

L

ω

arctg

Z

Re

Z

Im

tg

arc

φ

2

3

(6.225)

a przy oznaczeniu dobroci obwodu wyjściowego przez

R

/

C

/

L

k

Q

=

, zaś pulsacji rezo-

nansowej przez

LC

/

1

ω

=

, otrzymuje się































−













−

=

Q

Q

2

0

Q

0

k

1

k

ω

ω

k

ω

ω

arctg

φ

(6.226)

Moc czynna obciążenia

)

ω

τ

5

.

0

(

cos

1

φ

cos

1

R

U

8

π

P

k

2

2

2

d

2

=

(6.227)

przy czym do rezystancji obciążenia

R wlicza się także wszystkie rezystancje związane ze

stratami. Napięcie

U

d

jest wartością średnią napięcia na wejściu falownika,

ω

- pulsacją

prądu wyjściowego. Oznacza to również, że komutacja powinna być rozpoczęta z wyprzedze-
niem czasowym

w stosunku do momentu osiągnięcia zera przez napięcie na obciążeniu.

f

π

2

=

d

k

τ

τ

+

Czas komutacji w falownikach o mocy do 100 kW przy zastosowaniu tyrystorów o

dużych krytycznych stromościach narastania prądu przewodzenia

(

(parametr chara-

kteryzujący tyrystor związany ze zjawiskiem rozprzestrzeniania się prądu w strukturze załącza-
nego tyrystora) jest pomijalnie mały w porównaniu z czasem

i wynosi zaledwie kilka mikro-

sekund. Przy większych mocach czas ten zaczyna odgrywać istotną rolę i musi być mierzony
oraz uwzględniony w procesie sterowania impulsami bramkowymi tyrystorów [322]. Podobnie
jest w przypadku tyrystorów szybkich, czyli charakteryzujących się małymi czasami .

k

τ

crit

)

τ

d

/

di

d

τ

q

τ

Z uwagi na fakt, że wartość

nie powinna być przekroczona, ponieważ

spowodowałoby to uszkodzenie tyrystora, czas nie może być zbyt krótki. Ograniczenie stro-
mości narastania prądu tyrystorów poniżej wartości

w przypadku falowników o

małej mocy, gwarantuje indukcyjność rozproszenia przewodów łączeniowych. Przy dużej
mocy falowników w szereg z równoległym obwodem obciążenia włącza się dławik o induk-
cyjności

L

crit

)

τ

d

/

di

(

k

τ

crit

)

τ

d

/

di

(

k

, do której czas jest w przybliżeniu wprost proporcjonalny [322].

k

τ

Utrzymywanie częstotliwości pracy falownika w stanie ustalonym na poziomie bliskim

częstotliwości rezonansowej wymaga ciągłego pomiaru czasu dysponowanego

i porównywa-

nia go z zadanym czasem dysponowanym

, którego górna granica limitowana jest czasem

wyłączenia

. Dobór czasu

, zwłaszcza dla częstotliwości granicznych dla danego typu

tyrystorów, musi uwzględniać fakt, że zmiana parametrów obciążenia, np. w wyniku zmian
temperatury wsadu, powoduje zmianę częstotliwości

d

τ

∗

d

τ

q

τ

∗

d

τ

99

6. Nagrzewanie indukcyjne
___________________________________________________________________________

rezonansowej, a więc zmianę

, który nie powinien przekroczyć wartości bezpiecznej np.

. Dobór częstotliwości roboczej falownika sprowadza się wobec tego do ustalenia

wartości

.

Jeśli

, częstotliwość ulega zmniejszeniu, jeśli

, częs-

totliwość ulega zwiększeniu, przy

- nie ulega ona zmianie. Zależność (6.227)

pozwala określić zakres regulacji

U

d

τ

q

τ

3

.

1

∗

d

τ

0

τ

τ

d

d

>

−

∗

0

τ

τ

d

d

<

−

∗

0

τ

τ

d

d

=

−

∗

d

w funkcji

czyli odchylenia od częstotliwości

rezonansowej (wartość ta zawsze jest > l z uwagi na pojemnościowy charakter obwodu) przy
założeniu np. stałej mocy obciążenia

P dla określonej dobroci obwodu.

0

ω

/

ω

Przy spotykanych w praktyce obciążeniach, rozruch falownika w układzie jak na rys. 6.49b nie
jest możliwy. Przyczyną tego jest brak odpowiedniej wartości napięcia na kondensatorze

C

przy pierwszej komutacji. W celu przeprowadzenia rozruchu falownika mostkowego stosuje
się dodatkowy układ rozruchowy złożony z tyrystorów pomocniczych

T5, T6 i kondensatora C,

(rys. 6.50). W czasie rozruchu impulsy bramkowe są doprowadzane kolejno do par tyrystorów
T4, T5 oraz T2, T6. Obwód wyjściowy falownika stanowią wówczas obciążenia
skompensowane kondensatorem

C z szeregowo dołączonym kondensatorem C

1

. W chwili gdy

w falowniku pracującym w układzie rozruchowym nastąpi taki stan, że energia zgromadzona w
kondensatorze

C jest wystarczająca do przeprowadzenia komutacji wyłączonej pary tyrystorów

falownika, układ sterowania powinien włączyć tyrystory

T1, T3 zamiast T5, T6, a więc

odłączyć kondensator

C

1

. Powinna wówczas nastąpić także zmiana funkcji sterowania, polega-

jąca na zapewnieniu wyprzedzenia przez prąd

i

1

(ściśle rzecz biorąc

i

11

) napięcia

u

3

o zadany

czas

.

∗

d

τ

Sprawność przemiennika z falownikiem prądu z obwodem rezonansu równoległego jest
zależna od częstotliwości i zawiera się w przedziale od 91 ÷ 97%. Falownik taki jest
niewrażliwy na zwarcia w obwodzie obciążenia i może być bez problemów eksploatowany w
układach pracy równoległej (na szyny zbiorcze częstotliwości zwiększonej). Z tego względu
granica mocy źródeł z użyciem tych przemienników nie jest od góry ograniczona.
Przemiennik z falownikiem prądu ma oczywiście także wady, z których głównymi są: duży
wzrost napięcia przy malejącym prądzie obciążenia, a także przy zwiększającej się
częstotliwości. Towarzyszy temu malenie czasu

, co przy pewnej jego wartości prowadzi do

nieprawidłowej komutacji tyrystorów i przejścia falownika w stan zwarcia. Nie stanowi to
jednak dla niego zagrożenia, ponieważ

I

d

τ

d

nie zwiększa swojej wartości ponad wartość

dopuszczalną. Nie do pominięcia jest także energia strat wyłączania tyrystorów. Stosunkowo
duże jej wartości wynikają z konieczności rozpoczęcia komutacji znacznie wcześniej od chwili
przejścia napięcia przez zero (rys. 6.51). Energia tracona w tyrystorze zależy nie tylko od
częstotliwości obwodu rezonansowego i natężenia prądu komutowanego, lecz także od
napięcia występującego podczas komutacji. Straty te mogą być zmniejszone przy stosowaniu
tyrystorów wyłączalnych GTO w układzie jak na rys. 6.52.

Główne obwody przemiennika z tyrystorami GTO różnią się od przemiennika z

tyrystorami SCR obecnością szybkich diod szeregowych oraz eliminacją układu roz-
ruchowego. Zadaniem diod szeregowych jest zabezpieczenie GTO przed napięciami


100