staƒ i rozejrzyj si´

wko∏o. Przejdê si´, podskocz. Pomachaj r´kami. Je-
steÊ zbiorem czàstek poruszajàcych si´ w niewiel-
kim obszarze trójwymiarowej rozmaitoÊci – ota-
czajàcej nas przestrzeni trójwymiarowej – która
rozpoÊciera si´ we wszystkich kierunkach na mi-
liardy lat Êwietlnych.

RozmaitoÊç to poj´cie czysto matematyczne. Suk-

cesy fizyki od czasów Galileusza i Keplera polega-
∏y na skutecznym opisywaniu rzeczywistoÊci za po-
mocà takich lub innych narz´dzi matematycznych
– na przyk∏ad rozmaitoÊci. W fizyce trójwymiaro-
wa przestrzeƒ jest t∏em wszystkiego, co si´ w ogó-
le dzieje (zostawiamy na boku rozwa˝ania zwolen-
ników teorii strun, którzy twierdzà, ˝e prócz trzech
oczywistych wymiarów przestrzeni istniejà jeszcze
mikroskopijne wymiary dodatkowe) [patrz: Michael
J. Duff „Powrót teorii strun”; Âwiat Nauki, kwie-
cieƒ 1998]. Przestrzeƒ trójwymiarowa to taka, w
której okreÊlajàc po∏o˝enie punktu, trzeba podaç
trzy liczby. W pobli˝u Ziemi na przyk∏ad takimi trze-
ma liczbami mogà byç d∏ugoÊç i szerokoÊç geogra-
ficzna oraz wysokoÊç nad poziomem morza.

W fizyce Newtona i tradycyjnej mechanice kwan-

towej trójwymiarowa przestrzeƒ, w której zacho-
dzà wszelkie zdarzenia, jest ustalona i niezmien-
na. Natomiast w ogólnej teorii wzgl´dnoÊci
Einsteina przestrzeƒ staje si´ aktywnym uczest-
nikiem zdarzeƒ: odleg∏oÊç mi´dzy dwoma punk-
tami zale˝y od tego, ile w ich pobli˝u znajduje si´

68

ÂWIAT NAUKI SIERPIE¡ 2004

HENRI POINCARÉ wysunà∏ w 1904 roku przypuszczenie,

˝e ka˝dy trójwymiarowy obiekt, któremu przys∏uguje jedna

z w∏asnoÊci sfery trójwymiarowej, mo˝na przekszta∏ciç w sfer´

trójwymiarowà. Dowód tej hipotezy zabra∏ matematykom 99 lat.

(Prosz´ zwróciç uwag´, ˝e trójwymiarowa sfera

nie jest prawdopodobnie tym, o czym czytelnik myÊli).

Graham P. Collins

W

Kszta∏ty przestrzeni

Wszystko wskazuje, ˝e rosyjski matematyk dowiód∏ hipotezy Poincarégo,

dokonujàc jednoczeÊnie pe∏nej klasyfikacji wszystkich przestrzeni

trójwymiarowych. JeÊli tak, otrzyma milion dolarów

SIERPIE¡ 2004 ÂWIAT NAUKI

69

AIP EMILIO SEGRÈ

VISU

AL ARCHIVES (

zdj´cie

); IL

USTRACJE K

OMPUTEROWE

JANA BRENNING, TRÓJWYMIAROWE FIGURY

DON FOLEY (

popr

zednia str

ona

)

materii i energii, a tak˝e od fal gra-
witacyjnych [patrz: W. Wayt Gibbs
„Zmarszczki czasoprzestrzeni”; Âwiat
Nauki, maj 2002]. Niezale˝nie jednak
od tego, czy mamy do czynienia z fizy-
kà Newtona czy Einsteina i niezale˝nie,
czy przestrzeƒ jest skoƒczona czy nie,
przestrzeƒ fizyczna jest w geometrii
pewnà rozmaitoÊcià trójwymiarowà.
Zrozumienie w∏asnoÊci rozmaitoÊci trój-
wymiarowych jest wi´c sprawà zasad-
niczà, jeÊli chcemy w pe∏ni pojàç pod-
stawy, na których zbudowana jest niemal
ca∏a fizyka i wszystkie inne nauki przy-
rodnicze. (RozmaitoÊci czterowymiaro-
we sà równie˝ wa˝ne: przestrzeƒ i czas
tworzà razem w∏aÊnie rozmaitoÊç czte-
rowymiarowà).

Matematycy wiedzà o rozmaitoÊciach

trójwymiarowych wiele, lecz niektóre z
najbardziej zasadniczych pytaƒ okaza∏y
si´ szczególnie trudne. Jednà z ga∏´zi
matematyki badajàcych rozmaitoÊci jest
topologia. Podstawowymi pytaniami, ja-
kie na temat trójwymiarowych rozma-

itoÊci mo˝e zadaç topolog, sà: jaka jest
najprostsza rozmaitoÊç trójwymiarowa;
czy ma ona wiele „kuzynek” o równie
prostej budowie, czy te˝ jest jedyna,
jakie sà mo˝liwe rodzaje rozmaitoÊci
trójwymiarowych?

Odpowiedê na pierwsze pytanie zna-

my od dawna. Najprostszà zwartà roz-
maitoÊcià trójwymiarowà jest sfera
trójwymiarowa (mo˝na sobie wyobra-
˝aç, ˝e rozmaitoÊci niezwarte sà nie-
skoƒczone, tj. odleg∏oÊci mi´dzy punk-
tami mogà byç na nich dowolnie du˝e;
w tym tekÊcie b´dziemy rozwa˝aç jedy-
nie rozmaitoÊci zwarte). Odpowiedzi na
dwa pozosta∏e pytania by∏y nieuchwyt-
ne przez sto lat. Byç mo˝e jednak zna-
laz∏ je w roku 2002 Grigorij (Grisza, jak
o sobie mówi) Jakowlewicz Perelman,
z Instytutu Stiek∏owa w Sankt Peters-
burgu, który najprawdopodobniej udo-
wodni∏ twierdzenie nazywane hipotezà
Poincarégo [patrz: Pawe∏ Strzelecki
„Âwiat wed∏ug Perelmana”;

PANORAMA

,

Âwiat Nauki, listopad 2003].

Sformu∏owa∏ je po raz pierwszy do-

k∏adnie 100 lat temu francuski matema-
tyk Henri Poincaré. Hipoteza ta g∏osi,
˝e wÊród wszystkich rozmaitoÊci trój-
wymiarowych sfera trójwymiarowa ma
unikalny charakter: ˝adna inna rozma-
itoÊç nie dzieli ze sferà jej szczególnie
prostych w∏asnoÊci. RozmaitoÊci trój-
wymiarowe, które sà bardziej skompli-
kowane od sfery, majà albo brzeg, na
który mo˝na wpaÊç niczym na twardy
ceglany mur, albo istniejà w nich istot-
nie ró˝ne po∏àczenia dwóch rejonów w
rodzaju drogi przez las, która rozwidla
si´ i omija bagno z ró˝nych stron, by
póêniej znów si´ spotkaç sama ze sobà.
Hipoteza Poincarégo orzeka, ˝e jedynà
rozmaitoÊcià trójwymiarowà wolnà od
wszelkich komplikacji tego typu jest w∏a-
Ênie sfera. Dowód Perelmana pozwala
odpowiedzieç tak˝e na trzecie z naszych
pytaƒ – stanowi zwieƒczenie pracy, któ-
ra klasyfikuje wszelkie istniejàce rodza-
je rozmaitoÊci trójwymiarowych.

Trzeba troch´ pogimnastykowaç

umys∏, by wyobraziç sobie, jak wyglàda
trójwymiarowa sfera [ramka na stronach
72 i 73]. Ma ona jednak wiele w∏asnoÊci
wspólnych ze zwyk∏à sferà dwuwymia-
rowà, którà wszyscy dobrze znamy: jeÊli
weêmie si´ kulisty balon, to jego gu-
mowa pow∏oka jest dwuwymiarowà sfe-
rà. Dwuwymiarowà, gdy˝ do okreÊlenia
ka˝dego z jej punktów wystarczà dwie
wspó∏rz´dne – d∏ugoÊç i szerokoÊç geo-
graficzna. Niewielki kolisty fragment po-
wierzchni balonu oglàdany przez lup´

70

ÂWIAT NAUKI SIERPIE¡ 2004

CELENE CHANG

Daily P

rincetonian

n

Przez 100 lat matematycy usi∏owali udowodniç hipotez´, którà postawi∏ Henri Poincaré

na temat obiektu zwanego sferà trójwymiarowà i oznaczanego S

3

. Hipoteza orzeka,

˝e sfera trójwymiarowa jest w pewnym sensie unikatowa wÊród obiektów trójwymiarowych
nazywanych rozmaitoÊciami.

n

Dowód hipotezy Poincarégo pojawi∏ si´ w koƒcu w pracach rosyjskiego matematyka

Grigorija Perelmana. Jego prace stanowià tak˝e zwieƒczenie olbrzymiego programu
badawczego, który pozwala sklasyfikowaç wszystkie rozmaitoÊci trójwymiarowe.

n

Nasz WszechÊwiat móg∏by mieç kszta∏t sfery trójwymiarowej. Istnieje wiele intrygujàcych

zwiàzków geometrii z fizykà czàstek elementarnych i teorià grawitacji Einsteina.

Przeglàd /

Hipoteza Poincarégo

GRIGORIJ PERELMAN w kwietniu 2003 roku opowiada na
seminarium w Princeton University o swoim dowodzie hipo-
tezy Poincarégo i hipotezy geometryzacyjnej Thurstona.

b´dzie bardzo przypomina∏ kó∏ko wy-
ci´te z p∏askiej gumowej b∏ony. Ot, b´-
dzie troszk´ zakrzywiony. Ma∏a mrów-
ka w´drujàca po powierzchni balonu nie
odró˝ni go od p∏aszczyzny. Mimo to gdy-
by pow´drowa∏a dostatecznie daleko
wzd∏u˝ krzywej, która wydawa∏aby si´
jej idealnie prosta, to wróci∏aby do punk-
tu wyjÊcia.

Podobnie mrówka na sferze trójwy-

miarowej (lub cz∏owiek na sferze trój-
wymiarowej tak olbrzymiej jak nasz
WszechÊwiat) widzi swoje najbli˝sze
otoczenie jako fragment „zwyk∏ej” prze-
strzeni trójwymiarowej. JeÊli jednak
uda si´ w odpowiednio dalekà podró˝
w dowolnym kierunku wzd∏u˝ linii, któ-
ra w geometrii sfery jest idealnie pro-
sta, to okrà˝y ca∏à sfer´ i powróci do
punktu wyjÊcia – tak samo jak mrówka
na powierzchni balonu lub ktoÊ, kto od-
bywa podró˝ dooko∏a Êwiata.

Istniejà tak˝e sfery wymiarów ró˝-

nych od trzech. Sfer´ jednowymiarowà
znajà wszyscy: to zwyk∏y okràg, czyli
brzeg ko∏a. Sfer´ n-wymiarowà mate-
matycy oznaczajà symbolem S

n

.

Zmagania z hipotezami

MIN

¢¸O PÓ¸ WIEKU

, zanim dokona∏ si´ ja-

kikolwiek post´p w poszukiwaniach
dowodu wysuni´tej przez Poincarégo
hipotezy. W latach szeÊçdziesiàtych ma-
tematycy udowodnili jej odpowiednik
dla sfer S

n

o wymiarach n równych co

najmniej pi´ç. Okazuje si´, ˝e dla ka˝-
dego n

≥ 5 sfera S

n

istotnie jest jedynà

najprostszà rozmaitoÊcià n-wymiarowà.
Paradoksalnie dowód tego wyniku jest
∏atwiejszy dla sfer wysokich wymiarów
ni˝ dla sfery czterowymiarowej i trój-
wymiarowej. Dowód szczególnie trud-
nego przypadku czterowymiarowego
zosta∏ przeprowadzony w roku 1982.
Otwarty pozosta∏ jedynie przypadek sfe-
ry trójwymiarowej, czyli pierwotna wer-
sja hipotezy Poincarégo.

Olbrzymi krok w stron´ ostatecznego

rozwiàzania tego problemu wykona∏ w li-
stopadzie 2002 roku w∏aÊnie Perelman;
swój wywód umieÊci∏ na serwerze
www.arxiv.org (którego matematycy i fi-
zycy powszechnie u˝ywajà, by udost´p-
niaç kolegom nowe wyniki w∏asnych ba-
daƒ). Wprawdzie hipoteza Poincarégo
nie by∏a w niej w ogóle wymieniona, ale
eksperci w dziedzinie topologii, którzy
zajrzeli do tekstu, b∏yskawicznie si´ zo-
rientowali, ˝e praca Perelmana ma kapi-
talne znaczenie. Perelman drugà prac´

na ten sam temat udost´pni∏ w marcu
2003 roku, a w maju i kwietniu odwiedzi∏
Stany Zjednoczone i wyg∏osi∏ na ró˝nych
seminariach w MIT i Stony Brook Uni-
versity seri´ odczytów na temat swoich
wyników. Od tamtej pory zespo∏y mate-
matyków pracujàcych w kilkunastu naj-
lepszych instytutach na Êwiecie Êl´czà
nad tekstami Perelmana, sprawdzajàc
w nich ka˝dy szczegó∏ i szukajàc b∏´dów.

W Stony Brook Perelman mia∏ formal-

ne i nieformalne wyk∏ady przez dwa ty-
godnie; codziennie mówi∏ od trzech do
szeÊciu godzin. „Odpowiedzia∏ na wszyst-
kie pytania, jakie si´ pojawi∏y, i to bar-
dzo jasno – opowiada Michael Ander-
son, matematyk ze Stony Brook. – Na
razie nikt nie zg∏osi∏ do jego dowodu ˝ad-
nych powa˝nych zastrze˝eƒ”. Aby za-
koƒczyç dowód, trzeba wykonaç jeszcze
jeden stosunkowo niewielki krok – mó-
wi Anderson – „ale nie ma ˝adnych wàt-
pliwoÊci co do prawdziwoÊci wyniku”.
Pierwsza z prac Perelmana zawiera pod-
stawowe idee i jest ju˝ w∏aÊciwie zaak-
ceptowana jako wolna od b∏´dów. Dru-
ga to zastosowania i bardzo techniczne
argumenty; proces jej sprawdzania nie
osiàgnà∏ jeszcze tego poziomu ufnoÊci,
jakim cieszy si´ pierwsza praca.

Na badacza, który przeprowadzi do-

wód hipotezy Poincarégo, umieszczonej
przez Instytut Claya z Cambridge w sta-
nie Massachusetts na liÊcie siedmiu tzw.
problemów milenijnych, czeka milion
dolarów. Zanim jednak Perelman stanie
si´ kandydatem do nagrody, jego dowód
musi zostaç opublikowany i przetrwaç
dwa lata krytyki. (Instytut Claya mo˝e
postanowiç, ˝e udost´pnienie dowodu
na jednym z serwerów w Internecie by-
∏o w istocie opublikowaniem – prace Pe-
relmana sà bowiem recenzowane tak
skrupulatnie jak ˝adne inne). Wyniki Pe-
relmana sà rozwini´ciem i ukoronowa-
niem programu badaƒ, który przed 20
laty sformu∏owa∏, a nast´pnie w pewnej
mierze wykona∏ Richard S. Hamilton z
Columbia University. Pod koniec 2003
roku Instytut Claya uhonorowa∏ Hamil-
tona za te prace nagrodà. Perelman
dzi´ki swym pomys∏om i obliczeniom
przebi∏ si´ przez liczne zapory, które Ha-
milton napotka∏, ale wszystkich nie po-
trafi∏ pokonaç.

JeÊli – jak si´ wszyscy spodziewajà

– dowód Perelmana rzeczywiÊcie jest po-
prawny, to nie tylko zostanie udowodnio-
na hipoteza Poincarégo, ale uda si´ za-
mknàç równie˝ znacznie szerszy obszar

badaƒ. Rozpoczà∏ je William P. Thurston,
który dziÊ pracuje w Cornell University.
Jego hipoteza geometryzacyjna to w isto-
cie pe∏ny opis wszystkich mo˝liwych roz-
maitoÊci trójwymiarowych. Sfera trójwy-
miarowa, jedyna w swej niezwyk∏ej
prostocie, jest fundamentem tej wspania-
∏ej klasyfikacji. Gdyby okaza∏o si´, ˝e hi-
poteza Poincarégo jest fa∏szywa, tzn.
gdyby istnia∏o wiele przestrzeni trójwy-
miarowych równie „prostych” jak sfera
S

3

, to klasyfikacja rozmaitoÊci trójwymia-

rowych sta∏aby si´ nieskoƒczenie bardziej
skomplikowana ni˝ to, co zaproponowa∏
Thurston. Dzi´ki wynikom Thurstona i
Perelmana mo˝emy jednak poznaç pe∏-
ny katalog wszystkich kszta∏tów, jakie mo-
˝e przybieraç przestrzeƒ trójwymiarowa
– tzn. wszystkich form, które matematy-
ka uznaje za dopuszczalne kszta∏ty na-
szego WszechÊwiata (chodzi o samà prze-
strzeƒ, nie o przestrzeƒ i czas).

Gumowe obwarzanki

ABY LEPIEJ ZROZUMIE

å

hipotez´ Poincarégo

i pomys∏y Perelmana, trzeba coÊ wiedzieç
o topologii. W tej dziedzinie matematyki
nie majà znaczenia dok∏adne kszta∏ty
obiektu – zupe∏nie tak jakby wszystko by-
∏o zrobione z plasteliny lub gumy, którà
mo˝na dowolnie wyginaç, rozciàgaç i
Êciskaç. Dlaczego jednak mielibyÊmy za-
przàtaç sobie uwag´ przedmiotami czy
przestrzeniami wykonanymi z jakiejÊ uro-
jonej plasteliny? Przyczyna jest taka, ˝e
wierny kszta∏t przedmiotu – a wi´c na
przyk∏ad odleg∏oÊci mi´dzy ró˝nymi je-
go punktami – to tylko odbicie jego struk-
tury geometrycznej. Badajàc przedmiot
„wykonany z plasteliny”, topolog odkry-
wa, które cechy przedmiotu sà tak fun-
damentalne, ˝e istniejà niezale˝nie od
struktury geometrycznej. Zajmowanie si´
topologià mo˝na porównaç do odkrywa-
nia ogólnych cech cz∏owieka metodà roz-
wa˝ania „osoby z plasteliny”, której mo˝-
na nadaç dowolnà form´.

KtoÊ, kto czyta∏ jakiekolwiek popular-

ne teksty o topologii, prawdopodobnie
spotka∏ si´ ze starym, wyÊwiechtanym
dowcipem, ˝e dla topologa fili˝anka i
obwarzanek to przedmioty nieodró˝-
nialne. Istotnie, fili˝ank´ wykonanà z
plasteliny mo˝na przekszta∏ciç w pla-
stelinowy model obwarzanka, rozpro-
wadzajàc tworzywo palcami; nie trze-
ba przy tym nic rozcinaç ani zalepiaç.
˚eby natomiast zmieniç w obwarzanek
plastelinowà kulk´, trzeba albo wywier-
ciç w niej dziurk´ na wylot, albo zrobiç

SIERPIE¡ 2004 ÂWIAT NAUKI

71

z kulki wa∏eczek i skleiç jego koƒce. Po-
niewa˝ potrzebne jest rozcinanie lub
sklejanie, dla topologa kula nie jest tym
samym, co obwarzanek.

Tym, co interesuje topologa najbar-

dziej, sà powierzchnie kuli i obwarzan-
ka – zamiast wi´c myÊleç o bry∏ach,
powinniÊmy w obu przypadkach wy-
obra˝aç sobie baloniki. Ich topologie sà
ró˝ne: balonika w kszta∏cie sfery nie
mo˝na przekszta∏ciç w balonik w kszta∏-
cie d´tki rowerowej, nazywany torusem.
Tak wi´c dla topologa sfera i torus sà
istotnie ró˝nymi obiektami. W poczàt-
kach istnienia topologii matematycy po-
stanowili odpowiedzieç na pytanie, ile

jest takich istotnie ró˝nych obiektów i
jak mo˝na je scharakteryzowaç. Dla
obiektów dwuwymiarowych, nazywa-
nych powierzchniami, odpowiedê jest
jasna i elegancka: wszystko zale˝y tylko
od tego, ile „ràczek” ma dana powierzch-
nia [ilustracja na stronie 74].

Ostatni uniwersalista

POD KONIEC

XIX WIEKU

matematycy zro-

zumieli, jak nale˝y sklasyfikowaç po-
wierzchnie. Wiedzieli, ˝e sfer´ wyró˝nia
spoÊród wszystkich powierzchni jej uni-
kalna prostota. By∏o wi´c rzeczà natu-
ralnà, ˝e zacz´∏y ich ciekawiç rozmaito-
Êci trójwymiarowe. Pytanie na poczàtek:

czy sfer´ trójwymiarowà te˝ wyró˝nia
jej unikalna prostota, podobnie jak sfer´
dwuwymiarowà? W stuletniej historii,
której poczàtkiem by∏o to elementarne
pytanie, pe∏no jest b∏´dnych kroków i
b∏´dnych dowodów.

Osobà, która Êmia∏o wzi´∏a si´ za to

zagadnienie, by∏ Henri Poincaré, jeden
z dwóch najs∏ynniejszych matematy-
ków aktywnych zawodowo na poczàtku
XX wieku (drugim by∏ David Hilbert).
Nazywano go ostatnim uniwersalistà,
porusza∏ si´ bowiem swobodnie we
wszystkich ga∏´ziach matematyki, zarów-
no czystej, jak i stosowanej. Przyczyni∏
si´ nie tylko do post´pu w jej licznych

72

ÂWIAT NAUKI SIERPIE¡ 2004

DON FOLEY

Wielowymiarowa muzyka sfer

TRZEBA NIECO TRUDU, by wyobraziç sobie bohaterk´ hipotezy Poincarégo, trójwymiarowà sfer´ S

3

. Matematycy, którzy dowodzà twier-

dzeƒ o rozmaitych wielowymiarowych obiektach, jeszcze trudniejszych do ogarni´cia myÊlà, w gruncie rzeczy wcale nie muszà ich sobie wy-
obra˝aç. Wystarczajà im abstrakcyjne w∏asnoÊci, wsparte intuicjà opartà na analogiach z przypadkami niskowymiarowymi (matematycy
uwa˝ajà jednak, by nie braç tych analogii zbyt dos∏ownie). Dzi´ki analizie znanych przyk∏adów niskowymiarowych ka˝dy mo˝e nabraç pew-
nego wyobra˝enia o tym, jak zbudowane sà obiekty wielowymiarowe. Za przyk∏ad pos∏u˝y nam sfera S

3

.

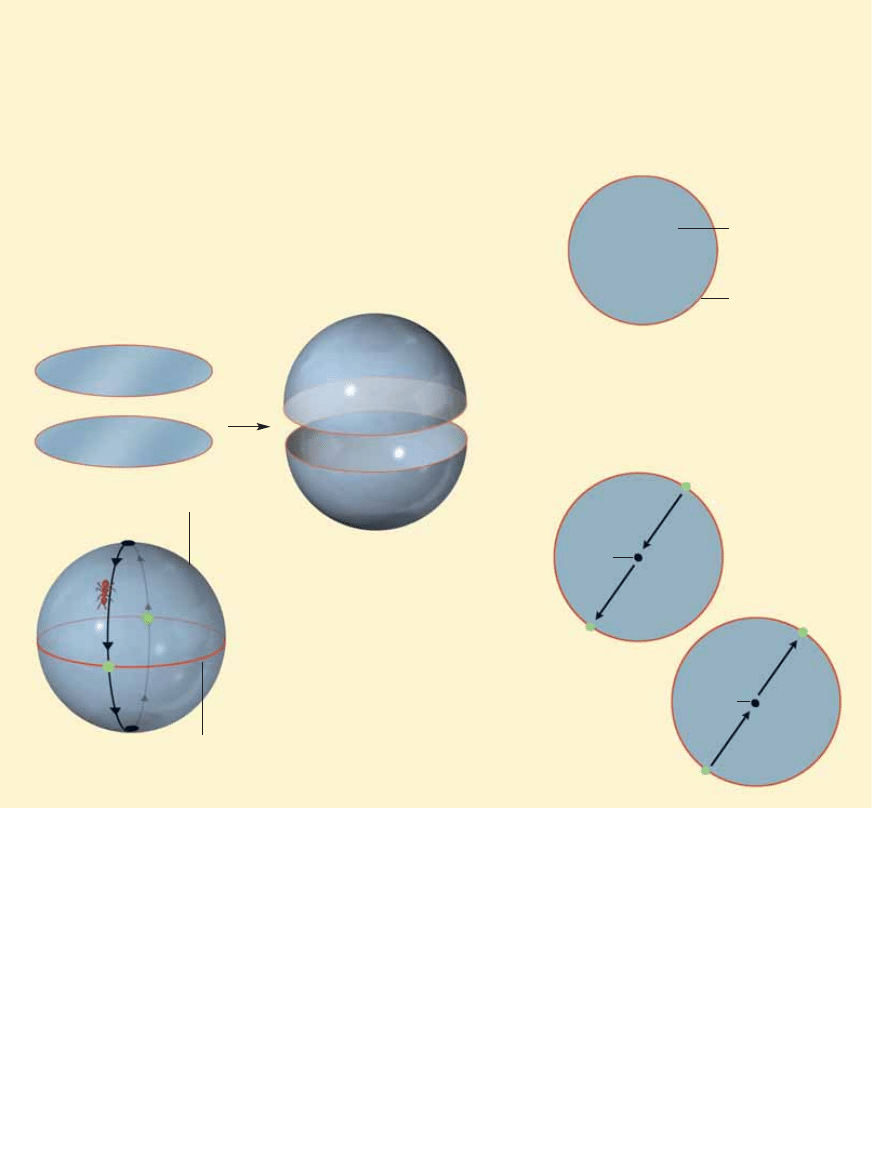
1

Zaczniemy od rozwa˝enia ko∏a, figury ograniczonej okr´giem. Matematycy
nazywajà ko∏o „kulà dwuwymiarowà”, okràg zaÊ „sferà jednowymiarowà”.

Dla matematyków „kula” dowolnego wymiaru to obiekt wype∏niony w Êrodku
niczym pi∏ka do gry w bejsbol, „sfera” zaÊ to powierzchnia kuli, ograniczajàcy
jà cieniutki balon. Okràg jest jednowymiarowy, gdy˝ po∏o˝enie punktu
na nim mo˝na opisaç za pomocà jednej liczby.

2

Z dwóch kopii dysku mo˝emy zbudowaç sfer´
dwuwymiarowà. Jeden z dysków trzeba zdeformowaç

do po∏ówki sfery, powiedzmy, do pó∏sfery pó∏nocnej,
drugi natomiast – do pó∏sfery po∏udniowej. Nast´pnie obie
po∏ówki sfery trzeba skleiç wzd∏u˝ brzegów, które po sklejeniu
utworzà równik. I prosz´ – sfera gotowa.

3

Wyobraêmy sobie teraz mrówk´, która wyrusza
z bieguna pó∏nocnego i w´druje wzd∏u˝ wielkiego

ko∏a, które tworzà linia zmiany daty i po∏udnik
Greenwich (z lewej). JeÊli zaznaczymy drog´ mrówki
w obu wyjÊciowych dyskach (z prawej), z których
sklejona zosta∏a sfera, to zobaczymy, ˝e mrówka
w´druje po prostej (1) do brzegu pó∏nocnego dysku (a),
a nast´pnie przechodzi do odpowiedniego punktu
na brzegu po∏udniowego dysku i w jego wn´trzu
nadal w´druje po prostej (2 i 3). Dotar∏szy do brzegu,
wraca do pó∏nocnego dysku, a w nim do punktu
wyjÊcia, tzn. do bieguna pó∏nocnego (4). Wiodàcà
dooko∏a sfery tras´ mrówki mo˝na wi´c przeÊledziç
w obu dyskach. Jedyna trudnoÊç polega na tym,
˝e kierunek podró˝y ulega pozornej zmianie,
gdy przechodzimy z jednego dysku na drugi.

Biegun

pó∏nocny

Biegun

pó∏nocny

Biegun

po∏udniowy

Biegun

po∏udniowy

Równik

Dwuwymiarowa
sfera

Dwuwymiarowa
kula

Jednowymiarowa
sfera

a

b

2

3

a

a

b

b

1

4

dziedzinach, lecz wniós∏ tak˝e wk∏ad do
mechaniki niebios, elektromagnetyzmu
i filozofii nauki (o tej ostatniej napisa∏ kil-
ka poczytnych ksià˝ek popularnych).

Poincaré w znacznej mierze stworzy∏

ga∏àê matematyki zwanà dziÊ topologià
algebraicznà. Oko∏o roku 1900, korzy-
stajàc z metod tej dziedziny, sformu∏o-
wa∏ nowy sposób „mierzenia” topologii
obiektu, nazywany homotopià. Aby zrozu-
mieç, jak okreÊla si´ homotopi´ rozma-
itoÊci

1

, nale˝y wyobraziç sobie zanurzo-

nà w tej rozmaitoÊci zamkni´tà p´telk´.
P´tla mo˝e byç pozawijana wokó∏ rozma-
itoÊci w dowolnie fantazyjny sposób. Za-
dajemy pytanie: czy mo˝na t´ p´tl´ p∏yn-

nie zdeformowaç – inaczej: Êciàgnàç – do
punktu, wykonujàc dowolne ruchy, ale
nie rozcinajàc jej i nie „wyjmujàc” ani na
chwil´ choçby fragmentu p´telki z roz-
maitoÊci. W przypadku torusa odpowiedê
brzmi: nie. JeÊli p´tla obiega torus dooko-
∏a, to nie mo˝na jej zdeformowaç do
punktu – uwi´ênie po wewn´trznej stro-
nie obwarzanka. Homotopia to miara te-
go, ile jest wszystkich mo˝liwych sposo-
bów uwi´êni´cia tych p´tli, które nie dajà
si´ zdeformowaç do punktu.

Na sferze n-wymiarowej ka˝dà p´tl´

– niezale˝nie od tego, jak dziwacznie zo-
sta∏a zaplàtana – mo˝na bez rozcinania
odplàtaç i Êciàgnàç do punktu. (Pozwala-

my, aby podczas tych manipulacji p´tla
przecina∏a siebie samà). Poincaré wy-
sunà∏ przypuszczenie, ˝e jedynà rozma-
itoÊcià trójwymiarowà, na której ka˝dà
p´tl´ mo˝na Êciàgnàç do punktu, jest
sfera trójwymiarowa. Nie potrafi∏ jed-
nak tego udowodniç. Po pewnym cza-
sie zacz´to to przypuszczenie nazywaç
hipotezà Poincarégo. Wiele osób zg∏a-
sza∏o dowody tej hipotezy – jak si´ póê-
niej okazywa∏o, b∏´dne. (Dla jasnoÊci:
w ca∏ym tekÊcie nie bior´ pod uwag´
dwóch mo˝liwych komplikacji – tzw.
rozmaitoÊci nieorientowalnych i rozma-
itoÊci z brzegiem. Nieorientowalna jest
na przyk∏ad wst´ga Möbiusa, którà

SIERPIE¡ 2004 ÂWIAT NAUKI

73

4

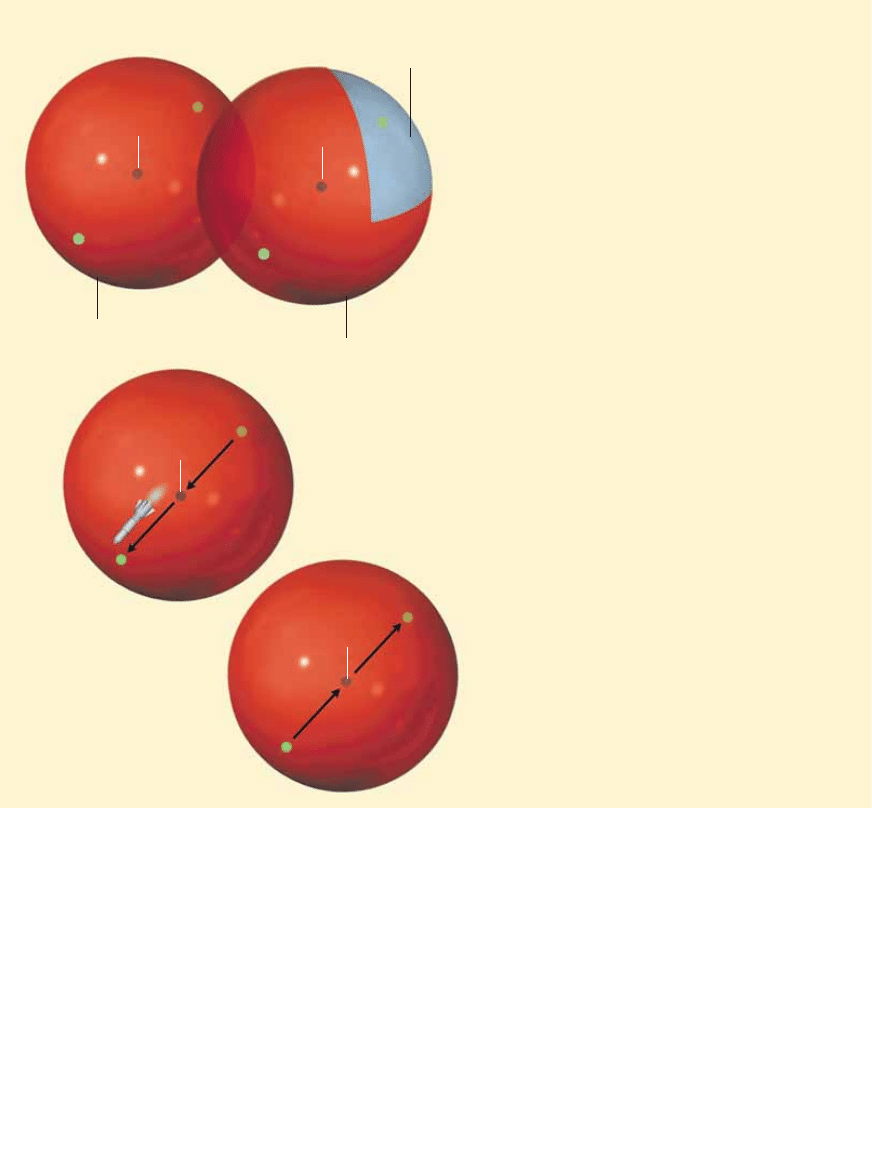
Rozwa˝my teraz sfer´ dwuwymiarowà i ograniczony
nià obszar przestrzeni trójwymiarowej (tzn. „trójwymiarowà

kul´”) i zróbmy to samo, co przed chwilà zrobiliÊmy
z okr´giem i dyskiem: weêmy dwie kopie kuli i sklejmy
ich brzegi. Nie mo˝emy sobie wyobraziç deformacji kul
do po∏ówek sfer w przestrzeni czterowymiarowej – lecz nie
musimy tego robiç. Wystarczy wiedzieç, ˝e odpowiednie punkty
na powierzchni brzegów kul – tzn. na dwuwymiarowych sferach
– ∏àczymy razem. Wynikiem takiego po∏àczenia dwóch kul jest
sfera trójwymiarowa, która stanowi brzeg kuli czterowymiarowej.
Jednà z kul mo˝emy nazwaç pó∏sferà pó∏nocnà, drugà zaÊ
– pó∏sferà po∏udniowà. Biegun pó∏nocny znajduje si´
w Êrodku kuli „pó∏nocnej” (podobnie wczeÊniej biegun
pó∏nocny znajdowa∏ si´ w Êrodku dysku pó∏nocnego).

5

Wyobraêmy sobie, ˝e sà to rozleg∏e obszary pustej
przestrzeni, a dzielna podró˝niczka wyrusza z bieguna

pó∏nocnego w podró˝ statkiem kosmicznym. W koƒcu dociera
do „równika”, który tym razem jest ca∏à dwuwymiarowà sferà
ograniczajàcà kul´ pó∏nocnà. Przeciàwszy równik, podró˝niczka
przedostaje si´ do kuli po∏udniowej i przemieszcza si´ przez jej
wn´trze po prostej, przez Êrodek, do punktu po przeciwnej
stronie równika. Tam wraca do kuli pó∏nocnej, a nast´pnie
do punktu wyjÊcia, do bieguna pó∏nocnego. WyobraziliÊmy
sobie w∏aÊnie kogoÊ, kto podró˝uje po brzegu kuli
czterowymiarowej, okrà˝ajàc jà dooko∏a! Ten brzeg
to trójwymiarowa sfera S

3

, której dotyczy hipoteza Poincarégo.

Byç mo˝e nasz WszechÊwiat ma kszta∏t takiej sfery.

Odpowiednik tej konstrukcji mo˝na przeprowadziç tak˝e

w pi´ciowymiarowej przestrzeni, by zbudowaç model sfery
czterowymiarowej – wtedy jednak jeszcze trudniej jest wyobraziç
sobie, co si´ dzieje. Zauwa˝my najpierw, ˝e brzegiem kuli
czterowymiarowej jest sfera S

3

(podobnie jak brzegiem zwyk∏ej

kuli trójwymiarowej jest dwuwymiarowa sfera S

2

). Weêmy dwie

kopie kuli czterowymiarowej i sklejmy je wzd∏u˝ brzegów
– tzn. po∏àczmy wszystkie pary odpowiednich punktów dwóch
ograniczajàcych te kule sfer trójwymiarowych. Otrzymamy wtedy
sfer´ czterowymiarowà, która jest brzegiem kuli pi´ciowymiarowej.
Ogólnie, podobnie buduje si´ sfer´ n-wymiarowà S

n

z dwóch kul

n-wymiarowych: trzeba po prostu skleiç brzegi obu kul. Ka˝dy
z tych brzegów jest sferà (n – 1)-wymiarowà, podobnie jak
brzegiem ko∏a (tzn. kuli dwuwymiarowej) jest okràg (sfera
jednowymiarowa). Wynikiem takiego sklejenia jest sfera
n-wymiarowa, stanowiàca brzeg kuli (n + 1)-wymiarowej.

Biegun

pó∏nocny

Biegun

pó∏nocny

Biegun

po∏udniowy

Biegun

po∏udniowy

Równik (dwuwymiarowa sfera,
ca∏a sferyczna pow∏oka)

Równik

Trójwymiarowa kula

a

b

2

3

a

b

b

b

a

a

1

4

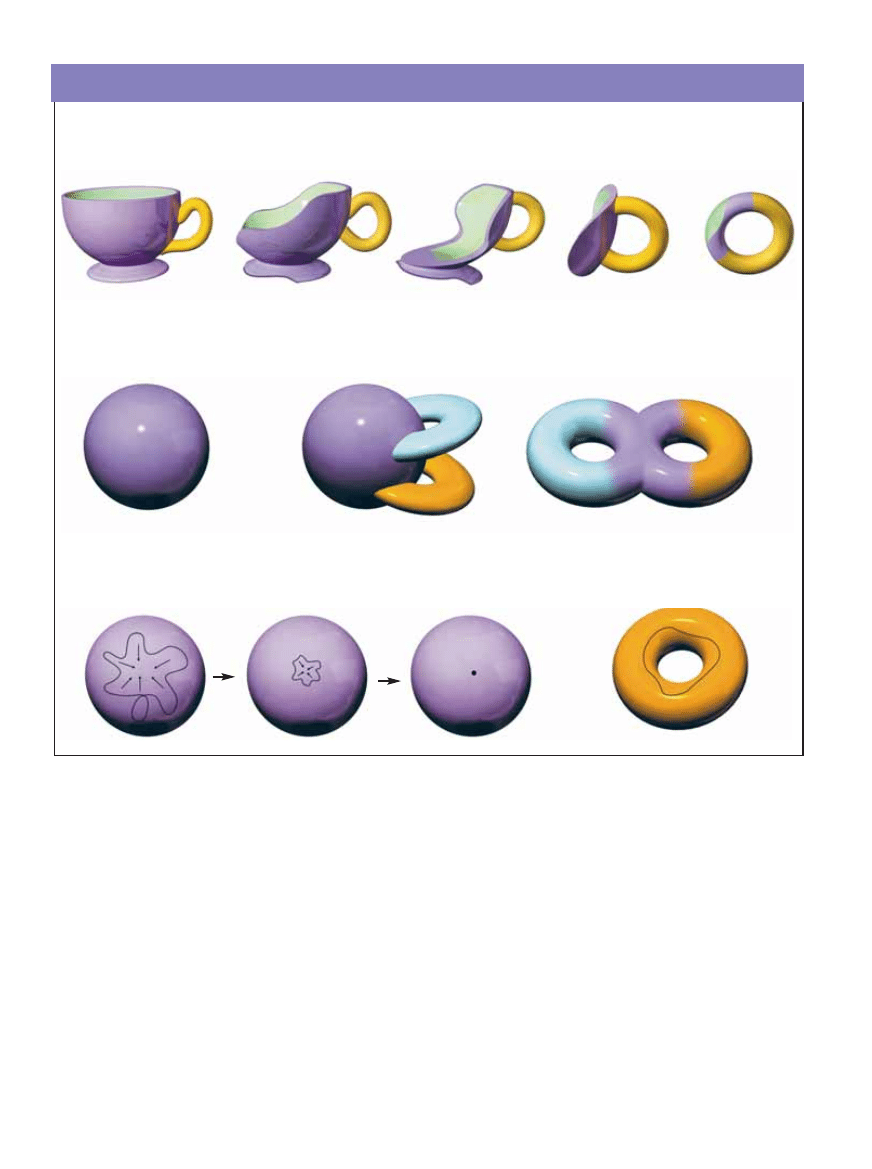
otrzymuje si´, sklejajàc dwa koƒce d∏u-
giego paska skr´conego w Êrodku o
180º. Sfera, z której wyci´to niewielki
dysk, jest rozmaitoÊcià z brzegiem. Wst´-
ga Möbiusa te˝ jest rozmaitoÊcià z brze-
giem. JeÊli WszechÊwiat jest nieograni-
czony, to z topologicznego punktu
widzenia jest tak, jakby mia∏ brzeg nie-
skoƒczenie daleko).

Wyg∏adzanie

DOWÓD PERELMANA

jest pierwszym, który

wytrzymuje szczegó∏owe sprawdzanie.
U˝yta w nim metoda badania topologii
rozmaitoÊci trójwymiarowych wià˝e si´
z zabiegiem nazywanym geometryzacjà.
Geometria opisuje rzeczywiste kszta∏ty
obiektu lub rozmaitoÊci: z punktu wi-
dzenia geometry przedmioty nie sà wy-

konane z mi´kkiej plasteliny, lecz z wy-
palonej gliny. Fili˝anka ma wi´c geo-
metri´ innà od obwarzanka; jego po-
wierzchnia jest zakrzywiona w inny
sposób. Mówi si´, ˝e fili˝anka i obwa-
rzanek sà (o ile fili˝anka ma jedno
uszko) dwoma modelami topologiczne-
go torusa o odmiennych geometriach.

Aby daç pewne wyobra˝enia o sposo-

bie, w jaki geometryzacja pomog∏a Perel-
manowi, opowiemy, jak mo˝na powià-
zaç geometri´ z klasyfikacjà rozmaitoÊci
dwuwymiarowych, czyli powierzchni.
Otó˝ ka˝dà powierzchni´ mo˝na wypo-
sa˝yç w specjalnà, unikalnà geometri´
– takà geometri´, która sprawia, ˝e krzy-
wizna powierzchni jest idealnie równo-
miernie roz∏o˝ona na ca∏ej rozmaitoÊci.
W przypadku sfery takà specjalnà geo-

metri´ ma doskonale symetryczna sfe-
ra obrotowa. Jajo to inny mo˝liwy
kszta∏t topologicznej sfery, ale jego krzy-
wizna nie jest równomiernie roz∏o˝ona
– wszak cienki koniec jaja jest bardziej
zakrzywiony ni˝ gruby.

RozmaitoÊci dwuwymiarowe dzielà

si´ na trzy geometryczne typy [ilustracja
na nast´pnej stronie]. Sfera ma krzywizn´
dodatnià (takà jak szczyt ob∏ego pagór-
ka). Zgeometryzowany torus jest p∏aski
– ma zerowà krzywizn´ niczym p∏asz-
czyzna. Wszystkie inne rozmaitoÊci dwu-
wymiarowe – o dwóch lub wi´kszej licz-
bie ràczek – majà krzywizn´ ujemnà.
Ujemna krzywizna charakteryzuje kszta∏-
ty w rodzaju prze∏´czy górskiej lub sio-
d∏a, które w dwóch ró˝nych kierunkach
sà wygi´te w przeciwne strony. T´ geo-

74

ÂWIAT NAUKI SIERPIE¡ 2004

DON FOLEY

TOPOLOGIA POWIERZCHNI

=

=

=

=

=

a

a

b

b

W TOPOLOGII

nie jest wa˝ne, jaki jest dok∏adny kszta∏t przedmiotu – zupe∏nie jakby wszystko by∏o zrobione z plasteliny lub gumy, którà

mo˝na dowolnie rozciàgaç, Êciskaç i deformowaç. Zabronione jest tylko rozcinanie i sklejanie. A zatem w topologii ka˝da bry∏a z jednà dziu-
rà na wylot, na przyk∏ad fili˝anka poni˝ej, jest tym samym co obwarzanek, czyli wype∏niony w Êrodku torus.

KA˚DÑ ROZMAITOÂå DWUWYMIAROWÑ

(dla uproszczenia wykluczamy z rozwa˝aƒ tzw. rozmaitoÊci nieorientowalne i rozmaito-

Êci z brzegiem) mo˝na skonstruowaç, dodajàc do sfery (a) ràczki. Dodajàc jednà ràczk´, otrzymuje si´ powierzchni´ genusu 1, czyli torus
(powy˝ej z prawej), a dwie (b) – precel, czyli powierzchni´ genusu 2. Topologia ka˝dej powierzchni jest jednoznacznie okreÊlona przez liczb´
ràczek. Nie jest wa˝ne, czy ràczki sà du˝e czy ma∏e ani jak sà u∏o˝one.

SPOÂRÓD WSZYSTKICH POWIERZCHNI

jedynie sfera dwuwymiarowa ma t´ w∏asnoÊç, ˝e ka˝dà p´tl´ zamkni´tà mo˝na w niej

p∏ynnie zdeformowaç do punktu (a), natomiast na przyk∏ad na torusie istniejà p´tle, które podczas ka˝dej próby deformacji do punktu „uwi´-
znà” wokó∏ dziury w Êrodku (b). Hipoteza Poincarégo orzeka, ˝e sfera trójwymiarowa jest jedynà rozmaitoÊcià trójwymiarowà o analogicznej
w∏asnoÊci: na niej i tylko na niej mo˝na ka˝dà zamkni´tà krzywà p∏ynnie zdeformowaç do punktu.

metrycznà klasyfikacj´ powierzchni za-
proponowa∏ Poincaré (któ˝by inny?)
wspólnie z Paulem Koebem i Feliksem
Kleinem (od którego nazwiska bierze na-
zw´ butelka Kleina).

Jest rzeczà naturalnà próbowaç po-

s∏u˝yç si´ podobnymi metodami w przy-
padku rozmaitoÊci trójwymiarowych.
Czy ka˝dà rozmaitoÊç trójwymiarowà
mo˝na wyposa˝yç w szczególnà, wyró˝-
nionà geometri´, która sprawia, ˝e krzy-
wizna jest roz∏o˝ona idealnie równomier-
nie na ca∏ej rozmaitoÊci?

Okazuje si´, ˝e rozmaitoÊci trójwymia-

rowe sà du˝o bardziej skomplikowane ni˝
powierzchnie: na ogó∏ nie mogà mieç tak
eleganckiej geometrii. Mo˝na pomyÊleç o
pewnej namiastce i zapytaç, czy da si´ roz-
ciàç rozmaitoÊç trójwymiarowà na cz´-
Êci, z których ka˝da b´dzie mieç (innà) ka-
nonicznà geometri´. Takich modelowych
kanonicznych rodzajów geometrii jest w
przypadku trójwymiarowym nie trzy jak
dla powierzchni, lecz osiem. Rozcinanie
rozmaitoÊci trójwymiarowych na odpo-
wiednie cz´Êci przypomina w jakimÊ sen-
sie rozk∏adanie liczby naturalnej na czyn-
niki pierwsze. Taki hipotetyczny sposób
klasyfikacji zaproponowa∏ pod koniec lat
siedemdziesiàtych Thurston, który wspól-
nie z kolegami po fachu utorowa∏ drog´
do pe∏nego opisu rozmaitoÊci trójwymia-
rowych. Kluczowe punkty systemu kla-
syfikacji, w tym ta jego cz´Êç, która za-
wiera hipotez´ Poincarégo, pozosta∏y
jednak poza zasi´giem matematyków. Czy
sfera trójwymiarowa jest jedyna? Prace
Perelmana przynoszà odpowiedê na to py-
tanie i wieƒczà sukcesem ca∏y program
Thurstona.

W jaki sposób mo˝na próbowaç zgeo-

metryzowaç rozmaitoÊç, tzn. nadaç jej w
ka˝dym miejscu identyczny rodzaj zakrzy-
wienia? Jeden ze sposobów polega na tym,
by zaczàç od zupe∏nie dowolnej geome-
trii – byç mo˝e od czegoÊ w kszta∏cie jaja
z najró˝niejszymi wypustkami i wg∏´bie-
niami – a nast´pnie wyg∏adziç wszelkie
nieregularnoÊci. Hamilton na poczàtku
lat osiemdziesiàtych zaczà∏ w taki w∏a-
Ênie sposób badaç rozmaitoÊci trójwymia-
rowe, wykorzystujàc do wyg∏adzania ich
kszta∏tów równanie zwane potokiem Ric-
ciego (od nazwiska geometry, Gregoria
Ricciego-Curbastra), które pod pewnymi
wzgl´dami przypomina równanie prze-
wodnictwa cieplnego. W ciele, w którym
sà miejsca zimne i goràce, ciep∏o dopóty
w naturalny sposób przep∏ywa z obsza-
rów mocniej nagrzanych do ch∏odniej-

SIERPIE¡ 2004 ÂWIAT NAUKI

75

DON FOLEY

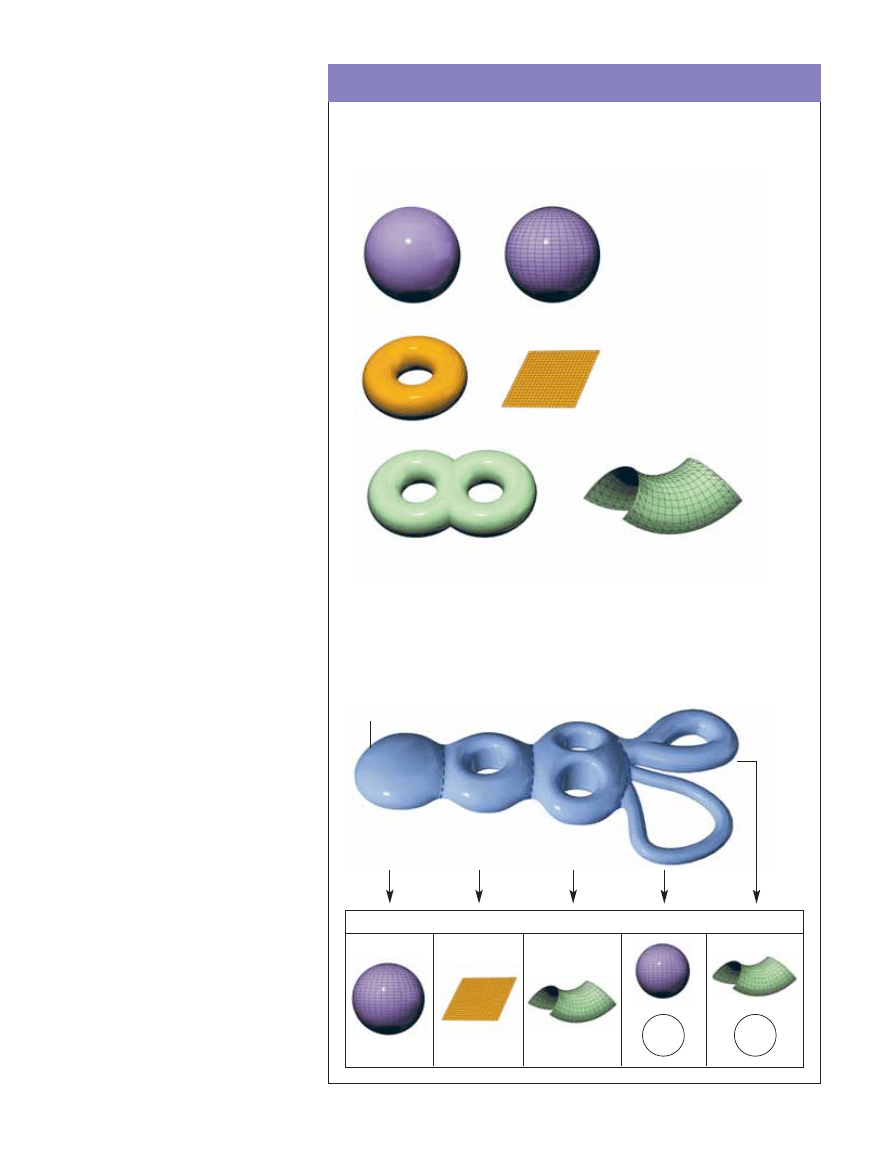
GEOMETRYZACJA

ROZMAITOÂCI DWUWYMIAROWE

mo˝na sklasyfikowaç, przypisujàc im szcze-

gólne geometrie, czyli nadajàc sztywne kszta∏ty. W szczególnoÊci ka˝dej powierzchni mo˝-
na nadaç taki kszta∏t, by mia∏a równomiernà (sta∏à) krzywizn´. Sfera (a) jest jedynà po-
wierzchnià o sta∏ej krzywiênie dodatniej, tzn. w ka˝dym punkcie jest zakrzywiona tak jak
szczyt pagórka. Torus (b) mo˝na – bez sklejania i rozcinania – sp∏aszczyç, tzn. nadaç mu

sta∏à krzywizn´ równà zeru. (Âci-
Êle bioràc, mo˝na to wykonaç w
przestrzeni czterowymiarowej. Ów
zabieg polega na zwini´ciu p∏asz-
czyzny w d∏ugi, nieskoƒczony wa-
lec, a nast´pnie zwini´ciu tego
walca w torus. Gdyby na p∏asz-
czyênie narysowaç równomiernà
krat´, to ka˝dy kwadrat tej kraty
przykry∏by w wyniku tego zwija-
nia ca∏y torus). Powierzchniom
genusu 2 i wi´kszego (c) mo˝na
nadaç sta∏à krzywizn´ ujemnà;
szczegó∏y tej procedury zale˝à od
liczby ràczek. Innym przyk∏adem
powierzchni z brzegiem, o krzy-
wiênie ujemnej jest siod∏o.

a

=

=

=

b

c

PRZYK¸ADY KANONICZNYCH GEOMETRII TRÓJWYMIAROWYCH

a

b

c

d

e

××

××

RozmaitoÊci trójwymiarowe

PE¸NÑ KLASYFIKACJÑ ROZMAITOÂCI TRÓJWYMIAROWYCH

dysponu-

jemy dzi´ki pracy Perelmana, podobnà w ogólnych zarysach do klasyfikacji powierzchni, tyl-
ko dalece bardziej skomplikowanà. Ogólnie bioràc, ka˝dà rozmaitoÊç trójwymiarowà trze-
ba najpierw pociàç na cz´Êci, tak jak liczb´ rozk∏ada si´ na czynniki pierwsze. Ka˝dà z
tych cz´Êci mo˝na nast´pnie wyposa˝yç w jednà z oÊmiu modelowych, kanonicznych geo-
metrii. Pokolorowana na niebiesko rozmaitoÊç trójwymiarowa poni˝ej (z koniecznoÊci przed-
stawiona na rysunku jako obiekt dwuwymiarowy zawiera odpowiedniki pi´ciu z nich: o sta-
∏ej krzywiênie dodatniej (a), zerowej (b) i ujemnej (c), produkt sfery dwuwymiarowej i okr´gu
(d) i wreszcie produkt powierzchni o krzywiênie ujemnej i okr´gu (e).

76

ÂWIAT NAUKI SIERPIE¡ 2004

DON FOLEY

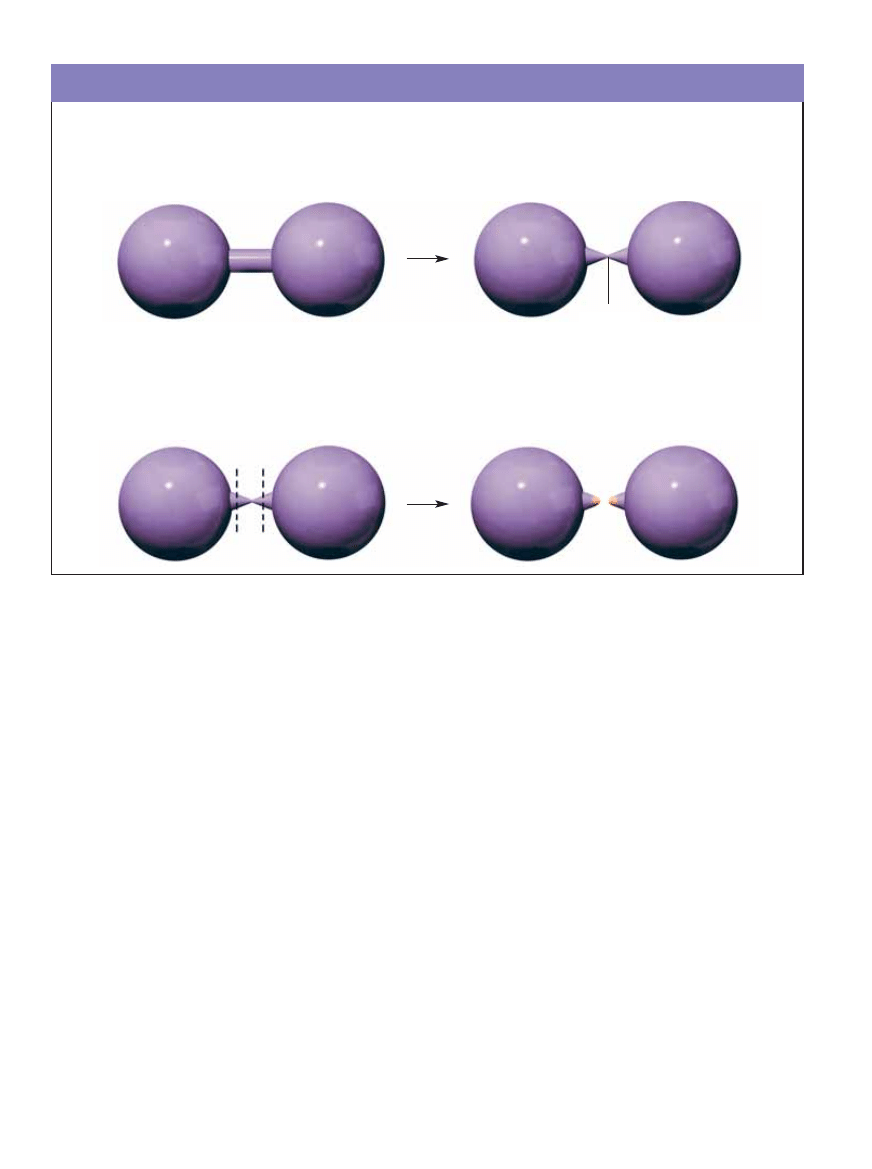
CO ROBIå Z OSOBLIWOÂCIAMI?

ZANIM GRIGORIJ PERELMAN

pojawi∏ si´ na scenie, próby zastosowania tzw. potoku Ricciego do udowodnienia hipotezy Poincarégo

natrafi∏y na powa˝nà przeszkod´. Potok Ricciego, który p∏ynnie deformuje kszta∏ty trójwymiarowych rozmaitoÊci, czasem napotyka k∏opotli-
we osobliwoÊci. Jeden z przyk∏adów to rozmaitoÊç w kszta∏cie hantli, tzn. dwie sfery po∏àczone rurkà (a). Gdy zacznie si´ jà deformowaç
zgodnie z potokiem Ricciego, pojawi si´ punktowe przew´˝enie (b). Inny hipotetyczny problem to tzw. cygaro – sytuacja, gdy d∏ugi, cienki i
ob∏y wyrostek zmienia si´ w zaostrzony szpic.

Z OSOBLIWOÂCIAMI,

które pojawiajà si´ w potoku Ricciego, mo˝na si´ uporaç, co wykaza∏ Perelman, za pomocà tzw. chirurgii. Gdy w

pewnym rejonie rozmaitoÊci pojawia si´ niebezpieczne przew´˝enie, mo˝na wyciàç niewielkà cz´Êç po dwóch stronach potencjalnego ostrza
(c). Miejsca po ci´ciach zalepia si´ niewielkimi sferycznymi ∏atkami. Potem otrzymane cz´Êci mo˝na dalej deformowaç zgodnie z potokiem Ric-
ciego (d). Mo˝e si´ okazaç, ˝e t´ procedur´ trzeba powtarzaç wiele razy, gdy˝ do narastania osobliwoÊci dochodzi w wielu miejscach i w ró˝-
nych chwilach. Perelman wykaza∏ jednak, ˝e ów proces kiedyÊ si´ zakoƒczy (i b´dziemy wtedy mieç pe∏nà kontrol´ nad kszta∏tem wszystkich
cz´Êci). Udowodni∏ równie˝, ˝e potok Ricciego nigdy nie doprowadza do pojawienia si´ cygar.

OsobliwoÊç

a

c

d

b

szych, dopóki nie nastàpi ca∏kowite wy-
równanie temperatur. Potok Ricciego ma
podobny wp∏yw na krzywizn´: deformu-
je „p∏ynàce” zgodnie z nim rozmaitoÊci,
wyrównujàc rozmaite pagórki i zag∏´bie-
nia. GdybyÊmy zacz´li na przyk∏ad od ja-
ja, stopniowo zacz´∏oby ono przybieraç
idealnie sferyczny kszta∏t.

Hamilton nie potrafi∏ jednak pokonaç

powa˝nej przeszkody. Otó˝ w pewnych
sytuacjach potok Ricciego powoduje p´-
kanie rozmaitoÊci lub pojawianie si´ w
nich d∏ugich, cieniutkich ostrzy. (Jest to
jedna z ró˝nic mi´dzy potokiem Riccie-
go a równaniem przewodnictwa cieplne-
go. Miejsca p´kni´ç lub ostrza sà jak
punkty, którym jakimÊ cudem uda∏o si´
osiàgnàç nieskoƒczonà temperatur´).
Jeden z przyk∏adów to rozmaitoÊç w
kszta∏cie hantli: dwóch sfer po∏àczonych
cienkà szyjkà. Potok Ricciego powi´k-
sza sfery, one zaÊ odciàgajà materia∏ z
szyjki, która wskutek tego zw´˝a si´ w
Êrodku do punktu [ilustracja powy˝ej].
Z innym przyk∏adem takiej sytuacji ma-
my do czynienia, gdy rozmaitoÊç ma
d∏ugi, cienki wyrostek: potok Ricciego
móg∏by spowodowaç, ˝e na jego koƒcu
pojawi si´ punktowe, szpiczaste ostrze;
ten k∏opot nazywa si´ osobliwoÊcià cy-

gara. Takie ostrza lub przew´˝enia poja-
wiajàce si´ na rozmaitoÊci nazywamy
osobliwoÊciami. Powodujà one, ˝e roz-
maitoÊç przestaje byç prawdziwà roz-
maitoÊcià trójwymiarowà. Na prawdzi-
wej rozmaitoÊci trójwymiarowej wokó∏
ka˝dego punktu mo˝na znaleêç niewiel-
ki obszar, który wyglàda jak niewielki
obszar w zwyk∏ej przestrzeni euklideso-
wej; w punktach ostrzy lub przew´˝eƒ
ju˝ tak nie jest. Odkrycie drogi, która
pozwala obejÊç t´ przeszkod´, musia∏o
poczekaç w∏aÊnie na Perelmana.

Kulturowo odmienny

PERELMAN PRZYJECHA

¸

do Stanów Zjed-

noczonych w 1992 roku jako stypendy-
sta po doktoracie. Sp´dzi∏ po semestrze
na uniwersytetach w Nowym Jorku i w
Stony Brook, a potem dwa lata w Uni-
versity of California w Berkeley. Szybko
zyska∏ s∏aw´ wschodzàcej gwiazdy, do-
wodzàc wielu g∏´bokich i wa˝nych
twierdzeƒ w pewnej ga∏´zi geometrii.
Przyznano mu Nagrod´ Europejskiego
Towarzystwa Matematycznego, której
przyj´cia odmówi∏. Dosta∏ te˝ presti˝o-
we zaproszenie do wyg∏oszenia wyk∏adu
na Mi´dzynarodowym Kongresie Mate-
matyków, którego nie odrzuci∏. Wiosnà

roku 1995 kilka najlepszych wydzia∏ów
matematyki w USA zaproponowa∏o mu
sta∏à prac´; nie przyjà∏ jednak ˝adnej
oferty i wróci∏ do rodzinnego Sankt Pe-
tersburga. „On kulturowo jest bardzo
rosyjski – skomentowa∏ to jeden z ame-
rykaƒskich kolegów Perelmana. – W
ogóle nie jest materialistà”.

Wróciwszy do Sankt Petersburga, Pe-

relman zniknà∏ matematykom z pola wi-
dzenia. Jedynym znakiem ˝ycia, jaki z
rzadka dawa∏ przez lata, by∏y nieliczne
e-maile do dawnych kolegów, pisywane
na przyk∏ad po to, by wytknàç b∏´dy w
udost´pnionych przez nich w Interne-
cie nowych pracach. Na listy z pytania-
mi, co sam robi, nie odpowiada∏. Wresz-
cie, pod koniec roku 2002, kilka osób
otrzyma∏o od niego e-mail, w którym
zwraca∏ uwag´ na swojà prac´, udost´p-
nionà w∏aÊnie na serwerze z preprinta-
mi matematycznymi. W lakonicznym jak
zwykle liÊciku Perelman stwierdza∏, ˝e
mo˝e ta praca oka˝e si´ interesujàca...

To niedomówienie zwiastowa∏o opis

pierwszego etapu jego ataku na hipote-
z´ Poincarégo. W preprincie, obok swo-
jego s∏u˝bowego adresu w Instytucie
Stiek∏owa, Perelman umieÊci∏ wzmian-
k´, ˝e prowadzi∏ badania, korzystajàc z

pieni´dzy zaoszcz´dzonych podczas po-
bytów w USA.

W swojej pracy Perelman doda∏ do

równania potoku Ricciego nowy sk∏ad-
nik. Dzi´ki tej temu nie zdo∏a∏ wpraw-
dzie pozbyç si´ k∏opotów z osobliwoÊcia-
mi, móg∏ jednak poprowadziç analiz´
znacznie dalej. Wykaza∏, ˝e w przypad-
ku osobliwoÊci w kszta∏cie hantli mo˝-
na przeprowadziç „chirurgi´”: przeciàç
cienkà rurk´ w dwóch miejscach, po obu
stronach rodzàcej si´ osobliwoÊci, a
nast´pnie zalepiç sferycznà czapeczkà
ka˝dà z otwartych rurek wystajàcych z
kul ci´˝arka. Po takiej operacji potok
Ricciego mo˝na przed∏u˝aç na zmienio-
nej przez chirurgi´ rozmaitoÊci a˝ do
chwili, gdy zacznie pojawiaç si´ nast´p-
na osobliwoÊç – wtedy zaÊ mo˝na ca∏à
procedur´ powtórzyç. Perelman wyka-
za∏ tak˝e, ˝e osobliwoÊci cygara nie mo-
gà si´ pojawiaç. Post´pujàc w taki spo-
sób, dowolnà rozmaitoÊç trójwymiarowà
mo˝na podzieliç na cz´Êci, z których ka˝-
da b´dzie mieç jednostajnà geometri´.

Gdy potok Ricciego z chirurgiami za-

stosujemy do wszystkich mo˝liwych
rozmaitoÊci trójwymiarowych, to ka˝-
da rozmaitoÊç, która jest tak „prosta” jak
sfera trójwymiarowa (formalnie bioràc,
ma t´ samà homotopi´, co sfera S

3

), przy-

bierze ostatecznie t´ samà jednostajnà
geometri´, którà ma sfera obrotowa

2

. Ten

wynik oznacza, ˝e w topologii owa roz-
maitoÊç jest w istocie sferà S

3

. Mówiàc

inaczej, sfera trójwymiarowa jest jedynà
najprostszà rozmaitoÊcià trójwymiarowà.

Prace Perelmana sà wa˝ne nie tylko z

powodu wyników, ale tak˝e ze wzgl´du
na nowatorskie metody, które zosta∏y w
nich wprowadzone. Inni matematycy
ju˝ piszà artyku∏y, w których opierajà
si´ na pracy Perelmana albo stosujà je-
go metody do innych zagadnieƒ. Ponad-
to ten dzia∏ matematyki ma intrygujàce
zwiàzki z fizykà. Potok Ricciego, wyko-
rzystany przez Hamiltona i Perelmana,
wià˝e si´ z tajemniczà grupà renorma-
lizacji, przewidujàcà, w jaki sposób si∏a
oddzia∏ywaƒ zmienia si´ w zale˝noÊci
od energii zderzeƒ. Na przyk∏ad w ni-
skich energiach si∏´ oddzia∏ywaƒ elek-
tromagnetycznych charakteryzuje licz-

ba 0.0073 (oko∏o

1

/

137

). JeÊli jednak dwa

elektrony zderzajà si´ czo∏owo z pr´dko-
Êciami bliskimi pr´dkoÊci Êwiat∏a, to ów
parametr jest bli˝szy 0.0078.

Zwi´kszenie energii zderzenia odpo-

wiada badaniu si∏y w skali mniejszych
odleg∏oÊci. Grupa renormalizacji jest
wi´c czymÊ w rodzaju mikroskopu, w
którym mo˝na regulowaç powi´kszenie,
˝eby oglàdaç rozmaitej wielkoÊci szcze-
gó∏y danego procesu. Podobnie potok
Ricciego jest czymÊ w rodzaju mikrosko-
pu do oglàdania rozmaitoÊci w ró˝nych
powi´kszeniach. Wzgórki i zag∏´bienia
widoczne w jednym powi´kszeniu zni-
kajà w innym. Fizycy spodziewajà si´,
˝e w skali 10

–35

m, tzn. w skali sta∏ej

Plancka, przestrzeƒ, w której ˝yjemy, wy-
glàda zupe∏nie inaczej – jak „pianka”, w
której jest mnóstwo p´tli, ràczek i innych
struktur topologicznych [patrz: Lee Smo-
lin „Atomy czasu i przestrzeni”; Âwiat
Nauki, luty 2004]. Matematyka, która
s∏u˝y do opisu zmian si∏ fizycznych, jest

bardzo podobna do tej, której u˝ywa si´
do opisu geometryzacji rozmaitoÊci.

Inny zwiàzek z fizykà polega na tym,

˝e z potokiem Ricciego sà blisko spo-
krewnione równania ogólnej teorii
wzgl´dnoÊci, opisujàce grawitacj´ i wiel-
koskalowà struktur´ WszechÊwiata. Po-
nadto sk∏adnik, który Perelman doda∏
do potoku Ricciego, pojawia si´ w teorii
strun, tzn. w kwantowej teorii grawita-
cji. Przysz∏oÊç poka˝e, czy metody Pe-
relmana pozwalajà dotrzeç do nowych,
ciekawych informacji w ogólnej teorii
wzgl´dnoÊci i teorii strun. Gdyby tak si´
sta∏o, to oka˝e si´, ˝e dowiedzieliÊmy si´
od Perelmana nie tylko o kszta∏tach abs-
trakcyjnych przestrzeni trójwymiaro-
wych, lecz tak˝e o kszta∏cie tej szczegól-
nej przestrzeni, w której ˝yjemy.

n

1

ÂciÊlej, pierwszà grup´ homotopii.

2

Dok∏adniej mówiàc, ka˝da z cz´Êci powsta∏ych w

wyniku chirurgii, które si´ wykonuje, by zapobiec
narastaniu osobliwoÊci, b´dzie mieç t´ samà geome-
tri´, co sfera obrotowa.

SIERPIE¡ 2004 ÂWIAT NAUKI

77

HUL

TON-DEUTSCH COLLECTION/CORBIS

POINCARÉ (rozmawia z Marià Sk∏odowskà-Curie) bra∏ udzia∏ w pierw-
szej Solvayowskiej Konferencji Fizycznej w Brukseli w paêdzierniku
1911 roku. Z ty∏u stojà: Ernest Rutherford, Heike Kamerlingh Onnes
(który nieco wczeÊniej w tym samym roku odkry∏ zjawisko nadprze-
wodnictwa) i Albert Einstein. Byç mo˝e by∏o to jedyne spotkanie
Einsteina i Poincarégo, który zmar∏ dziewi´ç miesi´cy póêniej.

The Poincaré Conjecture 99 Years Later: A Progress Report. John W. Milnor. II/2003. Tekst do-

st´pny w Internecie: www.math.sunysb.edu/~jack/PREPRINTS/poiproof.pdf

Biografia Henriego Poincarégo:

www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Poincare.html

Notatki i komentarze na temat prac Perelmana o potoku Ricciego, zgromadzone przez Bruce’a

Kleinera i Johna Lotta: http://www.math.lsa.umich.edu/research/ricciflow/perelman.html

Problemy milenijne Instytutu Claya: www.claymath.org/millennium/
Topology. Eric W. Weisstein; Mathworld – A Wolfram Web Resource. Dost´pne równie˝ na stronie

mathworld.wolfram.com/Topology.html

JEÂLI CHCESZ WIEDZIEå WI¢CEJ