CIŚNIENIE OSMOTYCZNE

1.

Zjawisko osmozy

występuje gdy czysty rozpuszczalnik i roztwór

składnika w tym rozpuszczalniku zostaną rozdzielone przegrodą
nie przepuszczającą cząsteczek substancji rozpuszczonej, lecz nie
stanowią przeszkody dla cząsteczek rozpuszczalnika ( w tym
układzie panuje stała, po obu stronach przegrody jednakowa
temperatura). Można stwierdzić, że zjawisko osmozy polega na
powolnym przepływie rozpuszczalnika do roztworu.

Przepływ ten można powstrzymać, działając na roztwór odpowiednio
dużym ciśnieniem zewnętrznym p

2

, większym niż ciśnienie p

1

panujące w tej części układu , w której znajduje się czysty
rozpuszczalnik. Przy wyższym ciśnieniu działającym na roztwór
nastąpi nawet odwrócenie kierunku przepływu. Wartość różnicy
(p

2

- p

1

), jaka jest potrzebna, by w układzie został osiągnięty stan

równowagi procesu osmozy, nosi nazwę ciśnienia osmotycznego
roztworu ( Π ).

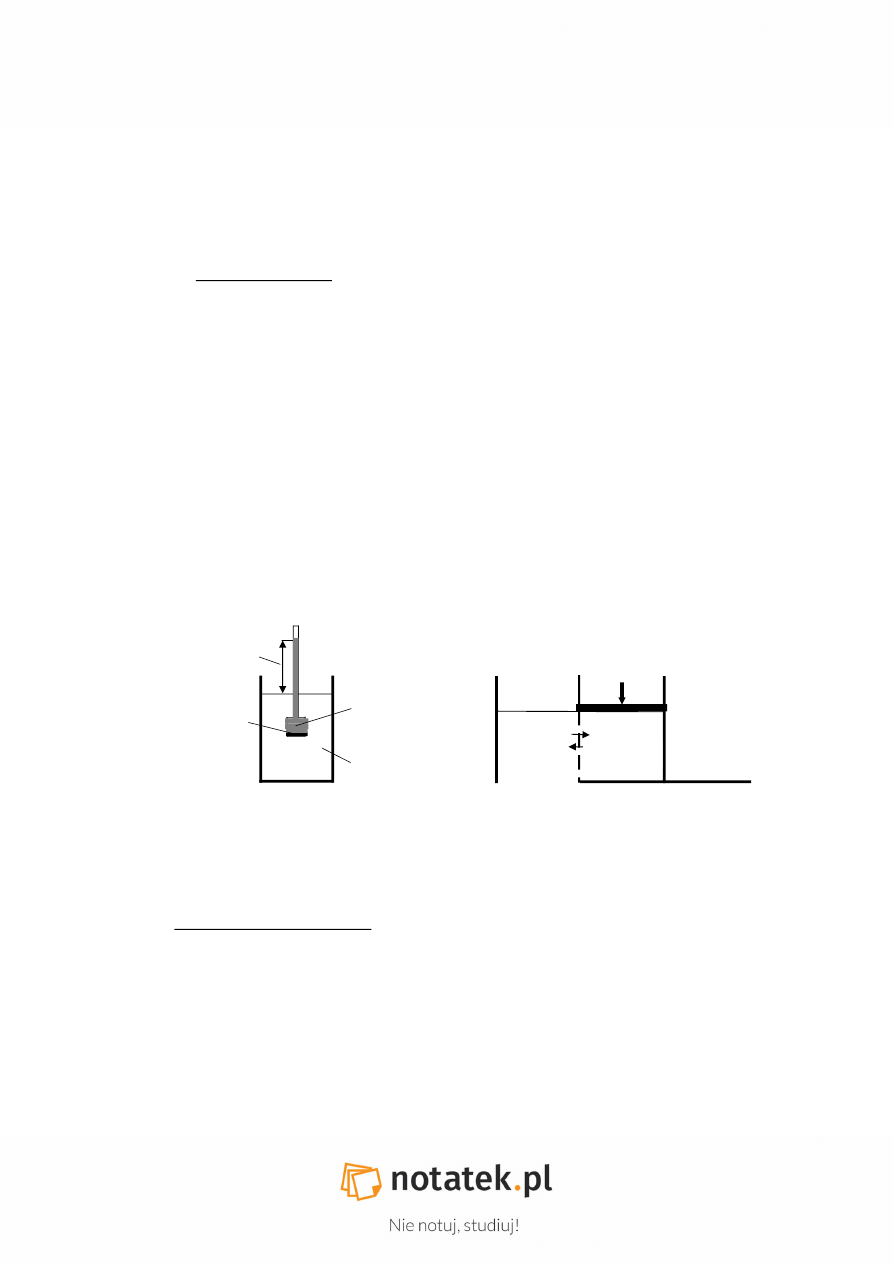
rys.1. uproszczony schemat osmometru

rys.2. odwrócenie kierunku osmozy pod

działaniem zewnętrznego ciśnienia p

2

Warunek równowagi: μ

H2O

L

= μ

H2O

r-rze (P)

(1)←μ

r

o

(p

1

,T) = μ

r

x

(p

2

,T)+ gRTlnx

r

→(2)

Proces samorzutny osmozy zachodzi, gdy potencjał chemiczny

rozpuszczalnika w roztworze (2) jest mniejszy od potencjału
chemicznego czystego rozpuszczalnika (1) w warunkach stałej
temperatury i ciśnienia.

roztwór

rozpuszczalnik

przegroda

półprzepusz-

czalna

wysokość
proporcjonalna do
ciśnienia
osmotycznego

p

2

p

1

rozpuszczalnik

roztwór

μ

r

=μ

r

o

μ

r

= μ

r

x

+gRTlnx

r

2. Ciśnienie osmotyczne ( Π ) równe jest ciśnieniu jakie należy
wywrzeć na roztwór (wewnętrzny), aby powstrzymać przepływ
rozpuszczalnika, a co za tym idzie by nie doszło do procesu osmozy.
Ciśnienie jest wyrażane w [ mm słupa roztworu ]. Na paskale
przeliczamy je wg wzoru

Π = delta h * g * ρ

roztw.

gdzie: g – przyspieszenie ziemskie;
delta h – wysokość słupa wyrażona w metrach;
ρ

roztw.

– gęstość roztworu wyrażona w kg/m

3

Dla roztworu doskonałego (zgodnie z prawem Raoulta) ciśnienie
osmotyczne wynosi :

Π = (-RT)/V * lnx

1

= (-RT)/V * ln(1-x

2

)

gdzie: V – objętość molowa rozpuszczalnika;
x

1

,x

2

– ułamki molowe rozpuszczalnika i substancji rozpuszczonej

Gdy x

2

jest bardzo małe (roztwory rozcieńczone) zamiast

ln(1-x

2

) = x

2

i otrzymujemy:

Π = RT/V * x

2

W warunkach stałej temperatury Π jest proporcjonalne do stężenia

(wzór van’t Hoffa) :

Π = cRT

pamiętając, że c = n/V = m/(MV) = c

w

/M, wzór można przekształcić

do często używanej postaci :

Π = c

w

RT/M

gdzie: c

w

– stężenie masowe;

M – masa molowa substancji rozpuszczonej.

Z równania wynika, że iloraz Π / c

w

powinien być niezależny od

stężenia. W roztworach rzeczywistych taka sytuacja nie jest
spotykana, natomiast jest powszechna w roztworach dyspersyjnych.
Iloraz ten jest zazwyczaj rosnąca funkcją stężenia. Do opisu ciśnienia
osmotycznego stosuje się wówczas równanie wirialne:

Π = c

w

RT/M * ( 1 + B

2

c

w

+B

3

c

w

2

+ ... )

gdzie : B2,B3,... – drugi , trzeci , ... współczynnik wiriału.

Pomiary ciśnienia osmotycznego stanowią metodę wyznaczania mas molowych

cząstek.

3.Współczynnik izotoniczny ( i ) jest miarą odchyleń ciśnienia
osmotycznego roztworów elektrolitów od ciśnienia osmotycznego
roztworów doskonałych.

i = Σn / n

0

Związek A

n

B

m

dysocjuje wg schematu: A

x

B

y

= xA

+

+ yB

-

n

0

(1-α) xn

0

α yn

0

α

Σn =

n

0

(1-α) + n

0

α(x+y) x+y = ν

i =

n

0

(1-α) + n

0

αν

/ n

0

i =

1 – α + αν

i = 1 + α (ν – 1) → końcowa postać, na obliczenie współczynnika
izotonicznego.

Wykres wykorzystywany przy wyznaczaniu masy molowej

metodą osmotyczną. Wartość masy molowej oblicza się z

punktu przecięcia prostej z osią rzędnych

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

0

2

4

6

8

10

c [ g/l]

h

/c

[

(

cm

*l

)/

g

http://notatek.pl/cisnienie-osmotyczne-omowienie?notatka