Chemia ogólna

i

nieorganiczna

ZADANIA

zadania pochodzą z kursu: Chemia ogólna i nieorganiczna,

dr Marcin Broniatowski

Chemia ogólna i nieorganiczna ZADANIA

1

Spis rzeczy:

1. Stężenia procentowe, molowe, przeliczanie stężeń , stechiometria

str. 1-8

2. pH, stała i stopień dysocjacji

str. 9-14

3. Roztwory buforowe

str. 15-20

4. Elektrochemia

str. 21-28

5. Iloczyn rozpuszczalności

str. 29-37

Chemia ogólna i nieorganiczna ZADANIA

2

Stężenia procentowe, molowe, przeliczanie stężeń , stechiometria

1. Oblicz stężenie procentowe r-u otrzymanego po rozpuszczeniu 35 g substancji w 150 g
wody.

Zapisujemy, to co wiemy z danych zadania w pierwszej linijce proporcji, w drugiej zaś odnosimy
się do definicji stężenia procentowego:

35g (subst. rozpuszczonej) - (150+35g) (roztworu)
xg (subst. rozpuszczonej) - 100g (roztworu); czyli

35g – 185g
x – 100g

x = 18,9g

Odp: Roztwór jest 18,9 %

Uwaga: roztwór składa się z wody i substancji rozpuszczonej, czyli jego masa wynosi 150 + 35g,
typowy błąd w tego typu zadaniu to napisanie w pierwszej linijce, że 35g substancji znajduje się w
150g.

2. Oblicz stężenie procentowe r-u otrzymanego po rozpuszczeniu 35 g substancji w 150 cm

3

alkoholu etylowego o gęstości 0,78 g/cm

3

.

Gęstość ρ zdefiniowana jest jako stosunek masy do objętości ρ = m/V, zaś jej jednostką jest

jednostka masy dzielona przez jednostkę objętości, czyli g/cm

3

lub kg/dm

3

. Gęstość czystej wody

wynosi 1 g/cm

3

. W przypadku bardzo rozcieńczonych roztworów można przyjąć, że ich gęstość nie

odbiega od gęstości czystej wody i wynosi 1 g/cm

3

. W przypadku roztworów bardziej stężonych

gęstość jest inna od 1 i jest podawana w danych zadania.

W tym zadaniu wiemy, że gęstość alkoholu etylowego wynosi 0,78 g/cm

3

, czyli jeden cm

3

tej substancji waży 0,78g. Chcemy wiedzieć ile waży 150 cm

3

, czyli zapisujemy odpowiednią

proporcję:

1cm

3

– 0,78g

150 cm

3

– x

x = 117g

Dalszy ciąg zadania rozwiązujemy tak jak poprzednio:
35g – (117 + 35g)
x – 100g

x = 23

Odp: Stężenie tego roztworu wynosi 23%

3. Ile wody zawiera 400 g roztworu o stężeniu 20%?

Zapisujemy proporcję:
20g (substancji rozpuszczonej) – 100 g (roztworu) – definicja
x – 400g

x = 80g

Jeżeli w 400g roztworu jest 80g substancji rozpuszczonej, to wody jest w nim 400 – 80 = 320g.

Chemia ogólna i nieorganiczna ZADANIA

3

4. Ile moli NaOH potrzeba do przygotowania 200 g r-u o stężeniu 5%.

Pytamy, ile gramów substancji rozpuszczonej jest w 200g roztworu:
5g (substancji rozpuszczonej) – 100g (roztworu)
x - 200g
x = 10g

Teraz pytamy ile moli NaOH stanowi 10g, czyli potrzebna nam jest masa molowa:
M

NaOH

= 23 + 16 + 1 = 40 g/mol, czyli:

1mol

NaOH

- 40g

x - 10g

x = 0,25 mol

Odp: Potrzeba 0,25 mol NaOH

5. W 250 cm

3

r-u znajduje się 50 g chlorku wapnia (CaCl

2

) Oblicz stężenie molowe r-u.

Należy policzyć masę molową CaCl

2

i zapytać ile moli stanowi 50g:

M

CaCl2

= 40 + 2*(35,5) = 111 g/mol

1 mol – 111g
x - 50g

x = 0,45 mol

Teraz należy dane z zadania porównać w proporcji z definicją stężenia molowego, czyli zapytać ile
moli CaCl

2

znajduje się w 1000 cm

3

roztworu:

0,45 mol – 250 cm

3

x - 1000 cm

3

;

x = 1,8 mol

Odp: Stężenie molowe tego roztworu wynosi 1,8 mol/dm

3

6. Oblicz stężenie molowe r-u otrzymanego po rozpuszczeniu 234 g siarczku sodu w 6 dm

3

wody, jeżeli gęstość tego r-u wynosi 1,14g/ cm

3

Liczymy masę molową Na

2

S i pytamy ile moli stanowi 234g M

Na2S

= 2*23+32 = 78g/mol

1 mol – 78g
x - 234g;

x = 3 mol

Teraz korzystamy z informacji o gęstości. Typowym błędem tego zadania może być pobieżne
przeczytanie jego treści i zapisanie, że 3 mole Na

2

S znajdują się w 6000 cm

3

roztworu, a wtedy

informacja o gęstości staje się zbędna. Roztwór zawiera 6 dm

3

wody i 234 g Na

2

S, więc trzeba

skorzystać z informacji o gęstości roztworu, żeby wiedzieć jaką objętość zajmuje 6234g tego
roztworu:
1cm

3

– 1,14g

x - 6234g;

x = 5468 cm

3

Znając tę objętość i korzystając z definicji stężenia molowego możemy obliczyć stężenie molowe
tego roztworu:
3 mole(Na

2

S) – 5468 cm

3

(roztworu)

x - 1000 cm

3

x = 0,55 mol
Odp; Stężenie molowe tego roztworu wynosi 0,55 mol/dm

3

.

Chemia ogólna i nieorganiczna ZADANIA

4

7. Jaką objętość 0,1M roztworu NaCl należy odmierzyć, aby sporządzić 250cm

3

0,02M

roztworu?

Jest to bardzo ważny typ zadania ze względu na znaczenie praktyczne – bardzo często trzeba

w laboratorium z roztworu stężonego sporządzić roztwór bardziej rozcieńczony, czyli należy za
pomocą naczynia miarowego (np. pipety) pobrać pewną objętość roztworu stężonego, przenieść do
odpowiednie kolby miarowej (tutaj 250 cm

3

), dodać wodę destylowaną do kreski kalibracyjnej i

wymieszać. Zadanie to rozwiązujemy w następujący sposób:

Jeżeli roztwór ma być 0,02 molowy, to pytamy il moli substancji rozpuszczonej ma być w 250 cm

3

:

0,02 mol – 1000 cm

3

x - 250 cm

3

;

x = 0,005 mol

Wiemy, że z roztworu bardziej stężonego mamy pobrać taką objętość, która zawiera 0,005 mol
substancji rozpuszczonej:
0,1 mol – 1000 cm

3

0,005 mol – x;

x = 50 cm

3

8. Ile gramów wody należy dodać do 300 gramów 18% r-u, aby otrzymać r-r 15 %?

Pytamy ile gramów substancji rozpuszczonej znajduje się w 300g 18% roztworu:
18g – 100g
x - 300g

x = 54g

Teraz zapisujemy definicje roztworu 15%, a następnie pytamy w jakiej objętości takiego roztworu
znajduje się 54g substancji rozpuszczonej:
15g – 100g
54g - x

x = 360g

Stąd widzimy, że należy dodać 60g wody (360 – 300).

9. Oblicz stężenie molowe 96 % r-u kwasu siarkowego (VI) o gęstości 1,84 g/ cm

3

.

Z definicji stężenia procentowego wiemy, że 100 g tego roztworu zawiera 96 g H

2

SO

4

.

Korzystając z gęstości pytamy jaką objętość zajmuje 100g tego roztworu, oraz korzystając z masy
molowej pytamy ile moli H

2

SO

4

zawiera 96g tej substancji.

1cm

3

– 1,84g

x - 100g;

x = 54,3 cm

3

M

H2SO4

= 2*1 + 32 + 4*16 = 98 g/mol

1mol – 98g
x - 96g;

x = 0,98 mol

0,98mol – 54,3 cm

3

x - 1000 cm

3

; x = 18mol/dm

3

Odp: Stężenie tego roztworu wynosi 18 mol/dm

3

.

Chemia ogólna i nieorganiczna ZADANIA

5

10. Oblicz stężenie procentowe 5,5 molowego roztworu kwasu azotowego (V) o gęstości 1,18 g/
cm

3

Liczymy masę molową HNO

3

, by móc przeliczyć ile gramów stanowi 5,5 mol tej substancji.

Poza tym korzystając z gęstości trzeba obliczyć masę 1000 cm

3

tego roztworu:

M

HNO3

= 1 + 14 + 3*16 = 63 g/mol

1 mol – 63g
5,5 mol – x;

x = 346,5g

1 cm

3

– 1,18g

1000cm

3

- x; x = 1180g

Teraz korzystamy z definicji stężenia molowego:
346,5g – 1180g
x - 100g; x = 29,4g

Odp: Stężenie procentowe tego roztworu wynosi 29,4%.

11. Ile moli H

2

SO

4

znajduje się w 150 cm

3

25 % r-u o gęstości 1,2 g/ cm

3

.

Korzystamy z gęstości, żeby przeliczyć ile waży 150 cm

3

tego roztworu:, a następnie z

definicji stężenia procentowego obliczamy ile gramów H

2

SO

4

zawiera ten roztwór:

1 cm

3

– 1,2g

150 cm

3

– x; x = 180g

25g – 100g
x - 180g; x = 45g

Teraz korzystamy z masy molowej i przeliczamy ile to jest moli:
M

H2SO4

= 2*1 + 32 + 4*16 = 98 g/mol

1 mol – 98g
x - 45g;

x = 0,46 mol

Odp: Roztwór ten zawiera 0,46 mol H

2

SO

4

.

12. Oblicz stężenie jonów sodowych w 0,1 molowym roztworze siarczanu(VI) sodu.

Jeżeli substancja dysocjuje na jony, to możemy określić, jakie jest stężenie roztworu

względem poszczególnych jonów:
Na

2

SO

4

→ 2Na

+

+ SO

4

2-

Czyli jeżeli stężenie roztworu Na

2

SO

4

wynosi 0,1M, to stężenie jonów Na

+

wynosi 0,2M, a stężenie

jonów siarczanowych SO

4

2-

0,1M.

Chemia ogólna i nieorganiczna ZADANIA

6

13. W 162g wody rozpuszczono 29,25g NaCl i 37,25g KCl. Obliczyć ułamki molowe
składników tego roztworu.

Ułamek molowy pewnej substancji „i” w roztworze X

i

definiowany jest jako stosunek liczby

moli substancji „i” do sumy moli wszystkich substancji obecnych w tym roztworze. Ten sposób
wyrażania stężeń czasami jest niezbędny, gdyż nie zależy od objętości układu. Np. wyobraźmy
sobie, ze mamy 1 dm

3

roztworu pewnej substancji o stężeniu 1 mol/dm

3

w temperaturze 20

o

C i pod

ciśnieniem 1 atm (w zamkniętym naczyniu). Załóżmy, że roztwór ten poddano działaniu wysokiej
temperatury i wysokiego ciśnienia, jego objętość nie wynosi już 1 dm

3

(bo objętość zależy od

ciśnienia i temperatury), a więc stężenie molowe nie wynosi już 1 mol/dm

3

, natomiast ułamki

molowe substancji rozpuszczonej i rozpuszczalnika są stałe i nie zależą od temperatury i ciśnienia.

Żeby rozwiązać to zadanie trzeba policzyć ilości moli wszystkich składników roztworu,

czyli NaCl, KCl i H

2

O, policzyć sumę moli wszystkich składników, po czym wyliczyć odpowiednie

ułamki:
M

NaCl

= 23 + 35,5 = 58,5

M

KCl

= 39 + 35,5 = 74,5

M

H2O

= 2*1 + 16 = 18

1 mol NaCl – 58,5 g;

1mol KCl – 74,5g;

1mol H

2

O – 18g

x - 29,25g;

x - 37,25;

x - 162g

x = 0,5 mol;

x = 0,5 mol

x = 9 mol

Liczymy sum moli wszystkich substancji: 0,5 + 0,5 + 9 = 10
Teraz liczymy poszczególne ułamki molowe:
X

NaCl

= 0,5/10 = 0,05;

X

KCl

= 0,5/10

= 0,05;

X

H2O

= 9/10 = 0,9

Suma ułamków molowych wszystkich składników roztworu musi być równa 1, więc możemy
sprawdzić, czy wynik jest prawidłowy: 0,05 + 0,05 + 0,9 = 1

14. Oblicz stężenie molowe r-u wodorotlenku sodu, jeżeli do zobojętnienia 100 cm

3

tego r-u

zużyto 200 cm

3

0,15 molowego kwasu solnego.

Takie zadanie zawsze trzeba zacząć od zapisania równania reakcji, żeby zobaczyć jaka jest
stechiometria:
NaOH + HCl → NaCl + H

2

O

Widzimy, ze stechiometria jest 1:1, czyli wracając do treści zadania w 100 cm

3

roztworu NaOH jest

tyle samo moli NaOH, co kwasu solnego w 200 cm

3

0,15M roztworu HCl.

Obliczamy, więc ile moli HCl jest w 200 cm

3

0,15M roztworu HCl:

0,15 mol (HCl) – 1000cm

3

x - 200cm

3

x = 0,03 mol
Czyli, w 100 cm

3

roztworu NaoH o nieznanym stężeniu jest również 0,03 mol NaOH. Teraz trzeba

policzyć stężenie molowe tego roztworu:
0,03 mol (NaOH) – 100 cm

3

x - 1000 cm

3

x = 0,3 mol/dm

3

Chemia ogólna i nieorganiczna ZADANIA

7

15. Ile gramów jodku potasu należy odważyć i jaką objętość 0,25M roztworu azotanu(V)
ołowiu należy odmierzyć, aby wytrącić 2g jodku ołowiu.

Zaczynamy od zapisania równania reakcji strącania jodku ołowiu:
2KI + Pb(NO

3

)

2

→ PbI

2↓

+ 2KNO

3

Na początek pytamy ile moli PbI

2

zawiera się w 2g tej substancji:

MPbI

2

= 207 + 2*127 = 461 g/mol

1mol (PbI

2

) – 461g

x - 2g

x = 0,0043 mol

Ze stechiometrii równania reakcji widać, że potrzebna jest taka sama liczba moli Pb(NO

3

)

2

, czyli

0,0043 oraz dwa razy większa liczba moli KI, czyli 0,0086
Pb(NO

3

)

2

mamy w roztworze o stężeniu 0,25 mol/dm

3

, pytamy, więc w jakiej objętości tego

roztworu znajduje się 0,0043mol Pb(NO

3

)

2

:

0,25 mol – 1000cm

3

0,0043mol – x

x = 17,2cm

3

Teraz pytamy ile waży 0,0086 mol KI:
M

KI

= 39 + 127 = 166g/mol

1mol – 166g
0,0086 – x

x = 1,43g

Odp: Żeby otrzymać 2g PbI

2

trzeba dodać 1,43g KI do 17,2cm

3

0,25M roztworu Pb(NO

3

)

2

.

16. W 162g wody rozpuszczono 29,25g NaCl i 37,25g KCl. Wiedząc, że gęstość powstałego
roztworu wynosi 1,2 g/cm

3

oblicz stężenia molowe:

a) jonów sodowych,
b) jonów potasowych;
c) jonów chlorkowych.

To zadanie utrwala obliczanie stężeń poszczególnych jonów w roztworze.
Z poprzednich zadań wiemy, że 29,25g NaCl to 0,5 mol, podobnie 37,25g KCl to również 0,5 mol.
Policzmy teraz masę roztworu: 162 + 29,25 + 37,25 = 228,5. Teraz korzystając z gęstości obliczmy
objętość tego roztworu:
1 cm

3

– 1,2g

x - 228,5g

x = 190,4cm

3

Liczymy stężenia molowe roztworu względem obu soli:
0,5 mol (NaCl) – 190,4cm

3

x - 1000cm

3

x = 2,63 mol/dm

3

Analogicznie stężenie roztworu względem KCl również wynosi 2,63 mol/dm

3

. Żeby wyrazić

stężenia jonów zapisujemy dysocjacje obu soli:
NaCl → Na

+

+ Cl

-

;

KCl → K

+

+ Cl

-

Stąd widzimy, że stężenie jonów Na

+

wynosi 2,63 mol/dm

3

; stężenie jonów K

+

wynosi 2,63

mol/dm

3

, zaś stężenie jonów Cl

-

wynosi 2*2,63 = 5,26 mol/dm

3

, bo jony te pochodzą z obu soli.

Chemia ogólna i nieorganiczna ZADANIA

8

PH, stała i stopień dysocjacji

1. Oblicz pH:
a) 0,05M HCl
b) 0,05M NaOH
c) oblicz stężenie jonów wodorowych w roztworze o pH = 2,35
d) oblicz stężenie jonów hydroksylowych w roztworze o pH 11,9

W tym przykładzie chodzi o wykonanie odpowiednich działań na kalkulatorze:
a) pH = -log(H

+

)=-log(0,05)=1,3

HCl jest moznym kwasem, który odszczepia jeden jon H

+

, więc stężenie jonów H

+

jest równe

stężeniu kwasu.
b) pOH= -log(OH

-

)= =log(0,05)=1,3

pH = 14 – 1,3 = 12,7
c) Tu trzeba skorzystać z zależności, że jeżeli pH = -log[H

+

], to [H

+

] = 10

-pH

[H

+

]=10

-2,35

= 0,0045

d) pOH = 14- pH = 14- 11,9 = 2,1
[OH

-

] = 10

-pOH

= 10

-2,1

= 0,008

2. Oblicz pH:
a) 1M HCl ;b) 10M HCl ;c) 10

-8

M HCl; d) 0,05M H

2

SO

4

a) pH = 0, b) pH = -1, c) pH = 6,97 (błędny wynik 8 o ile nie uwzględni się autodysocjacji wody),
d) pH = 1 o ile założymy, że oba jony H

+

się odszczepiły, 1,3, o ile założymy, że odszczepił się

tylko jeden, a tak naprawdę zawiera się pomiędzy 1 a 1,3, bo wiemy, że druga dysocjacja kwasu
siarkowego nie zachodzi w 100%.

3. Do 300 cm

3

wody dodano 100 cm

3

0,08M roztworu HNO

3

. Oblicz pH otrzymanego

roztworu.

Musimy obliczyć stężenie jonów H

+

po rozcieńczeniu:

Pytamy ile moli H

+

jest w 100 cm

3

0,08M roztworu przed rozcieńczeniem:

0,08mol – 1000cm

3

x - 100cm

3

;

x = 0,008 mol

Po rozcieńczeniu ta ilość moli H

+

znajduje się w 400 cm

3

roztworu, pytamy więc o stężenie molowe

rozcieńczonego roztworu:
0,008 mol – 400cm

3

x - 1000cm

3

;

x=0,02 mol/dm

3

pH = -log(0,02) = 1,7

4.Oblicz pH 0,05M NH

3aq

wiedząc, że α = 4%, a K = 1,78*10

-5

.

Piszemy równanie dysocjacji amoniaku:
NH

3

+ H

2

O ↔ NH

4

+

+ OH

-

Stopień dysocjacji wynosi 0,04, więc [OH

-

] = 0,04*0,05 = 0,002

pOH=2,7; pH=11,3
Jak widać, skoro w tym zadaniu podany jest stopień dysocjacji, to informacja o stałej dysocjacji jest
zbędna.

Chemia ogólna i nieorganiczna ZADANIA

9

5. Zmieszano 200 cm

3

0,03M H

2

SO

4

i 150 cm

3

0,1M NaOH. Oblicz pH powstałego roztworu.

Zaczynamy od zapisania równania reakcji:
H

2

SO

4

+ 2NaOH → Na

2

SO

4

+ 2H

2

O

Musimy teraz obliczyć ile moli kwasu i ile moli zasady wymieszaliśmy razem, umożliwiając ich
przereagowanie:
0,03mol H

2

SO

4

- 1000 cm

3

;

0,1mol NaOH- 1000cm

3

x - 200 cm

3

;

x - 150 cm

3

x = 0,006

x = 0,015

Teraz musimy się zastanowić ile moli NaOH trzeba dostarczyć, żeby zobojętnić 0,006 mol H

2

SO

4

–

ze stechiometrii reakcji widać, że 2 razy więcej, czyli 0,012 mol. My dodaliśmy 0,015 mol NaOH, a
więc wynika z tego, że NaOH jest w nadmiarze i nadmiar ten wynosi 0,015 – 0,012 = 0,003 mol.

Czyli odczyn roztworu po zmieszaniu na pewno będzie zasadowy. Trzeba jednak policzyć stężenie
molowe jonów OH

-

, by móc policzyć pH:

0,003 mol OH

-

- 350cm

3

(200 + 150)

x - 1000cm

3

;

0,0086 mol

pOH = -log(0,0086) = 2,07;
pH = 14 – 2,07 = 11,93

6. Oblicz pH oraz stopień dysocjacji 0,1M roztworu CH

3

COOH wiedząc, że K = 1,58*10

-5

Jest to typowe zadanie dotyczące słabego kwasu.

Na początku liczymy α (i to niezależnie od tego, czy w treści zadania o to α pytają, czy nie, bo po
prostu stopień dysocjacji jest potrzebny do wyliczenia pH).

1

,

0

/

10

*

58

,

1

/

5

−

=

=

c

K

α

=0,013

Zauważamy, że α < 0,05, czyli możemy stosować wzór uproszczony.
Następnie zauważamy, że [H

+

]

= α*c, bo liczba jonów H

+

, czyli cząsteczek, które dysocjowały jest

równa pewnemu procentowi wszystkich cząsteczek, co wyraża wzór αc.
[H

+

] = 0,013*0,1 = 0,0013 mol/dm

3

pH = -log(0,0013) = 2,89

7. Jak zmieni się stopień dysocjacji 0,2M roztworu kwasu mrówkowego po czterokrotnym
rozcieńczeniu roztworu? Stała dysocjacji tego kwasu K=1,76·10

-4

.

Trzeba wyliczyć α

1

przed rozcieńczeniem i α

2

po rozcieńczeniu (c

2

= c

1

/4), a potem te liczby

porównać, czyli np. podzielić α

2

/α

1

:

α

1

=

2

,

0

/

10

*

76

,

1

4

−

=0,03

α

2

=

05

,

0

/

10

*

76

,

1

4

−

= 0,06

α

2

/α

1

= 0,06/0,03 = 2

Czyli przy czterokrotnym rozcieńczeniu α wzrośnie dwukrotnie
Można to zrobić zupełnie teoretycznie na symbolach:
α

1

=

1

/ c

K

; α

2

=

4

/

/

1

c

K

=

1

/

4

c

K

Gdy napiszemy wyrażenie α

2

/α

1

, to równe jest ono:

2

4

/

/

/

4

1

1

=

=

c

K

c

K

Chemia ogólna i nieorganiczna ZADANIA

10

8. pH 0,15M roztworu kwasu octowego wynosi 2,79. Oblicz wartość stałej dysocjacji tego
kwasu.

Zapisujemy równanie dysocjacji kwasu octowego:
CH

3

COOH + H

2

O ↔ CH

3

COO

-

+ H

3

O

+

Zapisuję wyrażenie na stałą:

}

[

]

][

[

3

3

3

COOH

CH

O

H

COO

CH

K

+

−

=

Znamy stężenie jonów [H

3

O

+

] = 10

-pH

= 10

-2,79

= 0,0016 mol/dm

3

Stężenie [CH

3

COO

-

] wynosi tyle samo, tj. 0,0016 mol/dm

3

. Stężenie równowagowe [CH

3

COOH]

wynosi c – [H

3

O

+

], czyli 0,15-0,0016 = 0,1484 mol/dm

3

Teraz podstawiam te liczby i obliczam stałą:

1484

,

0

0016

,

0

*

0016

,

0

=

K

=0,0000173, co zapisujemy jako 1,73*10

-5

9 Zmieszano 200 cm

3

0,05M Ca(OH)

2

i 230cm

3

0,1M HNO

3

. Oblicz pH powstałego roztworu.

Zapisujemy równanie reakcji:
Ca(OH)

2

+ 2HNO

3

→ Ca(NO

3

)

2

+ 2H

2

O

Teraz obliczamy ile moli Ca(OH)

2

i ile moli HNO

3

zmieszaliśmy:

0,05 mol – 1000 cm

3

;

0,1 mol – 1000 cm

3

x - 200 cm

3

;

x - 250 cm

3

x = 0,01

x = 0,025

Teraz zastanawiamy się, która z tych substancji jest w nadmiarze: Na zobojętnienie 1 mola Ca(OH)

2

potrzeba 2 moli HNO

3

, czyli na zobojętnienie 0,01 mol Ca(OH)

2

potrzeba 0,02 mol HNO

3

. Stąd

widzimy, że mamy kwas w nadmiarze, a jego nadmiar wynosi:
0,025 – 0,01 = 0,005 mol
Teraz obliczamy stężenie molowe jonów H

+

0,005 mol – 430 cm

3

x - 1000 cm

3

x = 0.012 mol/dm

3

pH = -log(0,012) = 1,92

10. Zmieszano 300 cm

3

0,1M CH

3

COOH i 200cm

3

0,2M NaOH. Oblicz pH powstałego

roztworu, K = 1,58*10

-5

Zapisujemy równanie reakcji:
CH

3

COOH + NaOH → CH

3

COONa + H

2

O

Liczymy ilości moli obu składników:
0,1 mol – 1000 cm

3

;

0,2 mol – 1000 cm

3

x - 300 cm

3

;

x - 200 cm

3

x = 0,03 mol

x = 0,04

Widzimy, że zasada jest w nadmiarze i nadmiar ten wynosi: 0,04-0,03 = 0,01 mol
Teraz liczymy stężenie molowe jonów OH:
0,01 mol OH

-

- 500 cm

3

x - 1000 cm

3

;

x = 0,02

pOH = -log(0,02) = 1,7;
pH = 14- 1,7 = 12,3

Chemia ogólna i nieorganiczna ZADANIA

11

11 Zmieszano 100 cm

3

0,1M CH

3

COOH i 100cm

3

0,1M HCl. Oblicz pH powstałego roztworu.,

K = 1,58*10

-5

W zadaniu tym zmieszano kwas mocny (solny) z kwasem słabym (octowy). Obecność

jonów H

+

z kwasu solnego całkowicie wycofuje dysocjacje kwasu octowego, w związku z tym jony

H

+

pochodzą tylko od mocnego kwasu, a w warunkach zadania kwas ten się rozcieńczył. Zadanie to

trzeba tak rozwiązywać, jakby w treści było: dodano 100 cm

3

wody do 100 cm

3

0,1M HCl. Liczę

ilość moli HCl w 100 cm

3

0,1 – 1000
x – 100; x = 0,01mol
Teraz to jest w 200 cm

3

roztworu, a my pytamy o stężenie molowe:

0,01 – 200
x – 1000; x = 0,05 mol/dm

3

.

pH = -log [H

3

O

+

] = -log(0,05)=1,3

12 Zmieszano 250 cm

3

0,1M NaOH i 500cm

3

0,05M NH

3aq

.. Oblicz pH powstałego roztworu.

K = 1,78*10

-5

Analogicznie jak w zadaniu 11. Mieszamy mocną zasadę z zasadą słabą. Dysocjacjia zasady słabej
jest wycofana, czyli traktujemy to tak, jakby NaOH rozcieńczyło się wodą:
0,1 mol NaOH – 1000 cm

3

x – 250 cm

3

; x =0,025mol

Po zmieszaniu ta ilość moli NaOH znajduje się w 750 cm

3

, a my pytamy o stężenie molowe:

0,025 mol NaOH – 750 cm

3

x - 1000 cm

3

; x = 0,0333

pOH = -log(0,0333) = 1,48
pH = 14 – 1,48 = 12,52

13. W 0,1-molowym roztworze stopień dysocjacji pewnego jednoprotonowego kwasu wynosi
1%. Przy jakim stężeniu stopień dysocjacji osiągnie wartość 90% ? [1,23·10

-6

]

Trzeba policzyć stałą dysocjacji tego kwasu. Kwas jednoprotonowy zapisujemy HX:
HX + H

2

O ↔ H

3

O

+

+ X

-

K=

]

[

]

][

[

3

HX

X

O

H

−

+

Znamy [H

3

O

+

] = α*c = 0,01*0,1 = 0,001, stąd

K =

001

,

0

1

,

0

)

001

,

(

2

−

O

=0,00001, czyli 10

-5

Znając stałą podstawimy sobie dane przy α = 0,9 (90%):

K=

c

c

c

c

9

,

0

9

,

0

*

9

,

0

−

=

c

c

1

,

0

81

,

0

2

=8,1c

c=K/8,1 = 10

-5

/8,1 = 1,23*10

-6

Pamiętajmy, że dla α>0,05 nie wolno stosować wzoru uproszczonego – w rozwiązaniu tego zadania
nie były stosowane żadne uproszczenia.

Możemy jednak zobaczyć, co by się stało, gdyby zastosować wzór uproszczony: α

2

=K/c, czyli c =

K/α

2

= K/(0,9)

2

= 1,23*10

-5

– wynik wyszedł 10 razy za duży.

Chemia ogólna i nieorganiczna ZADANIA

12

14. Wodny roztwór słabego, jednoprotonowego kwasu













=

4

10

K

C

mol

rozcieńczono

dziesięciokrotnie wodą. Ile razy wzrośnie stopień dysocjacji? [3,16]

Wyrażenie C

mol

/K = 10

6

oznacza, że stała dysocjacji jest rzędu 10

-6

.

Podobne zadanie było już rozwiązane:
Na początku mamy stężenie c

1

i stopień α

1

, po rozcieńczeniu mamy stopień α

2

i stężenie c

1

/10. α

1

=

1

/ c

K

; α

2

=

10

/

/

1

c

K

=

1

/

*

10

c

K

Czyli α

2

/α

1

= 10 =3,16

15. Obliczyć pH 0,5-molowego roztworu kwasu octowego, którego stała dysocjacji wynosi
1,75·10

-5

. [2,53]

Liczymy stopień dysocjacji: α=

c

K / =

5

,

0

10

*

75

,

1

5

−

=0,006

α< 0,05, czyli można stosować wzór uproszczony.
[H

3

O

+

] = α*c= 0,006*0,5=0,003

pH = -log[H

3

O

+

] = 2,52

16. W 500 cm

3

roztworu znajduje się 0,05 g NaOH. Ile wynosi pH roztworu? [11,4]

Tu oczywiście należy przeliczyć masę NaOH na mole:
M

NaOH

= 23 + 1 + 16 = 40 g/mol

1mol – 40g
x - 0,05g,

x = 0,00125mol

Teraz obliczamy stężenie molowe jonów OH

-

:

0,00125 mol – 500 cm

3

x - 1000 cm

3

,

x = 0,0025 mol/dm

3

pOH = -log(0,0025) = 2,6
pH = 14 – 2,6 = 11,4

17. Obliczyć stałą dysocjacji kwasu azotowego(III), wiedząc że jego roztwór o pH=2 ma
stopień dysocjacji 2%. [2·10

-4

]

Zapiszmy równanie dysocjacji tego kwasu:
HNO

2

+ H

2

O ↔ H

3

O

+

+ NO

2

-

K=

]

[

]

][

[

2

2

3

HNO

NO

O

H

−

+

Jeżeli pH = 2, to [H

3

O

+

] = 10

-2

= 0,01 mol/dm

3

,

Jeżeli α= 0,02, to wiedząc, że [H

3

O

+

] = α*c obliczamy c:

c = [H

3

O

+

]/α

= 0,01/0,02= 0,5 mol/dm

3

W takim razie podstawiamy dane liczbowe do wyrażenia na stałą:

K=

01

,

0

5

,

0

01

,

0

*

01

,

0

−

=2*10

-4

Chemia ogólna i nieorganiczna ZADANIA

13

18. 1 cm

3

91% roztworu kwasu siarkowego(VI) o gęstości 1,82 g/cm

3

rozcieńczono wodą do

objętości 5 dm

3

. Gęstość otrzymanego roztworu przyjąć za równą 1 g/cm

3

. Obliczyć pH

uzyskanego roztworu. [2,17]

Trzeba obliczyć liczbę moli H

2

SO

4

zawartą w 1 cm

3

91% roztworu:

Pytamy, ile waży 1 cm

3

(korzystamy z gęstości) – od razu widać, z wartości gęstości, że waży on

1,82g. W takim razie z definicji stężenia procentowego, pytamy ile gramów H

2

SO

4

znajduje się w

tej masie roztworu:
91g – 100g
x - 1,82g

x = 1,6562g

M

H2SO4

= 2*1 + 32 + 4*16 = 98 g/mol

1mol – 98g
x - 1,6562g

x = 0,0169 mol

Po rozcieńczeniu ta ilość moli znajduje się w 5000 cm

3

. Pytamy o stężenie molowe:

0,0169 mol – 5000 cm

3

x - 1000 cm

3

x = 0,00338 mol/dm

3

Przy przeliczaniu pH możemy założyć, że H

2

SO

4

oddaje 2 jony H

+

, czyli, że stężenie molowe tych

jonów wynosi: 0,00676 mol/dm

3

pH = -log(0,00676) = 2,17

Chemia ogólna i nieorganiczna ZADANIA

14

Roztwory buforowe

1. Zmieszano 200 cm

3

0,1M kwasu octowego i 200 cm

3

0,15M roztworu octanu sodu. Wiedząc,

że stała
K = 1,58*10

-5

wykonaj następujące polecenia:

a) Oblicz pH powstałego roztworu
b) Do 400 cm

3

roztworu z zadania 1 dodano 2cm

3

1M roztworu HCl. Jak zmieniło się pH?

c) Do 400 cm

3

wody destylowanej dodano 2cm

3

1M roztworu HCl. Jak zmieniło się pH?

d) Do 400 cm

3

roztworu z zadania 1 dodano 2cm

3

1M NaOH. Jak zmieniło się pH?

e) Do 400 cm

3

wody destylowanej dodano 2 cm

3

1M NaOH. Jak zmieniło się pH?

f) Do 400 cm

3

roztworu z zadania 1 dodano 40 cm

3

1M HCl. Jak zmieniło się pH?

g) Do 400 cm

3

roztworu z zadania 1 dodano 40 cm

3

1M NaOH. Jak zmieniło się pH?

h) Do 400 cm

3

roztworu z zadania 1 dodano 500 cm

3

wody destylowanej. Jak zmieniło się pH?

i) Do 400 cm

3

roztworu z zadania 1 dodano 500 cm

3

0,1M roztworu chloku potasu. Jak

zmieniło się pH?
j) Do 400 cm

3

roztworu z zadania 1 dodano 2g stałego octanu potasu. Jak zmieniło się pH?

k) Do 400 cm

3

roztworu z zadania 1 dodano 40 cm

3

1M roztworu kwasu octowego. Jak

zmieniło się pH?

a) pH = pK +log(n

S

/n

A

)

obliczamy n

S

i n

A

:

0,1 CH

3

COOH - 1000 cm

3

0,15 CH

3

COONa – 1000 cm

3

x

-

200 cm

3

x

-

200 cm

3

x = 0,02

x = 0,03

pH = 4,8 +log (0,03/0,02)
pH = 4,8 + 0,18 = 4,98

b) dodano 2cm

3

1 M HCl. Obliczamy ile to jest moli:

1 mol – 1000 cm

3

x - 2 cm

3

; x = 0,002 mol

Zaszła następująca reakcja chemiczna:
CH

3

COONa + HCl = CH

3

COOH + NaCl

pH = 4,8 + log(n

S

-x)/(n

S

+x) = 4,8 + log ((0,03 – 0,002)/(0,02 + 0,002) = 4,8 + log(0,028/0,022) =

4,8 + 0,1 = 4,90
ΔpH = 4,90 – 4,98 = -0,08

c) ten punkt liczymy normalnie z rozcieńczenia HCl. Wiemy już, że 2 cm

3

1M HCl zawierają 0,002

mol tej substancji, więc:
0,002 mol - 402cm

3

x

-

1000cm

3

; x = 0,005 mol/dm

3

pH = -log(0,005) = 2,3
ΔpH = 2,3 – 7 = 4,7

d)
NaOH + CH

3

COOH = CH

3

COONa + H

2

O

1 mol NaOH – 1000 cm

3

x - 2cm

3

; x = 0,002 mol

pH = 4,8 + log(n

S

+x)/(n

A

-x) = 4,8 + log(0,03+0,002)/(0,02-0,002) = 4,8 + log(0,032/0,018) = 4,8 +

0,25 = 5,05
ΔpH = 5,05 – 4,98 = 0,07

Chemia ogólna i nieorganiczna ZADANIA

15

e) liczymy z rozcieńczenia:
0,002 mol NaOH – 402 cm

3

x

- 1000cm

3

x = 0,005 mol

pOH = -log(0,005) = 2,3; pH = 11,7

f) dodano 40 cm

3

1 M HCl

HCl + CH

3

COONa = CH

3

COOH + NaCl

1 mol HCl

-

1000cm

3

x

-

40cm

3

x = 0,04 mol
Zauważamy, że kwasu HCl jest więcej niż całego octanu sodu (którego jest 0,03 mol)
Nadmiar kwasu HCl = 0,04 – 0,03 = 0,01 mol
W tej sytuacji, skoro zanikła jedna z cząsteczek tworzących parę buforową, to bufor przestał
działać. W układzie mamy na raz 2 kwasu: słaby octowy i mocny solny. Ponieważ ilości molowe
obu kwasów są porównywalne (są tego samego rzędu) pomijamy kwas słaby i liczymy pH tylko z
mocnego:
0,01 mol HCl – 440cm

3

x - 1000 cm

3

x = 0,023 mol/dm

3

pH = -log(0,023) = 1,64 ΔpH = 1,64 – 4,98 = -3,34

g) dodano 40 cm

3

1M NaOH

Sytuacja analogiczna jak poprzednio:
CH

3

COOH + NaOH = CH

3

COONa + H

2

O

1 mol NaOH -

1000cm

3

x - 40cm

3

x = 0,04 mol

Zauważamy, że cały kwas octowy, którego było 0,02 mol przereagował i pozostało 0,02 mol NaOH:
0,02 mol NaOH

-

440 cm

3

x - 1000cm

3

x = 0,045

pOH = - log(0,045) = 1,34; pH = 12,66
ΔpH = 12,66 – 4,98 = 7,68

h) dodano wodę
pH buforu nie zmienia się pod wpływem rozcieńczenia roztworu.

i) dodano chlorek potasu
Sól ta nie ma wspólnych jonów z octanem sodu i w związku z tym jej dodatek nie zmieni pH.

j) Octan potasu ma wspólny jon octanowy z octanem sodu, więc jego dodatek zmieni pH
M CH

3

COOK = 2*12 + 3 + 2*16 + 39 = 98 g/mol

1 mol – 98 g
x - 2g

x = 0,02

pH = 4,8 + log((0,03+0,02)/0,02)) = 4,8 + 0,4 = 5,2
ΔpH = 5,2 – 4,98 = 0,22

k) Kwas octowy jest jedną z części pary buforowej, więc jego dodatek zmieni pH:
1 mol - 1000cm

3

x - 40 cm

3

; x = 0,04 mol

pH = 4,8 + log(0,03/(0,02+0,04)) = 4,8 – 0,3 = 4,5
ΔpH = 4,5 – 4,98 = -0,48.

Chemia ogólna i nieorganiczna ZADANIA

16

2. Zmieszano 300 cm

3

0,1M kwasu octowego i::

a) 200 cm

3

0,1M roztworu NaOH

b) 400 cm

3

0,1M roztworu NaOH

Jakie było pH powstałych roztworów?
Stała dysocjacji kwasu octowego K = 1,58*10

-5

a)
NaOH + CH

3

COOH = CH

3

COONa + H

2

O

0,1 mol NaOH - 1000 cm

3

; 0,1 mol CH

3

COOH – 1000 cm

3

x - 200 cm

3

x - 300 cm

3

x = 0,02 mol

x = 0,03 mol

Wniosek: kwasu octowego jest więcej niż zasady, więc powstał bufor octanowy, zawierający: 0,01
mol CH

3

COOH i 0,02 mol CH

3

COONa

pH = 4,8 + log(0,02/0,01) = 4,8 + 0,3 = 5,1
0,1 mol NaOH – 1000cm

3

x - 400 cm

3

x = 0,04 mol
Zauważamy, że zasady mocnej NaOH było więcej niż kwasu octowego, jej nadmiar wynosi 0,01
mol, więc nie powstał bufor, a pH zasady liczymy z rozcieńczenia:
0,01 mol NaOH – 700 cm

3

x - 1000 cm

3

x = 0,014; pOH = -log(0,014) = 1,84; pH = 12,16

b) ANALOGICZNIE

3. Zmieszano 300 cm

3

0,1M kwasu solnego i:

a) 200 cm

3

0,1M roztworu NaOH

b) 400 cm

3

0,1M roztworu NaOH

Jakie było pH powstałych roztworów?

W tym zadaniu mieszamy mocny kwas z mocną zasadą, więc w żadnym wypadku nie powstanie
bufor.

a) NaOH + HCl = NaCl + H

2

O

0,1 mol HCl – 1000 cm

3

; 0,1 mol NaOH – 1000 cm

3

x - 300 cm

3

x -- 200 cm

3

x = 0,03 mol

x = 0,02 mol\

Zauważamy, że kwas jest w nadmiarze, a nadmiar ten wynosi: 0,01 mol, więc:
0,01 mol HCl - 500 cm

3

x - 1000 cm

3

x = 0,02; pH = -log(0,02) = 1,7

b)
0,1 NaOH – 1000 cm

3

x - 400 cm

3

x = 0,04
Zauważamy, że teraz jest nadmiar zasady i wynosi on 0,01 mol, więc:
0,01 mol – 700 cm

3

x - 1000 cm

3

x = 0,014; pOH = - log(0,014) = 1,84; pH = 12,14

Chemia ogólna i nieorganiczna ZADANIA

17

4. Do 300 cm

3

0,1M amoniaku dodano

a) 200 cm

3

0,1M HCl

b) 400 cm

3

0,1M HCl

Jakie było pH powstałych roztworów?
Stała dysocjacji amoniaku K = 1,6*10

-5

NH

3

+ HCl = NH

4

Cl

a) 0,1 mol NH

3

– 1000 cm

3

0,1 mol HCl - 1000 cm

3

x - 300 cm

3

x - 200 cm

3

x = 0,03

x = 0,02

Amoniaku jest więcej niż kwasu HCl, więc powstał bufor amonowy, zawierający 0,01 mol NH

3

i

0,02 mol NH

4

Cl

pOH = pK

B

+ log(n

S

/n

B

) = 4,8 + log(0,02/0,01) = 4,8 + 0,3 = 5,1

pH = 14 – 5,1 = 8,9

b) 0,1 mol HCl – 1000 cm

3

x - 400 cm

3

x = 0,04

Teraz mocny kwas jest w nadmiarze, a jego nadmiar wynosi 0,01 mol:
0,01 mol HCl – 700 cm

3

x - 1000 cm

3

x = 0,014; pH = -log(0,014) = 1,84

5. Ile gramów stałego NH

4

Cl należy rozpuścić w 200 cm

3

0,1M roztworu amoniaku, aby

otrzymać roztwór o pH = 10?, K

B

= 1,6*10

-5

pOH = pK

B

+ log(n

S

/n

B

)

pOH = 14 – pH = 14 – 10 = 4
Obliczamy ilość moli amoniaku:
0,1 mol – 1000 cm

3

x - 200 cm

3

x = 0,02 mol

wracamy do wzoru na pOH buforu zasadowego:
4 = 4,8 + log(n

S

/0,02)

log(n

S

/0,02) = -0,8

n

S

/0,02 = 10

-0,8

= 0,16

n

S

= 0,16*0,02 = 0,003 mol

M NH

4

Cl = 53,5 g/mol

1 mol – 53,5 g
0,003 mol – x
x = 0,16g
Odp: Należy naważyć 0,16g NH

4

Cl,

Chemia ogólna i nieorganiczna ZADANIA

18

6. Ile gramów octanu sodu należy rozpuścić w 200 cm

3

0,1M kwasu octowego, aby otrzymać

roztwór o pH = 4,5? K = 1,58*10

-5

Liczymy ilość moli kwasu octowego:
0,1 – 1000 cm

3

x - 200 cm

3

x = 0,02

pH = pK + log(n

S

/n

A

)

4,5 = 4,8 + log(n

S

/0,02)

log(n

S

/0,02) - -0,3

n

S

/0,02 = 10

-0,3

= 0,5

n

S

= 0,5*0,02 = 0,01 mol

M CH

3

COONa = 82 g/mol

1 mol – 82g
0,01 mol – x
x = 0,82g

Odp: Należy rozpuścić 0,82g octanu sodu.

7. W jakim stosunku powinno się zmieszać 0,1M roztwór kwasu octowego i 0,1M roztwór
octanu sodu, aby otrzymać roztwór o pH = 4? K = 1,58*10

-5

Pytamy o n

S

/n

A

pH = pK + log(n

S

/n

A

)

4 = 4,8 + log(n

S

/n

A

)

log(n

S

/n

A

) = -0,8

n

S

/n

A

= 10

-0,8

= 0,16

8. Zmieszano 200 cm

3

0,1M roztworu Na

2

HPO

4

i 100 cm

3

0,1M roztworu NaH

2

PO

4

. Oblicz pH

wiedząc, że druga stała dysocjacji kwasu octowego K

2

= 6,31*10

-8

W zadaniu z buforów solnych trzeba stwierdzić, która sól w naszej konwencji jest kwasem. Zgodnie
z teorią Bronsteda, jest to ta sól danego kwasu wieloprotonowego, która ma więcej protonów.
H

2

PO

4

-

+ H

2

O ↔ HPO

4

2-

+ H

3

O

+

Zastosujemy wzór pH = pK + log(n

S

/n

A

), przy czym za n

S

podstawimy ilość moli soli mającej mniej

wodorów, a za n

A

ilość moli soli mającej więcej wodorów:

0,1 mol Na

2

HPO

4

– 1000 cm

3

0,1 mol NaH

2

PO

4

- 1000cm

3

x - 200cm

3

x - 100 cm

3

x = 0,02 mol

x = 0,01 mol

pH = 7,2 + log(0,02/0,01) = 7,2 + 0,3 = 7,5

Chemia ogólna i nieorganiczna ZADANIA

19

9. Ile cm

3

0,1 M HCl należy dodać do 200 cm

3

buforu octanowego zawierającego 0,02 mol

CH

3

COOH i 0,02 mol CH

3

COONa, aby pH spadło o 0,2 jednostki. K = 1,58*10

-5

.

CH

3

COONa + HCl = CH

3

COOH + NaCl

pH = pK + log(n

S

/n

A

)

widzimy, że w reakcji z x molami HCl n

S

zmniejszy się o x, a n

A

zwiększy się o x:

pH = pK + log((n

S

-x)/(n

A

+ x))

Treść zadania mówi, że pH ma się zmniejszyć o 0,2 jednostki, czyli trzeba obliczyć jakie pH ma ten
bufor przed dodaniem HCl:

pH = 4,8 + log(0,02/0,02) = 4,8
Czyli po dodaniu HCl chcemy, żeby pH spadło o 0,2 jednostki, czyli do 4,6.
4,6 = 4,8 + log((0,02 –x)/(0,02+x))
log((0,02-x)/(0,02+x)) = -0,2
(0,02-x)/(0,02+x) = 10

-0,2

= 0,63

0,02 – x = 0,63*(0,02 + x)
0,02 – x = 0,0126 + 0,63x
1,63x = 0,0074
x = 0,0045 mol

Teraz sprawdzamy w jakiej objętości 0,1 M HCl znajduje się taka ilość moli:
0,1 – 1000cm

3

0,0045 – x
x = 45 cm

3

Odp: Do tego buforu należy dodać 45 cm

3

0,1M HCl aby pH zmniejszyło się o 0,2 jednostki.

10. Ile cm

3

NaOH o stężeniu 1 mol/dm

3

należy dodać do 300 cm

3

0,1M CH

3

COOH aby pH

powstałego roztworu wynosiło 5? K = 1,58*10

-5

CH

3

COOH + NaOH = CH

3

COONa + H

2

O

pH = pK + log(x/n

A

-x)

W tym przypadku niewiadomą jest ilość, ilość n

S

= x, a ilość moli NaOH którą trzeba dodać jest

taka sama, co widać z równania reakcji. Obliczamy ile mamy moli CH

3

COOH:

0,1 – 1000 cm

3

x - 300 cm

3

x = 0,03 mol

Podstawiamy dane do wzoru na pH buforu i obliczamy niewiadomą n

S

:

5 = 4,8 + log(x/0,03 - x)
log((x/(0,03-x)) = 0,2
x/0,03-x = 10

0,2

= 1,58

x = 1,58*(0,03-x)
x = 0,047 – 1,58x
2,58x = 0,047
x = 0,018

1 mol NaOH – 1000cm

3

0,018 - x x = 18,4 cm

3

Odp: Należy dodać 18,4 cm

3

1M NaOH.

Chemia ogólna i nieorganiczna ZADANIA

20

Elektrochemia

1. W zlewce zawierającej roztwór siarczanu (VI) cynku o stężeniu 0,5 mol/dm

3

zanurzono

blaszkę cynkową. Podobnie w zlewce zawierającej roztwór siarczanu )VI) miedzi (II) o
stężeniu 0,2 mol/dm

3

zanurzono blaszkę miedzianą. Tak skonstruowane półogniwa połączono

kluczem elektrolitycznym i zamknięto w obwód elektryczny. E

0

Zn/Zn2+

= -0,763 V; E

0

Cu/Cu2+

=

0,521 V.
a) Napisz schemat tego ogniwa
b) Zapisz reakcje zachodzące w półogniwach i reakcje sumaryczną
c) Za pomocą odpowiednich wzorów wyraź siłę elektromotoryczną tego ogniwa a następnie
oblicz jej wartość.
d) Zapisz wyrażenia na potencjały obu półogniw i oblicz ich wartość.
e) Oblicz zmianę entalpii swobodnej w tym ogniwie, jeżeli przez obwód przepłynęło 0,1 mola
elektronów.
a)

Zauważamy, że potencjał standardowy półogniwa miedziowego jest znacznie większy od

potencjału standardowego półogniwa cynkowego (w tym wypadku od razu to widać, bo jeden jest
dodatni, a drugi ujemny). Miedź ulega więc redukcji, a cynk utlenieniu, czyli schemat tego ogniwa
jest następujący: -Zn|Zn

2+

|| Cu

2+

| Cu+

b) W układzie zachodzą następujące reakcje:
Zn

0

– 2e

-

→ Zn

2+

Cu

2+

+ 2e

-

→Cu

0

Zn

0

+ Cu

2+

↔ Zn

2+

+ Cu

0

c) Ze wzoru Nernsta wiemy, że siła elektromotoryczna dana jest wzorem:

K

F

RT

E

E

SEM

L

P

ln

2

0

0

−

−

=

czyli:

]

[

]

[

log

2

059

,

0

2

2

0

2

/

0

2

/

+

+

+

+

−

−

=

Cu

Zn

E

E

SEM

Zn

Zn

Cu

Cu

bo stała reakcji sumarycznej wynosi: K = [Zn

2+

]/[Cu

2+

] (tylko formy jonowe rozpuszczone w

wodzie wchodzą do stałej).
SEM = 0,521 – (-0,763) – 0,059/2log(0,5/0,2) = 1,284 – 0,012 = 1,272 V

d) Potencjały półogniw:
Uwaga: Trzeba uważać, żeby we wzorze Nernsta na potencjały półogniw mieć dobre znaki, tak,
żeby później odjęcie potencjału lewego półogniwa od prawego dało dokładnie to samo wyrażenie,
co zapisane powyżej na SEM. Ponadto w tym zadaniu można zacząć od tego podpunktu, wyliczyć
wartości liczbowe potencjałów obu półogniw, a następnie w punkcie dotyczącym SEM napisać, że
SEM = E

P

– E

L

i odjąć dwie, uprzednio wyliczone liczby.

Uwaga: Rozpatrujemy półogniwa niespięte, czyli takie, w których nie wiemy, czy będzie
zachodziło utlenianie, czy redukcja, konwencja więc jest taka, żeby zawsze rozpatrywać
równowagę redukcji:
W lewym półogniwie (cynkowym) mamy następującą równowagę:
Zn

2+

+ 2e

-

↔ Zn

0

, czyli K = 1/[Zn

2+

] (bo Zn

0

nie wchodzi do stałej)

E

Zn

= E

0

Zn/Zn2+

- 0,059/2log(1/[Zn

2+

]) = -0,763V – (0,059/2)log(1/0,5) = -0,763 - 0,009 = - 0,772 V

W prawym półogniwie (miedzianym) mamy następującą równowagę:
Cu

2+

+ 2e

-

↔ Cu

0

, a więc K = 1/[Cu

2+

] (bo Cu

0

na górze nie piszemy)

E

Cu

= E

0

Cu/Cu2+

- (0,059/2)log(1/0,2) = 0,521 – 0,021 = 0,500V

Sprawdzamy: SEM = E

Cu

– E

Zn

= 0,500 V – (-0,772V) = 1,272 V

e) ΔG = - nFSEM ΔG = -0,1*96500*1,272V = -12275 J

Chemia ogólna i nieorganiczna ZADANIA

21

2. Zbudowano ogniwo Daniela zestawiając półogniwa glinowe i żelazowe. Potencjały
standardowe tych półogniw wynoszą odpowiednio E

0

(Al

3+

/Al.) = -1,662 V i E

0

(Fe

3+

/Fe) =

-0,036V. Wiedząc, że stężenie jonów Al

3+

wynosiło 0,12 mol/dm

3

, a jonów Fe

3+

0,24 mol/dm

3

:

a) Zapisz schemat tego ogniwa
b) Zapisz reakcje zachodzące w półogniwach i reakcje sumaryczną
c) Za pomocą odpowiednich wzorów wyraź siłę elektromotoryczną tego ogniwa, a następnie
oblicz jej wartość.
d) Zapisz wyrażenia na potencjały obu półogniw i oblicz i wartość.
e) Oblicz zmianę entalpii swobodnej w tym ogniwie, jeżeli przez obwód przepłynęło 0,05 mola
elektronów.

a)
Widzimy, że potencjał standardowy w ogniwie żelazowym jest wyższy niż w glinowym, czyli
żelazo się redukuje, a glin utlenia:

-Al|Al

3+

|| Fe

3+

| Fe+

b)
Al

0

– 3e

-

→ Al

3+

Fe

3+

+ 3e

-

→ Fe

0

Al

0

+ Fe

3+

↔ Al

3+

+ Fe

0

c)

K

F

RT

E

E

SEM

Al

Al

Fe

Fe

ln

3

0

3

/

0

3

/

−

−

=

+

+

widzimy, że K = [Al

3+

]/[Fe

3+

]

czyli:
SEM = -0,036V – (-1,662V) – (0,059/3)log(0,12/0,24) = 1,626 + 0,006 = 1,632 V

d)
W lewym półogniwie (glinowym, rozłączonym) rozpatrujemy równowagę w kierunku redukcji:
Al

3+

+ 3e

-

↔ Al

0

; K = 1/[Al

3+

]

E

Al

= E

0

Al/Al3+

- (0,059/3)log(1/[Al

3+

]) = -1,662V – 0,018 = -1,68 V

W prawym półogniwie (żelazowym, rozłączonym) rozpatrujemy równowagę w kierunku redukcji:
Fe

3=

+ 3e

-

↔ Fe

0

; K = 1/[Fe

3+

]

E

Fe

= E

0

Fe/Fe3+

- (0,059/3)log(1/[Fe

3+

]) = -0,036V – 0,012 = - 0,048 V

Sprawdzamy: SEM = E

Fe

– E

Al

= -0,048 – (-1,68) = 1,632 V

e) ΔG = -nFSEM = 0,05*96500*1,632 = -7874 J

Chemia ogólna i nieorganiczna ZADANIA

22

3. Zbudowano ogniwo Daniela zestawione z półogniwa kadmowego i półogniwa srebrowego.
E

0

(Cd

2+

/Cd) = -0,403 V; E

0

(Ag+/Ag) = 0,799 V. Wiedząc, że stężenie jonów kadmu wynosiło 0,4

mol/dm

3

, a jonów srebra 0,3 mol/dm

3

:

a) Zapisz schemat tego ogniwa
b) Zapisz reakcje zachodzące w półogniwach i reakcje sumaryczną
c) Za pomocą odpowiednich wzorów wyraź siłę elektromotoryczną tego ogniwa, a następnie
oblicz jej wartość.
d) Zapisz wyrażenia na potencjały obu półogniw i oblicz ich wartość
e) Oblicz zmianę entalpii swobodnej w tym ogniwie, jeżeli przez obwód przepłynęło 0,15 mola
elektronów.

a)
-Cd|Cd

2+

||Ag

+

|Ag+

b)
Cd

0

– 2e

-

→ Cd

2=

2Ag

+

+ 2e

-

→ 2Ag

0

Cd

0

+ 2Ag

+

↔ Cd

2+

+ 2Ag

0

c)

K

F

RT

E

E

SEM

Cd

Cd

Ag

Ag

ln

2

0

2

/

0

/

−

−

=

+

+

K = [Cd

2+

]/[Ag

+

]

2

, czyli:

SEM = 0,799 – (-0,403) – (0,059/2)log(0,4/(0,3)

2

) = 1,202 – 0,019 = 1,183 V

d) Piszemy równowagowo reakcje w półogniwach w kierunku redukcji:
Lewe: Cd

2+

+ 2e

-

↔ Cd

0

; K = 1/[Cd

2+

]

Czyli: E

Cd

= E

0

Cd/Cd2+

-(0,059/2)log(1/0,4) = -0,403 – 0,012 = - 0,415 V

Prawe: Ag

+

+ e

-

↔ Ag

0

K = 1/[Ag

+

]

Czyli: E

Ag

= E

0

Ag+/Ag

– 0,059log(1/0,3) = 0,799 – 0,031 = 0,768 V

SEM = E

Ag

– E

Cd

= 0,768 – (-0,415) = 1,183

Uwaga: przy rozpatrywaniu półogniwa pominąłem kwadrat przy stężeniu srebra, ale również
współczynnik 2 przy 0,059, bo (0,059/2)log(1/0,3)

2

= (0,059/2)*2log(1/0,3) (z praw o logarytmach.

e) ΔG = -nFSEM = -0,15*96500*1,183 = -17124 J

Chemia ogólna i nieorganiczna ZADANIA

23

4. W nasyconym roztworze siarczanu (VI) ołowiu zanurzono elektrodę zbudowaną z drutu
ołowianego pokrytego cienka warstwą siarczanu (VI) ołowiu. Tak skonstruowane półogniwo
połączono z normalna elektrodą wodorową. Wiedząc, że E

0

Pb/PbSO4

= -0,356 V, a zmierzona siła

elektromotoryczna wyniosła 0,241 V:
a) zapisz schemat półogniwa
b) zapisz reakcje połówkowe i reakcję sumaryczną
c) wyznacz iloczyn rozpuszczalności siarczanu (VI) ołowiu.

a) Potencjał elektrody drugiego rodzaju jest ujemny, czyli będzie ona półogniwem lewym, a
normalna elektroda wodorowa półogniwem prawym:

-Pb/PbSO

4

| SO

4

2-

|| H

+

, H

2

| Pt+

b)
Pb + SO

4

2-

- 2e

-

→ PbSO

4

2H

+

- 2e

-

→ H

2

Pb + SO

4

2-

+ 2H

+

↔ PbSO

4

+ H

2

K = 1/[SO

4

2-

][H

+

]

2

c)

K

F

RT

E

E

SEM

PbSO

Pb

H

H

ln

2

0

4

/

0

2

/

−

−

=

+

SEM = 0 – (-0,356) – (0,059/2)log(1/[SO

4

2-

]*1)

Przy okazji: log(1/[SO

4

2-

] = - log[SO

4

2-

], więc:

SEM = 0,356 + (0,059/2)log[SO

4

2-

]

[SO

4

2-

] jest niewiadomą, SEM = 0,241V

0,241 = 0,356 + 0,0295log[SO

4

2-

]

0,0295log[SO

4

2-

] = - 0,115

log[SO

4

2-

] = -3,9

[SO

4

2-

] = 10

-3,9

[SO

4

2-

] = 1,26*10

-4

Piszemy równanie dysocjacji PbSO

4

i wyrażenie na iloczyn rozpuszczalności:

PbSO

4

↔ Pb

2+

+ SO

4

2-

; K

SO

= [Pb

2+

][SO

4

2-

]

Czyli jest to iloczyn typu x

2

K

SO

= (1,26*10

-4

)

2

= 1,6*10

-8

.

Chemia ogólna i nieorganiczna ZADANIA

24

5. Zbudowano ogniwo redoksowe w następujący sposób: w roztworze o stężeniu 0,4 mol/dm

3

względem jonów Sn

4+

i 0,03 mol/dm

3

względem jonów Sn

2+

zanurzono elektrodę platynową.

Podobnie w drugim roztworze o stężeniu 0,25 mol/dm

3

względem jonów Fe

3+

i 0,05mol/dm

3

względem jonów Fe

2+

zanurzono elektrodę platynową. Roztwory połączono kluczem

elektrolitycznym i złączono obwód elektryczny. E

0

(Sn

4+

/Sn

2+

) = 0,150 V; E

0

(Fe

3+

/Fe

2+

) =

0,771V
a) Zapisz schemat tego ogniwa
b) Zapisz reakcje zachodzące w półogniwach i reakcje sumaryczną
c) Za pomocą odpowiednich wzorów wyraź siłę elektromotoryczną tego ogniwa, a następnie
oblicz jej wartość.
d) Zapisz wyrażenia na potencjały obu półogniw i oblicz ich wartość
e) Oblicz zmianę entalpii swobodnej w tym ogniwie, jeżeli przez obwód przepłynęło 0,04 mola
elektronów.

Z potencjałów standardowych wynika, że w układzie z żelazem będzie zachodziła redukcja, a w
układzie z cyną utlenienie.

a)
-Pt | Sn

2+

, Sn

4+

|| Fe

3+

, Fe

2+

| Pt+

Uwaga: W ogniwie redoksowym elektrodą jest metal szlachetny, np. drut platynowy, stąd symbol Pt
w układzie.

b)
Sn

2+

- 2e

-

→ Sn

4+

2Fe

3+

+ 2e

-

→ 2Fe

2+

Sn

2+

+ 2Fe

3+

↔ Sn

4+

+ 2 Fe

2+

K = [Sn

4+

][Fe

2+

]

2

/ [Sn

2+

][Fe

3+

]

2

c)

2

3

2

2

2

4

0

4

/

2

0

2

/

3

]

][

[

]

][

[

ln

2

+

+

+

+

+

+

+

+

−

−

=

Fe

Sn

Fe

Sn

F

RT

E

E

SEM

Sn

Sn

Fe

Fe

SEM = 0,771 – 0,150 – (0,059/2)log(0,4*0,05

2

/0,03*0,25

2

) = 0,621 + 0,008 = 0,629 V

d)
Reakcje w półogniwach zapisujemy również w kierunku redukcji:

Półogniwo cynowe:
Sn

4+

+ 2e

-

↔ Sn

2+

; K = [Sn

2+

]/[Sn

4+

]

E

Sn

= E

0

Sn4+/Sn2+

- (0,059/2)log(0,03/0,4) = 0,150 + 0,033 = 0,183 V

Półogniwo żelazowe:
Fe

3+

+ e

-

↔ Fe

2+

; K = [Fe

2+

]/[Fe

3+

]

E

Fe

= E

0

Fe3+?Fe2+

- 0,059log(0,05/0,25) = 0,771 + 0,041 = 0,812

SEM = E

Fe

– E

Sn

= 0,812 – 0,183 = 0,629

e)
ΔG = -nFSEM = -0,04*96500*0,629 = -2428 J

Chemia ogólna i nieorganiczna ZADANIA

25

6. Zbudowano ogniwo redoksowe w następujący sposób: W kwaśnym roztworze manganianu
(VII), w którym jony MnO

4

-

są w równowadze z jonami Mn

2+

zanurzono elektrodę platynową.

Stężenie jonów MnO

4

-

wynosiło 0,06 mol/dm

3

, a jonów Mn

2+

0,02 mol/dm

3

. Podobnie w drugim

półogniwie w roztworze zawierającym jony Cr

3+

(0,5 mol/dm

3

) i Cr

2+

(0,02 mol/dm

3

)

zanurzono elektrodę platynową. Półogniwa złączono kluczem elektrolitycznym i spięto w
obwód elektryczny. E

0

(MnO

4

-

/Mn

2+

) = 1,51 V; E

0

(Cr

3+

/Cr

2+

) = -0,408 V

a) Zapisz schemat tego ogniwa
b) Zapisz reakcje zachodzące w półogniwach i reakcje sumaryczną
c) Za pomocą odpowiednich wzorów wyraź siłę elektromotoryczną tego ogniwa, a następnie
oblicz jej wartość.
d) Zapisz wyrażenia na potencjały obu półogniw i oblicz ich wartość.
e) Oblicz zmianę entalpii swobodnej w tym ogniwie, jeżeli przez obwód przepłynęło 0,01 mola
elektronów.

a)
-Pt | Cr

2+

, Cr

3+

|| MnO

4

-

, Mn

2+

, H

+

| Pt+

b)
5Cr

2+

+ 5e

-

→ 5Cr

3+

MnO

4

-

- 5e

-

+ 8H

+

→ Mn

2+

+ 4 H

2

O

5Cr

2+

+ MnO

4

-

+ 8H

+

↔ Mn

2+

+ 5Cr

3+

4 H

2

O

K = [Mn

2+

][Cr

3+

]

5

/[Cr

2+

]

5

[MnO

4

-

] (H

+

pomijamy w wyrażeniu na stałą, zakładając, że jest go

nadmiar i jego stężenie jest stałe)

Obliczmy sobie od razu stałą:
K = (0,02*0,5

5

/0,02

5

*0,06) = 0,000625/1,92*10

-10

= 3,26*10

6

c)

K

F

RT

E

E

SEM

Cr

Cr

Mn

MnO

ln

5

0

2

/

3

0

2

/

4

−

−

=

+

+

+

−

SEM = 1,51 – (-0,408) – (0,059/5)log(3,26*10

6

) = 1,918 – 0,077 = 1,841 V

d)
Znowu piszemy oba półogniwa w kierunku redukcji:
Cr

3+

+ e

-

↔ Cr

2+

; K = [Cr

2+

]/[Cr

3+

]

E

Cr

= E

0

Cr3+/Cr2+

- 0,059log(0,02/0,5) = -0,408 + 0,082 = -0,326 V

MnO

4

-

+ 5e

-

+ 8H

+

↔ Mn

2+

+ 4H

2

O; K = [Mn

2+

]/[MnO

4

-

]

E

Mn

= E

0

MnO4-/Mn2+

- (0,059/5)log(0,02/0,06) = 1,51 + 0,006 = 1,516

SEM = E

Mn

– E

Cr

= 1,516 – (-0,326) = 1,842 V

e)
ΔG = -0,01*96500*1,842 = -1778 J

Chemia ogólna i nieorganiczna ZADANIA

26

7. Zbudowano półogniwo manganowe zanurzając blaszke manganową w roztworze chlorku
manganu o stężeniu 0,2 mol/dm

3

oraz półogniwo wodorowe zanurzając blaszke platynową w

roztworze kwasu solnego o stężeniu 0,5 mol/dm

3

. E

0

(Mn

2+

/Mn) = -1,18 V

a) Zapisz schemat tego ogniwa
b) Zapisz reakcje zachodzące w półogniwach i reakcje sumaryczną
c) Za pomocą odpowiednich wzorów wyraź siłę elektromotoryczną tego ogniwa, a następnie
oblicz jej wartość.
d)Zapisz wyrażenia na potencjały obu półogniw i oblicz ich wartość.
e) Oblicz zmianę entalpii swobodnej w tym ogniwie, jeżeli przez obwód przepłynęło 0,05 mola
elektronów.

a)
Uwaga: jedną z części ogniwa jest półogniwo wodorowe, nie jest to jednak normalna elektroda
wodorowa, bo stężenie H

+

= 0,5 , a nie 1. E

0

H+/H2

= 0

-Mn | Mn

2+

|| H

+

, H

2

| Pt+

b)
Mn

0

– 2e

-

→ Mn

2+

2H

+

+ 2e

-

→ H

2

Mn + 2H

+

↔ Mn

2+

+ H

2

;

K = [Mn

2+

]/[H

+

]

2

c)

K

F

RT

E

E

SEM

Mn

Mn

H

H

ln

2

0

/

2

0

2

/

−

−

=

+

+

SEM = 0 – (-1,18) – (0,059/2)log(0,2/0,5

2

) = 1,18 + 0,003 = 1,183 V

d)
lewe:
Mn

2+

+ 2e

-

↔ Mn

0

; K = 1/[Mn

2+

]

E

Mn

= E

0

Mn2+/Mn

–(0,059/2)log(1/0,2)= -1,18 – 0,021 = -1,201

prawe:
H

+

+ e

-

↔ 1/2H

2

; K = 1/[H

+

]

E

H

= 0 – 0,059log(1/0,5) = -0,018

SEM = E

H

– E

Mn

= -0,018 – (-1,201) = 1,183

e)
ΔG = -nFSEM = -0,05*96500*1,183 = -5708 J

Chemia ogólna i nieorganiczna ZADANIA

27

8. W nasyconym roztworze chlorku srebra zanurzono elektrodę chlorosrebrową i tak
skonstruowane półogniwo połączono z normalną elektrodą wodorową. Wiedząc, że E

0

Ag/AgCl

=

0,222 V, a zmierzona siła elektromotoryczna wynosiła 0,511 V:
a) zapisz schemat tego ogniwa
b) zapisz reakcje połówkowe i reakcję sumaryczną
c) wyznacz iloczyn rozpuszczalności chlorku srebra.

a)
Normalna elektroda wodorowa ma potencjał 0, czyli mniejszy niż E

0

Ag/AgCl

, więc będzie zachodziło

utlenianie wodoru i redukcja srebra.

-Pt | H

+

, H

2

|| Cl

-

|Ag/AgCl+

b)
1/2H

2

– e

-

→ H

+

AgCl + e

-

→ Ag + Cl

-

1/2H

2

+ AgCl ↔ Ag + Cl

-

+ H

+

K = [Cl

-

][H

+

] (bo inne substancje są albo stałe albo gazowe)

c)

K

F

RT

E

E

SEM

H

H

Ag

AgCl

ln

0

2

/

0

/

−

−

=

+

SEM = 0,222 – 0 – 0,059log[Cl

-

]*1

[Cl

-

] jest niewiadomą i mamy je wyliczyć, wiedząc, że zmierzone SEM wynosi 0,511V

0,511 = 0,222 – 0,059log[Cl

-

]

-0,059log[Cl

-

] = 0,289

log[Cl

-

] = -4,9

[Cl

-

] = 10

-4,9

[Cl

-

] = 1,26*10

-5

Piszemy równanie dysocjacji AgCl i wyrażenie na iloczyn rozpuszczalności:

AgCl ↔ Ag

+

+ Cl

-

;

K

SO

= [Ag

+

][Cl

-

], czyli jest to iloczyn postaci x

2

K

so

= (1,26*10

-5

)

2

= 1,58*10

-10

Chemia ogólna i nieorganiczna ZADANIA

28

Iloczyn rozpuszczalności

1. Ile g PbSO

4

znajduje się w 200 cm

3

nasyconego roztworu tej soli; pK

SO

= 7,8

PbSO

4

↔ Pb

2+

+ SO

4

2-

K

SO

= [Pb

2+

][SO

4

2-

]

x x
Zauważamy, że jest to iloczyn typu x

2

, więc

x

2

= K

SO

; x=

SO

K

; x =

8

,

7

10

−

= 0,000126 mol

M PbSO

4

= 303 g/mol

1 mol – 303g
0,000126mol – x; x = 0,038g
Ta ilość znajduje się w jednym litrze roztworu, pytamy ile jest w 200 cm

3

:

0,038g – 1000 cm

3

x - 200 cm

3

x = 0,00764g

Odp: W 200 cm

3

wody rozpuszcza się 0,00764g siarczanu (VI) ołowiu (II).

2. Oblicz rozpuszczalność chlorku ołowiu (II), wiedząc, że pK

SO

= 4,8

PbCl

2

↔ Pb

2+

+ 2Cl

-

K

SO

= [Pb

2+

][Cl

-

]

2

x 2x
Zauważamy, ze mamy iloczyn typu 4x

3

:

4x

3

= K

SO

, więc x =

3

4

SO

K

; x = 0,0158 mol

M PbCl

2

= 278 g/mol

1mol – 278g
0,0158 mol - x; x = 4,4g
Tyle gramów PBCl

2

rozpuszcza się w 1000 cm

3

(1000g, bo gęstość dla rozcieńczonych roztworów

soli jest równa 1 g/cm

3

) roztworu. Rozpuszczalność jest to ilość gramów substancji rozpuszczonej

w 100 g rozpuszczalnika.
Widzimy, że skoro w 1000g roztworu PbCl

2

jest 4,4g tej soli, to wody jest 995,6g, więc

4,4g PbCl

2

– 995,6g wody

x - 100g; x = 0,44g

W zadaniach tego typu, ponieważ zwykle bardzo mało soli rozpuszcza się w litrze wody, można
masę tej soli pominąć i zrobić następującą proporcję:
4,4 g PbCl

2

– 1000g wody

x - 100g x = 0,44g
Zauważamy, że przy zachowaniu dokładności do drugiego miejsca po przecinku wynik jest taki
sam.
Odp: W 100g wody rozpuszcza się 0,44g chlorku ołowiu (II).

Chemia ogólna i nieorganiczna ZADANIA

29

3. Która sól i ilokrotnie lepiej jest rozpuszczalna w wodzie: PbSO

4

czy PbF

2

? pK

SO

PbSO

4

=

7,8; pK

SO

PbF

2

= 7,6

Liczymy ilość moli tych soli jaka rozpuszcza się w 1000 cm

3

roztworu, a następnie przeliczamy to

na masę. Obliczone masy porównujemy.

PbSO

4

↔ Pb

2+

+ SO

4

2-

K

SO

= [Pb

2+

][SO

4

2-

] = x

2

; x =

SO

K

= 0,000126

M PbSO

4

= 303 g/mol

1 mol – 303g
0,000126 – x; x = 0,038g

PbF

2

↔ Pb

2+

+ 2F

-

K

SO

= [Pb

2+

][F

-

]

2

x 2x
Iloczyn typu 4x

3

x =

3

4

SO

K

= 0,0018 mol

M PbF

2

= 245 g/mol

1 mol – 245g
0,0018 - x; x = 0,44g

Nie przeliczamy już tego na 100g wody, bo stosunek jednej masy do drugiej jest stały:
0,44g/0,038g = 11,6

Odp: Fluorek ołowiu (II) rozpuszcza się w wodzie 11,6 razy lepiej niż siarczan (VI) ołowiu (II).

4. Oblicz stężenie molowe jonów Ag

+

w nasyconym roztworze Ag

3

PO

4

, pK

SO

= 15,8.

Ag

3

PO

4

↔ 3Ag

+

+ PO

4

3-

K

SO

= [Ag

+

]

3

[PO

4

3-

]

3x x
Zauważamy, że mamy iloczyn typu 27 x

4

, więc

x =

4

27

SO

K

= 4,9*10

-5

mol

Zauważamy, ze pytanie w zadaniu dotyczy kationów srebrowych, srebrowych nie całej soli.

Kationów Ag

+

jest 3 razy więcej niż cząsteczek soli, czyli jest ich 3x:

3*4,9*10

-5

= 1,48*10

-4

mol

Odp: Stężenie jonów srebrowych w nasyconym roztworze ortofosforanu (V) srebra wynosi
1,48*10

-4

mol/dm

3

.

Chemia ogólna i nieorganiczna ZADANIA

30

5. Wiedząc, że iloczyn rozpuszczalności Bi

2

S

3

, pK

SO

= 9,7, oblicz stężenia molowe jonów Bi

3+

i

S

2-

w nasyconym roztworze tej soli:

Bi

2

S

3

↔ 2Bi

3+

+ 3S

2-

K

SO

= [Bi

3+

]

2

[S

2-

]

3

= (2x)

2

(3x)

3

= 4x

2

*27x

3

= 108x

5

2x 3x
zauważamy, że mamy iloczyn rozpuszczalności typu 108x

5

, więc:

x =

5

108

SO

K

= 0,0045 mol

2x = 0,009 mol/dm

3

; 3x = 0,0135 mol/dm

3

Odp: Stężenie molowe jonów Bi

3+

wynosi 0,009 mol/dm

3

, zaś jonów S

2-

0,0135 mol/dm

3

6. Wiedząc, że rozpuszczalność CaF

2

wynosi 0,00156g oblicz iloczyn rozpuszczalności.

Zaczynamy od rozpisania równowagi dysocjacji i znalezienia wyrażenia na iloczyn
rozpuszczalności:

CaF

2

↔ Ca

2+

+ 2F

-

K

SO

= [Ca

2+

][F

-

]

2

= 4x

3

x 2x
Rozpuszczalność wyrażana jest w gramach substancji rozpuszczonej w 100g rozpuszczalnika, więc:
0,00156g – 100grozpuszczalnika (100 cm

3

roztworu)

x - 1000 x = 0,0156g
(przy tak małych ilościach substancji rozpuszczonej przyjmujemy, bez większego błędu, że 100 g
rozpuszczalnika to 100g/cm

3

roztworu)

M CaF

2

= 76g/mol

1 mol – 76g
x – 0,0156g; x = 2*10

-4

mol

To, co obliczyliśmy to jest x z wyrażenia na iloczyn rozpuszczalności, więc:
K

SO

= 4x

3

= 4*(2*10

-4

)

3

= 3,46*10

-11

; pK

SO

= 10,46

7. Wiedząc, że iloczyn rozpuszczalności Cd(OH)

2

wynosi pK

SO

= 13,6 oblicz pH nasyconego

roztworu tego wodorotlenku:

Potrzebujemy obliczyć stężenie molowe jonów OH

-

:

Cd(OH)

2

↔ Cd

2+

+ 2OH

-

K

SO

= [Cd

2+

][OH

-

]

2

= 4x

3

x 2x

x =

3

4

SO

K

= 1,84*10

-5

mol

[OH

-

] = 2x = 2*1,84*10

-5

= 3,69*10

-5

mol/dm

3

pOH = -log[OH

-

] = -log(3,69*10

-5

) = 4,43; pH = 9,57

Odp: pH nasyconego roztworu wodorotlenku kadmu wynosi 9,57

Chemia ogólna i nieorganiczna ZADANIA

31

8. Przy jakim pH zacznie się strącać Bi(OH)

3

z roztworu Bi(NO

3

)

3

o stężeniu 0,1 mol/dm

3

?

pK

SO

Bi(OH)

3

= 30,4

W roztworze zachodzi reakcja:
Bi

3+

+ 3OH

-

= Bi(OH)

3

Zapisujemy równowagę dysocjacji i wyrażenie na iloczyn:
Bi (OH)

3

↔ Bi

3+

+ 3OH

-

K

SO

= [Bi

3+

][OH

-

]

3

= 27x

4

x 3x

Wiemy, że w bardzo kwaśnym pH taki wodorotlenek się rozpuści, pytamy jakie jest graniczne pH,
przy którym osad Bi(OH)

3

zaczyna się wytrącać.

W tym zadaniu pojawia się nowość: znamy stężenie azotanu (V) bizmutu, a co za tym idzie stężenie
jonów Bi

3+

= 0,1 mol/dm

3

, więc:

[Bi

3+

][OH

-

]

3

= K

SO

0,1*[0H

-

]

3

= 3,98*10

-31

[OH

-

] =

3

1

,

0

SO

K

= 1,58*10

-10

pOH = -log[OH

-

] = -log(1,58*10

-10

) = 9,8

pH = 4,2

Odp: Bi(OH)

3

zaczyna się strącać przy pH 4,2 z 0,1 M roztworu Bi(NO

3

)

3

, czyli poniżej tego pH

osad Bi(OH)

3

rozpuści się zgodnie z reakcją: Bi(OH)

3

+ 3H

+

= Bi

3+

+ 3H

2

O

Uwaga: ja w tym zadaniu zapisałem, ze iloczyn jest typu 27x

4

, ale w ogóle nie korzystam z tego

wyrażenia, bo w tego typu zadaniu jest ono nie potrzebne.

9. Przy jakim stężeniu chlorków zacznie się strącać AgCl z roztworu AgNO

3

o stężeniu 0,005

mol/dm

3

? pK

SO

AgCl = 9,8

W roztworze zachodzi reakcja:
Ag

+

+ Cl

-

= AgCl

Zadanie podobne do poprzedniego:
AgCl ↔ Ag

+

+ Cl

-

K

SO

= [Ag

+

][Cl

-

]

Stężenie jonów Ag

+

wynosi 0,005 mol/dm

3

, więc:

0,005*[Cl

-

] = 1,58*10

-10

[Cl

-

] = 1,58*10

-10

/0,005 = 3,2*10

-8

Odp: AgCl zacznie się strącać z 0,005 M roztworu AgNO

3

jeżeli stężenie chlorków w tym układzie

przekroczy 3,2*10

-8

mol/dm

3

Chemia ogólna i nieorganiczna ZADANIA

32

10. Jakie pH roztworu należy zachować w 0,01M roztworze SnCl

2

, aby nie strącił się w nim

osad Sn(OH)

2

. pK

SO

Sn(OH)

2

= 28,1

W roztworze zachodzi reakcja:
Sn

2+

+ 2OH

-

= Sn(OH)

2

Piszemy wyrażenie na dysocjacje tego wodorotlenku oraz na jego iloczyn rozpuszczalności:
Sn(OH)

2

↔ Sn

2+

+ 2OH

-

K

SO

= [Sn

2+

][OH

-

]

2

Znamy stężenie jonów Sn

2+

i wynosi ono 0,01 mol/dm

3

, więc:

0,01*[OH

-

]

2

= 7,94*10

-29

[OH

-

] =

01

,

0

10

*

94

,

7

29

−

= 8,91*10

-14

pOH = -log(8,91*10

-14

) = 13,05; pH = 0,95

Odp: pH musi być mniejsze niż 0,95

11. Do 50 cm

3

roztworu BaCl

2

dodano 2 cm

3

roztworu H

2

SO

4

. Czy strąci się osad BaSO

4

, jeżeli

stężenie obu roztworów wynosiło 0,01 mol/dm

3

? pK

SO

BaSO

4

= 10

Zaczynamy od zapisania równania reakcji:
BaCl

2

+ H

2

SO

4

= BaSO

4

+ 2HCl

Obliczamy ilości moli obu substancji:
0,01 mol BaCl

2

– 1000cm

3

; 0,01 mol H

2

SO

4

- 1000cm

3

x - 50 cm

3

; x - 2 cm

3

x = 0,0005 mol ; x = 0,00002mol

Teraz postępujemy tak, jakby osad się nie strącił, a tylko roztwory się rozcieńczyły (bo iloczyn
rozpuszczalności można liczyć tylko ze stężeń molowych, a nie z ilości moli).
0,0005 mol BaCl

2

– 52cm

3

0,00002 mol H

2

SO

4

- 52cm

3

x - 1000cm

3

x - 1000cm

3

x = 0,0096 mol/dm

3

x = 0,00038 mol/dm

3

Teraz piszemy równanie dysocjacji BaSO

4

oraz wyrażenie na iloczyn rozpuszczalności:

BaSO

4

↔ Ba

2=

+ SO

4

2-

K

SO

= [Ba

2+

][SO

4

2-

]

Teraz wstawiamy obliczone stężenia jonów baru i jonów siarczanowych do tego wyrażenia. Jeżeli
otrzymany wynik jest większy niż wartość iloczynu rozpuszczalności, to osad się strąci, jeżeli jest
mniejszy to osad się nie strąci:
0,0096*0,00038 = 3,69*10

-6

Wartość iloczynu rozpuszczalności BaSO

4

wynosi 10

-10

, a więc: 3,69*10

-6

> 10

-10

, czyli osad się

wytrąci.

Chemia ogólna i nieorganiczna ZADANIA

33

12 Do 20 cm

3

nasyconego roztworu chlorku ołowiu zmieszano z 30 cm

3

0,01M roztworu

chromianu potasu. Czy w tych warunkach strąci się chromian ołowiu? pK

SO

PbCl

2

= 4,8; pK

SO

PbCrO

4

= 13,8.

Obliczam stężenie jonów Pb

2+

w nasyconym roztworze chlorku, korzystając z iloczynu

rozpuszczalności:
PbCl

2

↔ Pb

2+

+ 2Cl

-

K

SO

= [Pb

2+

][Cl

-

]

2

= 4x

3

x 2x

x =

3

4

SO

K

= 0,002 mol

Czyli stężenie jonów ołowiu w nasyconym roztworze PbCl

2

wynosi 0,002 mol/dm

3

Teraz jak w poprzednim zadaniu obliczam ilości moli substancji w użytych objętościach roztworów
przed zmieszaniem, a zmieszanie traktuję jak rozcieńczenie i obliczam nowe stężenia molowe:

0,002 mol Pb

2+

- 1000cm

3

; 0,01 CrO

4

2-

- 1000cm

3

x - 20 cm

3

; x - 30 cm

3

x = 0,00004 mol x = 0,0003 mol

0,00004 mol Pb

2+

- 50 cm

3

0,0003 mol – 50 cm

3

x - 1000 cm

3

x - 1000cm

3

x = 0,0008 mol/dm

3

x = 0,006 mol/dm

3

W układzie zachodzi reakcja:
Pb

2+

+ CrO

4

2-

= PbCrO

4

Sól ta dysocjuje pod wpływem wody zgodnie z równaniem:
PbCrO

4

↔ Pb

2+

+ CrO

4

2-

K

SO

= [Pb

2+

][CrO

4

2-

]

Teraz podstawiam obliczone powyżej stężenia do wzoru i porównuje z wartością iloczynu
rozpuszczalności:
0,0008*0,006 = 4,8*10

-6

Iloczyn rozpuszczalności PbCrO

4

wynosi 1,58*10

-14

, więc 4,8*10

-6

jest liczbą dużo większą i osad

się strąci.

Chemia ogólna i nieorganiczna ZADANIA

34

13. 20 cm

3

nasyconego roztworu chromianu ołowiu zmieszano z 30 cm

3

roztworu chlorku

potasu o stężeniu 4 mol/dm

3

. Czy w tych warunkach strąci się osad chlorku ołowiu? pK

SO

PbCrO

4

= 13,8; pK

SO

PbCl

2

= 4,8

Pytanie jest o osad PbCl

2

, więc można zacząć od rozpisania jego dysocjacji i rozpisania wyrażenia

na iloczyn rozpuszczalności:

PbCl

2

↔ Pb

2+

+ 2Cl

-

K

SO

= [Pb

2+

][Cl

-

]

2

Potrzebujemy znać stężenie molowe jonów Pb

2+

i Cl

-

, żeby podstawić to do wyrażenia na iloczyn.

Stężenie Pb

2+

obliczymy z iloczynu rozpuszczalności drugiej trudno rozpuszczalnej soli ołowiu, zaś

Cl

-

trzeba obliczyć z rozcieńczenia KCl:

PbCrO

4

↔ Pb

2+

+ CrO

4

-

K

SO

= [Pb

2+

][CrO

4

-

] = x*x = x

2

[Pb

2+

] = x =

SO

K

=

14

10

*

58

,

1

−

= 1,26*10

-7

taka ilość Pb

2+

byłaby w 1000 cm

3

, liczymy ile jest w 20cm

3

i jak się to stężenie zmieni po dodaniu

30 cm

3

KCl:

1,26*10

-7

– 1000 cm

3

2,52*10

-9

– 50 cm

3

roztworu (po dodaniu 30 cm

3

KCl)

x - 20cm

3

x - 1000 cm

3

x = 2,52*10

-9

mol x = 5*10

-8

mol/dm

3

teraz liczymy stężenie Cl

-

z rozcieńczenia roztworu KCl:

4 mole – 1000cm

3

0,12 mol KCl – 50 cm

3

x - 30cm

3

x - 1000cm

3

x = 0,12 mol x = 2,4 mol/dm

3

Podstawiamy do wyrażenia na iloczyn:

[Pb

2+

][Cl

-

]

2

= 5*10

-8

* (2,4)

2

= 2,88*10

-7

K

SO

PbCl

2

= 1,58*10

-5

, więc: 2,88*10

-7

< 1,58*10

-5

i osad się nie strąci.

Chemia ogólna i nieorganiczna ZADANIA

35

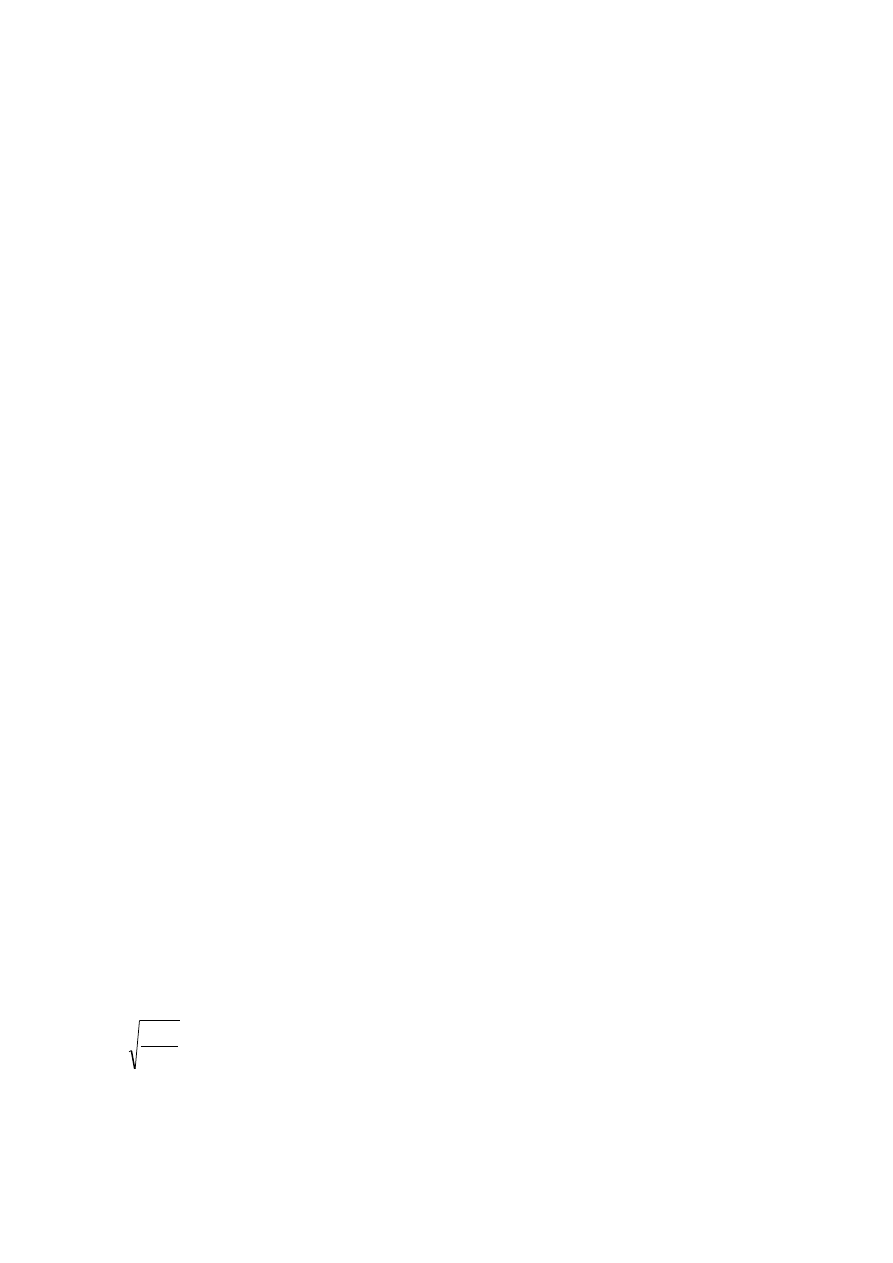
14. Do roztworu otrzymanego przez zmieszanie 30 cm

3

NH

4

NO

3

o stężeniu 0,4 mol/dm

3

i 20

cm

3

NH

3aq

o stężeniu 0,25 mol/dm

3

dodano 0,1 cm

3

roztworu chlorku magnezu o stężeniu 1

mol/dm

3

. Czy strąci się osad Mg(OH)

2

? K = 1,58*10

-5

; pK

SO

Mg(OH)

2

= 10,7

Zadanie łączy dwie rzeczy: bufory i iloczyn rozpuszczalności. Trzeba zacząć od rozpisania iloczynu
Mg(OH)

2

:

Mg(OH)

2

↔ Mg

2+

+ 2OH

-

K

SO

= [Mg

2+

][OH

-

]

2

Stężenie OH

-

wyliczamy z pH buforu, stężenie Mg

2+

z rozcieńczenia:

pOH = pK

B

+ log(n

S

/n

B

)

obliczamy n

S

i n

B

:

0,4 mol NH

4

NO

3

– 1000 cm

3

0,25 mol NH

3

- 1000 cm

3

x - 30 cm

3

x - 20 cm

3

x = 0,012 x = 0,005

pOH = 4,8 + log(0,012/0,005) = 4,8 + 0,38 = 5,18
[OH

-

] = 10

-5,18

= 6,6*10

-6

mol

Obliczamy stężenie Mg

2+

z rozcieńczenia:

1 mol MgCl

2

– 1000 cm

3

0,0001 – 50,1 cm

3

x - 0,1 cm

3

x - 1000 cm

3

x = 0,0001 x = 0,002 mol/dm

3

Podstawiamy do wyrażenia na iloczyn:
[Mg

2+

][OH

-

]

2

= 0,002*(6,6*10

-6

)

2

= 8,71*10

-14

K

SO

Mg(OH)

2

= 2*10

-11

; 8,71*10

-14

< 2*10

-11

Wniosek: Osad się nie strąci

15. Do roztworu o stężeniu 0,01 mol/dm

3

względem jonów Ag

+

i Bi

3+

dodawano kroplami

roztwór KI, która sól Agi, czy BiI

3

strąci się pierwsza? pK

SO

AgI = 16,1; pK

SO

BiI

3

19,0.

W tym zadaniu mamy zafiksowane stężenia kationów Ag

+

i Bi

3+

. Wynoszą one 0,01 mol/dm

3

i tę

liczbę należy podstawić do wyrażenia na iloczyn. Niewiadomą będzie stężenie jonów I

-

. Ta sól, dla

której w tych warunkach [I

-

] będzie mniejsze strąci się pierwsza,

AgI ↔ Ag

+

+ I

-

K

SO

= [Ag

+

][I

-

]

0,01*[I

-

] = 7,94*10

-17

[I

-

] = 7,94*10

-17

/0,01 = 7,94*10

-15

BiI

3

↔ Bi

3+

+ 3I

-

K

SO

= [Bi

3+

][I

-

]

3

0,01*[I

-

]

3

= 10

-19

[I

-

] =

3

19

01

,

0

10

−

= 2,15* 10

-6

Wniosek: 7,94*10

-15

< 2,15*10

-6

, więc AgI strąci się pierwszy

Chemia ogólna i nieorganiczna ZADANIA

36

16 Do 10 cm

3

roztworu zawierającego 20 mg Ba

2+

i 20 mg Pb

2+

dodawano kroplami roztwór

kwasu siarkowego. Który siarczan strąci się pierwszy? pK

SO

BaSO

4

= 10,0; pK

SO

PbSO

4

= 7,8.

Zadanie bardzo podobne do poprzedniego. Trzeba przeliczyć masy kationów na stężenia molowe.
M Pb

2+

= 207 g/mol M Ba

2+

= 137 g/mol

1 mol – 207g 1 mol - 137g
x - 0,02g x - 0,02g
x = 9,66*10

-5

mol x = 1,46*10

-4

Zauważamy, ze te ilości są w 10 cm

3

, a nam są potrzebne stężenia molowe, czyli obliczone ilości

moli trzeba przemnożyć przez 100:
[Pb

2+

] = 0,00966 mol/dm

3

[Ba

2+

] = 0,0146 mol/dm

3

Podstawiamy te stężenia do wyrażeń na odpowiednie iloczyny rozpuszczalności i sprawdzamy, dla
którego kationu stężenie [SO

4

2-

] wyjdzie mniejsze:

PbSO

4

↔ Pb

2+

+ SO

4

2-

K

SO

= [Pb

2+

][SO

4

2-

]

1,58*10

-8

= 0,00966*[SO

4

2-

]

[SO

4

2-

] = 1,58*10

-8

/0,00966 = 1,64*10

-6

BaSO

4

↔ Ba

2+

+ SO

4

2-

K

SO

= [Ba

2+

][SO

4

2-

]

10

-10

= 0,0146*[SO

4

2-

]

[SO

4

2-

] = 10

-10

/0,0146

[SO

4

2-

] = 6,85*10

-9

6,84*10

-9

< 1,64*10

-6

Wniosek: Pierwszy strąci się siarczan baru.

17. Podczas analizy kationów I i II grupy analitycznej ołów strącano w postaci chlorku, przy
czym stężenie HCl wynosiło 0,01 mol/dm

3

. Po odwirowaniu osadu do 2 cm

3

przesączu dodano

1 cm

3

roztworu KI o stężeniu 0,01 mol/dm

3

. Czy strąci się osad PbI

2

? pK

SO

PbCl

2

= 4,8; pK

SO

PbI

2

= 8,2.

Trzeba obliczyć stężenie wolnego Pb

2+

po strąceniu PbCl

2

:

PbCl

2

↔ Pb

2+

+ 2 Cl

-

K

SO

= [Pb

2+

][Cl

-

]

2

[Pb

2+

]*(0,01)

2

= 1,58*10

-5

[Pb

2+

] = 0,16 mol/dm

3

teraz obliczamy stężenia po rozcieńczeniu:
0,16 mol – 1000 cm

3

0,00032 mol Pb

2+

- 3 cm

3

x - 2 cm

3

x - 1000cm

3

x = 0,00032 x = 0,107 mol/dm

3

Teraz obliczamy stężenie jonów I

-

:

0,01 mol – 1000 cm

3

0,00001 mol I

-

- 3 cm

3

x - 1 cm

3

x - 1000 cm

3

x = 0,00001 mol x = 0,0033 mol

PbI

2

↔ Pb

2+

+ 2I

-

K

SO

= [Pb

2+

] [I

-

]

2

[Pb

2+

][I

-

]

2

= 0,107*(0,0033)

2

= 1,19*10

-6

K

SO

PbI

2

= 6,3*10

-9

1,19*10

-6

> 6,3*10

-9

Wniosek: W tych warunkach strąci się AgI

Chemia ogólna i nieorganiczna ZADANIA

37