Zadania2008 Dzienne

str 1

------------------------------------------------------------------------------------------------------------------------------------------------

Zadanie 1 .
a) Ocenić w przybliżeniu błąd bezwzględny i błąd względny, jaki popełniamy, obliczając wartość
funkcji
z = f(x,y),
jeżeli przyjęte do obliczeń x i y są niedokładne, przy czym oszacowania

∆

x

i

∆

y są niewielkie.

b) Ocenić błąd bezwzględny i błąd względny długości przekątnej prostokąta o bokach x = 5 cm
i y = 4 cm , jeżeli błąd przyrządu pomiarowego użytego do pomiaru wynosi

∆

= 0.2 cm

.

Komentarz
Zakładamy, że zamiast dokładnych wartości (X,Y) znamy wartości przybliżone (x,y) oraz oszacowania
błędów bezwzględnych:
X

x

−

∆

x

≤

, Y

y

−

∆

y

≤

.

Należy ocenić błędy: |f(X,Y) - f(x,y)| oraz |f(X,Y) - f(x,y)| / |f(x,y)|.

Rozwiązanie
(a)
Założymy, że funkcja f ma ciągłe pochodne cząstkowe do rzędu drugiego włącznie na pewnym otoczeniu
punktu (x,y) oraz x

∆

x

+

y

∆

y

+

,

(

)

jest punktem z tego otoczenia. Wtedy istnieje taka liczba

Θ,

0 <

Θ

< 1, że

f X Y

,

(

)

f x y

,

(

)

−

x

f x y

,

(

)

∂
∂













X

x

−

(

)

y

f x y

,

(

)

∂
∂













Y

y

−

(

)

+

=

+

+ 0.5 d

2

⋅

f x

Θ

X

x

−

(

)

+

y

Θ

Y

y

−

(

)

+

,

(

)

X

x

−

Y

y

−

,

(

)

(porównaj - Twierdzenie 6.8 Taylora, sem.1 wykład analizy matematycznej). Powyższą równość
nazywamy wzorem Taylora (dla funkcji dwóch zmiennych z 2-gą resztą).

Dla dostatecznie małych

∆

x i

∆

y, ostatni składnik (różniczka drugiego rzędu funkcji f) po prawej stronie

wzoru Taylora jest mały w porównaniu z pozostałymi składnikami (różniczka funkcji f). Zatem dla
błędów |f(X,Y) - f(x,y)| oraz |f(X,Y) - f(x,y)| / |f(x,y)| można przyjąć następujące oceny przybliżone

∆

f

x

f x y

,

(

)

∂
∂

∆

x

y

f x y

,

(

)

∂
∂

∆

y

+

=

,

δ

f

∆

f x y

,

(

)

f x y

,

(

)

=

.

(b)

f x y

,

(

)

x

2

y

2

+

=

,

x

f x y

,

(

)

∂
∂

x

x

2

y

2

+

=

,

y

f x y

,

(

)

∂
∂

y

x

2

y

2

+

=

;

x = 5, y = 4;

∆

=

∆

x =

∆

y = 0.2 ;

f 5 4

,

(

)

41

=

,

∆

f

9

41

0.2

⋅

=

,

δ

f

9

41

0.2

⋅

=

;

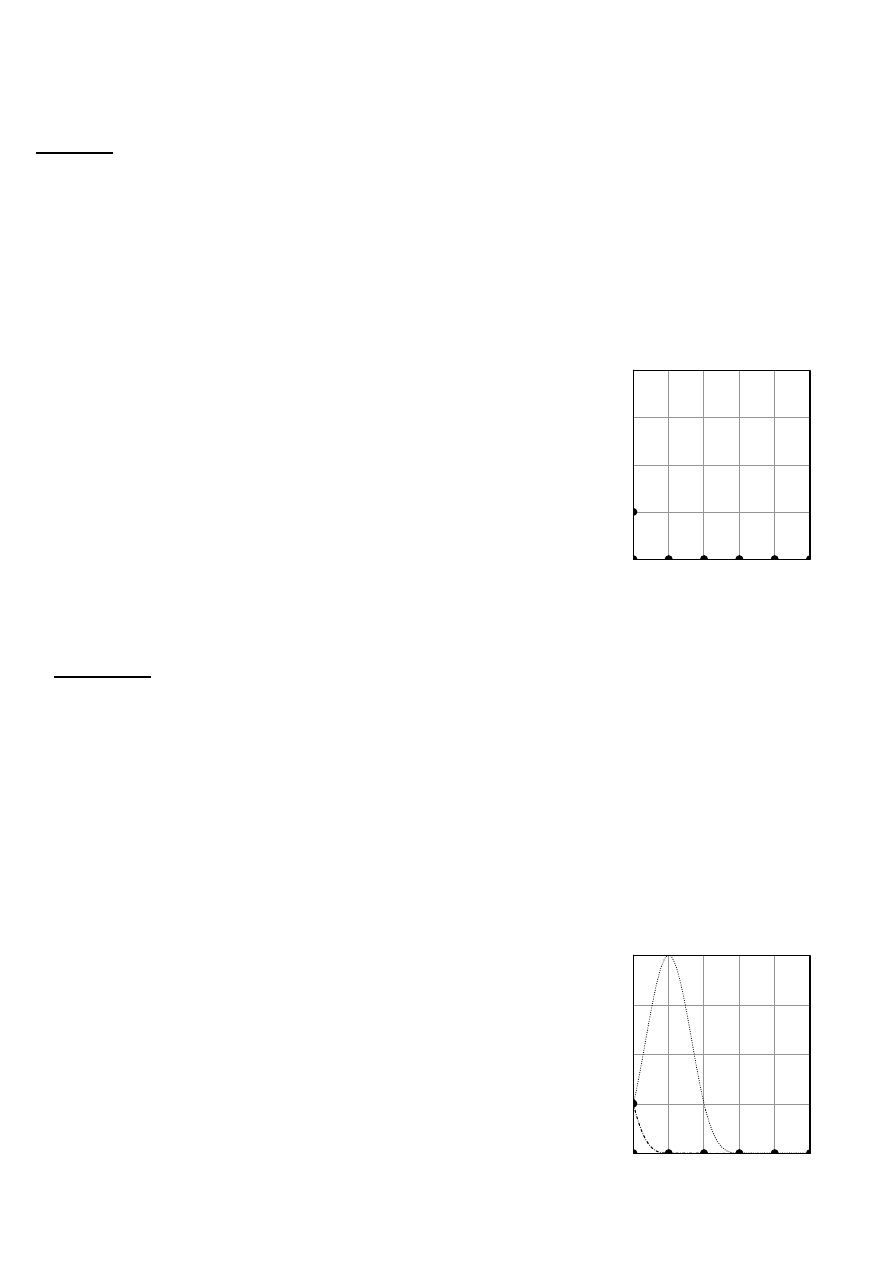
Zadania2008 Dzienne

str 2

---------------------------------------------------------------------------------------------------------------------------------------------

Zadanie 2.
W przedziale [a,b] danych jest (n+1) punktów x

0

x

1

,

....

,

x

n

,

, przy czym

a = x

0

< x

1

< ... < x

n

= b.

Punkty x

i

(i = 0, 1, 2, ...., n) są węzłami funkcji sklejanej.

a) Podać definicję funkcji sklejanej stopnia trzeciego. Od ilu parametrów zależy taka funkcja ?
b) Narysować wszystkie funkcje bazowe

Φ

i

takie, że

Φ

i

x

0

( )

1

=

.

0

1

2

3

4

x

0

x

1

x

2

x

3

x

4

x

5

Rozwiązanie
(a)
Funkcję s(x) określoną na przedziale [a,b] nazywamy funkcją sklejaną stopnia trzeciego, jeżeli

1) s(x) jest wielomianem stopnia co najwyżej trzeciego na każdym podprzedziale
(x

i

, x

i+1

) , i = 0,1,... , n-1 ;

2) s(x) jest funkcją klasy C

2

([a,b]) .

Funkcja sklejana stopnia trzeciego zależy od (n + 3) parametrów.

(b)
rysunek

0

1

2

3

4

x

0

x

1

x

2

x

3

x

4

x

5

Zadania2008 Dzienne

str 3

---------------------------------------------------------------------------------------------------------------------------------------------

Zadanie 3.

Rozważamy zagadnienie przybliżonego obliczania całki

1

−

1

x

f x

( )

⌠



⌡

d .

a) Omówić prosty wzór trapezów i wzór Gaussa-Legendre'a oparty na 2 węzłach.

b) Za pomocą tych wzorów wyznaczyć przybliżoną wartość całki

1

−

1

x

3 x

2

⋅

1

+

x

−

(

)

⌠



⌡

d

.

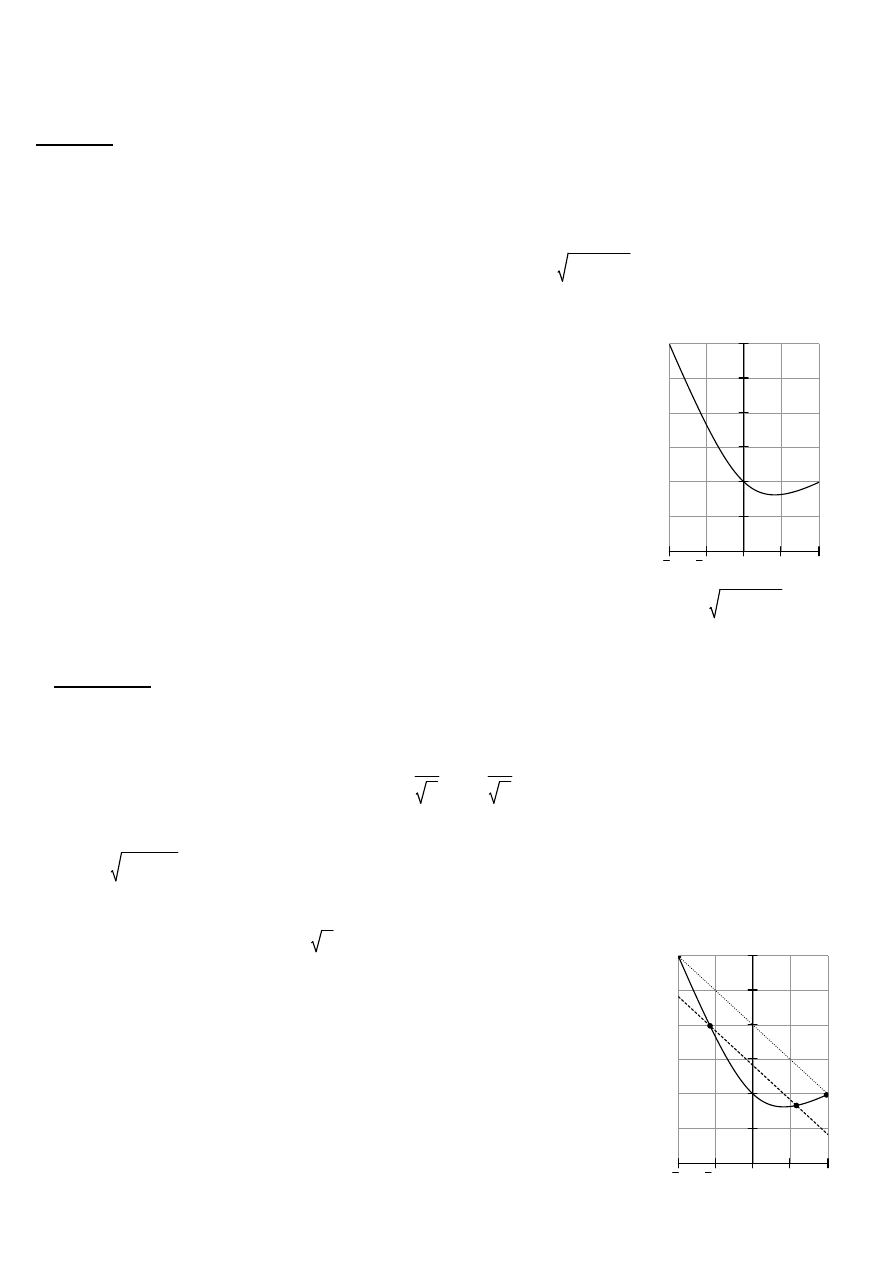
Obliczenia zilustrować graficznie.

Ad a. Podać wzory, przedstawić interpretację geometryczną.

1

0.5

0

0.5

1

0.5

1

1.5

2

2.5

3

y

3 x

2

⋅

1

+

x

−

=

Rozwiązanie
(a)
prosty wzór trapezów: S(f) = f(-1) + f(1) + interpretacja geometryczna;

2-punktowy wzór Gaussa-Legendre'a: S f

( )

f

1

−

3













f

1

3













+

=

+ interpretacja geometryczna;

(b)

f x

( )

3x

2

1

+

x

−

=

wzór trapezów: S(f) = 4 + rysunek

wzór Gaussa-Legendre'a: S f

( )

2 2

=

+ rysunek

1

0.5

0

0.5

1

0.5

1

1.5

2

2.5

3

Zadania2008 Dzienne

str 4

---------------------------------------------------------------------------------------------------------------------------------------------

Zadanie 4.
Zakładamy, że zagadnienie początkowe
y ' = f(x,y) , y(x

0

) = y

0

(*)

ma jednoznaczne rozwiązanie rozwijalne w szereg Taylora w pewnym otoczeniu punktu x

0

.

a) Omówić metodę rozwijania w szereg Taylora rozwiązania zagadnienia (*).
b) Wyznaczyć dwa pierwsze i trzy pierwsze wyrazy takiego rozwinięcia, gdy

y ' = - y

2

- 2x

2

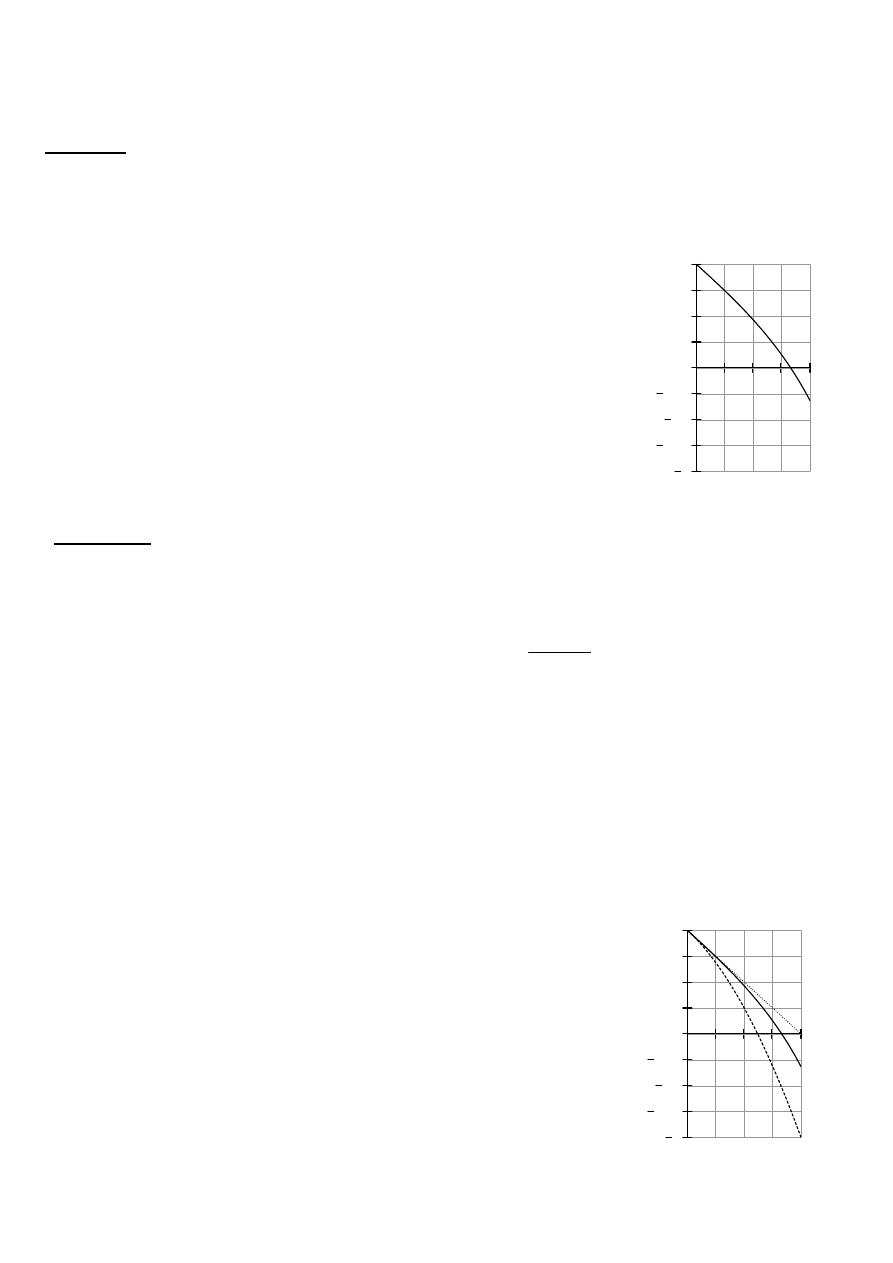
+ 2 , y(1) = 1. Obliczenia zilustrować graficznie.

1 1.25 1.5 1.75 2

1

0.75

0.5

0.25

0.25

0.5

0.75

1

y - rozwiązanie dokładne

Rozwiązanie
(a)
Zakładamy, że rozwiązanie zagadnienia Cauchy'ego (*) ma postać szeregu potęgowego w pewnym
otoczeniu punktu x

0

y x

( )

0

∞

k

a

k

x

x

0

−

(

)

k

⋅

∑

=

=

,

a

k

y

k

( )

x

0

( )

k

!

=

.

W każdym przedziale domkniętym zawartym w tym otoczeniu, sumy częściowe tego rozwinięcia

s

n

x

( )

0

n

k

a

k

x

x

0

−

(

)

k

⋅

∑

=

=

stanowią przybliżone rozwiązania.

Sumy częściowe s

n

, jako wielomiany, określone są dla dowolnego x . Stanowią one przybliżone rozwiązania

(przybliżenia rozwiązania dokładnego) jedynie w przedziałach domkniętych, w których rozwiązanie (dokładne)
jest rozwijalne w szereg potęgowy.

1 1.25 1.5 1.75 2

1

0.75

0.5

0.25

0.25

0.5

0.75

1

(b)

a

0

= 1, a

1

= y ' (1) = -1, s

1

(x) = 1 - (x-1); y "(x) = -2y(x)y '(x) - 4x,

y "(1) = -2, a

2

= -1, s

2

(x) = 1 - (x-1) - (x-1)

2

; rysunek

y = s

1

(x) (linia typu "kropka-kropka")

y = s

2

(x) (linia typu "kreska-kreska")