1

Wykład 9

Mechanika p

Mechanika p

ł

ł

yn

yn

ó

ó

w

w

Wrocław University of Technology

14-I-2012

2

Płyny

Mechanika płynów

14.I.2012

Płyn — w odróżnieniu od ciała stałego — to substancja zdolna do przepływu.
Gdy umieścimy go w naczyniu, przyjmie kształt tego naczynia.
Płyny — pod tą nazwą rozumiemy ciecze i gazy!

3

G

ę

sto

ść

Mechanika płynów

14.I.2012

Gęstość płynu jest równa

V

m

∆

∆

=

ρ

Aby wyznaczyć gęstość płynu ρ w pewnym jego punkcie, wydzielamy mały
element objętości ∆V w otoczeniu tego punktu i mierzymy masę ∆m płynu
zawartego w tej objętości.









=

3

3

1000

1

m

kg

cm

g

Substancja lub ciało

Gęstość [kg/m

3

]

Przestrzeń międzygwiazdowa

10

-20

Powietrze (20

o

C, 1 atm)

1.21

Styropian

60.5

Lód

0.917

.

10

3

Krew

1.060

.

10

3

Ziemia

5.5

.

10

3

Słońce

1.4

.

10

3

Jądro uranu

3

.

10

17

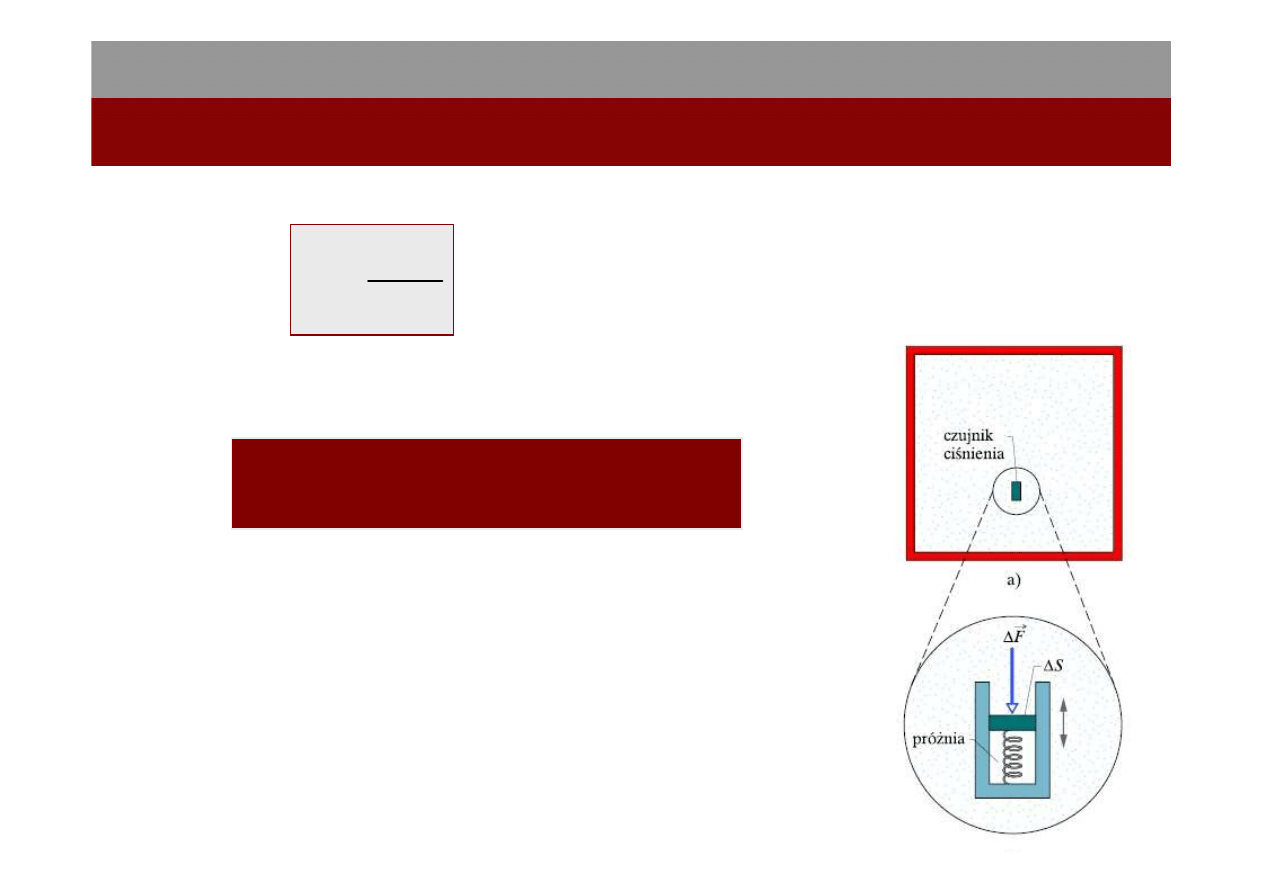
4

Ci

ś

nienie

S

F

p

∆

∆

=

⊥

Mechanika płynów

14.I.2012

Definicja:

[

]

2

/

1

1

1

m

N

Pa

Pascal

=

=

jednostkowa siła prostopadła do powierzchni ∆S

⊥

∆

F

1 Atm = 1.01

.

10

5

Pa = 1.013 bar =

= 760 Tr = 14.7 funt/in

2

Atmosfera (atm) jest to - jak wskazuje sama nazwa -
przybliżona wartość średnia ciśnienia atmosferycznego
na poziomie morza. Tor (Tr), nazwany tak na cześć
Evangelisty Toricellego, który wynalazł barometr
rtęciowy w 1647 roku, nazywany jest również
milimetrem słupa rtęci (mm Hg).

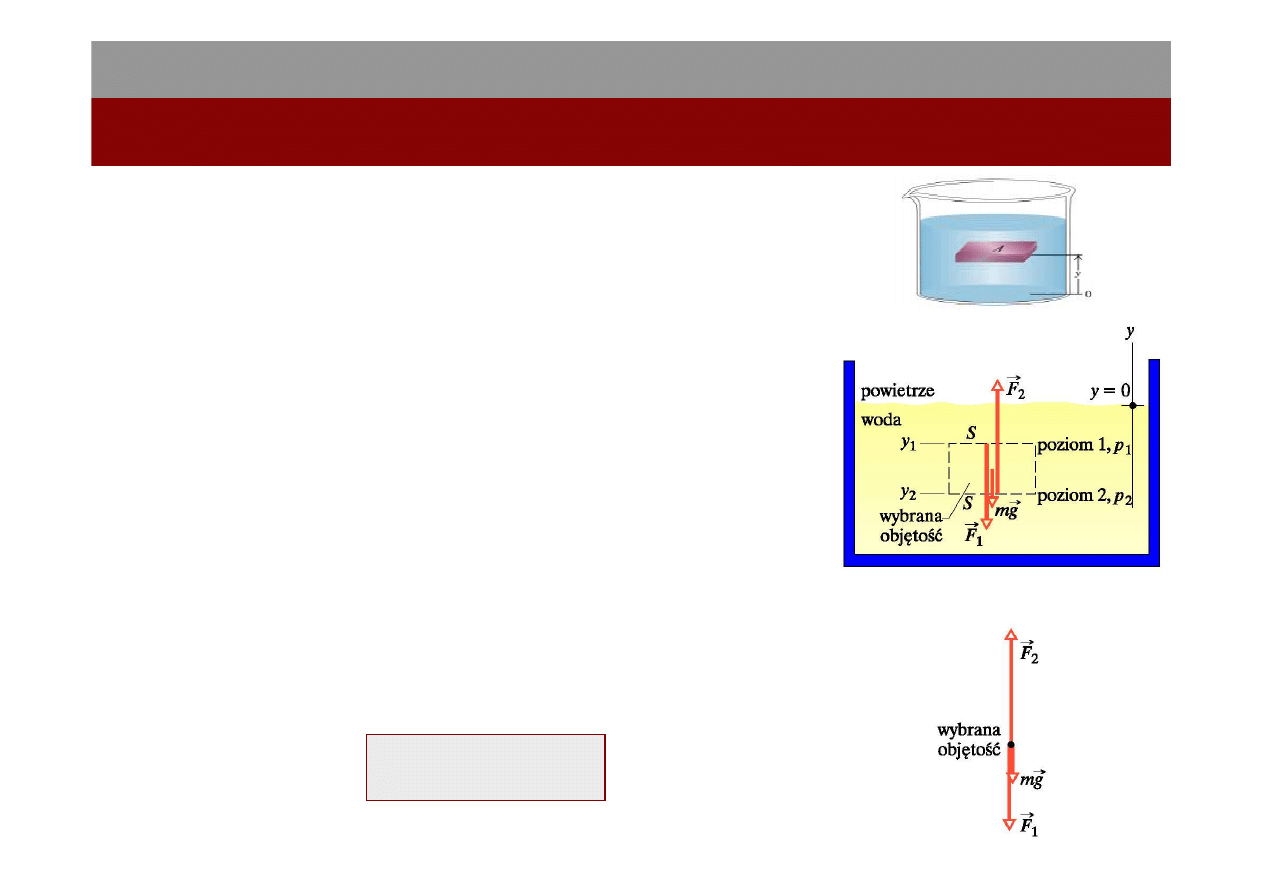
5

Płyny w spoczynku

mg

F

F

+

=

1

2

Mechanika płynów

14.I.2012

S

p

F

S

p

F

2

2

1

1

=

=

(

)

2

1

1

2

y

y

Sg

S

p

S

p

−

+

=

ρ

(

)

2

1

1

2

y

y

g

p

p

−

+

=

ρ

Oznaczając przez p

0

ciśnienie atmosferyczne na

powierzchni cieczy, otrzymujemy:

p

p

h

y

p

p

y

=

−

=

=

=

2

2

0

1

1

,

oraz

,

0

gh

p

p

ρ

+

=

0

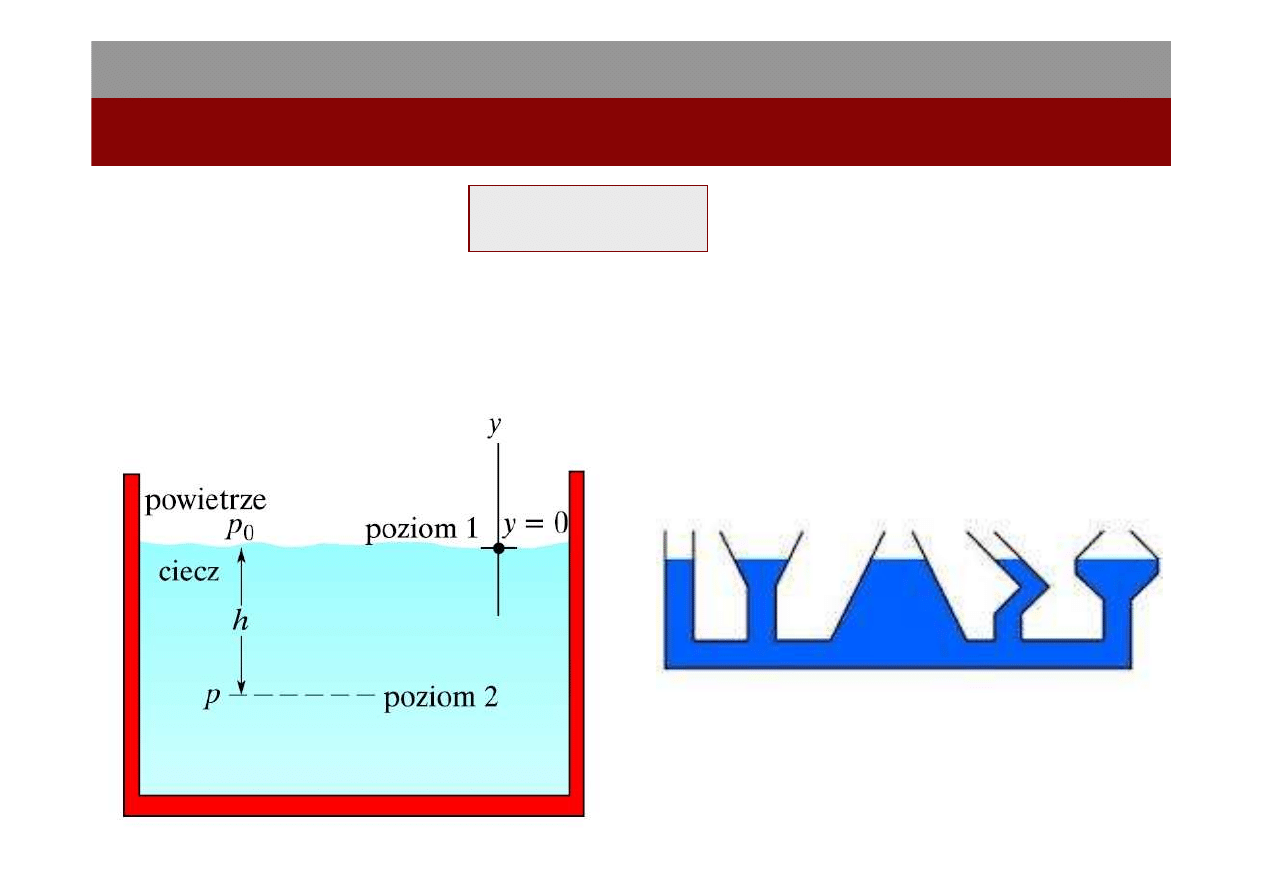
6

Płyny w spoczynku

Mechanika płynów

14.I.2012

Ciśnienie w pewnym punkcie w płynie znajdującym się w równowadze statycznej
zależy od głębokości tego punktu pod powierzchnią płynu, a nie zależy od
poziomych rozmiarów płynu ani zbiornika, w którym płyn jest zawarty.

gh

p

p

ρ

+

=

0

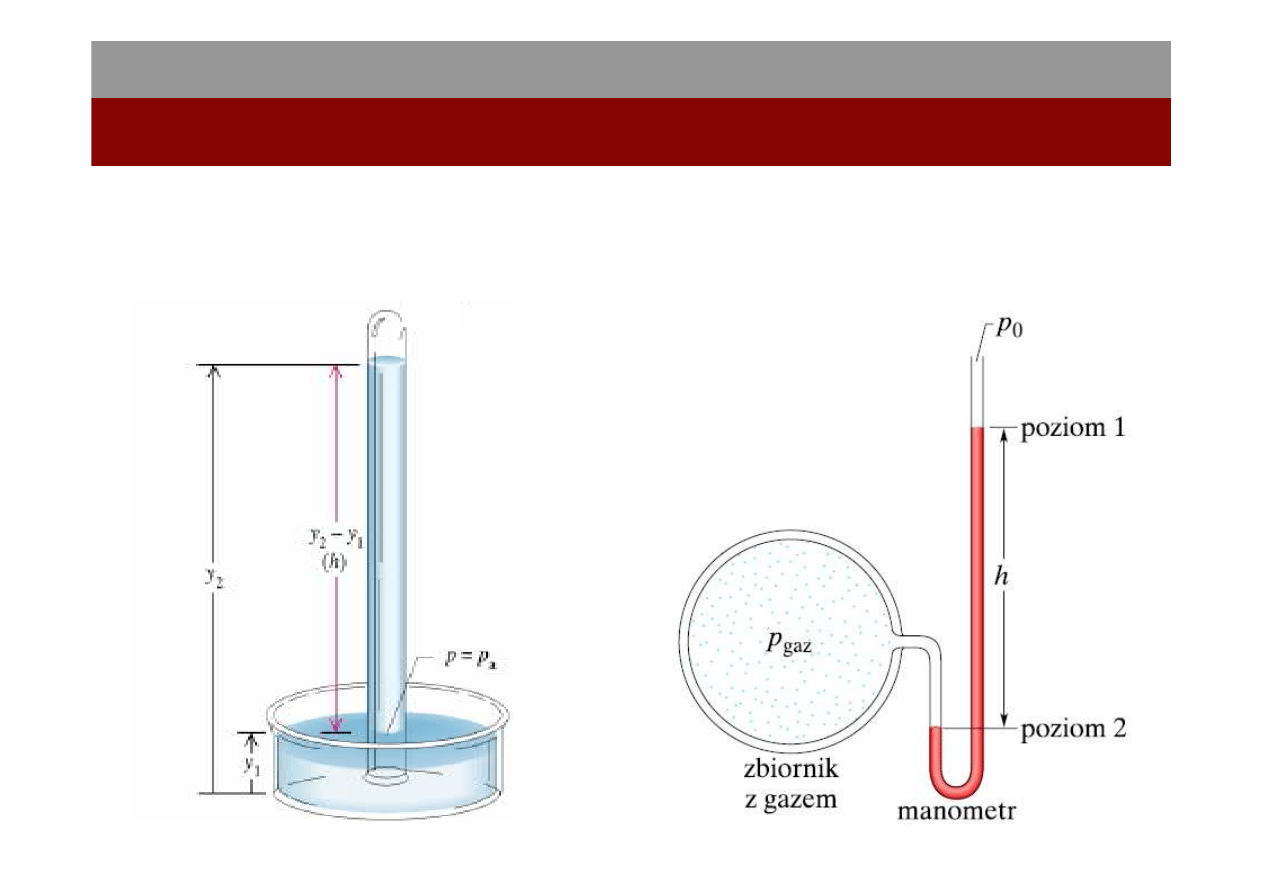
7

Pomiary ci

ś

nienia

Mechanika płynów

14.I.2012

Manometr rtęciowy

Manometr otwarty

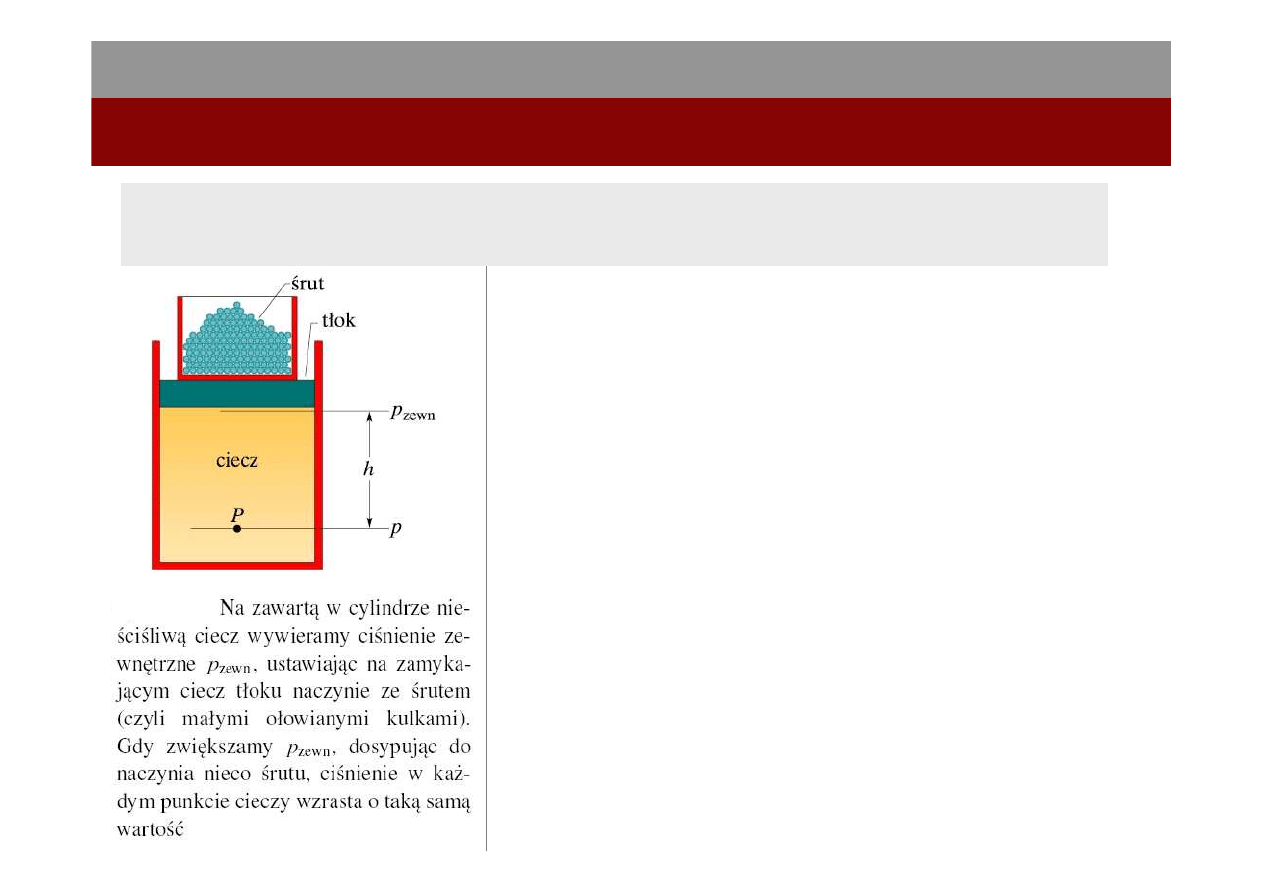
8

Prawo Pascala

Mechanika płynów

14.I.2012

W zamkniętej objętości nieściśliwego płynu zmiana ciśnienia jest przenoszona

bez zmiany wartości do każdego miejsca w płynie i do ścian zbiornika.

Ciśnienie p w dowolnym punkcie cieczy P wynosi:

gh

p

p

zewn

ρ

+

=

Następnie, do zbiornika ze śrutem dosypujemy nieco
ś

rutu, w wyniku czego ciśnienie p

zewn

wzrasta o

∆p

zewn

. Zatem zmiana ciśnienia w punkcie P jest

równa ∆p:

zewn

p

p

∆

=

∆

Ten przyrost ciśnienia nie zależy od h, a więc musi
być taki sam w każdym punkcie cieczy, co właśnie
stwierdza prawo Pascala.

9

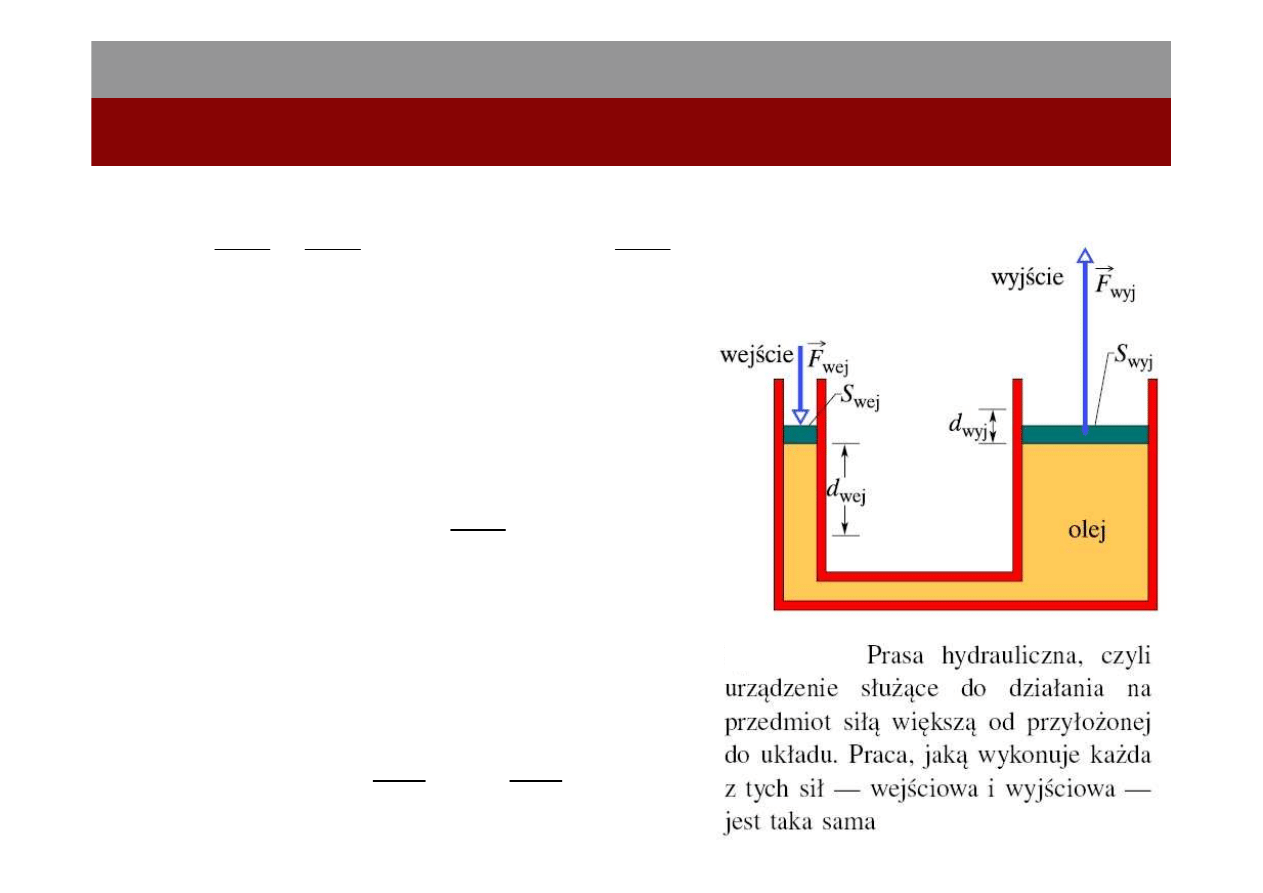
Prasa hydrauliczna

Mechanika płynów

14.I.2012

wyj

wyj

wej

wej

S

F

S

F

p

=

=

∆

wej

wyj

wej

wyj

S

S

F

F

=

Jeśli przesuniemy tłok wejściowy w dół o odcinek
d

wej

, to tłok wyjściowy przesunie się w górę o

odcinek d

wyj

wyj

wyj

wej

wej

d

S

d

S

V

=

=

wyj

wej

wej

wyj

S

S

d

d

=

stąd gdy S

wyj

> S

wej

, przemieszczenie tłoka

wyjściowego jest mniejsze niż przemieszczenie
tłoka wejściowego.
Praca wykonana przez siłę wyjściową:

wej

wej

wyj

wej

wej

wej

wyj

wej

wyj

wyj

d

F

S

S

d

S

S

F

d

F

W

=





























=

=

10

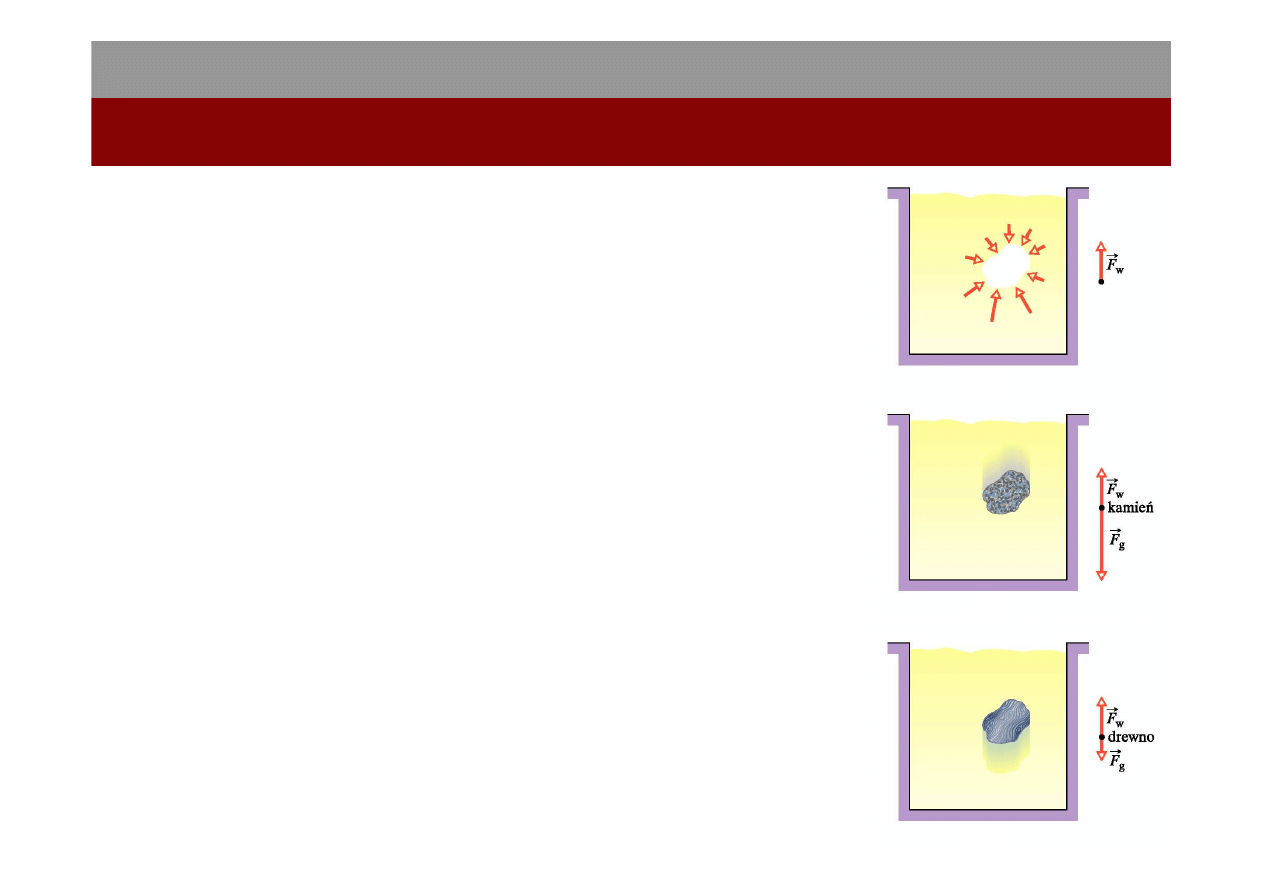
Prawo Archimedesa

Mechanika płynów

14.I.2012

Na ciało całkowicie lub częściowo zanurzone w
płynie działa ze strony płynu siła wyporu F

w

. Jest

ona skierowana pionowo do góry, a jej wartość
jest równa ciężarowi m

p

g płynu wypartego przez

to ciało.

Siła wyporu, jaka działa na ciało w płynie, ma
wartość:

g

m

F

p

wyp

=

przy czym m

p

jest masą płynu wypartego przez

ciało.

CIĘśAR

POZORNY

CIĘśAR

RZECZYWISTY

WARTOŚĆ SIŁY

WYPORU

=

-

11

Ruch płynów doskonałych

Mechanika płynów

14.I.2012

1. Przepływ ustalony. Przepływ jest ustalony
(nazywany też laminarnym), gdy prędkość
poruszającego się płynu w każdym wybranym
punkcie nie zmienia się w upływem czasu,
zarówno co do wartości, jak i co do kierunku.

2. Przepływ nieściśliwy. Będziemy zakładać,
podobnie jak to już robiliśmy dla płynów w
spoczynku, że nasz doskonały płyn jest
nieściśliwy, to znaczy, że jego gęstość jest stała.

3. Przepływ nielepki. Z grubsza rzecz biorąc,
lepkość płynu jest miarą oporu, jaki stawia płyn
jego przepływowi.

4. Przepływ bezwirowy.

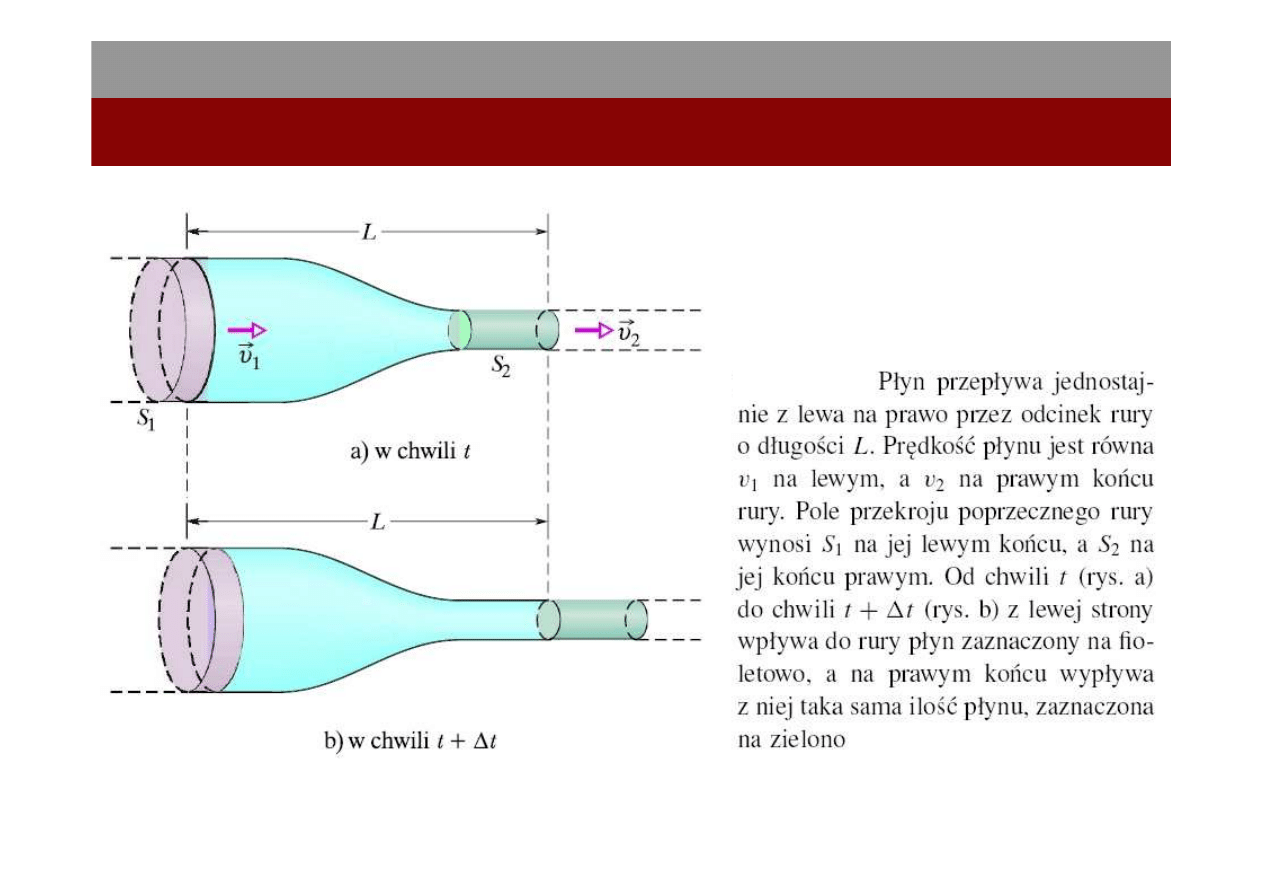
12

Równanie ci

ą

gło

ś

ci

Mechanika płynów

14.I.2012

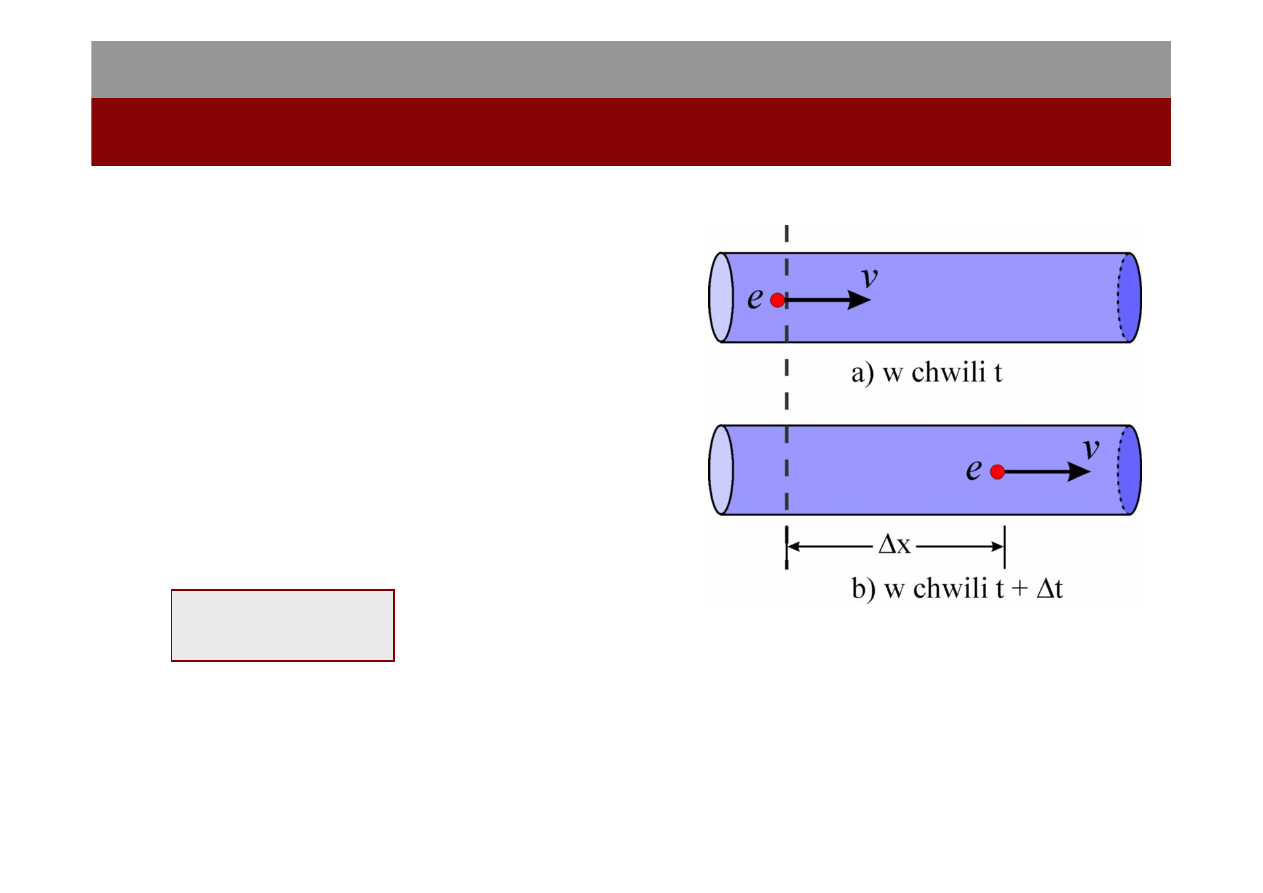
13

Równanie ci

ą

gło

ś

ci

Mechanika płynów

14.I.2012

Prędkość elementu e jest równa v, zatem w
przedziale czasu ∆t element ten przebywa
wzdłuż rury odcinek o długości ∆x = v ∆t.
Wobec tego w przedziale czasu ∆t przez linię
przerywaną przepływa płyn o objętości ∆V
równej

t

Sv

x

S

V

∆

=

∆

=

∆

t

v

S

t

v

S

V

∆

=

∆

=

∆

2

2

1

1

2

2

1

1

v

S

v

S

=

- równanie ciągłości

Wynika z niego, że prędkość przepływu wzrasta, gdy maleje pole przekroju
poprzecznego, przez który płyn przepływa.

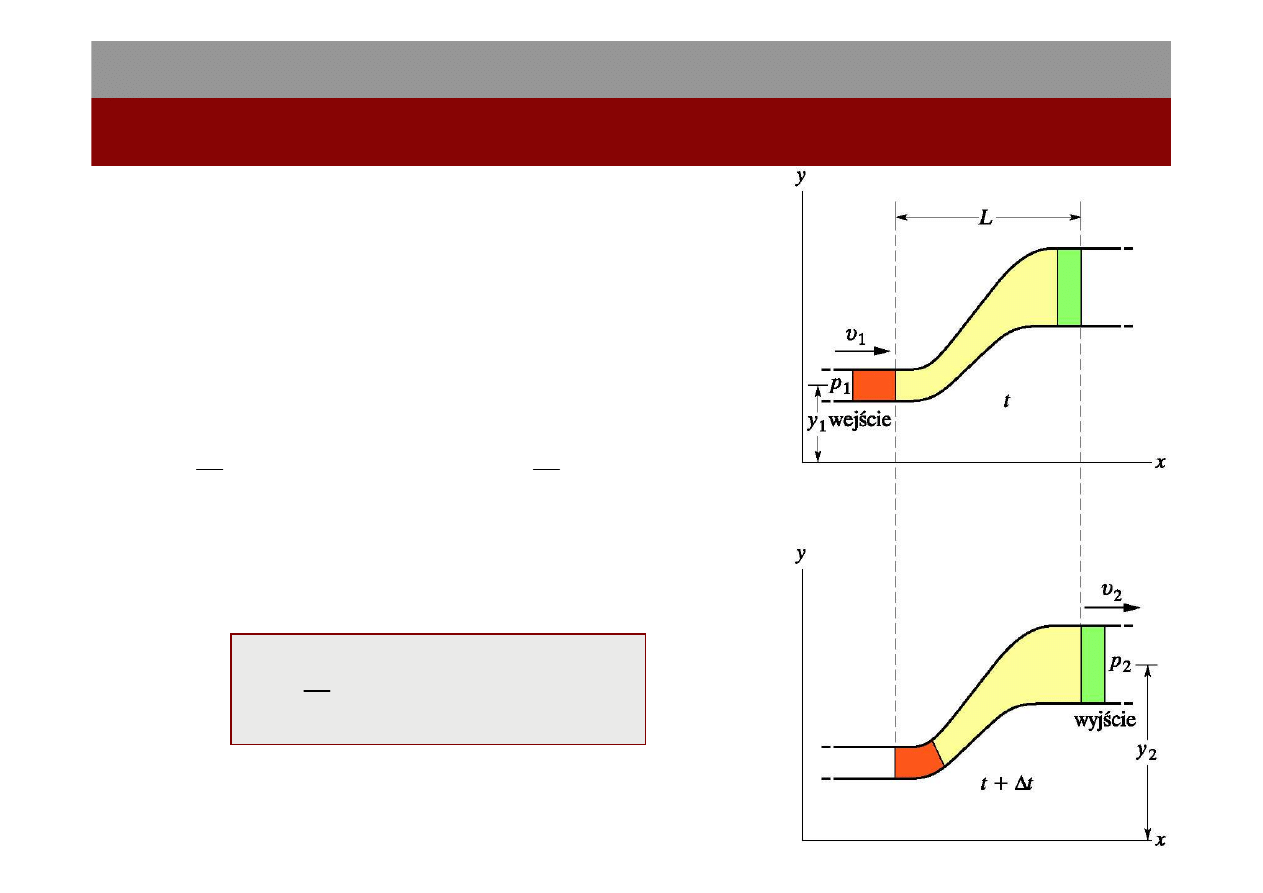
14

Równanie Bernoulliego

Mechanika płynów

14.I.2012

Oznaczenia:
y

1

, v

1

i p

1

- poziom, prędkość i ciśnienie płynu

wchodzącego do rury z lewej strony;
y

2

, v

2

i p

2

- odpowiednie wielkości odnoszące się

do płynu wychodzącego z rury z prawej strony.

2

2

2

2

1

2

1

1

2

1

2

1

gy

v

p

gy

v

p

ρ

ρ

ρ

ρ

+

+

=

+

+

const

gy

v

p

=

+

+

ρ

ρ

2

2

1

Równanie Bernoulliego:

15

Równanie Bernoulliego

Mechanika płynów

14.I.2012

• Równanie Bernoulliego dla płynu w spoczynku, v

1

= v

2

= 0

(

)

2

1

1

2

y

y

g

p

p

−

+

=

ρ

• Równanie Bernoulliego dla płynu, który w trakcie przepływu nie zmienia
położenia w pionie (y jest stałe np. y = 0)

2

2

2

2

1

1

2

1

2

1

v

p

v

p

ρ

ρ

+

=

+

Jeśli przy przepływie wzdłuż poziomej linii prądu prędkość elementu płynu
wzrasta, to ciśnienie płynu maleje i na odwrót.

Równanie Bernoulliego stosuje się ściśle jedynie dla płynu doskonałego. Gdy
występują siły lepkości, nie wolno nam pominąć zmian energii termicznej płynu.

16

Równanie Bernoulliego

Mechanika płynów

14.I.2012

Wyprowadzenie

Zasada zachowania energii w postaci związku pracy ze zmianą energii kinetycznej:

k

E

W

∆

=

Zmiana energii kinetycznej jest wynikiem zmiany prędkości płynu między końcami
rury, a zatem wynosi:

(

)

2

1

2

2

2

1

2

2

2

1

2

1

2

1

v

v

V

mv

mv

E

k

−

∆

=

∆

−

∆

=

∆

ρ

Praca wykonana nad układem ma dwa źródła. Po pierwsze, siła ciężkości
(

∆mg) wykonuje pracę W

g

nad płynem o masie

∆m, wznosząc go z poziomu

wejściowego na wyjściowy. Praca ta jest równa:

(

)

(

)

1

2

1

2

y

y

V

g

y

y

mg

W

g

−

∆

−

=

−

∆

−

=

ρ

Jest ona ujemna ze względu na przeciwne kierunki przemieszczenia płynu
(skierowanego w górę) i siły ciężkości (skierowanej w dół).

17

Równanie Bernoulliego

Mechanika płynów

14.I.2012

Po drugie, praca jest też wykonywana nad układem (na wejściowym końcu
rury), gdy płyn jest wtłaczany do rury, oraz przez układ (na wyjściowym końcu
rury), gdy płyn jest wypychany z rury. Całkiem ogólnie możemy powiedzieć,
ż

e praca wykonana przez siłę o wartości F, działającą na próbkę płynu o polu

przekroju poprzecznego S, przy przemieszczeniu płynu na odległość ∆x, jest
równa

( )( ) ( )

V

p

x

S

p

x

pS

x

F

∆

=

∆

=

∆

=

∆

Praca wykonana nad układem jest zatem równa p

1

∆V, a praca wykonana przez

okład wynosi - p

2

∆V. Ich suma W

p

jest równa:

(

)

V

p

p

V

p

V

p

W

p

∆

−

−

=

∆

+

∆

−

=

1

2

1

2

Związek pracy ze zmianą energii kinetycznej:

k

p

g

E

W

W

W

∆

=

+

=

(

)

(

)

(

)

2

1

2

2

1

2

1

2

2

1

v

v

V

p

p

V

y

y

V

g

−

∆

=

−

∆

−

−

∆

−

ρ

ρ

18

Efekt Magnusa

Mechanika płynów

14.I.2012

19

Efekt Magnusa

Mechanika płynów

14.I.2012

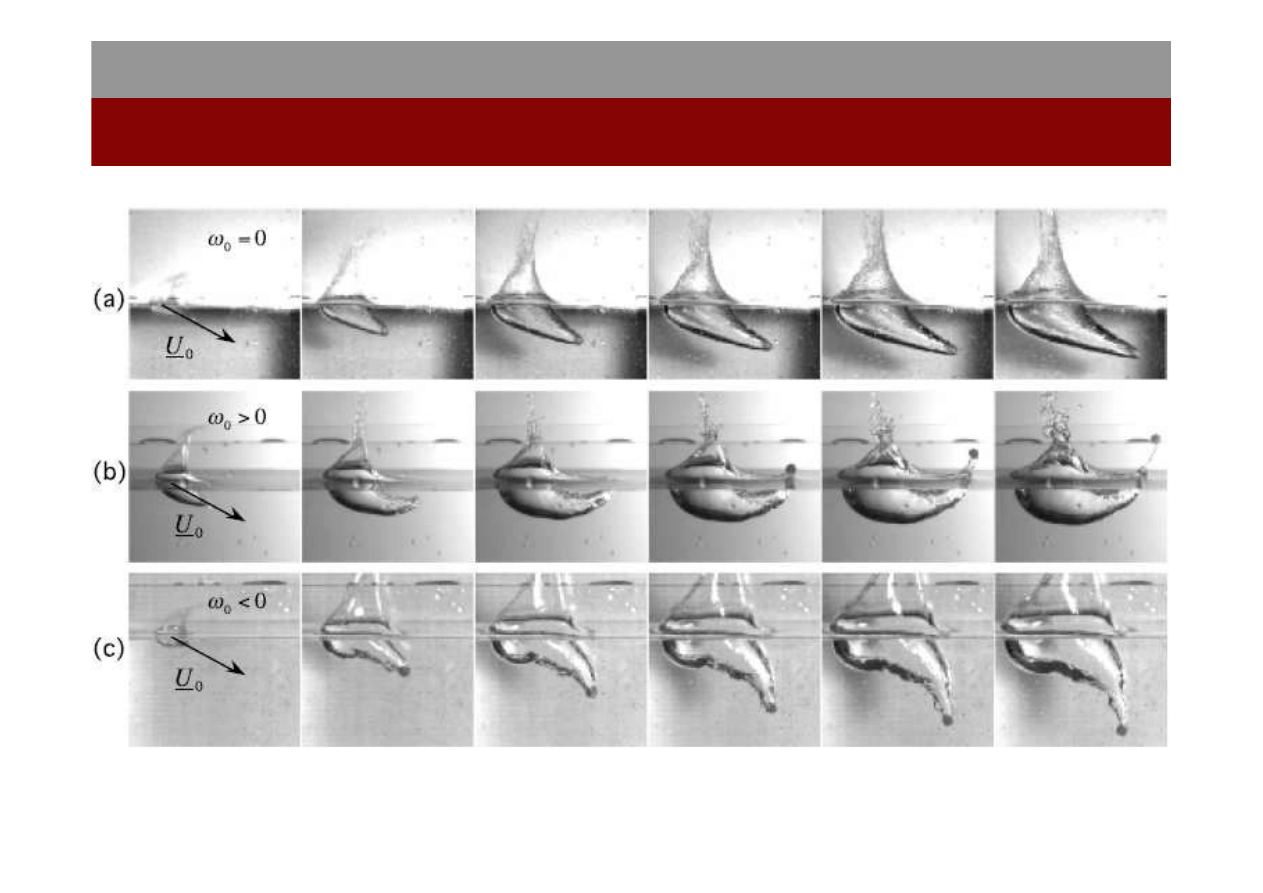
20

Efekt Magnusa

Mechanika płynów

14.I.2012

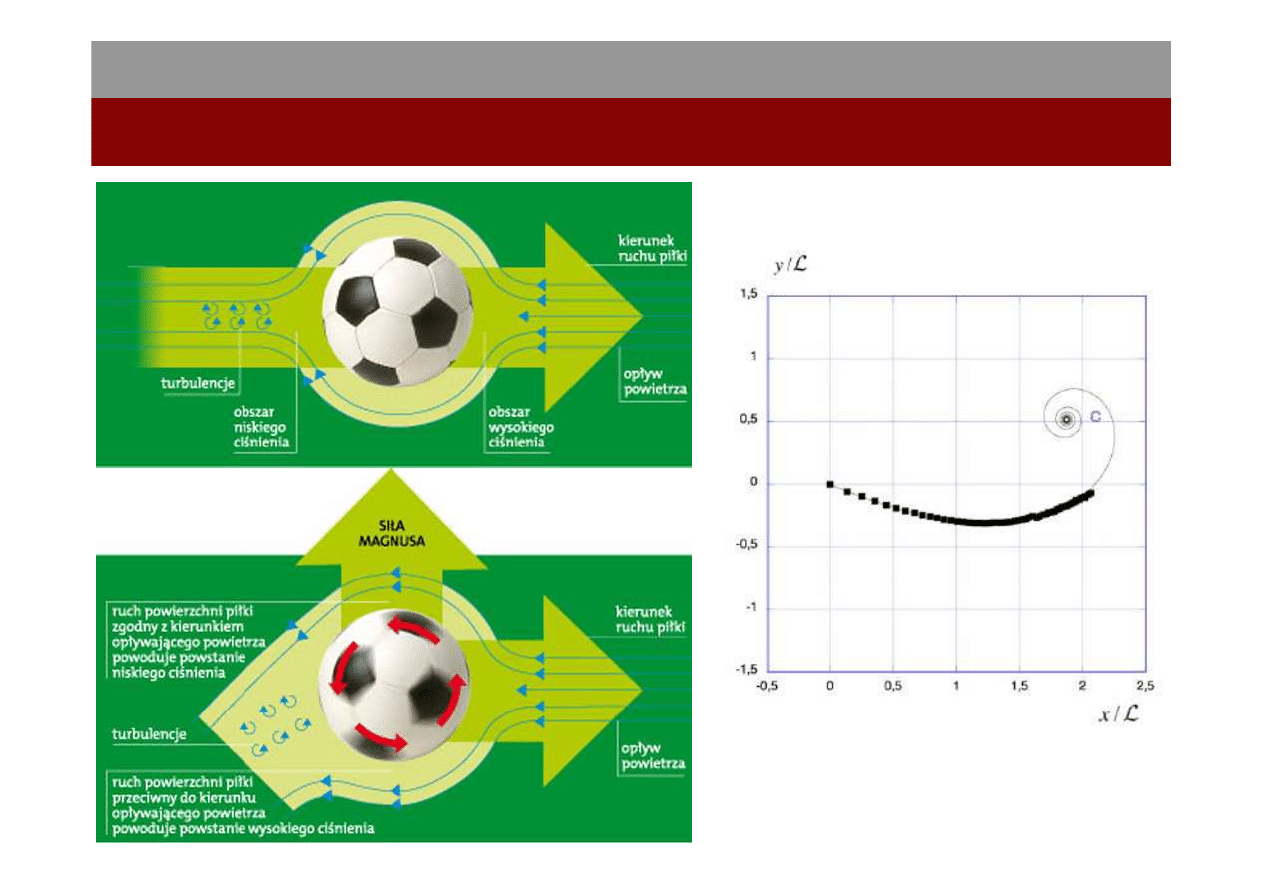
21

Efekt Magnusa

Mechanika płynów

14.I.2012