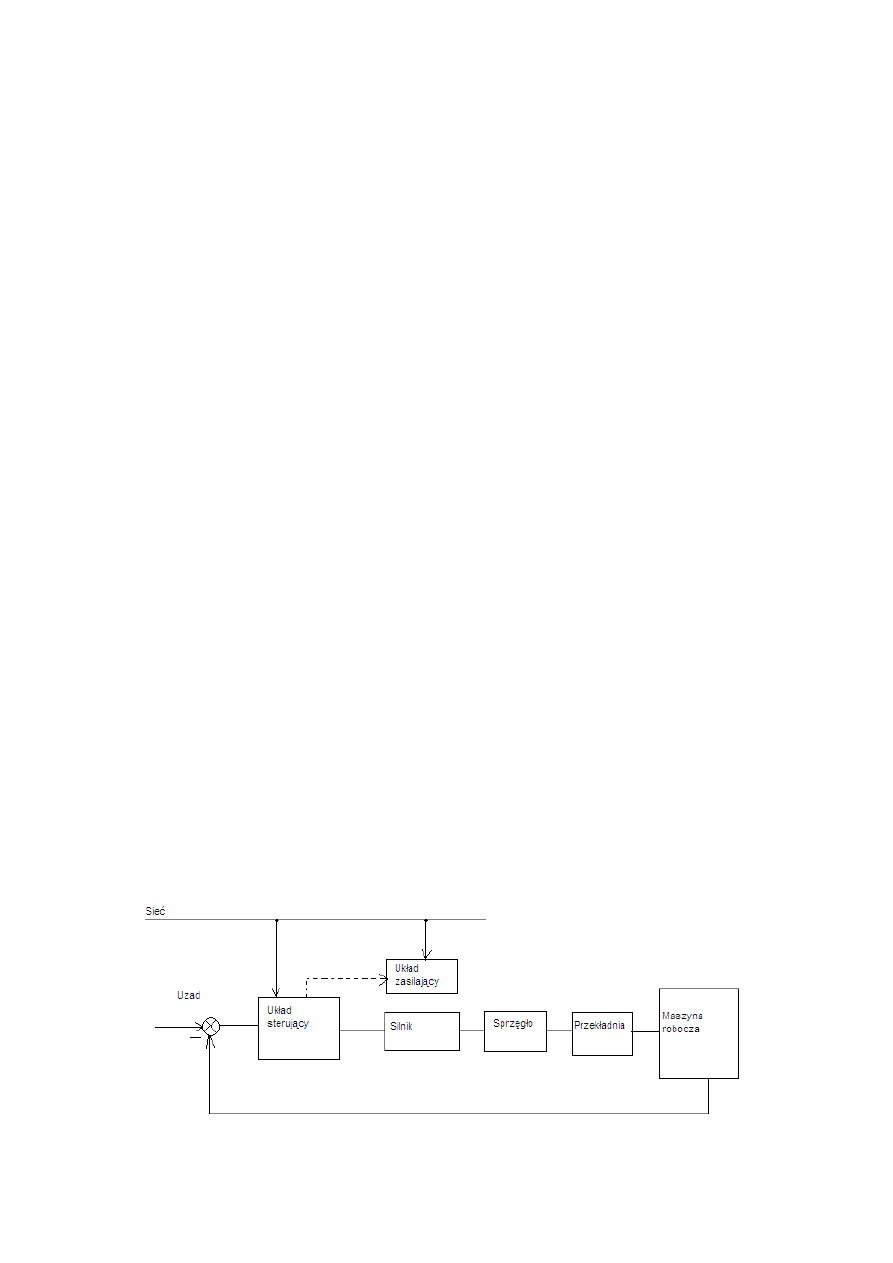
Podstawy napędu elektrycznego – wykład



Prof. J. Szewczyk


Zaliczenie: 5 pytań podzielonych na dwie części, trzeba odpowiedzieć na jeden temat z każdej
części by zaliczyć (opisówka)

Materiały:
Internet, notatki z wykładu, każda książka która ma w tytule „napęd elektryczny’

Literatura polecona przez prowadzącego:
Dotyczące klasycznego napędu;
Bielawski: Podstawy napędu elektrycznego 1979r
Praca zbiorowa pod redakcją prof. Grunwalda: Napęd elektryczny
Dotyczące układów przekształtnikowych:
Nowak, Barlik: Technika tyrystorowa

A.

Czajkowski: Napęd tyrystorowy prądu stałego

Wykład pierwszy 25.02.2010

Silniki mogą być sprzężone z pompami, charakteryzują się prostymi układami zasilania dużą
niezawodnością pracy.
Napędy elektryczne pokazują cztery kwadranty układów współrzędnych.
Budowane są w wieloraki sposób, maja różną obudowę przystosowaną do zadania które mają
wykonywać.
Mają stosunkową cicha pracę
Nie wymagają konserwacji (asynchroniczne), jeżeli posiadają komutator należy jednak
konserwować
Wady:
Trzeba ciągle dostarczać energię. Mają duże prędkości i dlatego niejednokrotnie trzeba
stosować przekładnie. Nasycanie się obwodu wirnika sprawia że stosunek masy do
wytworzonej mocy jest mały (lepiej zachowują się napędy pneumatyczne)

Struktura układu napędowego

Silnik musi być połączony z maszyną przez tzw. sprzęgło, czasami należy zastosować
przekładnie. Cały układ jest sterowany przez układ sterujący (najprostszym układem
sterującym jest wyłącznik). Całość jest zasilana z sieci. Układem zasilającym może być
np przekształtnik. Układ taki może pracować w systemie otwartym bądź w układzie
zamkniętym.

Równanie ruchu układu napędowego – wyprowadzenie (ważne)

W pracy układu możemy rozróżnić dwa stany:
- ustalony (statyczny) – prędkość kontowa jest stała
- nieustalony (dynamiczny, przejściowy) – zmiana prędkości po czasie jest różna od zera

Ω

= const =

dt

d

Ω

= 0 – prędkość dla stanu statycznego

ν

= const =

dt

dV

= 0

Ω

= var =

0

≠

Ω

dt

d

- prędkość dla stanu dynamicznego

ν

= var =

0

≠

dt

dV

op

n

d

M

M

M

−

=

Md – moment dynamiczny
Mn – moment napędowy silnika
Mop – moment opory stanowiony przez maszynę, składa się z dwóch części: samej maszyny i
momentu strat

Energia kinetyczna ruchu obrotowego jest równa:

2

2

v

j

E

k

=

j – moment bezwładności

2

2

v

m

E

k

=

Energia kinetyczna zależy od momentu bezwładności oraz od kwadratu prędkości
Moment bezwładności dla konkretnej bryły ma wartość stałą i jest to podane w katalogu.
Jeżeli różniczkujemy energię kinetyczną po czasie to otrzymujemy:

dt

dj

dt

d

j

j

dt

d

dt

dE

k

2

)

2

(

2

2

Ω

+

Ω

Ω

=

Ω

=

Zmiana energii kinetycznej po czasie określa moc.

dt

dj

dt

d

j

P

d

2

2

Ω

+

Ω

Ω

=

Wychodząc z wzoru ze moment jest to moc przez prędkość:

Ω

=

P

M

Uzyskujemy wyrażenie że moment jest równy:

dt

dj

dt

d

j

M

d

2

Ω

+

Ω

=

W zdecydowanej większości urządzeń moment dynamiczny jest stały ale są urządzenia w
których moment bezwładności się zmienia (np. wirówka)

Ponieważ w większości urządzeń w których moment bezwładności jest stały dla dalszych
rozważań ustalamy że:

j = const

I dlatego moment dynamiczny:

dt

d

j

M

M

M

op

n

d

Ω

=

−

=

- równanie dynamiczne napędu

Mn- moment napędowy (silnika) – może być momentem napędowym jak i hamującym

Moment wytworzony przez silnik którego znak jest zgodny z kierunkiem prędkości będziemy
nazywali momentem napędowym i oznaczali znakiem „+”
Moment napędowy którego znak jest przeciwny do kierunku prędkości będziemy nazywali
momentem hamującym i oznaczali znakiem „-„

Moment oporowy – jest to moment jakim maszyna robocza przeciwdziała momentowi
napędowemu (nieraz nazywany momentem statycznym)
Istnieją dwa rodzaje momentów oporowych:
- moment oporowy relaksacyjny (oznaczany symbolem

opr

M

) – jest to moment skierowany

zawsze przeciwnie do kierunku ruchu, przykładem jest tarcie
- moment oporowy potencjalny (czynny; oznaczany symbolem

opp

M

) – jest on skierowany w

określonym kierunku niezależnie od kierunku prędkości, przykładem jest moment sił
grawitacyjnych

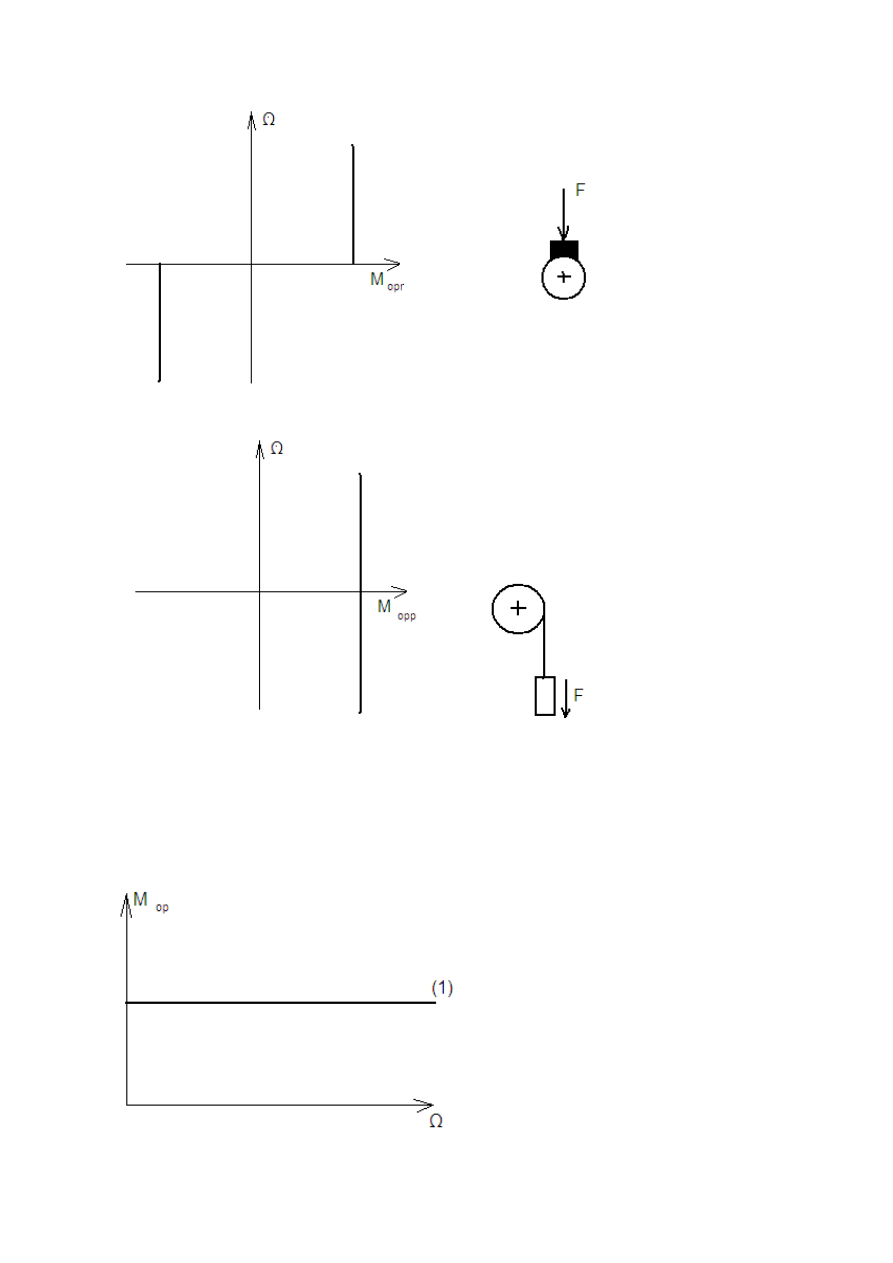
W ogólnym przypadku momenty opisane są funkcją, liniową itd.
Najczęściej spotykanymi rodzajami momentów oporowych w funkcji prędkości są:
- moment oporowy o stałej wartości (1)

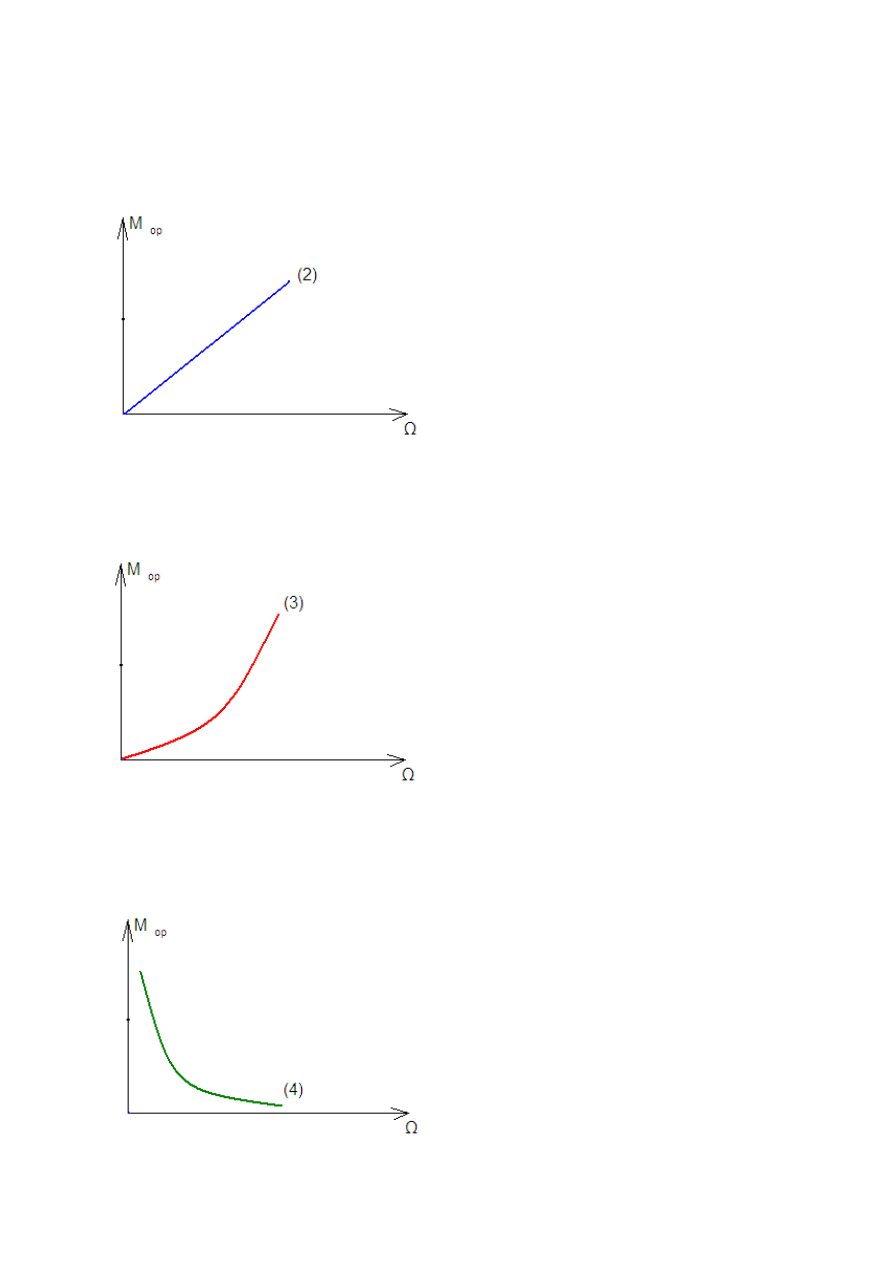
Mop = const
Mają mechanizmy jezdne (np. taśmociąg)

- moment zależny liniowo od prędkości (2)

Ω

=

k

M

op

Mają maszyny do obróbki metali

- moment zależny od prędkości w potędze (najczęściej spotykany to kwadrat) (3)

2

1

Ω

=

k

M

op

Występuje w wentylatorach – dlatego mówi się moment wentylatorowy

- moment hiperboliczny (4)

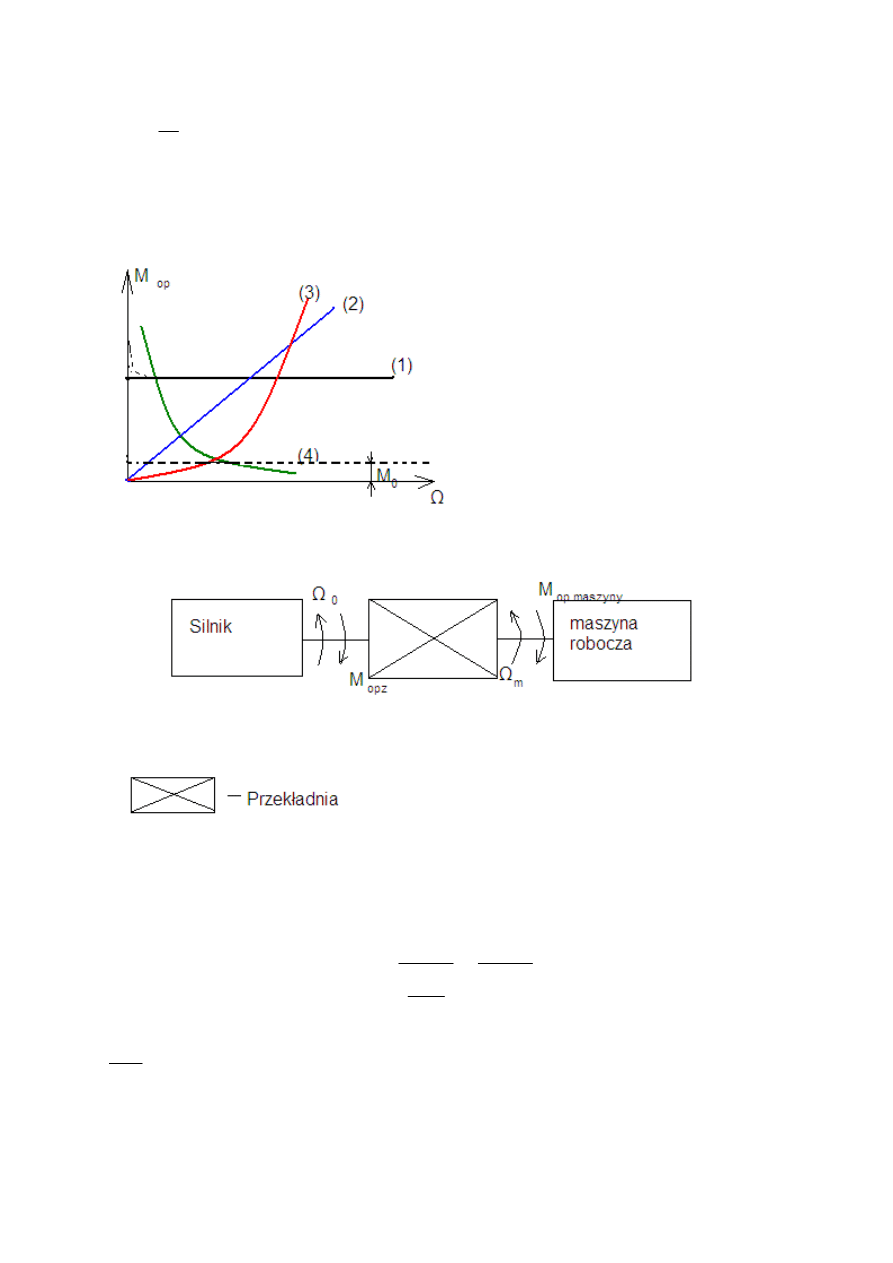
Ω

=

2

k

M

op

Występuje w maszynach do nawijania, przewijania (taśmy, drutu, papieru)

W praktyce nie ma idealnie i dlatego należy pamiętać o stratach więc wszystkie krzywe są
przeniesione o jakąś wartość (trzeba liczyć się np. z dodatkowym tarciem)

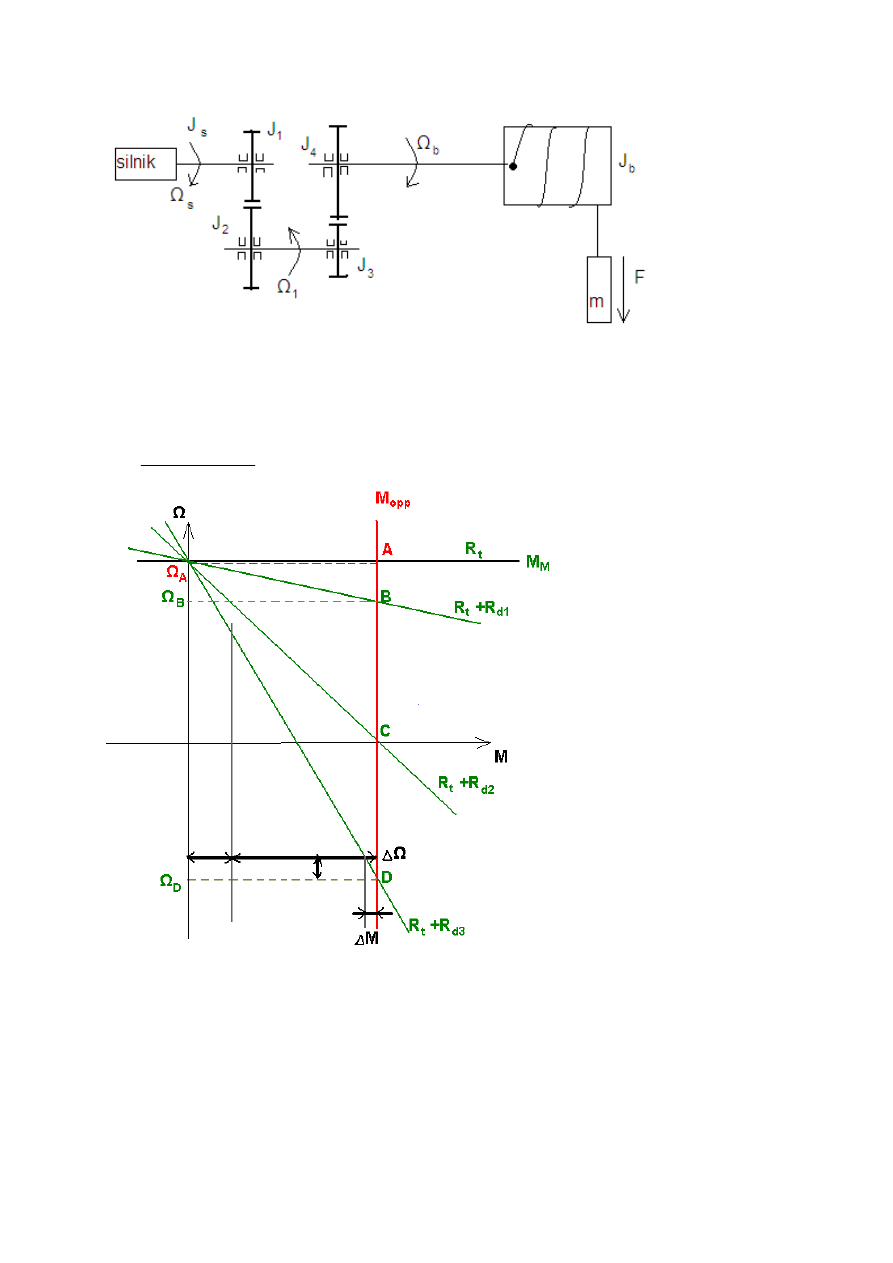
Przeliczenie momentu oporowego do prędkości silnika (przeliczenie momentu na wał silnika)

Przy doborze silnika będzie nas interesowało jak dobrać moment by zniwelować moment
oporowy. Wychodzimy z założenia że moc dostarczona jest równa pracy odebranej.

i

M

M

M

M

M

opm

m

s

opm

opz

m

opm

s

opz

=

Ω

Ω

=

⇒

Ω

=

Ω

i

m

s

=

Ω

Ω

- przełożenie przekładni

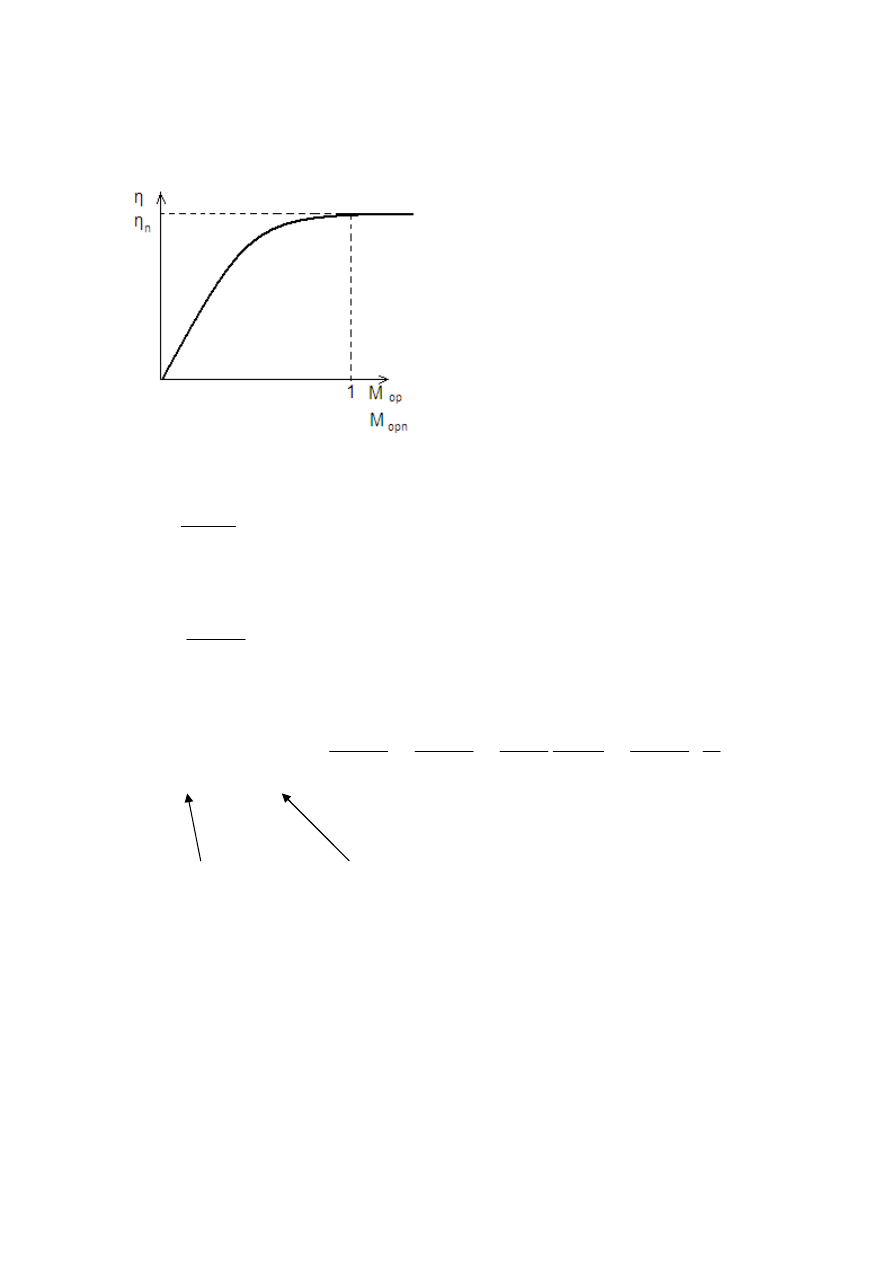
Zakłada się że w przekładni nie ma strat ale można je zaobserwować z wykresu sprawności
przekładni (wykres z poradnika mechanika)

Przy podnoszeniu nasz moment oporowy zastępczy wynosi:

η

i

M

M

opm

opz

=

Przy opuszczaniu przekładnia nam pomaga i ten moment jest mniejszy:

η

i

M

M

opm

opz

=

Straty przy podnoszeniu:

)

1

1

(

1

−

=

−

=

−

=

−

=

∆

η

η

η

η

i

M

i

M

i

M

i

M

M

M

M

opm

op

opm

opm

opz

opz

Z uwzględnieniem bez uwzględnienia
Sprawności sprawności

Przy opuszczaniu:

Φ

+

−

=

Ω

c

R

R

I

U

d

t

t

)

(

Hamowanie odzyskowe –odbywa się przy pomocy prędkości większej niż prędkość biegu
jałowego.

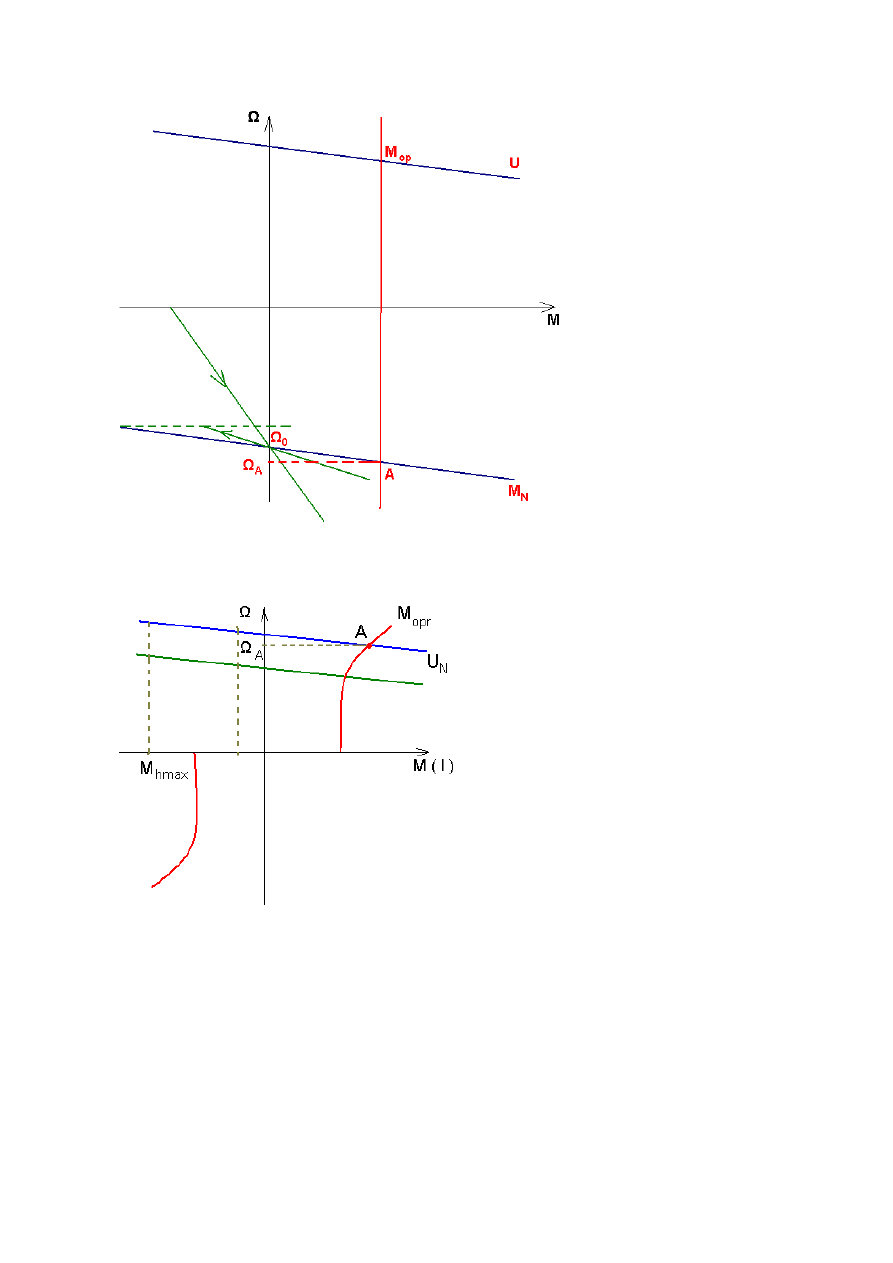
Możliwe jest także oddawanie energii do sieci przy momencie oporowym reakcyjnym

Sterowanie prędkości silników obcowzbudnych prądu stałego (sterowanie, bo układ otwarty /
Reg – układ zamknięty)

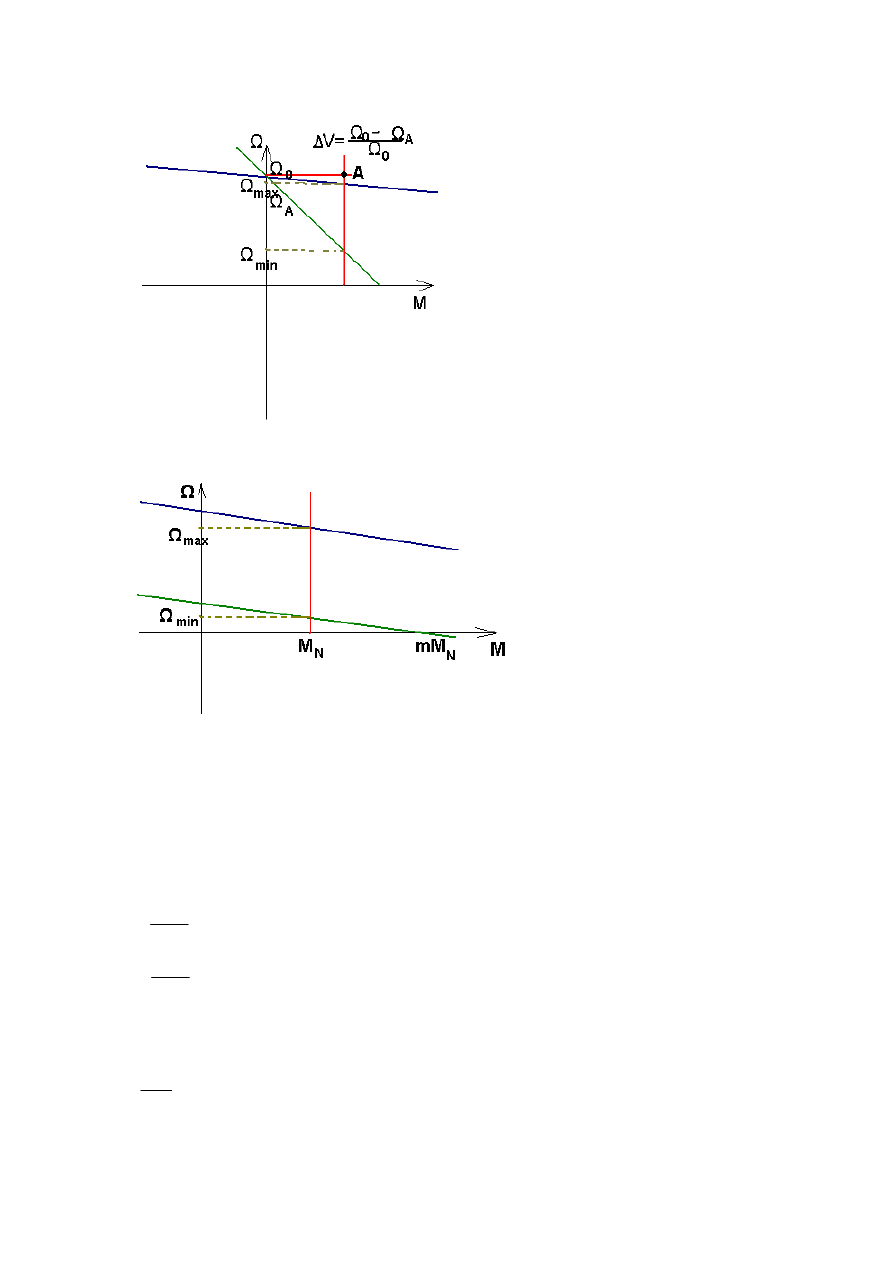
Def.
Zakresem regulacji prędkości nazywany stosunek prędkości maksymalnej do prędkości
minimalnej (lub odwrotnie). Obydwie te prędkości dotycza znamionowego obciążenia i
określonej przeciążalności m (momentem lub prądem). Winny być osiągnięte bez
przekroczenia dopuszczalnego ze względów technologicznych lub założonego względnego
spadku prędkości przy przejściu od biegu jałowego do obciążenia znamionowego.

1

:

'

1

:

max

min

min

max

x

x

=

Ω

Ω

=

=

Ω

Ω

=

ς

ς

m – przeciążalność

N

M

M

m

=

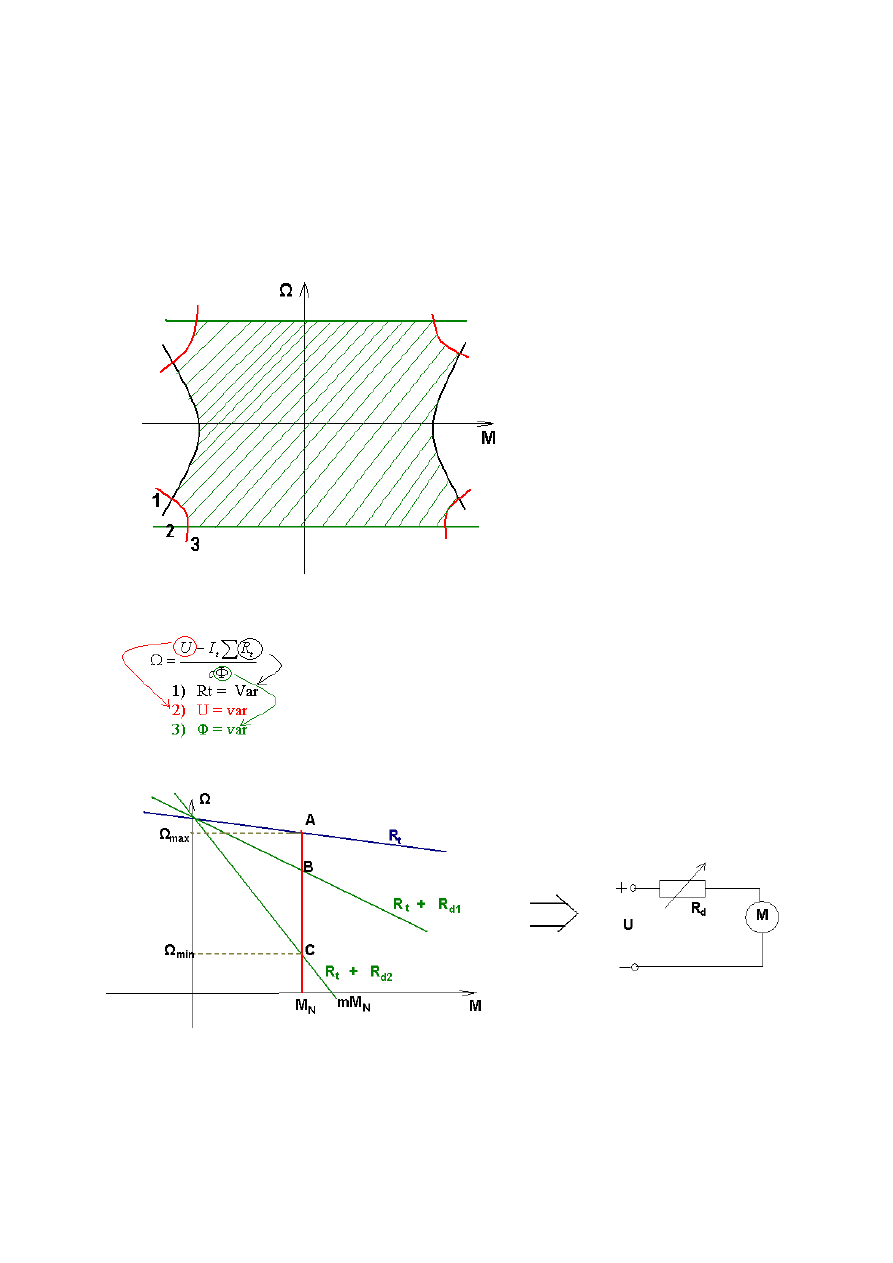
Ograniczenia:

1) górna wartość prędkości (zależy od wytrzymałości mechanicznej silnika)
2) zależy chłodzenia (nagrzewania)

- przewietrzenia własne

- przewietrzenie innym silnikiem

3) ze względu na prawidłową komutację

Sterowanie prędkością:

Ω

max – wynika z charakterystyki naturalnej

Ω

min- wynika z narzuconej przeciążalności

Zakres regulacji jest niewielki rzedu 2:1 do 3:1

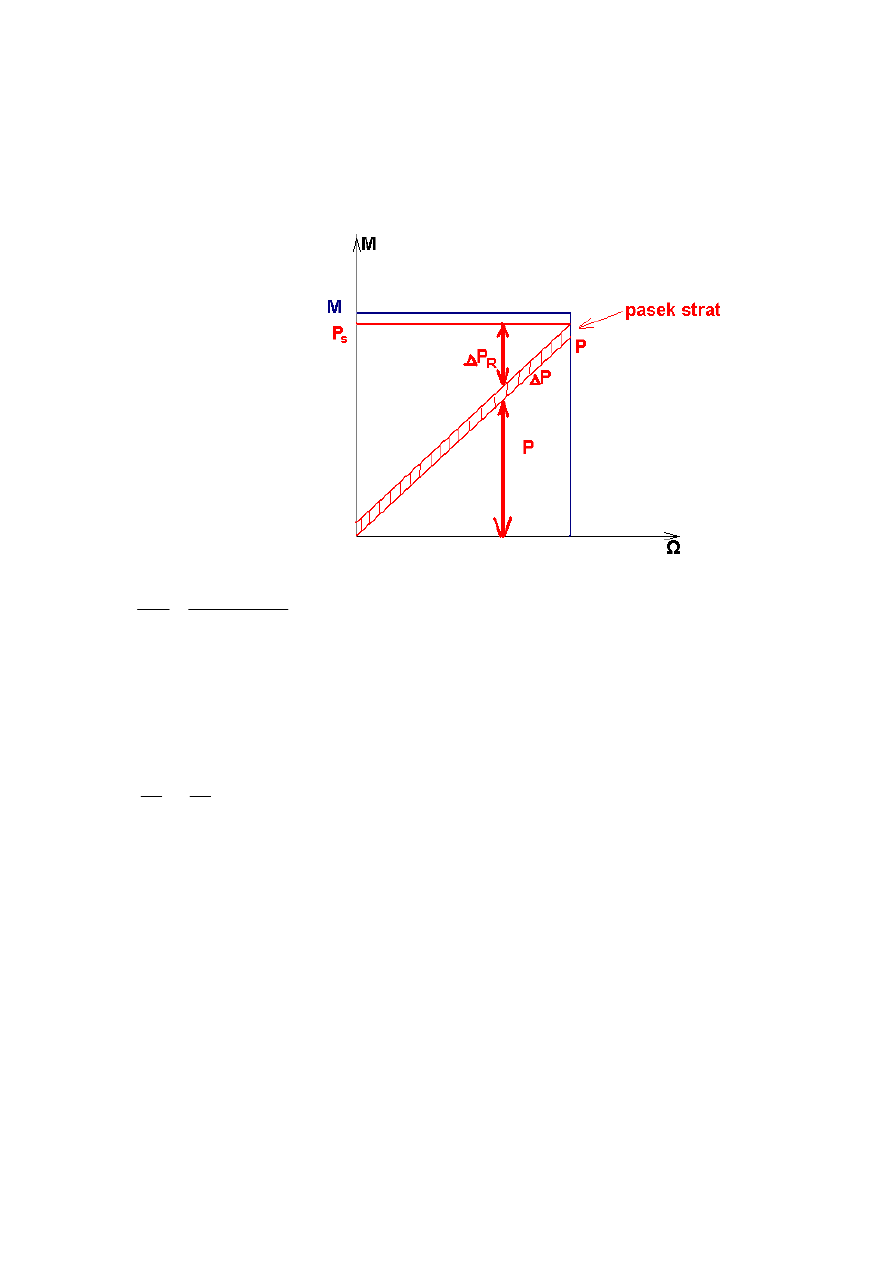
Cechy:
- regulacja związana z dużymi stratami na R
- stosuje się dla silników o niewielkiej mocy bądź silników w których niska prędkość jest
rzadko wykorzystywana
- regulacja przy stałym momencie i zmiennej mocy

R

dost

uż

N

P

P

P

P

P

P

M

P

I

c

M

∆

+

∆

+

=

=

Ω

=

=

η

φ

Sprawność spada wraz ze zmniejszeniem mocy

U = var
Φ

= const

φ

φ

c

R

I

c

U

const

R

R

t

t

t

−

=

Ω

=

=

∑

Cechy charakterystyczne regulacji:
- tylko ”w dół”:

- górna granica charakterystyka naturalna

- dolna wynika na wytrzymałość dielektryczną izolacji

- ze względu na wytrzymałość dielektryczna izolacji nie zwiększamy napięcia zasilającego
silnika (po za znamionowe)
- największy zakres regulacji z tych trzech metod od 5:1 do 10:1
- regulacja bez żadnych strat dodatkowych

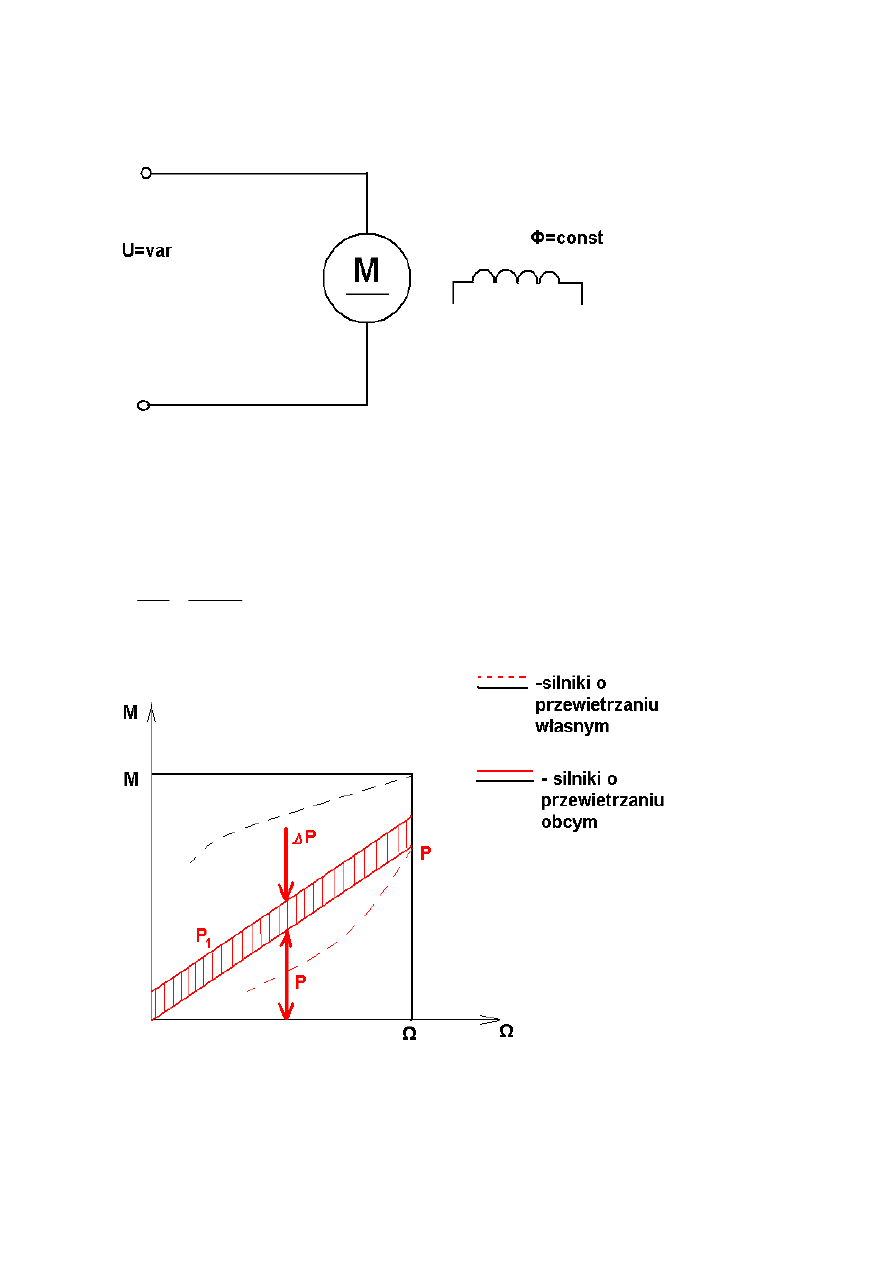
Układ:

Jest to regulacja przy stałym momencie i zmiennej mocy

P

P

P

P

P

M

P

I

c

M

dost

uż

N

N

∆

+

=

=

Ω

=

=

η

φ

Sprawność nieco spada przy obniżaniu prędkości

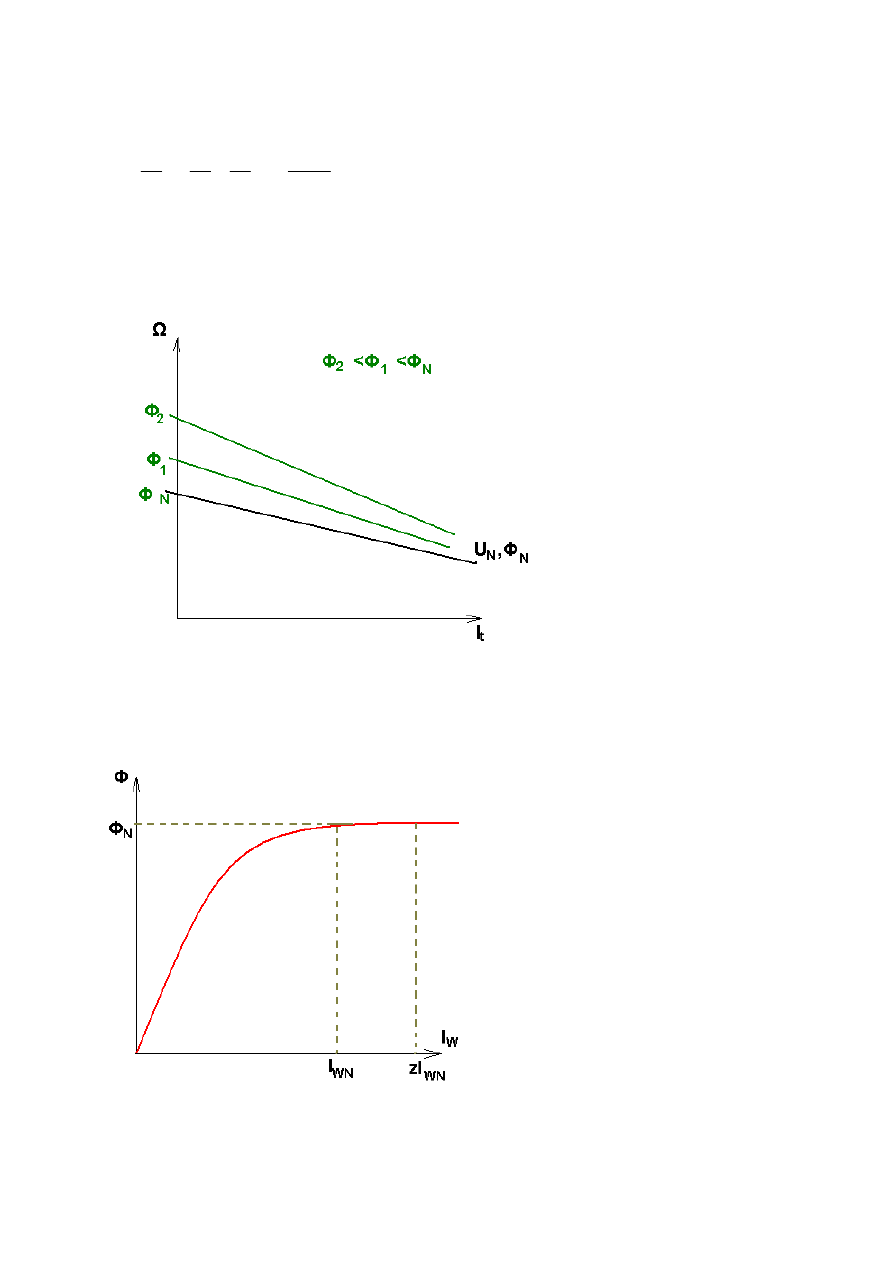
Φ

= var - sterowanie przez zmianę strumienia wzbudzenia

∑

=

=

=

−

=

−

=

Ω

const

R

const

U

c

R

M

c

U

c

R

I

c

U

t

t

t

var

)

(

2

φ

φ

φ

φ

φ

Nie powinny zwiększać strumienia.

Jest to nieopłacalne ze względu na mały wzrost strumienia przy ……

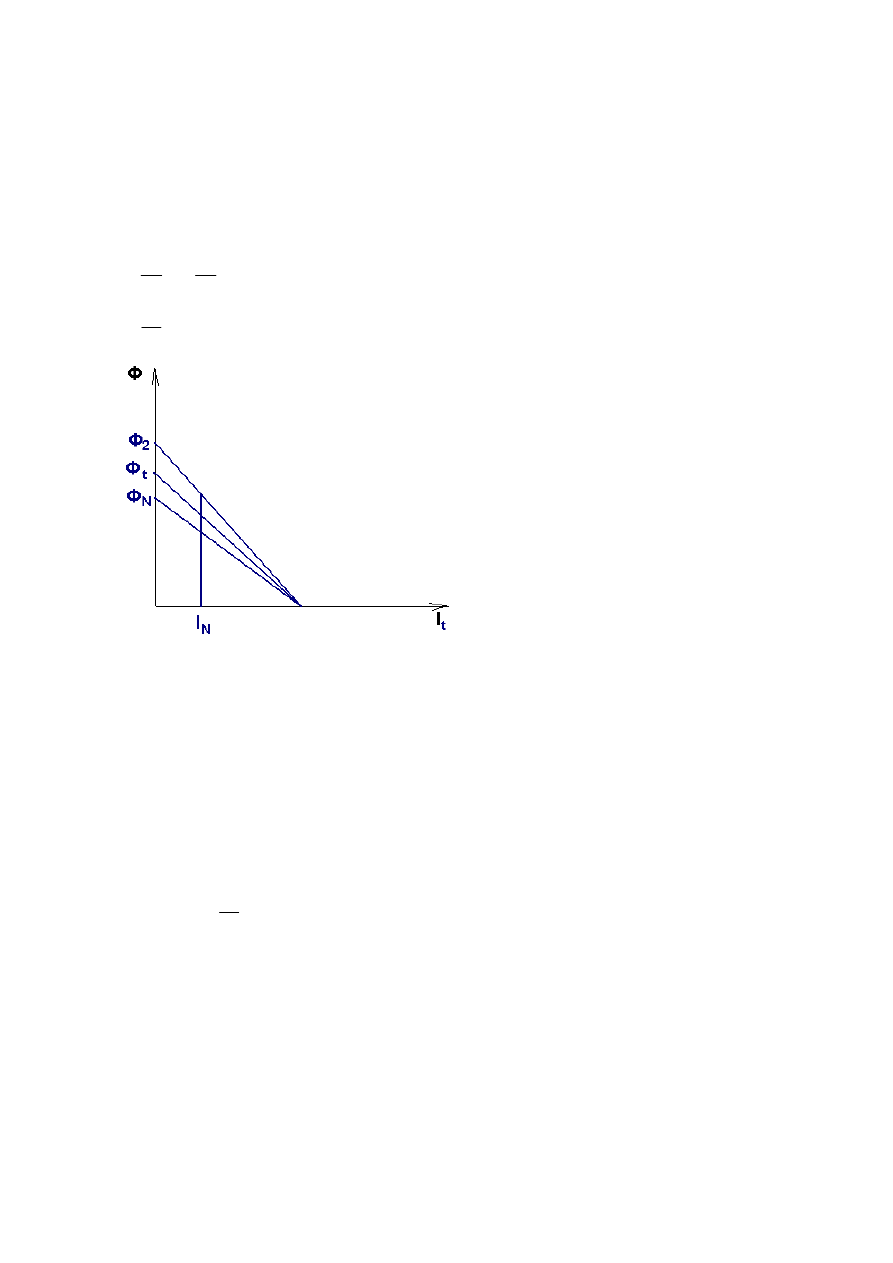
Cechy regulacji:
- tylko w „górę”
- ze względu na nasycanie się obwodu magnetycznego nie stosujemy zwiększenia strumienia
magnetycznego
- Ω max wynika z wytrzymałości mechanicznej silnika (najczęściej)
- nie należy zmieniać Φ zbyt mocno (do 0,5Φn co najwyżej)

t

t

t

t

R

U

I

c

R

I

c

U

=

=

−

=

Ω

0

φ

φ

W miarę zmniejszania strumienia charakterystyki są coraz mniej sztywne przy czym w
zakresie obciążeń można je traktować jako równoległe.

Jest to regulacja bez strat dodatkowych.

const

miedzi

w

straty

e

mechaniczn

straty

=

⇒

↑

⇒

Ω

_

_

_

Bo jest to regulacja przy stałym momencie.

r

t

N

N

I

c

R

U

c

M

UI

P

I

c

M

φ

φ

φ

=

=

=

=

1

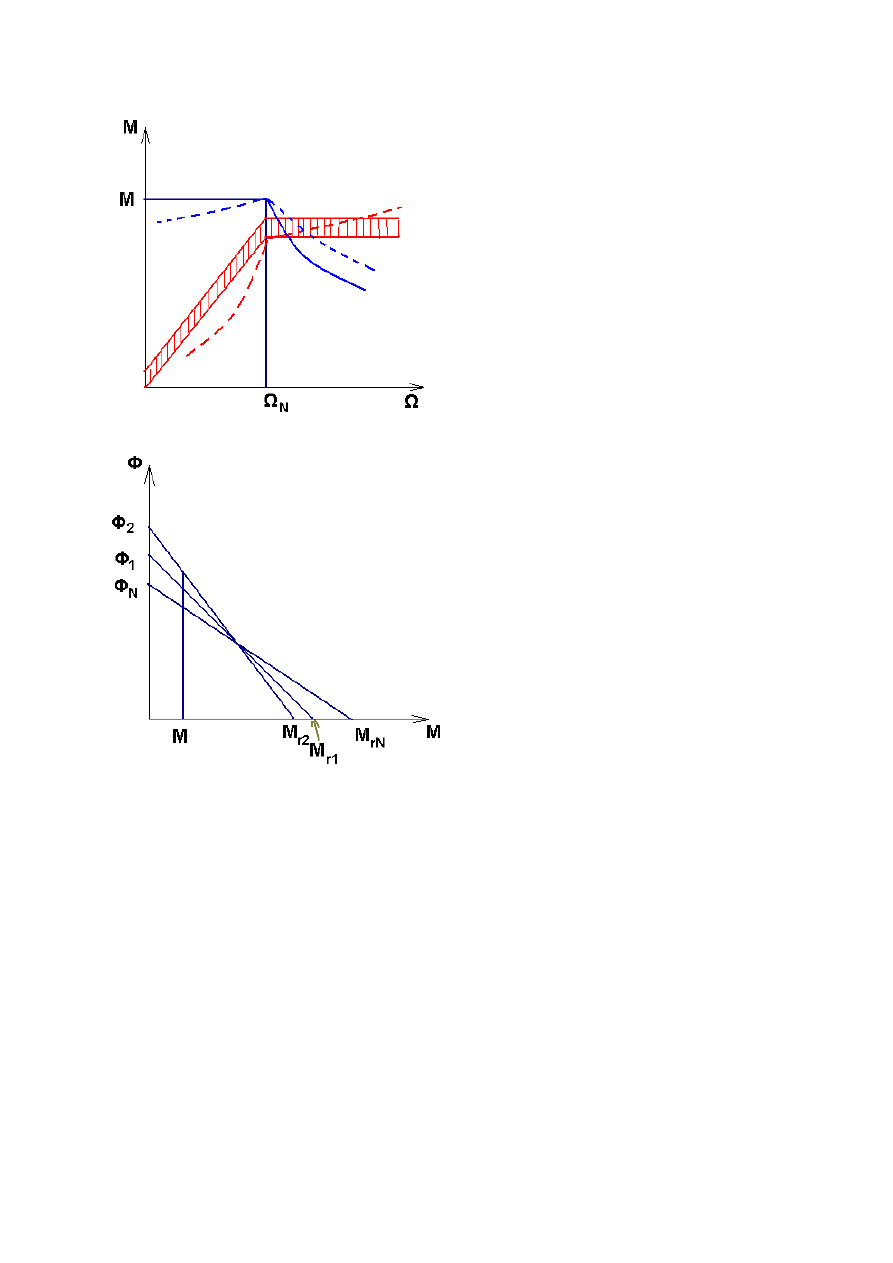
- praktyczne zastosowanie metod sterowania prędkości:

- Układ Leonarda