Strona 1 z 17

OPIS TECHNICZNY

Konstrukcja żelbetowa między piętrowego stropu płytowo-żebrowego:

Długość budynku 19,0 m

Szerokość budynku 10,0 m

Wysokość kondygnacji 2,7 m

Przeznaczenie budynku – Schronisko

Przyjęto:

Beton klasy B25;

= 13,3

;

= 1,0

;

Stal AI ;

= 210

;

Klasa ekspozycji – X0

Rodzaj konstrukcji - prefabrykowana

Rodzaj Podłogi:

Deszczułki podłogowe na lepiku o grubości 22 mm

Zaprawa cementowo-wapienna o grubości 30 mm

Styropian o grubości 100 mm

Zaprawa cementowo-wapienna o grubości 30 mm

Tynk od spodu o grubości 15 mm

Obciążenia i współczynniki obciążeń przyjęto zgodnie z PN-82/B-02000 ; PN-82/02001

Obliczenia przeprowadzono zgodnie z PN-B-03264:2002

Do pomocy w obliczeniach posłużyła książka „Konstrukcje z betonu” Stefan Pyrak

OBLICZENIA:

OBLICZENIE PŁYTY A

ZESTAWIENIE OBCIĄŻEŃ NA PŁYTĘ

Rodzaj Obciążeń

Obciążenie

Charakterystyczne

Współczynnik

Bezpieczeństwa

Obciążenie

Obliczeniowe

STAŁE

1) Deszczułki podłogowe na lepiku o
grubości 22 mm

0,23

0,23

1,30

0,30

2) Zaprawa Cementowo-wapienna 30 mm

19,00

0,03

0,57

1,30

0,74

3) Styropian 100 mm

0,45

0,01

0,00

1,20

0,01

4) Zaprawa Cementowo-wapienna 30 mm

19,00

0,03

0,57

1,30

0,74

5) Płyta żelbetowa

Strona 2 z 17

25,00

0,05

1,25

1,10

1,37

6) Tynk od spodu Cementowo-wapienny 15
mm

19,00

0,015

0,29

1,30

0,37

Suma

=2,91

=3,53

ZMIENNE

1) Schronisko

15,00

1,50

1,20

1,80

Suma

=1,50

=1,80

Suma całkowita

Σ

+

=4,41

1,20701

+

= ,

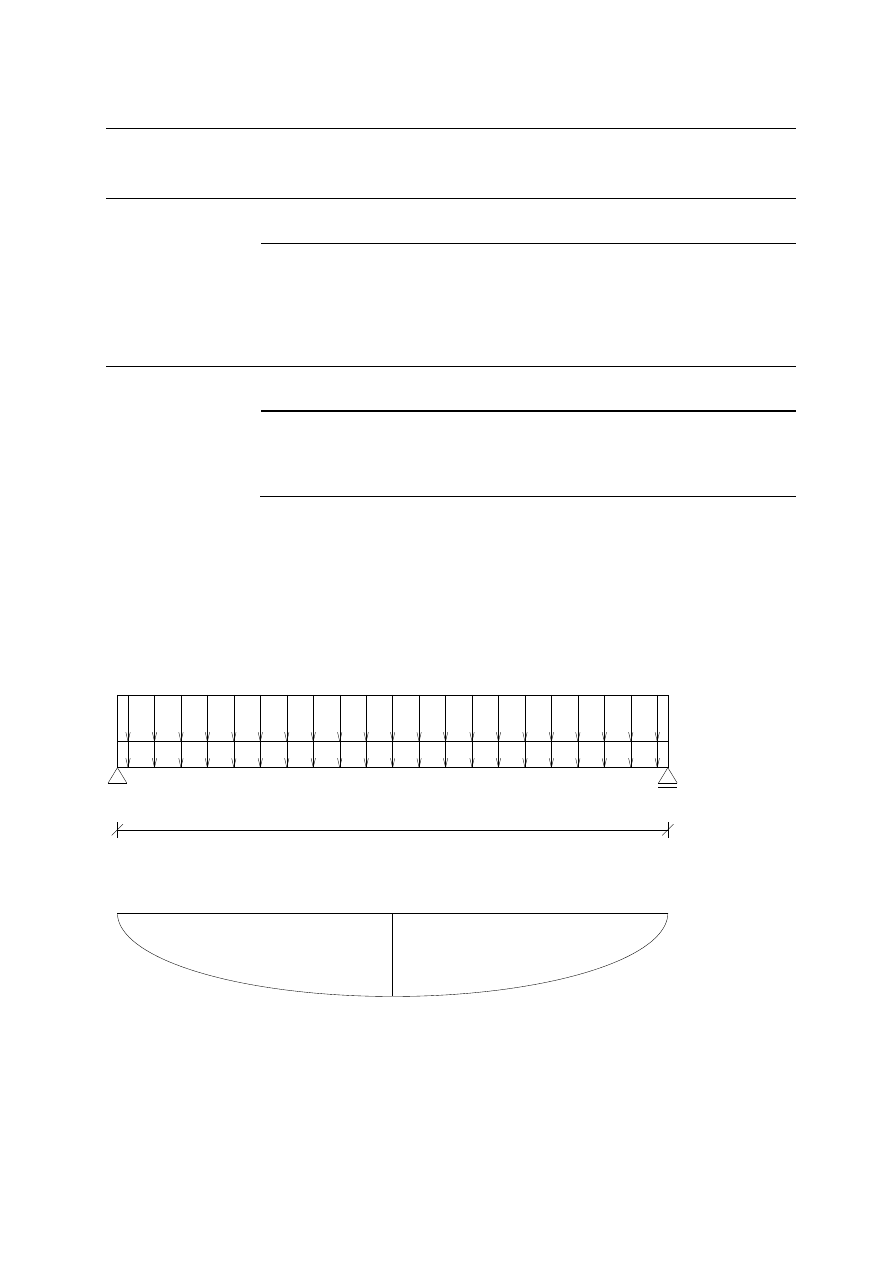
Wykres momentów dla płyty:

l

eff

M

sd

p - uzytkowe

q - stale

Strona 3 z 17

PN-B-03264:2002 str.25 p.4.4.3

=

+

+

=

=

ℎ

2

=

5
2

= 2,5

2

=

36

2

= 18,0

= 175 + 2,5 + 2,5 = 180

= 1,80

=

( + ) ∙

8

=

1,8

+ 3,53

∙ (1,80 )

8

= 2,16

Otulenie prętów zbrojenia:

PN-B-03264:2002 Tablica 21; str.90; Minimalna grubość otulenia

[

] dla klasy ekspozycji X0

= 10 [

]

PN-B-03264:2002 p.8.1.1.2; str.89; (185) – Otulenie prętów zbrojenia

=

+ ∆

∆ = 0 ÷ 5

−

ℎ

ℎ

Przyjmuję ∆ = 5

= 10

+ 5

= 15

- użyteczna wysokość przekroju

= ℎ −

+

∅

2

[ ]

= 0,05 − 0,015 +

0,006

2

= 0,032 [ ]

= 2,16

=

∙

∙

∙

Gdzie:

- współczynnik uwzględniający wpływ obciążenia długotrwałego, niekorzystny efekt

sposobu przyłożenia obciążenia, a w przypadku słupów również wpływ małych przekrojów na
wytrzymałość obliczeniową betonu na ściskanie PN-B-03264:2002 p.2.1.2; str.15; (3)(4)

= 1,0

– wytrzymałość obliczeniowa betonu na ściskanie w konstrukcjach żelbetowych i

sprężonych PN-B-03264:2002 Tab.2; str.15;

Strona 4 z 17

= 13,3

= 13300

- 1 m bieżący płyty

- użyteczna wysokość przekroju – 0,032 m

- moment zginający wywołany obciążeniem obliczeniowym

=

∙

∙

∙

=

2,16

1 ∙ 13300 ∙ 1 ∙ 0,032

= 0,158

,

- Graniczna wartość względnej wysokości strefy ściskanej przekroju PN-B-03264:2002 Tab.9;

str.33; Przyjmuję

,

= 0,62 dla stali klasy A-I

= 1 − 1 − 2 ∙

= 1 − 1 − 2 ∙ 0,158 = 0,17 <

,

= 0,62

= 1 − 0,5 ∙

= 1 − 0,5 ∙ 0,17 = 0,915

– użyteczna wysokość przekroju

- moment zginający wywołany obciążeniem obliczeniowym

– obliczeniowa granica plastyczności stali zbrojeniowej PN-B-03264:2002 Tab.3; str.19;

= 210

= 210000

=

∙

∙

=

2,16

210000 ∙ 0,915 ∙ 0,032

= 3,40 ∙ 10 [

] = 3,51 [

]

= 3,51 [

]

Przyjmuję ∅ 6 8

∶

∅ →

= 3,53 [

] > 3,51[

]

Pręty rozdzielcze:

0,1 ∙

∙

=

,

∙

0,1 ∙ 210000 ∙ 3,53 = 210000 ∙

= 0,353 [

]

∅ 6 33

OBLICZENIE PŁYTY B

Strona 5 z 17

PN-B-03264:2002 str.25 p.4.4.3

=

+

+

=

=

ℎ

2

=

5
2

= 2,5

2

=

36

2

= 18,0

= 182,5 + 2,5 + 2,5 = 187,5

= 1,875

=

( + ) ∙

8

=

1,8

+ 3,53

∙ (1,875 )

8

= 2,34

Otulenie prętów zbrojenia:

PN-B-03264:2002 Tablica 21; str.90; Minimalna grubość otulenia

[

] dla klasy ekspozycji X0

= 10 [

]

PN-B-03264:2002 p.8.1.1.2; str.89; (185) – Otulenie prętów zbrojenia

=

+ ∆

∆ = 0 ÷ 5

−

ℎ

ℎ

Przyjmuję ∆ = 5

= 10

+ 5

= 15

- użyteczna wysokość przekroju

= ℎ −

+

∅

2

[ ]

= 0,05 − 0,015 +

0,006

2

= 0,032 [ ]

= 2,34

=

∙

∙

∙

Gdzie:

- współczynnik uwzględniający wpływ obciążenia długotrwałego, niekorzystny efekt

sposobu przyłożenia obciążenia, a w przypadku słupów również wpływ małych przekrojów na
wytrzymałość obliczeniową betonu na ściskanie PN-B-03264:2002 p.2.1.2; str.15; (3)(4)

= 1,0

– wytrzymałość obliczeniowa betonu na ściskanie w konstrukcjach żelbetowych i

sprężonych PN-B-03264:2002 Tab.2; str.15;

Strona 6 z 17

= 13,3

= 13300

- 1 m bieżący płyty

- użyteczna wysokość przekroju – 0,032 m

- moment zginający wywołany obciążeniem obliczeniowym

=

∙

∙

∙

=

2,34

1 ∙ 13300 ∙ 1 ∙ 0,032

= 0,172

,

- Graniczna wartość względnej wysokości strefy ściskanej przekroju PN-B-03264:2002 Tab.9;

str.33; Przyjmuję

,

= 0,62 dla stali klasy A-I

= 1 − 1 − 2 ∙

= 1 − 1 − 2 ∙ 0,172 = 0,19 <

,

= 0,62

= 1 − 0,5 ∙

= 1 − 0,5 ∙ 0,19 = 0,905

– użyteczna wysokość przekroju

- moment zginający wywołany obciążeniem obliczeniowym

– obliczeniowa granica plastyczności stali zbrojeniowej PN-B-03264:2002 Tab.3; str.19;

= 210

= 210000

=

∙

∙

=

2,34

210000 ∙ 0,905 ∙ 0,032

= 3,85 ∙ 10 [

] = 3,85 [

]

= 3,85 [

]

Przyjmuję ∅ 8 13

∶ ∅ →

= 3,87 [

] > 3,85[

]

Pręty rozdzielcze:

0,1 ∙

∙

=

,

∙

0,1 ∙ 210000 ∙ 3,87 = 210000 ∙

= 0,387 [

]

∅ 6 33

OBLICZENIE ŻEBRA

=

+

+

Dla elementów prefabrykowanych wartość

można przyjmować równe połowie głębokości oparcia.

Strona 7 z 17

=

=

ą

2

=

12,0

2

= 6

ś

2

=

12,0

2

= 6

= 487,5 + 6 + 6 = 487

= 4,995

Wymiary żebra – Wytyczne:

ℎ =

1

15

;

1

12

→ ℎ − (

1

15

∙ 4,995 = 0,33;

1

12

∙ 4,995 = 0,42) → 0,35

=

1
2

;

1
3

ℎ →

− (

1
2

∙ 0,35 = 0,18;

1
3

∙ 0,35 = 0,12) → 0,15

ZESTAWIENIE OBCIĄŻEŃ NA ŻEBRO

Rodzaj Obciążeń

Obciążenie

Charakterystyczne

Współczynnik

Bezpieczeństwa

Obciążenie

Obliczeniowe

STAŁE

1) Deszczułki podłogowe na lepiku o grub. 22 mm

0,23

1,875

0,43

1,30

0,56

2) Zaprawa Cementowo-wapienna 30 mm

19,00

0,03

1,875

1,07

1,30

1,39

3) Styropian 100 mm

0,45

0,01

1,875

0,01

1,20

0,01

4) Zaprawa Cementowo-wapienna 30 mm

19,00

0,03

1,875

1,07

1,30

1,39

5) Płyta żelbetowa

25,00

0,05

1,875

2,34

1,10

2,57

6) Tynk od spodu Cementowo-wapienny 15 mm

19,00

0,015

1,875

0,53

1,30

0,69

7) Żebro

25,00

0,15

0,35

1,31

1,10

1,44

Suma

= 6,76

= 8,05

ZMIENNE

1) Schronisko

1,50

1,875

2,81

1,20

3,37

Suma

= 2,81

= 3,37

Σ

+

= 9,57

+

= 11,42

Strona 8 z 17

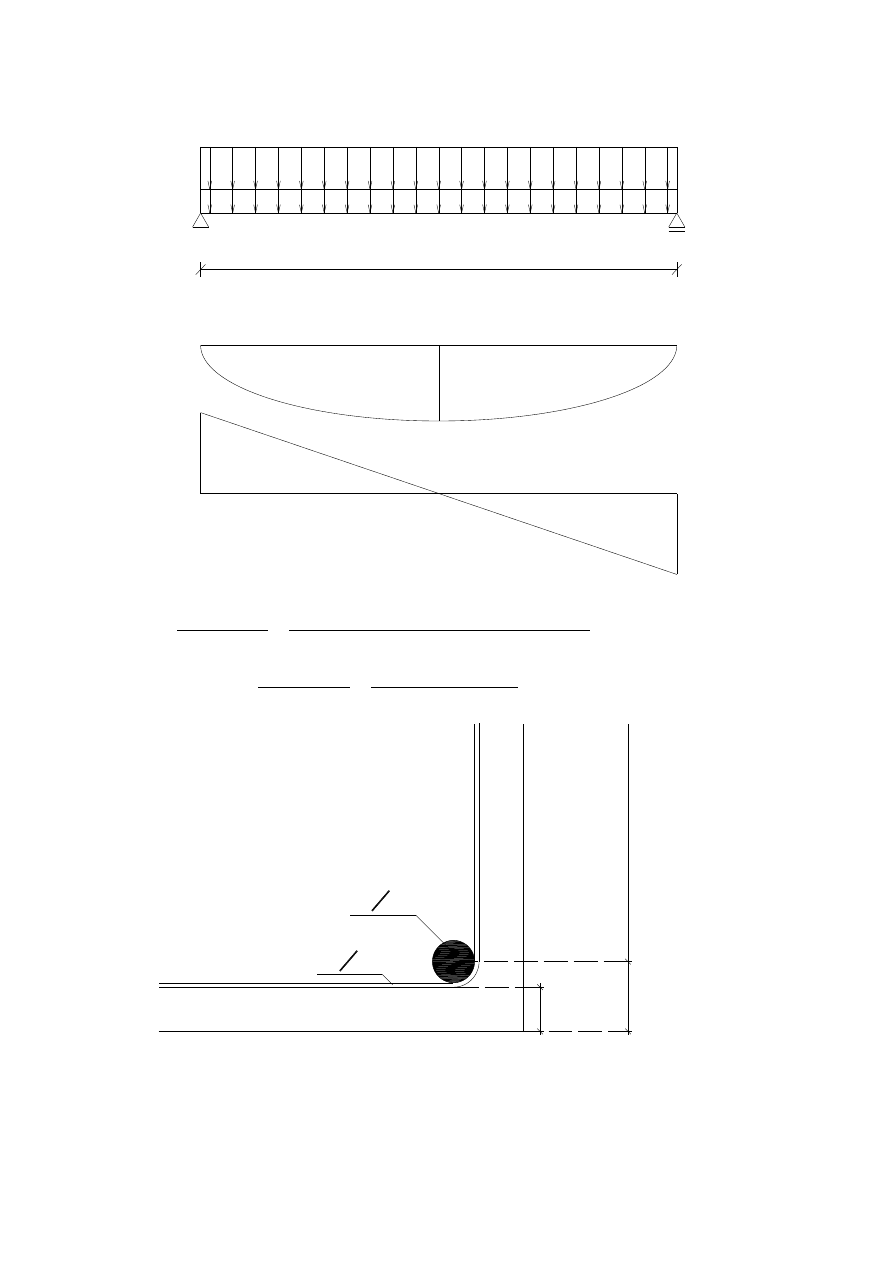
Momenty i Tnące dla Żebra:

l

eff

M

sd

p - uzytkowe

q - stale

V

sd

V

sd

=

( + ) ∙

8

=

8,05

+ 3,37

∙ (4,995 )

8

= 35,62

=

( + ) ∙

2

=

(8,05 + 3,37) ∙ 4,995

2

= 28,52

a

1

C

nom

d

o

o

s

PN-B-03264:2002 Tablica 21; str.90; Minimalna grubość otulenia

[

] dla klasy ekspozycji X0

= 10 [

]

PN-B-03264:2002 p.8.1.1.2; str.89; (185) – Otulenie prętów zbrojenia

Strona 9 z 17

=

+ ∆

∆ = 0 ÷ 5

−

ℎ

ℎ

Przyjmuję ∆ = 5

= 10

+ 5

= 15

- użyteczna wysokość przekroju

= ℎ −

+ ∅ +

∅

2

[ ]

= 0,35 − 0,015 + 0,006 +

0,016

2

= 0,32 [ ]

= 35,62

=

∙

∙

∙

Gdzie:

- współczynnik uwzględniający wpływ obciążenia długotrwałego, niekorzystny efekt

sposobu przyłożenia obciążenia, a w przypadku słupów również wpływ małych przekrojów na
wytrzymałość obliczeniową betonu na ściskanie PN-B-03264:2002 p.2.1.2; str.15; (3)(4)

= 1,0

– wytrzymałość obliczeniowa betonu na ściskanie w konstrukcjach żelbetowych i

sprężonych PN-B-03264:2002 Tab.2; str.15;

= 13,3

= 13300

– szerokość żebra – 0,15 m

- użyteczna wysokość przekroju – 0,32 m

- moment zginający wywołany obciążeniem obliczeniowym

=

∙

∙

∙

=

35,62

1 ∙ 13300 ∙ 0,15 ∙ 0,32

= 0,174

,

- Graniczna wartość względnej wysokości strefy ściskanej przekroju PN-B-03264:2002

Tab.9; str.33; Przyjmuję

,

= 0,62 dla stali klasy A-I

= 1 − 1 − 2 ∙

= 1 − 1 − 2 ∙ 0,174 = 0,19 <

,

= 0,62

OK.

= 1 − 0,5 ∙

= 1 − 0,5 ∙ 0,19 = 0,905

Strona 10 z 17

– użyteczna wysokość przekroju

- moment zginający wywołany obciążeniem obliczeniowym

– obliczeniowa granica plastyczności stali zbrojeniowej PN-B-03264:2002 Tab.3; str.19;

= 210

= 210000

=

∙

∙

=

35,62

210000 ∙ 0,905 ∙ 0,32

= 5,86 ∙ 10 [

] = 5,86 [

]

= 5,86[

]

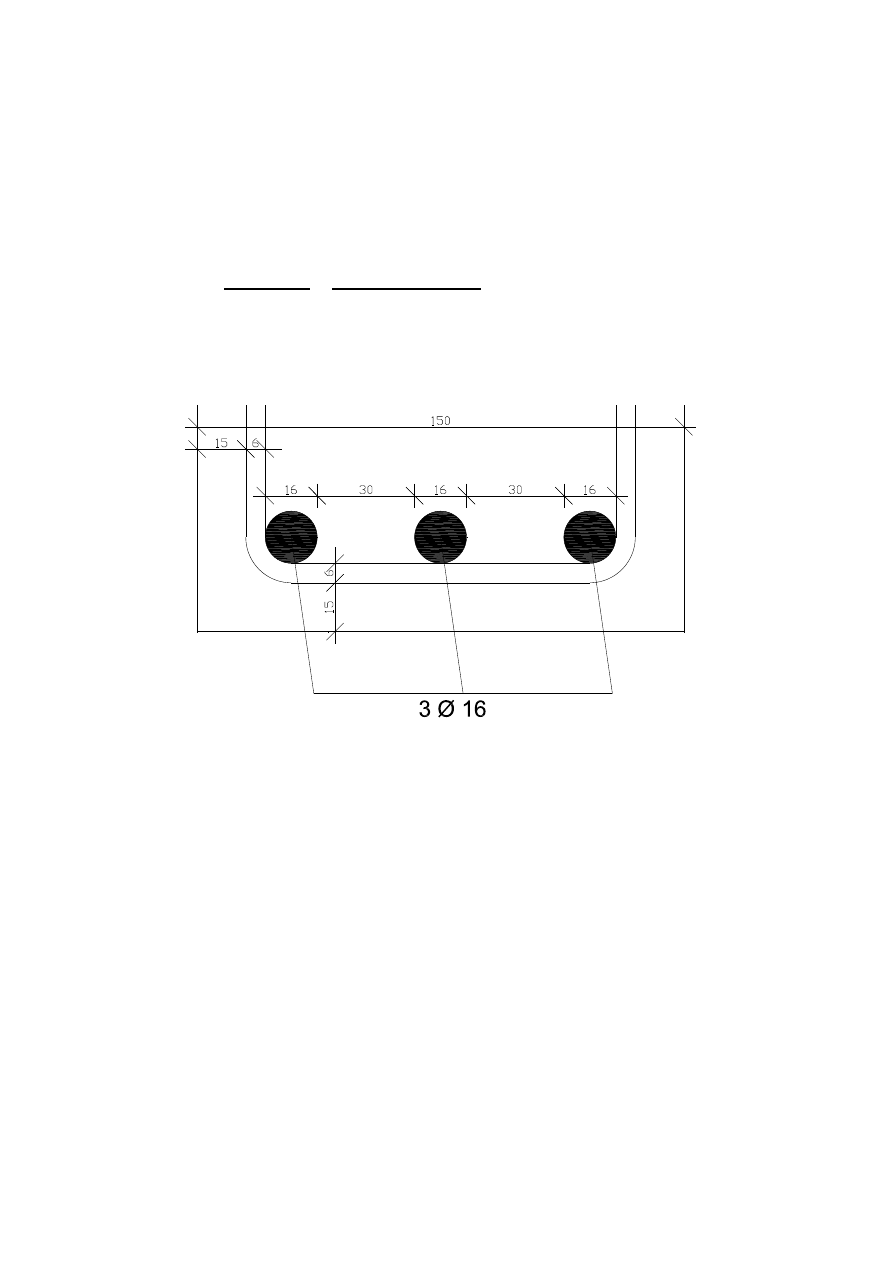
Przyjmuję

= 6,03

czyli 3 ∅ 16

PN-B-03264:2002 p.5.5.2.1 str.46

Sprawdzenie Stanu granicznego nośności obliczeniowej na ścinanie na odcinakach I rodzaju

= 28,52

=

−

∙ ( + ) = 28,52 − 0,32 ∙ (8,05 + 3,37) = 24,87

= [0,35 ∙

∙

(1,2 + 40 ∙

) + 0,15 ∙

]

∙

Gdzie:

− Współczynnik równy 1,0, gdy do podpory doprowadzono mniej niż 50% rozciąganego zbrojenia

przęsłowego, a w innych przypadkach wyznaczamy ze wzoru:

= 1,6 −

= 1,6 − 0,32 = 1,28

> 1,0

− Średnie naprężenie ściskające w betonie wywołanym w elementach żelbetowych przez siłę

podłużną

= 0

Strona 11 z 17

− wytrzymałość obliczeniowa betonu na rozciąganie w konstrukcjach żelbetowych i sprężonych

= 1,0

= 1000

=

− szerokość żebra

= 0,15

− użyteczna wysokość przekroju

= 0,32

− Stopień zbrojenia - PN-B-03264:2002 p.5.5.2.1 str.46

=

∙

≤ 0,01

Gdzie:

− pole przekroju prętów głównego zbrojenia rozciąganego

=

∙

=

6,03

15 ∙ 32,0

= 0,013 ≥ 0,01

= 0,35 ∙

∙

(1,2 + 40 ∙

) + 0,15 ∙

∙

= [0,35 ∙ 1,28 ∙ 1000 ∙ (1,2 + 40 ∙ 0,01) + 0,15 ∙ 0]0,15 ∙ 0,32 = 34,41

= 24,87

<

= 34,41

Odcinek I rodzaju

Nośność

na odcinkach I rodzaju:

= 0,5 ∙ ∙

∙

∙

= 0,6 −

250

= 0,6 −

250

= 0,6 −

16,0

250

= 0,536

= 0,9 ∙

= 0,9 ∙ 0,32 = 0,288

= 0,5 ∙ ∙

∙

∙

= 0,5 ∙ 0,536 ∙ 13300 ∙ 0,15 ∙ 0,288 = 153,98

= 24,87

<

= 153,98

Nie jest wymagane obliczanie zbrojenie poprzecznego

Maksymalny rozstaw ramion strzemion w kierunku podłużnym powinien spełniać warunki:

≤ 0,75 ∙

= 0,75 ∙ 320

= 240

Strona 12 z 17

Oraz

≤ 400

Przyjmuję

= 2,4

STAN GRANICZNY UŻYTKOWALNOŚCI

RYSY PROSTOPADŁE

Obliczeniowa szerokość

rys prostopadłych: PN-B-03264:2002 p. 6,3 str. 62

=

∙

∙

− Współczynnik wyrażający stosunek obliczeniowej szerokości rysy do szerokości średniej

= 1,3

300

− Średni końcowy rozstaw rys PN-B-03264:2002 p. 6.3 str. 63

− średnie odkształcenie zbrojenia rozciąganego

= 50 + 0,25 ∙

∙

∙

∅

∅ − średnia pręta

− współczynnik zależny od przyczepności prętów

= 0,8 −

ę ó ż

ℎ

− współczynnik zależny od rozkładu odkształceń w strefie rozciąganej

= 0,5 −

ł

ó ą

− efektywny stopień zbrojenia

=

,

− pole przekroju zbrojenia

,

− pole efektywne przekroju strefy rozciąganej

,

=

2,5a

(h − x )/3

=

2

1 + ℎ +

2

∙

=

1 −

∙

Strona 13 z 17

− naprężenie w zbrojeniu rozciąganym

=

∙

∙

=

0,9

≤ 0,5%

0,85 0,5% ≤

≤ 1%

0,8

> 1%

− naprężenie w zbrojeniu rozciąganym, obliczone w przekroju przez rysę, dla obciążenia

powodujące zarysowanie

− współczynnik zależny od przyczepności prętów

= 1,0 −

ę ó ż

ℎ

− współczynnik zależny od czasu działania i powtarzalności obciążenia

= 0,5 −

ąż

ł

ł

Zamiast stosunku

można przyjmować przy zginaniu

=

∙

− Moment rysujący

− Wytrzymałość średnia betonu na rozciąganie – 2,2

→ 2200

− Wskaźnik wytrzymałości przekroju betonowego na zginanie, obliczony jak dla materiału liniowo

sprężonego

=

∙ ℎ

6

Moment

− Charakterystyczne

− Współczynnik potrzebny do obliczenia części długotrwałej obciążenia zmiennego PN-B-82/B-

2003 w domach mieszkalnych współczynnik

= 0,35

,

=

(

+

∙

) ∙

8

=

6,76

+ 0,35 ∙ 2,81

∙ (4,995 )

8

= 24,15

,

= 24,15

=

∙ ℎ

6

=

0,15 ∙ 0,35

6

= 0,0030625

=

∙

= 2200 ∙ 0,0030625 = 6,73

=

∙

∙ 100% =

6,03

15 ∙ 32,0

∙ 100% = 1,26% > 1% →

= 0,8

Strona 14 z 17

=

,

∙

∙

=

24,15

0,8 ∙ 0,32 ∙ 6,03 ∙ 10

= 156444

= 156,444

=

∙

∙

=

6,73

0,8 ∙ 0,32 ∙ 6,03 ∙ 10

= 43597

=

1 −

∙

=

156444

200 ∙ 10

∙ 1 − 1 ∙ 0,5

43597

156444

= 7,518 ∙ 10

=

,

=

6,03 ∙ 10

0,15 ∙ 2,5 ∙ 0,029

= 0,0554

= 50 + 0,25 ∙

∙

∙

∅

= 50 + 0,25 ∙ 0,8 ∙ 0,5 ∙

16

0,0554

= 79

=

∙

∙

= 1,3 ∙ 79 ∙ 7,518 ∙ 10

= 0,077

PN-B-03264:2002 Tab. 7 str.30 Dla ekspozycji X0 -

= 0,3

= 0,077 <

= 0,3

Szerokość rys prostopadłych jest mniejsza od szerokości granicznej.

RYSY UKOŚNE

PN-B-03264:2002 p.6.4 str. 65

Tnąca

,

− Charakterystyczne

− Współczynnik potrzebny do obliczenia części długotrwałej obciążenia zmiennego PN-B-82/B-

2003 w domach mieszkalnych współczynnik

= 0,35

,

=

(

+

) ∙

2

=

(6,76 + 0,35 ∙ 2,81) ∙ 4,995

2

= 19,34

Szerokość rys ukośnych

w elementach zginanych

=

4 ∙

∙

∙

∙

Gdzie:

=

,

∙

=

∙

Stopień zbrojenia strzemionami prostopadłymi do osi elementu

oraz strzemionami ukośnymi lub

prętami odgiętymi

Dla strzemion prostopadłych

Strona 15 z 17

=

∙

− Pole przekroju strzemion do osi elementu, leżących w jednej płaszczyźnie,

− rozstaw strzemion prostopadłych do osi elementu,

=

1

3 ∙

+

;

− odpowiednio: średnia (w mm) strzemion pionowych i prętów ukośnych,

∅ = 6

;

− współczynnik zależnie od przyczepności strzemion pionowych i prętów ukośnych

1,0 −

ę ó ł

ℎ

= 2 ∙

= 2 ∙ 0,28 = 0,56

=

∙

=

0,56

24 ∙ 15

= 0,00155

=

1

3 ∙

+

=

1

3 ∙

0,00155

1,0 ∙ 6

= 1290

=

∙

=

19,34

15 ∙ 32

= 0,00769

= 0,0403

=

4 ∙

∙

∙

∙

=

4 ∙ 0,0403 ∙ 1290

0,00155 ∙ 200000 ∙ 20

= 0,00135

PN-B-03264:2002 Tab. 7 str.30 Dla ekspozycji X0 -

= 0,3

= 0,00135

<

= 0,3

Szerokość rysy ukośnej jest mniejsza od szerokości granicznej

UGIĘCIE

Wartości graniczne dla stropów i stropodachów:

≤ 6

→

=

200

=

4995

200

= 24,98

= 24,98

=

∙

,

∙

− Współczynnik zależny od rozkładu zginającego,

=

Strona 16 z 17

− Maksymalny moment zginający wywołany rozpatrywanym obciążeniem

− Sztywność przekroju, w którym osiąga się moment

=

,

∙

1 −

∙

∙

∙ 1 −

= 1,0

= 0,5

= 156444

= 43597

,

=

1 + ∅( ,

)

Współczynnik pełzania betonu ∅( , )

∅( ,

) = ∅(∞, ) ∙

( − )

ℎ =

2

= 150 ∙ 350 = 52500

= 150 + 350 + 350 = 850

ℎ =

2

=

2 ∙ 52500

850

= 123,53

≈ 150

Wartości końcowego współczynnika pełzania betonu ∅(∞,

) oraz funkcja ( − ) określająca

przyrost pełzania po przyłożeniu obciążenia, obliczone dla cementów zwykłych otrzymano z tablic A.1
i A.2 PN-B-03264:2002 Załącznik A str. 134 i 135. Przyjmuję wiek betonu w chwili obciążenia

= 28

, wilgotność względną RH = 80%

∅(∞,

) = 2,1

( − ) = 0,40

∅( ,

) = ∅(∞, ) ∙

( − ) = 2,1 ∙ 0,40 = 0,84

,

=

1 + ∅( , )

=

30 ∙ 10

1 + 0,84

= 16304347,83

=

,

=

200 ∙ 10

16304347,83

= 12,267

=

0,5 ∙

∙ ℎ ∙

∙

∙

∙ ℎ +

∙

=

0,5 ∙ 15 ∙ 35 + 12,267 ∙ 6,03 ∙ 32

15 ∙ 35 + 12,267 ∙ 6,03

= 19,29

= 0,193

Strona 17 z 17

=

∙

3

+

(ℎ −

)

3

+

∙

∙ ( −

)

=

0,15 ∙ 0,193

3

+

0,15 ∙ (0,35 − 0,193)

3

+ 12,267 ∙ 6,03 ∙ 10

∙ (0,32 − 0,193)

= 6,723 ∙ 10

=

∙

∙ 100% =

6,03

15 ∙ 32,0

∙ 100% = 1,26% > 1% →

= 0,8

=

2 ∙

1 + ℎ +

2

∙

=

2 ∙ 0,32

1 + 0,35 +

2

12,267 ∙ 0,8

= 0,367

=

∙

3

+

∙

∙ ( −

) =

0,15 ∙ 0,367

3

+ 12,267 ∙ 6,03 ∙ 10

∙ (0,32 − 0,367)

= 24,879 ∙ 10

=

,

∙

1 −

∙

∙

∙ 1 −

=

16304347,83 ∙ 24,879 ∙ 10

1 − 1,0 ∙ 0,5 ∙

43597

156444

∙ 1 −

24,879 ∙ 10

6,723 ∙ 10

= 36713,68

=

∙

,

∙

=

5

48

∙

24,15 ∙ 4,995

36713,68

= 0,0017

= 15

= 17

≤

= 24,98

Ugięcie nie przekroczy wartości granicznej